Embedded Fiber Bragg Grating Sensors for Monitoring Temperature and Thermo-Elastic Deformations in a Carbon Fiber Optical Bench
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fundamentals
2.1.1. Temperature and Strain Sensitivity of FBGs
2.1.2. Strain Measurement with Temperature Compensation
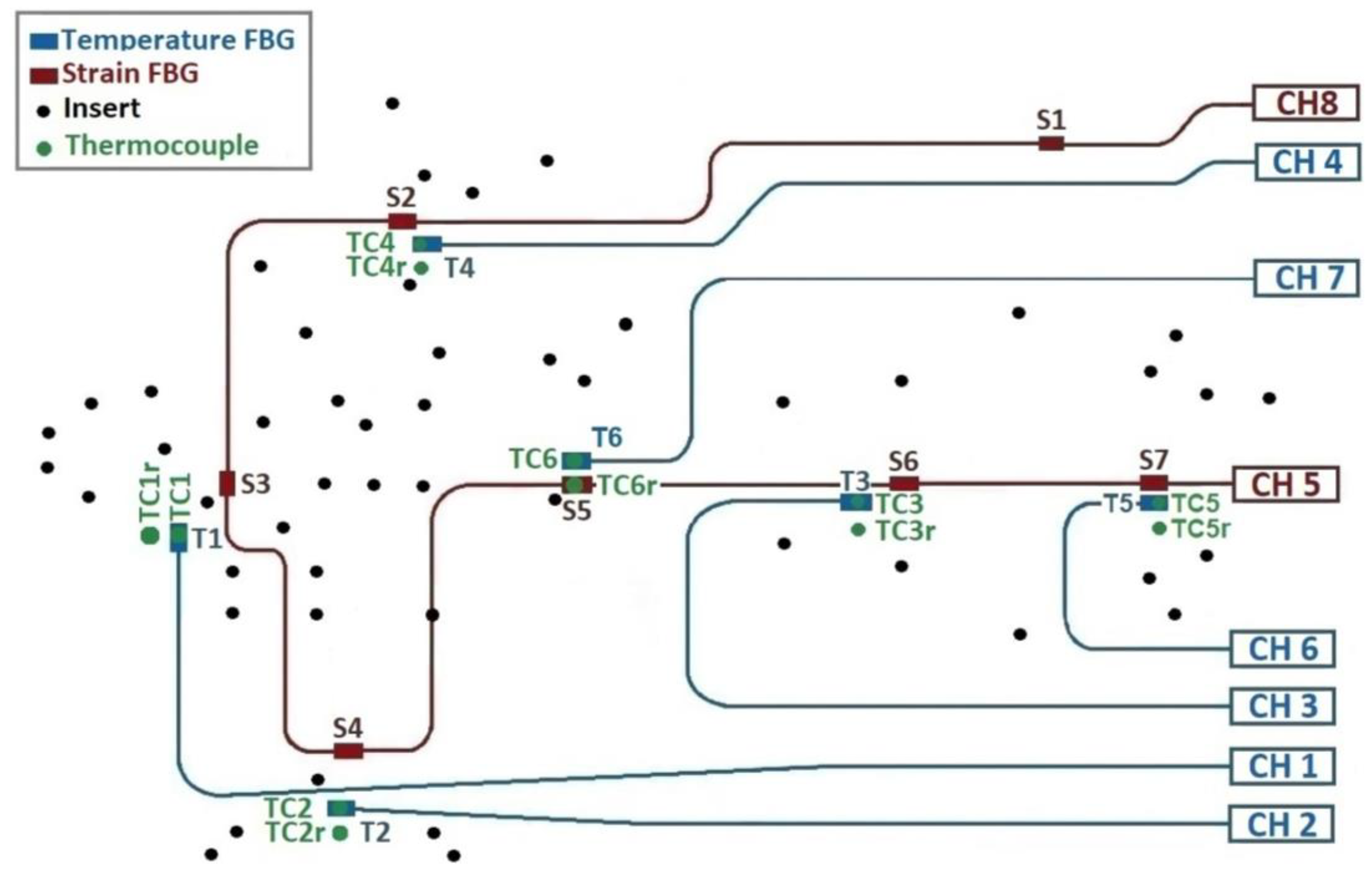
2.2. Optical Bench BB Design and Description
2.3. Sensors Design
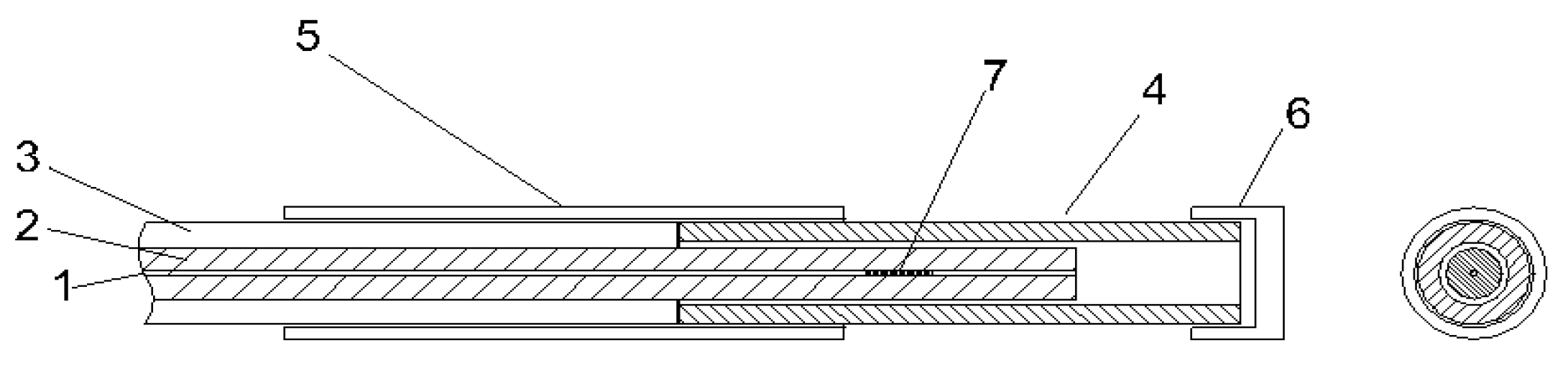
2.3.1. Temperature Sensors
2.3.2. Strain Sensors
2.4. Thermal Vacuum Test Description
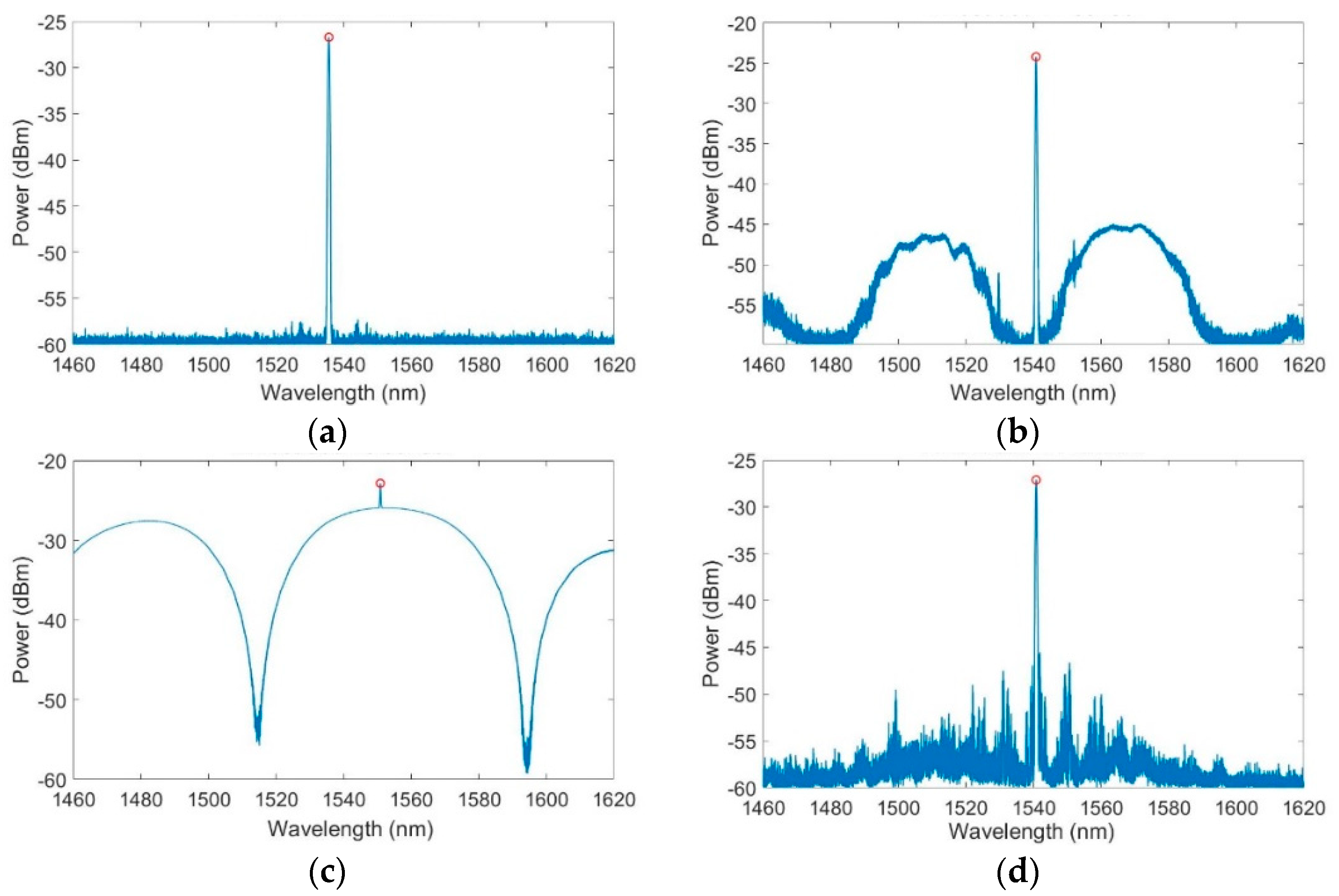
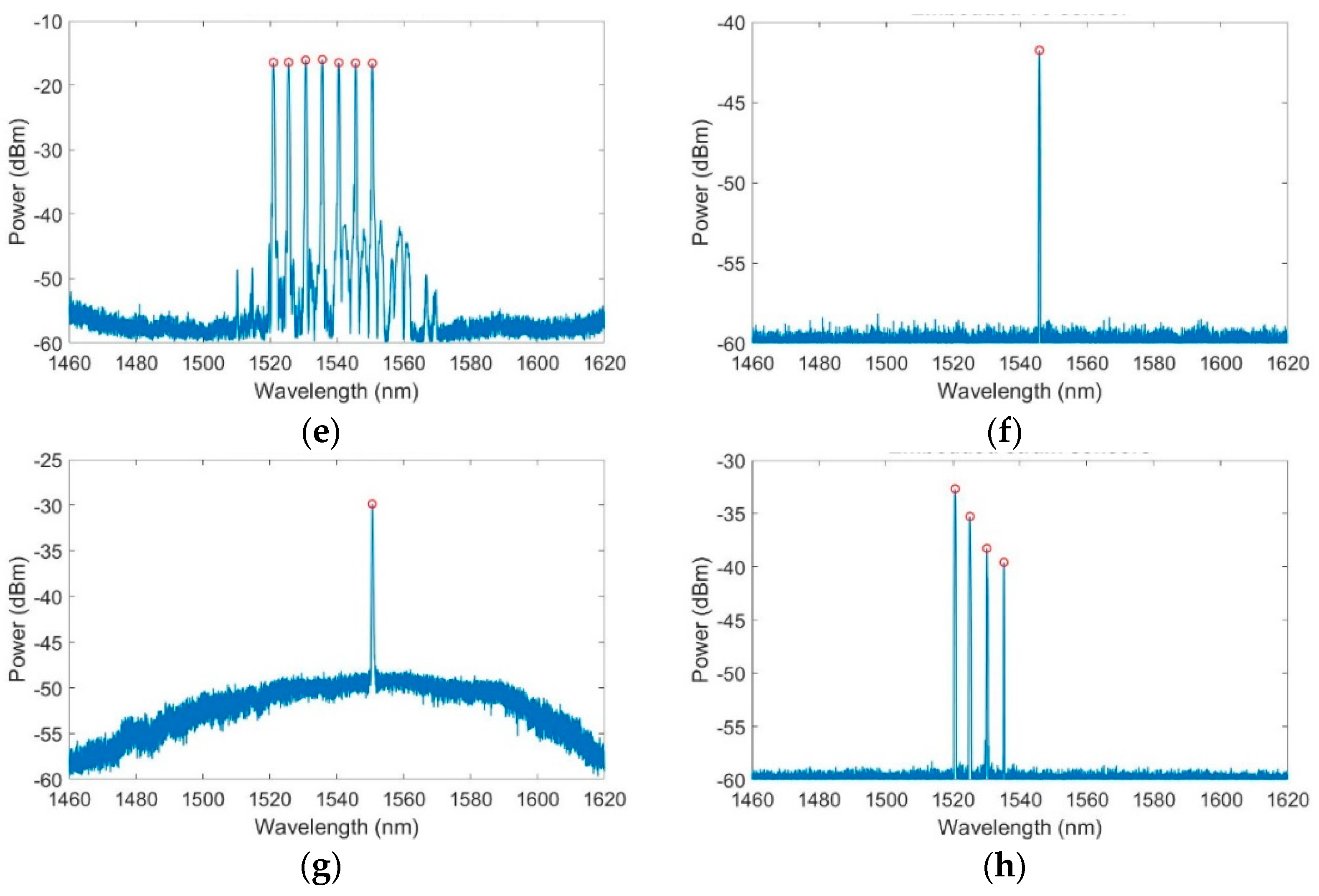
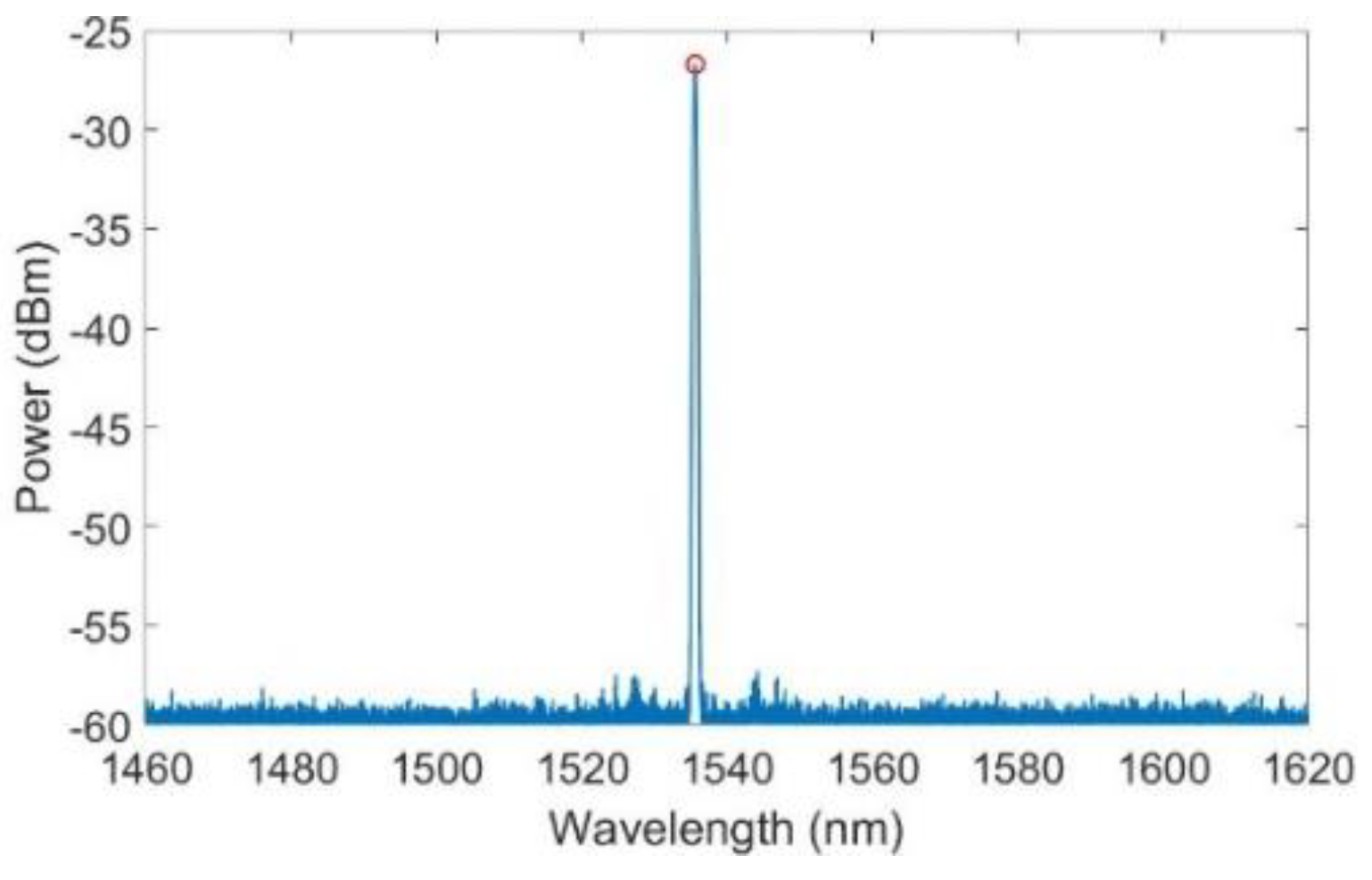
2.5. Peak Wavelength and Spectral Response Detection
3. Results
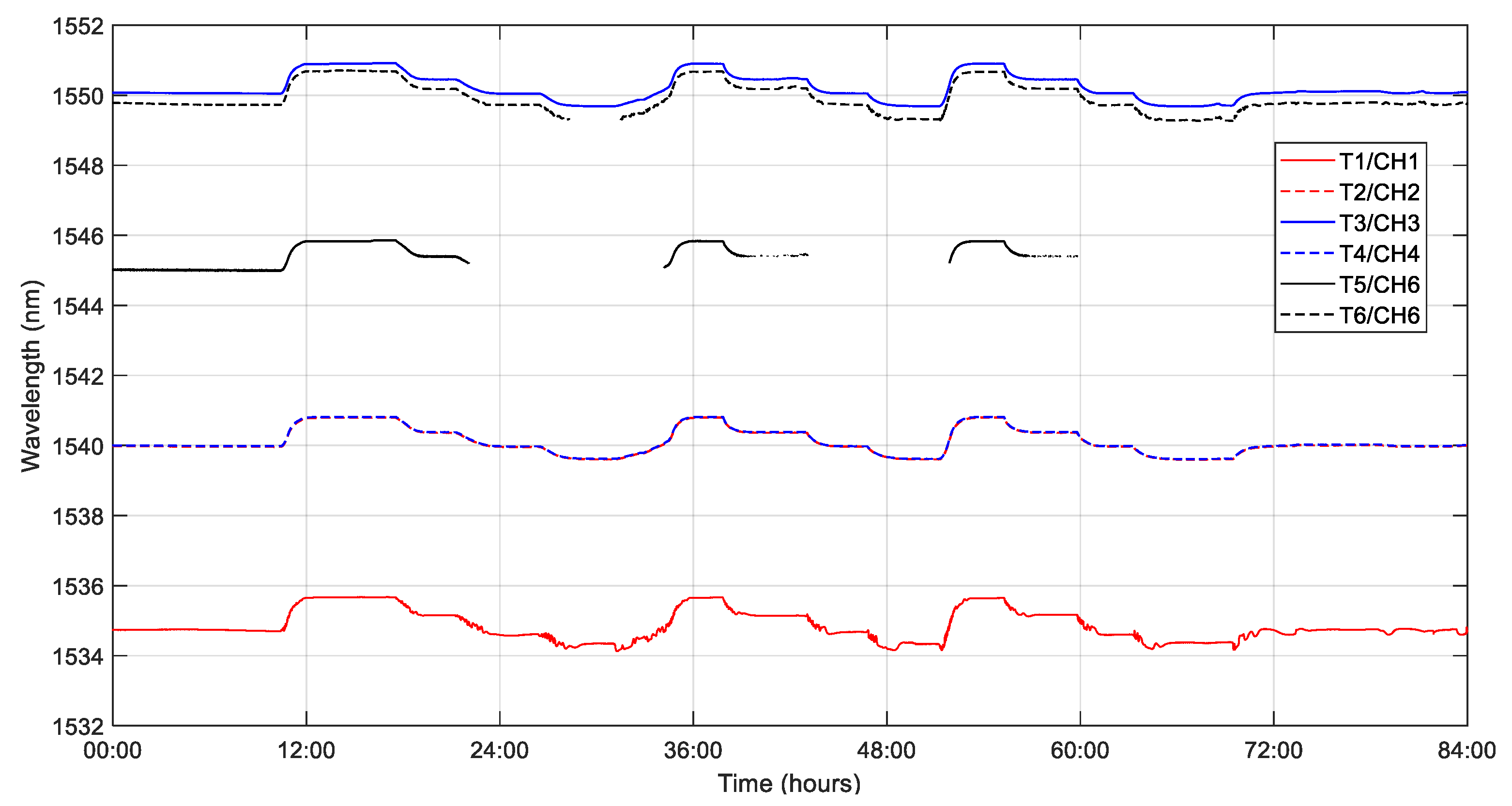
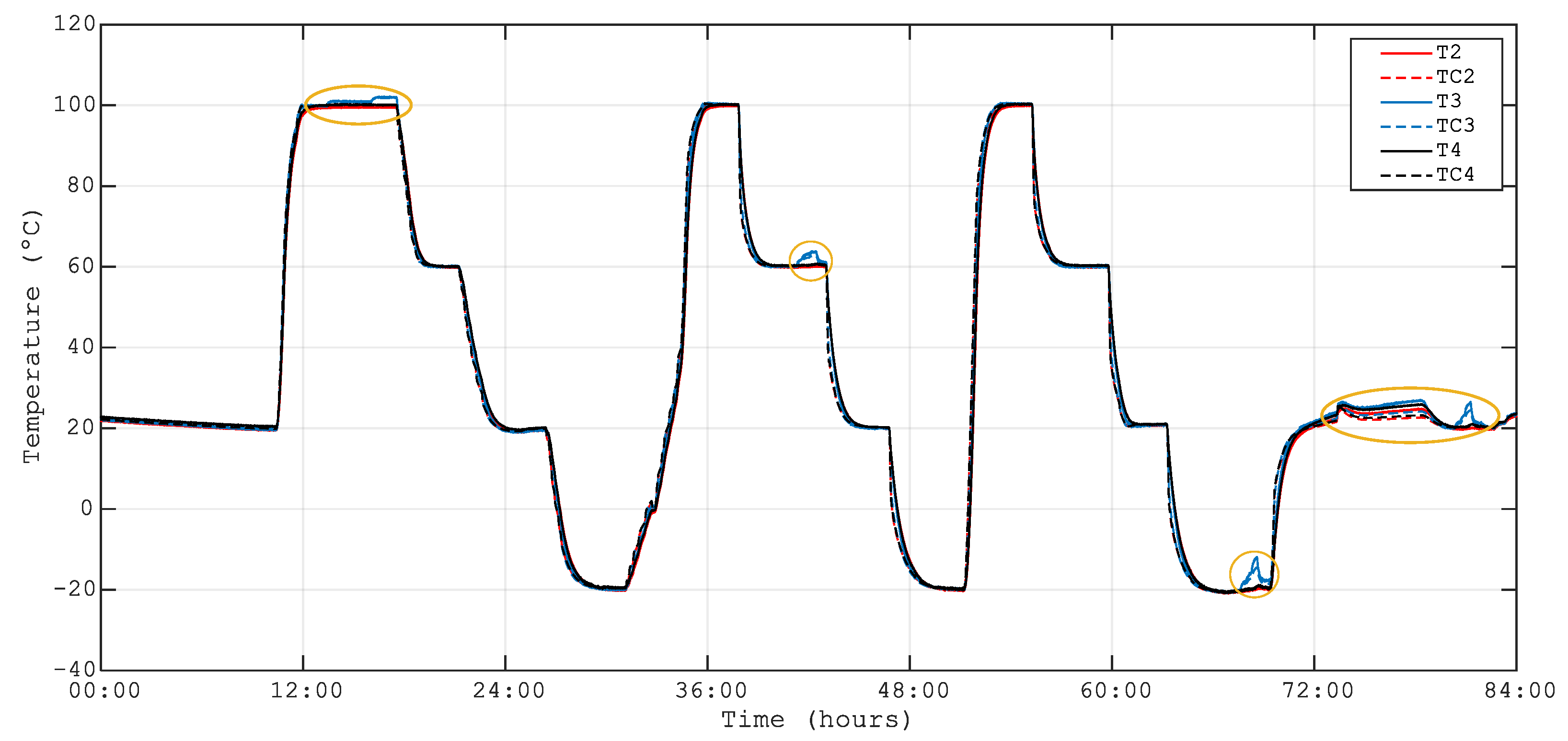
3.1. Temperature Sensors
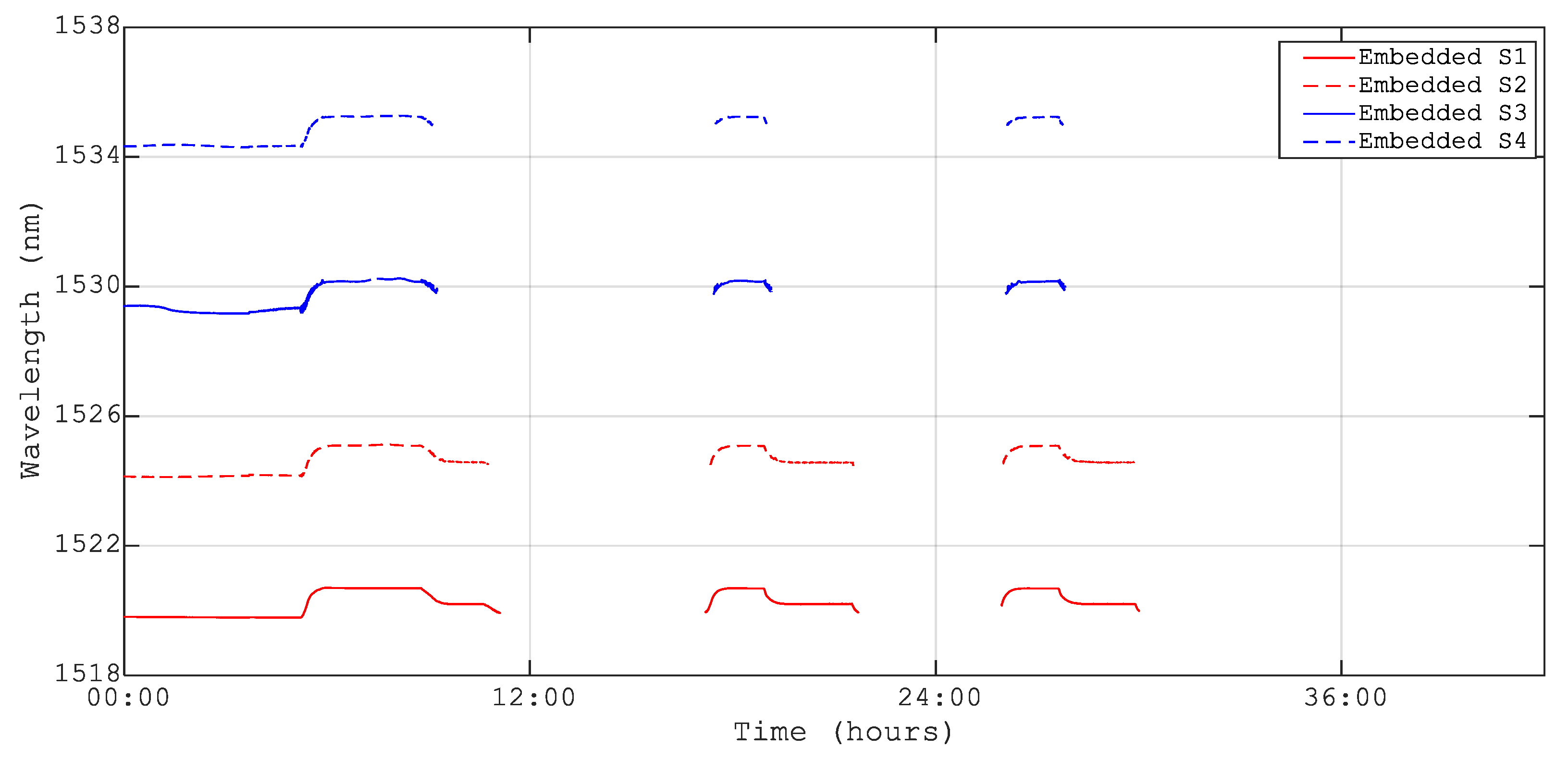
3.2. Strain Sensors
4. Discussion
4.1. Temperature Monitoring
4.2. Surface-Mounted Connectors
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Sensor | Cavity Length (μm) |
|---|---|
| T2 | 43.0 ± 0.7 |
| T3 | 30.2 ± 0.5 |
References
- Hill, K.O. Aperiodic Distributed-Parameter Waveguides for Integrated Optics. Appl. Opt. 1974, 13, 1853–1856. [Google Scholar] [CrossRef] [PubMed]
- Matsuhara, M.; Hill, K.O. Optical-Waveguide Band-Rejection Filters: Design. Appl. Opt. 1974, 13, 2886–2888. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, C.; Priye, V. Dispersion Compensation in a 24 × 20 Gbps DWDM System by Cascaded Chirped FBGs. Optik 2018, 164, 335–344. [Google Scholar] [CrossRef]
- Goh, C.S.; Set, S.Y.; Kikuchi, K. Widely Tunable Optical Filters Based on Fiber Bragg Gratings. IEEE Photon. Technol. Lett. 2002, 14, 1306–1308. [Google Scholar] [CrossRef]
- Sayed, A.F.; Mustafa, F.M.; Khalaf, A.A.M.; Aly, M.H. An Enhanced WDM Optical Communication System Using a Cascaded Fiber Bragg Grating. Opt Quant. Electron 2020, 52, 181. [Google Scholar] [CrossRef]
- Talam, D.B.; El-Badawy, E.-S.A.; Shalaby, H.M.H.; Aly, M.H. EDFA Gain Flattening Using Fiber Bragg Gratings Employing Different Host Materials. Opt Quant. Electron 2020, 52, 161. [Google Scholar] [CrossRef]
- Sahota, J.K.; Gupta, N.; Dhawan, D. Fiber Bragg Grating Sensors for Monitoring of Physical Parameters: A Comprehensive Review. Opt. Express 2020, 59, 060901. [Google Scholar] [CrossRef]
- Pevec, S.; Donlagić, D. Multiparameter Fiber-Optic Sensors: A Review. Opt. Express 2019, 58, 072009. [Google Scholar] [CrossRef] [Green Version]
- Bhaskar, C.V.N.; Pal, S.; Pattnaik, P.K. Recent Advancements in Fiber Bragg Gratings Based Temperature and Strain Measurement. Res. Opt. 2021, 5, 100130. [Google Scholar] [CrossRef]
- Herrero, A.Á.; Fernández-Medina, A.; Cebollero, M.; Garranzo-García, D.; Núñez, A.; Gonzalo, A.; Sánchez, A.; Villanueva, J.; Parejo, P.G.; Campos-Jara, A.; et al. TuMag for SUNRISE III Mission: Development of the Optical Unit of an Imaging Spectropolarimeter. In Proceedings of the Ground-Based and Airborne Instrumentation for Astronomy IX, Montréal, QC, Canada, 17–23 July 2022; SPIE: Bellingham, WA, USA, 2022; Volume 12184, pp. 803–818. [Google Scholar]
- Sunrise: Ein Ballongetragenes Sonnenobservatorium. Available online: https://www.mps.mpg.de/solar-physics/sunrise (accessed on 8 November 2022).
- Rajini-Kumar, R.; Suesser, M.; Narayankhedkar, K.G.; Krieg, G.; Atrey, M.D. Performance Evaluation of Metal-Coated Fiber Bragg Grating Sensors for Sensing Cryogenic Temperature. Cryogenics 2008, 48, 142–147. [Google Scholar] [CrossRef]
- Merberg, G.N.; Harrington, J.A. Optical and Mechanical Properties of Single-Crystal Sapphire Optical Fibers. Appl. Opt. 1993, 32, 3201–3209. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Xia, L.; Ran, Y.; Rohollahnejad, J.; Zhou, J.; Wen, Y. Interrogation of Ultrashort Bragg Grating Sensors Using Shifted Optical Gaussian Filters. IEEE Photon. Technol. Lett. 2015, 27, 1833–1836. [Google Scholar] [CrossRef]
- Zhu, C.; Gerald, R.E.; Huang, J. Progress Toward Sapphire Optical Fiber Sensors for High-Temperature Applications. IEEE Trans. Instrum. Meas. 2020, 69, 8639–8655. [Google Scholar] [CrossRef]
- Arao, Y.; Koyanagi, J.; Utsunomiya, S.; Takeda, S.; Kawada, H. Analysis of Time-Dependent Deformation of a CFRP Mirror under Hot and Humid Conditions. Mech. Time Depend. Mater. 2009, 13, 183–197. [Google Scholar] [CrossRef]
- Catanzaro, B.E.; Hylton, J.C.; Bass, P.; Stumm, B.D. Stability Testing of a Carbon Fiber Composite Optical Bench for Use in the Spacebased LIDAR Mission: CALIPSO (Picasso-Cena). In Proceedings of the Earth Observing Systems VII, Seattle, WA, USA, 7–11 July 2002; SPIE: Bellingham, WA, USA, 2002; Volume 4814, pp. 474–482. [Google Scholar]
- Meltz, G.; Morey, W.W.; Glenn, W.H. Formation of Bragg Gratings in Optical Fibers by a Transverse Holographic Method. Opt. Lett. 1989, 14, 823–825. [Google Scholar] [CrossRef] [PubMed]
- Hill, K.O.; Meltz, G. Fiber Bragg Grating Technology Fundamentals and Overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef] [Green Version]
- Marshall, G.D.; Williams, R.J.; Jovanovic, N.; Steel, M.J.; Withford, M.J. Point-by-Point Written Fiber-Bragg Gratings and Their Application in Complex Grating Designs. Opt. Express 2010, 18, 19844–19859. [Google Scholar] [CrossRef] [PubMed]
- Othonos, A.; Kalli, K. Fiber Bragg Gratings: Fundamentals and Applications in Telecommunications and Sensing; Artech House: Boston, MA, USA, 1999; ISBN 978-0-89006-344-6. [Google Scholar]
- Steenkiste, R.J.V. Strain and Temperature Measurement with Fiber Optic Sensors; CRC Press: Boca Raton, FL, USA, 1996; ISBN 978-1-56676-480-3. [Google Scholar]
- Trutzel, M.N.; Wauer, K.; Betz, D.; Staudigel, L.; Krumpholz, O.; Muehlmann, H.-C.; Muellert, T.; Gleine, W. Smart Sensing of Aviation Structures with Fiber Optic Bragg Grating Sensors. In Proceedings of the Smart Structures and Materials 2000: Sensory Phenomena and Measurement Instrumentation for Smart Structures and Materials, Newport Beach, CA, USA, 6–9 March 2000; SPIE: Bellingham, WA, USA, 2000; Volume 3986, pp. 134–143. [Google Scholar]
- Frövel, M.; Gutiérrez, C.; González, S.; Carrión, G.; Cabrerizo, F.; Pintado, J.M. Influence of Temperature and Humidity on the Performance of FBG-Strain Sensors Embedded in CFRP Composites. In Proceedings of the 4th European Workshop on Structural Health Monitoring, Krakow, Poland, 2–4 July 2008; pp. 1–8. [Google Scholar]
- Fróvel, M.; Fernández-Medina Maeso, A.B.; Mora, J.; Agüero, A.; Sor Mendi, S.; López Heredero, R.; García-Magariño García, A.; González Del Val, M. System and Method for Detecting Ice Formation on a Body. U.S. Patent 20210316869A1, 14 October 2020. [Google Scholar]
- Gao, H.; Jiang, Y.; Cui, Y.; Zhang, L.; Jia, J.; Jiang, L. Investigation on the Thermo-Optic Coefficient of Silica Fiber Within a Wide Temperature Range. J. Lightwave Technol. 2018, 36, 5881–5886. [Google Scholar] [CrossRef]



| Sensor | Peak Wavelength (nm) | Standard Deviation (nm) |
|---|---|---|
| T1 | 1534.61 | ±0.03 |
| T2 | 1539.947 | ±0.006 |
| T3 | 1550.049 | ±0.007 |
| T4 | 1539.970 | ±0.005 |
| T5 | 1544.99 | ±0.03 |
| T6 | 1549.710 | ±0.004 |
| Sensor | Sensitivity (pm/K) | Statistical Error (pm/K) |
|---|---|---|
| T1 | 11 | ±2 |
| T2 | 10.1 | ±0.8 |
| T3 | 10.0 | ±0.5 |
| T4 | 10.1 | ±0.6 |
| T5 | 11 | ±1 |
| T6 | 11 | ±2 |
| Compensation Sensor | Variation Rate of Strain (με/°C) | Statistical Error (με/°C) |
|---|---|---|
| T2 | 1.35 | ±0.03 |
| T3 | 1.41 | ±0.04 |
| T4 | 1.31 | ±0.06 |
| Surface-Mounted Sensor | Strain (με/°C) | Variation Rate (με/°C) | Variation Rate Percentage Difference (με/°C) |
|---|---|---|---|
| S1 | −35 ± 6 | 0.30 ± 0.02 | 20% |
| S2 | −164 ± 5 | 1.41 ± 0.04 | 4% |
| S3 | 10 ± 11 | −0.08 ± 0.04 | 55% |
| S4 | −18 ± 6 | 0.16 ± 0.03 | 60% |
| S5 | −80 ± 8 | 0.66 ± 0.03 | 9% |
| S6 | −153 ± 8 | 1.20 ± 0.05 | 8% |
| S7 | −103 ± 5 | 0.86 ± 0.03 | 13% |
| Sensor | Temperature (°C) | Surface Mounted (με) | Embedded (με) | Difference (με) |
|---|---|---|---|---|
| S1 | 100 | 0 ± 8 | 0 ± 6 | 0 ± 10 |
| 60 | −7 ± 3 | −48 ± 12 | −41 ± 15 | |
| 20 | −25 ± 10 | −30 ± 34 | −5 ± 44 | |
| S2 | 100 | 0 ± 9 | 0 ± 8 | 0 ± 17 |
| 60 | −44 ± 10 | −6 ± 45 | 38 ± 55 | |
| S3 | 100 | 0 ± 6 | 0 ± 9 | 0 ± 15 |
| 60 | 4 ± 20 | −13 ± 17 | −17 ± 37 | |
| S4 | 100 | 0 ± 5 | 0 ± 9 | 0 ± 10 |
| 60 | 0 ± 13 | −20 ± 23 | −20 ± 36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Medina, A.; Frövel, M.; López Heredero, R.; Belenguer, T.; de la Torre, A.; Moravec, C.; San Julián, R.; Gonzalo, A.; Cebollero, M.; Álvarez-Herrero, A. Embedded Fiber Bragg Grating Sensors for Monitoring Temperature and Thermo-Elastic Deformations in a Carbon Fiber Optical Bench. Sensors 2023, 23, 6499. https://doi.org/10.3390/s23146499
Fernández-Medina A, Frövel M, López Heredero R, Belenguer T, de la Torre A, Moravec C, San Julián R, Gonzalo A, Cebollero M, Álvarez-Herrero A. Embedded Fiber Bragg Grating Sensors for Monitoring Temperature and Thermo-Elastic Deformations in a Carbon Fiber Optical Bench. Sensors. 2023; 23(14):6499. https://doi.org/10.3390/s23146499
Chicago/Turabian StyleFernández-Medina, Ana, Malte Frövel, Raquel López Heredero, Tomás Belenguer, Antonia de la Torre, Carolina Moravec, Ricardo San Julián, Alejandro Gonzalo, María Cebollero, and Alberto Álvarez-Herrero. 2023. "Embedded Fiber Bragg Grating Sensors for Monitoring Temperature and Thermo-Elastic Deformations in a Carbon Fiber Optical Bench" Sensors 23, no. 14: 6499. https://doi.org/10.3390/s23146499
APA StyleFernández-Medina, A., Frövel, M., López Heredero, R., Belenguer, T., de la Torre, A., Moravec, C., San Julián, R., Gonzalo, A., Cebollero, M., & Álvarez-Herrero, A. (2023). Embedded Fiber Bragg Grating Sensors for Monitoring Temperature and Thermo-Elastic Deformations in a Carbon Fiber Optical Bench. Sensors, 23(14), 6499. https://doi.org/10.3390/s23146499







