Disguised Full-Duplex Covert Communications
Abstract
:1. Introduction
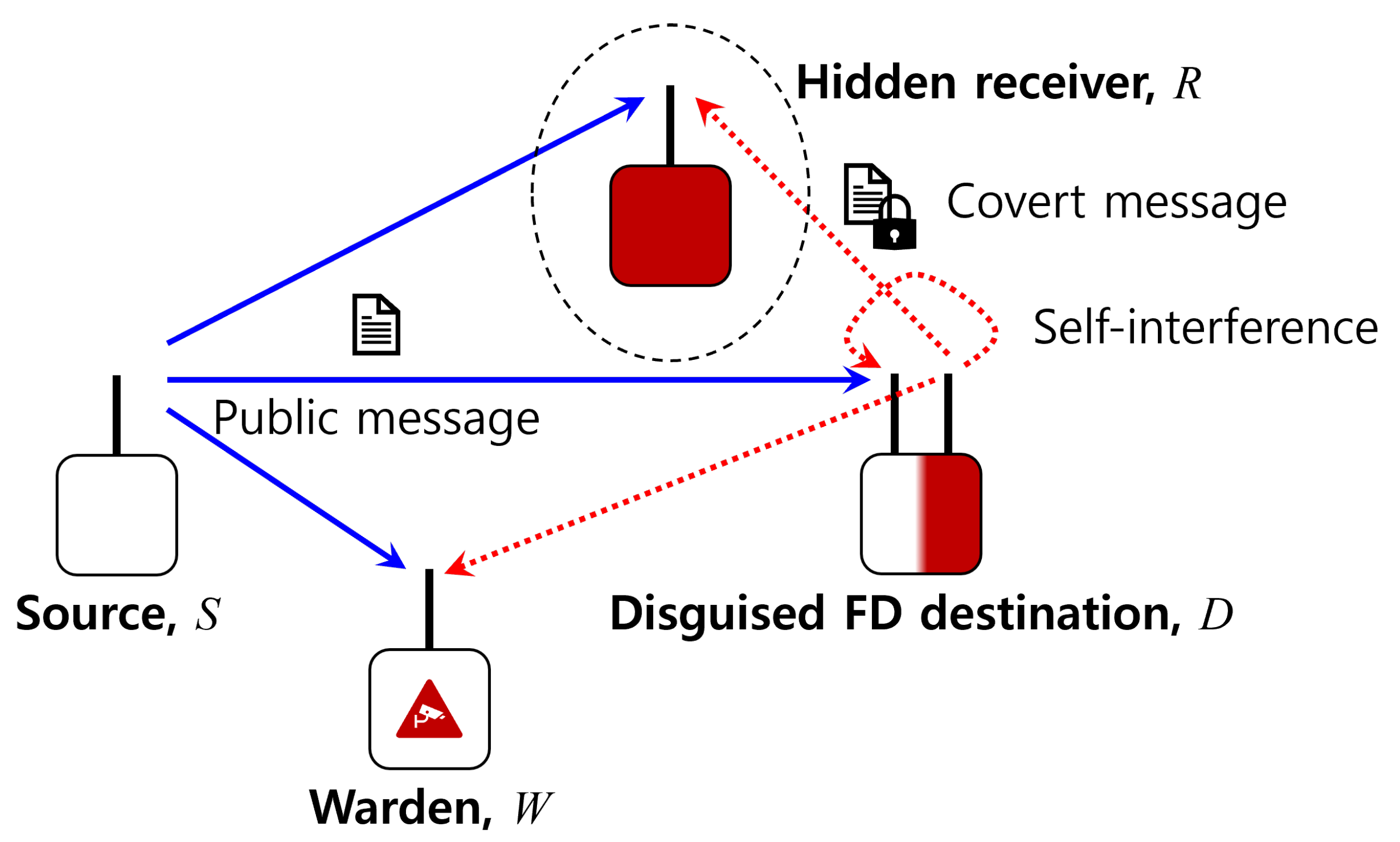
- Different from past works which assume that the surveillance party is confident of the hardware specifications of covert nodes, we take a step further and consider a practical scenario in which a covert communications node disguises itself as another functional entity for even more covertness.
- The worst-case DEP is derived in the presence of noise uncertainty at the warden node.
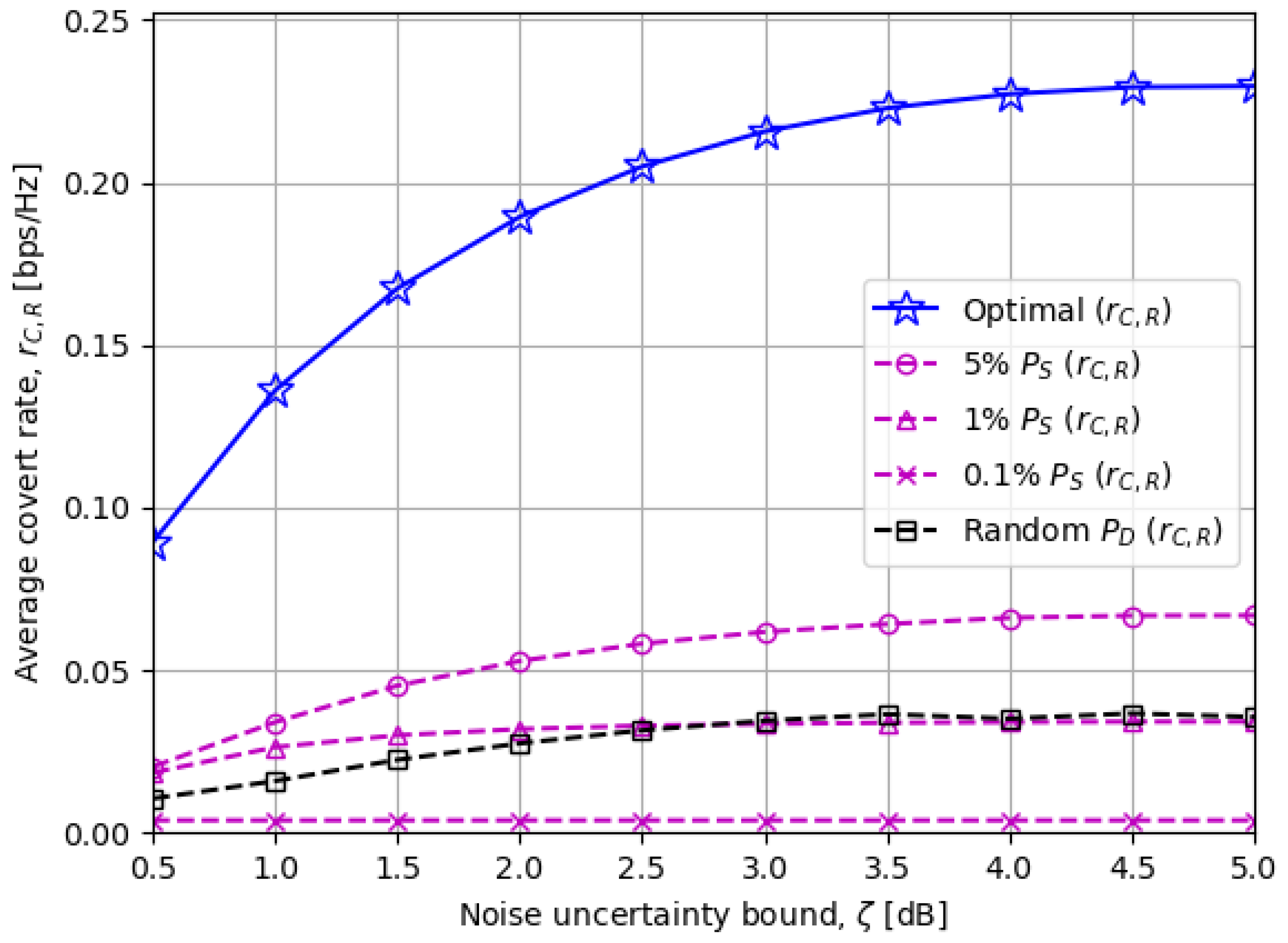
- Noting that covert communications typically suffer from a low data rate due to the stringent DEP requirements, we focus on maximizing the covert rate at the hidden receiver by optimizing the public data rate and the transmit power of the FD destination node subject to the worst-case DEP of the warden.
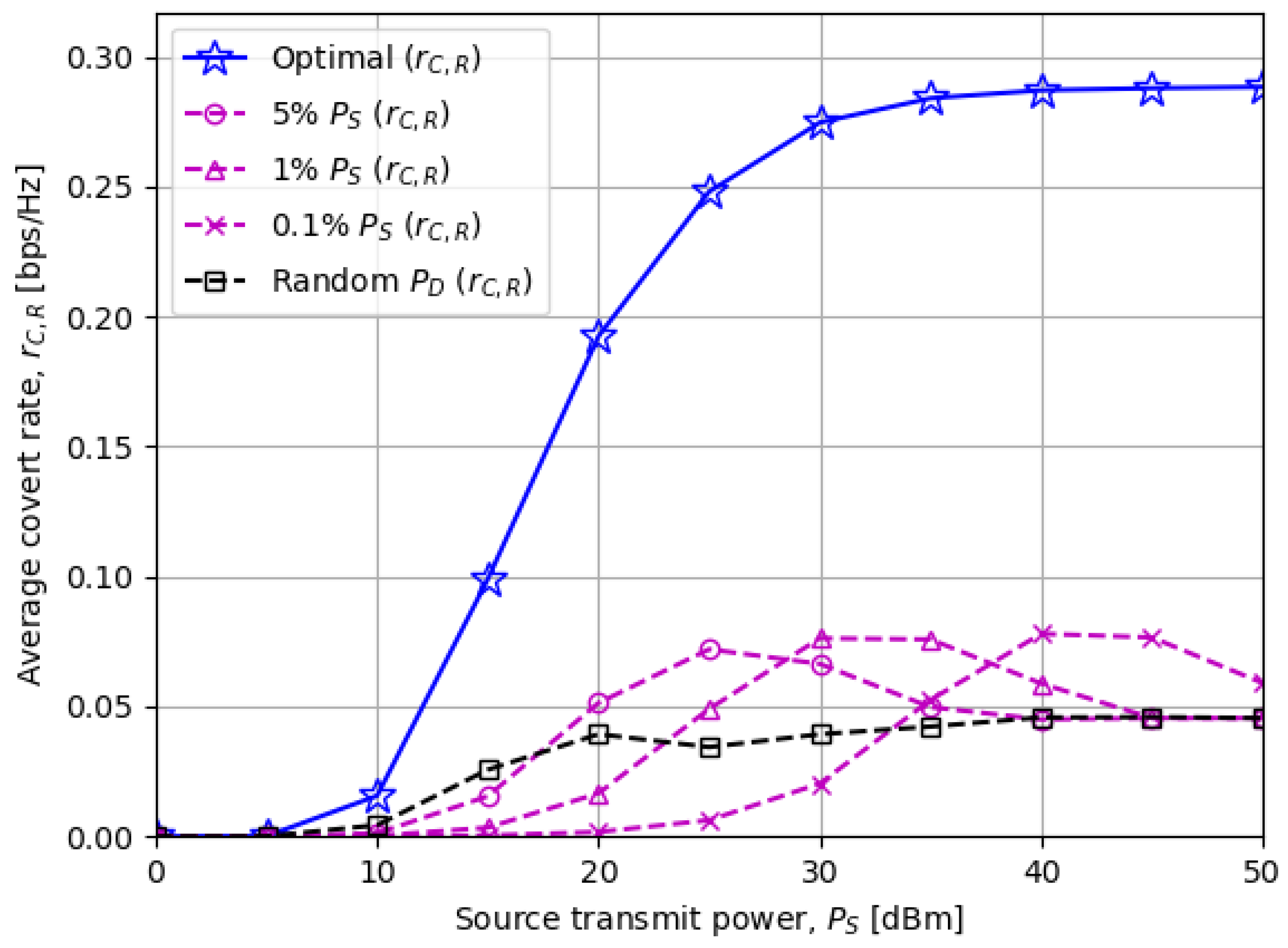
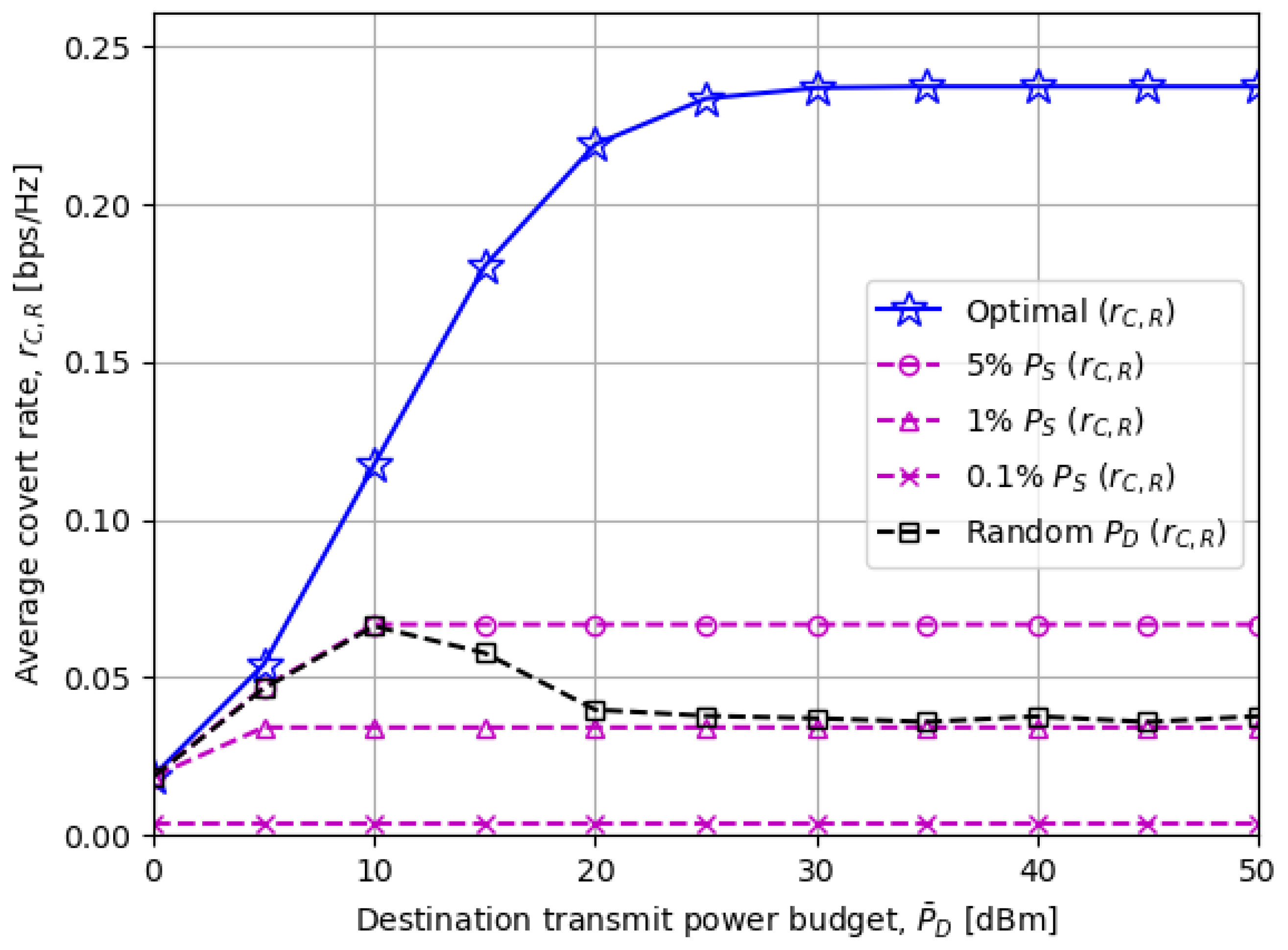
- We investigate the effects of various system parameters on the covert rate through numerical results, one of which reveals that applying more (less) destination transmit power achieves a higher covert rate when the source transmit power is low (high).
- Since our work provides a performance guideline from the information-theoretic point of view, we suggest analyses with practical modulations and imperfect CSI as valuable future research topics.
2. System Model
2.1. Received Signals
2.2. Covert Message Detection
3. Problem Formulation
4. Proposed Solutions
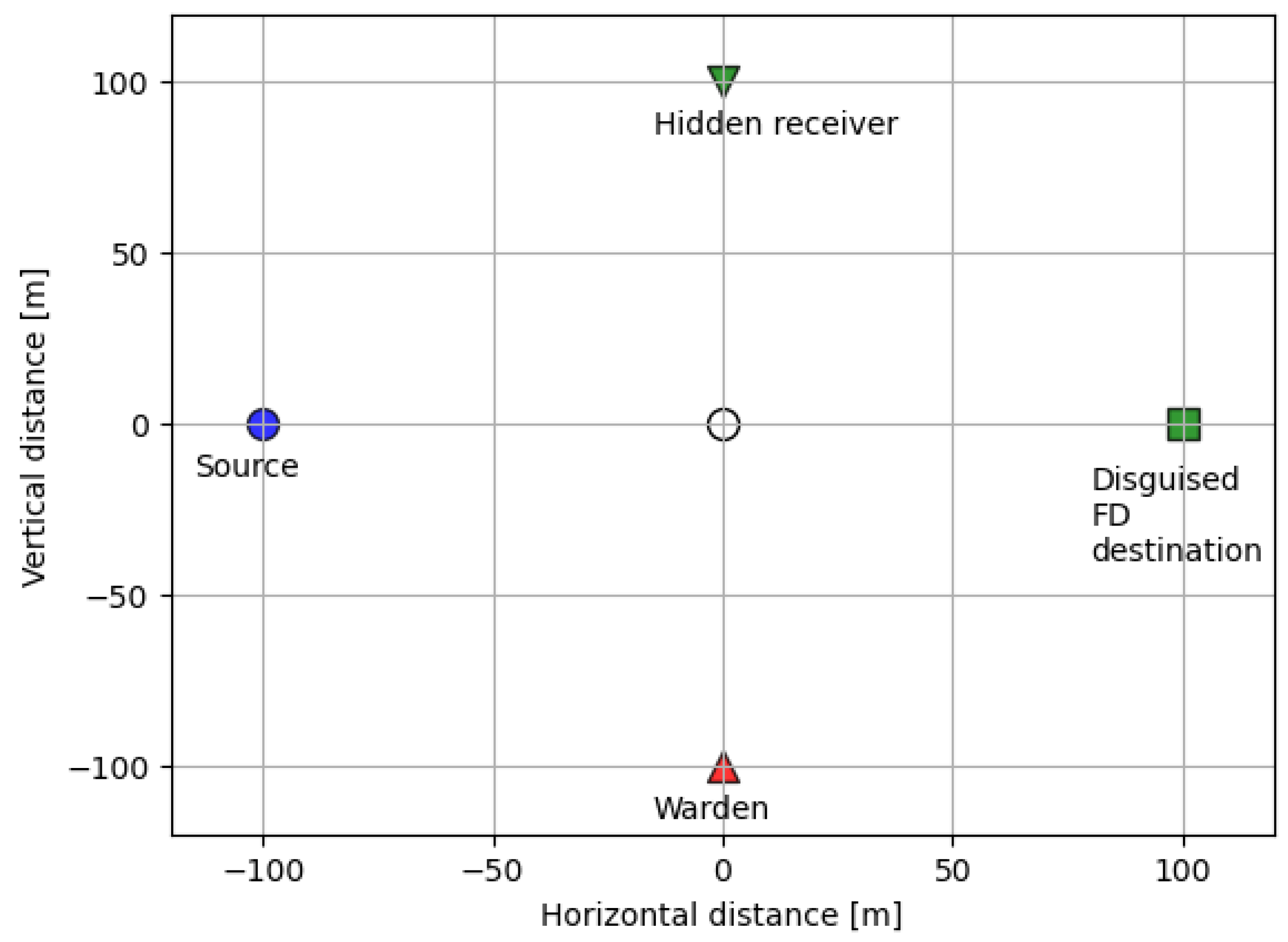
5. Numerical Results
6. Discussion
6.1. Performance
6.2. Applications
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Qazi, S.; Khawaja, B.A.; Farooq, Q.U. IoT-Equipped and AI-Enabled Next Generation Smart Agriculture: A Critical Review, Current Challenges and Future Trends. IEEE Access 2022, 10, 21219–21235. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, Z.; Fei, S.; Wang, M.; Li, T.; Wang, H. Is Today’s End-to-End Communication Security Enough for 5G and Its Beyond? IEEE Netw. 2022, 36, 105–112. [Google Scholar] [CrossRef]
- Forouzan, B.A. Cryptography and Network Security; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Wyner, A.D. The Wire-Tap Channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Angueira, P.; Val, I.; Montalbán, J.; Seijo, Ó.; Iradier, E.; Fontaneda, P.S.; Fanari, L.; Arriola, A. A Survey of Physical Layer Techniques for Secure Wireless Communications in Industry. IEEE Commun. Surv. Tutor. 2022, 24, 810–838. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, X.; Tang, J.; Zhao, N.; Zhang, X.Y.; Niyato, D.; Wong, K.-K. Covert Communication in UAV-Assisted Air-Ground Networks. IEEE Wirel. Commun. 2021, 28, 190–197. [Google Scholar] [CrossRef]
- Bash, B.A.; Goeckel, D.; Towsley, D.; Guha, S. Hiding information in noise: Fundamental limits of covert wireless communication. IEEE Commun. Mag. 2015, 53, 26–31. [Google Scholar] [CrossRef] [Green Version]
- Shahzad, K.; Zhou, X.; Yan, S.; Hu, J.; Shu, F.; Li, J. Achieving Covert Wireless Communications Using a Full-Duplex Receiver. IEEE Trans. Wirel. Commun. 2018, 17, 8517–8530. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Xu, L.; Liu, X.; Lu, Z. Covert Communication with A Full-Duplex Receiver Based on Channel Distribution Information. In Proceedings of the 2018 12th International Symposium on Antennas, Propagation and EM Theory (ISAPE), Hangzhou, China, 3–6 December 2018; pp. 1–4. [Google Scholar]
- Zheng, M.; Hamilton, A.; Ling, C. Covert Communications with a Full-Duplex Receiver in Non-Coherent Rayleigh Fading. IEEE Trans. Commun. 2021, 69, 1882–1895. [Google Scholar] [CrossRef]
- Yang, L.; Yang, W.; Xu, S.; Tang, L.; He, Z. Achieving Covert Wireless Communications Using a Full-Duplex Multi-Antenna Receiver. In Proceedings of the 2019 IEEE 5th International Conference on Computer and Communications (ICCC), Chengdu, China, 6–9 December 2019; pp. 912–916. [Google Scholar]
- Wang, J.; Li, Y.; Tang, W.; Li, X.; Li, S. Channel State Information Based Optimal Strategy for Covert Communication. In Proceedings of the 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi’an, China, 23–25 December 2019; pp. 1–6. [Google Scholar]
- Hu, J.; Yan, S.; Zhou, X.; Shu, F.; Li, J. Covert Wireless Communications With Channel Inversion Power Control in Rayleigh Fading. IEEE Trans. Veh. Technol. 2019, 68, 12135–12149. [Google Scholar] [CrossRef] [Green Version]
- Shu, F.; Xu, T.; Hu, J.; Yan, S. Delay-Constrained Covert Communications With a Full-Duplex Receiver. IEEE Wirel. Commun. Lett. 2019, 8, 813–816. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Li, Z.; Cheng, N.; Wang, D.; Quan, W.; Shen, X. Joint Power and Position Optimization for the Full-Duplex Receiver in Covert Communication. In Proceedings of the ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 July 2020; pp. 1–6. [Google Scholar]
- Xu, R.; Guan, L.; Zhao, Y.; Li, Z.; Wang, D. Robust Power and Position Optimization for the Full-Duplex Receiver in Covert Communication. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Chen, X.; Sun, W.; Xing, C.; Zhao, N.; Chen, Y.; Yu, F.R.; Nallanathan, A. Multi-Antenna Covert Communication via Full-Duplex Jamming Against a Warden With Uncertain Locations. IEEE Trans. Wirel. Commun. 2021, 20, 5467–5480. [Google Scholar] [CrossRef]
- Che, B.; Yang, W.; Lu, X. Covert Communication for Multi-Channel Transmission with A Full-Duplex Receiver. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–5. [Google Scholar]
- Wang, Y.; Yan, S.; Yang, W.; Cai, Y. Covert Communications With Constrained Age of Information. IEEE Wirel. Commun. Lett. 2021, 10, 368–372. [Google Scholar] [CrossRef]
- Sun, R.; Yang, B.; Ma, S.; Shen, Y.; Jiang, X. Covert Rate Maximization in Wireless Full-Duplex Relaying Systems With Power Control. IEEE Trans. Commun. 2021, 69, 6198–6212. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, R.; Deng, Y.; Shu, F.; Nie, Z.; Aghvami, A.H. Harvest-and-Opportunistically-Relay: Analyses on Transmission Outage and Covertness. IEEE Trans. Wirel. Commun. 2020, 19, 7779–7795. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, K.; Zhu, S. Covert Communication for Integrated Satellite–Terrestrial Relay Networks with Cooperative Jamming. Electronics 2023, 12, 999. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Shi, J.; Ng, D.W.K. Intelligent Reflecting Surface-Assisted Multi-Antenna Covert Communications: Joint Active and Passive Beamforming Optimization. IEEE Trans. Commun. 2021, 69, 3984–4000. [Google Scholar] [CrossRef]
- Pejoski, S.; Hadzi-Velkov, Z.; Zlatanov, N. Full-Duplex Covert Communications Assisted by Intelligent Reflective Surfaces. IEEE Commun. Lett. 2022, 26, 2846–2850. [Google Scholar] [CrossRef]
- Wang, M.; Xu, Z.; Xia, B.; Guo, Y. Active Intelligent Reflecting Surface Assisted Covert Communications. IEEE Trans. Veh. Technol. 2023, 72, 5401–5406. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Zheng, T.-X.; Ng, D.W.K.; Al-Dhahir, N. Intelligent Reflecting Surface-Aided Full-Duplex Covert Communications: Information Freshness Optimization. IEEE Trans. Wirel. Commun. 2023, 22, 3246–3263. [Google Scholar] [CrossRef]
- Zhou, X.; Yan, S.; Shu, F.; Chen, R.; Li, J. UAV-Enabled Covert Wireless Data Collection. IEEE J. Sel. Areas Commun. 2021, 39, 3348–3362. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, S.; Wang, J.; Lit, H.; Shen, Y. Optimal Location Design for UAV Covert Communications with a Full-Duplex Receiver. In Proceedings of the 2022 International Conference on Networking and Network Applications (NaNA), Urumqi, China, 3–5 December 2022; pp. 35–40. [Google Scholar]
- Zhang, R.; Chen, X.; Liu, M.; Zhao, N.; Wang, X.; Nallanathan, A. UAV Relay Assisted Cooperative Jamming for Covert Communications Over Rician Fading. IEEE Trans. Veh. Technol. 2022, 71, 7936–7941. [Google Scholar] [CrossRef]
- Li, M.; Tao, X.; Wu, H.; Li, N. Joint Trajectory and Resource Optimization for Covert Communication in UAV-Enabled Relaying Systems. IEEE Trans. Veh. Technol. 2023, 72, 5518–5523. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, H.; Chen, R.; Shi, J.; Li, Z. Covert Communication Against a Full-Duplex Adversary in Cognitive Radio Networks. In Proceedings of the GLOBECOM 2022-2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 3144–3149. [Google Scholar]
- Yang, Y.; Yang, B.; Shen, S.; She, Y.; Taleb, T. Covert Rate Study for Full-Duplex D2D Communications Underlaid Cellular Networks. IEEE Internet Things J. 2023. [Google Scholar] [CrossRef]
- Sun, R.; Yang, B.; Shen, Y.; Jiang, X.; Taleb, T. Covertness and Secrecy Study in Untrusted Relay-Assisted D2D Networks. IEEE Internet Things J. 2023, 10, 17–30. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, S.; Yang, W.; Zhong, C.; Ng, D.W.K. Probabilistic Accumulate-Then-Transmit in Wireless-Powered Covert Communications. IEEE Trans. Wirel. Commun. 2022, 21, 10393–10406. [Google Scholar] [CrossRef]
- Feng, S.; Lu, X.; Sun, S.; Niyato, D. Mean-Field Artificial Noise Assistance and Uplink Power Control in Covert IoT Systems. IEEE Trans. Wirel. Commun. 2022, 21, 7358–7373. [Google Scholar] [CrossRef]
- Liu, J.; Yu, J.; Chen, X.; Zhang, R.; Wang, S.; An, J. Covert Communication in Ambient Backscatter Systems With Uncontrollable RF Source. IEEE Trans. Commun. 2022, 70, 1971–1983. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons, Inc.: New Jersey, NJ, USA, 2005. [Google Scholar]
- Kim, S.W.; Ta, H.Q. Covert Communications Over Multiple Overt Channels. IEEE Trans. Commun. 2022, 70, 1112–1124. [Google Scholar] [CrossRef]
- He, B.; Yan, S.; Zhou, X.; Lau, V.K.N. On Covert Communication With Noise Uncertainty. IEEE Commun. Lett. 2017, 21, 941–944. [Google Scholar] [CrossRef] [Green Version]
- Sobers, T.V.; Bash, B.A.; Guha, S.; Towsley, D.; Goeckel, D. Covert Communication in the Presence of an Uninformed Jammer. IEEE Trans. Wirel. Commun. 2017, 16, 6193–6206. [Google Scholar] [CrossRef]
- Si, J.; Li, Z.; Zhao, Y.; Cheng, J.; Guan, L.; Shi, J.; Al-Dhahir, N. Covert Transmission Assisted by Intelligent Reflecting Surface. IEEE Trans. Commun. 2021, 69, 5394–5408. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zeng, Y.; Ma, J. Covert Wireless Communications in IoT Systems: Hiding Information in Interference. IEEE Wirel. Commun. 2018, 25, 46–52. [Google Scholar] [CrossRef]
- Moon, J.; Lee, S.H.; Lee, H.; Lee, I. Proactive Eavesdropping With Jamming and Eavesdropping Mode Selection. IEEE Trans. Wirel. Commun. 2019, 18, 3726–3738. [Google Scholar] [CrossRef]
- Grayver, E.; Keating, R.; Parower, A. Feasibility of full duplex communications for LEO satellite. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–8. [Google Scholar]
- Ross, S. A First Course in Probability, 10th ed.; Pearson: London, UK, 2019. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, J. Disguised Full-Duplex Covert Communications. Sensors 2023, 23, 6515. https://doi.org/10.3390/s23146515
Moon J. Disguised Full-Duplex Covert Communications. Sensors. 2023; 23(14):6515. https://doi.org/10.3390/s23146515
Chicago/Turabian StyleMoon, Jihwan. 2023. "Disguised Full-Duplex Covert Communications" Sensors 23, no. 14: 6515. https://doi.org/10.3390/s23146515
APA StyleMoon, J. (2023). Disguised Full-Duplex Covert Communications. Sensors, 23(14), 6515. https://doi.org/10.3390/s23146515





