1. Introduction
A phase camera is an instrument that can simultaneously measure intensity and wavefront aberrations of the incoming light. In general, a phase camera is a combination of a CCD (charge-coupled device) or CMOS (complementary metal-oxide-semiconductor) sensor with a special optical arrangement or a wavefront sensor, and a computer system to translate data to phase maps, intensity maps or a combination of both.
Wavefront phase sensors were first developed to measure the aberration of an optical wavefront produced by an imaging system or other surrounding information acquired by the system [
1]. They were developed mainly, and independently, in two fields as different as astronomy [
2,
3] and ophthalmology [
4,
5], where, in the first case, they correct the wavefront aberrations produced by the huge telescopic lenses and changes in composition, and in the second, conditions in the atmosphere and aberrations of the human vision system.
Shack–Hartmann (SH) wavefront sensors are widely used in many applications [
3,
6]. They fit a lenslet array between the camera sensor and the sample, and ultimately measure a set of discrete slopes, so the lateral resolution is limited to the number of lenslets. SH wavefront sensors became the gold standard, due to their simplicity, precision and wide dynamic range and, above all, because these sensors are principally used in adaptive optics (AO) in telescopes [
7], where their main drawback, the low resolution, is not a serious problem, since the resolution of these systems is currently limited, not by the resolution of the sensor, but by the resolution of the corrective elements, whether deformable mirrors (DMs), spatial light modulators (SLM), or other corrective elements [
8,
9].
Interferometric methods have been commonly used to retrieve the wavefront phase of an optical field, although they are not normally considered wavefront sensors, due to the use of a laser and an aberrated reference beam [
10,
11]. These characteristics limit their applications, especially in fields such as ophthalmology or microscopy, where laser phototoxicity limits either the sensor exposure time or the laser power.
In recent years, many wavefront sensing techniques have emerged as alternatives to the SH system. Some are evolutions of the SH, which use some diffractive element between the sensor and the sample, and present improvements in accuracy [
12,
13], speed [
14], dynamic range [
15,
16,
17,
18], or lateral resolution [
19,
20]. These sensors are still limited in the latter aspect, as they cannot reach full sensor resolution and have other drawbacks typical of an SH sensor, such as low-frequency phase detection, without the possibility of extracting high variations inside the wavefront.
Deterministic or iterative mathematical techniques, phase imaging [
21,
22] or curvature sensing [
23], for instance, can provide wavefront estimation. In these techniques, lateral resolution is limited only by the resolution of the images used to calculate wavefront measurements [
24]. The most common approach, used specially in microscopy because it is limited to short defocused distances, is based on the transport of intensity equation (TIE) [
21]. These wavefront sensors suffer from linearity problems and narrow dynamic range, and their applications to video recording are limited, because these sensors take multiple images to obtain one phase map.
As wavefront sensors have evolved technically, so have their fields of application. The characterisation of lenses [
25], lasers [
26], ophthalmic diseases such as keratoconus [
27,
28], microscopy [
29] or medicine [
30] are just some of the current and future applications of wavefront sensors. In all these applications it will be convenient to use the highest possible resolution within the largest possible field of view, since in terms of computer vision we have moved from determining the low frequencies required for atmospheric correction to determining high frequencies, which are necessary to elucidate small details within an image. Despite the researcher efforts, the notable evolution of many types of wavefront sensor that have been described above, and the growing number of applications, there are a relatively reduced number of commercial instruments.
We have developed a compact real-time high-resolution phase camera that is able to recover the wavefront phase distortions and the amplitude of an optical field simultaneously. It is a combination of a deterministic wavefront phase sensor that obtains the information from two symmetrically out-of-focus images and an electrically tunable lens (ETL), which allows minimizing capture time and avoiding a mechanical system that moves the camera or the sample. In our technique, we obtain wavefront phase information from defocused images in symmetrical planes before and after the focal point, as was proposed in the original work of Roddier in 1988, with the introduction of the curvature wavefront sensor [
31], which avoided using diffractive elements or lenslets. The main innovation in our setup is the placement of the ETL before the Fourier plane, in the pupil plane, which enables us to reduce the setup size, unlike other state of the art works [
32] which place it in the Fourier plane. It simplifies the current state-of-the-art setup, which often requires additional control electronics and physical separation of the lens from the camera, and it involves adapting a camera with a fixed lens, along with ETL, specifically designed to capture intensity images.
2. Materials and Methods
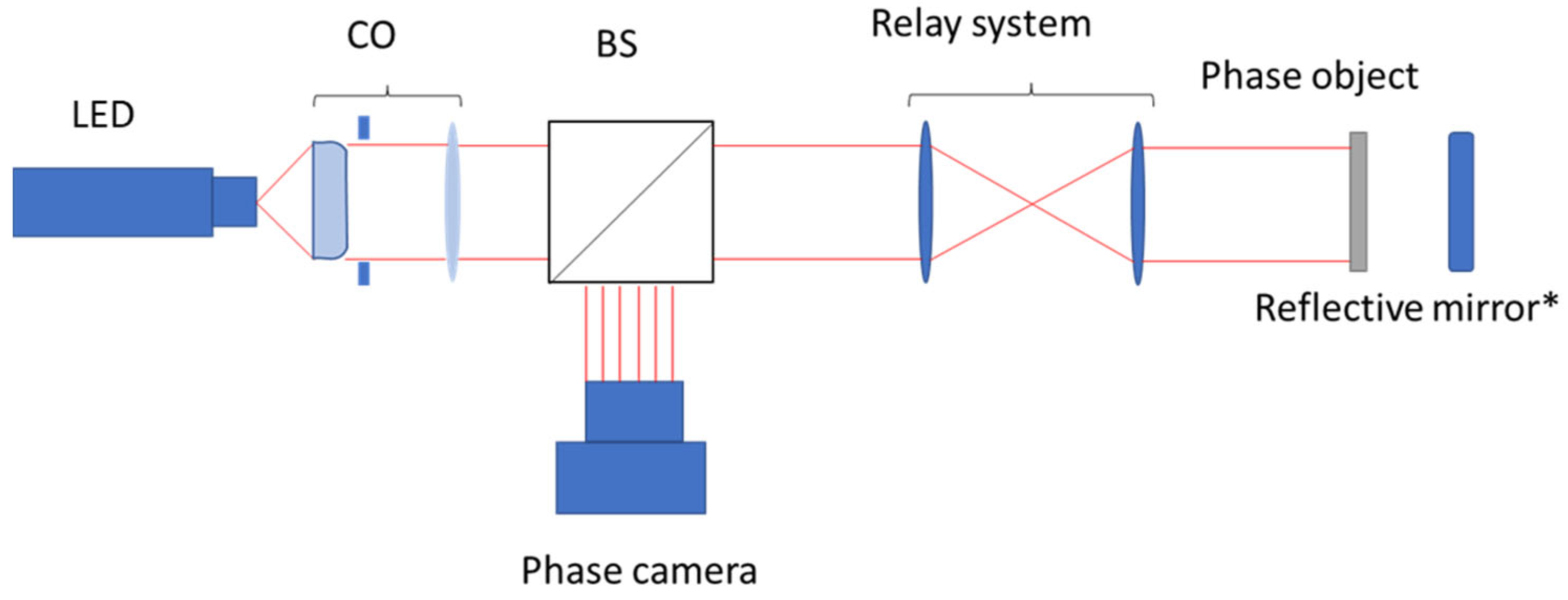
Our approach consists of a common intensity imaging system combined with an ETL, an optimized optical arrangement and a Jetson AGX microcontroller to manage the electronics, obtain the high frame rate data, and process the outputs with low power consumption. This measuring procedure needs a lens relay to capture around the phase object with a collimated light beam. The most common approaches that captures out-of-focus images use external translation stages to move either the sensor or the object, which requires a high amount of time to stabilise the system and capture both images. This capture system was first designed as an ophthalmologic device [
28], using a prism system and one sensor to capture multiple images at the same time. In the presented approach, an ETL was used to enhance the capture process, but the approach requires image processing to solve the aberrations and magnification produced by the lens.
The system consists of a wavefront phase image sensor [
28,
33], which employs a lens relay to reverse the object space and captures two out-of-focus images on either side of the pupil plane, as depicted in
Figure 1. This approach eliminates the need for mechanical translation or prism stages, by utilizing an ETL. This methodology provides the capability of modifying the propagation distance rapidly and automatically, enabling real-time measurements. The potential of merging different images obtained at various propagation distances using fast focus switching holds promise [
34], and will be explored in future studies to fully leverage the advantages of the system equipped with an ETL. The lack of physical displacement needs image corrections to account for the focal length variations, along with a comprehensive characterisation of the ETL to control defocused distances. This process is crucial to ensure quantitative and accurate measurements.
A lens with a focal length of 30 mm was placed on top of the ETL to enhance the details of the phase object, resulting in a fivefold increase. The relay system is composed of a 150 mm and a 75 mm lenses, augmenting by a factor of 2. The light is located at 25 cm from the BS, and the phase object at over 8 cm in front of the 75 mm lens. Finally, the camera is placed in front of the BS at 12 cm, which is the focal combination that provides the centre of the range for varying the ETL. The telecentric system is common hardware which is added to an ETL optical setup [
32], generally used to correct the magnification produced by the focal shift. Our configuration avoids the use of this element, simplifying the mechanical design by solving the problem through a computational approach using the method developed specifically for this work, which is described below.
The phase camera was positioned in front of the beam splitter to ensure that the pupil plane was at the midpoint of the maximum range available with ETL. This allowed for an increased range of defocus distances within the maximum limits of the ETL, which is not necessarily the median of the allowed voltage.
We designed a case holder to incorporate the necessary electronics for cooling the sensor, avoiding temperature effect on dark noise. The holder employs a common Peltier cell with a heat sink, and it is powered using a modified power supply. The design was built using a 3D printer.
In our approach the propagation distance depends on the focal movement of the ETL. In the lens selected [
35], the mechanical system provides an application-specific integrated circuit (ASIC) to control the focus actuator, with a 10 bit digital-to-analog converter (DAC). Our method to calibrate the focus distances uses a concentric circle reticule target [
36] to detect the most focused value on each DAC position, moving a stage on the object side to obtain the distances. Each image was captured every 500 µm in the linear stage. The procedure captures each 1.60 V from 0 V to 60 V, obtaining the characterisation curve. Using the Laplacian kernel [
37] and the Radon transform [
38] makes it possible to find the maximum variance over the oriented axis of the target, obtaining the maximum variability to decide the correct focus.
Figure 2 presents a selection of images with different focuses, showing the variability of the high frequencies when the lens is well focused. Before the calibration, a pupil plane must be chosen, using the lens datasheet, to obtain the central position in distance, not in voltage.
The algorithm finds the minimum thickness of the lines across the oriented angles, as shown in
Figure 2b. After the algorithm execution, it is possible to fit a polynomial relation of the voltage-versus-propagation distance, to use this method as a quantitative one, as shown in
Figure 2c.
Magnification due to changes in focus distance must be corrected. Our proposal requires the calibration target to obtain the sensor-acquired dimension differences; the magnification is calculated with the size of each target, as in Equation (1),
where
M is the magnification factor,
T the target size and
v1 and
v2 the voltage at each DAC. Target size is obtained using the intensity information. In this case, the target is circular, so the diameter of each circle is chosen as
T, each value of
v determines the distance in the object space, and the medium point is chosen to locate the pupil plane. To avoid intensity value manipulation, the algorithm always chooses the smallest shape to expand without modifying the values obtained by the sensor. By extracting both shapes from the target, it is possible to obtain the different number of steps needed to adjust the size, as shown in Equation (2),
where
D represents the final difference between the two circular pupils. The minimum diameter is chosen to expand the intensity image, ensuring that the information captured by the sensor is not lost.
With the difference between the images, the step (
S) for generating the grid is shown in Equation (3),
where a linear regression is characterised using
N neighbours to fill the intermediate values;
I is the intensity image and
v each voltage, assuming that the images are square. By obtaining the trend in both axis
X and
Y, the medium values without information are filled. The idea behind the procedure is to enlarge the image without losing the information captured by the sensor. The intermediate step displays a grid of the S-by-S-sized images, filling the intermediate values with neighbours, so that a common interpolation, such as nearest neighbour or linear interpolation, is not necessary.
Figure 3 shows the images before and after the correction.
The last step to obtain the phase map with our approach consists of capturing two intensity images around the pupil plane with an equal defocus, Δz, on each side. With both images, the phase gradients are recovered along two orthogonal directions. Δz must be chosen according to the phase object we are measuring, in order to maximise the frequencies that should be extracted from the object [
21,
39]. The optical setup presented is comparable to those used in curvature sensors [
23,
31].
The mathematical computation required to extract the wavefront phase information differs from the variations observed in the state-of-the-art TIE methods [
21], as depicted in Bonaque-González et al. [
28]. The following equations describe the algorithm behaviour and how to extract the phase of the two images. It should be noted that when we refer to phase, we are indicating the aberrated wavefront, i.e., the points where the electromagnetic waves have the same phase. The algorithm quantifies the differences between a reference wavefront and an aberrated wavefront by measuring the path of light rays at various locations and detecting the optical path difference. SH sensors operate on the same principle, and provide a phase image of the wavefront aberration too.
where
H(
x,
y) is a continuous bidimensional function defined for positive values
x, y and with positive numbers, and
V the auxiliary transformation of
H. The character
α is a variable of
k discrete angles distributed in the interval [−π/2, π/2], defining a line with y origin and angular separation from the
x axis equal to
α.
Another auxiliary function that represents the abscissa axis between two unidimensional continuous functions represented by
f(
x) and
g(
x) defined for positive values of
x, represented here as
D, is described in Equation (5).
The captured images named
I1 and
I2 are different intensity maps, and to recover the phase with our method, Equation (6) is applied.
It is necessary to apply a factor, represented by Equation (7), to obtain the wavefront phase
φo in real units (
o denotes real units). This factor considers the pixel size (s) along with Δz, which represents the propagation distance from the pupil to one of the defocused images. We assume a symmetrical distribution of defocus distances relative to the midpoint (pupil plane) for both defocused images. In our case, the pixel size was chosen in the pupil position, extracted with the calibration target in 11 mm (
Figure 4).
A numerical integration of both gradients is needed to obtain the phase maps [
40]. The
k number of discrete angles to evaluate the images with algorithm is 80, achieving the desired accuracy of our prototype λ/60 without sacrificing the speed of the algorithm; as we checked, more angles do not improve the accuracy when compensated by the execution time, and with more angles it would not be possible to extract the wavefront in real time. In our tests, by adding 120 angles, the accuracy increases to λ/63.
To design our experiment a 4K Sony sensor was chosen, using the half of the height sensor to avoid lens distortions and to limit the pupil of the prototype to 9 mm. It is possible to reach 25 frames per second in the 1200 × 1200 pixels pupils, and 120 with a 650 × 650 pixels pupil. Due to the high amount of data to manage, a Jetson AGX Xavier was chosen to compute the algorithm at a maximum of 25 phase maps per second, allowing real time applications.
The SH sensor was purchased from Thorlabs, model WFS20-14AR, 300 µm pitch, 8–32 taps. The deformable mirror used was DM140A-35-UP01, a 12 × 12 continuous deformable mirror with aluminium coating. The rest of the optical arrangement consists of common lenses and beam splitter 50-50. We chose the ETL, given its speed of movement, a Polight T-Lens Silver [
31], and the Sony sensor to obtain a high frame rate. The liquid lens studied with our sensor was an Optotune EL-10-30 [
41].
The light source is based in a point-source-type LED (Marktech MTPS9067) emitting at 650 nm, with a window size of 160 um. The beam divergence is adjusted by modifying the distance between the lens and the LED. Note the divergence adjustment is not critical, as any deviation from collimation is seen as a defocus aberration in the wave-front-phase maps that is subtracted from the results. We used achromatic lenses for the entire setup so that the setup would be insensitive to the spectral width of the LED. These achromatic lenses are optimised for the 400–700 nm wavelength range; hence, the same configuration works with the same performance for any LED within the optical range.
4. Conclusions
This work presents the design of a highly versatile phase camera that can be easily adapted for use in various experimental settings without the need for significant modifications to the optical system. The limitations of the ETL have been thoroughly characterised and addressed by software correction, and the optical setup has been optimised to achieve maximum displacement. This adaptable system allows for changes in magnification and other optical adjustments to expand its use in fields such as microscopy, biomedicine, astronomy, and semiconductor metrology. The use of ETLs can be valuable for obtaining the wavefront of an object, solving the limitations outlined in the current literature, such as magnification correction. By integrating this technology into a basic optical setup, several advantages can be gained, including the effortless use of different propagation distances, eliminating the need for a stage to capture multiple images, and avoiding the use of specific prisms, which can reduce sampling resolution. The principal novelty of our camera is the location of the liquid lens, placed before the Fourier plane, in the pupil plane, unlike Zuo et al. [
32], who place it in the Fourier plane. The Zuo setup often requires additional control electronics and the physical separation of the lens from the camera, and it involves adapting a camera with a fixed lens, along with a liquid lens specifically designed to capture intensity. This separation delays the synchronisation between the camera and the lens, which is crucial to achieve real-time performance and minimise temporal variability. Therefore, the assembly process becomes more complicated. With this configuration, a pre-assembled liquid-lens capture system can be easily integrated into a phased-imaging system.
We have made a comparison with one of the most widespread phase sensors, and considered a standard in the field, the SH sensor. Our camera has been shown to achieve SH-equivalent results in normal situations, and to improve on SH in situations where lateral resolution is a critical issue. We have seen that better lateral resolution will yield more detail in high frequencies, and better sensibility and accuracy in Z in relatively low frequencies.
Our compact system is suitable for studying and characterising lenses in the visible range of the spectrum, even though, with another design including a different sensor, we could shift to the IR spectral region. Moving forward, metasurfaces are expected to gain prominence, due to their lighter weight and tunability, and their small dimension and complicated spatial design make them ideal candidates for maximum resolution techniques such as the one presented in this article.
We have shown the potential of our camera to work in real-time situations. By providing real-time capture capabilities, this type of camera can be utilised to study a diverse range of samples that exhibit temporal variability in their behaviour. As a result, it is possible to introduce these cameras into fields such as microscopy, where cells undergo structural changes sensitive to phase measurements. Another growing field is real-time laser beam characterisation, where the ability to utilise compact systems that can work in diverse positions and allow for quick interchangeability of resolutions can be an asset.
In summary, our results show that the phase camera developed has a wide range of applications and produces outcomes that are comparable to the SH sensor in low spatial frequencies. By working at the maximum resolution of the sensor with a very small effective pixel size, it becomes possible to achieve the highest level of detail in lateral resolution. This, in turn, enhances the sensitivity to potential high-frequency signals. However, it also increases the Z-sensitivity in intermediate situations and at relatively low frequencies. While such signals can be detected by the SH, their accuracy tends to be lower (
Figure 5a).
The future perspectives for phase sensors lie in the development and commercial availability of more instruments that can cover a wider range of fields of application and detect a broader range of spatial frequencies. Such instruments should allow for the simultaneous detection of low- and high-frequency details on the same phase images. In this regard, research studies that combine images captured using techniques like ours, at various propagation distances, represent one of the most important lines of investigation to follow in the coming years.