Vehicle State Estimation Combining Physics-Informed Neural Network and Unscented Kalman Filtering on Manifolds
Abstract
1. Introduction
- We use PINN as a data-driven vehicle dynamics model to establish a VS, using the IMU calibration values as the output. By leveraging the loss calculation method of PINN, the vehicle dynamics can be integrated with the data-driven model, enabling the incorporation of information from multiple sensor sources during vehicle operation. The experimental results in a real vehicle platform indicated that the PINN-based model effectively integrates multiple sensor inputs to achieve improved estimation of the vehicle’s state, surpassing both the physical and neural network-based models.
- Based on the IMU calibration values, we utilize the UKF-M algorithm to estimate the altitude, velocity, and position of the vehicle. By fusing data from multiple sensors, PINN UKFM provided accurate and comprehensive vehicle states that included six-dimensional vehicle dynamics, 3D attitude, speed, and position, which can be used in various vehicle dynamic control systems. For example, the six-dimensional vehicle dynamics can define the chassis motion, which can be used in OCCS. The 3D position can be applied to vehicle navigation in a GNSS-denied environment. The experimental results indicated that the PINN-based model can effectively incorporate multiple sensor inputs to mitigate IMU biases and enhance the accuracy of the existing state-of-the-art integrated navigation algorithm, UKF-M.
2. Estimation Problem
2.1. The Vehicle Model
2.2. The Sensor States
2.3. Problem Definition
3. Methodology
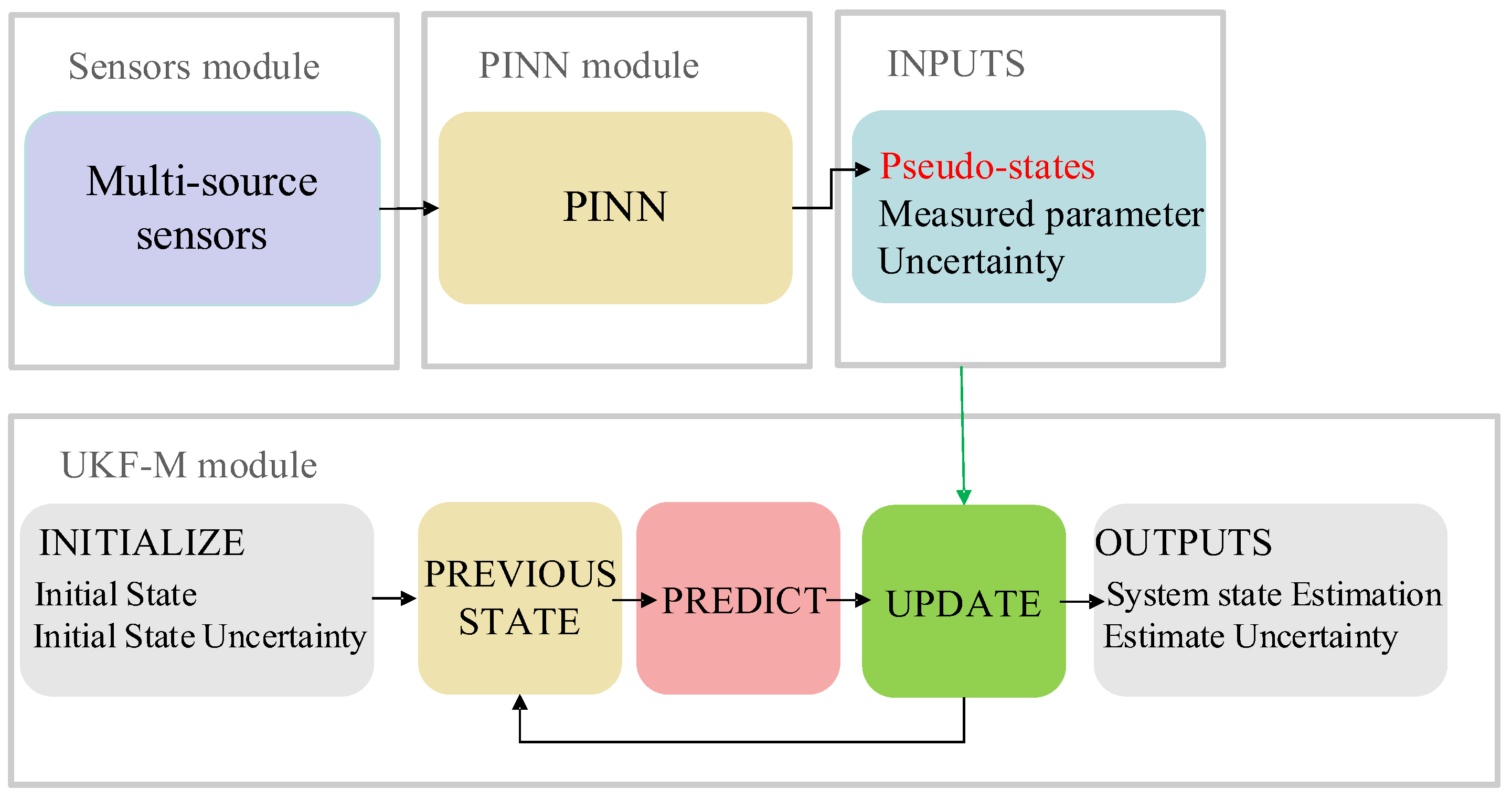
3.1. Structure of the Proposed VSE
3.2. The PINN Module
3.3. The UKF-M Module
4. Experimental Results
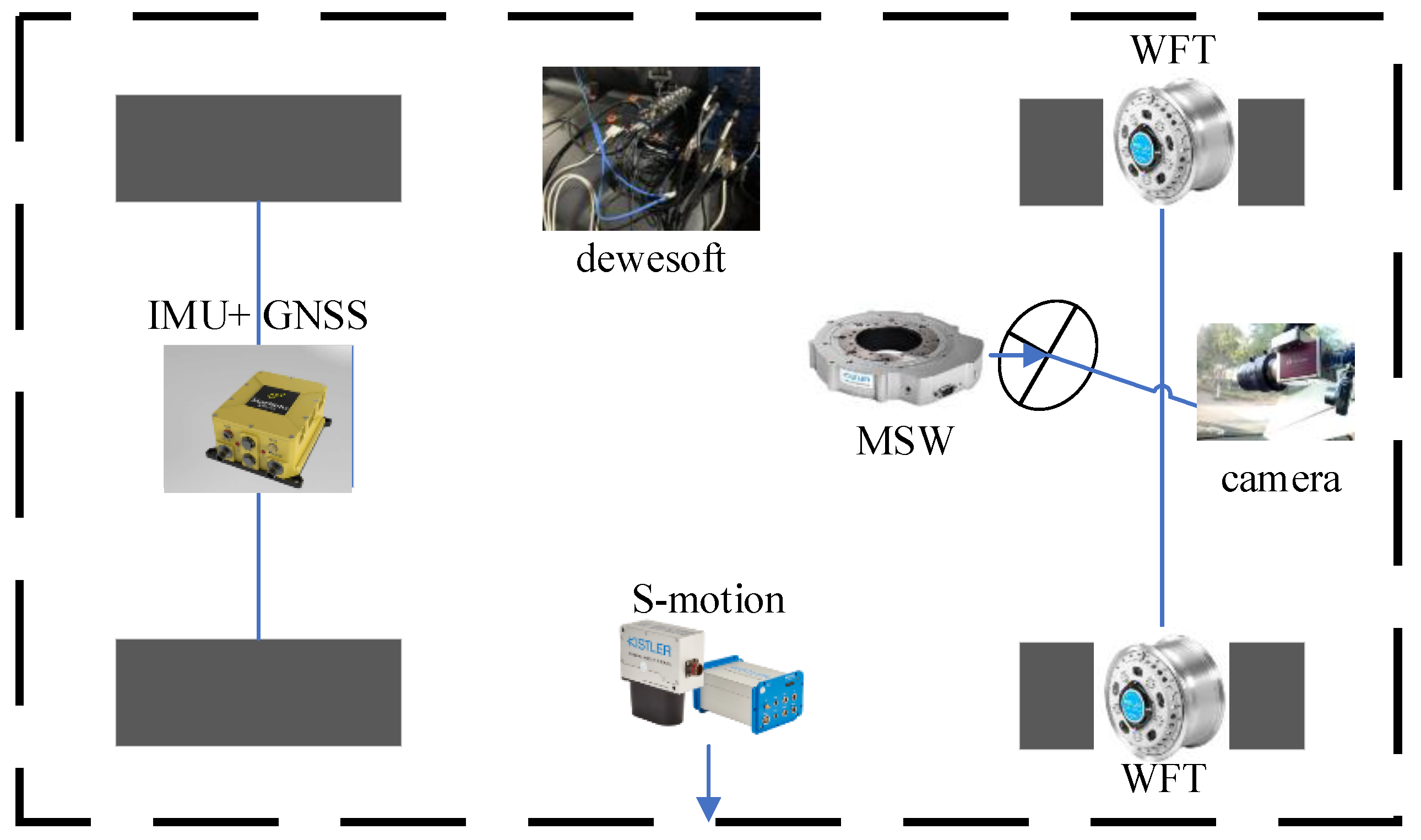
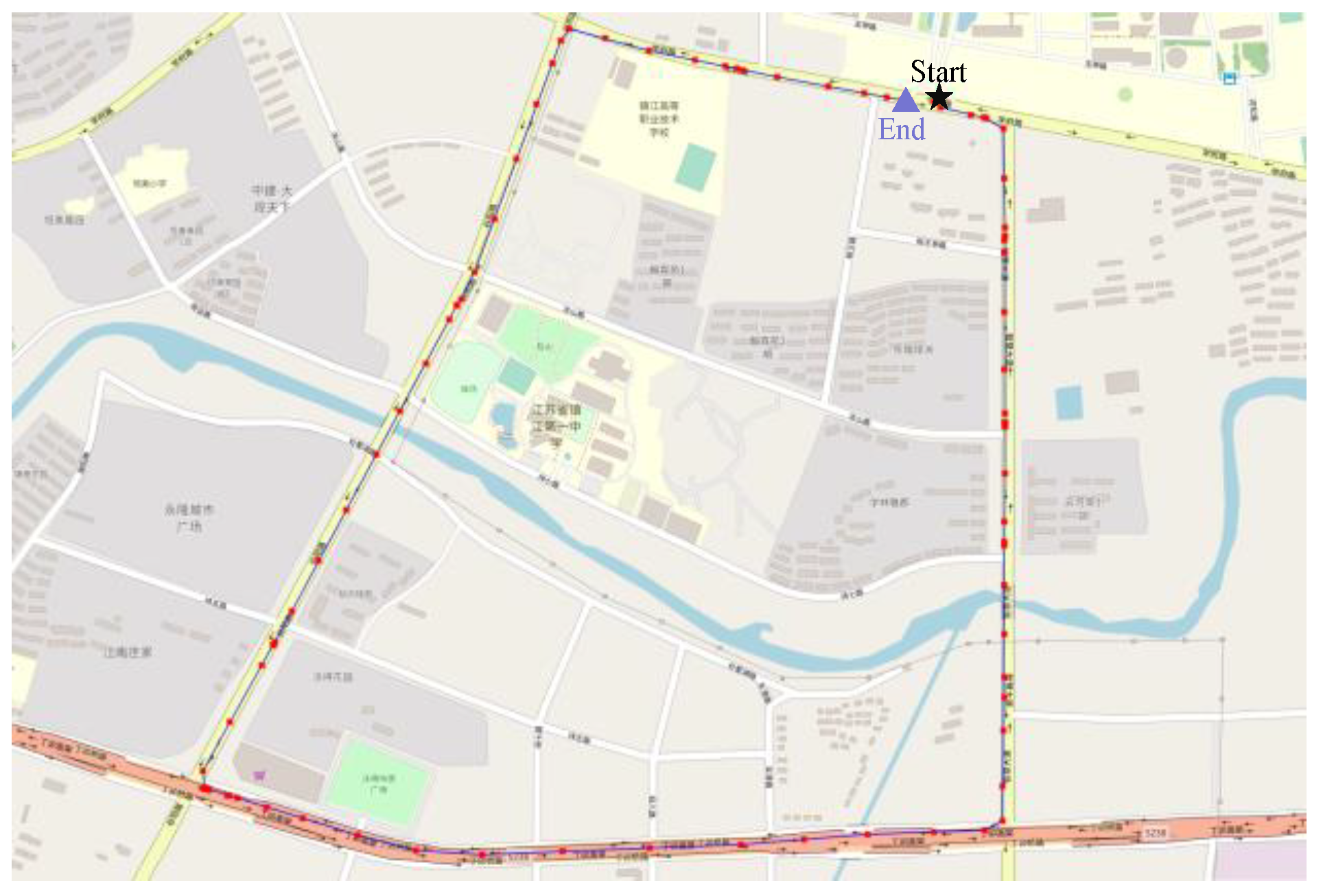
4.1. Vehicle Platform
4.2. Parameter Settings and Training of All Comparative Methods
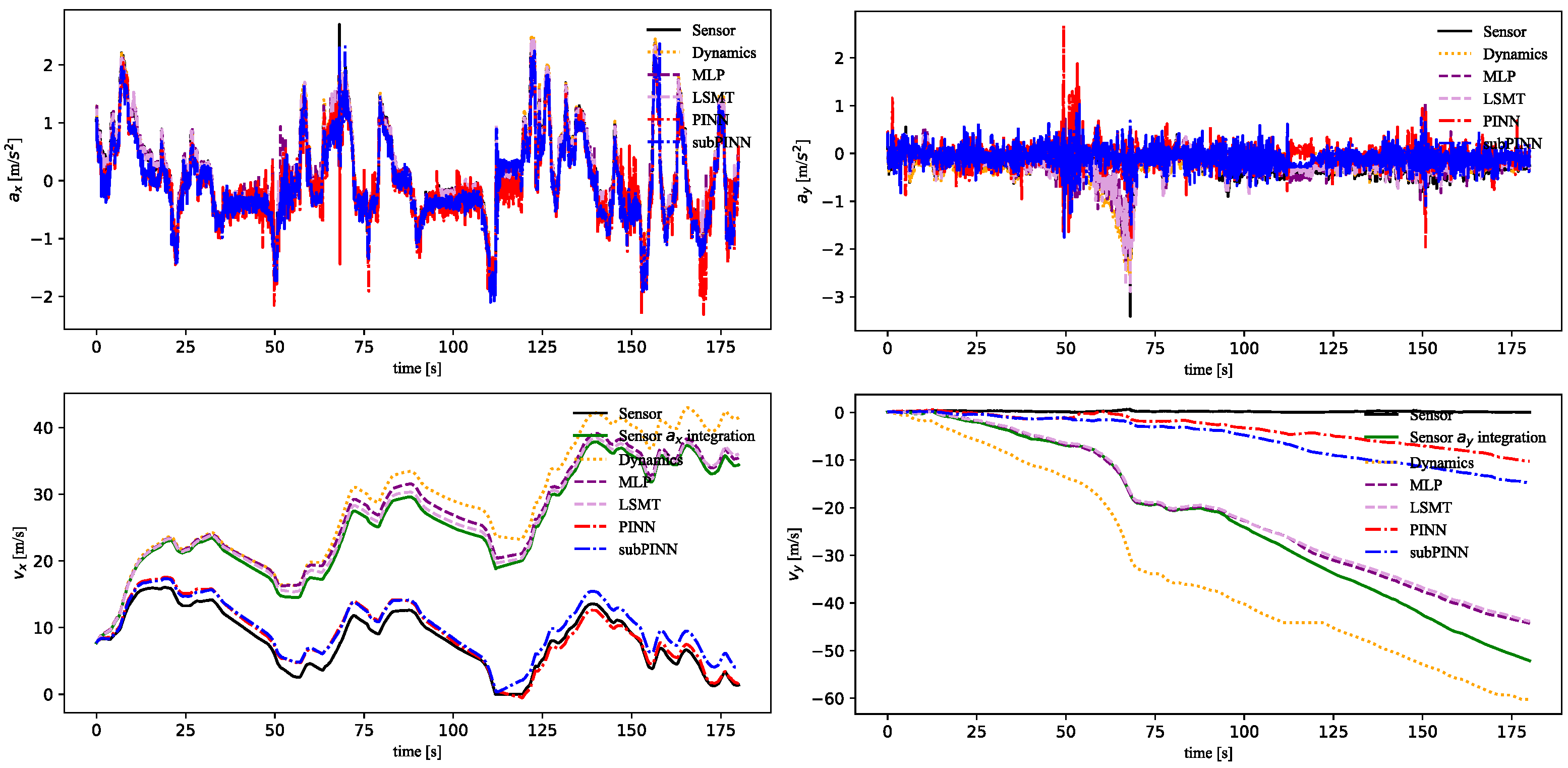
4.3. Validation of the PINN Module
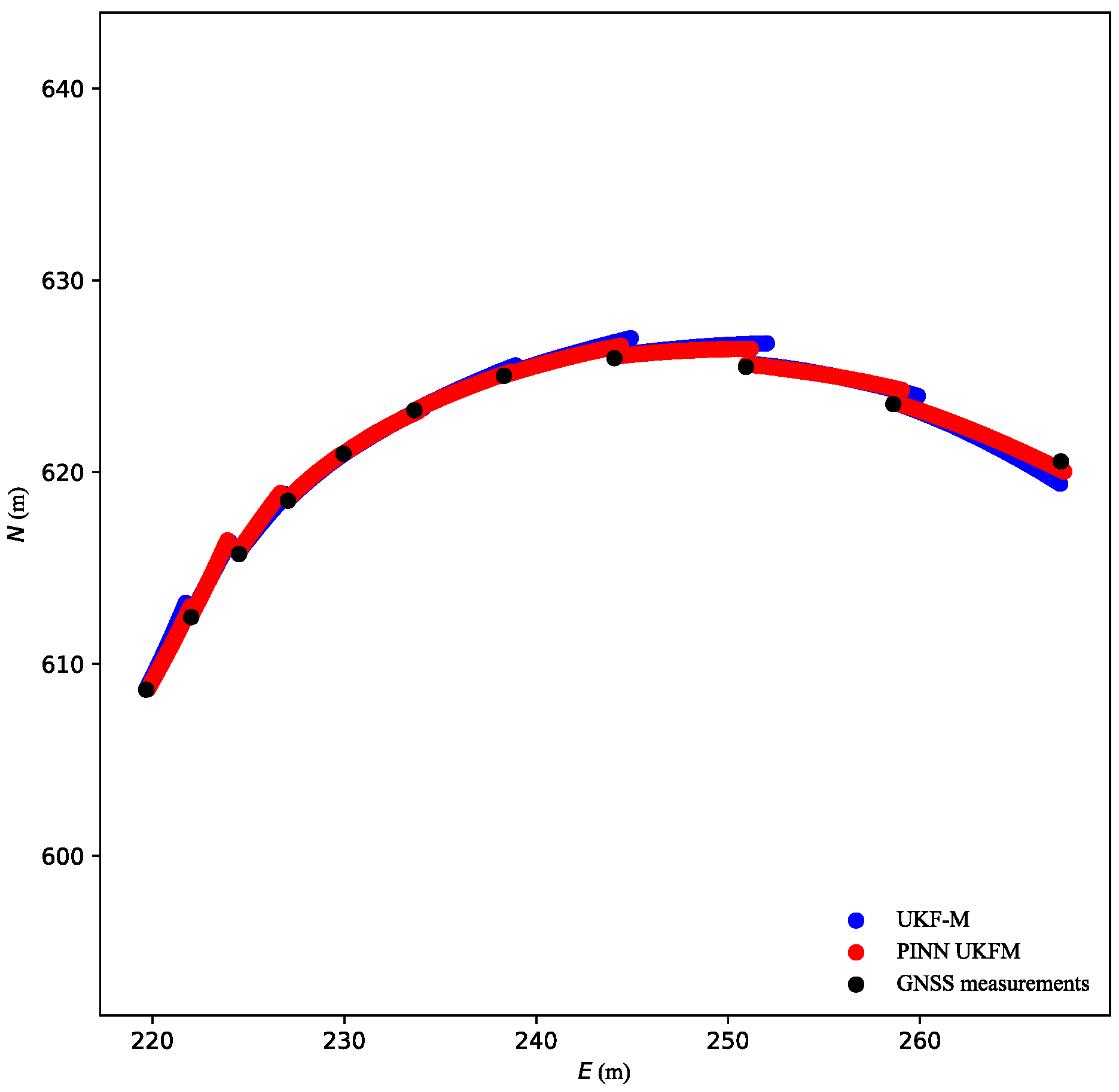
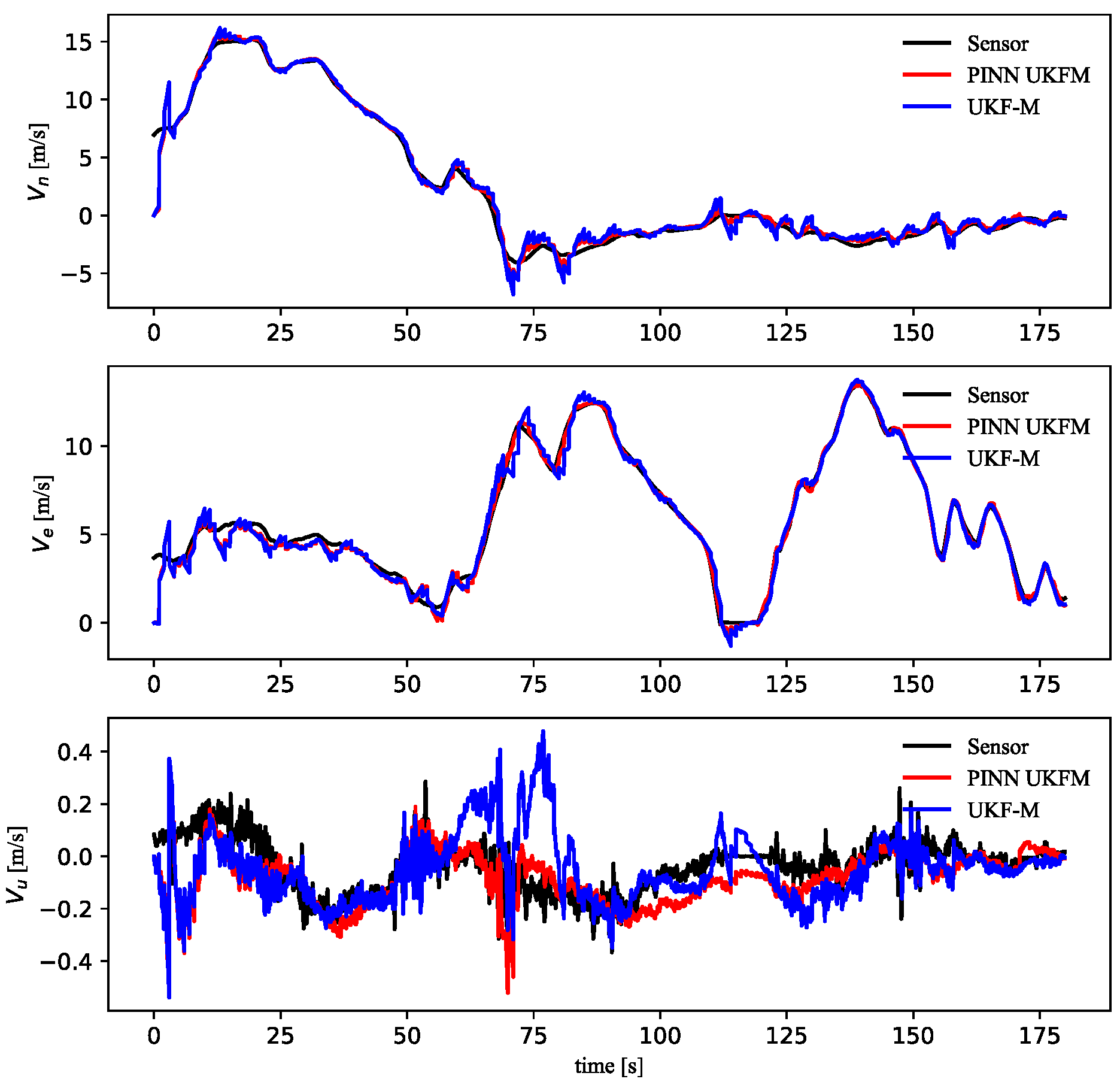
4.4. Validation of PINN UFM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guerrero-Ibáñez, J.; Zeadally, S.; Contreras-Castillo, J. Sensor Technologies for Intelligent Transportation Systems. Sensors 2018, 18, 1212. [Google Scholar] [CrossRef]
- Kissai, M.; Monsuez, B.; Tapus, A. Review of integrated vehicle dynamics control architectures. In Proceedings of the 2017 European Conference on Mobile Robots (ECMR), Paris, France, 6–8 September 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Kissai, M. Optimal Coordination of Chassis Systems for Vehicle Motion Control. Ph.D. Thesis, Université Paris-Saclay (ComUE), Orsay, France, 2019. [Google Scholar]
- Zhang, L.; Zhang, Z.; Wang, Z.; Deng, J.; Dorrell, D. Chassis coordinated control for full X-by-wire vehicles-A review. Chin. J. Mech. Eng. 2021, 34, 42. [Google Scholar] [CrossRef]
- Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Vehicle sideslip angle estimation by fusing inertial measurement unit and global navigation satellite system with heading alignment. Mech. Syst. Signal Process. 2021, 150, 107290. [Google Scholar] [CrossRef]
- Melzi, S.; Sabbioni, E. On the vehicle sideslip angle estimation through neural networks: Numerical and experimental results. Mech. Syst. Signal Process. 2011, 25, 2005–2019. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J.; Guo, M.; Ning, X.; Wang, Y.; Lu, J. Sensor Fusion of GNSS and IMU Data for Robust Localization via Smoothed Error State Kalman Filter. Sensors 2023, 23, 3676. [Google Scholar] [CrossRef]
- Laftchiev, E.I.; Lagoa, C.M.; Brennan, S.N. Vehicle localization using in-vehicle pitch data and dynamical models. IEEE Trans. Intell. Transp. Syst. 2014, 16, 206–220. [Google Scholar] [CrossRef]
- Xia, X.; Xiong, L.; Huang, Y.; Lu, Y.; Gao, L.; Xu, N. Estimation on IMU yaw misalignment by fusing information of automotive onboard sensors. Mech. Syst. Signal Process. 2022, 162, 107993. [Google Scholar] [CrossRef]
- Song, R.; Fang, Y. Vehicle state estimation for INS/GPS aided by sensors fusion and SCKF-based algorithm. Mech. Syst. Signal Process. 2021, 150, 107315. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Z.; Xie, R. Quadratic extended Kalman filter approach for GPS/INS integration. Aerosp. Sci. Technol. 2006, 10, 709–713. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Z.; Zou, C.; Drugge, L.; Nybacka, M. Advanced vehicle state monitoring: Evaluating moving horizon estimators and unscented Kalman filter. IEEE Trans. Veh. Technol. 2019, 68, 5430–5442. [Google Scholar] [CrossRef]
- Hauberg, S.; Lauze, F.; Pedersen, K.S. Unscented Kalman filtering on Riemannian manifolds. J. Math. Imaging Vis. 2013, 46, 103–120. [Google Scholar] [CrossRef]
- Du, S.; Huang, Y.; Lin, B.; Qian, J.; Zhang, Y. A lie group manifold-based nonlinear estimation algorithm and its application to low-accuracy SINS/GNSS integrated navigation. IEEE Trans. Instrum. Meas. 2022, 71, 1–27. [Google Scholar] [CrossRef]
- Chen, T.; Cai, Y.; Chen, L.; Xu, X.; Jiang, H.; Sun, X. Design of vehicle running states-fused estimation strategy using Kalman filters and tire force compensation method. IEEE Access 2019, 7, 87273–87287. [Google Scholar] [CrossRef]
- Park, G.; Choi, S.B.; Hyun, D.; Lee, J. Integrated observer approach using in-vehicle sensors and GPS for vehicle state estimation. Mechatronics 2018, 50, 134–147. [Google Scholar] [CrossRef]
- Šabanovič, E.; Kojis, P.; Šukevičius, Š.; Shyrokau, B.; Ivanov, V.; Dhaens, M.; Skrickij, V. Feasibility of a Neural Network-Based Virtual Sensor for Vehicle Unsprung Mass Relative Velocity Estimation. Sensors 2021, 21, 7139. [Google Scholar] [CrossRef]
- Kim, D.; Min, K.; Kim, H.; Huh, K. Vehicle sideslip angle estimation using deep ensemble-based adaptive Kalman filter. Mech. Syst. Signal Process. 2020, 144, 106862. [Google Scholar] [CrossRef]
- Kim, D.; Kim, G.; Choi, S.; Huh, K. An integrated deep ensemble-unscented Kalman filter for sideslip angle estimation with sensor filtering network. IEEE Access 2021, 9, 149681–149689. [Google Scholar] [CrossRef]
- Vargas-Meléndez, L.; Boada, B.L.; Boada, M.J.L.; Gauchía, A.; Díaz, V. A Sensor Fusion Method Based on an Integrated Neural Network and Kalman Filter for Vehicle Roll Angle Estimation. Sensors 2016, 16, 1400. [Google Scholar] [CrossRef]
- Soriano, M.A.; Khan, F.; Ahmad, R. Two-axis accelerometer calibration and nonlinear correction using neural networks: Design, optimization, and experimental evaluation. IEEE Trans. Instrum. Meas. 2020, 69, 6787–6794. [Google Scholar] [CrossRef]
- Boada, B.L.; Boada, M.J.L.; Diaz, V. Vehicle sideslip angle measurement based on sensor data fusion using an integrated ANFIS and an Unscented Kalman Filter algorithm. Mech. Syst. Signal Process. 2016, 72, 832–845. [Google Scholar] [CrossRef]
- Vicente, B.A.H.; James, S.S.; Anderson, S.R. Linear system identification versus physical modeling of lateral–longitudinal vehicle dynamics. IEEE Trans. Control. Syst. Technol. 2020, 29, 1380–1387. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, X.; Xu, X.; Liu, X.; Liu, J. Deep neural networks with Koopman operators for modeling and control of autonomous vehicles. IEEE Trans. Intell. Veh. 2023, 8, 135–146. [Google Scholar] [CrossRef]
- Spielberg, N.A.; Brown, M.; Kapania, N.R.; Kegelman, J.C.; Gerdes, J.C. Neural network vehicle models for high-performance automated driving. Sci. Robot. 2019, 4, eaaw1975. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.; Xiao, D.; Havyarimana, V.; Jiang, H.; Liu, D.; Wang, D.; Zeng, F. Toward accurate vehicle state estimation under non-Gaussian noises. IEEE Internet Things J. 2019, 6, 10652–10664. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Xu, P.-F.; Han, C.-B.; Cheng, H.-X.; Cheng, C.; Ge, T. A Physics-Informed Neural Network for the Prediction of Unmanned Surface Vehicle Dynamics. J. Mar. Sci. Eng. 2022, 10, 148. [Google Scholar] [CrossRef]
- Franklin, T.S.; Souza, L.S.; Fontes, R.M.; Martins, M.A. A Physics-Informed Neural Networks (PINN) oriented approach to flowmetering in oil wells: An ESP lifted oil well system as a case study. Digit. Chem. Eng. 2022, 5, 100056. [Google Scholar] [CrossRef]
- Wong, J.C.; Chiu, P.H.; Ooi, C.C.; Da, M.H. Robustness of Physics-Informed Neural Networks to Noise in Sensor Data. arXiv 2022, arXiv:2211.12042. [Google Scholar]
- Arnold, F.; King, R. State–space modeling for control based on physics-informed neural networks. Eng. Appl. Artif. Intell. 2021, 101, 104195. [Google Scholar] [CrossRef]
- Alatise, M.B.; Hancke, G.P. Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter. Sensors 2017, 17, 2164. [Google Scholar] [CrossRef]
- Gräber, T.; Lupberger, S.; Unterreiner, M.; Schramm, D. A hybrid approach to side-slip angle estimation with recurrent neural networks and kinematic vehicle models. IEEE Trans. Intell. Veh. 2018, 4, 39–47. [Google Scholar] [CrossRef]
- Brossard, M.; Barrau, A.; Bonnabel, S. A code for unscented Kalman filtering on manifolds (UKF-M). In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 5701–5708. [Google Scholar]
- Zhang, W.; Al Kobaisi, M. On the Monotonicity and Positivity of Physics-Informed Neural Networks for Highly Anisotropic Diffusion Equations. Energies 2022, 15, 6823. [Google Scholar] [CrossRef]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Rai, R.; Sahu, C.K. Driven by data or derived through physics? a review of hybrid physics guided machine learning techniques with cyber-physical system (cps) focus. IEEE Access 2020, 8, 71050–71073. [Google Scholar] [CrossRef]
- Fioretto, F.; Van Hentenryck, P.; Mak, T.W.; Tran, C.; Baldo, F.; Lombardi, M. Lagrangian duality for constrained deep learning. In Proceedings of the Applied Data Science and Demo Track: European Conference, ECML PKDD 2020, Part, V.. Ghent, Belgium, 14–18 September 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 118–135. [Google Scholar]
- Bajaj, C.; McLennan, L.; Andeen, T.; Roy, A. Recipes for when Physics Fails: Recovering Robust Learning of Physics Informed Neural Networks. Mach. Learn. Sci. Technol. 2023, 4, 015013. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y. A Dual-Dimer method for training physics-constrained neural networks with minimax architecture. Neural Netw. 2021, 136, 112–125. [Google Scholar] [CrossRef]
- Chen, T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D.K. Neural ordinary differential equations. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Munich, Germany, 8–14 September 2018; pp. 6571–6583. [Google Scholar]
- Yuan, L.; Ni, Y.Q.; Deng, X.Y.; Hao, S. A-PINN: Auxiliary physics informed neural networks for forward and inverse problems of nonlinear integro-differential equations. J. Comput. Phys. 2022, 462, 111260. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Deo, N.; Trivedi, M.M. Convolutional social pooling for vehicle trajectory prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1468–1476. [Google Scholar]
- Kong, J.; Pfeiffer, M.; Schildbach, G.; Borrelli, F. Kinematic and dynamic vehicle models for autonomous driving control design. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Republic of Korea, 28 June–1 July 2015; pp. 1094–1099. [Google Scholar]
- Gao, Z.; Wang, J.; Wang, D. Dynamic modeling and steering performance analysis of active front steering system. Procedia Eng. 2011, 15, 1030–1035. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. Intrinsic filtering on Lie groups with applications to attitude estimation. IEEE Trans. Autom. Control 2014, 60, 436–449. [Google Scholar] [CrossRef]
- Barfoot, T.D.; Furgale, P.T. Associating uncertainty with three-dimensional poses for use in estimation problems. IEEE Trans. Robot. 2014, 30, 679–693. [Google Scholar] [CrossRef]
- Brossard, M.; Bonnabel, S.; Condomines, J.P. Unscented Kalman filtering on Lie groups. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2485–2491. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. Signal Process. Sens. Fusion Target Recognit. VI. Spie 1997, 3068, 182–193. [Google Scholar]
- Liu, Z.; Cai, Y.; Wang, H.; Chen, L.; Gao, H.; Jia, Y.; Li, Y. Robust target recognition and tracking of self-driving cars with radar and camera information fusion under severe weather conditions. IEEE Trans. Intell. Transp. Syst. 2021, 23, 6640–6653. [Google Scholar] [CrossRef]
- Yin, C.; Jiang, H.; Tang, B.; Zhu, C.; Lin, Z.; Yin, Y. Handling Stability and Energy-Saving of Commercial Vehicle Electronically Controlled Hybrid Power Steering System. J. Jiangsu Univ. Nat. Sci. 2019, 40, 269. [Google Scholar]
- Wang, H.; Ming, L.; Yin, C.; Long, C. Vehicle target detection algorithm based on fusion of lidar and millimeter wave radar. J. Jiangsu Univ. Nat. Sci. 2021, 4, 003. [Google Scholar]
- Wang, H.; Chen, Z.; Cai, Y.; Chen, L.; Li, Y.; Sotelo, M.A.; Li, Z. Voxel-rcnn-complex: An effective 3-d point cloud object detector for complex traffic conditions. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Cai, Y.; Chen, L.; Li, Y.; Sotelo, M.A.; Li, Z. SFNet-N: An improved SFNet algorithm for semantic segmentation of low-light autonomous driving road scenes. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21405–21417. [Google Scholar] [CrossRef]
- Wang, H.; Cheng, L.; Yin, C.; Long, C.; You, H. Real-time visual vehicle detection method based on DSP platform. J. Jiangsu Univ. Nat. Sci. 2019, 1, 001. [Google Scholar]
- Hermansdorfer, L.; Trauth, R.; Betz, J.; Lienkamp, M. End-to-end neural network for vehicle dynamics modeling. In Proceedings of the 2020 6th IEEE Congress on Information Science and Technology (CiSt), Agadir-Essaouira, Morocco, 5–12 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 407–412. [Google Scholar]
- Xu, J.; Luo, Q.; Xu, K.; Xiao, X.; Yu, S.; Hu, J.; Miao, J.; Wang, J. An automated learning-based procedure for large-scale vehicle dynamics modeling on baidu apollo platform. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Ro- bots and Systems (IROS), Macau, China, 3–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5049–5056. [Google Scholar]
- Nie, X.; Min, C.; Pan, Y.; Li, Z.; Królczyk, G. An Improved Deep Neural Network Model of Intelligent Vehicle Dynamics via Linear Decreasing Weight Particle Swarm and Invasive Weed Optimization Algorithms. Sensors 2022, 22, 4676. [Google Scholar] [CrossRef]







| Sensor Types | Signal Name | Symbol | Units |
|---|---|---|---|
| GNSS | Easting | ||
| GNSS | Northing | ||
| GNSS | Altitude | ||
| GNSS | UTM velocity | ||
| IMU | Roll angle | rad | |
| IMU | Pitch angle | rad | |
| IMU | Yaw angle | rad | |
| IMU | Vertical velocity | ||
| S-Motion | Longitudinal velocity | ||
| S-Motion | Longitudinal acceleration | ||
| S-Motion | Lateral velocity | ||
| S-Motion | Longitudinal acceleration | ||
| S-Motion | Vertical acceleration | ||
| S-Motion | Roll rate | rad/s | |
| S-Motion | Pitch rate | rad/s | |
| S-Motion | Yaw rate | rad/s | |
| WFT | Wheel force | ||
| WFT | Wheel torque | ||
| MSW | Steering wheel angle | rad |
| Model | ||||||
| MLP | 0.1117 | 0.1524 | 0.2729 | 0.0164 | 0.0171 | 0.0174 |
| LSTM | 0.1167 | 0.1444 | 0.2626 | 0.0171 | 0.0175 | 0.0167 |
| PINN | 0.2733 | 0.3904 | 0.2806 | 0.0110 | 0.0084 | 0.0058 |
| subPINN | 0.2301 | 0.3606 | 0.2167 | 0.0076 | 0.0049 | 0.0036 |
| Model | ||||||
| MLP | 20.2365 | 25.2757 | 2.7479 | 0.1027 | 0.1865 | 0.3334 |
| LSTM | 19.6955 | 24.8413 | 0.5609 | 0.0613 | 0.1391 | 0.3856 |
| PINN | 1.3007 | 4.6707 | 0.5609 | 0.0806 | 0.0429 | 0.0475 |
| subPINN | 1.8171 | 7.3559 | 0.4169 | 0.0312 | 0.0113 | 0.0217 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, C.; Cai, Y.; Wang, H.; Sun, X.; Chen, L. Vehicle State Estimation Combining Physics-Informed Neural Network and Unscented Kalman Filtering on Manifolds. Sensors 2023, 23, 6665. https://doi.org/10.3390/s23156665
Tan C, Cai Y, Wang H, Sun X, Chen L. Vehicle State Estimation Combining Physics-Informed Neural Network and Unscented Kalman Filtering on Manifolds. Sensors. 2023; 23(15):6665. https://doi.org/10.3390/s23156665
Chicago/Turabian StyleTan, Chenkai, Yingfeng Cai, Hai Wang, Xiaoqiang Sun, and Long Chen. 2023. "Vehicle State Estimation Combining Physics-Informed Neural Network and Unscented Kalman Filtering on Manifolds" Sensors 23, no. 15: 6665. https://doi.org/10.3390/s23156665
APA StyleTan, C., Cai, Y., Wang, H., Sun, X., & Chen, L. (2023). Vehicle State Estimation Combining Physics-Informed Neural Network and Unscented Kalman Filtering on Manifolds. Sensors, 23(15), 6665. https://doi.org/10.3390/s23156665







