Adaptive Optics Tip-Tilt Correction Based on Smith Predictor and Filter-Optimized Linear Active Disturbance Rejection Control Method
Abstract
:1. Introduction
2. AO Tip-Tilt Correction Principle Based on the FLADRC–Smith Control
2.1. Mathematical Model of AO Tip-Tilt Correction
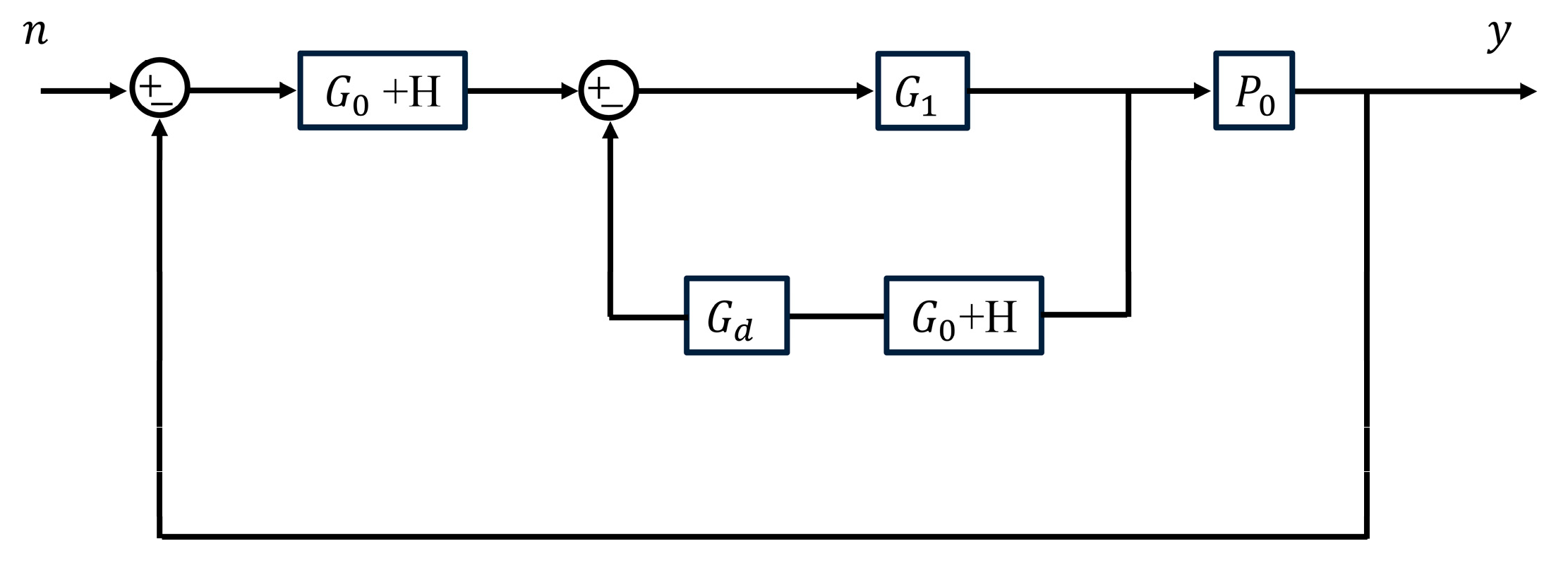
2.2. Design of FLADRC–Smith Control Method
2.3. Bandwidth Analysis
2.4. Noise Analysis
3. Results
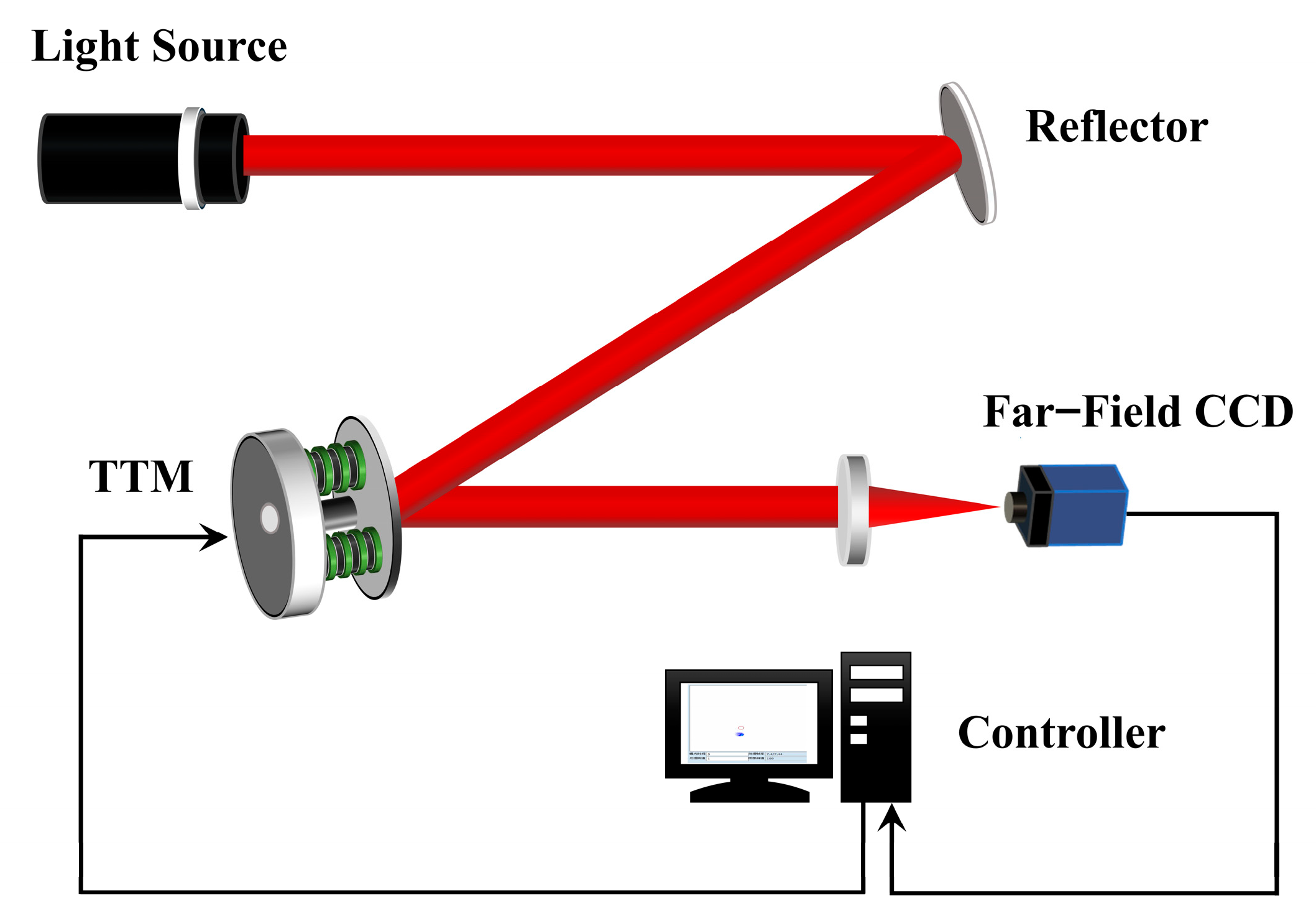
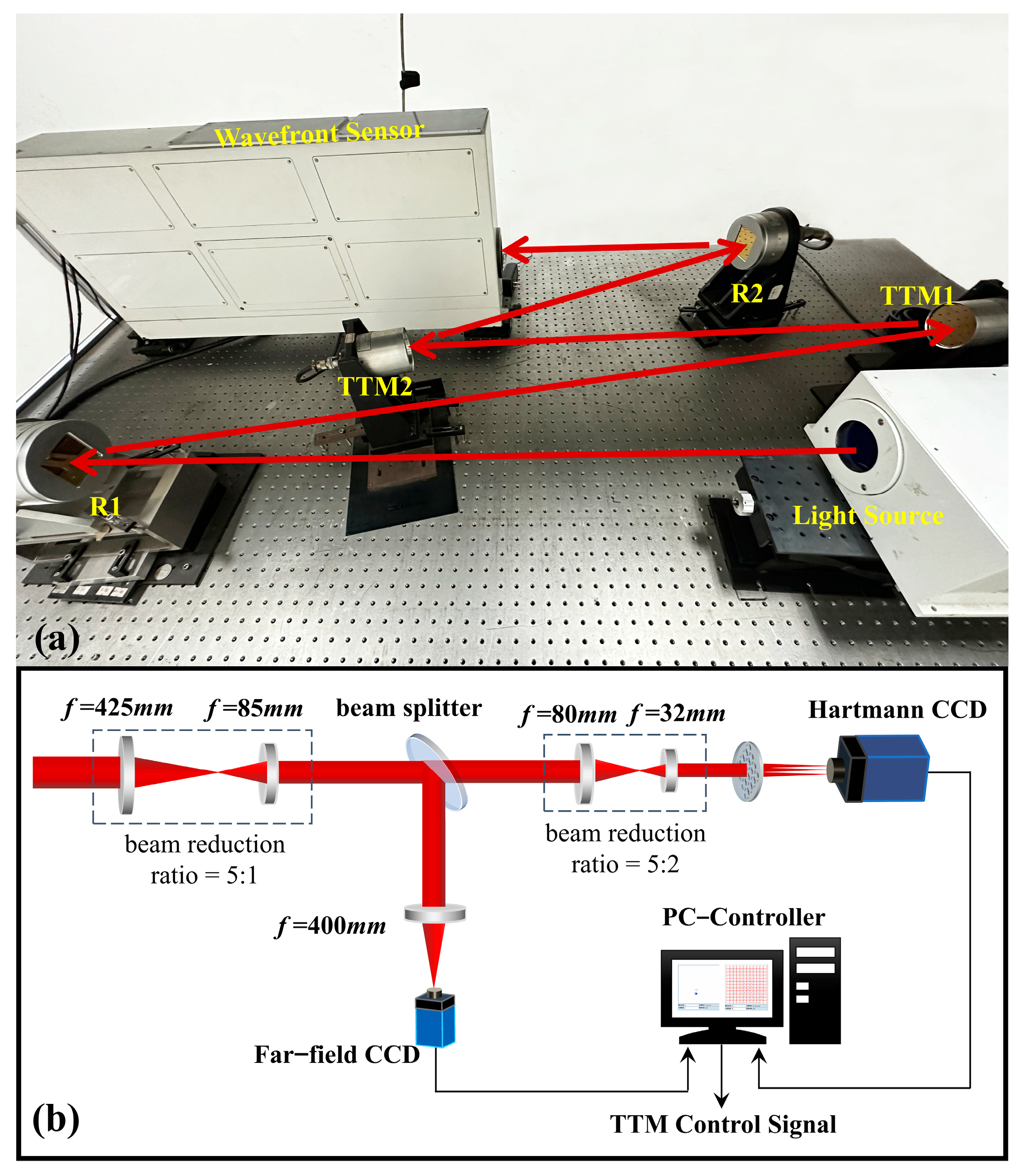
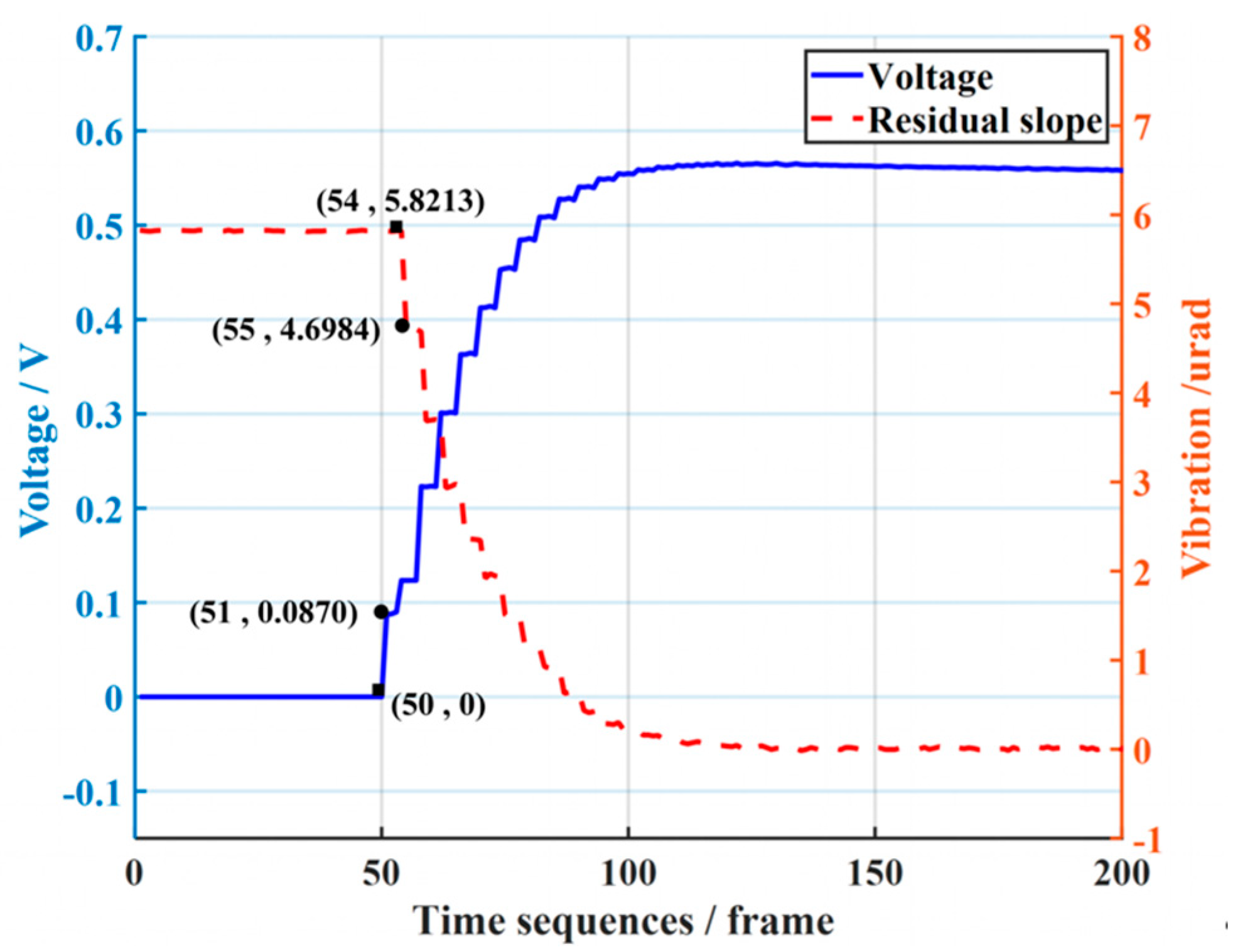
3.1. AO Tip-Tilt Correction Experimental Platform
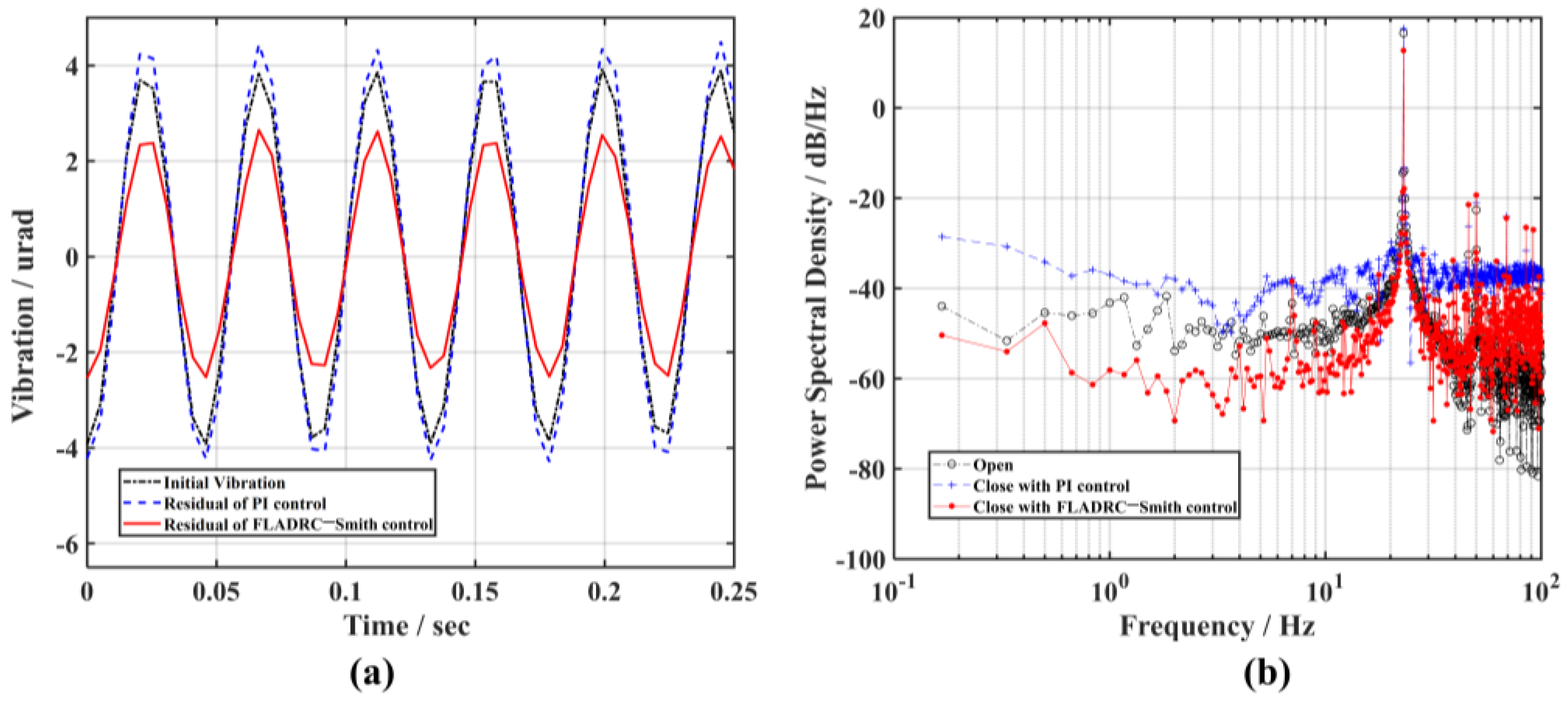
3.2. Comparison with PI Control Method
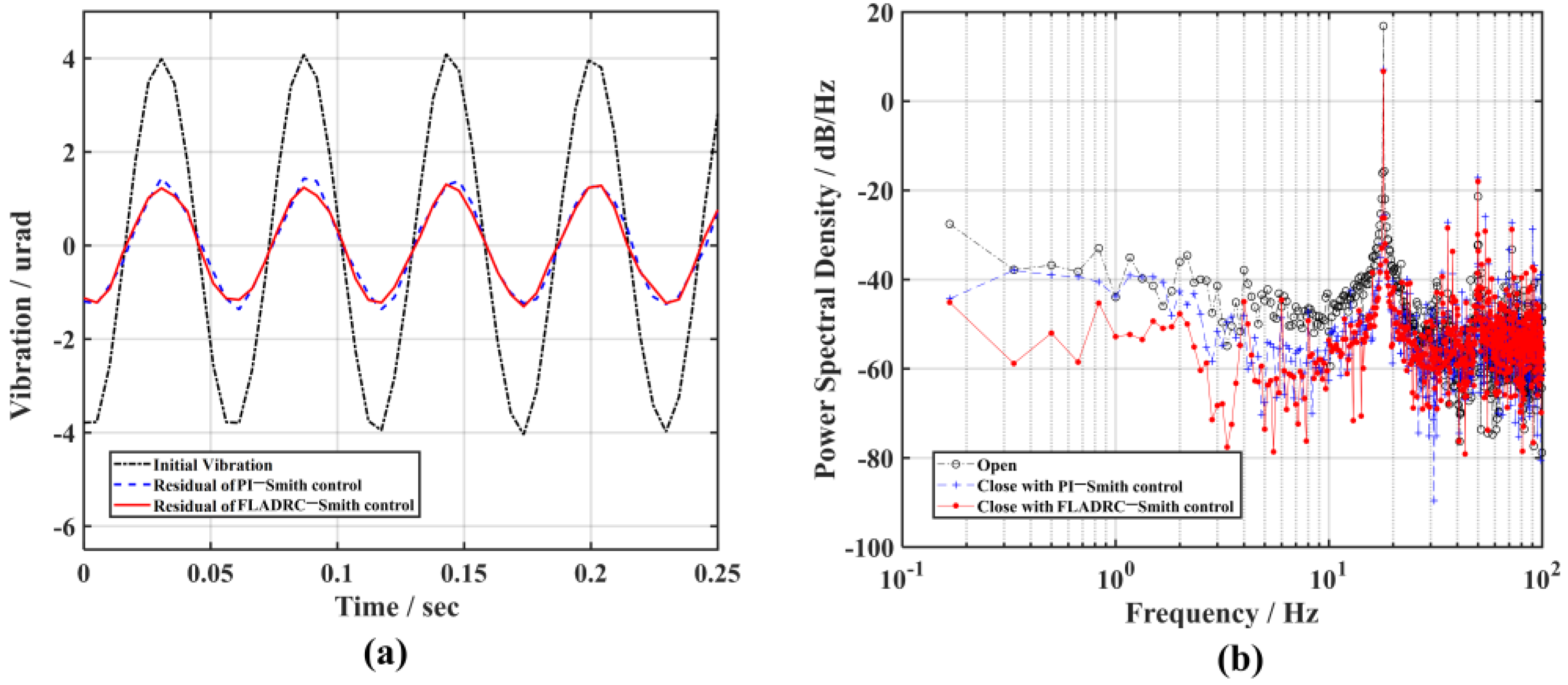
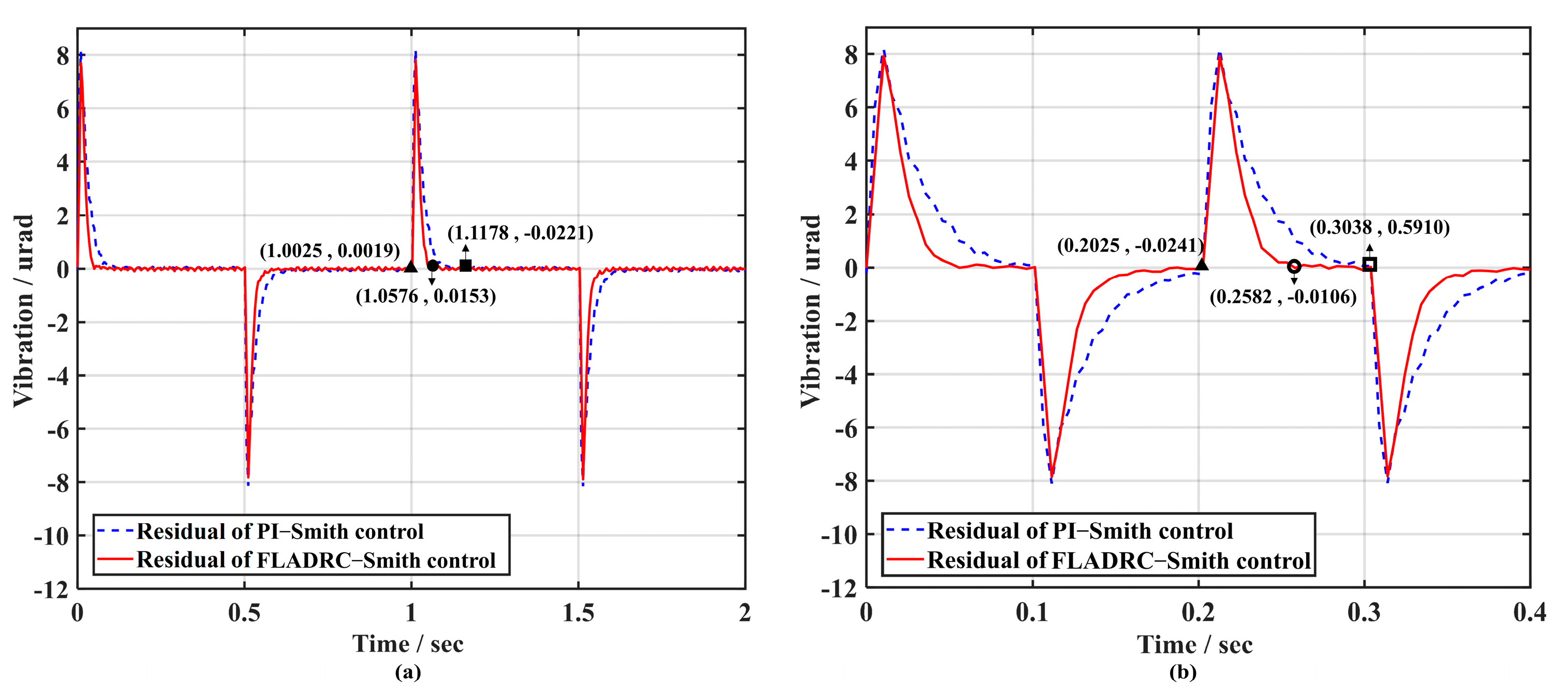
3.3. Comparison with PI–Smith Control Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AO | adaptive optics |
| TTM | tip-tilt mirror |
| PI | proportional–integral |
| PI–Smith | Smith predictor and proportional–integral |
| LADRC | linear active disturbance rejection |
| FLADRC–Smith | Smith predictor and filter-optimized linear active disturbance rejection |
References
- Jiang, W. Overview of adaptive optics development. Opto-Electron. Eng. 2018, 45, 170489. [Google Scholar] [CrossRef]
- Samarkin, V.V.E.; Alexandrov, A.G.; Galaktionov, I.V.; Kudryashov, A.V.E.; Nikitin, A.N.; Rukosuev, A.L.V.; Toporovsky, V.V.; Sheldakova, Y.V. Large-aperture adaptive optical system for correcting wavefront distortions of a petawatt Ti: Sapphire laser beam. Quant. Electron. 2022, 52, 187. [Google Scholar] [CrossRef]
- Zhou, Z.; Feng, Z.; Huang, L.; Xian, H. Structure Design of Compact Piezoelectric Fast Steering Mirror with High Performance. Chin. J. Lasers 2021, 48, 1305002. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, K.; Yang, F.; Wen, X.; Huang, Y.; Guo, S.; Ren, Y.; Li, T. Observation and compensation control of sliding mode compound layered interference for the fast steering mirror system. Opto-Electron. Eng. 2023, 50, 220330. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, Q.; Liao, Y.; Gan, Y.; Shen, F.; Li, X. Research on Beam Jitter Control Technology Base on Hybrid Adaptive Filter. Laser Optoelectron. Prog. 2021, 58, 1314004. [Google Scholar] [CrossRef]
- Fan, M.; Huang, L.; Li, M.; Rao, C. High-bandwidth control of piezoelectric steering mirror for suppression of laser beam jitter. Acta Phys. Sin. 2016, 65, 024209. [Google Scholar] [CrossRef]
- Su, C.; Dong, L.; Lai, B.; Chen, S.; Zhao, W.; Yang, K.; Ma, S.; Fan, X.; Wen, L.; Xu, B. Adaptive beam clean-up of high power slab lasers using least-squares wavefront reconstruction algorithm with performance-based filtering. Opt. Commun. 2021, 490, 126886. [Google Scholar] [CrossRef]
- Li, X.; Jiang, W. Effective bandwidth analysis of adaptive optics control system. Acta Opt. Sin. 1997, 12, 1697–1702. [Google Scholar]
- Guo, Y.; Zhong, L.; Min, L.; Wang, J.; Wu, Y.; Chen, K.; Wei, K.; Rao, C. Adaptive optics based on machine learning: A review. Opto-Electron. Adv. 2022, 5, 200082. [Google Scholar] [CrossRef]
- Nie, K.; Ren, W.; Zhou, X.; Mao, Y. Virtual dual-loop feedback control with model-construction Linear extended state observer for free space optical communication. Sensors 2019, 19, 3846. [Google Scholar] [CrossRef] [Green Version]
- Xiang, W.; Yang, P.; Wang, S.; Xu, B.; Liu, H. Underwater image enhancement based on red channel weighted compensation and gamma correction model. Opto-Electron. Adv. 2018, 1, 180024. [Google Scholar] [CrossRef]
- Dong, R.; Ai, Y.; Xiao, Y.; Shan, X. Design and communication experiment of fine tracking system for free space optic. Infrared Laser Eng. 2012, 41, 2718–2722. [Google Scholar]
- Glück, M.; Pott, J.U.; Sawodny, O. Investigations of an accelerometer-based disturbance feedforward control for vibration suppression in adaptive optics of large telescopes. Publ. Astron. Soc. Pac. 2017, 129, 065001. [Google Scholar] [CrossRef]
- Yang, K.; Yang, P.; Chen, S.; Wang, S.; Wen, L.; Dong, L.; He, X.; Lai, B.; Yu, X.; Xu, B. Vibration identification based on Levenberg–Marquardt optimization for mitigation in adaptive optics systems. Appl. Opt. 2018, 57, 2820–2826. [Google Scholar] [CrossRef] [PubMed]
- Luo, Q.; Luo, X.; Li, X. Optical axis jitter rejection for double overlapped adaptive optics systems. Opt. Rev. 2016, 23, 273–283. [Google Scholar] [CrossRef]
- Ruan, Y.; Xu, T.; Yang, T.; Tang, T. Position-rate control for the time delay control system of tip-tilt mirror. Opto-Electron. Eng. 2020, 47, 49–55. [Google Scholar] [CrossRef]
- Zhao, X.; Ma, C. Design and simulation of the adaptive optics system based on mixed H2/Hꝏ control. Acta Opt. Sin. 2014, 43, 1201003. [Google Scholar] [CrossRef]
- Yang, K.; Yang, P.; Wang, S.; Dong, L.; Xu, B. Tip-tilt disturbance model identification based on non-linear least squares fitting for Linear Quadratic Gaussian control. Opt. Commun. 2018, 415, 31–38. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y.; Kong, L.; Chen, K.; Rao, C. Hybrid Control Method for Adaptive Optics System. Laser Optoelectron. Prog. 2020, 57, 230101. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y.; Kong, L.; Rao, C. Experimental demonstration of LQG control with disturbance mitigation on multiple modes in adaptive optics system. Optik 2020, 202, 163594. [Google Scholar] [CrossRef]
- Li, J.; Dong, Y.; Lin, B.; Liu, Y. Improved active disturbance rejection control algorithm based on optical communication fast mirror. Laser Optoelectron. Prog. 2023, 60, 0706007. [Google Scholar] [CrossRef]
- Kong, L.; Cheng, T.; Su, C.; Yang, K.; Zhao, M.; Wang, S.; Yang, P. A tip-tilt mirror control method using the Smith predictor and filter-based linear active disturbance rejection. Chin. J. Lasers 2023, 50, 1305001. [Google Scholar] [CrossRef]
- Chu, X.; Qian, J. Research on discretization problem of Smith predictor. Ind. Control. Comput. 2010, 3, 60–62. [Google Scholar]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Yang, K.; Su, C.; Guo, S.; Wang, S.; Cheng, T.; Yang, P. Adaptive Optics Tip-Tilt Correction Based on Smith Predictor and Filter-Optimized Linear Active Disturbance Rejection Control Method. Sensors 2023, 23, 6724. https://doi.org/10.3390/s23156724
Kong L, Yang K, Su C, Guo S, Wang S, Cheng T, Yang P. Adaptive Optics Tip-Tilt Correction Based on Smith Predictor and Filter-Optimized Linear Active Disturbance Rejection Control Method. Sensors. 2023; 23(15):6724. https://doi.org/10.3390/s23156724
Chicago/Turabian StyleKong, Lingxi, Kangjian Yang, Chunxuan Su, Sicheng Guo, Shuai Wang, Tao Cheng, and Ping Yang. 2023. "Adaptive Optics Tip-Tilt Correction Based on Smith Predictor and Filter-Optimized Linear Active Disturbance Rejection Control Method" Sensors 23, no. 15: 6724. https://doi.org/10.3390/s23156724
APA StyleKong, L., Yang, K., Su, C., Guo, S., Wang, S., Cheng, T., & Yang, P. (2023). Adaptive Optics Tip-Tilt Correction Based on Smith Predictor and Filter-Optimized Linear Active Disturbance Rejection Control Method. Sensors, 23(15), 6724. https://doi.org/10.3390/s23156724





