Preliminary Test for 3D Surface Strain Measurement in the Tower and Foundation of Offshore Wind Turbines Using DOFS
Abstract
:1. Introduction
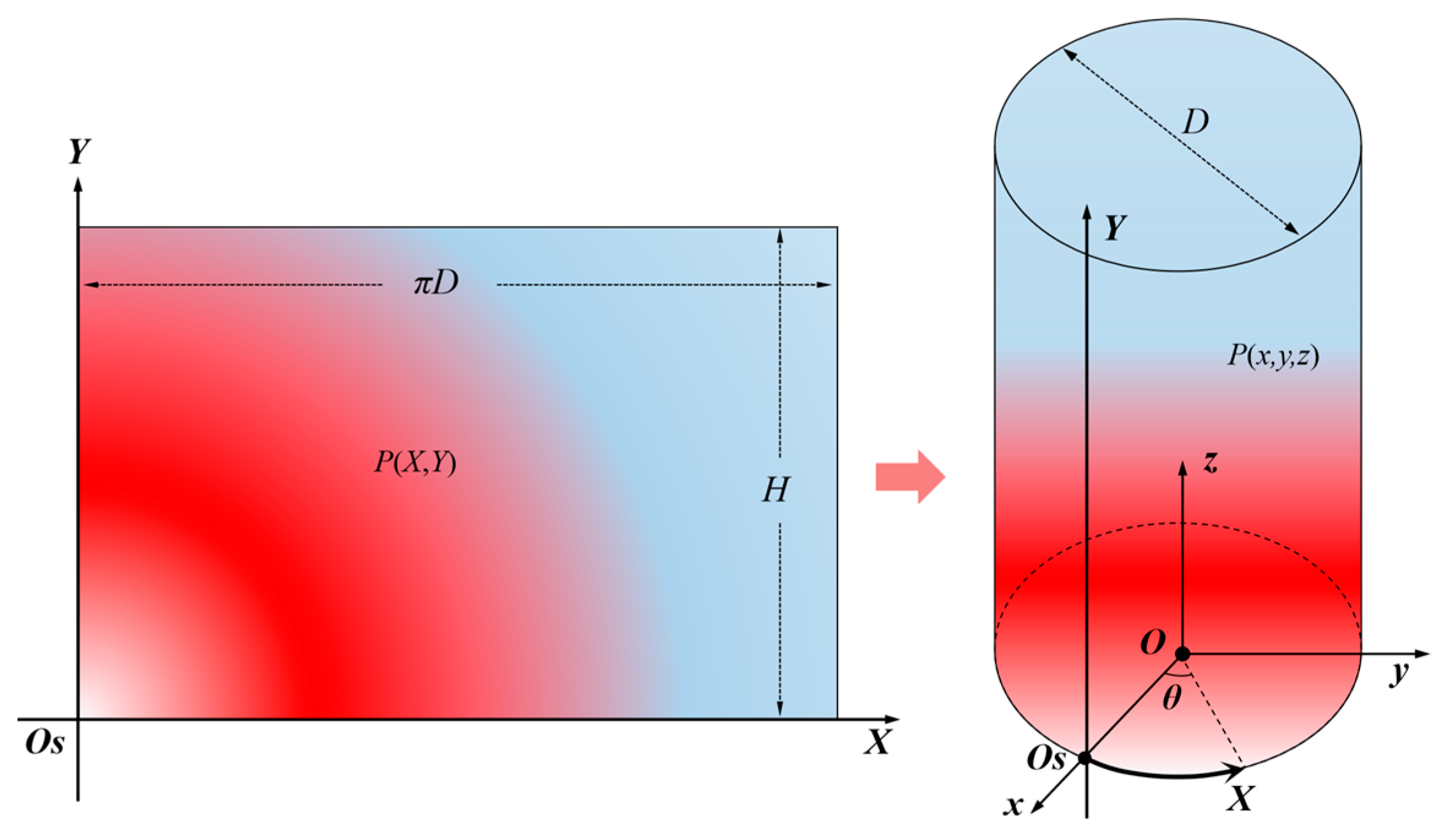
2. The Temperature/Strain Field Reconstruction Method
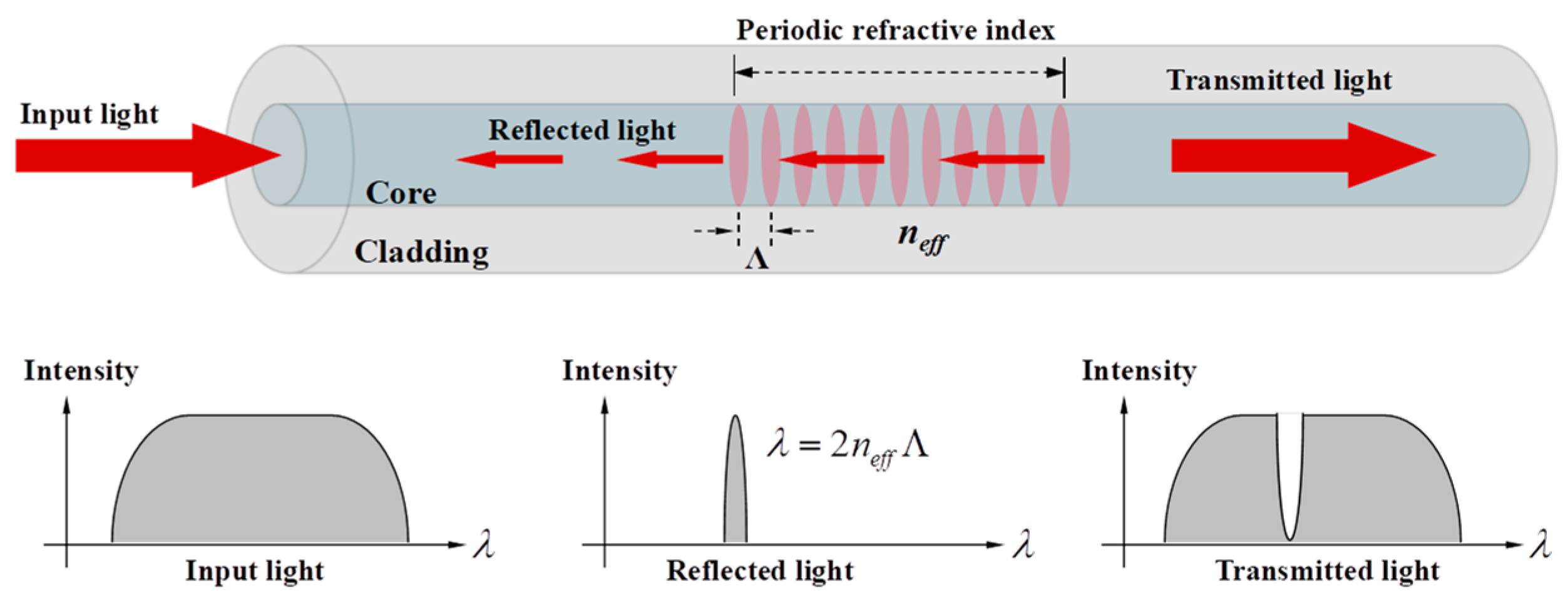
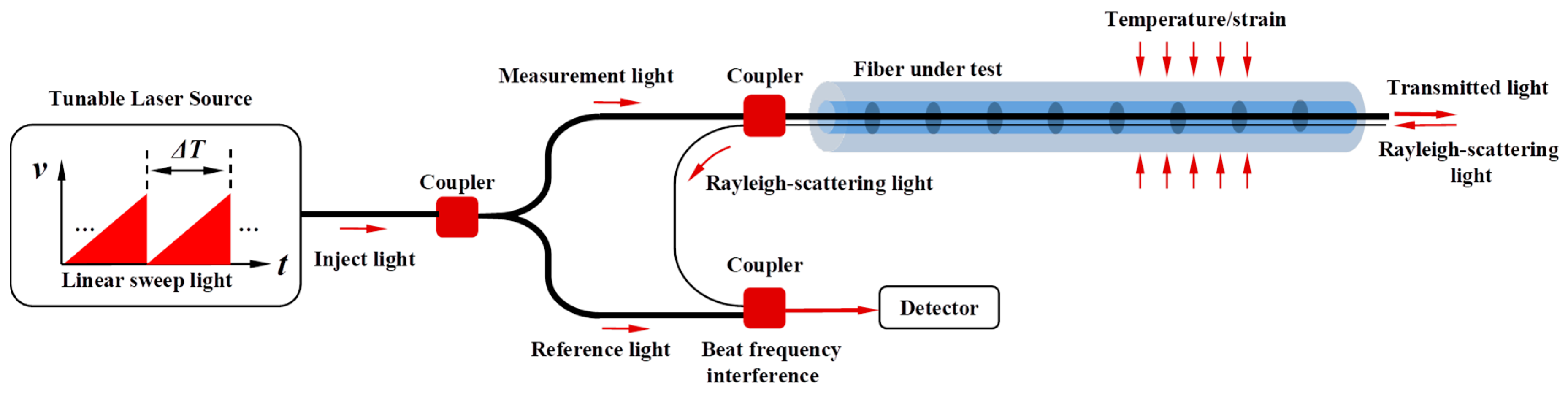
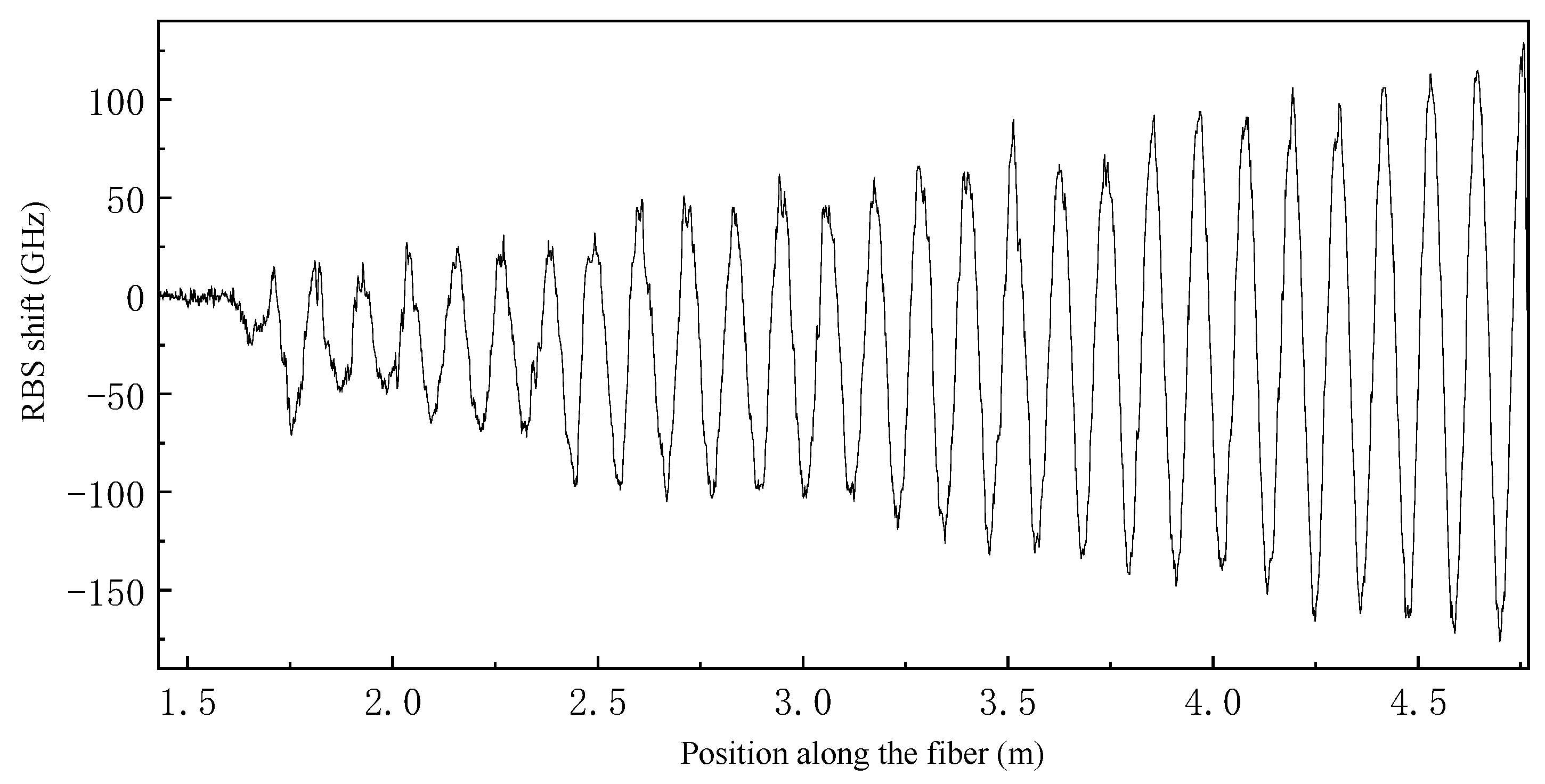
2.1. Optical Fiber Sensing Principle
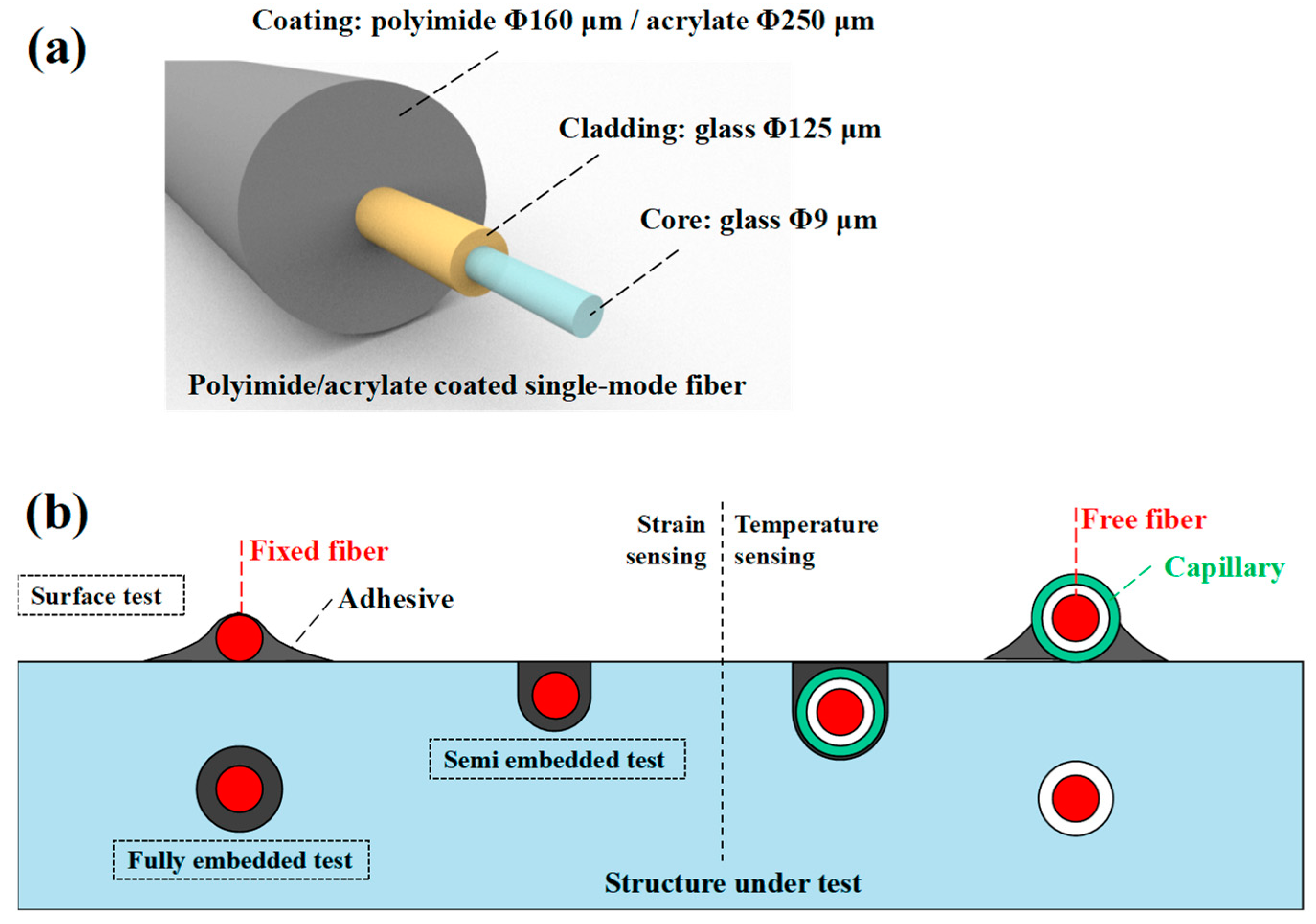
2.2. Installation of Optical Fiber Sensors
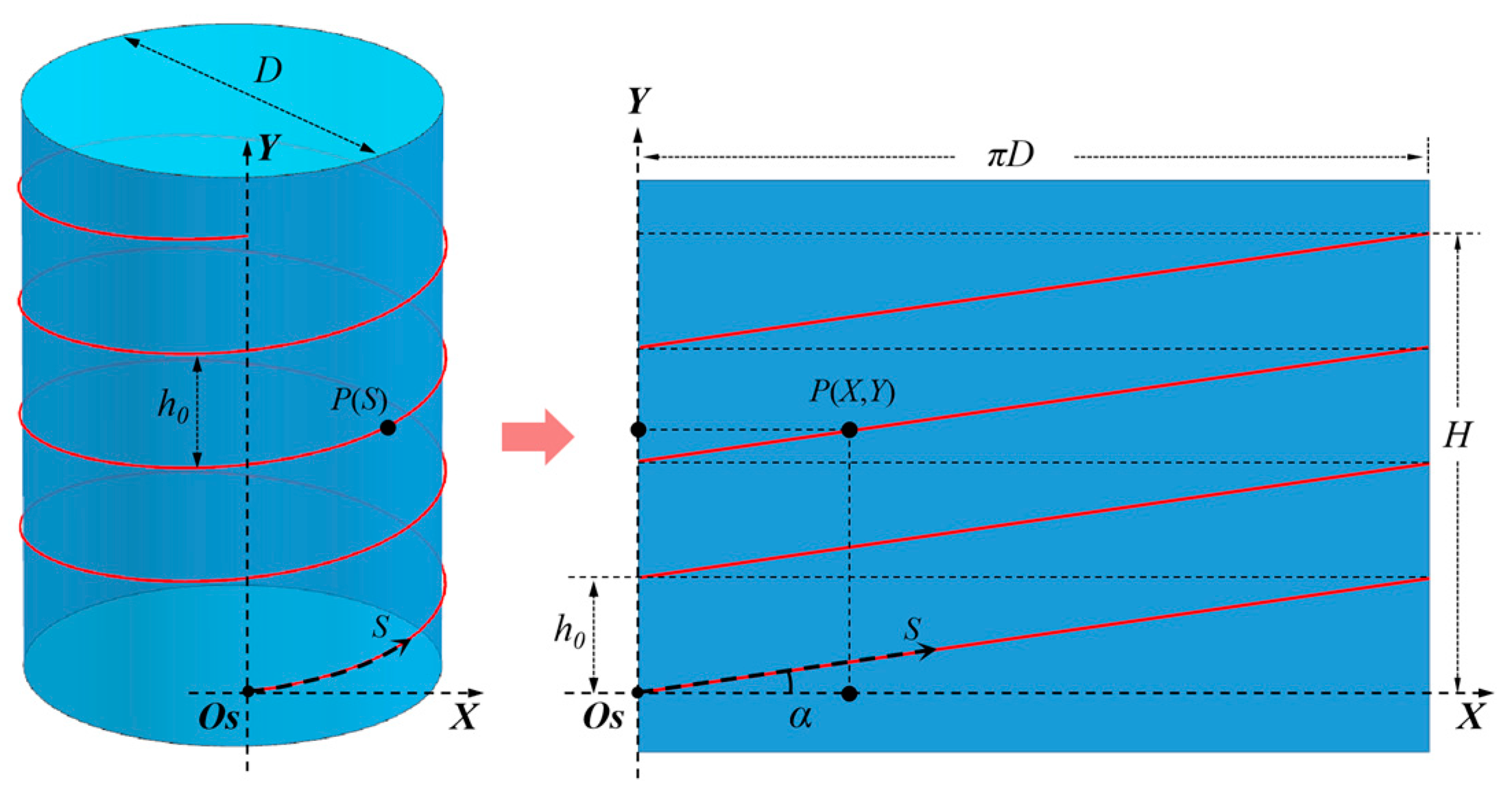
2.3. Reconstruction Principle of the Measuring Signal
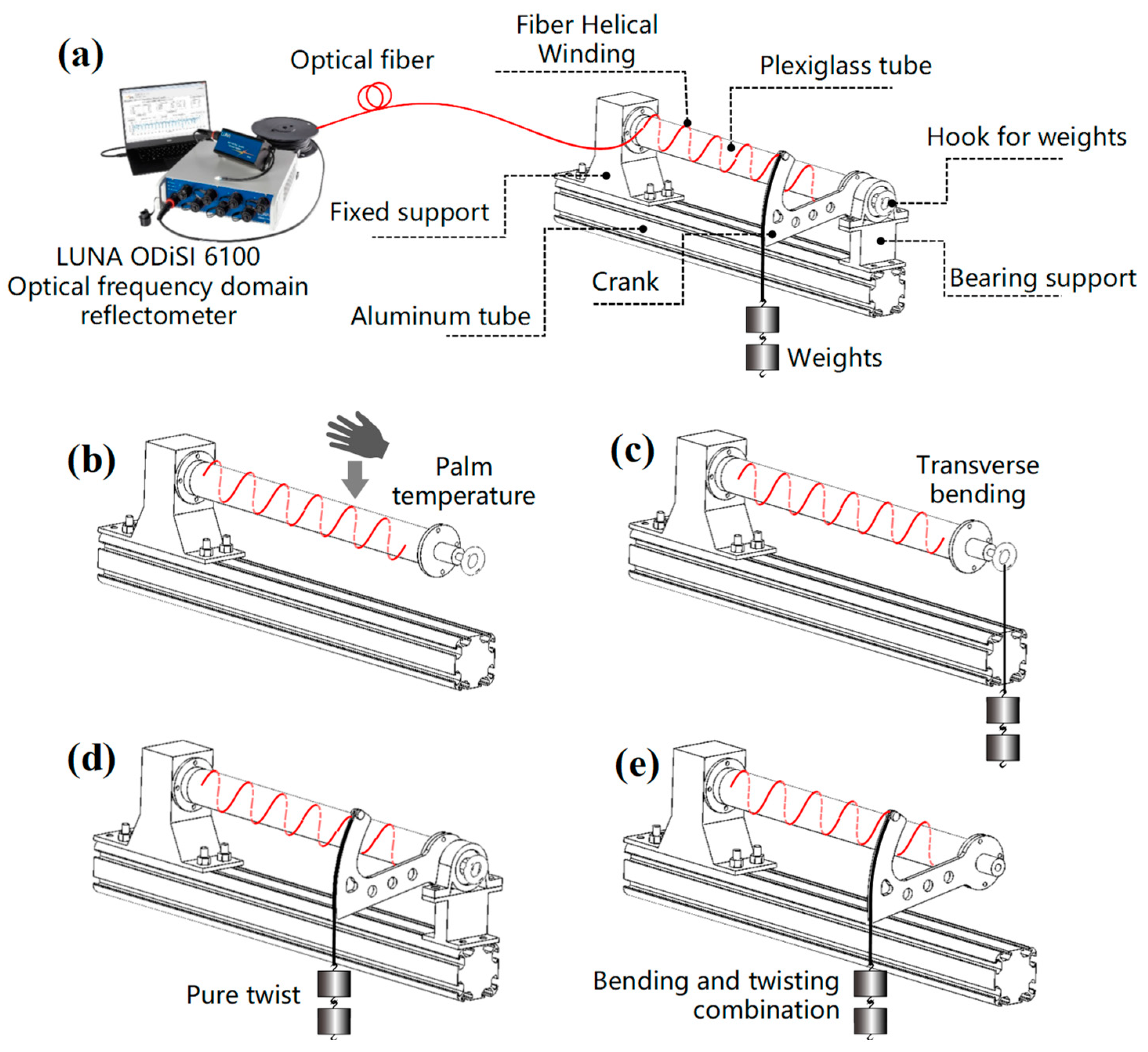
3. Test Bench
4. Experimental Results
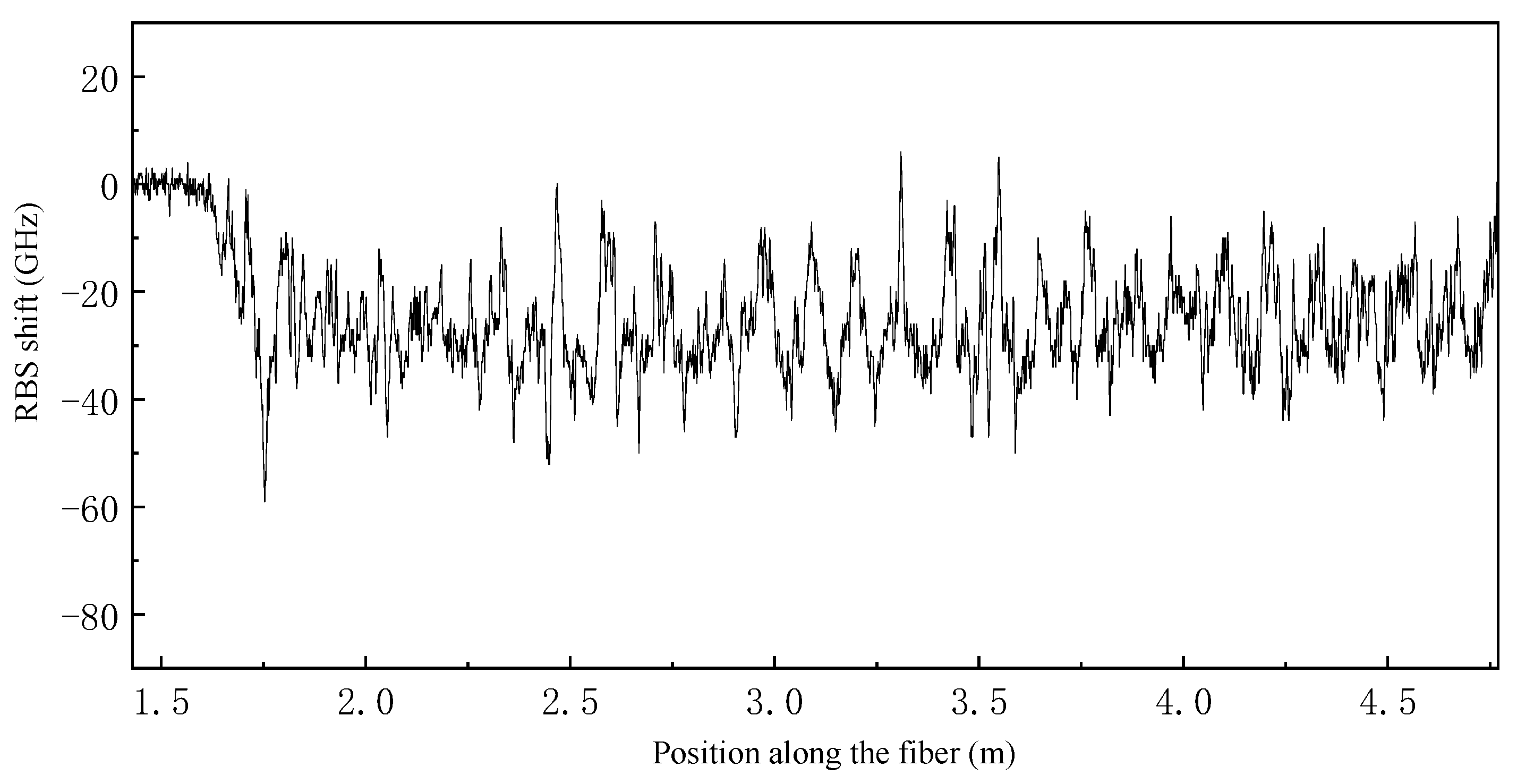
4.1. Palm-Shaped Temperature Field Reconstruction
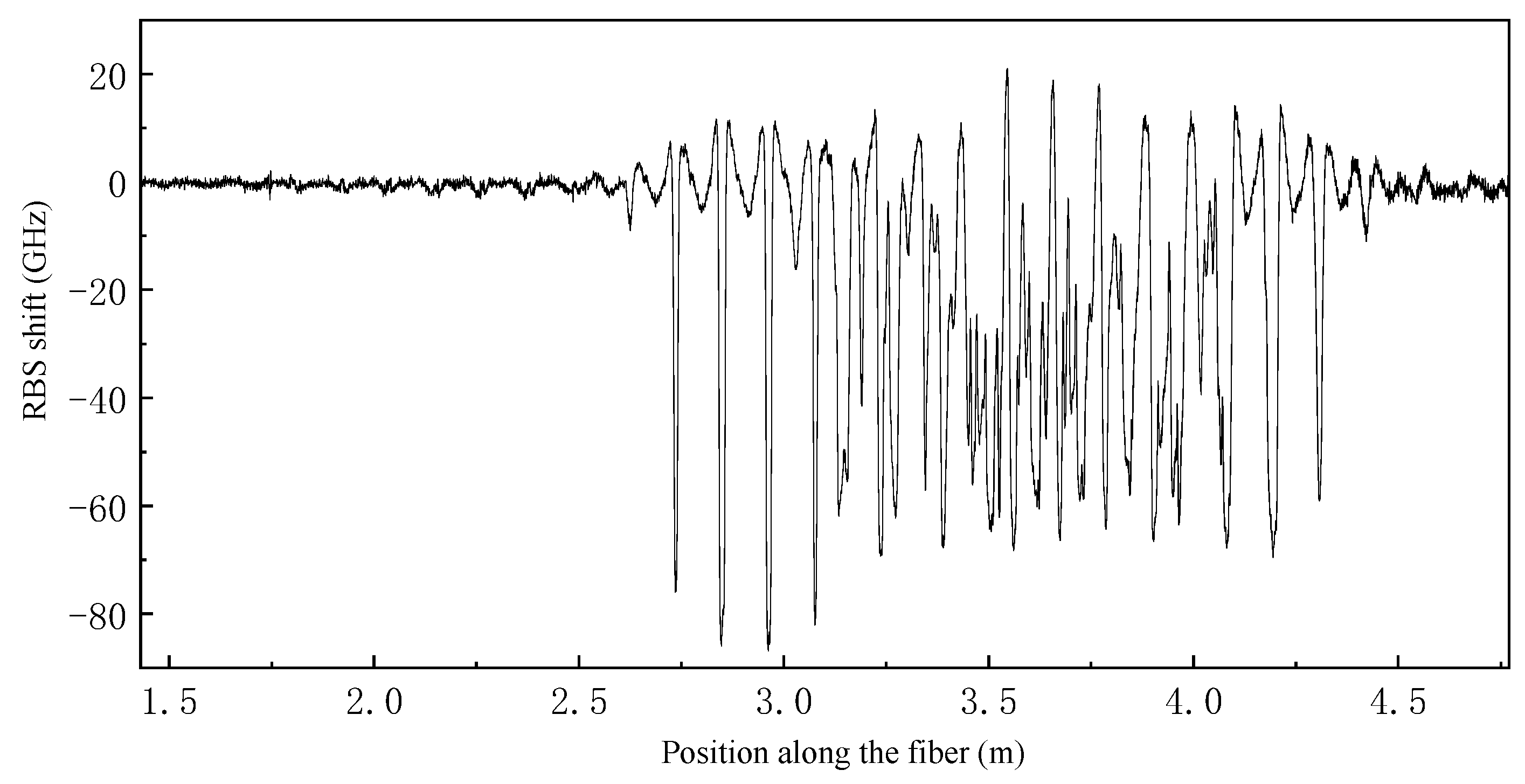
4.2. Transverse Bending Strain Field Reconstruction
4.3. Pure Torsion Strain Field Reconstruction
4.4. Combined Bending and Torsion Strain Field Reconstruction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chou, J.S.; Tu, W.T. Failure analysis and risk management of a collapsed large wind turbine tower. Eng. Fail. Anal. 2011, 18, 295–313. [Google Scholar] [CrossRef]
- Lian, J.; Cai, O.; Dong, X.; Jiang, Q.; Zhao, Y. Health monitoring and safety evaluation of the offshore wind turbine structure: A review and discussion of future development. Sustainability 2019, 11, 494. [Google Scholar] [CrossRef] [Green Version]
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Measur. Sci. Technol. 2008, 19, 122001. [Google Scholar] [CrossRef] [Green Version]
- Avdelidis, N.P.; Almond, D.P.; Ibarra-Castanedo, C.; Bendada, A.; Kenny, S.; Maldague, X. Structural integrity assessment of materials by thermography. In Proceeding of the Conference on Damage in Composite Materials CDCM, Stuttgart, Germany, 18–19 September 2006. [Google Scholar]
- Li, S.; Shi, K.; Yang, K.; Xu, J. Research on the defect types judgment in wind turbine blades using ultrasonic NDT. IOP Conf. Ser. Mater. Sci. Eng. 2015, 87, 012056. [Google Scholar] [CrossRef]
- Jang, J.H.; Yeo, I.; Shin, S.; Chang, S.P. Experimental investigation of system-identification-based damage assessment on structures. J. Struct. Eng. 2002, 128, 673–682. [Google Scholar] [CrossRef]
- Carne, T.G.; James, G.H., III. The inception of OMA in the development of modal testing technology for wind turbines. Mech. Syst. Signal Process. 2010, 24, 1213–1226. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, L.; Smolka, U.; Cosack, N.; Muskulus, M. Brief communication: Structural monitoring for lifetime extension of offshore wind monopiles: Can strain measurements at one level tell us everything? Wind Energy Sci. 2017, 2, 469–476. [Google Scholar] [CrossRef] [Green Version]
- Dongming, F.; Feng, M.Q. Vision-based multipoint displacement measurement for structural health monitoring. Struct. Control Health Monitor. 2016, 23, 876–890. [Google Scholar]
- Sendra, S.; Parra, L.; Jimenez, J.M.; Garcia, L.; Lloret, J. LoRa-based network for water quality monitoring in coastal areas. Mob. Netw. Appl. 2022, 1–17. [Google Scholar] [CrossRef]
- Wu, T.D.; Chen, Z.J.; Chang, C.C.; Wang, H.F. Design of a Wireless Sensor Network for Open Ocean Aquaculture Based on 802.11 ac Wireless Bridge and LoRa™ Technology. In Proceedings of the 2020 International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Penghu, Taiwan, 26–28 August 2020; pp. 1–2. [Google Scholar]
- Rattan, K.T.V.; Sun, T. Fiber optic sensor technology: An overview. Sensors Actuat. A Phys. 2000, 82, 40–61. [Google Scholar] [CrossRef]
- Chen, J.; Liu, B.; Zhang, H. Review of fiber Bragg grating sensor technology. Front. Optoelectron. China 2011, 4, 204–212. [Google Scholar] [CrossRef]
- Mihailov, S.J. Fiber Bragg grating sensors for harsh environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Z. Distributed acoustic sensing turns fiber-optic cables into sensitive seismic antennas. Seismol. Res. Lett. 2020, 91, 1–15. [Google Scholar] [CrossRef]
- Du, C.; Dutta, S.; Kurup, P.; Yu, T.; Wang, X. A review of railway infrastructure monitoring using fiber optic sensors. Sensors Actuat. A Phys. 2020, 303, 111728. [Google Scholar] [CrossRef]
- Girard, S.; Morana, A.; Ladaci, A.; Robin, T.; Mescia, L.; Bonnefois, J.J.; Boutillier, M.; Mekki, J.; Paveau, A.; Cadier, B.; et al. Recent advances in radiation-hardened fiber-based technologies for space applications. J. Opt. 2018, 20, 093001. [Google Scholar] [CrossRef] [Green Version]
- Chai, Q.; Luo, Y.; Ren, J.; Zhang, J.; Yang, J.; Yuan, L.; Peng, G.D. Review on fiber-optic sensing in health monitoring of power grids. Opt. Eng. 2019, 58, 072007. [Google Scholar] [CrossRef] [Green Version]
- Min, R.; Liu, Z.; Pereira, L.; Yang, C.; Sui, Q.; Marques, C. Optical fiber sensing for marine environment and marine structural health monitoring: A review. Opt. Laser Technol. 2021, 140, 107082. [Google Scholar] [CrossRef]
- Data Sheet of ODiSI 6000 Series Optical Distributed Sensor Interrogators (20 March 2022) ODiSI6 REV.5.7. Luna Innovations Incorporated, Web. 6 May 2022. Available online: https://lunainc.com (accessed on 6 May 2022).
- Shajiee, S.; Pao, L.Y.; Wagner, P.N.; Moore, E.D.; McLeod, R.R. Direct ice sensing and localized closed-loop heating for active de-icing of wind turbine blades. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 634–639. [Google Scholar]
- Eickhoff, W.; Ulrich, R. Optical frequency domain reflectometry in single-mode fiber. Appl. Phys. Lett. 1981, 39, 693–695. [Google Scholar] [CrossRef]
- Zhang, Z.; Guan, P.; Xu, J.; Wang, B.; Li, H.; Dong, Y. Horizontal loading performance of offshore wind turbine pile foundation based on DPP-BOTDA. Appl. Sci. 2020, 10, 492. [Google Scholar] [CrossRef] [Green Version]
- Lally, E.M.; Reaves, M.; Horrell, E.; Klute, S.; Froggatt, M.E. Fiber optic shape sensing for monitoring of flexible structures. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2012, San Diego, CA, USA, 12–15 March 2012; pp. 831–839. [Google Scholar]
- Grave JH, L.; Håheim, M.L.; Echtermeyer, A.T. Measuring changing strain fields in composites with Distributed Fiber-Optic Sensing using the optical backscatter reflectometer. Compos. Part B Eng. 2015, 74, 138–146. [Google Scholar] [CrossRef]
- Choi, B.H.; Kwon, I.B. Damage mapping using strain distribution of an optical fiber embedded in a composite cylinder after low-velocity impacts. Compos. Part B Eng. 2019, 173, 107009. [Google Scholar] [CrossRef]
- Sierra-Pérez, J.; Torres-Arredondo, M.A.; Güemes, A. Damage and nonlinearities detection in wind turbine blades based on strain field pattern recognition. FBGs, OBR and strain gauges comparison. Compos. Struct. 2016, 135, 156–166. [Google Scholar] [CrossRef]
- Tan, X.; Guo, P.; Zou, X.; Bao, Y. Buckling detection and shape reconstruction using strain distributions measured from a distributed fiber optic sensor. Measurement 2022, 200, 111625. [Google Scholar] [CrossRef]
- Hubbard, P.G.; Xu, J.; Zhang, S.; Dejong, M.; Luo, L.; Soga, K.; Papa, C.; Zulberti, C.; Malara, D.; Fugazzotto, F.; et al. Dynamic structural health monitoring of a model wind turbine tower using distributed acoustic sensing (DAS). J. Civil Struct. Health Monitoring 2021, 11, 833–849. [Google Scholar] [CrossRef]
- Yang, T.; Wang, Y.; Wang, X. High-precision calibration for strain and temperature sensitivities of Rayleigh-scattering-based DOFS at cryogenic temperatures. Cryogenics 2022, 124, 103481. [Google Scholar] [CrossRef]
- Yang, T.; Wang, H.; Wang, X. Strain Transfer Characteristics of Multi-Layer Optical Fiber Sensors with Temperature-Dependent Properties at Low Temperature. Sensors 2021, 21, 495. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.G.; Archambault, J.L.; Reekie, L.; Dakin, J.P. Discrimination between strain and temperature effects using dual-wavelength fibre grating sensors. Electron. Lett. 1994, 30, 1085–1087. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.; Wang, X. Decoupling and Simultaneous Measurement of Nonuniform Strain and Temperature Using a Single Distributed Optical Fiber Ring. Exp. Mech. 2022, 62, 1–22. [Google Scholar] [CrossRef]
- Kreger, S.T.; Gifford, D.K.; Froggatt, M.E.; Soller, B.J.; Wolfe, M.S. High resolution distributed strain or temperature measurements in single-and multi-mode fiber using swept-wavelength interferometry. In Optical Fiber Sensors; Optica Publishing Group: Washington, DC, USA, 2006; p. ThE42. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Tao, T.; Guo, X.; Yang, Y.; Liu, S. Preliminary Test for 3D Surface Strain Measurement in the Tower and Foundation of Offshore Wind Turbines Using DOFS. Sensors 2023, 23, 6734. https://doi.org/10.3390/s23156734
Yang T, Tao T, Guo X, Yang Y, Liu S. Preliminary Test for 3D Surface Strain Measurement in the Tower and Foundation of Offshore Wind Turbines Using DOFS. Sensors. 2023; 23(15):6734. https://doi.org/10.3390/s23156734
Chicago/Turabian StyleYang, Taolue, Tao Tao, Xinran Guo, Yi Yang, and Shi Liu. 2023. "Preliminary Test for 3D Surface Strain Measurement in the Tower and Foundation of Offshore Wind Turbines Using DOFS" Sensors 23, no. 15: 6734. https://doi.org/10.3390/s23156734
APA StyleYang, T., Tao, T., Guo, X., Yang, Y., & Liu, S. (2023). Preliminary Test for 3D Surface Strain Measurement in the Tower and Foundation of Offshore Wind Turbines Using DOFS. Sensors, 23(15), 6734. https://doi.org/10.3390/s23156734









