Modelling and Analysis of Expansion Joints’ Effect on Dynamic Performance of Railway Rigid Overhead System
Abstract
1. Introduction
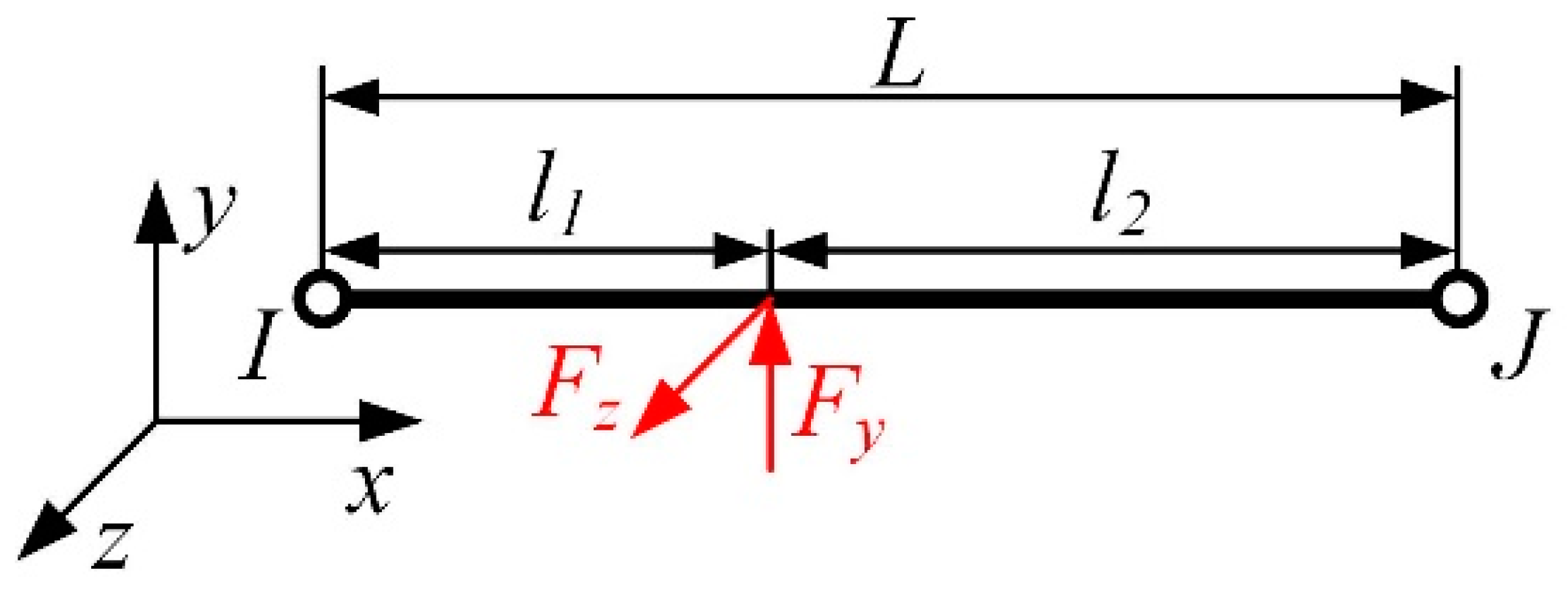
2. Numerical Modelling of Rigid Overhead System
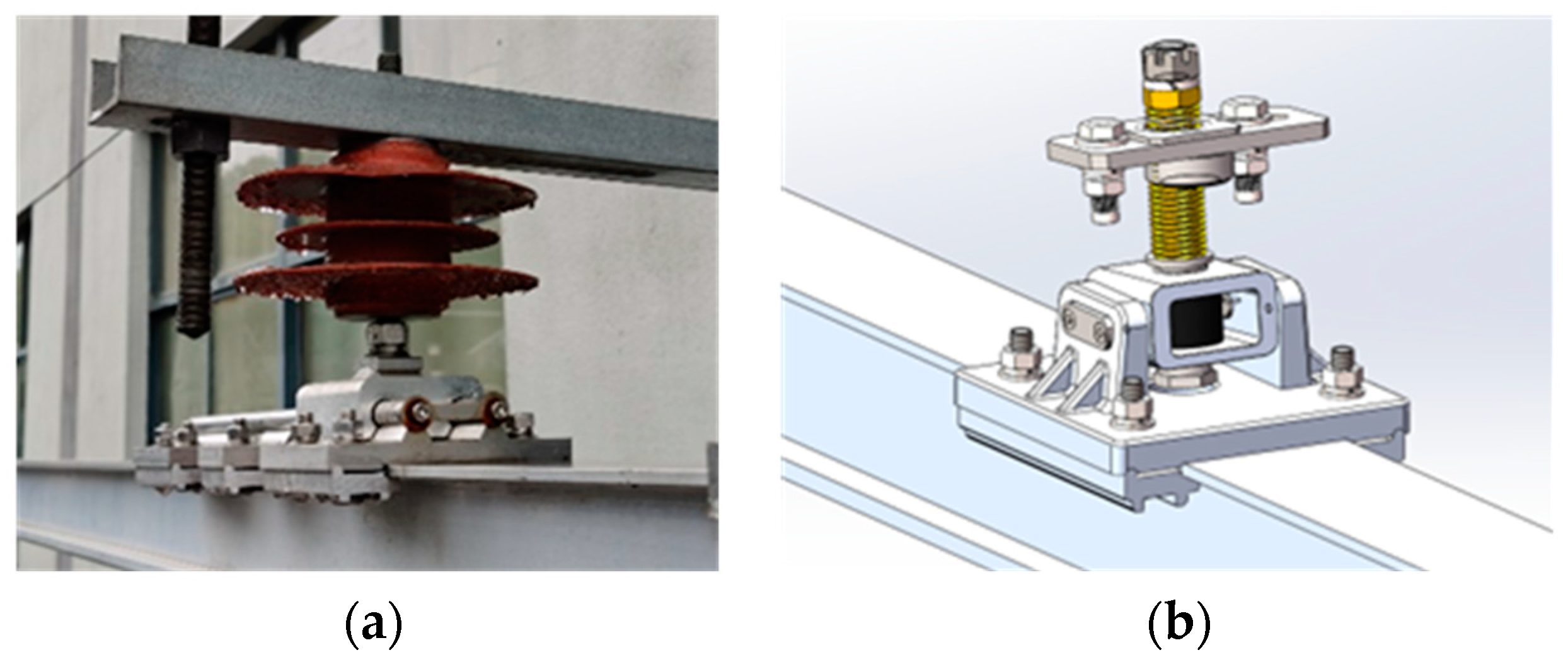
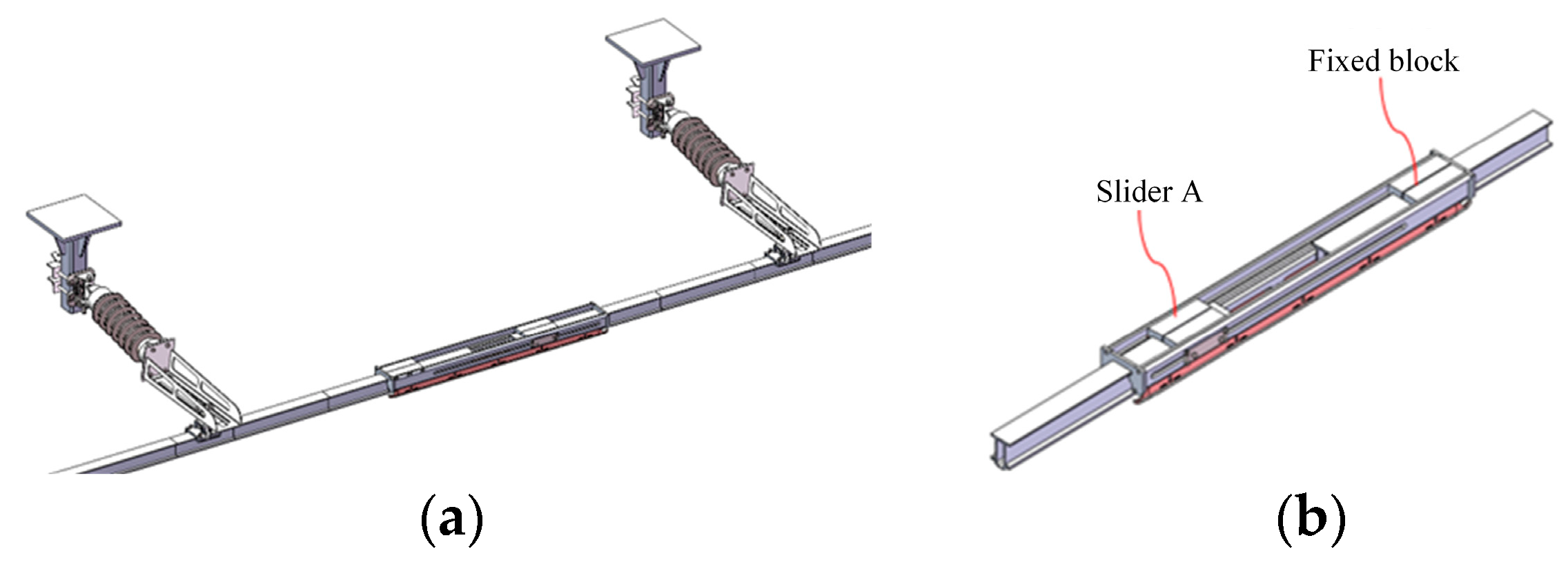
3. Modelling of Expansion Joint
4. Analysis of Expansion Joint Stress Distribution
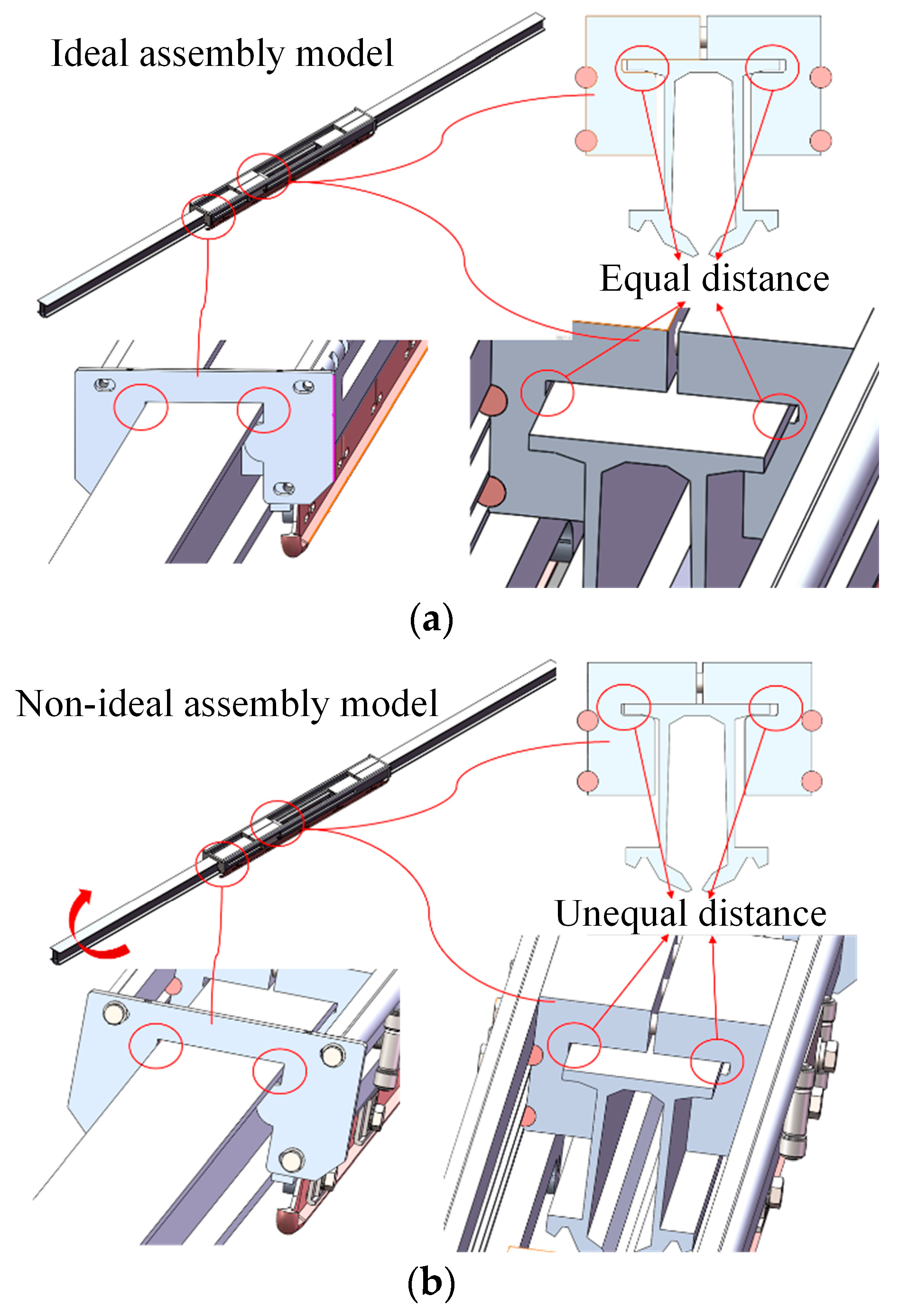
4.1. Stress Variation under Thermal Expansion and Contraction Effects (Normal Assembly)
4.2. Stress Variation under Thermal Expansion and Contraction Effects (Deflected Assembly)
4.3. Optimization of Expansion Joints under Thermal Expansion and Contraction Effects
4.3.1. Installation Deflection Angle of the Expansion Joint
4.3.2. Geometric Design Optimization of Expansion Joint
5. Dynamics Performance with Expansion Joints
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zuleta, E.C.; Lupi, C.; Felli, F.; Paris, C.; Vendittozzi, C. Railway overhead contact wire monitoring system by means of FBG sensors. Frat. Integrita Strutt. 2021, 15, 246–258. [Google Scholar] [CrossRef]
- Duan, F.; Liu, Z.; Zhai, D.; Rønnquist, A. A Siamese network-based non-contact measurement method for railway catenary uplift trained in a free vibration test. Sensors 2020, 20, 3984. [Google Scholar] [CrossRef] [PubMed]
- Garramiola, F.; del Olmo, J.; Poza, J.; Madina, P.; Almandoz, G. Integral sensor fault detection and isolation for railway traction drive. Sensors 2018, 18, 1543. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zou, D.; Tan, M.; Zhou, N.; Li, R.; Mei, G. Review of pantograph and catenary interaction. Front. Mech. Eng. 2018, 13, 311–322. [Google Scholar] [CrossRef]
- Bruni, S.; Ambrosio, J.; Carnicero, A.; Cho, Y.H.; Finner, L.; Ikeda, M.; Kwon, S.Y.; Massat, J.-P.; Stichel, S.; Tur, M.; et al. The results of the pantograph–catenary interaction benchmark. Veh. Syst. Dyn. 2015, 53, 412–435. [Google Scholar] [CrossRef]
- Song, Y.; Rønnquist, A.; Jiang, T.; Nåvik, P. Railway pantograph-catenary interaction performance in an overlap section: Modelling, validation and analysis. J. Sound Vib. 2023, 548, 117506. [Google Scholar] [CrossRef]
- Song, Y.; Rønnquist, A.; Jiang, T.; Nåvik, P. Identification of short-wavelength contact wire irregularities in electrified railway pantograph–catenary system. Mech. Mach. Theory 2021, 162, 104338. [Google Scholar] [CrossRef]
- Yang, K.; Peng, J.; Jiang, C.; Jiang, X.; Xiao, L.; Wang, B.; Gao, X.; Xie, L.; Peng, H. Design of the fall-block sensing of the railway line pantograph based on 3d machine vision sensors. Sensors 2018, 18, 2305. [Google Scholar] [CrossRef]
- EN 50318; Railway Applications—Current Collection Systems—Validation of Simulation of the Dynamic Interaction between Pantograph and Overhead Contact Line. European Committee for Electrotechnical Standardization: Brussels, Belgium, 2018; Volume 3.
- Antunes, P.; Ambrósio, J.; Pombo, J.; Facchinetti, A. A new methodology to study the pantograph–catenary dynamics in curved railway tracks. Veh. Syst. Dyn. 2020, 58, 425–452. [Google Scholar] [CrossRef]
- Shimizu, M.; Fujii, Y. Improvement of structure of contact wire on overlap sections of Shinkansen. Q. Rep. RTRI 2000, 41, 159–162. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Duan, F.; Xu, Z.; Lu, X. Wave propagation analysis in high-speed railway catenary system subjected to a moving pantograph. Appl. Math. Model. 2018, 59, 20–38. [Google Scholar] [CrossRef]
- Xu, Z.; Song, Y.; Liu, Z. Effective measures to improve current collection quality for double pantographs and catenary based on wave propagation analysis. IEEE Trans. Veh. Technol. 2020, 69, 6299–6309. [Google Scholar] [CrossRef]
- Song, Y.; Duan, F.; Liu, Z. Analysis of Critical Speed for High-Speed Railway Pantograph-Catenary System. IEEE Trans. Veh. Technol. 2022, 71, 3547–3555. [Google Scholar] [CrossRef]
- Vesali, F.; Rezvani, M.A.; Molatefi, H. Analysis of conceptual similarities and differences of wave speed and critical speed in the overhead catenary system. Measurement 2021, 176, 109164. [Google Scholar] [CrossRef]
- Metrikine, A.V.; Bosch, A.L. Dynamic response of a two-level catenary to a moving load. J. Sound Vib. 2006, 292, 676–693. [Google Scholar] [CrossRef]
- Ambrósio, J.; Pombo, J.; Pereira, M.; Antunes, P.; Mósca, A. Recent Developments in Pantograph-Catenary Interaction Modelling and Analysis. Int. J. Railw. Technol. 2012, 1, 249–278. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Patel, M.D.; Tinsley, B.; Shabana, A.A. Contact force control in multibody pantograph/catenary systems. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2016, 230, 307–328. [Google Scholar] [CrossRef]
- Lopez-Garcia, O.; Carnicero, A.; Maroño, J. Influence of stiffness and contact modelling on catenary–pantograph system dynamics. J. Sound Vib. 2007, 299, 806–821. [Google Scholar] [CrossRef]
- Lee, K.; Cho, Y.; Chung, J. Dynamic contact analysis of a tensioned beam with a moving mass–spring system. J. Sound Vib. 2012, 331, 2520–2531. [Google Scholar] [CrossRef]
- Facchinetti, A.; Bruni, S. Hardware-in-the-loop hybrid simulation of pantograph–catenary interaction. J. Sound Vib. 2012, 331, 2783–2797. [Google Scholar] [CrossRef]
- Correcher, A.; Ricolfe-Viala, C.; Tur, M.; Gregori, S.; Salvador-Muñoz, M.; Fuenmayor, F.J.; Gil, J.; Pedrosa, A.M. Hardware-in-the-Loop Test Bench for Simulation of Catenary–Pantograph Interaction (CPI) with Linear Camera Measurement. Sensors 2023, 23, 1773. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Lu, X. Dynamic Performance of High-Speed Railway Overhead Contact Line Interacting with Pantograph Considering Local Dropper Defect. IEEE Trans. Veh. Technol. 2020, 69, 5958–5967. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.G.; Rxnnquist, A.; Navik, P.; Liu, Z.D. Contact wire irregularity stochastics and effect on high-speed railway pantograph-catenary interactions. IEEE Trans. Instrum. Meas. 2020, 69, 8196–8206. [Google Scholar] [CrossRef]
- Zhang, W.; Mei, G.; Zeng, J. A study of pantograph/catenary system dynamics with influence of presag and irregularity of contact wire. Veh. Syst. Dyn. 2003, 37, 593–604. [Google Scholar] [CrossRef]
- Van Vo, O.; Massat, J.-P.; Balmes, E. Waves, modes and properties with a major impact on dynamic pantograph-catenary interaction. J. Sound Vib. 2017, 402, 51–69. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A spatial coupling model to study dynamic performance of pantograph-catenary with vehicle-track excitation. Mech. Syst. Signal Process. 2021, 151, 107336. [Google Scholar] [CrossRef]
- Yao, Y.; Zou, D.; Zhou, N.; Mei, G.; Wang, J.; Zhang, W. A study on the mechanism of vehicle body vibration affecting the dynamic interaction in the pantograph–catenary system. Veh. Syst. Dyn. 2021, 59, 1335–1354. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Øiseth, O.; Rønnquist, A. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test. Mech. Mach. Theory 2021, 168, 104608. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Duan, F.; Lu, X.; Wang, H. Study on wind-induced vibration behavior of railway catenary in spatial stochastic wind field based on nonlinear finite element procedure. J. Vib. Acoust. 2018, 140, 011010. [Google Scholar] [CrossRef]
- Duan, F.; Song, Y.; Gao, S.; Liu, Y.; Chu, W.; Lu, X.; Liu, Z. Study on Aerodynamic Instability and Galloping Response of Rail Overhead Contact Line Based on Wind Tunnel Tests. IEEE Trans. Veh. Technol. 2023, 72, 7211–7220. [Google Scholar] [CrossRef]
- Zhang, Y.; Yue, Y.; Zhao, S.; Sihua, W. Research on galloping response of catenary positive feeder in gale area considering surface roughness of stranded wire. J. Railw. Sci. Eng. 2021, 18, 1885–1894. [Google Scholar] [CrossRef]
- Su, K.; Zhang, J.; Zhang, J.; Yan, T.; Mei, G. Optimisation of current collection quality of high-speed pantograph-catenary system using the combination of artificial neural network and genetic algorithm. Veh. Syst. Dyn. 2022, 61, 260–285. [Google Scholar] [CrossRef]
- Song, Y.; Wang, H.; Frøseth, G.; Nåvik, P.; Liu, Z.; Rønnquist, A. Surrogate modelling of railway pantograph-catenary interaction using deep Long-Short-Term-Memory neural networks. Mech. Mach. Theory 2023, 187, 105386. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, J.; Liu, J.; Cao, Y.; Li, H.; Xu, X. Comprehensive evaluation method of catenary status based on improved multivariate statistical control chart. J. Railw. Sci. Eng. 2021, 18, 3048–3056. [Google Scholar] [CrossRef]
- Feng, X.; Gao, S.; Song, Y.; Hu, Z.; Chen, L.; Liang, T. Static and Dynamic Analysis of Conductor Rail with Large Cross-Sectional Moment of Inertia in Rigid Catenary Systems. Energies 2023, 16, 1810. [Google Scholar] [CrossRef]
- Vera, C.; Suarez, B.; Paulin, J.; Rodríguez, P. Simulation model for the study of overhead rail current collector systems dynamics, focused on the design of a new conductor rail. Veh. Syst. Dyn. 2006, 44, 595–614. [Google Scholar] [CrossRef]
- Bautista, A.; Montesinos, J.; Pintado, P. Dynamic interaction between pantograph and rigid overhead lines using a coupled FEM—Multibody procedure. Mech. Mach. Theory 2016, 97, 100–111. [Google Scholar] [CrossRef]
- Shimizu, M.; Harada, S.; Oya, A.; Tokuda, K. Improving performance of type T overhead rigid conductor lines. Q. Rep. RTRI 2006, 47, 52–58. [Google Scholar] [CrossRef][Green Version]
- Simarro, M.; Castillo, J.J.; Cabrera, J.A.; Postigo, S. Evaluation of the influence of the speed, preload and span length on the contact forces in the interaction between the pantograph and the overhead conductor rail. Eng. Struct. 2021, 243, 112678. [Google Scholar] [CrossRef]
- Álvarez-Monteserín, J.A.C.; Esteban, B.S.; Rodríguez, P. Simulation techniques for design of overhead conductor rail lines for speeds over 140 km/h. In Proceedings of the 22nd International Symposium on Dynamics of Vehicles on Roads and Tracks, Manchester, UK, 14–19 August 2011; Available online: http://www.iavsd2011.org/ (accessed on 9 July 2023).
- Su, Z.N.; Shao, L.T. Three-dimensional slope stability based on the finite element limit equilibrium method. Chin. J. Eng. 2022, 44, 2048–2056. [Google Scholar] [CrossRef]
- Kong, D.S.; Liu, Y.; Deng, M.X.; Li, Y.Z. Dynamic response characteristics of an offshore, wind-power monopile foundation in heterogeneous soil. Chin. J. Eng. 2021, 43, 710–719. [Google Scholar] [CrossRef]
- TB/T 3252-2010; Overhead Conductor Rail for Overhead Contact System in Electrification Railway. China Railway Electrification Bureau Group Co., Ltd.: Beijing, China, 2010. Available online: https://www.chinesestandard.net/Related.aspx/TBT3252-2010 (accessed on 28 December 2022).
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Hoboken, NJ, USA, 2005; Available online: https://books.google.ca/books?hl=en&lr=&id=rWvefGICfO8C&oi=fnd&pg=PR13&dq=Bathe,+K.J.+Finite+Element+Procedures+%5BM%5D.+Prentice+Hall,+2005.+&ots=gHLzyTttF3&sig=NPpkWMd9Xn9o3vpDY6HVrBJZb7M#v=onepage&q&f=false (accessed on 13 June 2023).
- Element, F.; Program, A.; Fortran, C. Computer procedures for finite. Program 2002, 1, 2–5. Available online: http://www.ncbi.nlm.nih.gov/pubmed/15500471 (accessed on 13 June 2023).
- Song, Y.; Jiang, T.; Ronnquist, A.; Navik, P.; Froseth, G. The effects of spatially distributed damping on the contact force in railway pantograph-catenary interactions. IEEE Trans. Instrum. Meas. 2021, 70, 7503110. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. Nonlinear static and dynamic analysis of cable structures. Finite Elem. Anal. Des. 2011, 47, 237–246. [Google Scholar] [CrossRef]
- Chen, L.; Duan, F.; Song, Y.; Hu, Z.; Liu, Z.; Feng, X. Assessment of Dynamic Interaction Performance of High-Speed Pantograph and Overhead Conductor Rail System. IEEE Trans. Instrum. Meas. 2022, 71, 9001914. [Google Scholar] [CrossRef]





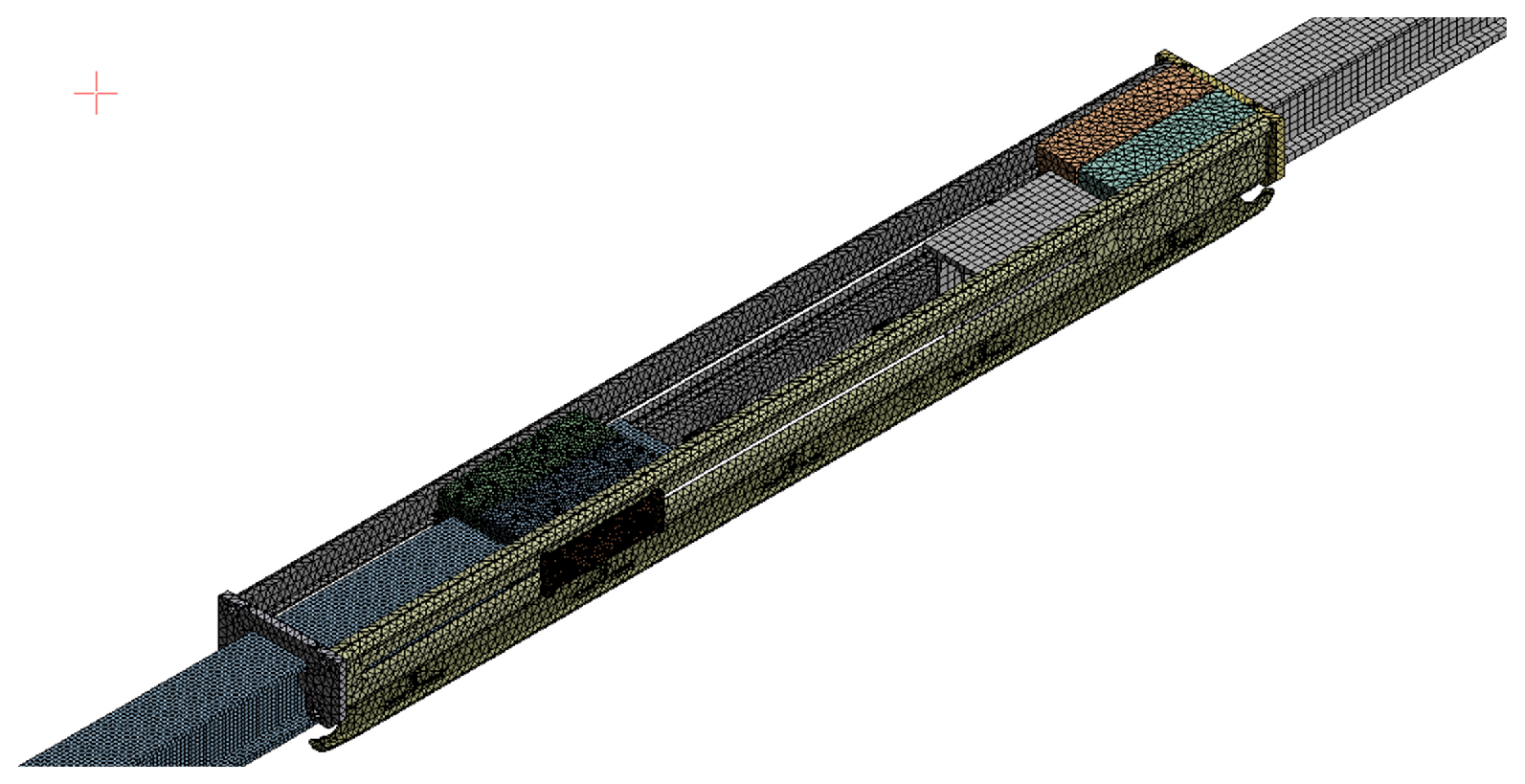
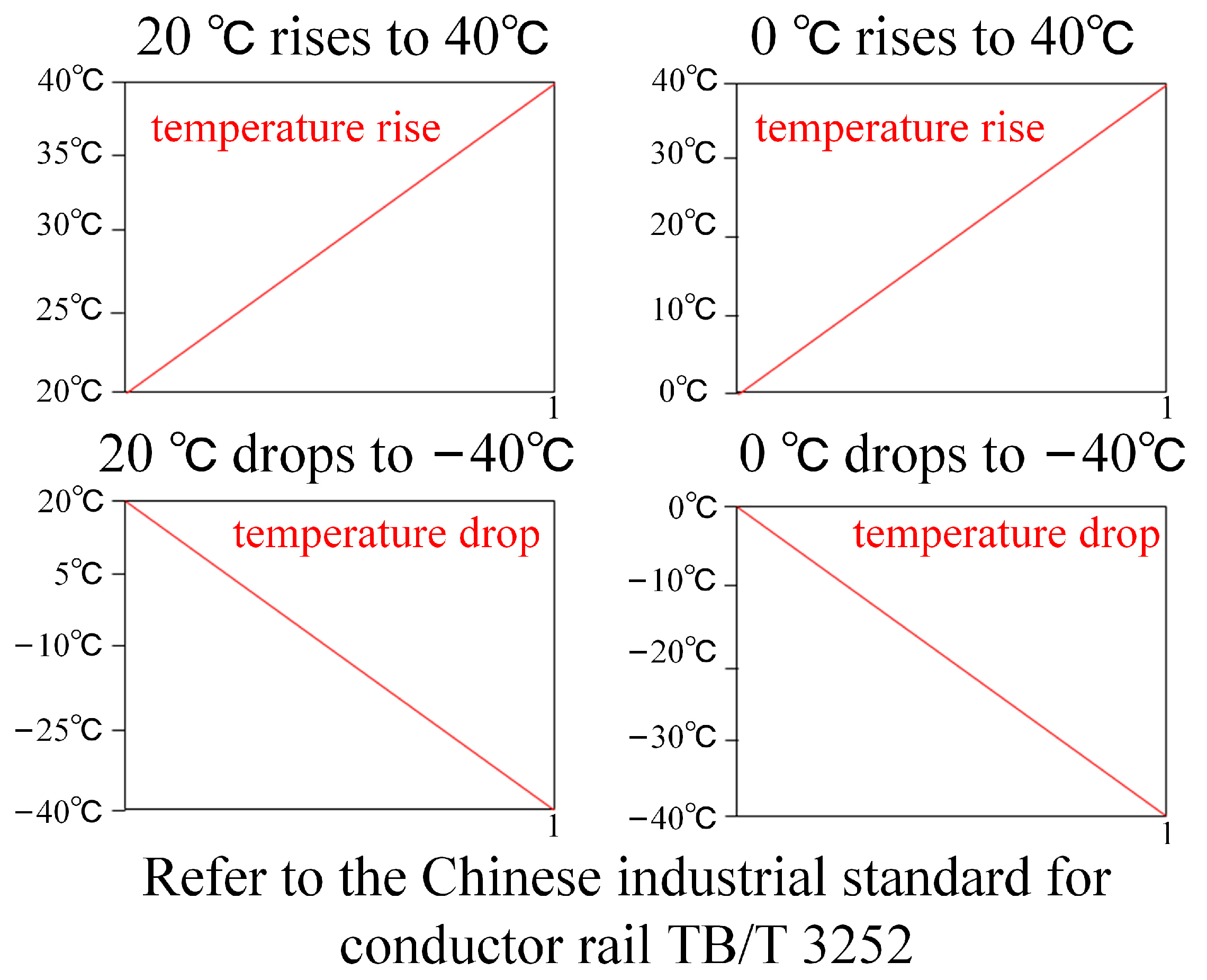

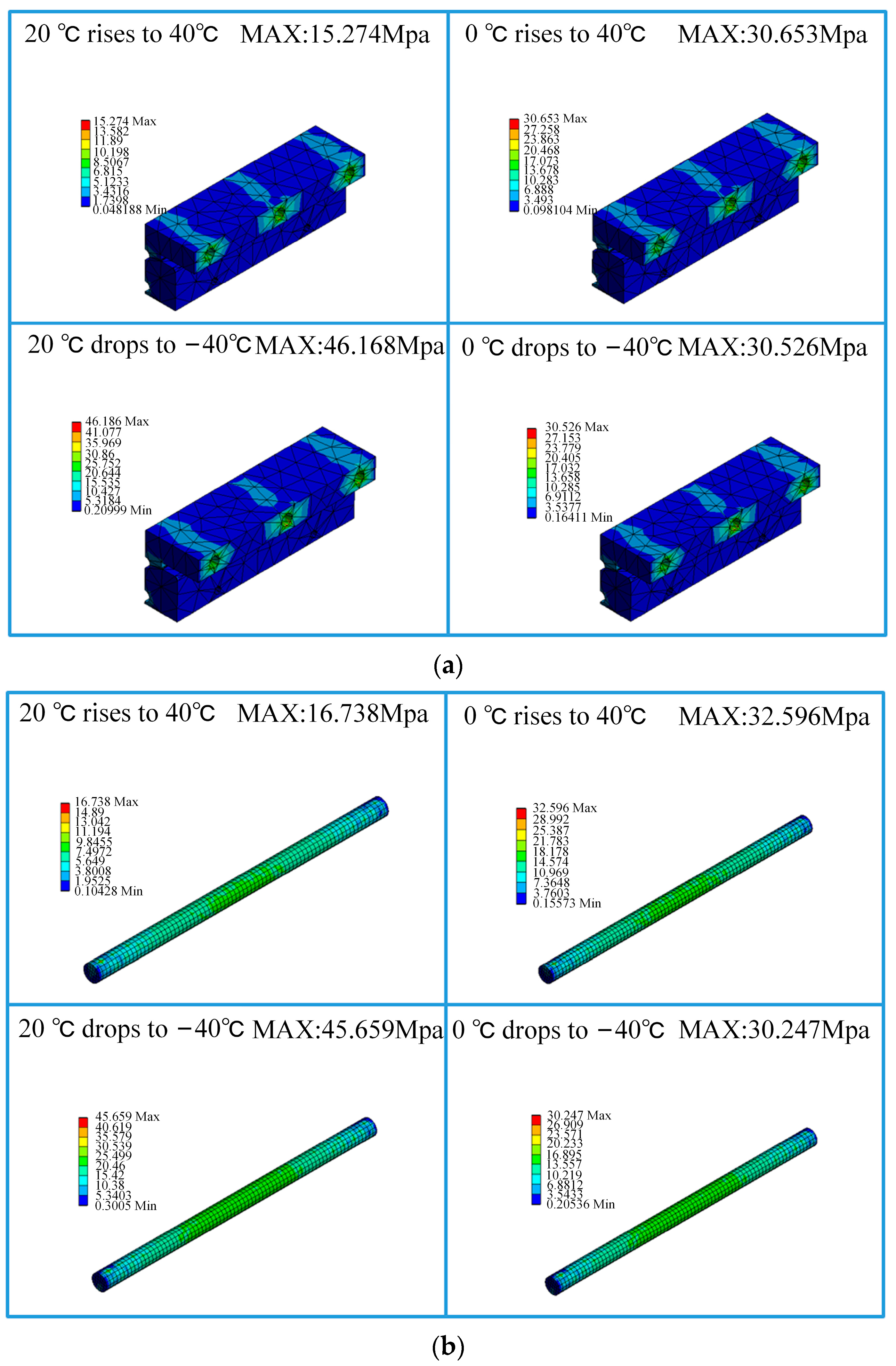
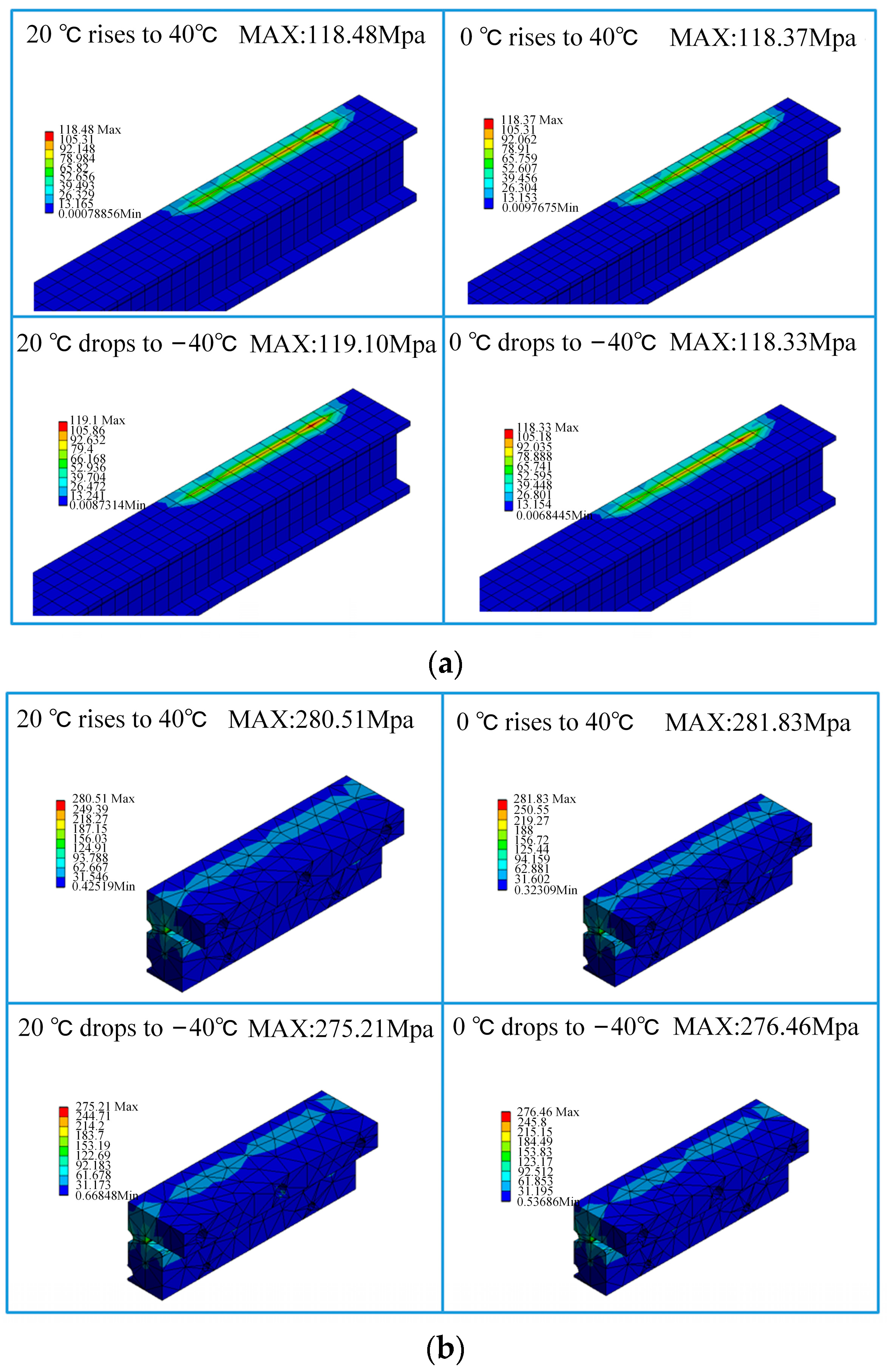

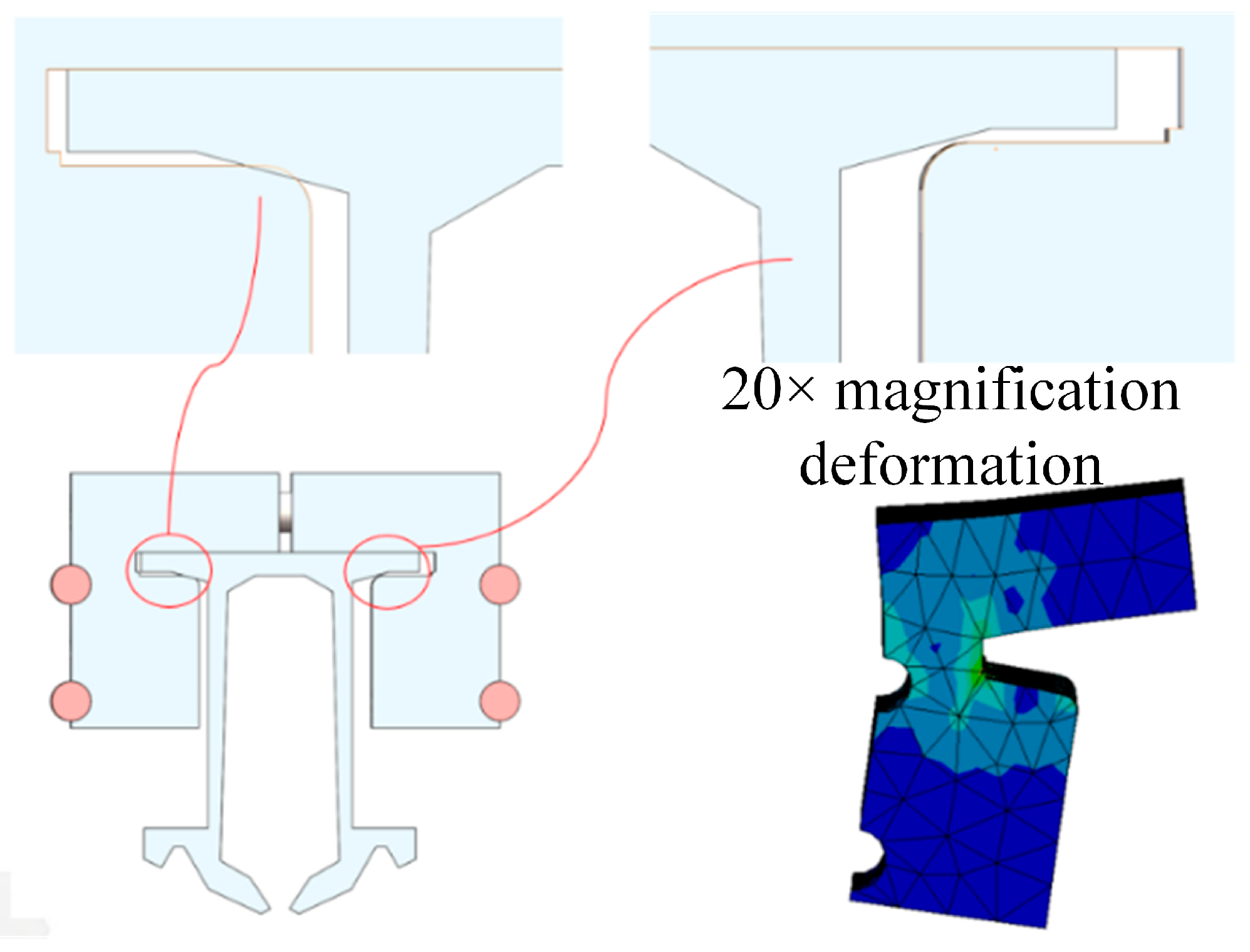

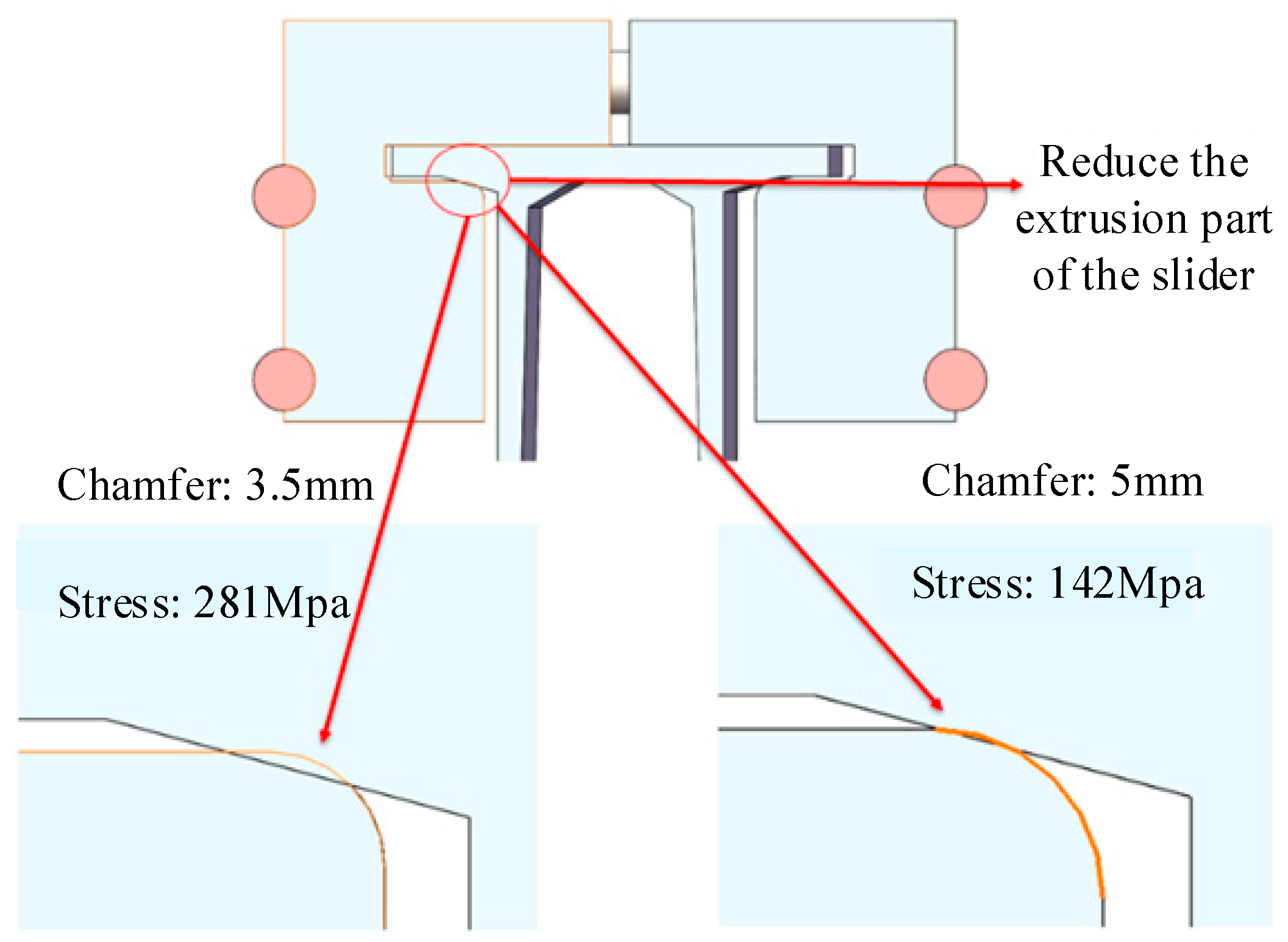



| Item | Cross-Sectional Area [mm2] | Linear Density [kg/m] | Inertia of Moment [m4] |
|---|---|---|---|
| Value | 2322 | 7.3 | 3.76 × 10−6 |
| Copper Alloy | Aluminium Alloy | Structural Steel. | Units | |
|---|---|---|---|---|
| Density | 8.3 × 10−6 | 2.77 × 10−6 | 7.85 × 10−6 | kg/mm3 |
| Elastic modulus | 1.1 × 105 | 7.1 × 104 | 2 × 105 | MPa |
| Thermal conductivity | 0.401 | 0.14862 | 0.0605 | W/mm·°C |
| Specific heat | 3.85 × 105 | 8.75 × 105 | 4.34 × 105 | mJ/kg·°C |
| Components | Busbar | Sliding Block A | Sliding Block B | Sliding Rod A | Sliding Rod B | Body A | Body B | Cover Plate | |
|---|---|---|---|---|---|---|---|---|---|
| Temperature | |||||||||
| 20–40 °C | 2.15 | 9.04 | 15.27 | 16.74 | 7.47 | 5.30 | 5.33 | 6.67 | |
| 0–40 °C | 5.24 | 18.19 | 30.65 | 32.60 | 14.91 | 10.18 | 10.33 | 7.76 | |
| 20–40 °C | 6.70 | 26.99 | 46.19 | 45.66 | 22.19 | 15.52 | 15.70 | 6.82 | |
| 0–40 °C | 4.62 | 17.84 | 30.53 | 30.25 | 14.78 | 10.18 | 10.95 | 7.64 | |
| Components | Busbar | Sliding Block A | Sliding Block B | Sliding Rod A | Sliding Rod B | Body A | Body B | Cover Plate | |
|---|---|---|---|---|---|---|---|---|---|
| Temperature | |||||||||
| 20–40 °C | 118.48 | 9.53 | 280.51 | 122.8 | 16.14 | 9.94 | 10.99 | 14.81 | |
| 0–40 °C | 118.37 | 18.23 | 281.83 | 121.81 | 15.65 | 11.88 | 12.61 | 15.77 | |
| 20–40 °C | 119.10 | 27.48 | 275.21 | 143.98 | 23.65 | 15.19 | 23.21 | 10.33 | |
| 0–40 °C | 118.33 | 18.44 | 276.46 | 137.03 | 19.06 | 10.25 | 19.74 | 11.24 | |
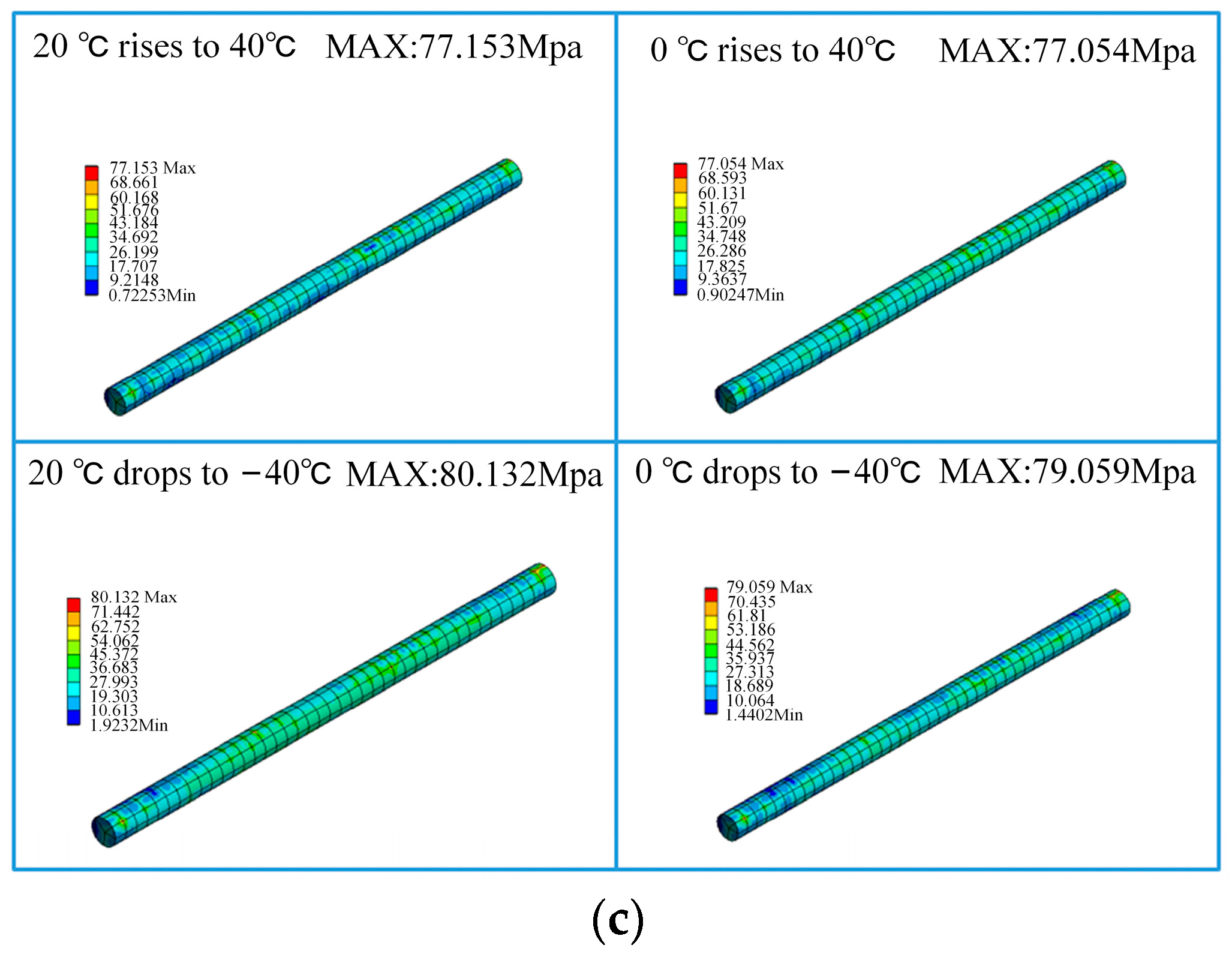
| Components | Deflection Angle (10°) | Deflection Angle (5°) | |||||
|---|---|---|---|---|---|---|---|
| Temperature | Busbar | Sliding Block B | Sliding Rod A | Busbar | Sliding Block B | Sliding Rod A | |
| 20 °C–40 °C | 118.48 | 280.51 | 122.8 | 80.16 | 193.31 | 77.15 | |
| 0 °C–40 °C | 118.37 | 281.83 | 121.81 | 80.14 | 197.21 | 77.05 | |
| 20 °C–40 °C | 119.10 | 275.21 | 143.98 | 81.00 | 187.89 | 80.13 | |
| 0 °C–40 °C | 118.33 | 276.46 | 137.03 | 79.93 | 189.30 | 79.06 | |
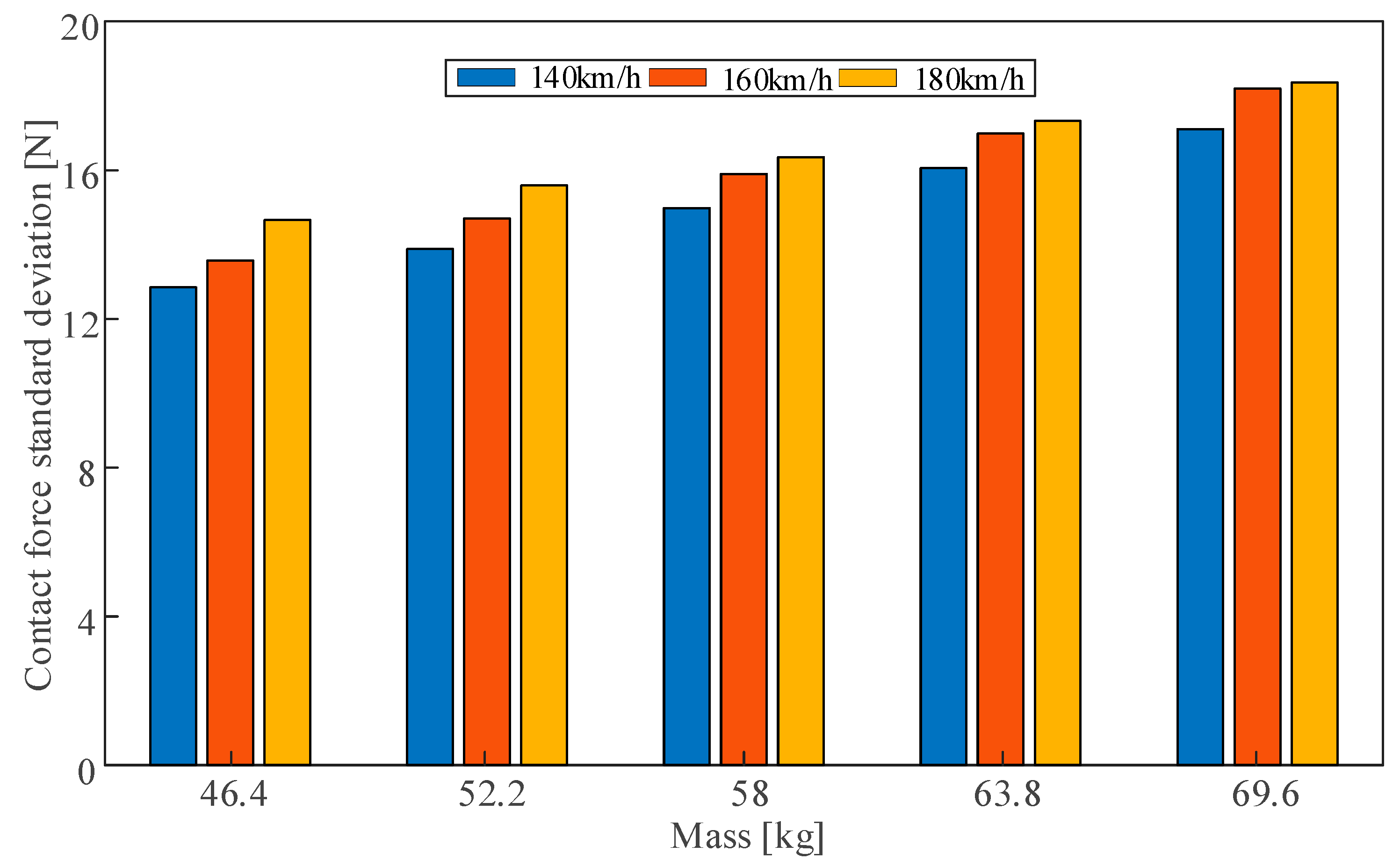
| Speed [km/h] | Expansion Joint Mass [kg] | Maximum Contact Force [N] | Average Contact Force Fm [N] | Minimum Contact Force [N] | Contact Force Standard Deviation σ (N) | 0.3 Fm-σ (N) |
|---|---|---|---|---|---|---|
| 140 | 46.4 | 133.55 | 112.19 | 89.07 | 12.85 | 20.81 |
| 52.2 | 135.91 | 112.35 | 87.63 | 13.88 | 19.82 | |
| 58 | 138.14 | 112.47 | 85.11 | 14.98 | 18.76 | |
| 63.8 | 140.39 | 112.62 | 83.36 | 16.06 | 17.73 | |
| 69.6 | 142.22 | 112.73 | 80.90 | 17.11 | 16.71 | |
| 160 | 46.4 | 135.62 | 111.64 | 87.12 | 13.57 | 19.92 |
| 52.2 | 138.26 | 111.66 | 88.05 | 14.71 | 18.79 | |
| 58 | 143.02 | 111.66 | 87.72 | 15.90 | 17.60 | |
| 63.8 | 143.67 | 111.64 | 86.21 | 16.99 | 16.50 | |
| 69.6 | 144.65 | 111.67 | 82.60 | 18.20 | 15.30 | |
| 180 | 46.4 | 136.81 | 110.88 | 80.96 | 14.66 | 18.61 |
| 52.2 | 137.21 | 110.83 | 78.01 | 15.59 | 17.66 | |
| 58 | 137.45 | 110.77 | 74.67 | 16.35 | 16.88 | |
| 63.8 | 141.13 | 110.63 | 72.23 | 17.32 | 15.87 | |
| 69.6 | 144.13 | 110.57 | 69.79 | 18.36 | 14.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Hu, Z.; Gao, S.; Duan, F.; Chu, W.; Song, Y. Modelling and Analysis of Expansion Joints’ Effect on Dynamic Performance of Railway Rigid Overhead System. Sensors 2023, 23, 6797. https://doi.org/10.3390/s23156797
Feng X, Hu Z, Gao S, Duan F, Chu W, Song Y. Modelling and Analysis of Expansion Joints’ Effect on Dynamic Performance of Railway Rigid Overhead System. Sensors. 2023; 23(15):6797. https://doi.org/10.3390/s23156797
Chicago/Turabian StyleFeng, Xiaohe, Zeyao Hu, Shibin Gao, Fuchuan Duan, Wenping Chu, and Yang Song. 2023. "Modelling and Analysis of Expansion Joints’ Effect on Dynamic Performance of Railway Rigid Overhead System" Sensors 23, no. 15: 6797. https://doi.org/10.3390/s23156797
APA StyleFeng, X., Hu, Z., Gao, S., Duan, F., Chu, W., & Song, Y. (2023). Modelling and Analysis of Expansion Joints’ Effect on Dynamic Performance of Railway Rigid Overhead System. Sensors, 23(15), 6797. https://doi.org/10.3390/s23156797








