Beam Steering 3D Printed Dielectric Lens Antennas for Millimeter-Wave and 5G Applications
Abstract
:1. Introduction
2. GRIN Lens Antenna Design Procedure
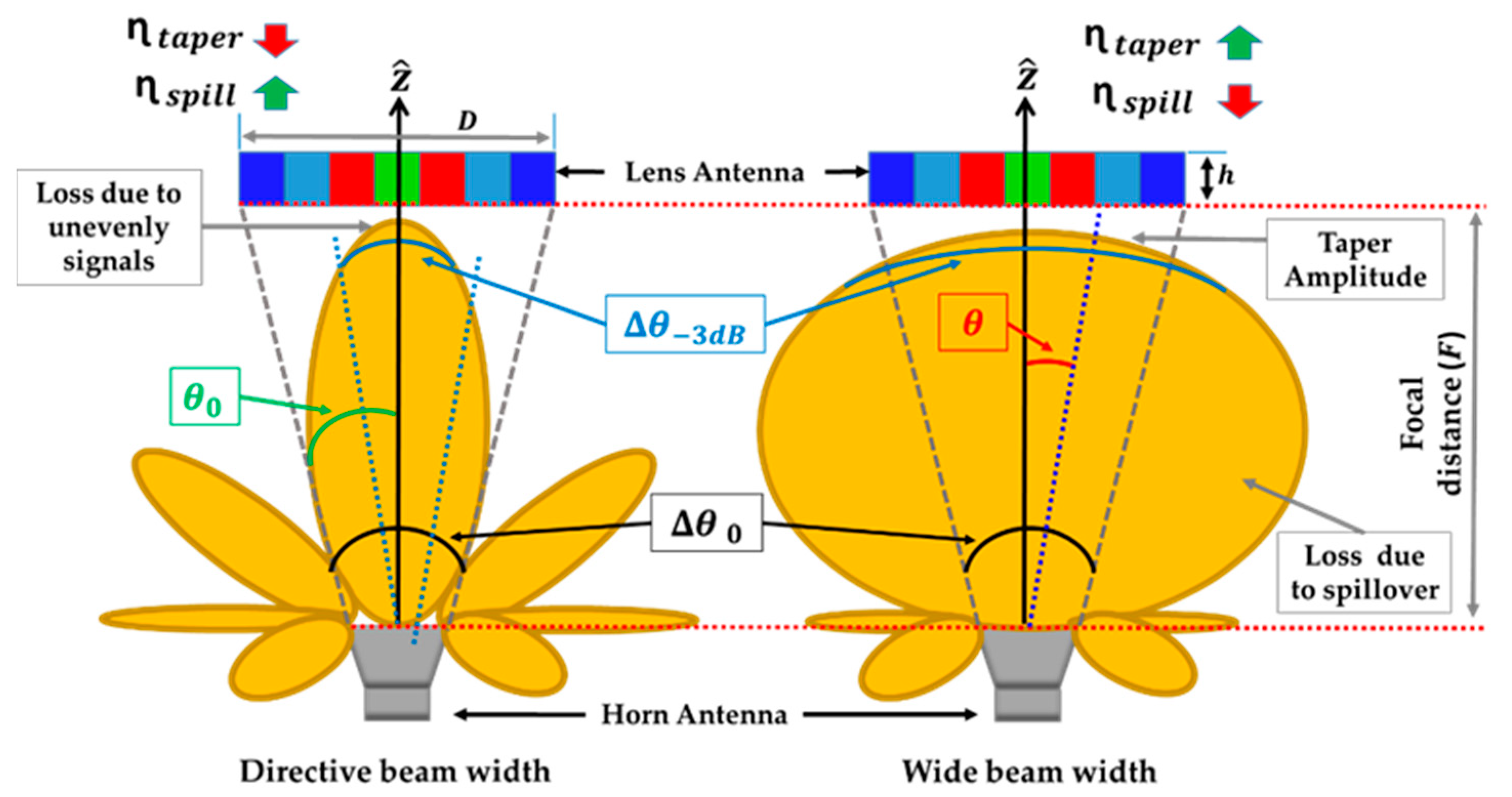
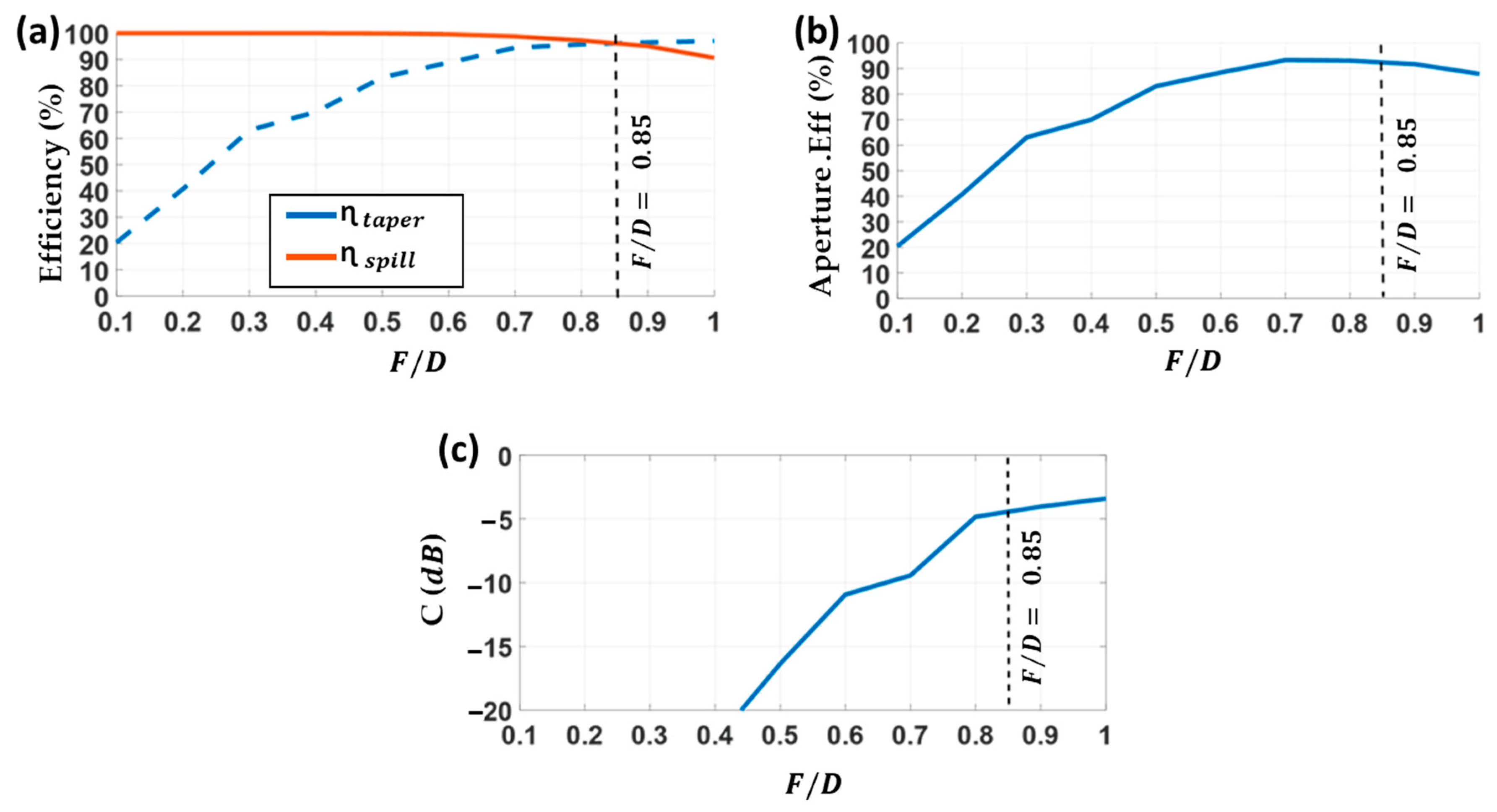
2.1. Aperture Efficiency Optimization
2.1.1. Feeder Radiation Pattern Influence
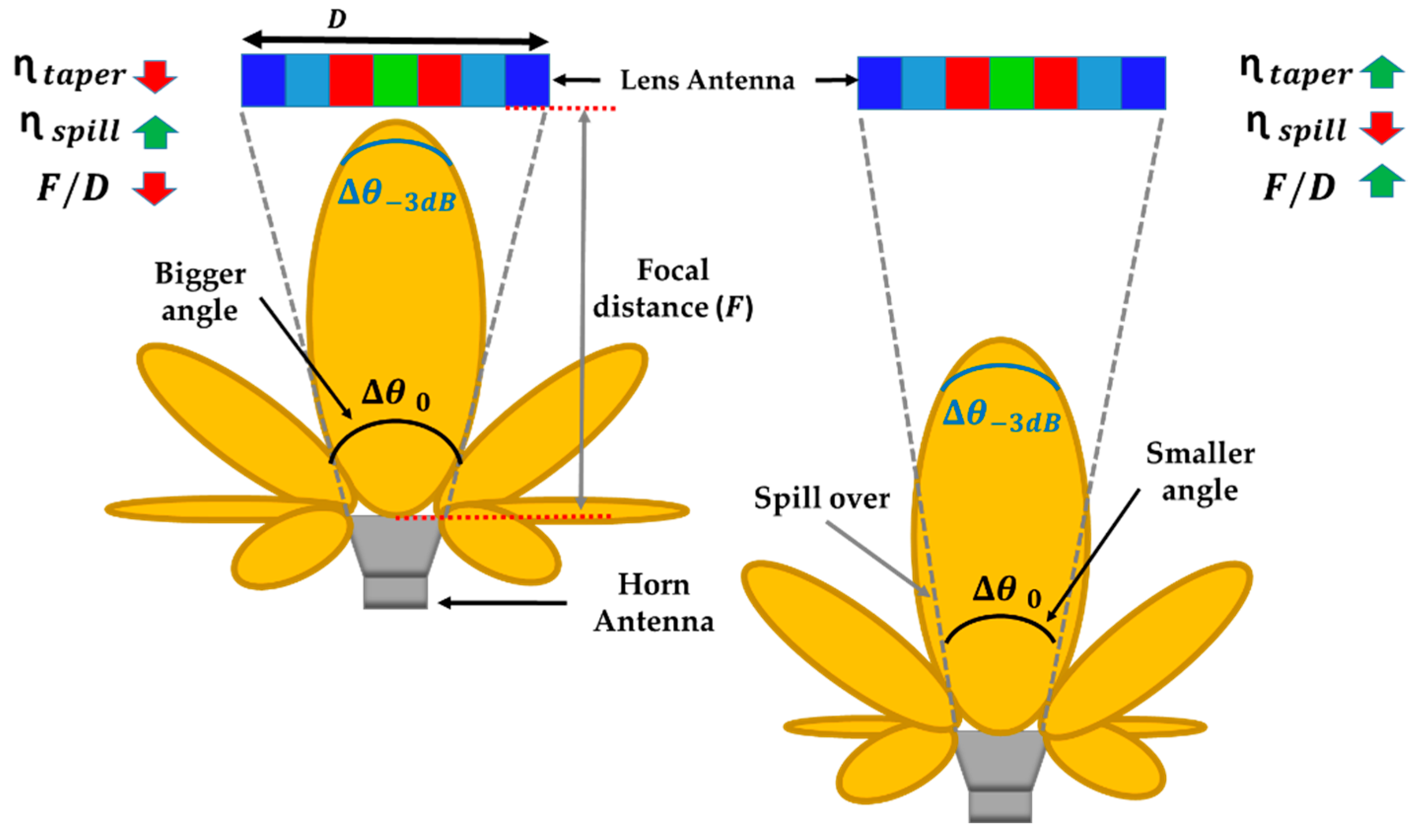
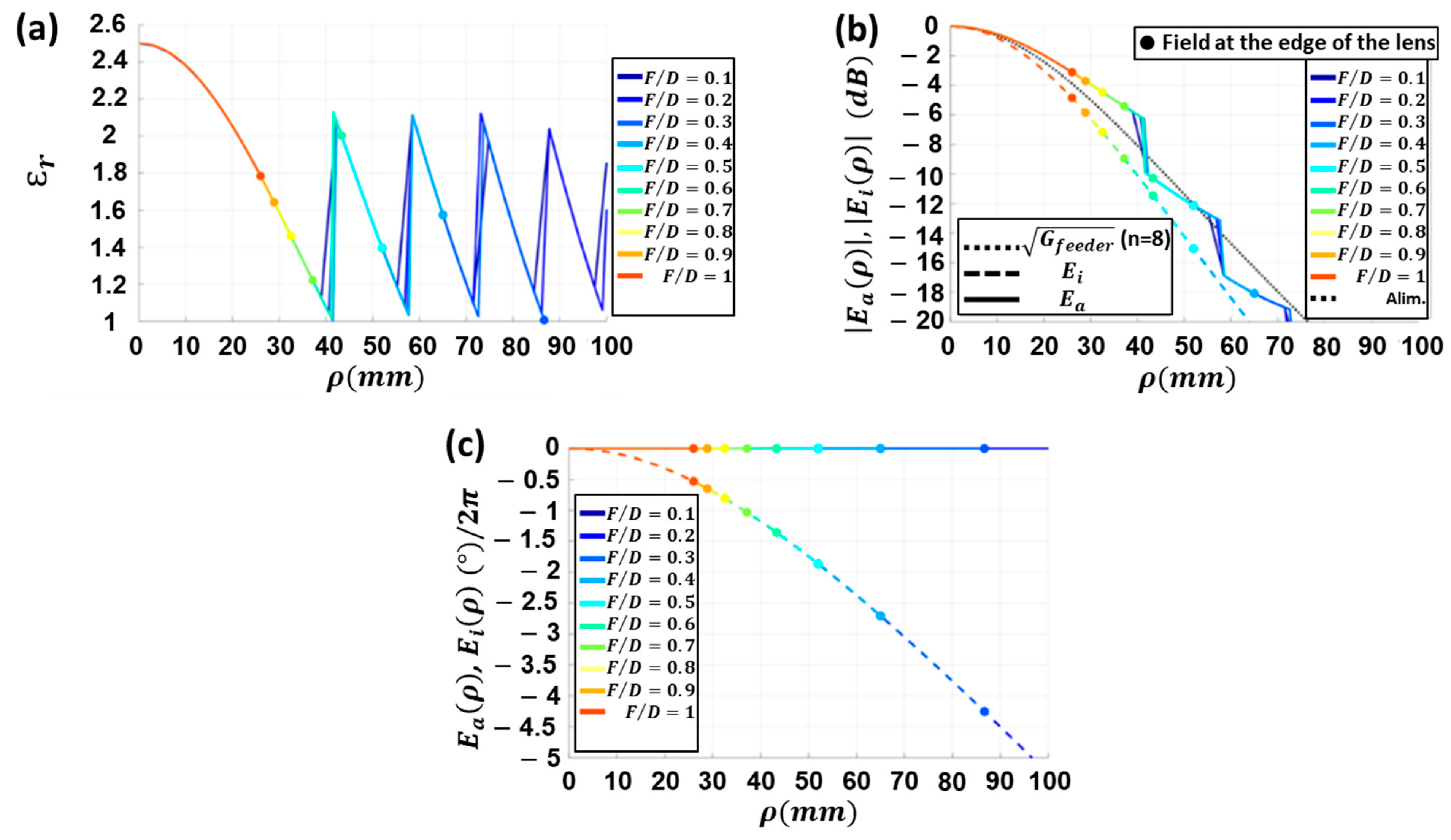
2.1.2. Focal Distance and Lens Diameter
2.2. Optimum Design
2.3. Phase Efficiency Optimization
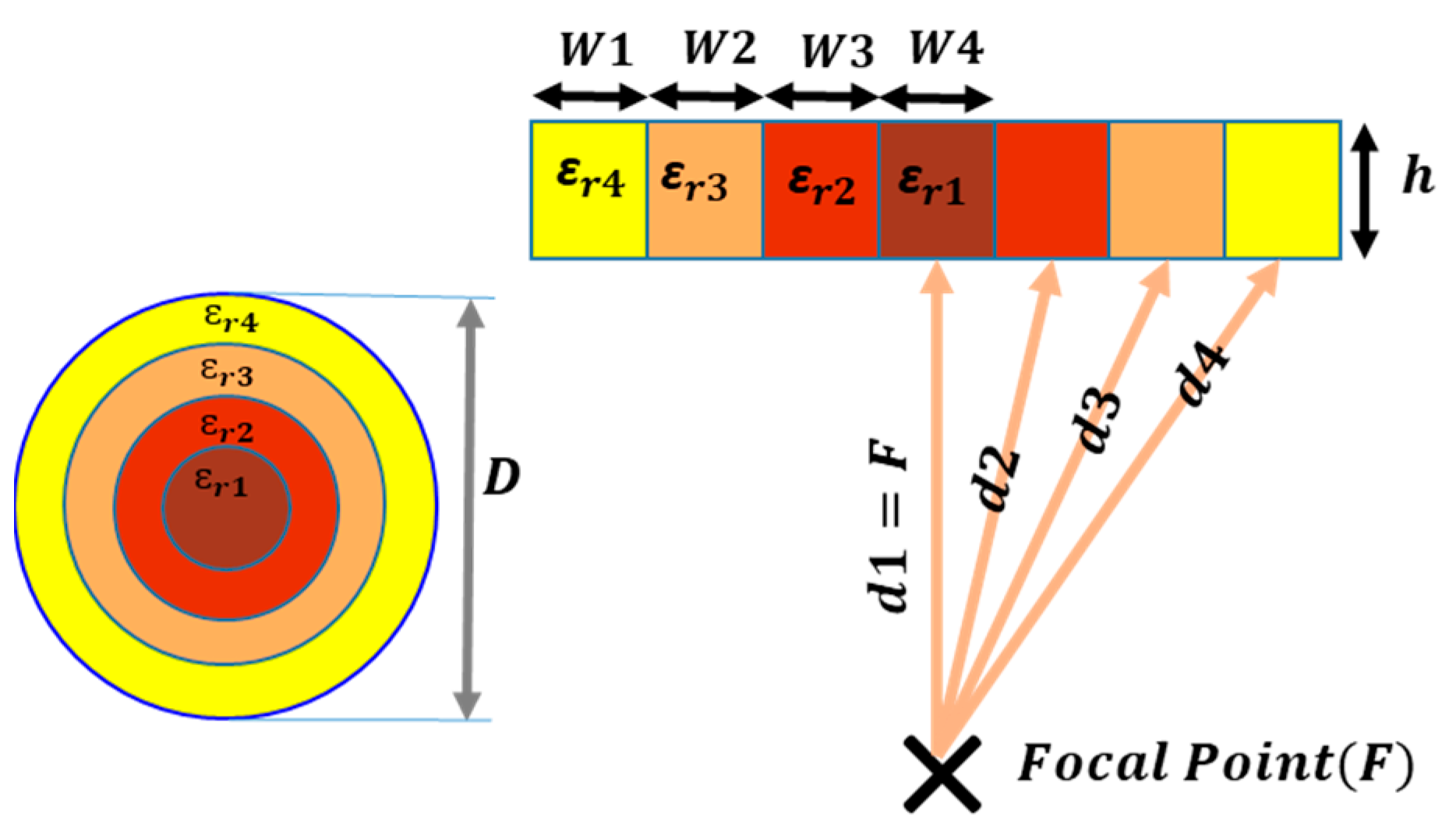
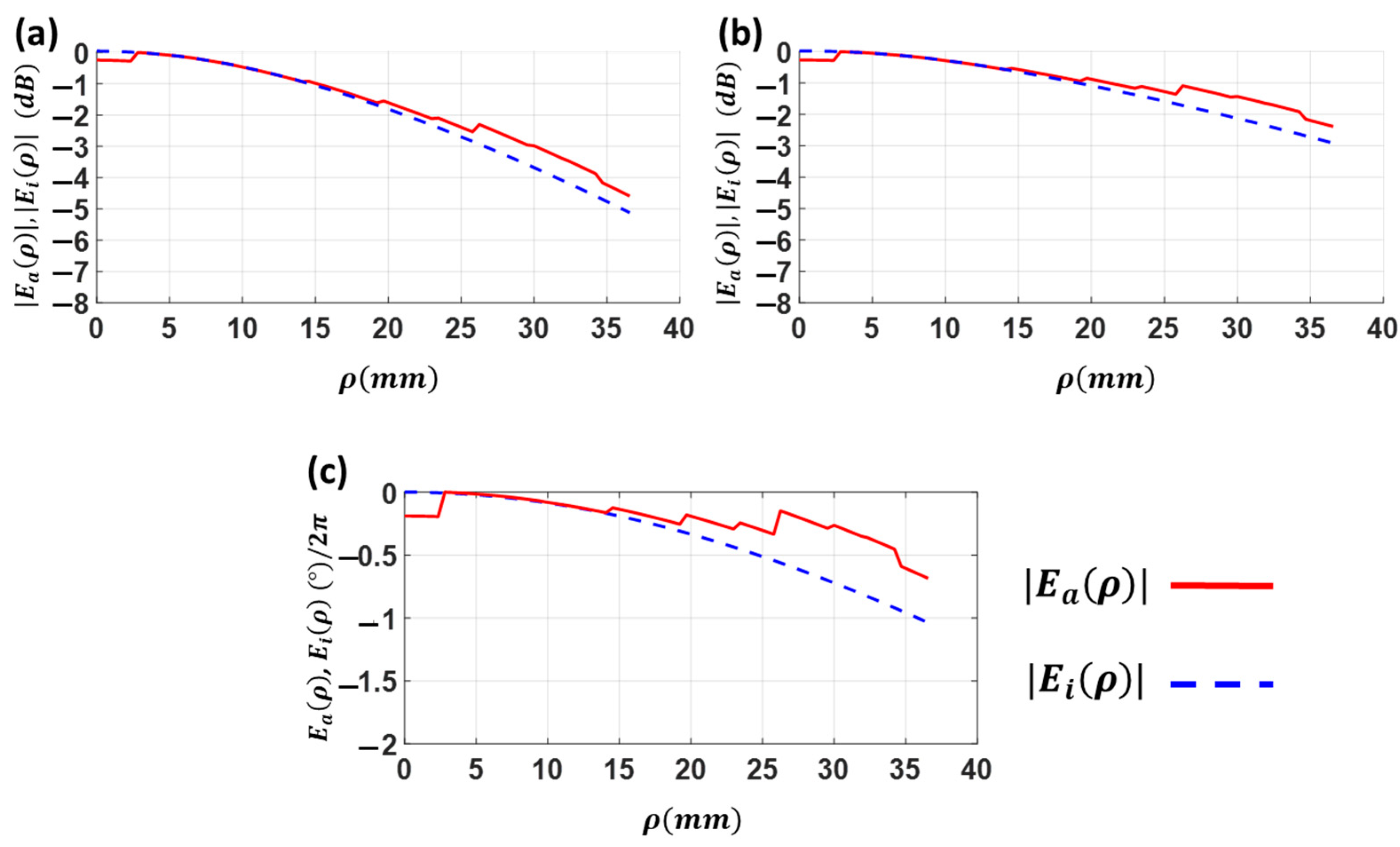
2.4. Perforated GRIN Lens
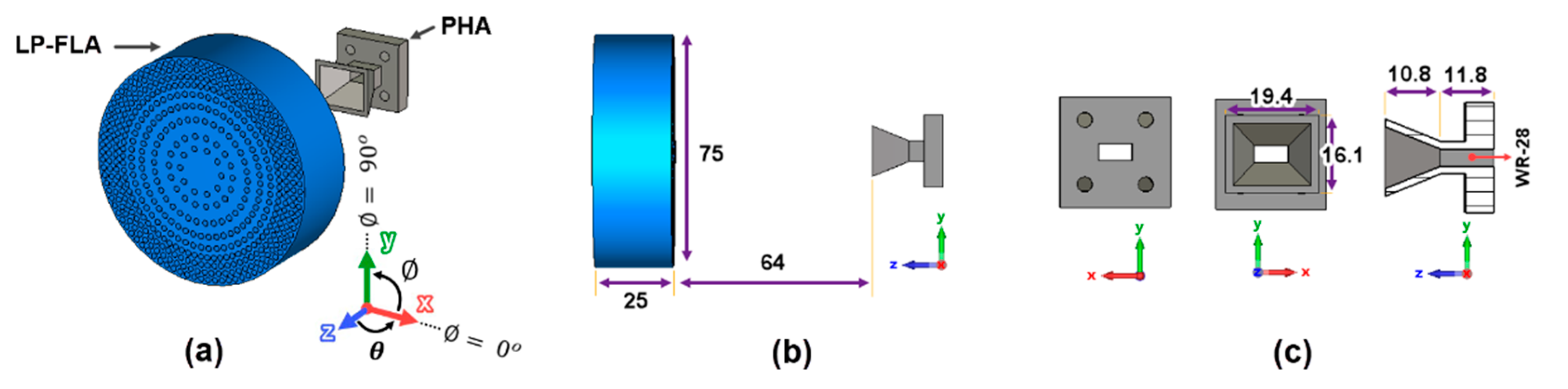
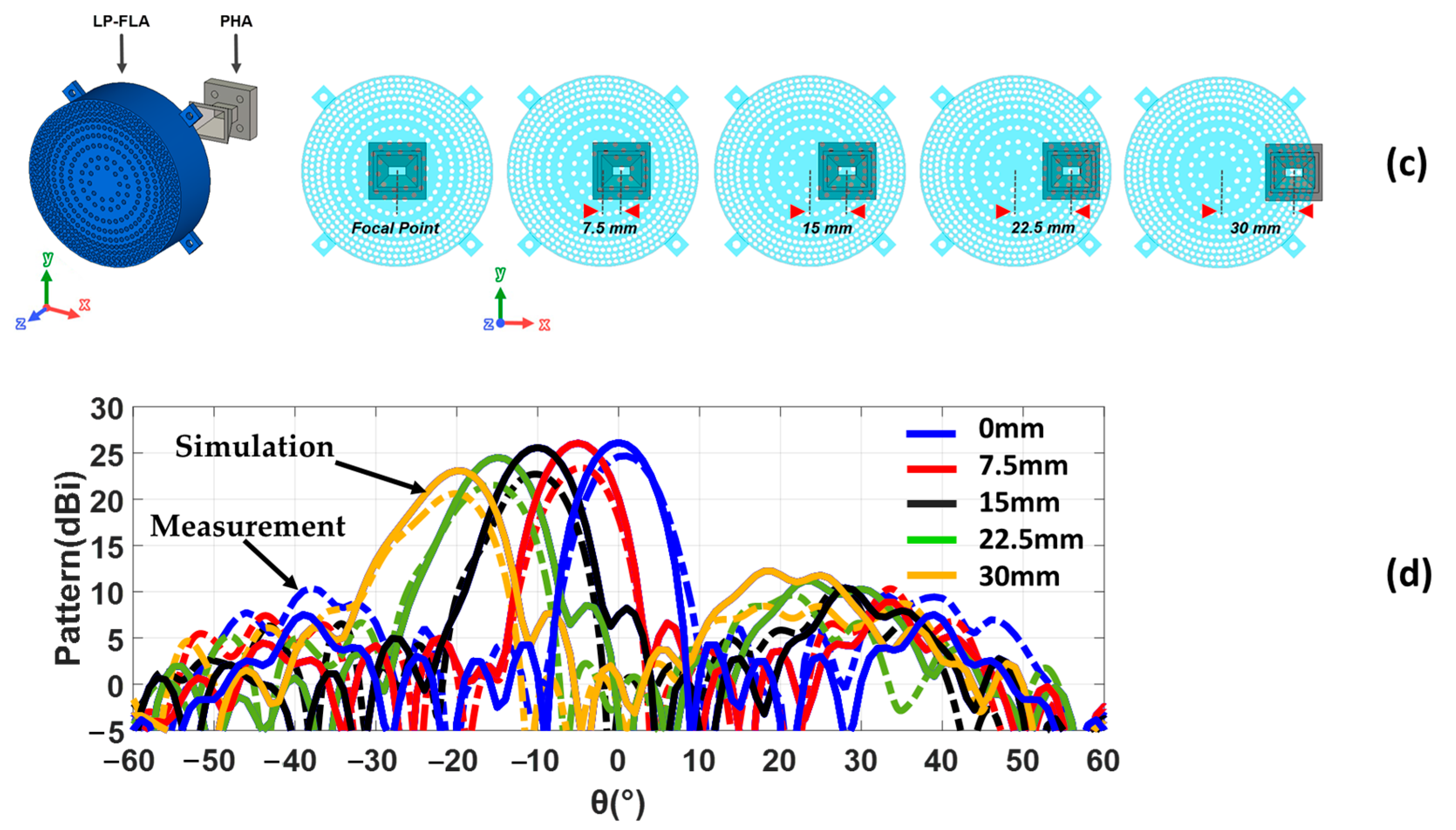
3. Linearly Polarized Flat Lens Antenna Fed by a Pyramidal Horn Antenna (LP-FLA + PHA)
3.1. Design Description
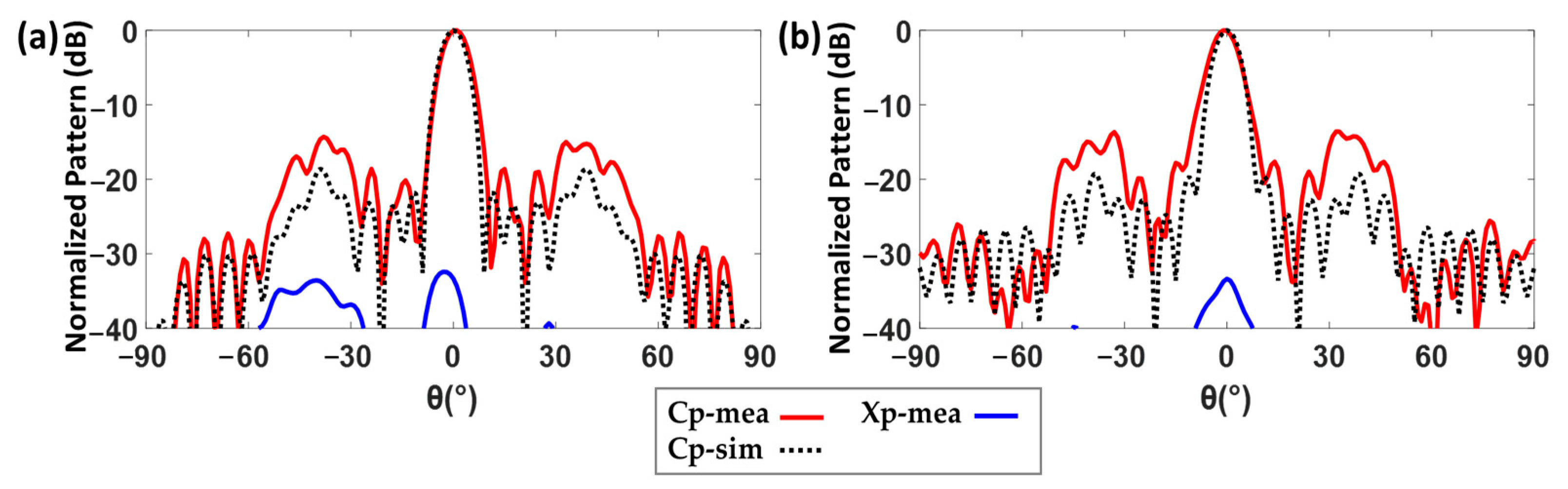
3.2. Experimental Results
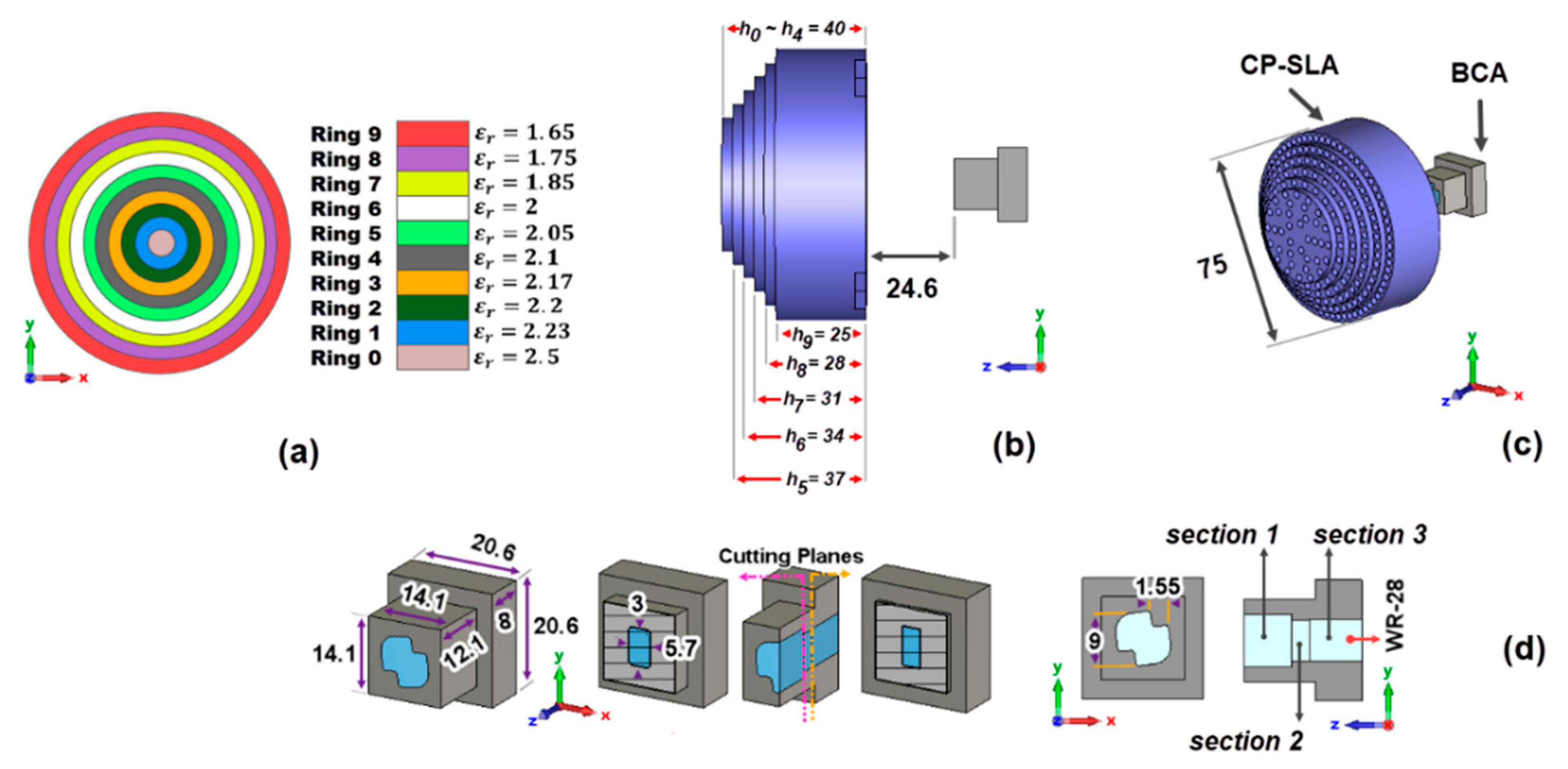
4. Circularly Polarized Stepped Lens Antenna Fed by a Bow-Tie Cavity Waveguide Antenna (CP-SLA + BCA) for Satellite 5G Applications
4.1. Design Description
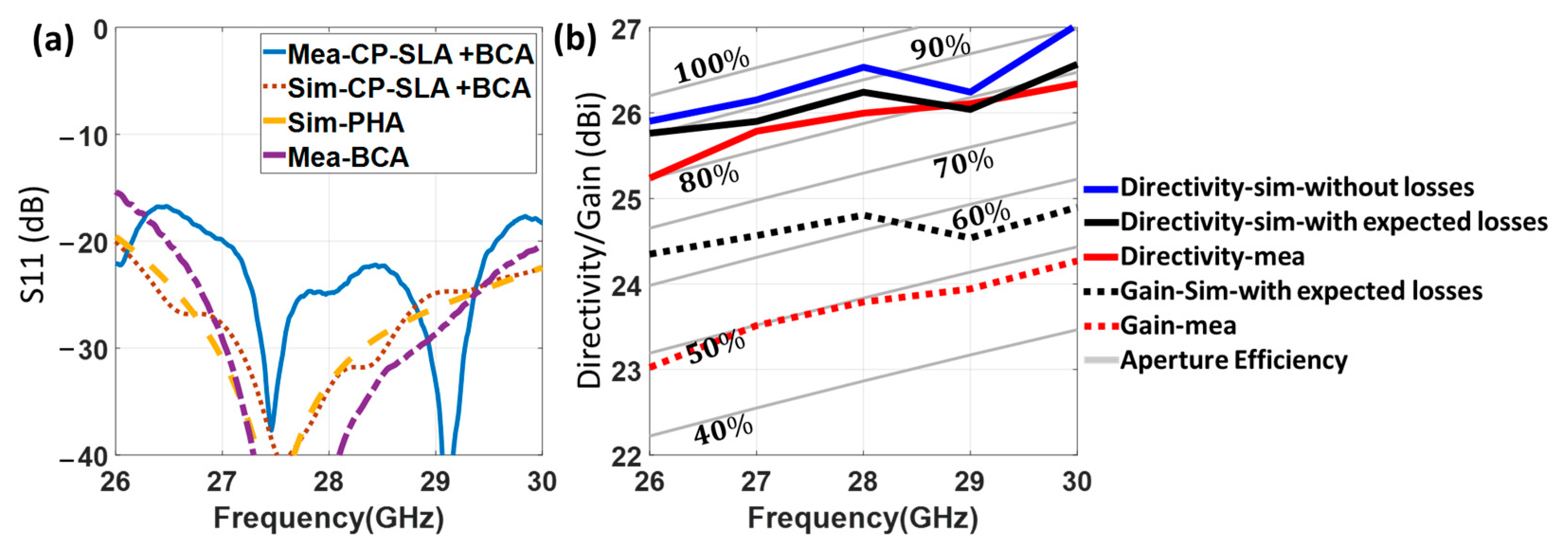
4.2. Experimental Results
5. Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.N.; Liu, D.; Nakano, H.; Qing, X.; Zwick, T. (Eds.) Handbook of Antenna Technologies; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Rao, K.S.; Cuchanski, M.; Tang, M.Q. Multiple beam antenna concepts for satellite communications. In Proceedings of the Symposium on Antenna Technology and Applied Electromagnetics [ANTEM 1994], Ottawa, ON, Canada, 3–5 August 1994. [Google Scholar]
- Chen, Z.N.; Luk, K.-M. (Eds.) Antennas for Base Stations in Wireless Communications; McGraw Hill: New York, NY, USA, 2009. [Google Scholar]
- Aljaloud, K.; Aladadi, Y.T.; Alkanhal, M.A.S.; Abdulkawi, W.M.; Hussain, R. A Wideband GRIN Dielectric Lens Antenna for 5G Applications. Micromachines 2023, 14, 997. [Google Scholar] [CrossRef]
- Hong, W.; Jiang, Z.H.; Yu, C.; Zhou, J.; Chen, P.; Yu, Z.; Zhang, H.; Yang, B.; Pang, X.; Jiang, M.; et al. Multibeam Antenna Technologies for 5G Wireless Communications. IEEE Trans. Antennas Propag. 2017, 65, 6231–6249. [Google Scholar] [CrossRef]
- Shen, L.P.; Wang, H.; Farzaneh, S.; Lotz, W.; Hojjat, N.; Gavrilovic, M. Dual band multi-beam base station antennas. In Proceedings of the IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017. [Google Scholar]
- Gao, F.; Xu, L.; Ma, S. Integrated Sensing and Communications with Joint Beam-Squint and Beam-Split for mmWave/THz Massive MIMO. IEEE Trans. Commun. 2023, 71, 2963–2976. [Google Scholar] [CrossRef]
- Wang, C.; Pang, M.; Zhong, D.; Cui, Y.; Wang, W. A MmWave communication testbed based on IEEE 802.11ad with scalable PtMP configuration. China Commun. 2022, 19, 44–56. [Google Scholar] [CrossRef]
- Tseng, C.H.; Chen, C.J.; Chu, T.H. A Low-Cost 60-GHz Switched-Beam Patch Antenna Array with Butler Matrix Network. IEEE Antennas Wirel. Propag. Lett. 2008, 7, 432–435. [Google Scholar] [CrossRef]
- Chieh, J.-C.S.; Dick, B.; Loui, S.; Rockway, J.D. Development of a Ku-Band Corrugated Conical Horn Using 3-D Print Technology. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 201–204. [Google Scholar] [CrossRef]
- Shao, W.; Chen, Q. 2-D Beam-Steerable Generalized Mikaelian Lens with Unique Flat-Shape Characteristic. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 2033–2037. [Google Scholar] [CrossRef]
- Garcia-Marin, E.; Filipovic, D.S.; Masa-Campos, J.L.; Sanchez-Olivares, P. Ka-band Multi-beam Planar Lens Antenna for 5G Applications. In Proceedings of the 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020. [Google Scholar]
- Costa, J.R.; Lima, E.B.; Fernandes, C.A. Compact Beam-Steerable Lens Antenna for 60-GHz Wireless Communications. IEEE Trans. Antennas Propag. 2009, 57, 2926–2933. [Google Scholar] [CrossRef] [Green Version]
- Baba, A.A.; Hashmi, R.M.; Attygalle, M.; Esselle, K.P.; Borg, D. Ultrawideband Beam Steering at mm-Wave Frequency with Planar Dielectric Phase Transformers. IEEE Trans. Antennas Propag. 2022, 70, 1719–1728. [Google Scholar] [CrossRef]
- Manafi, S.; González, J.M.F.; Filipovic, D.S. Design of a Perforated Flat Luneburg Lens Antenna Array for Wideband Millimeter-Wave Applications. In Proceedings of the 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019. [Google Scholar]
- Saleem, M.K.; Alkanhal, M.A.S.; Sheta, A.F.; Abdel-Rahman, M.; Himdi, M. Integrated lens antenna array with full azimuth plane beam scanning capability at 60 GHz. Microw. Opt. Technol. Lett. 2017, 59, 116–120. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Pichot, C.; Migliaccio, C.; Menzel, W. Study of Folded Reflector Multibeam Antenna with Dielectric Rods as Primary Source. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 786–789. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Jiao, Y.C.; Liu, S.B. 3-D-Printed Comb Mushroom-Like Dielectric Lens for Stable Gain Enhancement of Printed Log-Periodic Dipole Array. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2099–2103. [Google Scholar] [CrossRef]
- Farooqui, M.F.; Shamim, A. 3-D Inkjet-Printed Helical Antenna with Integrated Lens. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 800–803. [Google Scholar] [CrossRef] [Green Version]
- Mrnka, M.; Raida, Z. An Effective Permittivity Tensor of Cylindrically Perforated Dielectrics. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 66–69. [Google Scholar] [CrossRef]
- Su, Y.; Chen, Z.N. A Flat Dual-Polarized Transformation-Optics Beamscanning Luneburg Lens Antenna Using PCB-Stacked Gradient Index Metamaterials. IEEE Trans. Antennas Propag. 2018, 66, 5088–5097. [Google Scholar] [CrossRef]
- Ma, H.F.; Cai, B.G.; Zhang, T.X.; Yang, Y.; Jiang, W.X.; Cui, T.J. Three-Dimensional Gradient-Index Materials and Their Applications in Microwave Lens Antennas. IEEE Trans. Antennas Propag. 2013, 61, 2561–2569. [Google Scholar] [CrossRef]
- Melendro-Jimenez, J.; Sanchez-Olivares, P.; Tamayo-Dominguez, A.; Sun, X.; Fernandez-Gonzalez, J.M. 3D Printed Directive Beam-Steering Antenna Based on Gradient Index Flat Lens with an Integrated Polarizer for Dual Circular Polarization at W-Band. IEEE Trans. Antennas Propag. 2023, 71, 1059–1064. [Google Scholar] [CrossRef]
- Garcia-Marin, E.; Masa-Campos, J.L.; Sanchez-Olivares, P.; Ruiz-Cruz, J.A. Bow-Tie-Shaped Radiating Element for Single and Dual Circular Polarization. IEEE Trans. Antennas Propag. 2020, 68, 754–764. [Google Scholar] [CrossRef]
- Maeso, J.C.; Muriel Barrado, A.T.; Dominguez, A.T.; Olivares, P.S.; Gonzalez, J.M.F. Dual-band Multi-Polarization Metallic Cavity Antenna Design for Satellite Communications. In Proceedings of the 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design; Wiley-Interscience: New York, NY, USA, 2005. [Google Scholar]
- Garcia-Marin, E.; Filipovic, D.S.; Masa-Campos, J.L.; Sanchez-Olivares, P. Low-cost lens antenna for 5G multi-beam communication. Microw. Opt. Technol. Lett. 2020, 62, 3611–3622. [Google Scholar] [CrossRef]
- Ridler, N. Recommendations for waveguide sizes at submillimeter wavelengths. In Proceedings of the 73rd ARFTG Microwave Measurement Conference, Boston, MA, USA, 12 June 2009. [Google Scholar]
- Imbert, M.; Papió, A.; De Flaviis, F.; Jofre, L.; Romeu, J. Design and Performance Evaluation of a Dielectric Flat Lens Antenna for Millimeter-Wave Applications. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 342–345. [Google Scholar] [CrossRef] [Green Version]
- Erfani, E.; Niroo-Jazi, M.; Tatu, S. A High-Gain Broadband Gradient Refractive Index Metasurface Lens Antenna. IEEE Trans. Antennas Propag. 2016, 64, 1968–1973. [Google Scholar] [CrossRef]
- Qu, Z.; Qu, S.-W.; Zhang, Z.; Yang, S.; Chan, C.H. Wide-Angle Scanning Lens Fed by Small-Scale Antenna Array for 5G in MillimeterWave Band. IEEE Trans. Antennas Propag. 2020, 68, 3635–3643. [Google Scholar] [CrossRef]








| Ring (i) | No. of Holes | |||
|---|---|---|---|---|
| 0 | 2.75 | 0 | 0 | 2.5 |
| 1 | 9.5 | 2.75 | 10 | 2.241 |
| 2 | 14.5 | 9.5 | 18 | 2.244 |
| 3 | 19.25 | 14.5 | 34 | 2.18 |
| 4 | 23.4 | 19.25 | 48 | 2.07 |
| 5 | 26.25 | 23.4 | 66 | 1.99 |
| 6 | 29.7 | 26.25 | 76 | 1.75 |
| 7 | 32.25 | 29.7 | 80 | 1.70 |
| 8 | 34.65 | 32.25 | 82 | 1.69 |
| 9 | 37.5 | 34.65 | 88 | 1.82 |
| Ring (i) | No. of Holes | Height | |||
|---|---|---|---|---|---|
| 0 | 3.75 | 0 | 0 | 40 | 2.5 |
| 1 | 7.5 | 3.75 | 5 | 40 | 2.23 |
| 2 | 11.25 | 7.5 | 6 | 40 | 2.2 |
| 3 | 15 | 11.25 | 10 | 40 | 2.17 |
| 4 | 18.75 | 15 | 16 | 40 | 2.1 |
| 5 | 22.5 | 18.75 | 21 | 37 | 2.05 |
| 6 | 26.25 | 22.5 | 27 | 34 | 2 |
| 7 | 30 | 26.25 | 41 | 31 | 1.85 |
| 8 | 33.75 | 30 | 53 | 28 | 1.75 |
| 9 | 37.5 | 33.75 | 67 | 25 | 1.65 |
| Directivity-Mea | Directivity-Max (Theoretical) | Total Aper. Efficiency (%)-Mea | Realized Gain-Mea | Rad-Efficiency (%)-Mea | |||
|---|---|---|---|---|---|---|---|
| LP-FLA | 24.6 | 26.8 | 60 | 0.3 | 1.1 | 23.2 | 72 |
| CP-SLA | 26 | 26.8 | 82 | 0.2 | 2 | 23.8 | 60 |
| Ref. [27] | Ref. [29] | Ref. [30] | Ref. [4] | Ref. [31] | LP-FLA | CP-SLA | |
|---|---|---|---|---|---|---|---|
| Design Frequency () | 26 | 60 | 9.5 | 28 | 28 | 28 | 28 |
| Lens Type | Perforated Planar | Perforated Planar | Metamaterial lens | Perforated Planar | Perforated spherical | Perforated Planar | Perforated Stepped |
| Lens diameter | 6.7 λ0 | 6 λ0 | 4.56 λ0 | 3.2 λ0 | 10 λ0 | 7 λ0 | 7 λ0 |
| Lens Thickness | 2.2 λ0 | 1.4 λ0 | 0.38 λ0 | 0.7 λ0 | 7.3 λ0 | 2.3 λ0 | 2.3–3.7 λ0 |
| Lens feeder Spacing | 4.5 λ0 | 1.5 λ0 | 3.2 λ0 | 5.9 λ0 | 0.22 λ0 | 5.9 λ0 | 2.3 λ0 |
| Max measured Realized gain () | 20.2 | 18.3 | 21.5 | 20.7 | 21.2 | 23.6 | 24.3 |
| Feeder | Multi-port | WR-15 | antipodal exponential taper slot antenna | microstrip patch antenna | Phased Array antenna | Horn | Bow-tie antenna |
| Total Aper. efficiency (%) | 38 | N.A | 50 | N.A | 67 | 60 | 82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piroutiniya, A.; Rasekhmanesh, M.H.; Masa-Campos, J.L.; López-Hernández, J.; García-Marín, E.; Tamayo-Domínguez, A.; Sánchez-Olivares, P.; Ruiz-Cruz, J.A. Beam Steering 3D Printed Dielectric Lens Antennas for Millimeter-Wave and 5G Applications. Sensors 2023, 23, 6961. https://doi.org/10.3390/s23156961
Piroutiniya A, Rasekhmanesh MH, Masa-Campos JL, López-Hernández J, García-Marín E, Tamayo-Domínguez A, Sánchez-Olivares P, Ruiz-Cruz JA. Beam Steering 3D Printed Dielectric Lens Antennas for Millimeter-Wave and 5G Applications. Sensors. 2023; 23(15):6961. https://doi.org/10.3390/s23156961
Chicago/Turabian StylePiroutiniya, Asrin, Mohamad Hosein Rasekhmanesh, José Luis Masa-Campos, Javier López-Hernández, Eduardo García-Marín, Adrián Tamayo-Domínguez, Pablo Sánchez-Olivares, and Jorge A. Ruiz-Cruz. 2023. "Beam Steering 3D Printed Dielectric Lens Antennas for Millimeter-Wave and 5G Applications" Sensors 23, no. 15: 6961. https://doi.org/10.3390/s23156961
APA StylePiroutiniya, A., Rasekhmanesh, M. H., Masa-Campos, J. L., López-Hernández, J., García-Marín, E., Tamayo-Domínguez, A., Sánchez-Olivares, P., & Ruiz-Cruz, J. A. (2023). Beam Steering 3D Printed Dielectric Lens Antennas for Millimeter-Wave and 5G Applications. Sensors, 23(15), 6961. https://doi.org/10.3390/s23156961







