Sensor-Location-Specific Joint Acquisition of Peripheral Artery Bioimpedance and Photoplethysmogram for Wearable Applications
Abstract
:1. Introduction
2. Background and State of the Art
2.1. Features of Regional Impedance Measurements
2.2. Small Data Deep Learning for Biomedical Signals
3. Materials and Methods
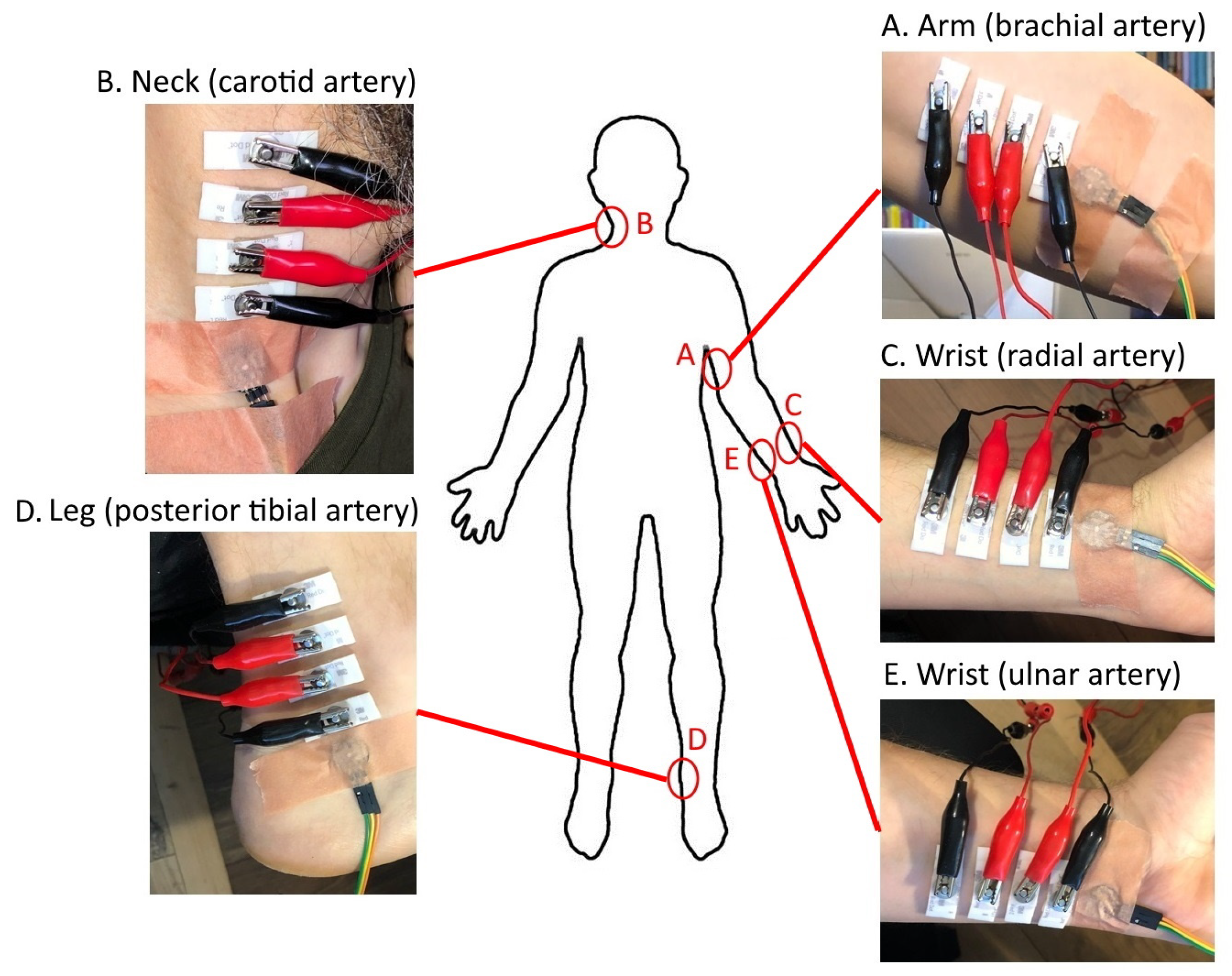
3.1. Measurement Devices
3.2. Measurement Method
- Closeness of the artery to the skin surface—enabling compact electrode configurations;
- Possibility of attaching a wearable device (sensor(s)) to the selected acquisition site.
3.3. Deep-Learning-Based Method and the Proposed CNN-Architecture-Based Model for Pulse Wave Signal Evaluation
- The mean value was removed, i.e., set to zero by subtracting from all of the values;
- The unit variance was found by dividing the values by the standard deviation (SD), marked as .
Proposed CNN Architecture for ICG and PPG Signal Evaluation
- Starting with average pooling (averagePooling1D)—as the initial data sample rate is high (1666 Hz), which is not necessary in EBI and PPG signal feature extraction, it is downsampled by averaging five values;
- One-dimensional convolution layer (Conv1D) with a kernel size of 4 for picking up the trivial features—activated by the rectified linear activation function (ReLU);
- Pooling layer (MaxPooling1D) for reducing the dimensions of features map;
- Convolution layer (Conv1D) with a kernel size of 20 for extracting more abstracted features;
- Pooling layer (MaxPooling1D) for further reduction in dimensions;
- Flattening of the previous layer (Flatten)—although the input is one-dimensional, an empty layer has been added previously to continue with fully connected layers;
- Fully connecting layer (Dense);
- Reduction in the overfitting by using dropout layer (rate of 0.3) (Dropout);
- Fully connected output layer (Dense) with a length dimension of 5 as the data have five different classes.
4. Results
5. Discussion
6. Limitations of the Work
7. Conclusions and Future Work
- For ΔZ(t), the carotid artery exhibits the highest sensitivity, while the posterior tibial artery outperforms all other locations in rPPG detection. In the case of summing the sensitivities of EBI and rPPG, the suggested location for a joint EBI and PPG acquisition-based wearable device would be the posterior tibial artery;
- The best average performance, i.e., continuity, throughout the four chosen excitation frequencies in the case of a joint acquisition of EBI and rPPG was experimentally proved to be delivered by the posterior tibial artery;
- The best average probability is provided when utilizing a classical excitation signal frequency of 100 kHz.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CVDs | Cardiovascular Diseases |
| PPG | Photoplethysmography |
| ECG | Electrocardiography |
| ICG | Impedance Cardiography |
| EBI | Electrical Bioimpedance |
| CAP | Central Aortic Pressure |
| rPPG | Reflection mode PPG |
| RICG | Regional ICG |
| CNN | Convolutional Neural Network |
| VAE | Variational Autoencoder |
| SD | Standard Deviation |
| CCA | Common Carotid Artery |
References
- Martinsen, O.G.; Grimnes, S. Bioimpedance and Bioelectricity Basics, 3rd ed.; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Sel, K.; Osman, D.; Huerta, N.; Edgar, A.; Pettigrew, R.; Jafari, R. Continuous cuffless blood pressure monitoring with a wearable ring bioimpedance device. NPJ Digit. Med. 2023, 6, 59. [Google Scholar] [CrossRef]
- Sokas, D.; Tamulevičiūtė-Prascienė, E.; Beigienė, A.; Barasaitė, V.; Marozas, J.; Kubilius, R.; Bailón, R.; Petrėnas, A. Wearable-Based Assessment of Heart Rate Response to Physical Stressors in Patients after Open-Heart Surgery with Frailty. IEEE J. Biomed. Health Inform. 2023, 27, 1825–1834. [Google Scholar] [CrossRef]
- Rachim, V.P.; Huynh, T.H.; Chung, W.Y. Wrist Photo-Plethysmography and Bio-Impedance Sensor for Cuff-Less Blood Pressure Monitoring. In Proceedings of the 2018 IEEE Sensors, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Priidel, E.; Pesti, K.; Min, M.; Ojarand, J.; Martens, O. FPGA-based 16-bit 20 MHz device for the inductive measurement of electrical bio-impedance. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Yao, Y.; Shin, S.; Mousavi, A.; Kim, C.S.; Xu, L.; Mukkamala, R.; Hahn, J.O. Unobtrusive Estimation of Cardiovascular Parameters with Limb Ballistocardiography. Sensors 2019, 19, 2922. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.V.; Mizuki, Y.; Tsukagoshi, T.; Takahata, T.; Ichiki, M.; Shimoyama, I. MEMS-Based Pulse Wave Sensor Utilizing a Piezoresistive Cantilever. Sensors 2020, 20, 1052. [Google Scholar] [CrossRef] [Green Version]
- Min, M.; Annus, P.; Kõiv, H.; Krivošei, A.; Uuetoa, T.; Lamp, J. Bioimpedance sensing–A viable alternative for tonometry in non-invasive assessment of central aortic pressure. In Proceedings of the 2017 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rochester, MN, USA, 7–10 May 2017; pp. 373–378. [Google Scholar] [CrossRef]
- Huynh, T.H.; Jafari, R.; Chung, W.Y. Noninvasive Cuffless Blood Pressure Estimation Using Pulse Transit Time and Impedance Plethysmography. IEEE Trans. Biomed. Eng. 2019, 66, 967–976. [Google Scholar] [CrossRef]
- Ibrahim, B.; Roozbeh, J. Cuffless blood pressure monitoring from a wristband with calibration-free algorithms for sensing location based on bio-impedance sensor array and autoencoder. Sci. Rep. 2022, 12, 319. [Google Scholar] [CrossRef] [PubMed]
- Sel, K.; Osman, D.; Jafari, R. Non-Invasive Cardiac and Respiratory Activity Assessment From Various Human Body Locations Using Bioimpedance. IEEE Open J. Eng. Med. Biol. 2021, 2, 210–217. [Google Scholar] [CrossRef]
- Charlton, P.H.; Paliakaitė, B.; Pilt, K.; Bachler, M.; Zanelli, S.; Kulin, D.; Allen, J.; Hallab, M.; Bianchini, E.; Mayer, C.C.; et al. Assessing hemodynamics from the photoplethysmogram to gain insights into vascular age: A review from VascAgeNet. Am. J. Physiol. Heart Circ. Physiol. 2022, 322, H493–H522. [Google Scholar] [CrossRef] [PubMed]
- Metshein, M.; Annus, P.; Land, R.; Min, M.; Aabloo, A. Availability and variations of cardiac activity in the case of measuring the bioimpedance of wrist. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, P.W.; Liu, C.P.; Lin, S.K.; Hu, W.C.; Kao, T. Evaluation of changes in cardiac output from the electrical impedance waveform in the forearm. Physiol. Meas. 2007, 28, 989–999. [Google Scholar] [CrossRef] [PubMed]
- Patterson, R. Fundamentals of impedance cardiography. IEEE Eng. Med. Biol. Mag. 1989, 8, 35–38. [Google Scholar] [CrossRef] [PubMed]
- Rahman, T.M.; Siddiqua, S.; Rabby, S.E.; Hasan, N.; Imam, M.H. Early Detection of Kidney Disease Using ECG Signals Through Machine Learning Based Modelling. In Proceedings of the 2019 International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 10–12 January 2019; pp. 319–323. [Google Scholar] [CrossRef]
- Moeyersons, J.; Morales, J.; Seeuws, N.; Van Hoof, C.; Hermeling, E.; Groenendaal, W.; Willems, R.; Van Huffel, S.; Varon, C. Artefact Detection in Impedance Pneumography Signals: A Machine Learning Approach. Sensors 2021, 21, 2613. [Google Scholar] [CrossRef]
- Trabelsi, I.; Francoise, J.; Bellik, Y. Sensor-Based Activity Recognition Using Deep Learning: A Comparative Study. In Proceedings of the 8th International Conference on Movement and Computing, MOCO’22, New York, NY, USA, 22–24 June 2022. [Google Scholar] [CrossRef]
- Shin, H.; Noh, G.; Choi, B.M. Photoplethysmogram based vascular aging assessment using the deep convolutional neural network. Sci. Rep. 2022, 12, 11377. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Watanabe, K.; Anzai, H.; Song, X.; Qiao, A.; Makoto, O. Pulse-Wave-Pattern Classification with a Convolutional Neural Network. Sci. Rep. 2019, 9, 14930. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Escalona, O.; Cullen, N.; Weli, I.; McCallan, N.; Ng, K.Y.; Finlay, D. Robust Arm Impedocardiography Signal Quality Enhancement Using Recursive Signal Averaging and Multi-Stage Wavelet Denoising Methods for Long-Term Cardiac Contractility Monitoring Armbands. Sensors 2023, 23, 5892. [Google Scholar] [CrossRef] [PubMed]
- Metshein, M.; Gautier, A.; Larras, B.; Frappe, A.; John, D.; Cardiff, B.; Annus, P.; Land, R.; Martens, O. Study of Electrode Locations for Joint Acquisition of Impedance- and Electro-cardiography Signals. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Mexico, 1–5 November 2021; p. 7264. [Google Scholar] [CrossRef]
- Brandao, A.A.; Amodeo, C.; Alcantara, C.; Barbosa, E.; Nobre, F.; Pinto, F.; Vilela-Martin, J.F.; Bastos, J.M.; Yugar-Toledo, J.C.; Mota-Gomes, M.A.; et al. I Luso-Brazilian Positioning on Central Arterial Pressure. Arq. Bras. Cardiol. 2017, 108, 100–108. [Google Scholar] [CrossRef]
- Cho, M.C.; Kim, J.Y.; Cho, S.H. A bio-impedance measurement system for portable monitoring of heart rate and pulse wave velocity using small body area. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems (ISCAS), Taipei, Taiwan, 24–27 May 2009; pp. 3106–3109. [Google Scholar] [CrossRef]
- Anand, G.; Lowe, A. Investigating Electrical Impedance Spectroscopy for Estimating Blood Flow-Induced Variations in Human Forearm. Sensors 2020, 20, 5333. [Google Scholar] [CrossRef]
- Ibrahim, B.; Jafari, R. Cuffless Blood Pressure Monitoring from an Array of Wrist Bio-Impedance Sensors Using Subject-Specific Regression Models: Proof of Concept. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 1723–1735. [Google Scholar] [CrossRef]
- Wang, T.W.; Chu, H.W.; Chou, L.; Sung, Y.L.; Shih, Y.T.; Hsu, P.C.; Cheng, H.M.; Lin, S.F. Bio-Impedance Measurement Optimization for High-Resolution Carotid Pulse Sensing. Sensors 2021, 21, 1600. [Google Scholar] [CrossRef]
- Bernstein, D.P.; Henry, I.C.; Banet, M.J.; Dittrich, T. Stroke volume obtained by electrical interrogation of the brachial artery: Transbrachial electrical bioimpedance velocimetry. Physiol. Meas. 2012, 33, 629. [Google Scholar] [CrossRef] [Green Version]
- Patterson, R.P. Impedance cardiography: What is the source of the signal? J. Phys. Conf. Ser. 2010, 224, 012118. [Google Scholar] [CrossRef]
- Pesti, K.; Metshein, M.; Annus, P.; Kõiv, H.; Min, M. Electrode Placement Strategies for the Measurement of Radial Artery Bioimpedance: Simulations and Experiments. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Metshein, M.; Annus, P.; Land, R.; Rist, M.; Min, M.; Märtens, O. Correlation between Electrical Bioimpedance and Pressure Waveform in Radial Artery and in Mechanical Pulsating Pipe System. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Kuba, W.; Conrad, T.O.F. Transfer learning for ECG classification. Sci. Rep. 2021, 11, 5251. [Google Scholar] [CrossRef]
- Romero, M.; Interian, Y.; Solberg, T.; Valdes, G. Targeted transfer learning to improve performance in small medical physics datasets. Med. Phys. 2020, 47, 6246–6256. [Google Scholar] [CrossRef]
- Stabenau, H.F.; Bridge, C.P.; Waks, J.W. ECGAug: A novel method of generating augmented annotated electrocardiogram QRST complexes and rhythm strips. Comput. Biol. Med. 2021, 134, 104408. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef] [Green Version]
- Nonaka, N.; Seita, J. RandECG: Data Augmentation for Deep Neural Network Based ECG Classification. In Proceedings of the Advances in Artificial Intelligence; Takama, Y., Matsumura, N., Yada, K., Matsushita, M., Katagami, D., Abe, A., Kashima, H., Hiraoka, T., Uchiya, T., Rzepka, R., Eds.; Springer: Cham, Switzerland, 2022; pp. 178–189. [Google Scholar] [CrossRef]
- Do, E.; Boynton, J.; Lee, B.S. Data Augmentation for 12-Lead ECG Beat Classification. SN Comput. Sci. 2022, 3, 70. [Google Scholar] [CrossRef]
- Zhu, F.; Ye, F.; Fu, Y.; Liu, Q.; Shen, B. Electrocardiogram generation with a bidirectional LSTM-CNN generative adversarial network. Sci. Rep. 2019, 9, 6734. [Google Scholar] [CrossRef] [Green Version]
- Kiyasseh, D.; Tadesse, G.A.; Nhan, L.N.T.; Van Tan, L.; Thwaites, L.; Zhu, T.; Clifton, D. PlethAugment: GAN-Based PPG Augmentation for Medical Diagnosis in Low-Resource Settings. IEEE J. Biomed. Health Inform. 2020, 24, 3226–3235. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Kuznetsov, V.V.; Moskalenko, V.A.; Gribanov, D.V.; Zolotykh, N.Y. Interpretable Feature Generation in ECG Using a Variational Autoencoder. Front. Genet. 2021, 12, 638191. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar] [CrossRef]
- Zurich Instruments. HF2 User Manual–ziControl Edition; Zurich Instruments: Zurich, Switzerland, 2019. [Google Scholar]
- Tamura, T.; Maeda, Y.; Sekine, M.; Yoshida, M. Wearable Photoplethysmographic Sensors—Past and Present. Electronics 2014, 3, 282–302. [Google Scholar] [CrossRef]
- Aliau-Bonet, C.; Pallas-Areny, R. A Novel Method to Estimate Body Capacitance to Ground at Mid Frequencies. IEEE Trans. Instrum. Meas. 2013, 62, 2519–2525. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef] [Green Version]
- Krejza, J.; Arkuszewski, M.; Kasner, S.E.; Weigele, J.; Ustymowicz, A.; Hurst, R.W.; Cucchiara, B.L.; Messe, S.R. Carotid Artery Diameter in Men and Women and the Relation to Body and Neck Size. Stroke 2006, 37, 1103–1105. [Google Scholar] [CrossRef] [Green Version]
- Wahood, W.; Ghozy, S.; Al-Abdulghani, A.; Kallmes, D.F. Radial artery diameter: A comprehensive systematic review of anatomy. J. Neurointerventional Surg. 2022, 14, 1274–1278. [Google Scholar] [CrossRef]
- Andreuccetti, D.; Fossi, R.; Petrucci, C. An Internet Resource for the Calculation of the Dielectric Properties of Body Tissues in the Frequency Range 10 Hz–100 GHz. 1997. Based on Data Published by C. Gabriel et al. in 1996. Available online: http://niremf.ifac.cnr.it/tissprop/ (accessed on 3 January 2023).
- Ibrahim, B.; Hall, D.A.; Jafari, R. Bio-impedance spectroscopy (BIS) measurement system for wearable devices. In Proceedings of the 2017 IEEE Biomedical Circuits and Systems Conference (BioCAS), Turin, Italy, 19–21 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Heiman, D.F.; Rodbard, S.; Shaffer, A.B.; Snider, G.L. Respiratory Factors Affecting Pulmonary Arterial Blood Pressure and Flow Through the Lungs. J. Appl. Physiol. 1957, 10, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Sel, K.; Brown, A.; Jang, H.; Krumholz, H.M.; Lu, N.; Jafari, R. A Wrist-worn Respiration Monitoring Device using Bio-Impedance. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 3989–3993. [Google Scholar] [CrossRef]
- Tronstad, C.; Callender, N.A.; Badeli, V.; Hisdal, J. A Flexible Electrode Strap for Impedance Plethysmography of the Dorsalis Pedis Artery. In Proceedings of the 2023 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4.0 & IoT), Brescia, Italy, 6–8 June 2023; pp. 113–117. [Google Scholar] [CrossRef]
- Diaz, D.H.; Casas, O.; Pallas-Areny, R. Heart rate detection from single-foot plantar bioimpedance measurements in a weighing scale. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 6489–6492. [Google Scholar] [CrossRef]
- Metshein, M.; Krivošei, A.; Abdullayev, A.; Annus, P.; Märtens, O. Non-Standard Electrode Placement Strategies for ECG Signal Acquisition. Sensors 2022, 22, 9351. [Google Scholar] [CrossRef]





| Layer Type | No. Channels | Length Dimension | No. of Parameters |
|---|---|---|---|
| AveragePooling1D | 1 | 299 | - |
| Conv1D | 4 | 296 | 20 |
| MaxPooling1D | 4 | 74 | - |
| Conv1D | 10 | 55 | 810 |
| MaxPooling1D | 10 | 5 | - |
| Flatten | - | 50 | - |
| Dense | - | 64 | 3264 |
| Dropout | - | 64 | - |
| Dense | - | 5 | 325 |
| Signal Acquisition Site | Z(t)mean ± () | rPPG(t)mean ± (V) |
|---|---|---|
| Brachial artery (A) | 0.029 ± 0.0005 | 0.068 ± 0.0039 |
| Carotid artery (B) | 11.123 ± 0.1500 | 0.225 ± 0.0164 |
| Radial artery (C) | 0.085 ± 0.0229 | 0.216 ± 0.0227 |
| Posterior tibial artery (D) | 0.304 ± 0.0253 | 0.413 ± 0.0598 |
| Ulnar artery (E) | 0.167 ± 0.0279 | 0.158 ± 0.0336 |
| Signal | Av. Acc. (%) | Av. Prob. (%) |
|---|---|---|
| EBI at 50 kHZ | 70.00 | 45.91 |
| EBI at 100 kHZ | 80.00 | 52.35 |
| EBI at 500 kHZ | 84.00 | 43.35 |
| EBI at 1000 kHZ | 96.00 | 47.02 |
| rPPG | 98.00 | 77.22 |
| Signal Acquisition Site | Av. Prob. of EBI at 50 kHZ (%) | Av. Prob. of EBI at 100 kHZ (%) | Av. Prob. of EBI at 500 kHZ (%) | Av. Prob. of EBI at 1000 kHZ (%) | Av. Prob. of rPPG (%) |
|---|---|---|---|---|---|
| Brachial artery (A) | 23.15 | 16.67 | 20.74 | 32.50 | 77.41 |
| Carotid artery (B) | 50.19 | 64.81 | 59.07 | 63.52 | 61.20 |
| Radial artery (C) | 57.13 | 45.65 | 48.52 | 41.39 | 71.48 |
| Posterior tibial artery (D) | 36.57 | 54.72 | 53.06 | 53.70 | 97.87 |
| Ulnar artery (E) | 62.50 | 79.81 | 35.37 | 43.98 | 78.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Metshein, M.; Abdullayev, A.; Gautier, A.; Larras, B.; Frappe, A.; Cardiff, B.; Annus, P.; Land, R.; Märtens, O. Sensor-Location-Specific Joint Acquisition of Peripheral Artery Bioimpedance and Photoplethysmogram for Wearable Applications. Sensors 2023, 23, 7111. https://doi.org/10.3390/s23167111
Metshein M, Abdullayev A, Gautier A, Larras B, Frappe A, Cardiff B, Annus P, Land R, Märtens O. Sensor-Location-Specific Joint Acquisition of Peripheral Artery Bioimpedance and Photoplethysmogram for Wearable Applications. Sensors. 2023; 23(16):7111. https://doi.org/10.3390/s23167111
Chicago/Turabian StyleMetshein, Margus, Anar Abdullayev, Antoine Gautier, Benoit Larras, Antoine Frappe, Barry Cardiff, Paul Annus, Raul Land, and Olev Märtens. 2023. "Sensor-Location-Specific Joint Acquisition of Peripheral Artery Bioimpedance and Photoplethysmogram for Wearable Applications" Sensors 23, no. 16: 7111. https://doi.org/10.3390/s23167111
APA StyleMetshein, M., Abdullayev, A., Gautier, A., Larras, B., Frappe, A., Cardiff, B., Annus, P., Land, R., & Märtens, O. (2023). Sensor-Location-Specific Joint Acquisition of Peripheral Artery Bioimpedance and Photoplethysmogram for Wearable Applications. Sensors, 23(16), 7111. https://doi.org/10.3390/s23167111






