A Mechanical Defect Localization and Identification Method for High-Voltage Circuit Breakers Based on the Segmentation of Vibration Signals and Extraction of Chaotic Features
Abstract
:1. Introduction
2. Chaotic Feature Extraction Method of Vibration Signals Based on Phase-Space Reconstruction
2.1. Phase-Space Reconstruction
2.1.1. Time Delay
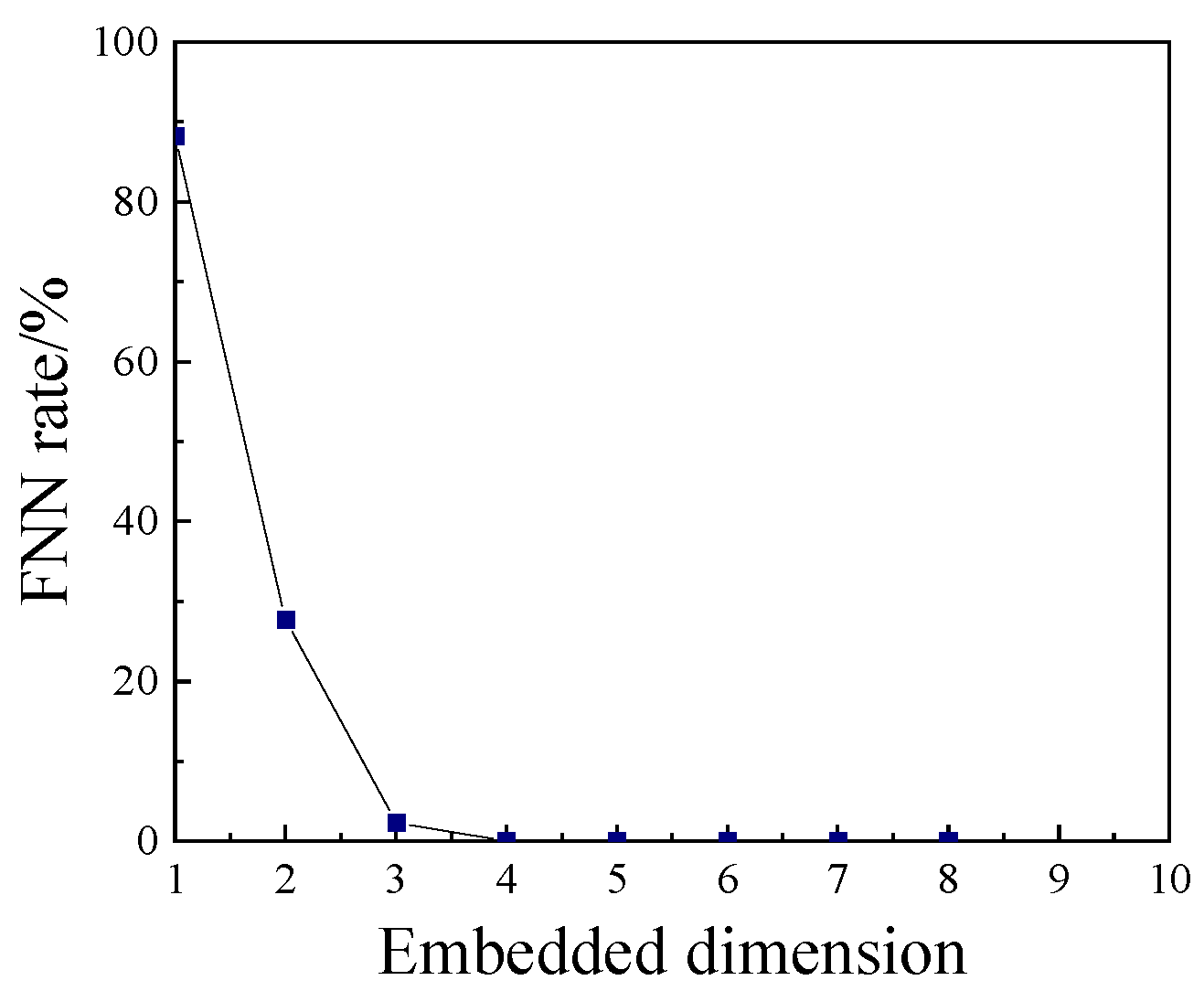
2.1.2. Embedding Dimension
2.2. Chaotic Features of the Vibration Signal
2.2.1. Largest Lyapunov Exponent
- First, the initial vector is constructed, the initial point corresponding to the initial time is selected in the time series, and the phase locus point , which is closest to , is selected in the high-dimensional phase space to form the initial vector. The Euclidean distance between the two phase points is calculated as ;
- Assume that the time step is . After a time step, , a new vector is obtained, and the Euclidean distance between the base point and the endpoint is calculated. In the corresponding time step, the exponential growth rate of the phase point distance is ;
- The estimated value of LLE is obtained by summing the growth rate of each linear index of the system and taking the average value: , where N is the number of phase points;
- While increasing the embedding dimension , repeat the above steps until LLE changes smoothly; the resulting value is the largest Lyapunov exponent.
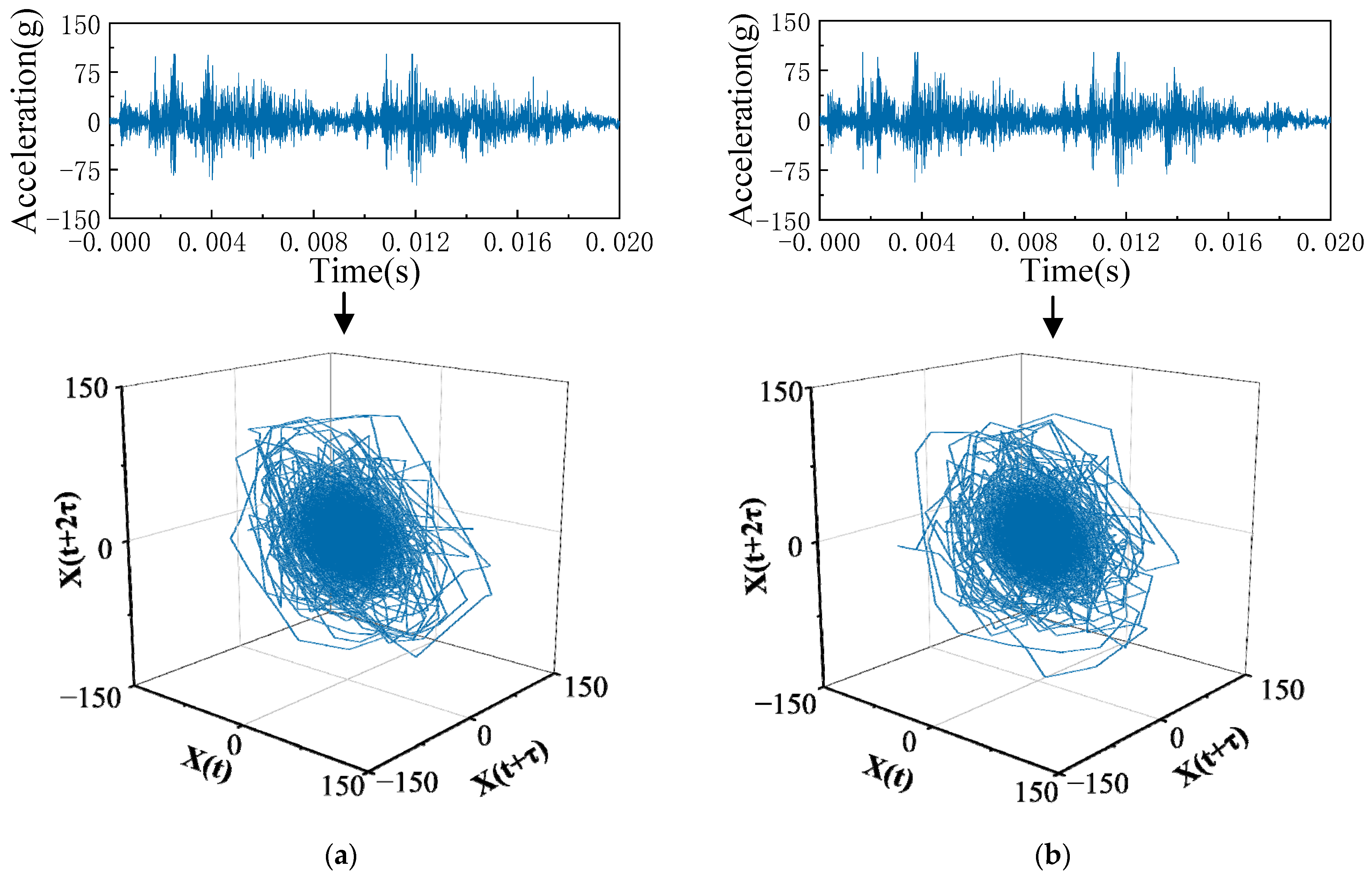
2.2.2. Phase Trajectory Feature
3. A Time-Sharing Division Processing Method for Vibration Signals during Circuit Breaker Operation
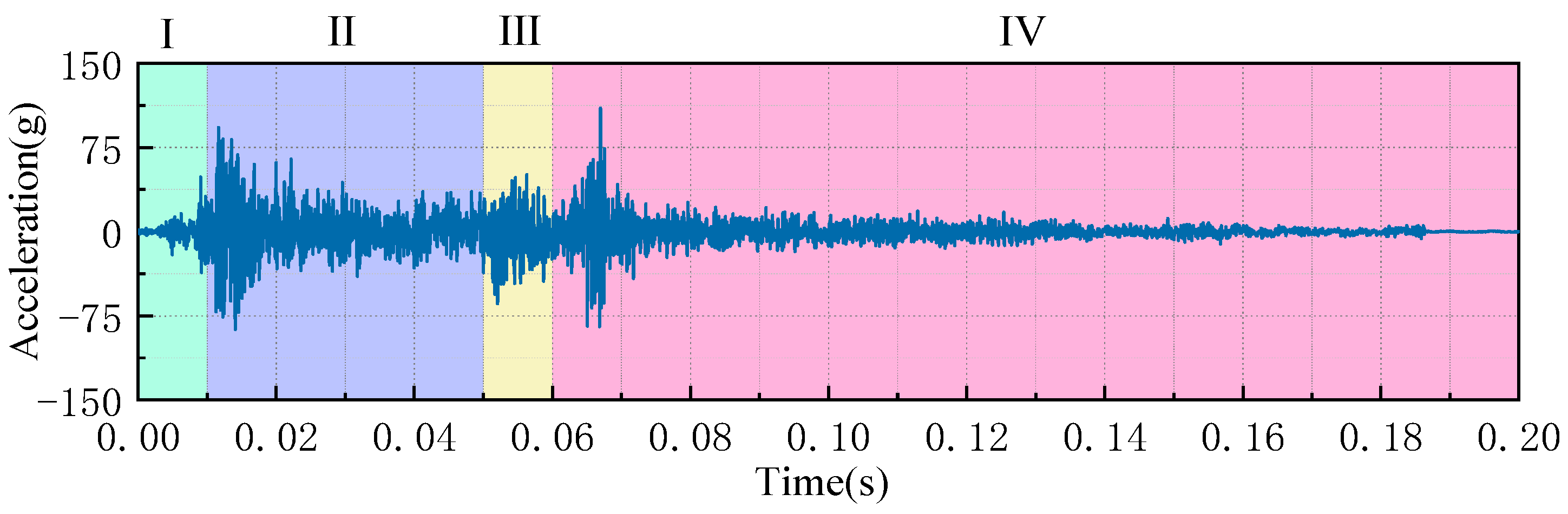
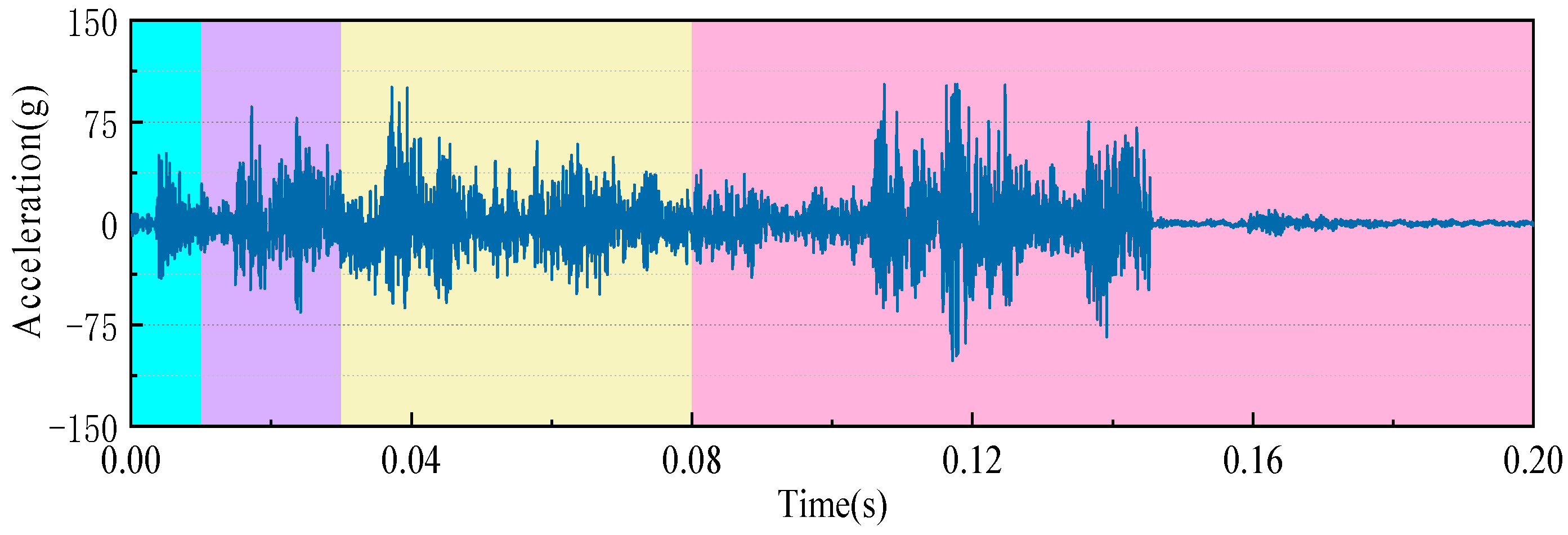
3.1. Time-Sharing Division of Vibration Signals
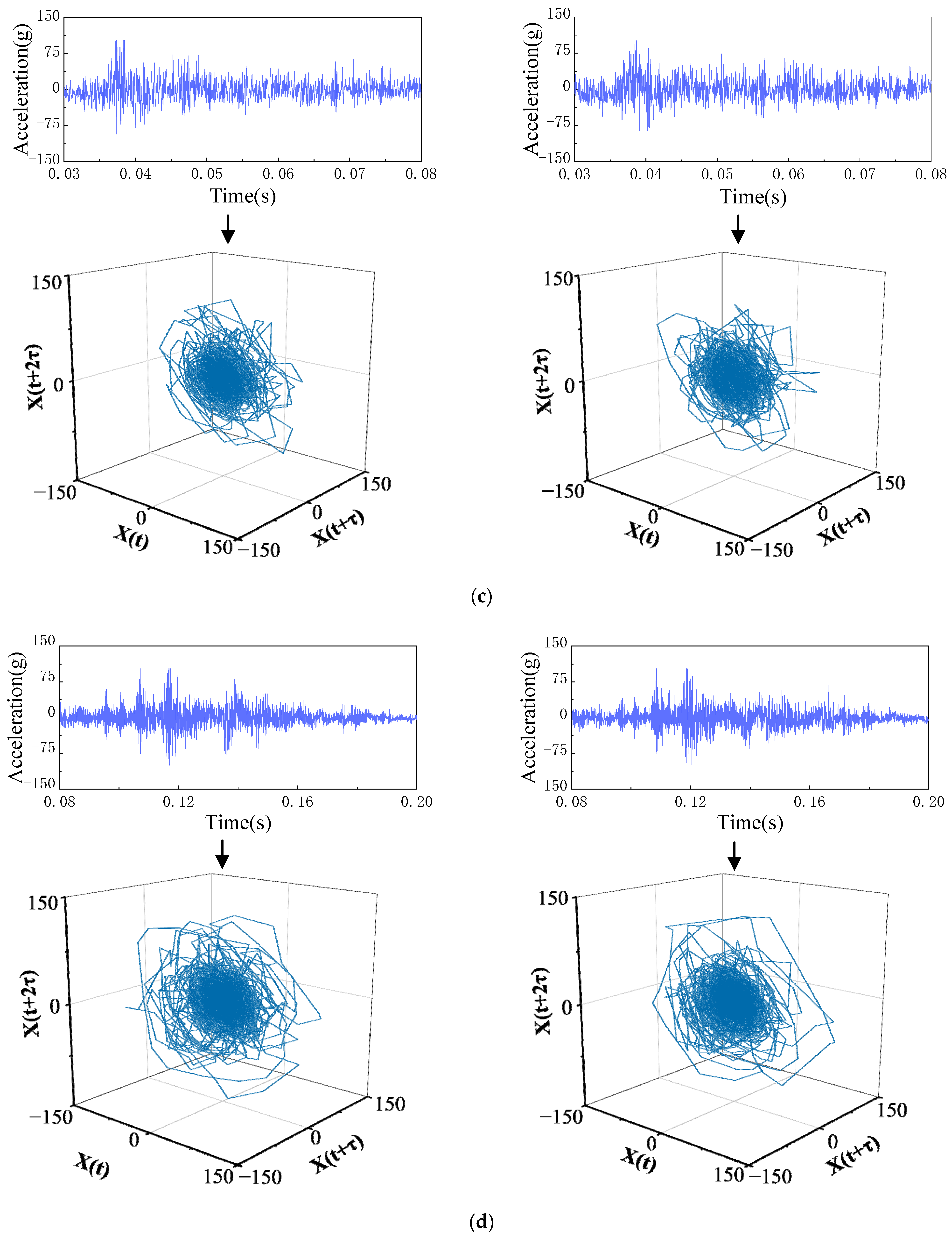
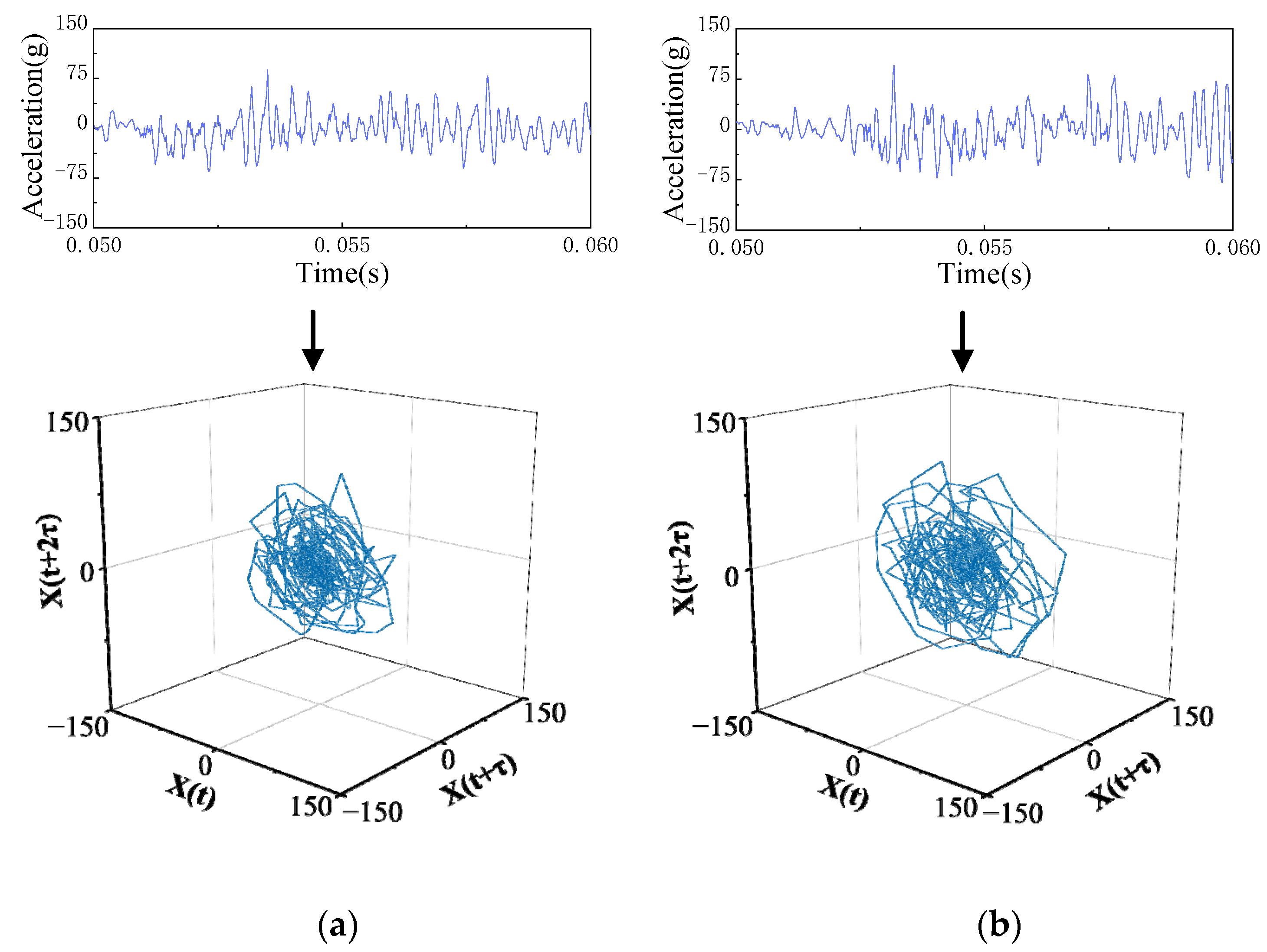
3.2. Vibration Signal Phase-Space Reconstruction in Substages
4. Vibration Signal Feature Extraction and Mechanical Defect Identification of the Circuit Breaker Operating Mechanism
4.1. Mechanical Defect Simulation and Vibration Signal Monitoring of the Circuit Breaker Operating Mechanism
4.2. Chaotic Feature Extraction of the Vibration Signal Substage
4.2.1. LLE of the Vibration Signal Substage
4.2.2. Trajectory Features of the Vibration Signal Substage
4.3. Mechanical Defect Identification of the Circuit Breaker Operating Mechanism
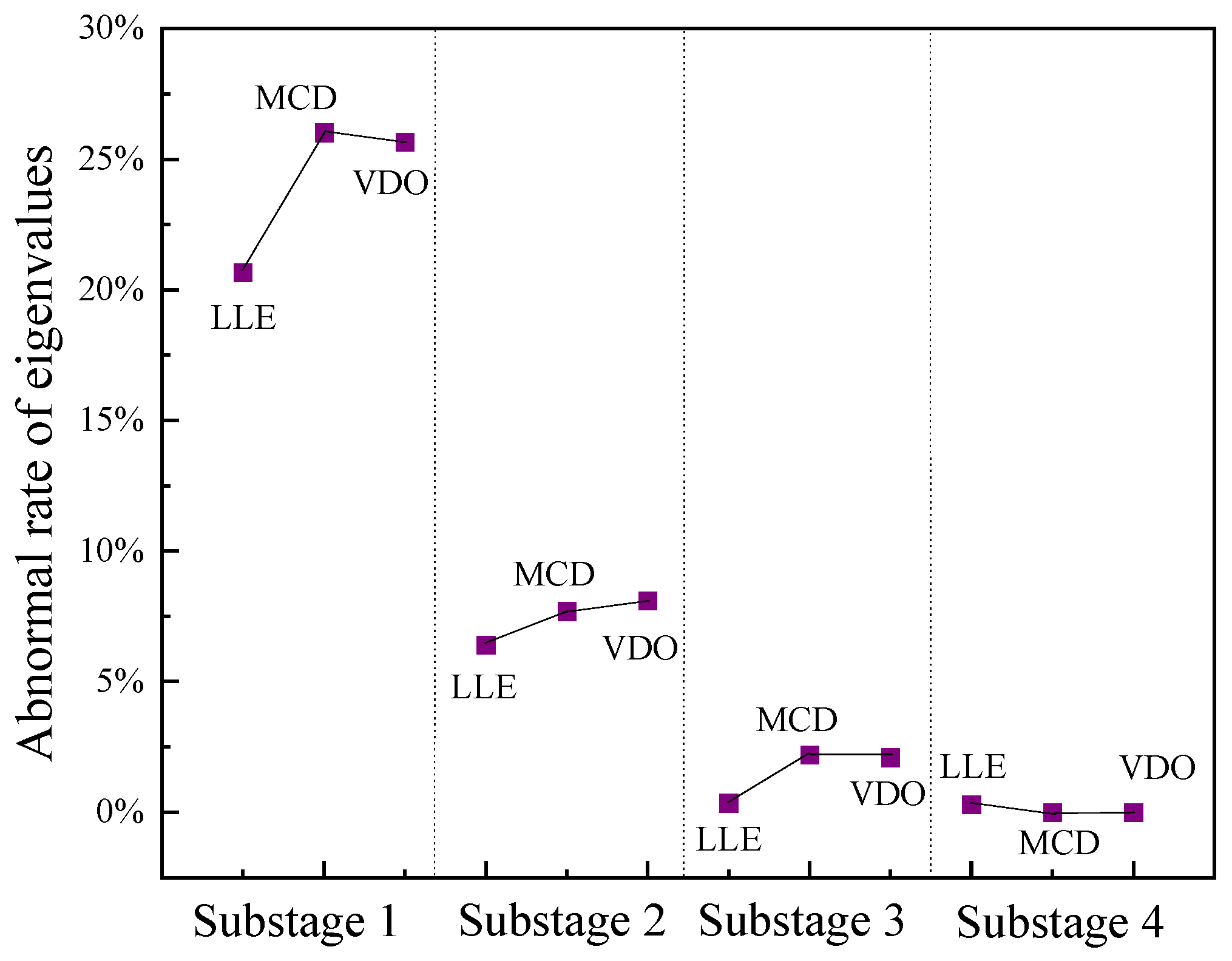
4.3.1. Mechanical Defect Vibration Substage Localization
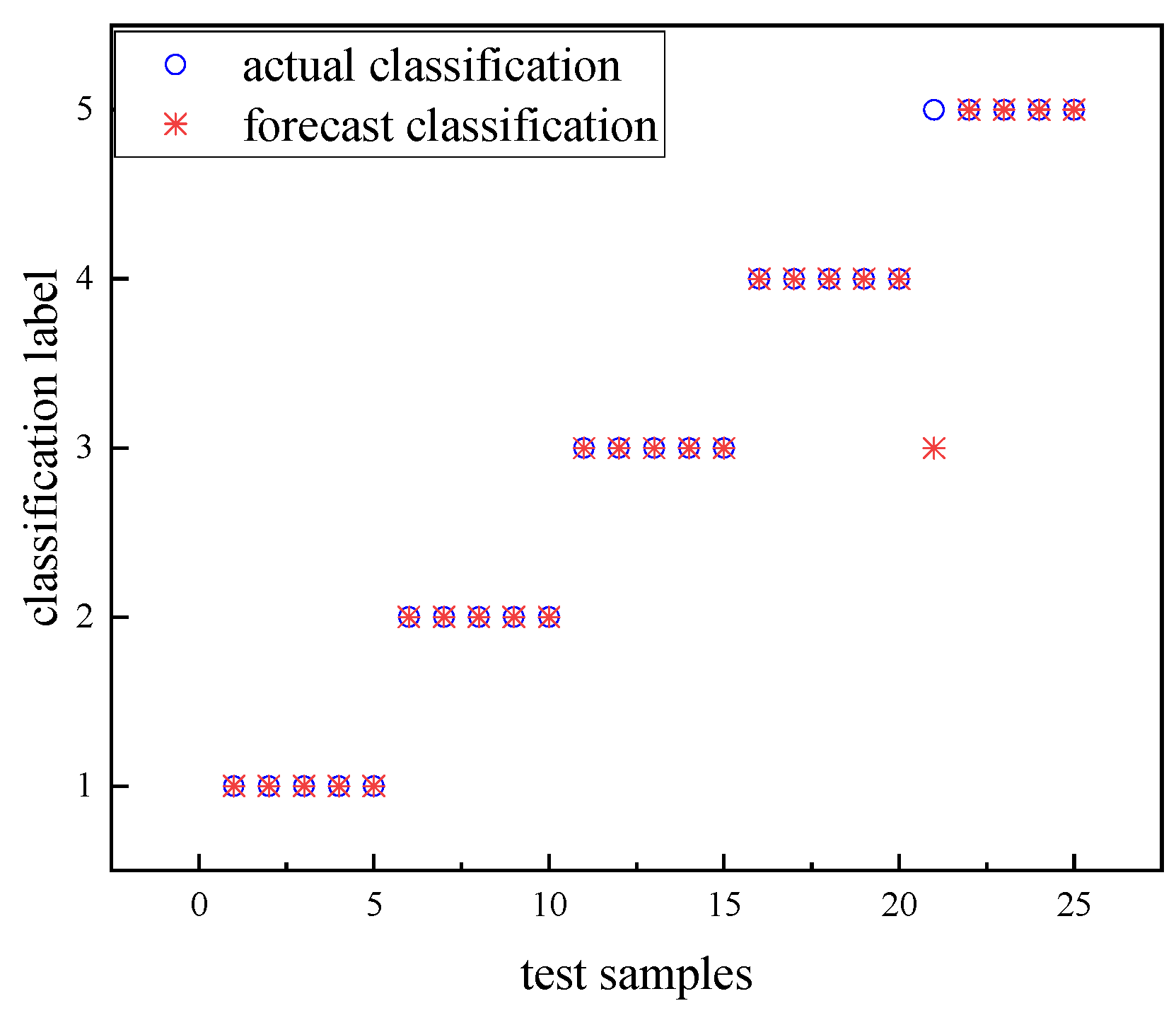
4.3.2. GA-SVM Classification and Recognition
5. Conclusions
- (1)
- According to the operation characteristics of the spring operating mechanism of the HVCB, the vibration signal of the switch is divided into four substages, namely, the switch release substage, the spring release substage, the mechanism transmission substage, and the mechanism brake substage, by using the method of time-sharing division;
- (2)
- Selecting the LLE, MCD, and VDO as chaotic features to identify the mechanical defect state of the circuit breaker helps achieve a better recognition effect;
- (3)
- Calculating the eigenvalue anomaly rate k for each substage of vibration and comparing it to a threshold value of 15%, the vibration substage of the abnormal signal can be quickly determined, and the mechanical defect can be located according to the actions of the circuit breaker parts. Finally, a GA-SVM classifier is used to identify the mechanical defects of circuit breakers with an accuracy of 96%;
- (4)
- The method of time-sharing division of the vibration signal proposed in this paper is suitable for spring-operated circuit breakers. Future work will involve dividing vibration substages according to different types and operation characteristics of circuit breakers in engineering practice.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, Z.; Li, L.; Han, W.; Guo, Z. SF6 High-Voltage Circuit Breaker Contact Status Detection at Different Currents. Sensors 2022, 22, 8490. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Chen, M.; Wu, J.; Wang, Y.; Jia, B.; Jiang, Y. Intelligent Fault Diagnosis of HVCB with Feature Space Optimization-Based Random Forest. Sensors 2018, 18, 1221. [Google Scholar] [CrossRef] [PubMed]
- Razi-Kazemi, A.A.; Vakilian, M.; Niayesh, K.; Lehtonen, M. Priority assessment of online monitoring investment for power system circuit breakers—Part I: Qualitative-quantitative approach. IEEE Trans. Power Del. 2013, 28, 928–938. [Google Scholar] [CrossRef]
- Bagherpoor, A.; Rahimi-Pordanjani, S.; Razi-Kazemi, A.A.; Niayesh, K. Online condition assessment of interruption chamber of gas circuit breakers using arc voltage measurement. IEEE Trans. Power Del. 2017, 32, 1776–1783. [Google Scholar] [CrossRef]
- Janssen, A.; Makareinis, D.; Solver, C.E. International surveys on circuit-breaker reliability data for substation and system studies. IEEE Trans. Power Del. 2014, 29, 808–814. [Google Scholar] [CrossRef]
- Li, B.; Liu, M.; Guo, Z.; Ji, Y. Mechanical Fault Diagnosis of High Voltage Circuit Breakers Utilizing EWT-Improved Time Frequency Entropy and Optimal GRNN Classifier. Entropy 2018, 20, 448. [Google Scholar] [CrossRef]
- Huang, N.; Fang, L.; Cai, G.; Xu, D.; Chen, H.; Nie, Y. Mechanical Fault Diagnosis of High Voltage Circuit Breakers with Unknown Fault Type Using Hybrid Classifier Based on LMD and Time Segmentation Energy Entropy. Entropy 2016, 18, 322. [Google Scholar] [CrossRef]
- Huang, N.; Chen, H.; Cai, G.; Fang, L.; Wang, Y. Mechanical Fault Diagnosis of High Voltage Circuit Breakers Based on Variational Mode Decomposition and Multi-Layer Classifier. Sensors 2016, 16, 1887. [Google Scholar] [CrossRef]
- Dou, L.; Wan, S.; Zhan, C. Application of Multiscale Entropy in Mechanical Fault Diagnosis of High Voltage Circuit Breaker. Entropy 2018, 20, 325. [Google Scholar] [CrossRef]
- Huang, N.; Chen, H.; Zhang, S.; Cai, G.; Li, W.; Xu, D.; Fang, L. Mechanical Fault Diagnosis of High Voltage Circuit Breakers Based on Wavelet Time-Frequency Entropy and One-Class Support Vector Machine. Entropy 2016, 18, 7. [Google Scholar] [CrossRef]
- Qi, J.; Gao, X.; Huang, N. Mechanical Fault Diagnosis of a High Voltage Circuit Breaker Based on High-Efficiency Time-Domain Feature Extraction with Entropy Features. Entropy 2020, 22, 478. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Ruan, J.; Zhou, T.; Peng, X.; Deng, Y.; Yang, Q. Data Mining in the Vibration Signal of the Trip Mechanism in Circuit Breakers Based on VMD-PSR. Electronics 2022, 11, 3700. [Google Scholar] [CrossRef]
- Runde, M.; Ottesen, G.E.; Skyberg, B.; Ohlen, M. Vibration analysis for diagnostic testing of circuit-breakers. IEEE Trans. Power Del. 1996, 11, 1816–1823. [Google Scholar] [CrossRef]
- Hoidalen, H.K.; Runde, M. Continuous monitoring of circuit breakers using vibration analysis. IEEE Trans. Power Del. 2005, 20, 2456–2465. [Google Scholar] [CrossRef]
- Lee, D.S.S.; Lithgow, B.J.; Morrison, R.E. New fault diagnosis of circuit breakers. IEEE Trans. Power Del. 2003, 18, 454–459. [Google Scholar] [CrossRef]
- Huang, J.; Hu, X.; Gong, Y. Machinery fault diagnosis of high voltage circuit breaker based on empirical mode decomposition. Proc. CSEE 2011, 31, 108–113. [Google Scholar]
- Yang, Q.; Ruan, J.; Zhuang, Z.; Huang, D.; Qiu, Z. A New Vibration Analysis Approach for Detecting Mechanical Anomalies on Power Circuit Breakers. IEEE Access 2019, 7, 14070–14080. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, X.; Zhou, Y. Deep PCA-Based Incipient Fault Diagnosis and Diagnosability Analysis of High-Speed Railway Traction System via FNR Enhancement. Machines 2023, 11, 475. [Google Scholar] [CrossRef]
- You, K.; Qiu, G.; Gu, Y. Rolling Bearing Fault Diagnosis Using Hybrid Neural Network with Principal Component Analysis. Sensors 2022, 22, 8906. [Google Scholar] [CrossRef]
- Chen, H.; Li, S.; Li, M. Multi-Channel High-Dimensional Data Analysis with PARAFAC-GA-BP for Nonstationary Mechanical Fault Diagnosis. Int. J. Turbomach. Propuls. Power 2022, 7, 19. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D.; Zhang, X.; Sun, Y. Intelligent Diagnosis Method for Rotating Machinery Using Dictionary Learning and Singular Value Decomposition. Sensors 2017, 17, 689. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, W.; Huang, M.; Yang, X. Analysis of characteristics of vibration signals in high-voltage circuit breakers based on phase space reconstruction. Modern Elect. Power 2006, 23, 10–14. [Google Scholar]
- Li, Z.; Wei, L.; Han, D.; Teng, W. Research on mechanical fault diagnosis of high voltage vacuum circuit breaker based on phase space reconstruction. Power Syst. Prot. Control 2018, 46, 129–135. [Google Scholar]
- Liu, X.; Zhang, X.; Jiang, W.; Chen, H.; Chen, J.; Song, B.A. Method of Mechanical Fault Identification of Permanent Magnet Repulsion Mechanism of Vacuum Circuit Breaker Based on Chaos Attractor. Transac. China Electro Soc. 2022, 37, 5334–5346. [Google Scholar]
- Yang, Q.; Ruan, J.; Zhuang, Z.; Huang, D. Chaotic Analysis and Feature Extraction of Vibration Signals from Power Circuit Breakers. IEEE Trans. Power Del. 2020, 35, 1124–1135. [Google Scholar] [CrossRef]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a time series. Phys. Rev. Lett. 1980, 45, 712–716. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- Yang, Q.; Ruan, J.; Zhuang, Z.; Huang, D.; Qiu, Z. Vibration Signature Extraction of High-Voltage Circuit Breaker by Frequency and Chaotic Analysis. IEEE Access 2019, 7, 80884–80892. [Google Scholar] [CrossRef]
- Gebereselassie, S.A.; Roy, B.K. The Impact of the Largest Lyapunov Exponent and Complexity of a Hyperchaotic System on the Secure Speech Communication. In Proceedings of the 2021 Advanced Communication Technologies and Signal Processing (ACTS), Rourkela, India, 14–17 December 2021. [Google Scholar]
- Zhao, R.; Zhang, L.; Wang, Z. A study on rolling bearing fault diagnosis based on maximum Lyapunov exponent. J. Univ. Pet. China 2005, 86–89. [Google Scholar]
- Cui, R.; Li, Z.; Tong, D. Aviation arc fault detection based on phase space reconstruction and PCA. Proc. Chin. Soc. Electr. Eng. 2021, 41, 5054–5065. [Google Scholar]
- Yang, Q.; Ruan, J.; Zhang, C. Study and Application of Mechanical Defect Identification for High-Voltage Circuit Breakers Using Recurrence Quantification Analysis. Transac. China Electro. Soc. 2020, 35, 3848–3859. [Google Scholar]
- Wan, S.; Chen, L.; Dou, L.; Zhou, J. Mechanical Fault Diagnosis of HVCBs Based on Multi-Feature Entropy Fusion and Hybrid Classifier. Entropy 2018, 20, 847. [Google Scholar] [CrossRef] [PubMed]









| Status of Operation | Substage I | Substage II | Substage III | Substage IV |
|---|---|---|---|---|
| NC | 0.3051 | 0.2446 | 0.2372 | 0.0447 |
| LCE | 0.1900 | 0.2479 | 0.2417 | 0.0551 |
| NO | 0.3130 | 0.2019 | 0.3666 | 0.1089 |
| SAM | 0.2903 | 0.1989 | 0.3642 | 0.1304 |
| OMJ | 0.2977 | 0.2533 | 0.3265 | 0.0978 |
| NC | LCE | |||||
|---|---|---|---|---|---|---|
| LLE | MCD | VDO | LLE | MCD | VDO | |
| Whole signal | 0.1868 | 26.7 | 15.4 | 0.1837 | 26.9 | 15.5 |
| Substage Ⅰ | 0.2748 | 19.6 | 11.3 | 0.2180 | 14.5 | 8.4 |
| Substage Ⅱ | 0.1939 | 32.3 | 18.6 | 0.1815 | 34.8 | 20.1 |
| Substage Ⅲ | 0.2613 | 32.4 | 18.7 | 0.2604 | 33.1 | 19.1 |
| Substage Ⅳ | 0.2348 | 24.1 | 13.9 | 0.2355 | 24.1 | 13.9 |
| Status of Operation | Training Samples | Test Samples | Tag Type |
|---|---|---|---|
| NC | 1~10 | 11~15 | 1 |
| LCE | 16~25 | 26~30 | 2 |
| NO | 31~40 | 41~45 | 3 |
| SAM | 46~55 | 56~60 | 4 |
| OMJ | 61~70 | 71~75 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, S.; Zhao, T.; Wang, G.; Zhang, T.; Liu, C.; Liu, Q.; Zhang, Z.; Wang, X. A Mechanical Defect Localization and Identification Method for High-Voltage Circuit Breakers Based on the Segmentation of Vibration Signals and Extraction of Chaotic Features. Sensors 2023, 23, 7201. https://doi.org/10.3390/s23167201
Cao S, Zhao T, Wang G, Zhang T, Liu C, Liu Q, Zhang Z, Wang X. A Mechanical Defect Localization and Identification Method for High-Voltage Circuit Breakers Based on the Segmentation of Vibration Signals and Extraction of Chaotic Features. Sensors. 2023; 23(16):7201. https://doi.org/10.3390/s23167201
Chicago/Turabian StyleCao, Shi, Tong Zhao, Gang Wang, Tigui Zhang, Chenlei Liu, Qinzhe Liu, Zhenming Zhang, and Xiaolong Wang. 2023. "A Mechanical Defect Localization and Identification Method for High-Voltage Circuit Breakers Based on the Segmentation of Vibration Signals and Extraction of Chaotic Features" Sensors 23, no. 16: 7201. https://doi.org/10.3390/s23167201
APA StyleCao, S., Zhao, T., Wang, G., Zhang, T., Liu, C., Liu, Q., Zhang, Z., & Wang, X. (2023). A Mechanical Defect Localization and Identification Method for High-Voltage Circuit Breakers Based on the Segmentation of Vibration Signals and Extraction of Chaotic Features. Sensors, 23(16), 7201. https://doi.org/10.3390/s23167201






