Microwave Electrometry with Multi-Photon Coherence in Rydberg Atoms
Abstract
:1. Introduction
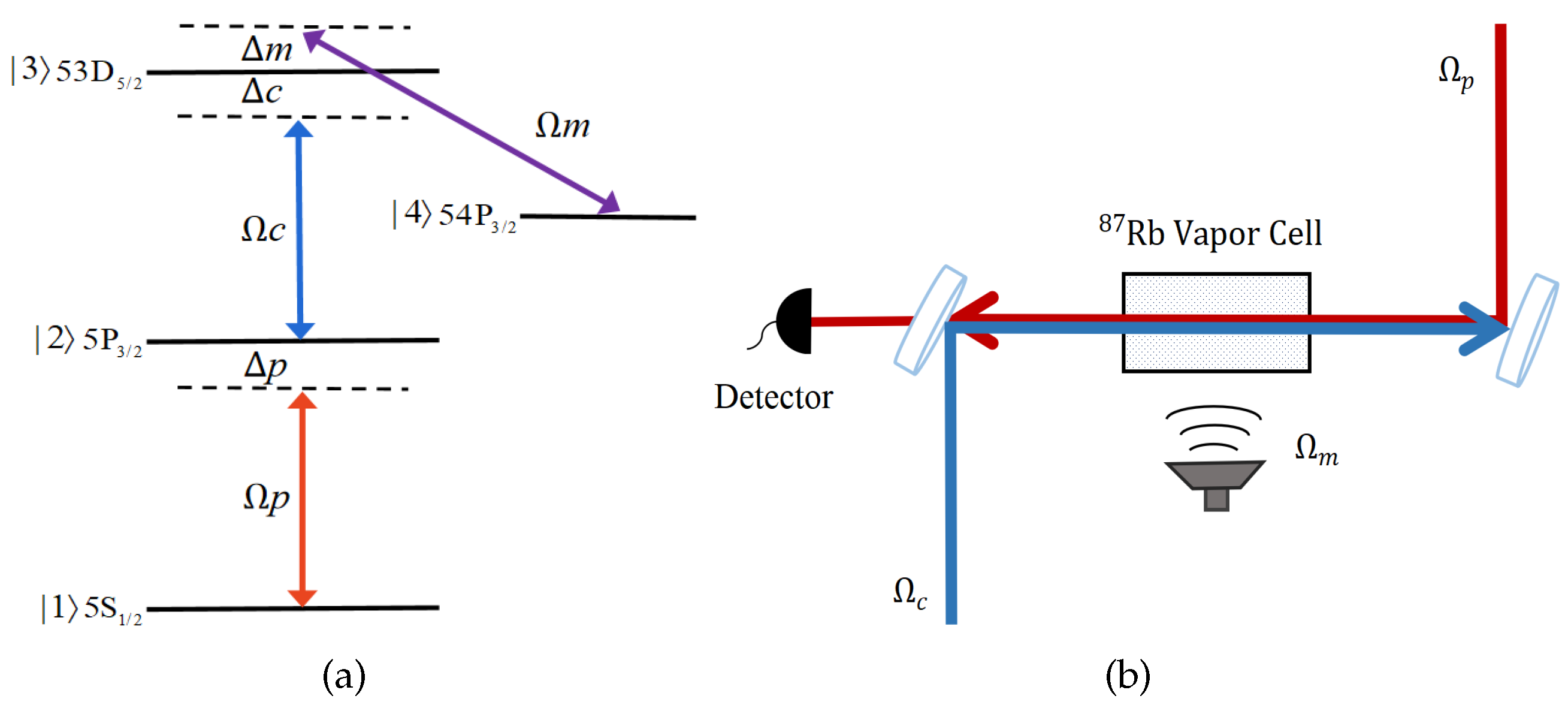
2. Model and Methods
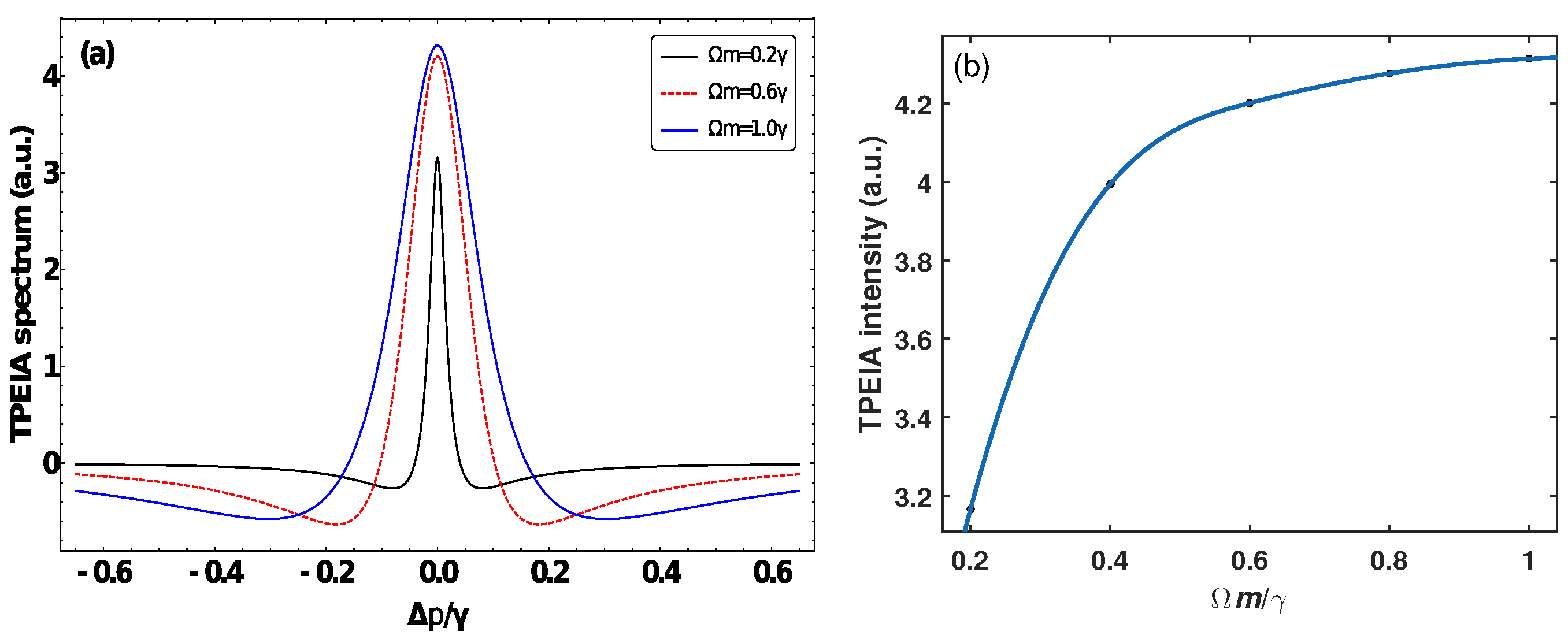
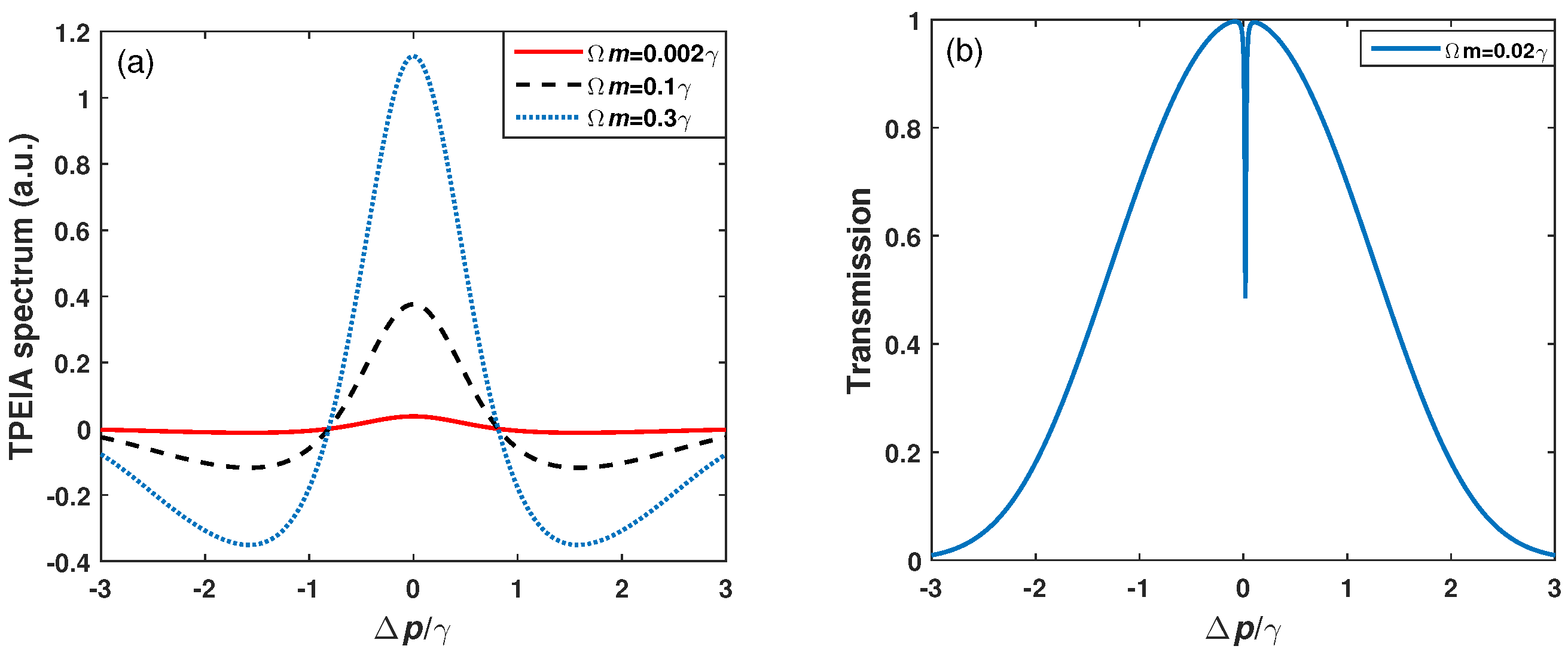
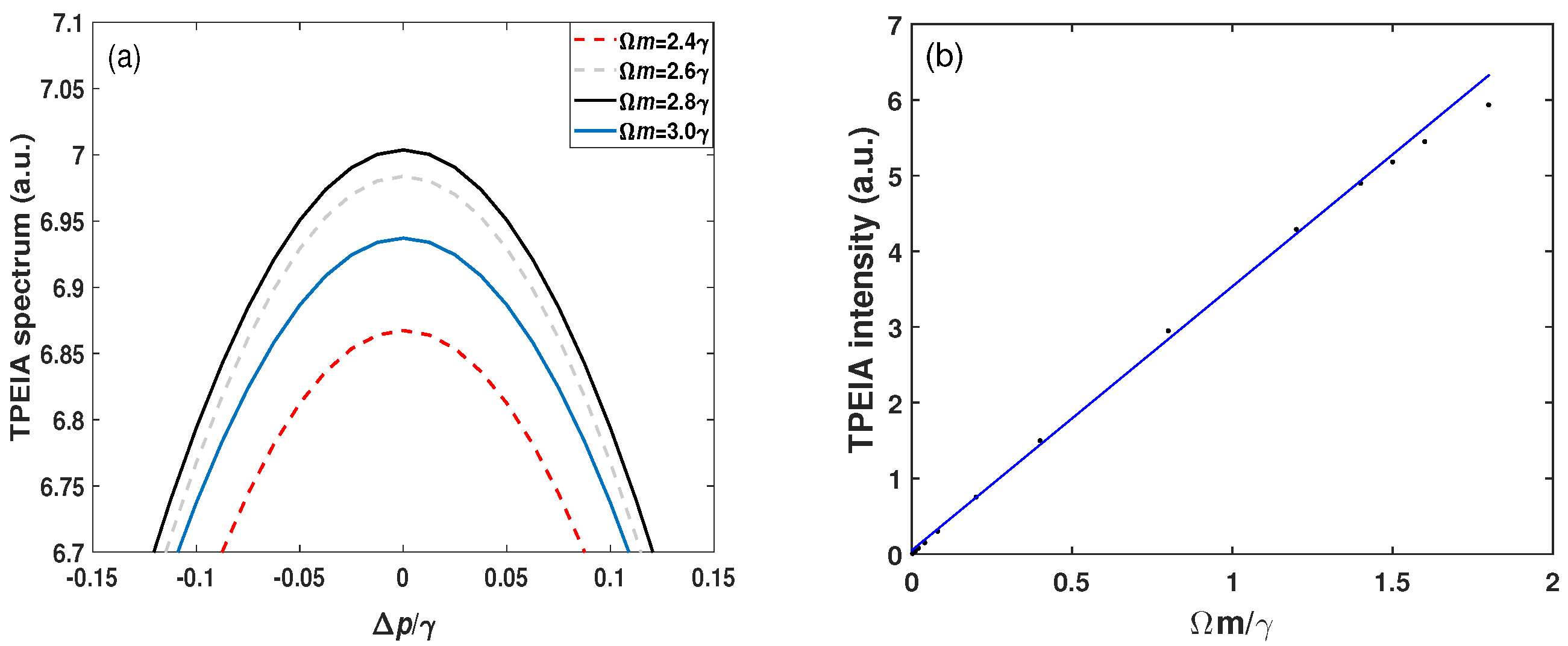
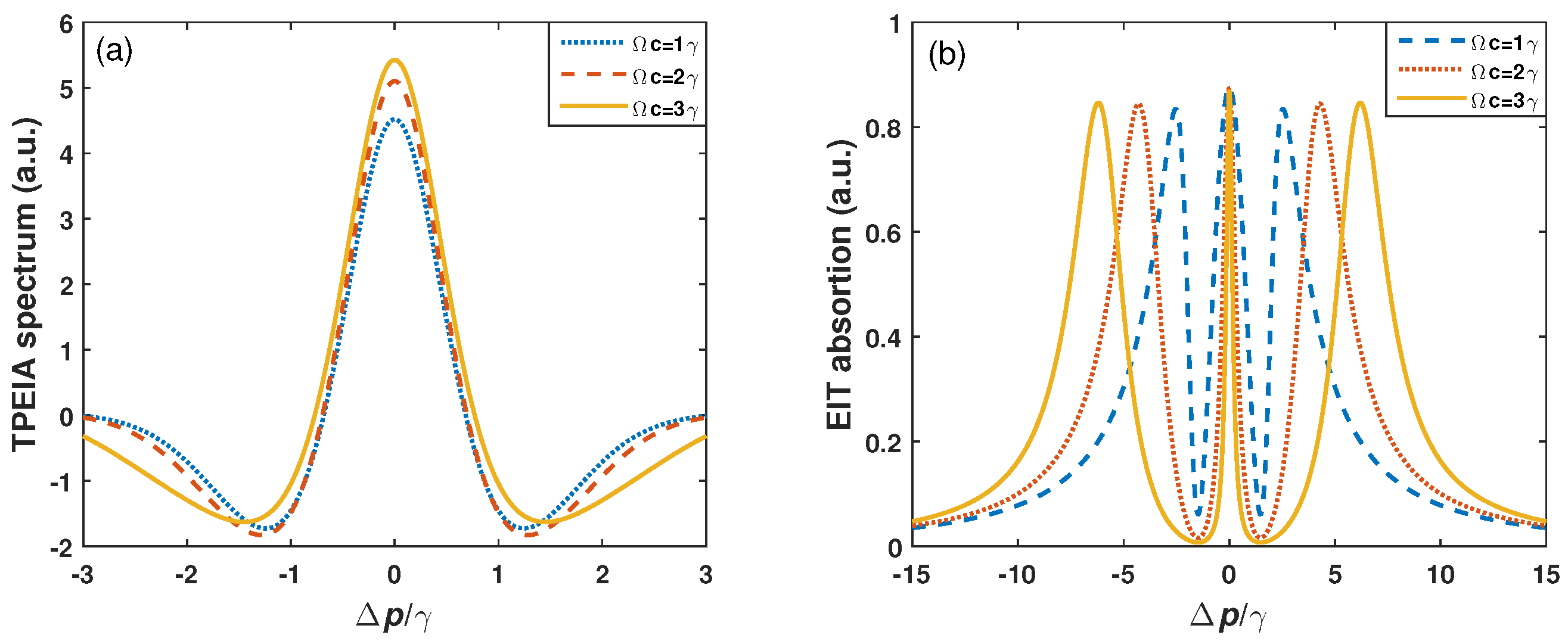
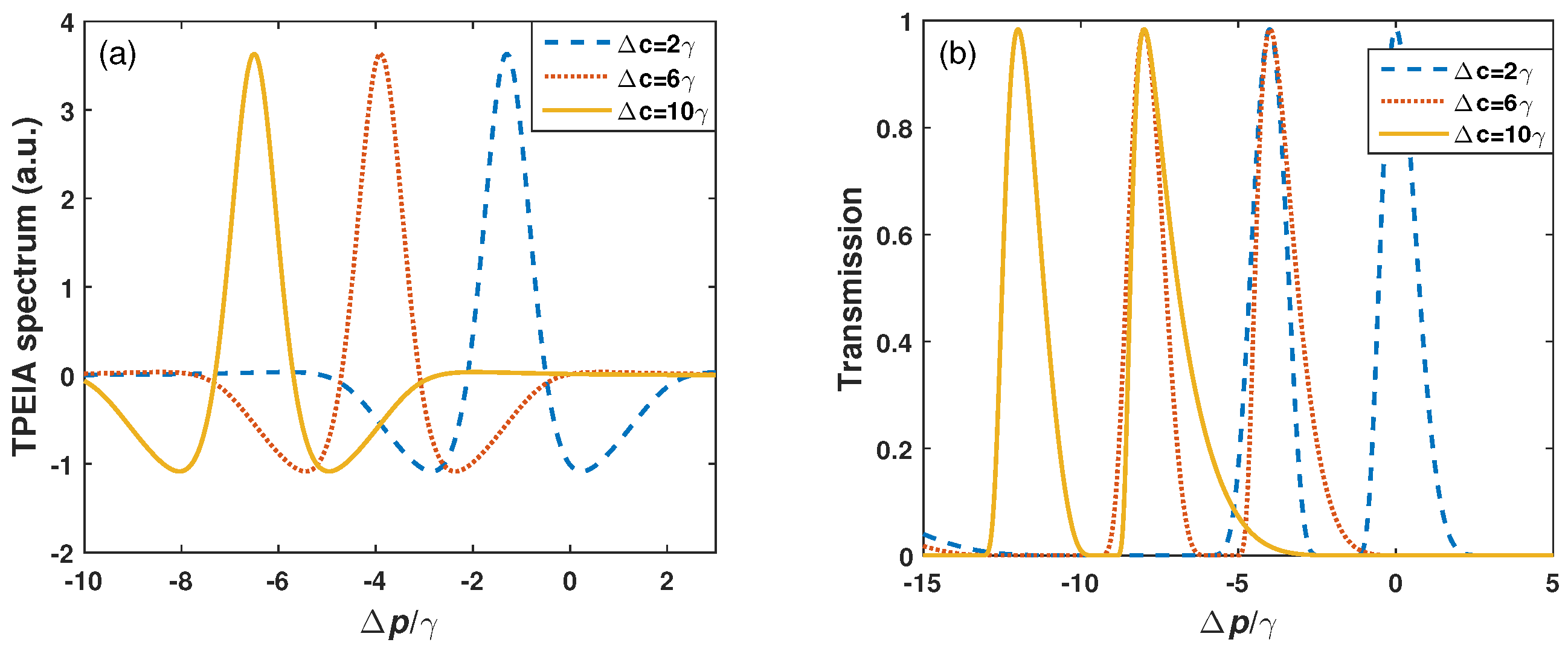
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical atomic clocks. Rev. Mod. Phys. 2015, 87, 637. [Google Scholar] [CrossRef]
- Kucsko, G.; Maurer, P.C.; Yao, N.Y.; Kubo, M.; Noh, H.J.; Lo, P.K.; Park, H.; Lukin, M.D. Nanometre-scale thermometry in a living cell. Nature 2013, 500, 54–58. [Google Scholar] [CrossRef] [PubMed]
- Sun, F.; Ma, J.; Bai, Q.; Huang, X.; Gao, B.; Hou, D. Measuring microwave cavity response using atomic Rabi resonances. Appl. Phys. Lett. 2017, 111, 051103. [Google Scholar] [CrossRef]
- Kominis, I.; Kornack, T.; Allred, J.; Romalis, M.V. A subfemtotesla multichannel atomic magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef]
- Sedlacek, J.A.; Schwettmann, A.; Kübler, H.; Löw, R.; Pfau, T.; Shaffer, J.P. Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances. Nat. Phys. 2012, 8, 819–824. [Google Scholar] [CrossRef]
- Osterwalder, A.; Merkt, F. Using high Rydberg states as electric field sensors. Phys. Rev. Lett. 1999, 82, 1831. [Google Scholar] [CrossRef]
- Gallagher, T. Rydberg Atoms; Cambridge University: Cambridge, UK, 2005. [Google Scholar]
- Wang, F.; Gou, C. Magnon-induced absorption via quantum interference. Opt. Lett. 2023, 48, 1164–1167. [Google Scholar] [CrossRef]
- Boller, K.J.; Imamoğlu, A.; Harris, S.E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 1991, 66, 2593. [Google Scholar] [CrossRef]
- Xu, J.; Wang, F. Perfect higher-order squeezing via strong nonlinearity in microwave-modified electromagnetically induced transparency. Phys. Rev. A 2021, 104, 013706. [Google Scholar] [CrossRef]
- Harris, S.E. Electromagnetically induced transparency. Phys. Today 1997, 50, 36–42. [Google Scholar] [CrossRef]
- Yang, K.; Mao, R.; An, Q.; Li, J.; Sun, Z.; Fu, Y. Amplitude-modulated RF field Rydberg atomic sensor based on homodyne technique. Sens. Actuators A Phys. 2023, 351, 114167. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, H.; Zhang, S.; Xin, P.; Luo, J.; Liu, H. High resolution electromagnetically induced transparency spectroscopy of Rydberg 87 Rb atom in a magnetic field. Opt. Exp. 2017, 25, 33575–33587. [Google Scholar] [CrossRef]
- Simons, M.T.; Gordon, J.A.; Holloway, C.L.; Anderson, D.A.; Miller, S.A.; Raithel, G. Using frequency detuning to improve the sensitivity of electric field measurements via electromagnetically induced transparency and Autler-Townes splitting in Rydberg atoms. Appl. Phys. Lett. 2016, 108, 174101. [Google Scholar] [CrossRef]
- Holloway, C.L.; Simons, M.T.; Gordon, J.A.; Dienstfrey, A.; Anderson, D.A.; Raithel, G. Electric field metrology for SI traceability: Systematic measurement uncertainties in electromagnetically induced transparency in atomic vapor. J. Appl. Phys. 2017, 121, 233106. [Google Scholar] [CrossRef]
- Fan, H.; Kumar, S.; Sedlacek, J.; Kübler, H.; Karimkashi, S.; Shaffer, J.P. Atom based RF electric field sensing. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 202001. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, W.; Wu, Q.; Mu, H.; Liu, X.; Zhang, L.; Qu, J. Field distortion and optimization of a vapor cell in Rydberg atom-based radio-frequency electric field measurement. Sensors 2018, 18, 3205. [Google Scholar] [CrossRef]
- Zhou, F.; Jia, F.; Liu, X.; Yu, Y.; Mei, J.; Zhang, J.; Xie, F.; Zhong, Z. Improving the spectral resolution and measurement range of quantum microwave electrometry by cold Rydberg atoms. J. Phys. B At. Mol. Opt. Phys. 2023, 56, 025501. [Google Scholar] [CrossRef]
- Jing, M.; Hu, Y.; Ma, J.; Zhang, H.; Zhang, L.; Xiao, L.; Jia, S. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy. Nat. Phys. 2020, 16, 911–915. [Google Scholar] [CrossRef]
- Prajapati, N.; Robinson, A.K.; Berweger, S.; Simons, M.T.; Artusio-Glimpse, A.B.; Holloway, C.L. Enhancement of electromagnetically induced transparency based Rydberg-atom electrometry through population repumping. Appl. Phys. Lett. 2021, 119, 214001. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, R.; Zhang, J.; Zhang, L.; Song, Z.; Feng, Z.; Peng, Y. Theoretical Investigation on the Mechanism and Law of Broadband Terahertz Wave Detection Using Rydberg Quantum State. IEEE Photon. J. 2022, 14, 5931808. [Google Scholar] [CrossRef]
- Tu, Z.; Wen, A.; Xiu, Z.; Zhang, W.; Chen, M. Angle-of-arrival estimation of broadband microwave signals based on microwave photonic filtering. IEEE Photon. J. 2017, 9, 5503208. [Google Scholar] [CrossRef]
- Simons, M.T.; Artusio-Glimpse, A.B.; Holloway, C.L.; Imhof, E.; Jefferts, S.R.; Wyllie, R.; Sawyer, B.C.; Walker, T.G. Continuous radio-frequency electric-field detection through adjacent Rydberg resonance tuning. Phys. Rev. A 2021, 104, 032824. [Google Scholar] [CrossRef]
- Cui, Y.; Jia, F.D.; Hao, J.H.; Wang, Y.H.; Zhou, F.; Liu, X.B.; Yu, Y.H.; Mei, J.; Bai, J.H.; Bao, Y.Y.; et al. Extending bandwidth sensitivity of Rydberg-atom-based microwave electrometry using an auxiliary microwave field. Phys. Rev. A 2023, 107, 043102. [Google Scholar] [CrossRef]
- Hao, J.; Jia, F.; Cui, Y.; Wang, Y.; Zhou, F.; Liu, X.; Zhang, J.; Xie, F.; Zhong, Z. Microwave electrometry with Rydberg atoms in a vapor cell using microwave amplitude modulation. arXiv 2023, arXiv:2304.09316. [Google Scholar]
- Simons, M.T.; Haddab, A.H.; Gordon, J.A.; Holloway, C.L. A Rydberg atom-based mixer: Measuring the phase of a radio frequency wave. Appl. Phys. Lett. 2019, 114, 114101. [Google Scholar] [CrossRef]
- Lin, L.; He, Y.; Yin, Z.; Li, D.; Jia, Z.; Zhao, Y.; Chen, B.; Peng, Y. Sensitive detection of radio-frequency field phase with interacting dark states in Rydberg atoms. Appl. Opt. 2022, 61, 1427–1433. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Chen, B.; Qi, Y.; Peng, Y. Multicolor coherence-induced grating in a three-level-type atomic system. J. Mod. Opt. 2018, 65, 852–857. [Google Scholar] [CrossRef]
- Dixon, K.; Nickerson, K.; Booth, D.W.; Shaffer, J.P. Rydberg-Atom-Based Electrometry Using a Self-Heterodyne Frequency-Comb Readout and Preparation Scheme. Phys. Rev. A 2023, 19, 034078. [Google Scholar] [CrossRef]
- Shaffer, J.; Kübler, H. A read-out enhancement for microwave electric field sensing with Rydberg atoms. Proc. SPIE 2018, 10674, 106740C. [Google Scholar] [CrossRef]
- Ripka, F.; Amarloo, H.; Erskine, J.; Liu, C.; Ramirez-Serrano, J.; Keaveney, J.; Gillet, G.; Kübler, H.; Shaffer, J.P. Application-Driven Problems in Rydberg Atom Electrometry; SPIE: Bellingham, WA, USA, 2021; Volume 11700, pp. 152–161. [Google Scholar] [CrossRef]
- You, S.; Cai, M.; Zhang, S.; Xu, Z.; Liu, H. Microwave-field sensing via electromagnetically induced absorption of Rb irradiated by three-color infrared lasers. Opt. Exp. 2022, 30, 16619–16629. [Google Scholar] [CrossRef]
- Bai, J.; Jiao, Y.; He, Y.; Song, R.; Zhao, J.; Jia, S. Autler-Townes splitting of three-photon excitation of cesium cold Rydberg gases. Opt. Exp. 2022, 30, 16748–16757. [Google Scholar] [CrossRef]
- Moon, H.S.; Jeong, T. Three-photon electromagnetically induced absorption in a ladder-type atomic system. Phys. Rev. A 2014, 89, 033822. [Google Scholar] [CrossRef]
- McGloin, D.; Fulton, D.; Dunn, M. Electromagnetically induced transparency in N-level cascade schemes. Opt. Commun. 2001, 190, 221–229. [Google Scholar] [CrossRef]
- Carr, C.; Tanasittikosol, M.; Sargsyan, A.; Sarkisyan, D.; Adams, C.S.; Weatherill, K.J. Three-photon electromagnetically induced transparency using Rydberg states. Opt. Lett. 2012, 37, 3858–3860. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.S.; Noh, H.R.; Moon, H.S. Relationship between two-and three-photon coherence in a ladder-type atomic system. Opt. Exp. 2015, 23, 2999–3009. [Google Scholar] [CrossRef] [PubMed]
- Noh, H.R.; Moon, H.S. Discrimination of one-photon and two-photon coherence parts in electromagnetically induced transparency for a ladder-type three-level atomic system. Opt. Exp. 2011, 19, 11128–11137. [Google Scholar] [CrossRef]
- Noh, H.R.; Moon, H.S. Diagrammatic analysis of multiphoton processes in a ladder-type three-level atomic system. Phys. Rev. A 2011, 84, 053827. [Google Scholar] [CrossRef]
- Kwak, H.M.; Jeong, T.; Lee, Y.S.; Moon, H.S. Microwave-induced three-photon coherence of Rydberg atomic states. Opt. Commun. 2016, 380, 168–173. [Google Scholar] [CrossRef]
- Gutekunst, J.; Weller, D.; Kübler, H.; Negel, J.P.; Ahmed, M.A.; Graf, T.; Löw, R. Fiber-integrated spectroscopy device for hot alkali vapor. Appl. Opt. 2017, 56, 5898–5902. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, J.; Yang, A.; Jia, Z.; Li, D.; Chen, B. Cavity-enhanced microwave electric field measurement using Rydberg atoms. J. Opt. Soc. Am. B 2018, 35, 2272–2277. [Google Scholar] [CrossRef]
- Zhi Wen, C.; Zhen Yue, S.; Kai Yu, L.; Wei, H.; Hui, Y.; Shi Liang, Z. Terahertz measurement based on Rydberg atomic antenna. Acta Phys. Sin. 2021, 70. [Google Scholar]
- Zhao, S.; Zhou, W.; Cai, Y.; Chang, Z.; Zeng, Q.; Peng, Y. Enhancing optical delay using cross-Kerr nonlinearity in Rydberg atoms. Appl. Opt. 2020, 59, 10076–10081. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Zubairy, M. Quantum Optics; Cambridge University: Cambridge, UK, 1997. [Google Scholar]
- Smith, D.G. Field Guide to Physical Optics; SPIE Press: Bellingham, WA, USA, 2013; Volume FG17, p. 115. [Google Scholar]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633. [Google Scholar] [CrossRef]
- Zhou, K.; Yan, X.a.; Han, Y.; Xu, W.; Ti, H.; Liu, H.; Chen, Y. Three-photon electromagnetically induced absorption in a dressed atomic system. J. Opt. Soc. Am. B 2022, 39, 501–507. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Li, Q.; Song, X.; Jia, Z.; Parniak, M.; Lu, X.; Peng, Y. Microwave Electrometry with Multi-Photon Coherence in Rydberg Atoms. Sensors 2023, 23, 7269. https://doi.org/10.3390/s23167269
Yin Z, Li Q, Song X, Jia Z, Parniak M, Lu X, Peng Y. Microwave Electrometry with Multi-Photon Coherence in Rydberg Atoms. Sensors. 2023; 23(16):7269. https://doi.org/10.3390/s23167269
Chicago/Turabian StyleYin, Zheng, Qianzhu Li, Xiaoyun Song, Zhengmao Jia, Michal Parniak, Xiao Lu, and Yandong Peng. 2023. "Microwave Electrometry with Multi-Photon Coherence in Rydberg Atoms" Sensors 23, no. 16: 7269. https://doi.org/10.3390/s23167269




