A Multiscale Method for Infrared Ship Detection Based on Morphological Reconstruction and Two-Branch Compensation Strategy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Morphological Reconstruction
2.2. Multiscale Saliency Map
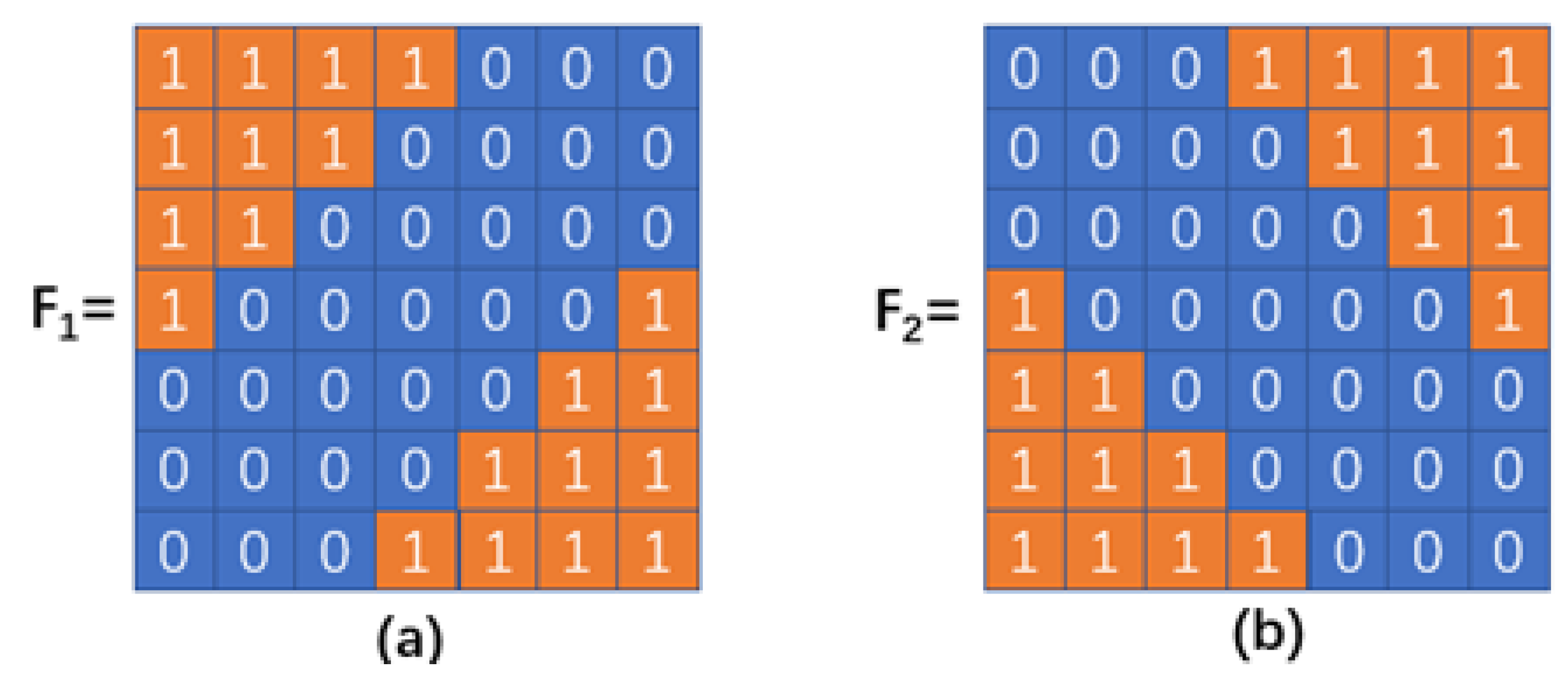
2.3. Feature-Based Structure Tensor
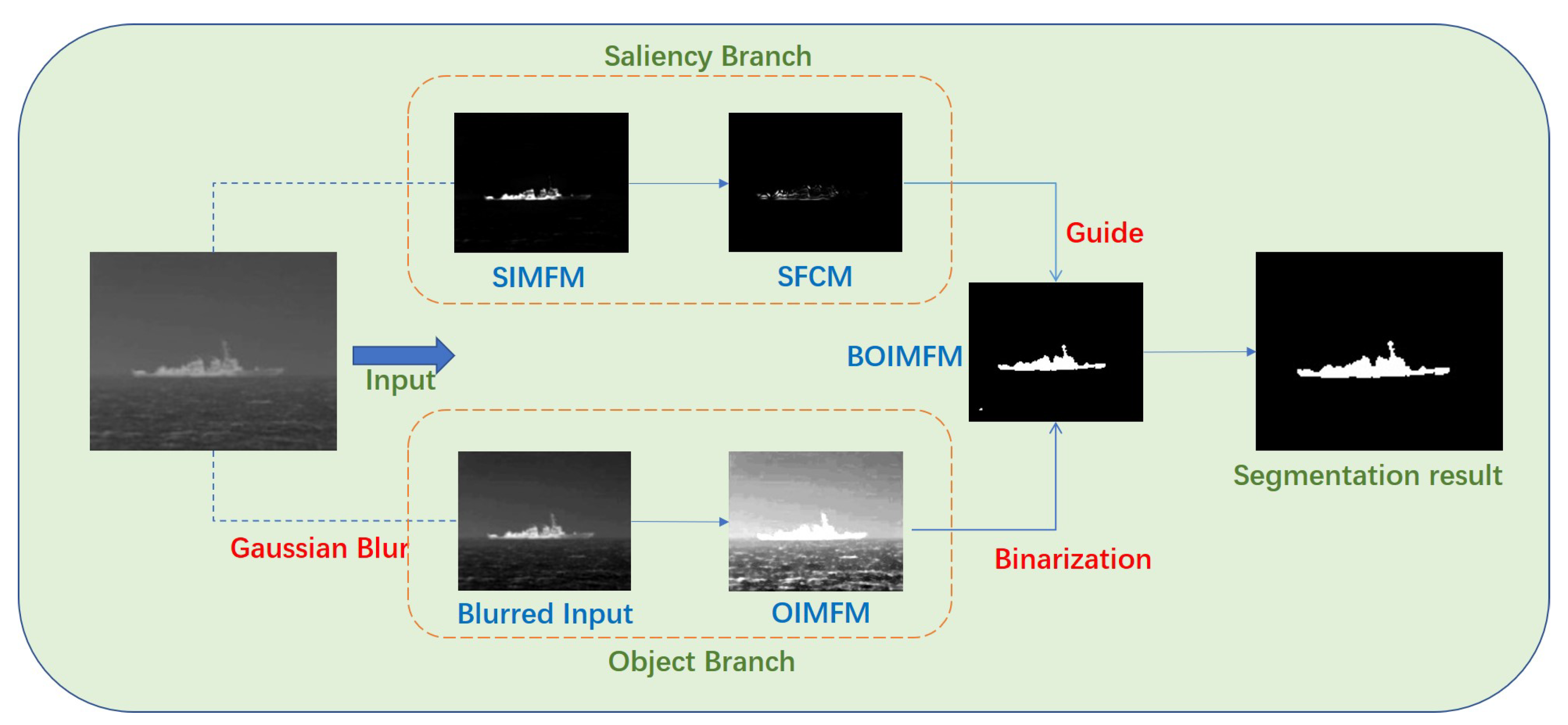
2.4. Two-Branch Compensation Strategy
| Algorithm 1: MRMSP-TBC |
| Input: |
| The original infrared image, I; |
| Output: |
| The detection binarized result of I; |
|
3. Experiments
3.1. Test Dataset
3.2. Discussion of Key Parameters
3.3. Qualitative Comparison
3.4. Quantitative Comparison
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.; Dong, L.; Ma, D.; Xu, W. Infrared target detection in marine images with heavy waves via local patch similarity. Infrared Phys. Technol. 2022, 125, 104283. [Google Scholar] [CrossRef]
- Dong, L.; Wang, B.; Zhao, M.; Xu, W. Robust infrared maritime target detection based on visual attention and spatiotemporal filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3037–3050. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, L.; Zheng, H.; Xu, W. Infrared maritime small target detection based on edge and local intensity features. Infrared Phys. Technol. 2021, 119, 103940. [Google Scholar] [CrossRef]
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Cui, H.; Li, L.; Liu, X.; Su, X.; Chen, F. Infrared small target detection based on weighted three-layer window local contrast. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7505705. [Google Scholar] [CrossRef]
- Yang, P.; Dong, L.; Xu, H.; Dai, H.; Xu, W. Robust Infrared Maritime Target Detection via Anti-Jitter Spatial–Temporal Trajectory Consistency. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7506105. [Google Scholar] [CrossRef]
- Zhang, T.X.; Zhao, G.Z.; Wang, F.; Zhu, G.X. Fast recursive algorithm for infrared ship image segmentation. J. Infrared Millim. Waves 2006, 25, 295–300. [Google Scholar]
- Fang, L.; Wang, X.; Wan, Y. Adaptable active contour model with applications to infrared ship target segmentation. J. Electron. Imaging 2016, 25, 041010. [Google Scholar] [CrossRef]
- Fang, L.; Zhao, W.; Li, X.; Wang, X. A convex active contour model driven by local entropy energy with applications to infrared ship target segmentation. Opt. Laser Technol. 2017, 96, 166–175. [Google Scholar] [CrossRef]
- Zhou, A.; Xie, W.; Pei, J. Background Modeling in the Fourier Domain for Maritime Infrared Target Detection. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2634–2649. [Google Scholar] [CrossRef]
- Zhou, A.; Xie, W.; Pei, J. Background modeling combined with multiple features in the Fourier domain for maritime infrared target detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4202615. [Google Scholar] [CrossRef]
- Zhou, M.; Jing, M.; Liu, D.; Xia, Z.; Zou, Z.; Shi, Z. Multi-resolution networks for ship detection in infrared remote sensing images. Infrared Phys. Technol. 2018, 92, 183–189. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Zhang, T.; Zhang, X.; Sun, C.; Rehman, S.u.; Ahmad, J. Infrared Ship Image Saliency Detection Based on Two-Branch Edge Guided Lightweight Network. Available online: https://ssrn.com/abstract=4487558 (accessed on 25 February 2023).
- Wang, F.; Qian, W.; Ren, K.; Wan, M.; Gu, G.; Chen, Q. Maritime Small Target Detection Based on Appearance Stability and Depth-Normalized Motion Saliency in Infrared Video with Dense Sunglints. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5605919. [Google Scholar]
- Liu, Z.; Waqas, M.; Yang, J.; Rashid, A.; Han, Z. A multi-task CNN for maritime target detection. IEEE Signal Process. Lett. 2021, 28, 434–438. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Zhu, Y.; Li, B.; Xiong, W.; Huang, Y. Thermal infrared small ship detection in sea clutter based on morphological reconstruction and multi-feature analysis. Appl. Sci. 2019, 9, 3786. [Google Scholar]
- Li, Y.; Li, Z.; Xu, B.; Dang, C.; Deng, J. Low-contrast infrared target detection based on multiscale dual morphological reconstruction. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7001905. [Google Scholar] [CrossRef]
- Jiang, B.; Ma, X.; Lu, Y.; Li, Y.; Feng, L.; Shi, Z. Ship detection in spaceborne infrared images based on Convolutional Neural Networks and synthetic targets. Infrared Phys. Technol. 2019, 97, 229–234. [Google Scholar]
- Wang, N.; Li, B.; Wei, X.; Wang, Y.; Yan, H. Ship detection in spaceborne infrared image based on lightweight CNN and multisource feature cascade decision. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4324–4339. [Google Scholar] [CrossRef]
- Vincent, L. Morphological grayscale reconstruction in image analysis: Applications and efficient algorithms. IEEE Trans. Image Process. 1993, 2, 176–201. [Google Scholar] [CrossRef]
- Shi, J.; Wang, Y.; Xu, D.; Yan, C.; Chen, T.; He, Y.; Tang, L.; Nie, M.; Duan, P.; Yan, D.; et al. Terahertz imaging based on morphological reconstruction. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 6800107. [Google Scholar]
- Roychowdhury, S.; Koozekanani, D.D.; Parhi, K.K. Iterative vessel segmentation of fundus images. IEEE Trans. Biomed. Eng. 2015, 62, 1738–1749. [Google Scholar] [PubMed]
- Liao, W.; Bellens, R.; Pizurica, A.; Philips, W.; Pi, Y. Classification of hyperspectral data over urban areas using directional morphological profiles and semi-supervised feature extraction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1177–1190. [Google Scholar] [CrossRef]
- Lei, T.; Jia, X.; Zhang, Y.; He, L.; Meng, H.; Nandi, A.K. Significantly fast and robust fuzzy c-means clustering algorithm based on morphological reconstruction and membership filtering. IEEE Trans. Fuzzy Syst. 2018, 26, 3027–3041. [Google Scholar] [CrossRef]
- Lei, T.; Jia, X.; Liu, T.; Liu, S.; Meng, H.; Nandi, A.K. Adaptive Morphological Reconstruction for Seeded Image Segmentation. IEEE Trans. Image Process. 2019, 28, 5510–5523. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Pedrycz, W.; Li, Z.; Zhou, M. Kullback–Leibler divergence-based fuzzy c-means clustering incorporating morphological reconstruction and wavelet frames for image segmentation. IEEE Trans. Cybern. 2021, 52, 7612–7623. [Google Scholar] [CrossRef]
- Salazar-Colores, S.; Cabal-Yepez, E.; Ramos-Arreguin, J.M.; Botella, G.; Ledesma-Carrillo, L.M.; Ledesma, S. A Fast Image Dehazing Algorithm Using Morphological Reconstruction. IEEE Trans. Image Process. 2019, 28, 2357–2366. [Google Scholar] [CrossRef] [PubMed]
- Mo, W.; Pei, J. Nighttime infrared ship target detection based on Two-channel image separation combined with saliency mapping of local grayscale dynamic range. Infrared Phys. Technol. 2022, 127, 104416. [Google Scholar] [CrossRef]
- Zhao, E.; Dong, L.; Dai, H. Infrared Maritime Small Target Detection Based on Multidirectional Uniformity and Sparse-Weight Similarity. Remote Sens. 2022, 14, 5492. [Google Scholar]
- Bigün, J.; Granlund, G.H.; Wiklund, J. Multidimensional orientation estimation with applications to texture analysis and optical flow. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 775–790. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, C. Corner detection using multi-directional structure tensor with multiple scales. Int. J. Comput. Vis. 2020, 128, 438–459. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y. Anisotropic diffusion filtering method with weighted directional structure tensor. Biomed. Signal Process. Control 2019, 53, 101590. [Google Scholar] [CrossRef]
- Prasath, V.S.; Pelapur, R.; Seetharaman, G.; Palaniappan, K. Multiscale structure tensor for improved feature extraction and image regularization. IEEE Trans. Image Process. 2019, 28, 6198–6210. [Google Scholar] [CrossRef] [PubMed]
- Paul, M.; Danelljan, M.; Mayer, C.; Van Gool, L. Robust visual tracking by segmentation. In Proceedings of the Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Proceedings, Part XXII. Springer: Berlin, Germany, 2022; pp. 571–588. [Google Scholar]
- Haddad, R.A.; Akansu, A.N. A class of fast Gaussian binomial filters for speech and image processing. IEEE Trans. Signal Process. 1991, 39, 723–727. [Google Scholar] [CrossRef]
- Zeng, M.; Li, J.; Peng, Z. The design of Top-Hat morphological filter and application to infrared target detection. Infrared Phys. Technol. 2006, 48, 67–76. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Liu, C.; Zhang, H.; Zhao, Q. A Local Contrast Method for Infrared Small-Target Detection Utilizing a Tri-Layer Window. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1822–1826. [Google Scholar] [CrossRef]
- Shi, J.F.; Ulrich, S.; Ruel, S. Real-time saliency detection for greyscale and colour images. Vis. Comput. 2021, 37, 1277–1296. [Google Scholar] [CrossRef]
- Zhou, D.; Fang, J.; Song, X.; Guan, C.; Yin, J.; Dai, Y.; Yang, R. Iou loss for 2D/3D object detection. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Quebec City, QC, Canada, 16–19 September 2019; pp. 85–94. [Google Scholar]
- Ma, D.; Dong, L.; Xu, W. Detecting Maritime Infrared Targets in Harsh Environment by Improved Visual Attention Model Preselector and Anti-Jitter Spatiotemporal Filter Discriminator. Remote Sens. 2022, 14, 5213. [Google Scholar] [CrossRef]
- Han, Y.; Liao, J.; Lu, T.; Pu, T.; Peng, Z. KCPNet: Knowledge-Driven Context Perception Networks for Ship Detection in Infrared Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 61, 5000219. [Google Scholar] [CrossRef]
- Wu, T.; Li, B.; Luo, Y.; Wang, Y.; Xiao, C.; Liu, T.; Yang, J.; An, W.; Guo, Y. MTU-Net: Multi-level TransUNet for Space-based Infrared Tiny Ship Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5601015. [Google Scholar]







| Sequences | Seq1 | Seq2 | Seq3 | Seq4 | Seq5 | Seq6 | Seq7 | Seq8 | Seq9 |
|---|---|---|---|---|---|---|---|---|---|
| Target size | Medium, Large | Small, Medium | Large | Medium | Small | Small | Large | Large | Large |
| Background | Coast | Mountain | Sea wave | Sea wave | Sea wave | Mountain | Sea wave | Tree | Sea wave |
| Target Number | 2 | 8 | 1 | 1 | 1 | 1 | 1 | 1 | 2 |
| Metrics | Methods | Seq1 | Seq2 | Seq3 | Seq4 | Seq5 | Seq6 | Seq7 | Seq8 | Seq9 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ME | Top-Hat | 0.5270 | 0.3715 | 0.8774 | 0.2239 | 1.0000 | 0.5283 | 0.7109 | 0.8369 | 0.8779 | 0.6615 |
| TLLCM | 0.9059 | 0.9180 | 0.9954 | 1.0000 | 0.2632 | 0.5283 | 0.8707 | 0.9190 | 0.9591 | 0.8177 | |
| PSTNN | 0.2848 | 0.2628 | 0.1816 | 1.0000 | 1.0000 | 0.8302 | 0.1406 | 0.1870 | 0.1494 | 0.4485 | |
| TCS-SMoLGDR | 1.0000 | 0.9662 | 0.7069 | 1.0000 | 1.0000 | 1.0000 | 0.4184 | 1.0000 | 0.9465 | 0.8931 | |
| MRMFA | 0.4993 | 0.3715 | 0.9290 | 0.1343 | 0.2105 | 0.2830 | 0.8821 | 0.9749 | 1.0000 | 0.5872 | |
| FRFCM | 0.1588 | 0.1132 | 1.0000 | 1.0000 | 1.0000 | 0.3396 | 0.0011 | 0.0743 | 1.0000 | 0.5208 | |
| KLDFCM | 0.2274 | 1.0000 | 1.0000 | 0.4328 | 1.0000 | 0.7358 | 0.0000 | 0.0942 | 1.0000 | 0.6100 | |
| Proposed | 0.0776 | 0.1457 | 0.1097 | 0.0746 | 0.0526 | 0.0943 | 0.0261 | 0.1321 | 0.0881 | 0.0890 | |
| TPR | Top-Hat | 0.4730 | 0.6285 | 0.1226 | 0.7761 | 0.0000 | 0.4717 | 0.2891 | 0.1631 | 0.1221 | 0.3385 |
| TLLCM | 0.0941 | 0.0820 | 0.0046 | 0.0000 | 0.7368 | 0.4717 | 0.1293 | 0.081 | 0.0409 | 0.1823 | |
| PSTNN | 0.7152 | 0.7372 | 0.8184 | 0.0000 | 0.0000 | 0.1698 | 0.8594 | 0.8130 | 0.8506 | 0.5515 | |
| TCS-SMoLGDR | 0.0000 | 0.0338 | 0.2931 | 0.0000 | 0.0000 | 0.0000 | 0.5816 | 0.0000 | 0.0535 | 0.1069 | |
| MRMFA | 0.5007 | 0.6285 | 0.0710 | 0.8657 | 0.7895 | 0.7170 | 0.1179 | 0.0251 | 0.0000 | 0.4128 | |
| FRFCM | 0.8412 | 0.8868 | 0.0000 | 0.0000 | 0.0000 | 0.6604 | 0.9989 | 0.9257 | 0.0000 | 0.4792 | |
| KLDFCM | 0.7726 | 0.0000 | 0.0000 | 0.5672 | 0.0000 | 0.2642 | 0.5509 | 1.0000 | 0.9058 | 0.0000 | |
| Proposed | 0.9224 | 0.8543 | 0.8903 | 0.9254 | 0.9474 | 0.9057 | 0.9739 | 0.8679 | 0.9119 | 0.9110 | |
| FPR | Top-Hat | 0.3334 | 0.8420 | 0.9380 | 0.8506 | 1.0000 | 0.9984 | 0.7319 | 0.7048 | 0.8961 | 0.8106 |
| TLLCM | 0.9456 | 0.9828 | 0.9940 | 1.0000 | 0.9397 | 0.9982 | 0.6715 | 0.6701 | 0.9767 | 0.9087 | |
| PSTNN | 0.5655 | 0.9254 | 0.7741 | 1.0000 | 1.0000 | 0.9996 | 0.1444 | 0.5008 | 0.4222 | 0.7036 | |
| TCS-SMoLGDR | 1.0000 | 0.9613 | 0.5825 | 1.0000 | 1.0000 | 1.0000 | 0.2338 | 1.0000 | 0.6027 | 0.8200 | |
| MRMFA | 0.0162 | 0.3682 | 0.3851 | 0.4328 | 0.6500 | 0.9426 | 0.2332 | 0.0393 | 1.0000 | 0.4519 | |
| FRFCM | 0.9447 | 0.9641 | 1.0000 | 1.0000 | 1.0000 | 0.9991 | 0.5509 | 0.5903 | 1.0000 | 0.8943 | |
| KLDFCM | 0.9479 | 1.0000 | 1.0000 | 0.9952 | 1.0000 | 0.9999 | 0.6547 | 0.5430 | 1.0000 | 0.9045 | |
| Proposed | 0.0360 | 0.2057 | 0.1949 | 0.3841 | 0.5915 | 0.8399 | 0.1250 | 0.0142 | 0.0891 | 0.2756 | |
| IoU | Top-Hat | 0.3041 | 0.1032 | 0.0362 | 0.0934 | 0.0000 | 0.0014 | 0.1325 | 0.1018 | 0.0497 | 0.0914 |
| TLLCM | 0.0296 | 0.0103 | 0.0026 | 0.0000 | 0.0378 | 0.0017 | 0.0862 | 0.0638 | 0.0122 | 0.0271 | |
| PSTNN | 0.2944 | 0.0508 | 0.1843 | 0.0000 | 0.0000 | 0.0002 | 0.5557 | 0.3983 | 0.4314 | 0.2128 | |
| TCS-SMoLGDR | 0.0000 | 0.0179 | 0.1485 | 0.0000 | 0.0000 | 0.0000 | 0.2895 | 0.0000 | 0.0491 | 0.0561 | |
| MRMFA | 0.4381 | 0.3426 | 0.0659 | 0.4056 | 0.2344 | 0.0486 | 0.1071 | 0.0248 | 0.0000 | 0.1852 | |
| FRFCM | 0.0420 | 0.0239 | 0.0000 | 0.0000 | 0.0000 | 0.0008 | 0.1493 | 0.3446 | 0.0000 | 0.0623 | |
| KLDFCM | 0.0386 | 0.0000 | 0.0000 | 0.0027 | 0.0000 | 0.0001 | 0.1138 | 0.3543 | 0.0000 | 0.0566 | |
| Proposed | 0.6993 | 0.5038 | 0.6531 | 0.4336 | 0.2500 | 0.1429 | 0.5808 | 0.7659 | 0.7011 | 0.5256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Qiu, C.; Zhang, Z. A Multiscale Method for Infrared Ship Detection Based on Morphological Reconstruction and Two-Branch Compensation Strategy. Sensors 2023, 23, 7309. https://doi.org/10.3390/s23167309
Chen X, Qiu C, Zhang Z. A Multiscale Method for Infrared Ship Detection Based on Morphological Reconstruction and Two-Branch Compensation Strategy. Sensors. 2023; 23(16):7309. https://doi.org/10.3390/s23167309
Chicago/Turabian StyleChen, Xintao, Changzhen Qiu, and Zhiyong Zhang. 2023. "A Multiscale Method for Infrared Ship Detection Based on Morphological Reconstruction and Two-Branch Compensation Strategy" Sensors 23, no. 16: 7309. https://doi.org/10.3390/s23167309
APA StyleChen, X., Qiu, C., & Zhang, Z. (2023). A Multiscale Method for Infrared Ship Detection Based on Morphological Reconstruction and Two-Branch Compensation Strategy. Sensors, 23(16), 7309. https://doi.org/10.3390/s23167309





