Low-Cost Distributed Optical Waveguide Shape Sensor Based on WTDM Applied in Bionics
Abstract
:1. Introduction
2. Principles and Methods
2.1. Sensing Principles
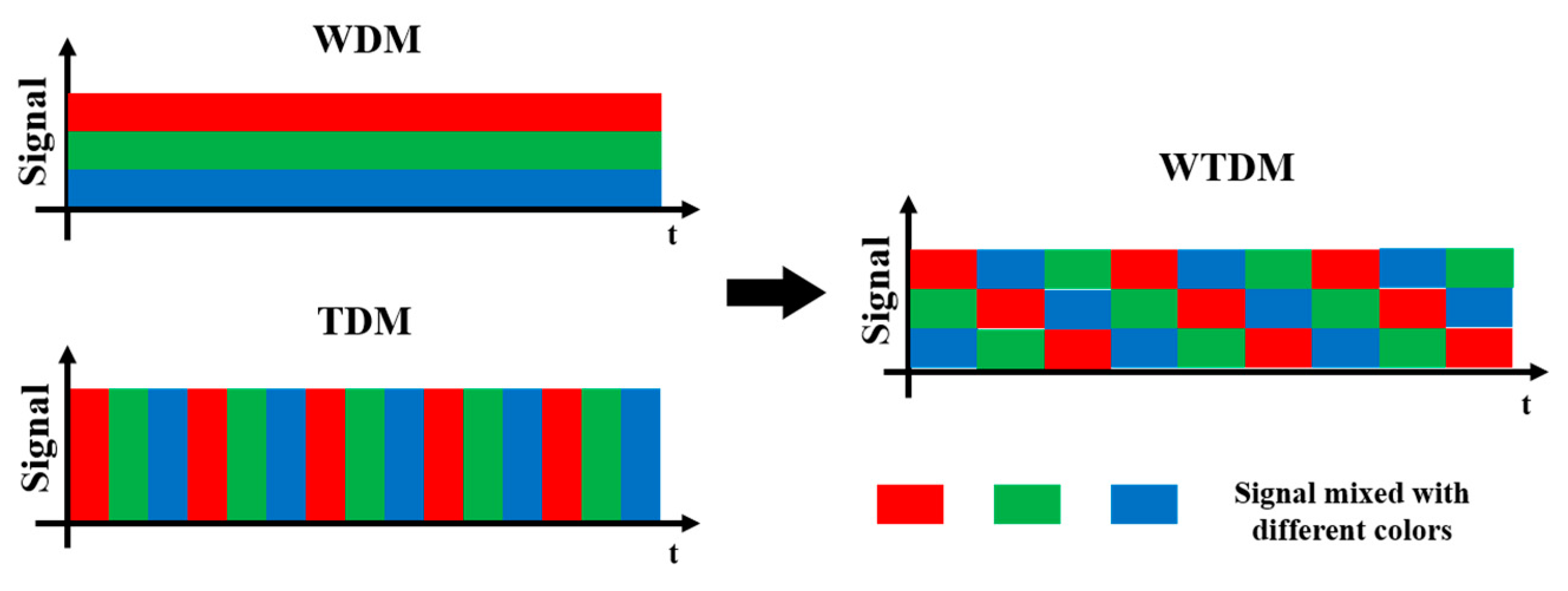
2.2. Sensing Methods
3. Results and Analysis
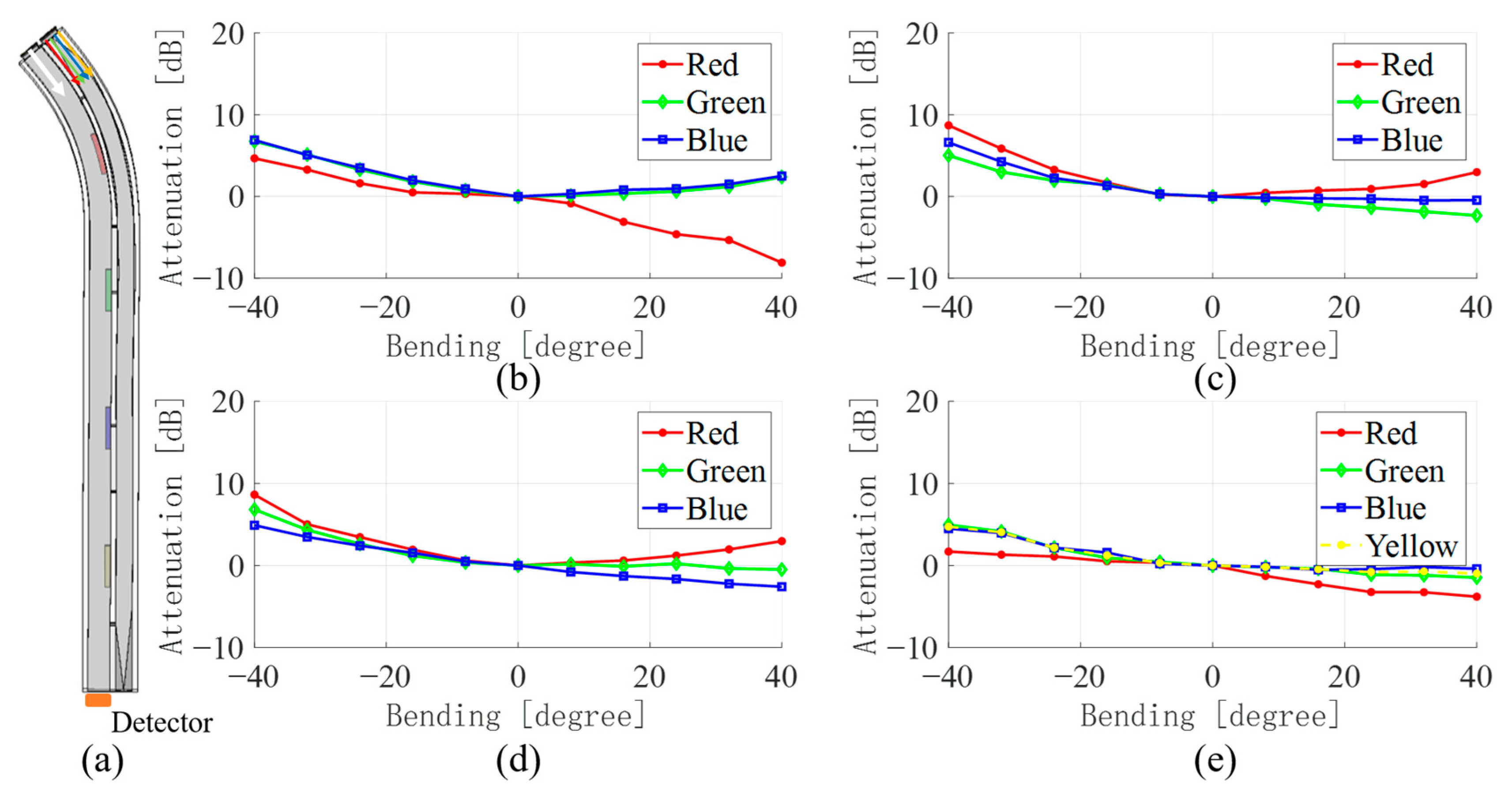
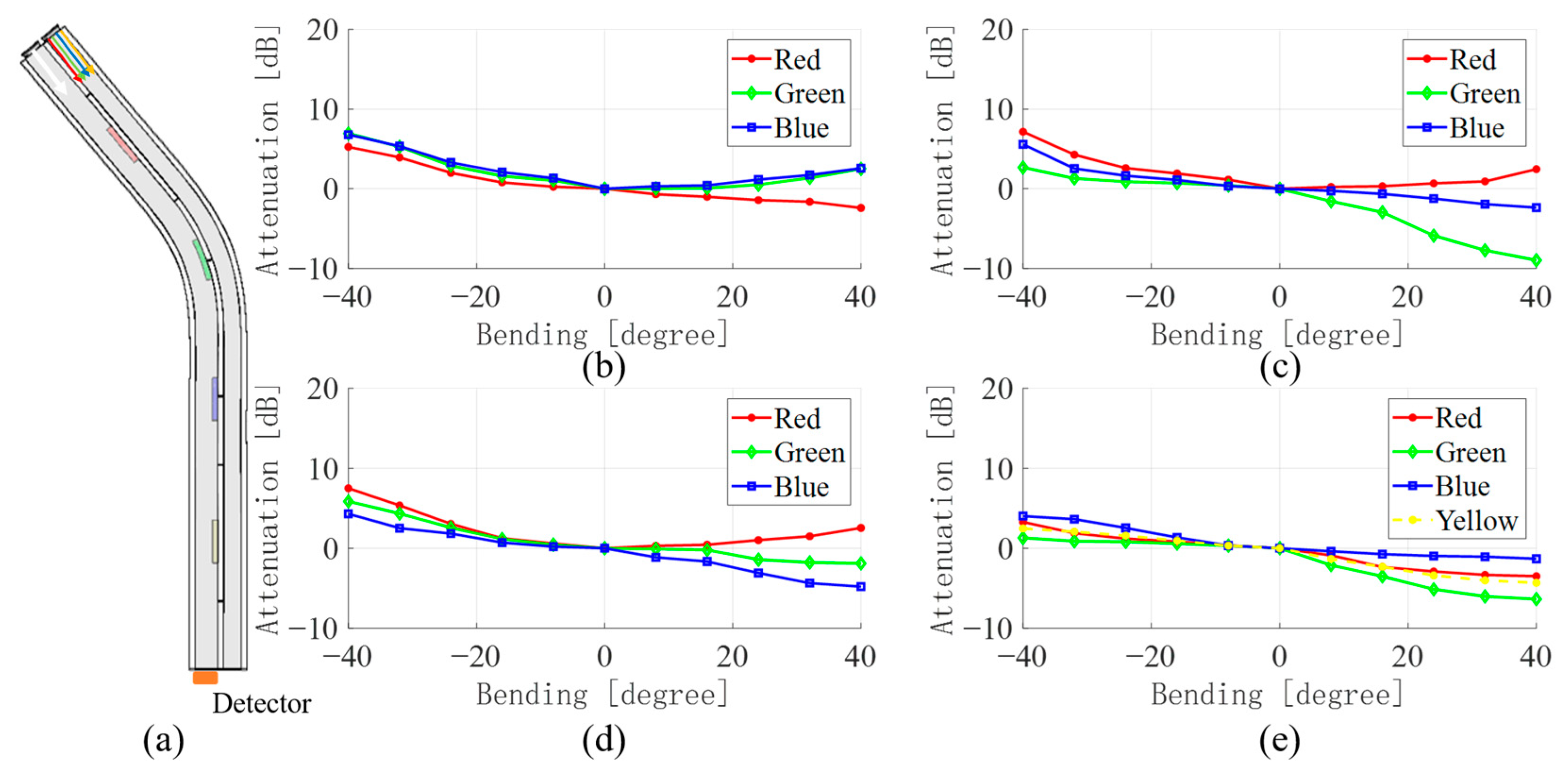
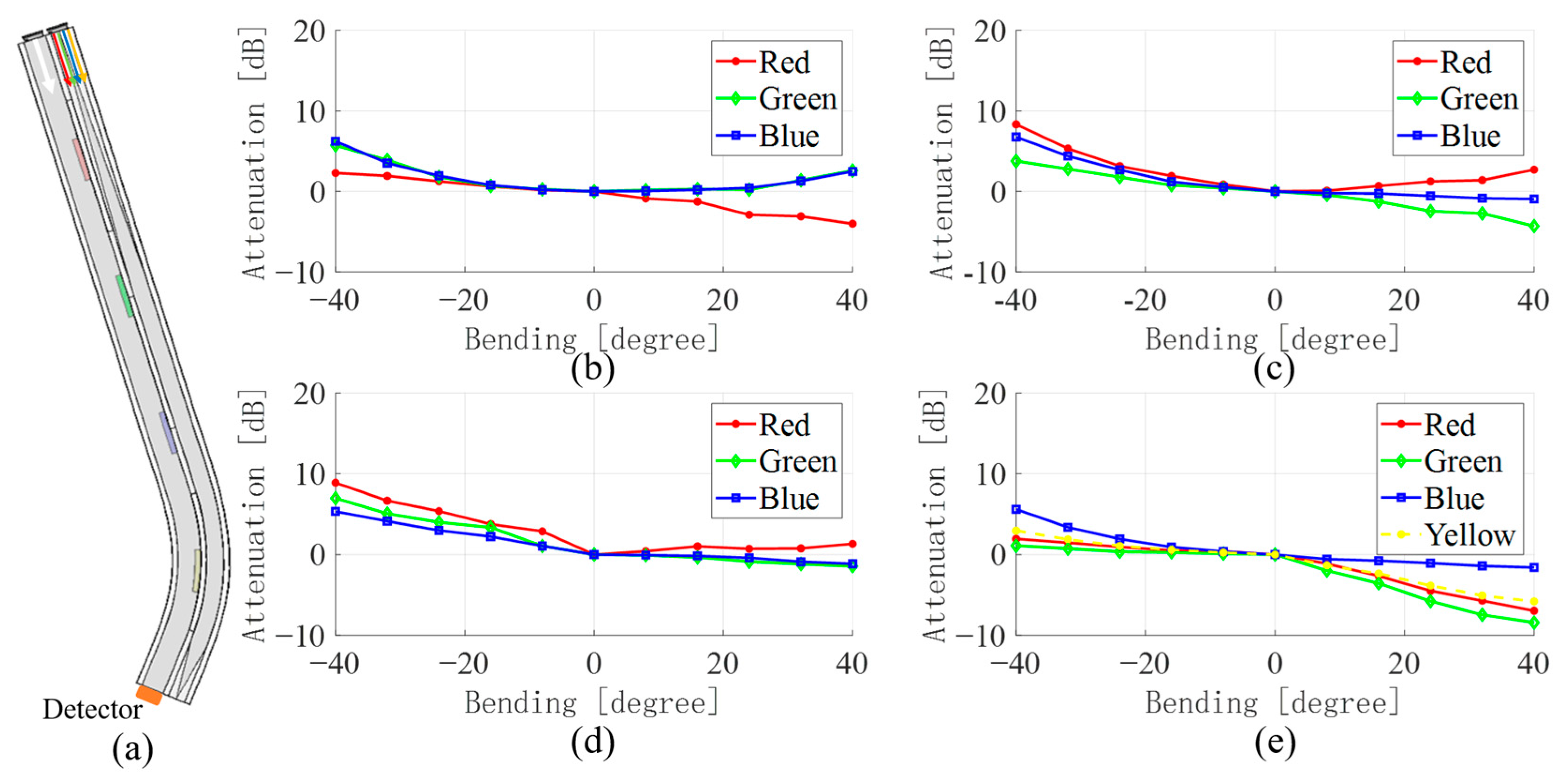
3.1. Single Bending Sensing
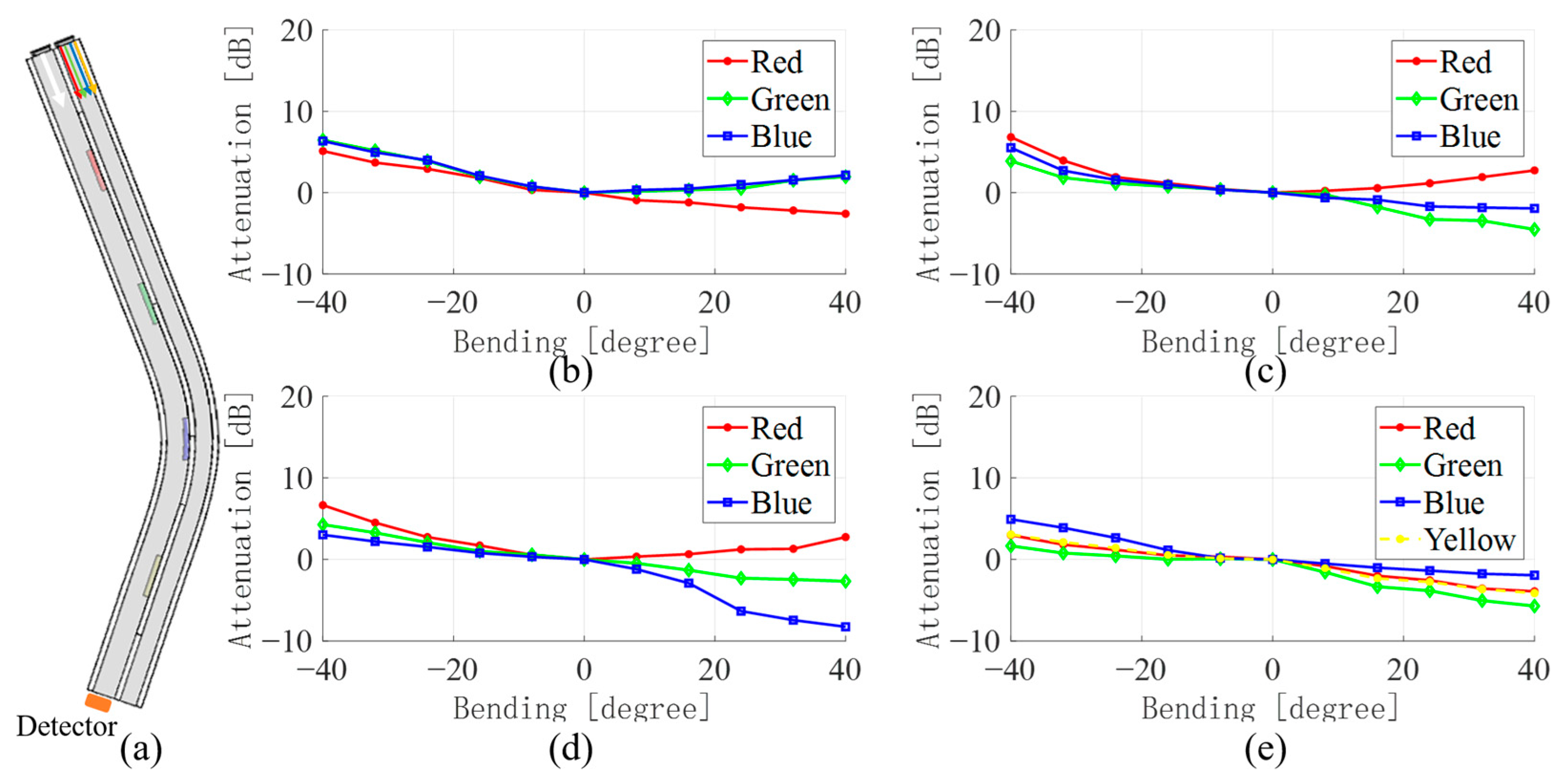
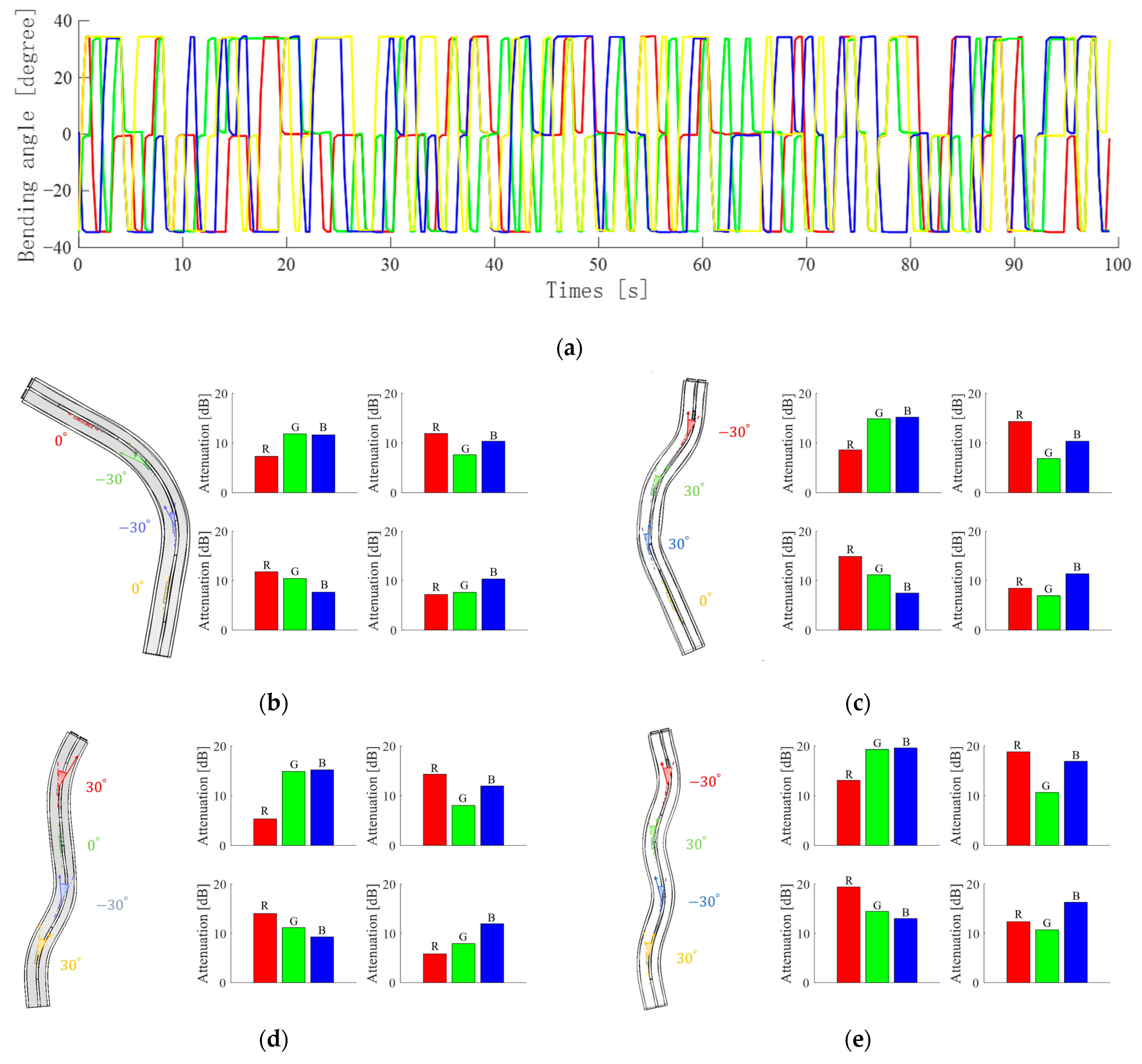
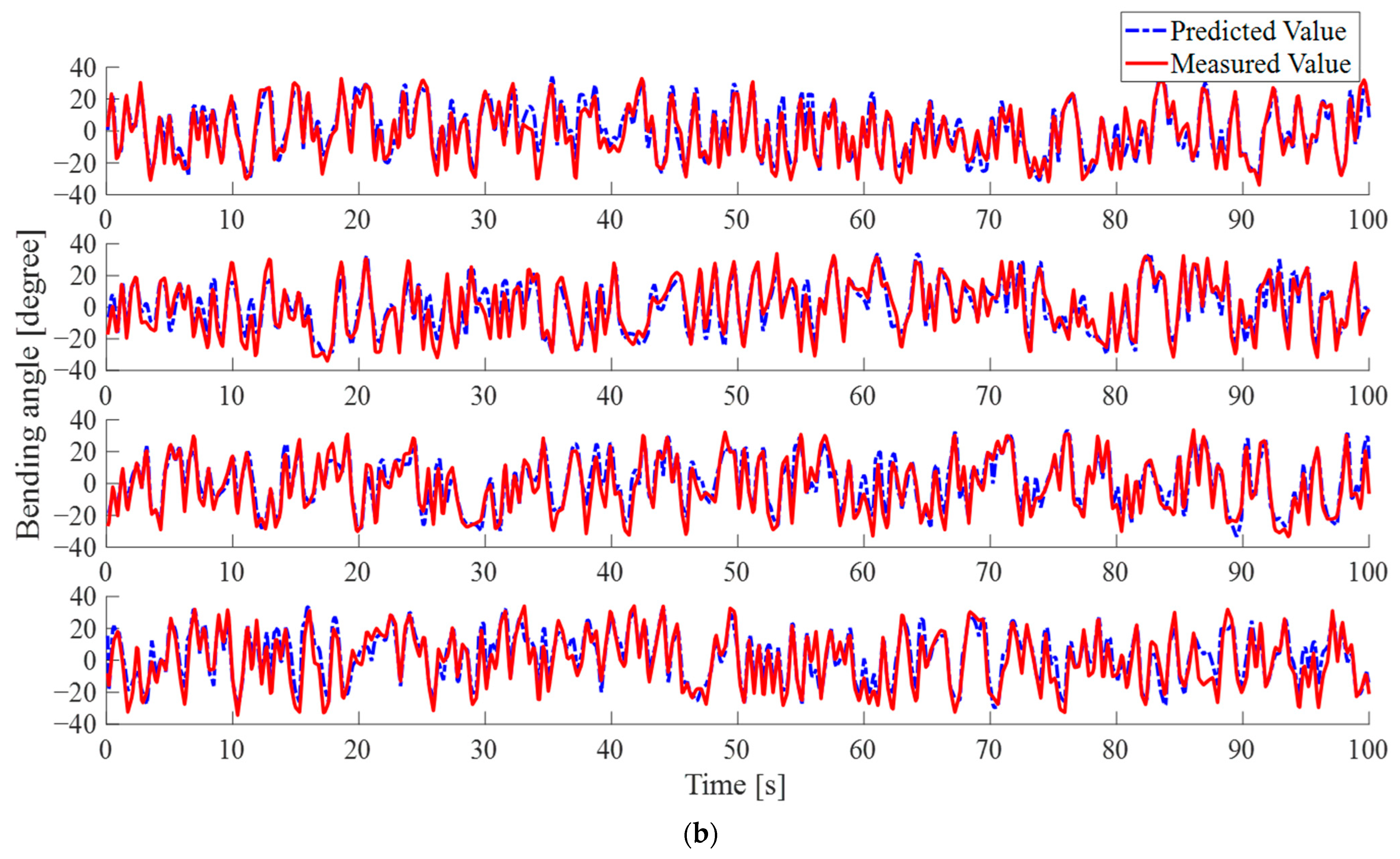
3.2. Random Multi-Bending Sensing
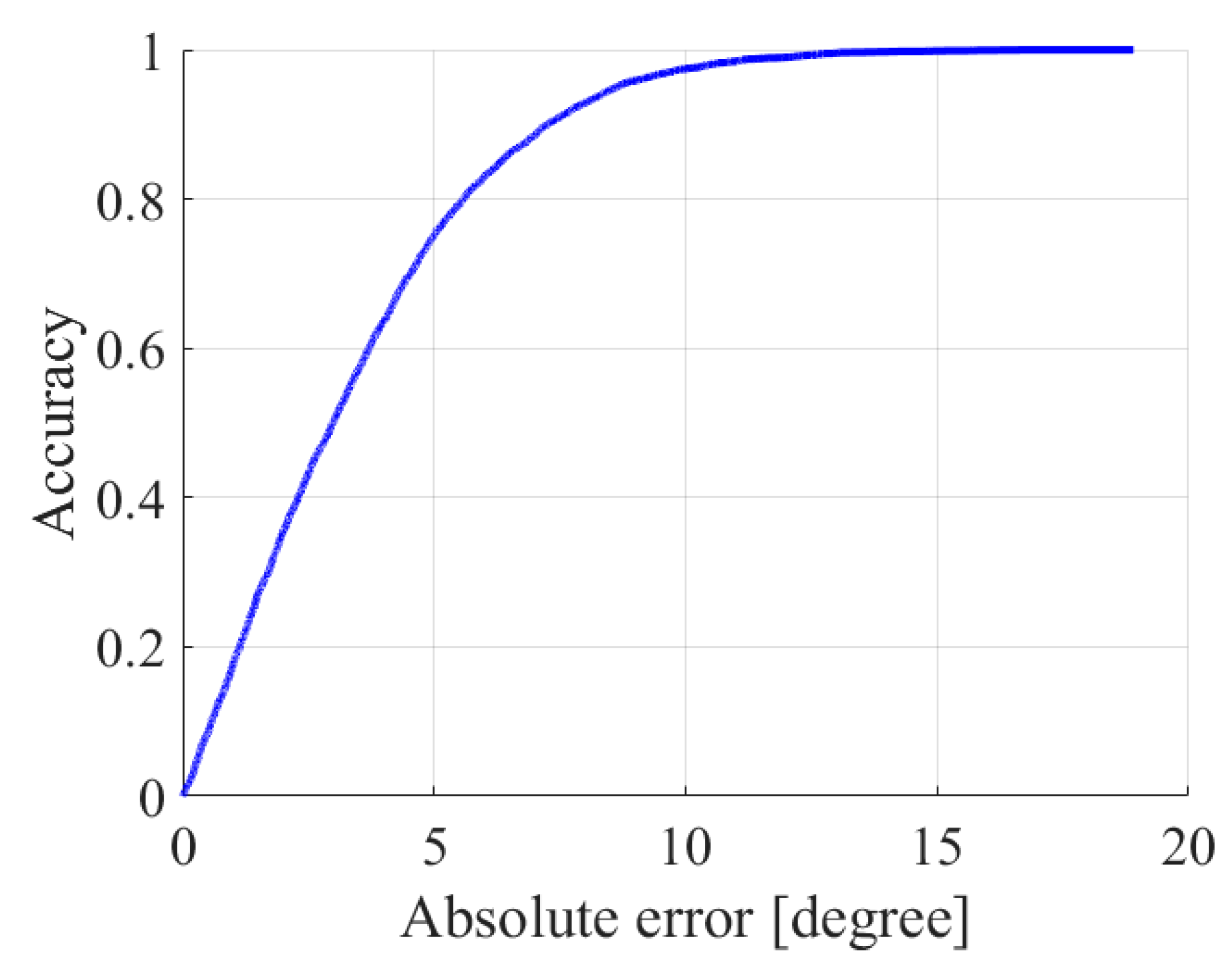
4. Application and Discussion
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ballard, Z.; Brown, C.; Madni, A.M.; Ozcan, A. Machine learning and computation-enabled intelligent sensor design. Nat. Mach. Intell. 2021, 3, 556–565. [Google Scholar] [CrossRef]
- Sun, B.; Li, W.; Wang, Z.; Zhu, Y.; He, Q.; Guan, X.; Dai, G.; Yuan, D.; Li, A.; Cui, W.; et al. Recent Progress in Modeling and Control of Bio-Inspired Fish Robots. J. Mar. Sci. Eng. 2022, 10, 773. [Google Scholar] [CrossRef]
- Zhang, H.; Lee, S. Robot Bionic Vision Technologies: A Review. Appl. Sci. 2022, 12, 7970. [Google Scholar] [CrossRef]
- Wang, K.; Mak, C.H.; Ho, J.D.L.; Liu, Z.; Sze, K.Y.; Wong, K.K.Y.; Althoefer, K.; Liu, Y.; Fukuda, T.; Kwok, K.-W. Large-scale surface shape sensing with learning-based computational mechanics. Adv. Intell. Syst. 2021, 3, 2100089. [Google Scholar] [CrossRef]
- Sun, K.; Wang, Z.; Liu, Q.; Chen, H.; Li, W.; Cui, W. Data-driven multi-joint waveguide bending sensor based on time series neural network. Optics Express 2023, 31, 2359–2372. [Google Scholar] [CrossRef]
- Wang, C.; Liu, C.; Shang, F.; Niu, S.; Ke, L.; Zhang, N.; Ma, B.; Li, R.; Sun, X.; Zhang, S. Tactile sensing technology in bionic skin: A review. Biosens. Bioelectron. 2023, 220, 114882. [Google Scholar] [CrossRef]
- Gruber, D.F.; Wood, R.J. Advances and future outlooks in soft robotics for minimally invasive marine biology. Sci. Robot. 2022, 7, eabm6804. [Google Scholar] [CrossRef]
- Sun, K.; Ding, Z.; Zhang, Z. Fiber directional position sensor based on multimode interference imaging and machine learning. Appl. Opt. 2020, 59, 5745–5751. [Google Scholar] [CrossRef]
- Yang, Z.; Albrow-Owen, T.; Cai, W.; Hasan, T. Miniaturization of optical spectrometers. Science 2021, 371, eabe0722. [Google Scholar] [CrossRef]
- Lim, H.R.; Kim, H.S.; Qazi, R.; Kwon, Y.T.; Jeong, J.W.; Yeo, W.H. Advanced Soft Materials, Sensor Integrations, and Applications of Wearable Flexible Hybrid Electronics in Healthcare, Energy, and Environment. Adv. Mater. 2020, 32, 1901924. [Google Scholar] [CrossRef]
- Homayounfar, S.Z.; Andrew, T.L. Wearable Sensors for Monitoring Human Motion: A Review on Mechanisms, Materials, and Challenges. SLAS Technol. 2020, 25, 9–24. [Google Scholar] [CrossRef] [PubMed]
- Cai, D.K.; Neyer, A.; Kuckuk, R.; Heise, H.M. Optical absorption in transparent PDMS materials applied for multimode waveguides fabrication. Opt. Mater. 2008, 30, 1157–1161. [Google Scholar] [CrossRef]
- Han, S.T.; Peng, H.; Sun, Q.; Venkatesh, S.; Chung, K.S.; Lau, S.C.; Zhou, Y.; Roy, V. An overview of the development of flexible sensors. Adv. Mater. 2017, 29, 1700375. [Google Scholar] [CrossRef]
- Sabri, N.; Aljunid, S.A.; Salim, M.S.; Fouad, S. Fiber Optic Sensors: Short Review and Applications. In Recent Trends in Physics of Material Science and Technology; Springer: Berlin/Heidelberg, Germany, 2015; pp. 299–311. [Google Scholar]
- Krauss, H.; Takemura, K. Stretchable Optical Waveguide Sensor Capable of Two-Degree-of-Freedom Strain Sensing Mediated by a Semidivided Optical Core. IEEE/ASME Trans. Mechatron. 2022, 27, 2151–2157. [Google Scholar] [CrossRef]
- Heiden, A.; Preninger, D.; Lehner, L.; Baumgartner, M.; Drack, M.; Woritzka, E.; Schiller, D.; Gerstmayr, R.; Hartmann, F.; Kaltenbrunner, M. 3D printing of resilient biogels for omnidirectional and exteroceptive soft actuators. Sci. Robot. 2022, 7, eabk2119. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; O’Brien, K.; Li, S.; Shepherd, R.F. Optoelectronically innervated soft prosthetic hand via stretchable optical waveguides. Sci. Robot. 2016, 1, eaai7529. [Google Scholar] [CrossRef]
- Kim, T.; Lee, S.; Hong, T.; Shin, G.; Kim, T.; Park, Y.-L. Heterogeneous sensing in a multifunctional soft sensor for human-robot interfaces. Sci. Robot. 2020, 5, eabc6878. [Google Scholar] [CrossRef]
- Bai, H.; Li, S.; Barreiros, J.; Tu, Y.; Pollock, C.R.; Shepherd, R.F. Stretchable distributed fiber-optic sensors. Science 2020, 370, 848–852. [Google Scholar] [CrossRef]
- Ishio, H.; Minowa, J.; Nosu, K. Review and status of wavelength-division-multiplexing technology and its application. J. Light. Technol. 1984, 2, 448–463. [Google Scholar] [CrossRef]
- Tucker, R.S.; Eisenstein, G.; Korotky, S.K. Optical time-division multiplexing for very high bit-rate transmission. J. Light. Technol. 1988, 6, 1737–1749. [Google Scholar] [CrossRef]
- Giusfredi, G. Physical Optics: Concepts, Optical Elements, and Techniques; Springer Nature: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Mayerhofer, T.G.; Pahlow, S.; Popp, J. The Bouguer-Beer-Lambert Law: Shining Light on the Obscure. Chemphyschem 2020, 21, 2029–2046. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Payne, F.P. Numerical Investigation of Microbending Loss in Optical Fibres. J. Light. Technol. 2016, 34, 1247–1253. [Google Scholar] [CrossRef]
- Delcourt, C.; Cubeau, J.; Balkan, B.; Papoz, L. Limitations of the Correlation Coefficient in the Validation of Diet Assessment Methods. Epidemiology 1994, 5, 518–524. [Google Scholar] [PubMed]
- Kovacic, J.; Varnai, V.M. Intraclass correlation coefficient for grouped data. Epidemiology 2014, 25, 769–770. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Chen, H.; Li, W.; Cui, W.; Yang, P.; Chen, L. Multi-Objective Multidisciplinary Design Optimization of a Robotic Fish System. J. Mar. Sci. Eng. 2021, 9, 478–502. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Confidence interval estimation of interaction. Epidemiology 1992, 3, 452–456. [Google Scholar] [CrossRef]




| Color Proportion | Red | Green | Blue |
|---|---|---|---|
| Red light | 82% | 8% | 10% |
| Green light | 7% | 66% | 27% |
| Blue light | 5% | 30% | 65% |
| Yellow light | 45% | 37% | 18% |
| Bending Location | Correlation Coefficient | Total Correlation Coefficient |
|---|---|---|
| Bend 1 (R) | 0.9211 | 0.9134 |
| Bend 2 (G) | 0.9106 | |
| Bend 3 (B) | 0.9219 | |
| Bend 4 (Y) | 0.9046 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, K.; Wang, Z.; Liu, Q.; Chen, H.; Cui, W. Low-Cost Distributed Optical Waveguide Shape Sensor Based on WTDM Applied in Bionics. Sensors 2023, 23, 7334. https://doi.org/10.3390/s23177334
Sun K, Wang Z, Liu Q, Chen H, Cui W. Low-Cost Distributed Optical Waveguide Shape Sensor Based on WTDM Applied in Bionics. Sensors. 2023; 23(17):7334. https://doi.org/10.3390/s23177334
Chicago/Turabian StyleSun, Kai, Zhenhua Wang, Qimeng Liu, Hao Chen, and Weicheng Cui. 2023. "Low-Cost Distributed Optical Waveguide Shape Sensor Based on WTDM Applied in Bionics" Sensors 23, no. 17: 7334. https://doi.org/10.3390/s23177334






