Optical Measurement of Ligament Strain: Opportunities and Limitations for Intraoperative Application
Abstract
1. Introduction
2. Determination of Technical Requirements
2.1. Postulated Workflow for an Intraoperative Strain Measurement of Ligaments and According Requirements
- Sterilize surfaces of the surgical equipment.
- Create surgical access.
- Irrigation of measuring area.
- First imaging of the measuring area.
- Apply stoichiometric pattern on the relevant anatomical structure(s). *
- Set the measuring area (manually).
- First image measurement:
- (a)
- Optical measurement of the three-dimensional topology (3D-topology) (vertical measurement);
- (b)
- Optical measurement of positions of the stoichiometric pattern (lateral measurement).
- First image analysis:
- (a)
- Analysis of the 3D-topology based on 7(a);
- (b)
- Assign the positions measured in 7(b) to the calculated surface of step 8(a).
- Manual manipulation of the joint to alter the strain state of the ligament.
- Second image measurement:
- (a)
- Optical measurement of the (altered) 3D-topology (vertical measurement);
- (b)
- Optical measurement of altered positions of the stoichiometric pattern (lateral measurement).
- Second image analysis:
- (a)
- Analysis of the 3D-topology based on 10(a);
- (b)
- Assign the positions measured in 10(b) to the calculated surface of step 11(a);
- (c)
- Calculate the displacement vectors of the elements of the stoichiometric pattern based on 8(b) and 11(b);
- (d)
- Derive the alteration of the strain state of the measuring area via 11(c) in comparison to the measurement in step 8.
- Diagramming the obtained data for the surgeon.
| No. | Description of Requirement | Referencing Step of Procedure |
|---|---|---|
| 1 | Sterilizability of the surfaces of invasive surgical equipment | Step 1 |
| 2 | Highly compact design of invasive surgical equipment and small surgical access | Step 2 |
| 3 | Compatibility of the measurement system with the optical properties of medical rinse (e.g., refractive index, adsorption, and speed of light within fluid) | Step 3 |
| 4 | Biocompatibility/resorbability of the colorant of the stoichiometric pattern * | Step 5 |
| 5 | Feasibility of surgical application of the stoichiometric pattern * | Step 5 |
| 6 | Technical suitability of the stoichiometric pattern (e.g., high edge definition, contrast, and refractive index) * | Step 5 |
| 7 | Graphical user interface (GUI): set measurement area | Step 6 |
| 8 | Accuracy demand for measurement system | Step 7, 10 |
| 9 | Nearly simultaneous imaging for step 7(a) and (b) as well as step 10(a) and (b) to avoid movement artifacts | Step 7, 10 |
| 10 | Software requirements from: Step 4, 6, 7, 8(a,b) and 11(c,d) | Step 4, 6, 7, 8, 11 |
| 11 | GUI: ascertainable evaluation of the measurement results | Step 12 |
2.2. Requirements for Measurement Accuracy: Model Assumptions and Case Study
2.3. Requirements for Image Resolution: Field-of-View
3. Screening for Applicable Technical Systems
3.1. Screening Method for Medical Endoscopic Systems
3.2. Screening Method for Non-Medical Optical Measurement Techniques
3.3. Screening Results of the Medical Endoscopic Systems
3.4. Preselection of Non-Medical Measuring Techniques Based on Achievable Measurement Accuracy and Field-of-View
4. Evaluation and Discussion
4.1. Evaluation of the Medical Endoscopic Systems
4.2. Evaluation of Non-Medical Measuring Techniques
4.2.1. Promising Candidates
4.2.2. Non-Suitable Techniques
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Consideration of the Extreme Case
Appendix A.2. Mathematical Description of the Circular Segment via Three Spatial Measurement Points

Appendix A.3. Mathematical Description of the Measuring Errors of the Arc Length s
Appendix A.4. Choice of a Suitable Coordinate System
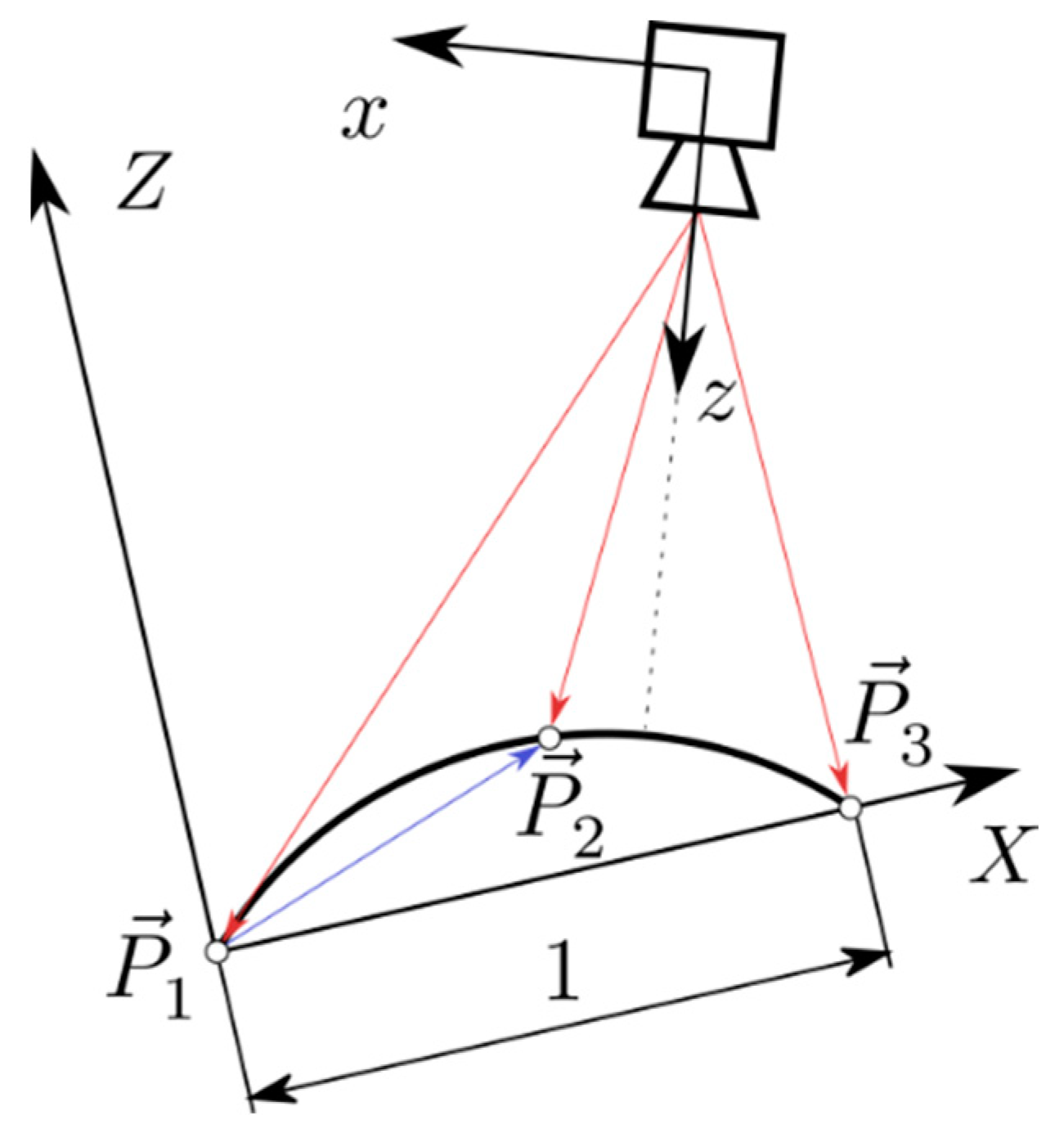
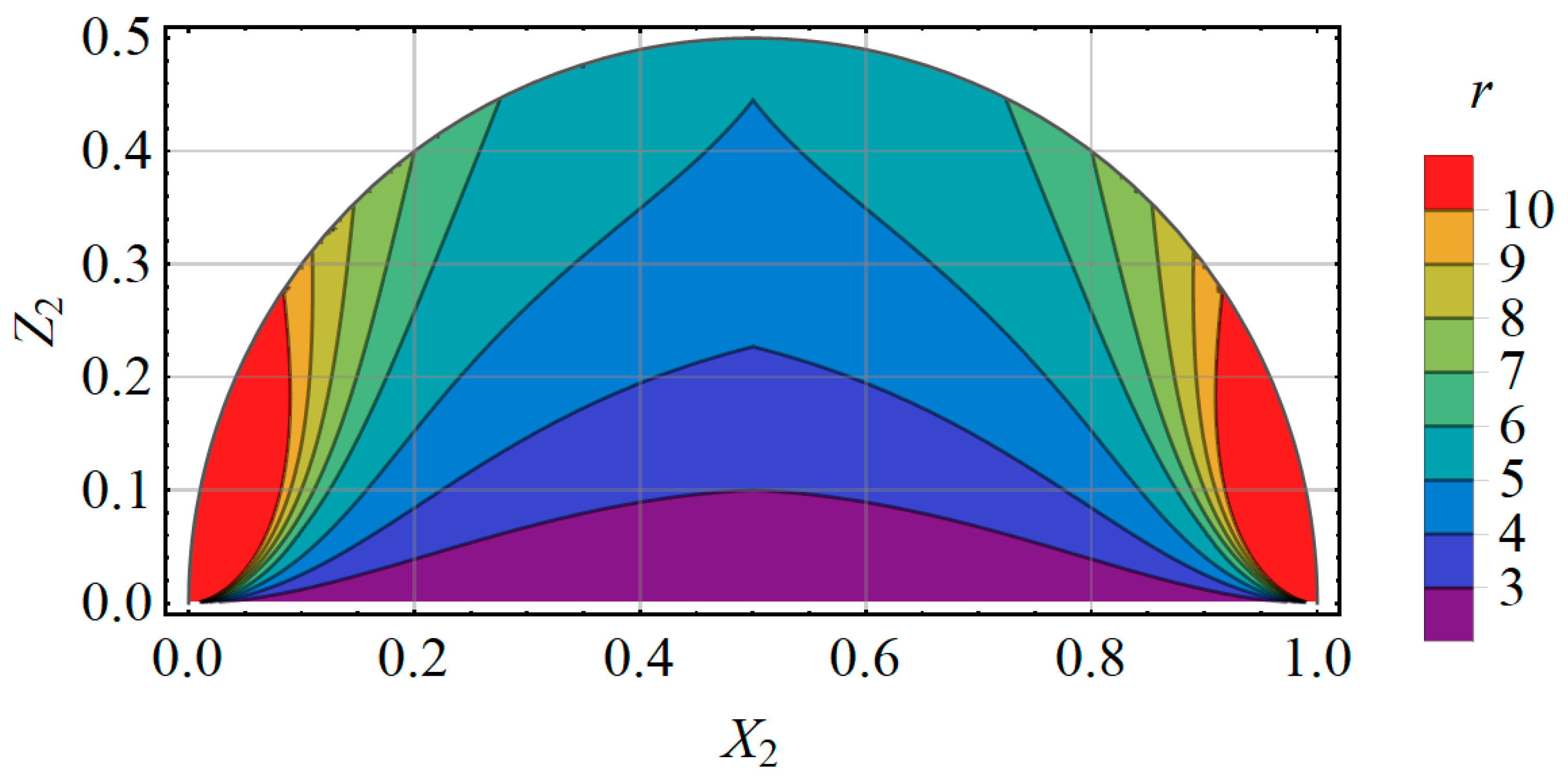
Appendix A.5. A Prediction for the Measuring Error of the Technical System
References
- Fallpauschalenbezogene Krankenhausstatistik (DRG-Statistik) Operationen und Prozeduren der Vollstationären Patientinnen und Patienten in Krankenhäusern (4-Steller)—2021. 2021. Available online: https://www.statistischebibliothek.de/mir/servlets/MCRFileNodeServlet/DEHeft_derivate_00071976/5231401217014.pdf (accessed on 25 May 2022).
- Senner, V. Biomechanische Methoden am Beispiel der Sportgeräteentwicklung. 2001. Available online: https://www.semanticscholar.org/paper/Biomechanische-Methoden-am-Beispiel-der-Senner/f10cd71e94cbe33682e69d740c0c4d9cd4a914e9 (accessed on 19 January 2022).
- Chuang, B.-I.; Hsu, J.-H.; Kuo, L.-C.; Jou, I.-M.; Su, F.-C.; Sun, Y.-N. Tendon-motion tracking in an ultrasound image sequence using optical-flow-based block matching. Biomed. Eng. Online 2017, 16, 47. [Google Scholar] [CrossRef]
- Edwards, R.G.; Lafferty, J.F.; Lange, K.O. Ligament Strain in the Human Knee Joint. J. Basic Eng. 1970, 92, 131–136. [Google Scholar] [CrossRef]
- Kennedy, J.C.; Hawkins, R.J.; Willis, R.B. Strain Gauge Analysis of Knee Ligaments. Clin. Orthop. Relat. Res. 1977, 129, 225–229. [Google Scholar] [CrossRef]
- Colville, M.R.; Marder, R.A.; Boyle, J.J.; Zarins, B. Strain measurement in lateral ankle ligaments. Am. J. Sports Med. 1990, 18, 196–200. [Google Scholar] [CrossRef]
- Ravary, B.; Pourcelot, P.; Bortolussi, C.; Konieczka, S.; Crevier-Denoix, N. Strain and force transducers used in human and veterinary tendon and ligament biomechanical studies. Clin. Biomech. 2004, 19, 433–447. [Google Scholar] [CrossRef]
- Howe, J.G.; Wertheimer, C.; Johnson, R.J.; Nichols, C.E.; Pope, M.H.; Beynnon, B. Arthroscopic strain gauge measurement of the normal anterior cruciate ligament. Arthroscopy 1990, 6, 198–204. [Google Scholar] [CrossRef]
- Beynnon, B.; Howe, J.G.; Pope, M.H.; Johnson, R.J.; Fleming, B.C. The measurement of anterior cruciate ligament strain in vivo. Int. Orthop. 1992, 16, 1–12. [Google Scholar] [CrossRef]
- Beynnon, B.D.; Fleming, B.C.; Johnson, R.J.; Nichols, C.E.; Renström, P.A.; Pope, M.H. Anterior cruciate ligament strain behavior during rehabilitation exercises in vivo. Am. J. Sports Med. 1995, 23, 24–34. [Google Scholar] [CrossRef]
- Fleming, B.C.; Beynnon, B.D. In vivo measurement of ligament/tendon strains and forces: A review. Ann. Biomed. Eng. 2004, 32, 318–328. [Google Scholar] [CrossRef]
- Zhang, Q.; Adam, N.C.; Hosseini Nasab, S.H.; Taylor, W.R.; Smith, C.R. Techniques for In Vivo Measurement of Ligament and Tendon Strain: A Review. Ann. Biomed. Eng. 2021, 49, 7–28. [Google Scholar] [CrossRef]
- Beynnon, B.D.; Fleming, B.C. Anterior cruciate ligament strain in-vivo: A review of previous work. J. Biomech. 1998, 31, 519–525. [Google Scholar] [CrossRef]
- Markolf, K.L.; Willems, M.J.; Jackson, S.R.; Finerman, G.A.M. In situ calibration of miniature sensors implanted into the anterior cruciate ligament. Part I: Strain measurements. J. Orthop. Res. 1998, 16, 455–463. [Google Scholar] [CrossRef] [PubMed]
- Hollis, J.M.; Pearsall, A.W.; Niciforos, P.G. Change in Meniscal Strain with Anterior Cruciate Ligament Injury and after Reconstruction. Am. J. Sports Med. 2000, 28, 700–704. [Google Scholar] [CrossRef] [PubMed]
- Kamineni, S.; ElAttrache, N.S.; O’driscoll, S.W.; Ahmad, C.S.; Hirohara, H.; Neale, P.G.; An, K.-N.; Morrey, B.F. Medial collateral ligament strain with partial posteromedial olecranon resection. A biomechanical study. J. Bone Jt. Surg. Am. 2004, 86, 2424–2430. [Google Scholar] [CrossRef] [PubMed]
- Withrow, T.J.; Huston, L.J.; Wojtys, E.M.; Ashton-Miller, J.A. Effect of Varying Hamstring Tension on Anterior Cruciate Ligament Strain During in Vitro Impulsive Knee Flexion and Compression Loading. J. Bone Jt. Surg. Am. 2008, 90, 815–823. [Google Scholar] [CrossRef]
- Kasisari, R. Bestimmung der Kräfte, Die in Den Humanen Meniscotibialen Bändern Wirken. Ph.D. Dissertation, Universität Ulm, Ulm, Germany, 2015. [Google Scholar] [CrossRef]
- Schilaty, N.D.; Bates, N.A.; Krych, A.J.; Hewett, T.E. Frontal Plane Loading Characteristics of Medial Collateral Ligament Strain Concurrent to Anterior Cruciate Ligament Failure. Am. J. Sports Med. 2019, 47, 2143–2150. [Google Scholar] [CrossRef]
- Bates, N.A.; Schilaty, N.D.; Nagelli, C.V.; Krych, A.J.; Hewett, T.E. Multiplanar Loading of the Knee and Its Influence on Anterior Cruciate Ligament and Medial Collateral Ligament Strain During Simulated Landings and Noncontact Tears. Am. J. Sports Med. 2019, 47, 1844–1853. [Google Scholar] [CrossRef]
- Yan, C.; Wang, J.; Kang, W.; Cui, M.; Wang, X.; Foo, C.Y.; Chee, K.J.; Lee, P.S. Highly stretchable piezoresistive graphene-nanocellulose nanopaper for strain sensors. Adv. Mater. 2014, 26, 2022–2027. [Google Scholar] [CrossRef]
- Zens, M.; Ruhhammer, J.; Goldschmidtboeing, F.; Woias, P.; Feucht, M.J.; Mayr, H.O.; Niemeyer, P. A new approach to determine ligament strain using polydimethylsiloxane strain gauges: Exemplary measurements of the anterolateral ligament. J. Biomech. Eng. 2014, 136, 124504. [Google Scholar] [CrossRef]
- Zens, M.; Niemeyer, P.; Bernstein, A.; Feucht, M.J.; Kühle, J.; Südkamp, N.P.; Woias, P.; Mayr, H.O. Novel approach to dynamic knee laxity measurement using capacitive strain gauges. Knee Surg. Sports Traumatol. Arthrosc. 2015, 23, 2868–2875. [Google Scholar] [CrossRef]
- Ruhhammer, J. Polymerbasierte Dehnmessstreifen zur Intra- und Extrakorporalen Applikation. Ph.D. Dissertation, Universität Freiburg, Freiburg im Breisgau, Germany, 2017. [Google Scholar] [CrossRef]
- Li, R.; Wang, L.; Yin, L. Materials and Devices for Biodegradable and Soft Biomedical Electronics. Materials 2018, 11, 2108. [Google Scholar] [CrossRef] [PubMed]
- Hirokawa, S.; Yamamoto, K.; Kawada, T. A photoelastic study of ligament strain. IEEE Trans. Rehabil. Eng. 1998, 6, 300–308. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, K.; Hirokawa, S.; Kawada, T. Strain distribution in the ligament using photoelasticity. A direct application to the human ACL. Med. Eng. Phys. 1998, 20, 161–168. [Google Scholar] [CrossRef] [PubMed]
- Sanghavi, P.; Bose, D.; Kerrigan, J.; Madeley, N.J.; Crandall, J. Non-contact strain measurement of biological tissue. Biomed. Sci. Instrum. 2004, 40, 51–56. [Google Scholar]
- Lujan, T.J.; Lake, S.P.; Plaizier, T.A.; Ellis, B.J.; Weiss, J.A. Simultaneous measurement of three-dimensional joint kinematics and ligament strains with optical methods. J. Biomech. Eng. 2005, 127, 193–197. [Google Scholar] [CrossRef][Green Version]
- Phatak, N.S.; Sun, Q.; Kim, S.-E.; Parker, D.L.; Sanders, R.K.; Ellis, B.J.; Weiss, J.A. Noninvasive Determination of Ligament Strain with Deformable Image Registration. Ann. Biomed. Eng. 2007, 35, 1175–1187. [Google Scholar] [CrossRef][Green Version]
- Brett, A.W.; Oliver, M.L.; Agur, A.M.R.; Edwards, A.M.; Gordon, K.D. Quantification of the transverse carpal ligament elastic properties by sex and region. Clin. Biomech. 2014, 29, 601–606. [Google Scholar] [CrossRef]
- Komi, P.V.; Belli, A.; Huttunen, V.; Bonnefoy, R.; Geyssant, A.; Lacour, J.R. Optic fibre as a transducer of tendomuscular forces. Eur. J. Appl. Physiol. Occup. Physiol. 1996, 72, 278–280. [Google Scholar] [CrossRef]
- Dillon, E.M.; Erasmus, P.J.; Müller, J.H.; Scheffer, C.; de Villiers, R.V. Differential Forces within the Proximal Patellar Tendon as an Explanation for the Characteristic Lesion of Patellar Tendinopathy. Am. J. Sports Med. 2008, 36, 2119–2127. [Google Scholar] [CrossRef]
- Ren, L.; Song, G.; Conditt, M.; Noble, P.C.; Li, H. Fiber Bragg grating displacement sensor for movement measurement of tendons and ligaments. Appl. Opt. 2007, 46, 6867–6871. [Google Scholar] [CrossRef]
- Arthroskopie und Sportmedizin|KARL STORZ Endoskope|Österreich. Available online: https://www.karlstorz.com/at/de/area-of-expertise.htm?cat=1000106621 (accessed on 8 February 2022).
- Wani, S.A.; Al Salmi, L.A.; Habib, O.; Uzair Ul Haq, M. Use of Permanent Markers for Intraoperative Marking in Body Contouring Surgery: An Innovative Technique. World J. Plast. Surg. 2018, 7, 387–388. [Google Scholar] [CrossRef] [PubMed]
- Mintz, D.; Falk, V.; Salisbury, J.K., Jr. Comparison of Three High-End Endoscopic Visualization Systems on Telesurgical Performance. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2000, Third International Conference, Pittsburgh, PA, USA, 11–14 October 2000; Delp, S.L., DiGioia, A.M., Jaramaz, B., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2000; Volume 1935, pp. 385–394. [Google Scholar]
- Petersen, W.; Tillmann, B. Anatomie und Funktion des vorderen Kreuzbandes. Orthopäde 2002, 31, 710–718. [Google Scholar] [CrossRef] [PubMed]
- Ekwueme, E.C.; Kwansa, A.L.; Sharif, K.; El-Amin, S.F.; Freeman, J.W. Recent Advancements in Ligament Replacement; Recent Patents on Biomedical Engineering (Discontinued); Bentham Science Publishers: Sharjah, United Arab Emirates, 2011; Volume 4, pp. 196–204. [Google Scholar]
- PubMed. Available online: https://pubmed.ncbi.nlm.nih.gov/ (accessed on 2 May 2022).
- Schuth, M.; Buerakov, W. Handbuch Optische Messtechnik: Praktische Anwendungen für Entwicklung, Versuch, Fertigung und Qualitätssicherung; Carl Hanser Verlag GmbH & Co. KG: München, Germany, 2017; ISBN 978-3-446-43634-3. [Google Scholar]
- Deliyski, D.D.; Shishkov, M.; Mehta, D.D.; Ghasemzadeh, H.; Bouma, B.; Zañartu, M.; de Alarcon, A.; Hillman, R.E. Laser-Calibrated System for Transnasal Fiberoptic Laryngeal High-Speed Videoendoscopy. J. Voice 2021, 35, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Sui, C.; Wu, J.; Wang, Z.; Ma, G.; Liu, Y.-H. A Real-Time 3D Laparoscopic Imaging System: Design, Method, and Validation. IEEE Trans. Biomed. Eng. 2020, 67, 2683–2695. [Google Scholar] [CrossRef]
- Furukawa, R.; Oka, S.; Kotachi, T.; Okamoto, Y.; Tanaka, S.; Sagawa, R.; Kawasaki, H. Fully Auto-calibrated Active-stereo-based 3D Endoscopic System using Correspondence Estimation with Graph Convolutional Network. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 4357–4360. [Google Scholar] [CrossRef]
- Chadebecq, F.; Vasconcelos, F.; Lacher, R.; Maneas, E.; Desjardins, A.; Ourselin, S.; Vercauteren, T.; Stoyanov, D. Refractive Two-View Reconstruction for Underwater 3D Vision. Int. J. Comput. Vis. 2020, 128, 1101–1117. [Google Scholar] [CrossRef]
- Kim, J.; Al Faruque, H.; Kim, S.; Kim, E.; Hwang, J.Y. Multimodal endoscopic system based on multispectral and photometric stereo imaging and analysis. Biomed. Opt. Express 2019, 10, 2289. [Google Scholar] [CrossRef]
- Wang, D.; Liu, H.; Cheng, X. A Miniature Binocular Endoscope with Local Feature Matching and Stereo Matching for 3D Measurement and 3D Reconstruction. Sensors 2018, 18, 2243. [Google Scholar] [CrossRef]
- Lin, J.; Clancy, N.T.; Qi, J.; Hu, Y.; Tatla, T.; Stoyanov, D.; Maier-Hein, L.; Elson, D.S. Dual-modality endoscopic probe for tissue surface shape reconstruction and hyperspectral imaging enabled by deep neural networks. Med. Image Anal. 2018, 48, 162–176. [Google Scholar] [CrossRef]
- Le, H.N.D.; Nguyen, H.; Wang, Z.; Opfermann, J.; Leonard, S.; Krieger, A.; Kang, J.U. Demonstration of a laparoscopic structured-illumination three-dimensional imaging system for guiding reconstructive bowel anastomosis. J. Biomed. Opt. 2018, 23, 1. [Google Scholar] [CrossRef]
- Howlett, I.D.; Han, W.; Gordon, M.; Rice, P.; Barton, J.K.; Kostuk, R.K. Volume holographic imaging endoscopic design and construction techniques. J. Biomed. Opt. 2017, 22, 056010. [Google Scholar] [CrossRef][Green Version]
- Furukawa, R.; Sanomura, Y.; Tanaka, S.; Yoshida, S.; Sagawa, R.; Visentini-Scarzanella, M.; Kawasaki, H. 3D endoscope system using DOE projector. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 2091–2094. [Google Scholar] [CrossRef]
- Furukawa, R.; Masutani, R.; Miyazaki, D.; Baba, M.; Hiura, S.; Visentini-Scarzanella, M.; Morinaga, H.; Kawasaki, H.; Sagawa, R. 2-DOF auto-calibration for a 3D endoscope system based on active stereo. In Proceedings of the 2015 37th IEEE Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 7937–7941. [Google Scholar]
- Malti, A.; Bartoli, A. Combining Conformal Deformation and Cook–Torrance Shading for 3-D Reconstruction in Laparoscopy. IEEE Trans. Biomed. Eng. 2014, 61, 1684–1692. [Google Scholar] [CrossRef]
- Schmalz, C.; Forster, F.; Schick, A.; Angelopoulou, E. An endoscopic 3D scanner based on structured light. Med. Image Anal. 2012, 16, 1063–1072. [Google Scholar] [CrossRef] [PubMed]
- Maurice, X.; Albitar, C.; Doignon, C.; de Mathelin, M. A structured light-based laparoscope with real-time organs’ surface reconstruction for minimally invasive surgery. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 5769–5772. [Google Scholar]
- Clancy, N.T.; Stoyanov, D.; Maier-Hein, L.; Groch, A.; Yang, G.-Z.; Elson, D.S. Spectrally encoded fiber-based structured lighting probe for intraoperative 3D imaging. Biomed. Opt. Express 2011, 2, 3119. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Narasimhan, S.G.; Jaramaz, B. A Multi-Image Shape-from-Shading Framework for Near-Lighting Perspective Endoscopes. Int. J. Comput. Vis. 2010, 86, 211–228. [Google Scholar] [CrossRef]
- Pilonis, N.D.; Januszewicz, W.; di Pietro, M. Confocal laser endomicroscopy in gastro-intestinal endoscopy: Technical aspects and clinical applications. Transl. Gastroenterol. Hepatol. 2022, 7, 7. [Google Scholar] [CrossRef]
- Teubner, D.; Kiesslich, R.; Matsumoto, T.; Rey, J.W.; Hoffman, A. Beyond Standard Image-enhanced Endoscopy Confocal Endomicroscopy. Gastrointest. Endosc. Clin. N. Am. 2014, 24, 427–434. [Google Scholar] [CrossRef][Green Version]
- Akarsu, M.; Akarsu, C. Evaluation of New Technologies in Gastrointestinal Endoscopy. J. Soc. Laparoendosc. Surg. 2018, 22, e00053. [Google Scholar] [CrossRef]
- Haidegger, T.; Kovács, L.; Benyó, B.; Benyó, Z. Spatial Accuracy of Surgical Robots. In Proceedings of the 2009 5th International Symposium on Applied Computational Intelligence and Informatics, SACI 2009, Timisoara, Romania, 28–29 May 2009; pp. 133–138. [Google Scholar] [CrossRef]
- Wise, E.S.; Cheung-Flynn, J.; Brophy, C.M. Standard Surgical Skin Markers Should Be Avoided for Intraoperative Vein Graft Marking during Cardiac and Peripheral Bypass Operations. Front. Surg. 2016, 3, 36. Available online: https://www.frontiersin.org/article/10.3389/fsurg.2016.00036 (accessed on 23 May 2022). [CrossRef]
- 120 Megapixel High Resolution CMOS Sensor|Canon USA. Canon Industrial Sensors. Available online: https://canon-cmos-sensors.com/canon-120mxs-cmos-sensor/ (accessed on 24 May 2022).
- Sony Semiconductor Solutions Group. Products|Image Sensor: Consumer Camera|Products|Sony Semiconductor Solutions Group. Available online: https://www.sony-semicon.co.jp/e/products/IS/camera/product.html (accessed on 24 May 2022).
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements; University Science Books: Sausalito, CA, USA, 1997; ISBN 978-0-935702-42-2. [Google Scholar]
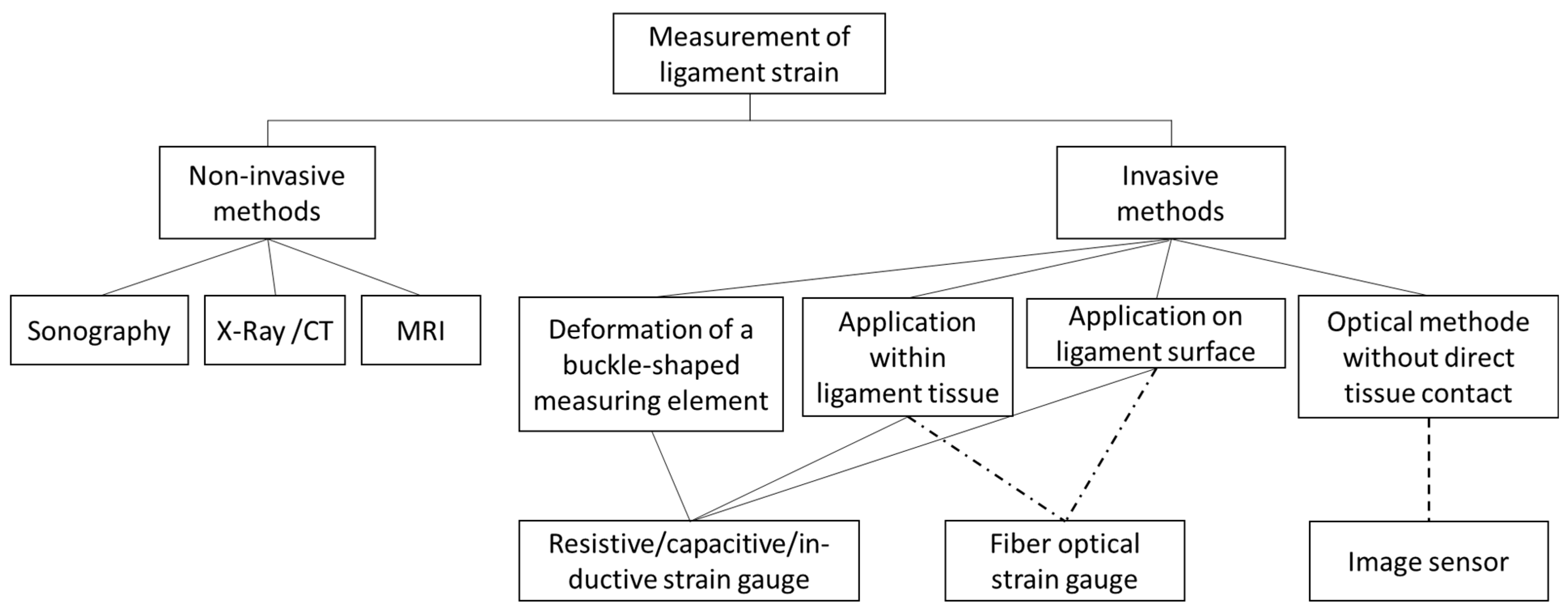

| No. | Objectives |
|---|---|
| 1 | Non-destructive towards the ligaments tissue |
| 2 | No irreversible application of parts of the measurement setup on the ligaments tissue (such as markers, etc.) |
| 3 | Compatibility with minimal invasive surgery (MIS) |
| 4 | Minimal or no influence of the measurement setup on the measurement results |
| 5 | Compatibility with curvature of ligaments surface |
| 6 | No hindering of ligaments twisting |
| 7 | Measurement duration of 1–20 min |
| 8 | High measurement accuracy (see Section 2.2) |
| Refs. | Meas. Object | Application | Meas. Setup | Limitations for an Application in the Clinical Routine |
|---|---|---|---|---|
| [4,5,6,7] | Surface | Surgical suture | LMSG |
|
| [8,9,10,11,12] | Surface | Barbs | HEST |
|
| [11,12,13,14,15,16,17,18,19,20] | Surface | Barbs | DVRT |
|
| [21,22,23,24,25] | Surface | Adhesive | Polymeric strain gauge with very low Young’s modulus |
|
| [32,33] | Tissue | Adhesive | Fiber Bragg grating |
|
| [34] | Surface | Adhesive | Fiber Bragg grating |
|
| [26,27] | Surface | Surface coating | Reflective photoelastic method |
|
| [31,32,33,34] | Surface | Needles/Adhesive for markers | DIC via CCD or CMOS sensors |
|
| Case | in mm | r | in mm | ||
|---|---|---|---|---|---|
| Ideal | 10 | 0.05 | 0.001 | 5 | 9.75 × 10−4 |
| Minimal | 20 | 0.1 | 0.01 | 5 | 1.90 × 10−2 |
| Case | Dimension of FoV | Pixel per Dimension | Total Number of Pixel | |
|---|---|---|---|---|
| In mm | ||||
| Ideal | Length | 15 | 1.54 × 104 | 7.89 × 107 |
| Width | 5 | 5.17 × 103 | ||
| Minimal | Length | 30 | 1.58 × 103 | 8.35 × 105 |
| Width | 10 | 5.27 × 102 | ||
| Keyword | Keyword |
|---|---|
| 3D endoscope development | Endoscope holography |
| Endoscope structured light 3D | Endoscope shearography |
| Endoscope strain measurement | Endoscope Speckle pattern shearing interferometry |
| Endoscope diffractive optical element | Endoscope confocal |
| Refs. | Technique | Max. Error of Measuring System in mm | FoV in mm × mm |
|---|---|---|---|
| [42] | Laser pattern | - | - |
| [43] | Active stereo | 0.3–0.4 | - |
| [44] | Active stereo | - | - |
| [45] | Multi view stereo, structure from motion | 0.2–0.3 | - |
| [46] | Photometric stereo | 0.5 | - |
| [47] | Weighted orthogonal-symmetric local binary pattern (WOS-LBP), multi view stereo | 0.03 | - |
| [48] | Structured light projection | 0.3 | - |
| [49] | Structured light projection | 0.25 | - |
| [50] | Holography | 0.0022 | 0.390 × 0.244 |
| [51,52] | Grid pattern projector, active stereo | - | - |
| [53] | Shapes from shading | 0.3 | - |
| [54] | Structured light projection | 0.092 | 30 × 30 |
| [55] | Structured light projection | - | - |
| [56] | Structured light projection | 0.15 | - |
| [57] | Shapes from shading | 1.45 | - |
| [58] | Confocal laser | 0.0035 | - |
| [59,60] | Confocal laser | 0.0007 | 0.475 × 0.475 |
| Method | Measurement Accuracy Criterion | FoV Criterion (Lateral) | ||
|---|---|---|---|---|
| Ideal | Minimal | Minimal | Ideal | |
| Structured light projection | No | Yes | Yes | Yes |
| Triangulation sensor | Yes | Yes | Yes | Yes |
| White light interferometry | Yes | Yes | No | No |
| Confocal microscopy | Yes | Yes | No | No |
| Confocal chromatic sensors | Yes | Yes | No | Yes |
| Scattered light sensor | Yes | Yes | No | Yes |
| Laser tracker | No | Yes | Yes | Yes |
| Autofocus optical system | Yes | Yes | Yes | Yes |
| Heterodyne and homodyne interferometry | Yes | Yes | No | Yes |
| Conoscopic holography | Yes | Yes | Yes | Yes |
| Ellipsometry | Yes | Yes | No | No |
| Multiple-Wavelength Interferometry | Yes | Yes | Yes | Yes |
| Maykoh sensor | Yes | Yes | Yes | Yes |
| Shadow casting method | Yes | Yes | No | No |
| Holography | Yes | Yes | Yes | Yes |
| Shearography | Yes | Yes | Yes | Yes |
| Image correlation | No | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marx, C.; Wulff, P.; Fink, C.; Baumgarten, D. Optical Measurement of Ligament Strain: Opportunities and Limitations for Intraoperative Application. Sensors 2023, 23, 7487. https://doi.org/10.3390/s23177487
Marx C, Wulff P, Fink C, Baumgarten D. Optical Measurement of Ligament Strain: Opportunities and Limitations for Intraoperative Application. Sensors. 2023; 23(17):7487. https://doi.org/10.3390/s23177487
Chicago/Turabian StyleMarx, Christian, Paul Wulff, Christian Fink, and Daniel Baumgarten. 2023. "Optical Measurement of Ligament Strain: Opportunities and Limitations for Intraoperative Application" Sensors 23, no. 17: 7487. https://doi.org/10.3390/s23177487
APA StyleMarx, C., Wulff, P., Fink, C., & Baumgarten, D. (2023). Optical Measurement of Ligament Strain: Opportunities and Limitations for Intraoperative Application. Sensors, 23(17), 7487. https://doi.org/10.3390/s23177487







