Frequency Limits of Sequential Readout for Sensing AC Magnetic Fields Using Nitrogen-Vacancy Centers in Diamond
Abstract
:1. Introduction
2. Results and Discussion
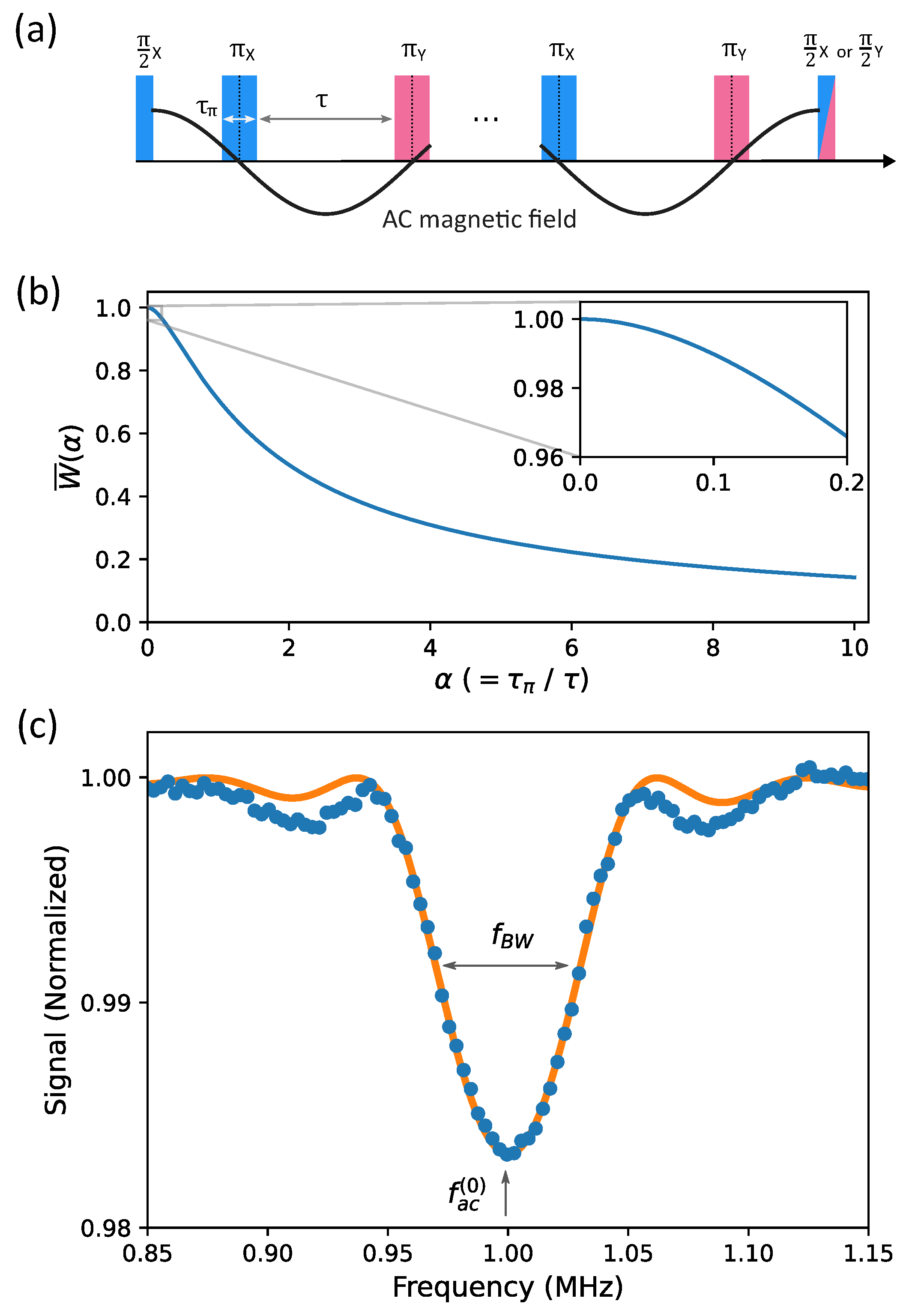
2.1. The Effect of Finite-Width Pulses
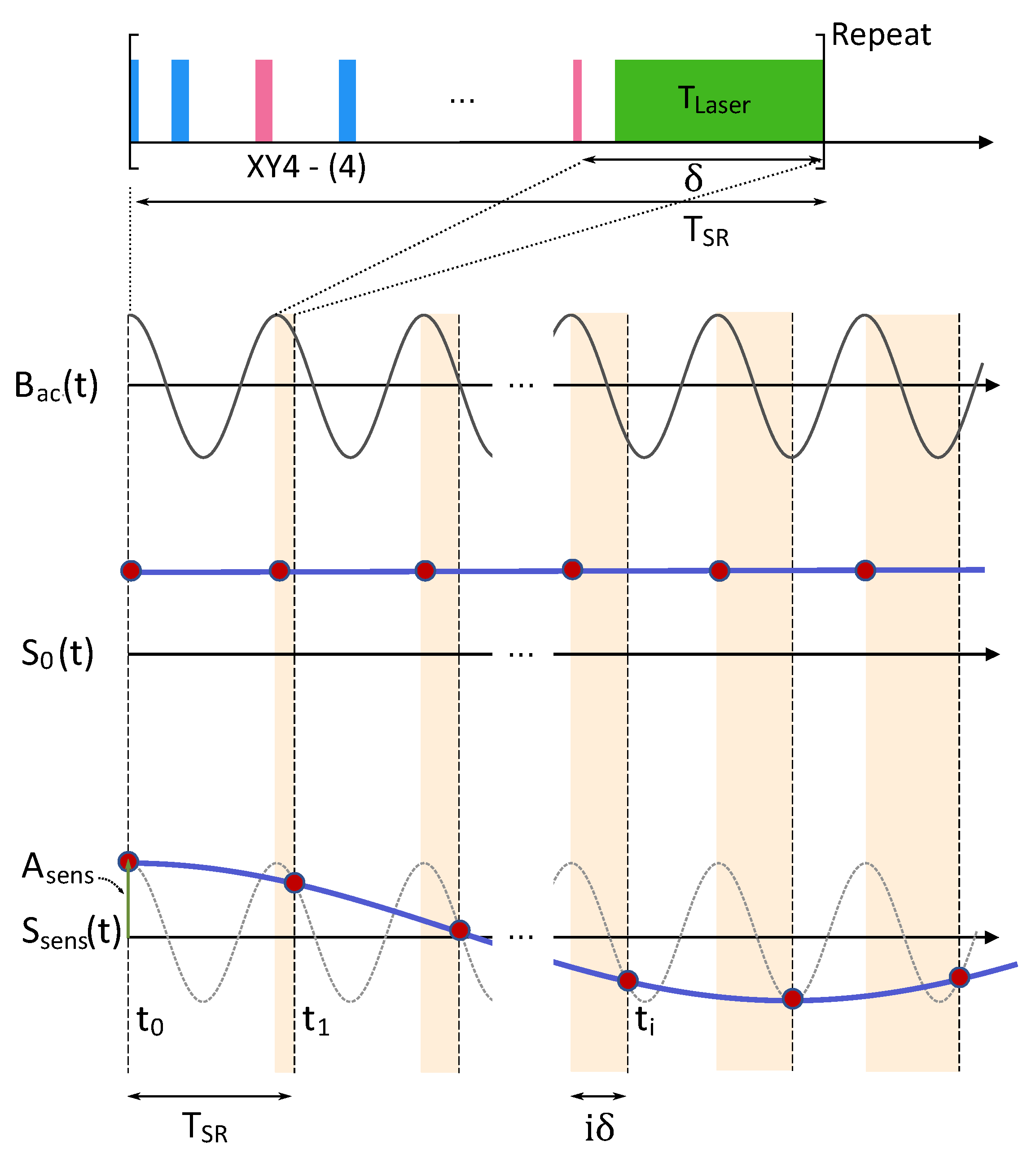
2.2. Sequential Readout Method
2.3. Bandwidth
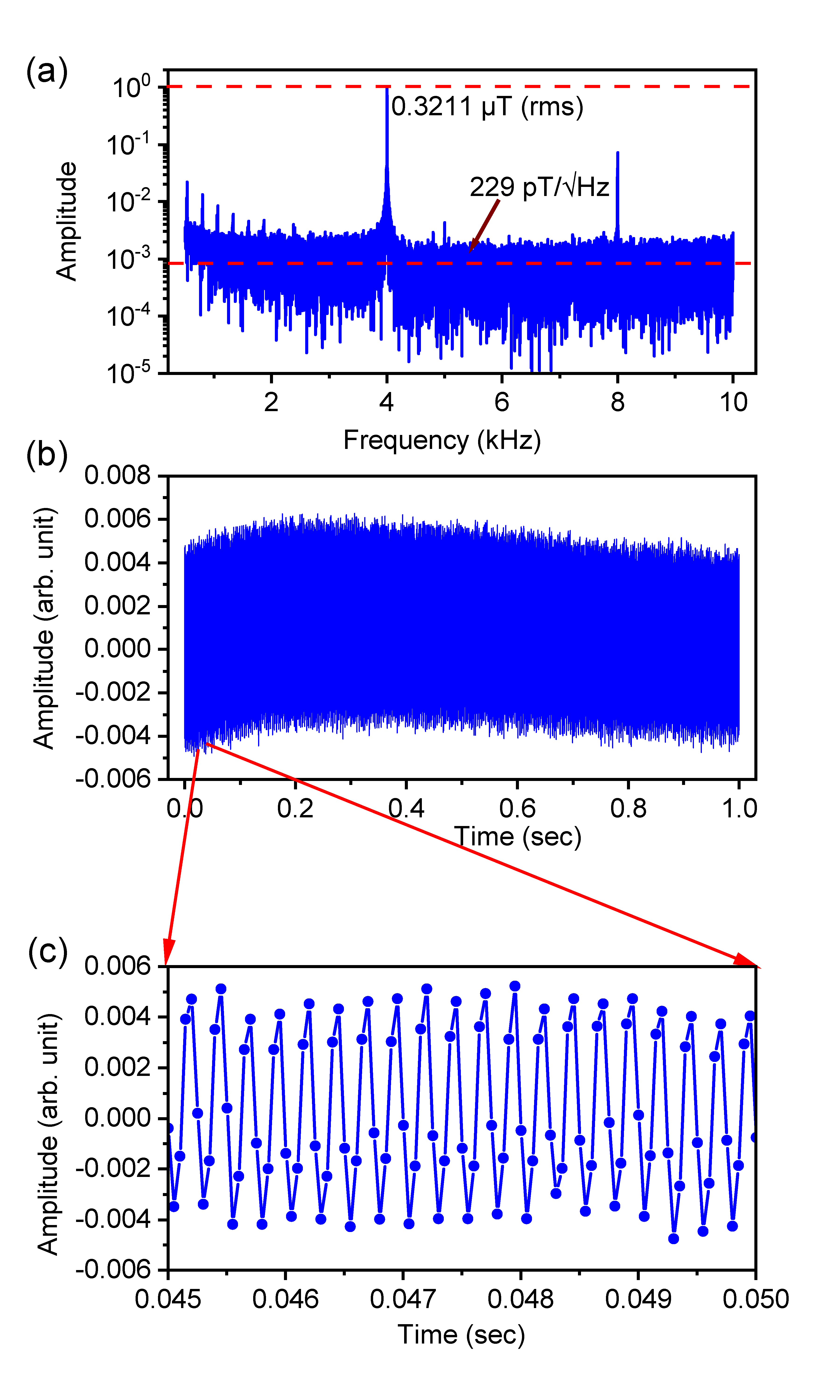
2.4. Sensitivity
2.5. Frequency Dependence of Sensitivity
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Experimental Methods
Appendix A.1. Optical and Microwave System
Appendix A.2. Diamond Sensor
References
- Glenn, D.R.; Bucher, D.B.; Lee, J.; Lukin, M.D.; Park, H.; Walsworth, R.L. High-resolution magnetic resonance spectroscopy using a solid-state spin sensor. Nature 2018, 555, 351–354. [Google Scholar] [CrossRef] [PubMed]
- Deans, C.; Cohen, Y.; Yao, H.; Maddox, B.; Vigilante, A.; Renzoni, F. Electromagnetic induction imaging with a scanning radio frequency atomic magnetometer. Appl. Phys. Lett. 2021, 119, 014001. [Google Scholar] [CrossRef]
- Gerginov, V.; da Silva, F.C.S.; Howe, D. Prospects for magnetic field communications and location using quantum sensors. Rev. Sci. Instrum. 2017, 88, 125005. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, G.; Chan, I.Y.; Kolesov, R.; Al-Hmound, M.; Tisler, J.; Shin, C.; Kim, C.; Wojcik, A.; Hemmer, P.R.; Krueger, A.; et al. Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 2008, 455, 648–651. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J.M.; Cappellaro, P.; Childress, L.; Jiang, L.; Budker, D.; Hemmer, P.R.; Yacoby, A.; Walsworth, R.L.; Lukin, M.D. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2008, 4, 810–816. [Google Scholar] [CrossRef]
- Wolf, T.; Neumann, P.; Nakamura, K.; Sumiya, H.; Ohshima, T.; Isoya, J.; Wrachtrup, J. Subpicotesla Diamond Magnetometry. Phys. Rev. X 2015, 5, 041001. [Google Scholar] [CrossRef]
- Maze, J.R.; Stanwix, P.L.; Hodges, J.S.; Hong, S.; Taylor, J.M.; Cappellaro, P.; Jiang, L.; Dutt, M.V.G.; Togan, E.; Zibrov, A.S.; et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 2008, 455, 644–647. [Google Scholar] [CrossRef]
- Degen, C.L. Scanning magnetic field microscope with a diamond single-spin sensor. Appl. Phys. Lett. 2008, 92, 243111. [Google Scholar] [CrossRef]
- Balasubramanian, G.; Neumann, P.; Twitchen, D.; Markham, M.; Kolesov, R.; Mizuochi, N.; Isoya, J.; Achard, J.; Beck, J.; Tissler, J.; et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Matter. 2009, 8, 383–387. [Google Scholar] [CrossRef]
- Maurer, P.C.; Maze, J.R.; Stanwix, P.L.; Jiang, L.; Gorshkov, A.V.; Zibrov, A.A.; Harke, B.; Hodges, J.S.; Zibrov, A.S.; Yacoby, A.; et al. Far-field optical imaging and manipulation of individual spins with nanoscale resolution. Nat. Phys. 2008, 6, 912–918. [Google Scholar] [CrossRef]
- Dolde, F.; Fedder, H.; Doherty, M.W.; Nobauer, T.; Rempp, F.; Balasubramanian, G.; Wolf, T.; Reinhard, F.; Hollenberg, L.C.L.; Jelezko, F.; et al. Electric-field sensing using single diamond spins. Nat. Phys. 2011, 7, 459–463. [Google Scholar] [CrossRef]
- Grinolds, M.S.; Maletinsky, P.; Hong, S.; Lukin, M.D.; Walsworth, R.L.; Yacoby, A. Quantum control of proximal spins using nanoscale magnetic resonance imaging. Nat. Phys. 2011, 7, 687–692. [Google Scholar] [CrossRef]
- Appel, P.; Ganzhorn, M.; Neu, E.; Maletinsky, P. Nanoscale microwave imaging with a single electron spin in diamond. New J. Phys. 2015, 17, 112001. [Google Scholar] [CrossRef]
- Siyushev, P.; Nesladek, M.; Bourgeois, E.; Gulka, M.; Hruby, J.; Yamamoto, T.; Trupke, M.; Teraji, T.; Isoya, J.; Jelezko, F. Photoelectrical imaging and coherent spin-state readout of single nitrogen-vacancy centers in diamond. Science 2019, 363, 728–731. [Google Scholar] [CrossRef]
- Barson, M.S.; Oberg, L.M.; McGuinness, L.P.; Denisenko, A.; Manson, N.B.; Wrachtrup, J.; Doherty, M.W. Nanoscale vector electric field imaging using a single electron spin. Nano Lett. 2011, 21, 2962–2967. [Google Scholar] [CrossRef] [PubMed]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Savukov, I.M.; Seltzer, S.J.; Romalis, M.V.; Sauer, K.L. Tunable Atomic Magnetometer for Detection of Radio-Frequency Magnetic Fields. Phys. Rev. Lett. 2005, 95, 063004. [Google Scholar] [CrossRef]
- Rondin, L.; Tetienne, J.P.; Hingant, T.; Roch, J.-F.; Maletinsky, P.; Jacques, V. Magnetometry with nitrogen-vacancy defects in diamond. Rep. Prog. Phys. 2014, 77, 056503. [Google Scholar] [CrossRef]
- Suter, D.; Jelezko, F. Single-spin magnetic resonance in the nitrogen-vacancy center of diamond. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 98–99, 50–62. [Google Scholar] [CrossRef]
- deLange, G.; Rist‘e, D.; Dobrovitski, V.V.; Hanson, R. Single-Spin Magnetometry with Multipulse Sensing Sequences. Phys. Rev. Lett. 2011, 106, 080802. [Google Scholar] [CrossRef]
- Pham, L.M.; Sage, D.L.; Stanwix, P.L.; Yeung, T.K.; Glenn, D.; Trifonov, A.; Cappellaro, P.; Hemmer, P.R.; Lukin, M.D.; Park, H.; et al. Magnetic field imaging with nitrogen-vacancy ensembles. New J. Phys. 2011, 13, 045021. [Google Scholar] [CrossRef]
- Pham, L.M.; Bar-Gill, N.; Belthangady, C.; Le Sage, D.; Cappellaro, P.; Lukin, M.D.; Yacoby, A.; Walsworth, R.L. Enhanced solid-state multispin metrology using dynamical decoupling. Phys. Rev. B 2012, 86, 045214. [Google Scholar] [CrossRef]
- Acosta, V.M.; Bauch, E.; Ledbetter, M.P.; Santori, C.; Fu, K.M.C.; Barclay, P.E.; Beausoleil, R.G.; Linget, H.; Roch, J.F.; Treussart, F.; et al. Diamonds with a high density of nitrogenvacancy centers for magnetometry applications. Phys. Rev. B 2009, 80, 115202. [Google Scholar] [CrossRef]
- Levine, E.V.; Turner, M.J.; Kehayias, P.; Hart, C.A.; Langellier, N.; Trubko, R.; Glenn, D.R.; Fu, R.R.; Walsworth, R.L. Principles and techniques of the quantum diamond microscope. Nanophotonics 2019, 8, 1945–1973. [Google Scholar] [CrossRef]
- Jordan, A.N. Classical-quantum sensors keep better time. Science 2017, 356, 802–803. [Google Scholar] [CrossRef] [PubMed]
- Boss, J.M.; Cujia, K.S.; Zopes, J.; Degen, C.L. Quantum sensing with arbitrary frequency resolution. Science 2017, 356, 837–840. [Google Scholar] [CrossRef]
- Schmitt, S.; Gefen, T.; Stürner, F.M.; Unden, T.; Wolff, G.; Müller, C.; Scheuer, J.; Naydenov, B.; Markham, M.; Pezzagna, S.; et al. Submillihertz magnetic spectroscopy performed with a nanoscale quantum sensor. Science 2017, 356, 832–837. [Google Scholar] [CrossRef]
- Smits, J.; Damron, J.T.; Kehayias, P.; McDowell, A.F.; Mosavian, N.; Fescenko, I.; Ristoff, N.; Laraoui, A.; Jarmola, A.; Acosta, V.M. Two-dimensional nuclear magnetic resonance spectroscopy with a microfluidic diamond quantum sensor. Sci. Adv. 2019, 5, eaaw7895. [Google Scholar] [CrossRef]
- Bruckmaier, F.; Allert, R.D.; Neuling, N.R.; Amrein, P.; Littin, S.; Briegel, K.D.; Schatzle, P.; Knittel, P.; Zaitsev, M.; Bucher, D.B. Imaging local diffusion in microstructures using NV-based pulsed field gradient NMR. arXiv 2023, arXiv:2303.03516. [Google Scholar] [CrossRef]
- Ishikawa, T.; Yoshizawa, A.; Mawatari, Y.; Watanabe, H.; Kashiwaya, S. Influence of Dynamical Decoupling Sequences with Finite-Width Pulses on Quantum Sensing for AC Magnetometry. Phys. Rev. Appl. 2018, 10, 054059. [Google Scholar] [CrossRef]
- Allert, R.D.; Briegel, K.D.; Bucher, D.B. Advances in nano- and microscale NMR spectroscopy using diamond quantum sensors. Chem. Commun. 2018, 58, 8165–8181. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghimire, S.; Lee, S.-j.; Oh, S.; Shim, J.H. Frequency Limits of Sequential Readout for Sensing AC Magnetic Fields Using Nitrogen-Vacancy Centers in Diamond. Sensors 2023, 23, 7566. https://doi.org/10.3390/s23177566
Ghimire S, Lee S-j, Oh S, Shim JH. Frequency Limits of Sequential Readout for Sensing AC Magnetic Fields Using Nitrogen-Vacancy Centers in Diamond. Sensors. 2023; 23(17):7566. https://doi.org/10.3390/s23177566
Chicago/Turabian StyleGhimire, Santosh, Seong-joo Lee, Sangwon Oh, and Jeong Hyun Shim. 2023. "Frequency Limits of Sequential Readout for Sensing AC Magnetic Fields Using Nitrogen-Vacancy Centers in Diamond" Sensors 23, no. 17: 7566. https://doi.org/10.3390/s23177566
APA StyleGhimire, S., Lee, S.-j., Oh, S., & Shim, J. H. (2023). Frequency Limits of Sequential Readout for Sensing AC Magnetic Fields Using Nitrogen-Vacancy Centers in Diamond. Sensors, 23(17), 7566. https://doi.org/10.3390/s23177566





