Dynamic Electromagnetic Scattering Simulation of Tilt-Rotor Aircraft in Multiple Modes
Abstract
:1. Introduction
2. Dynamic Scattering Simulation Method of Tilt-Rotor Aircraft
2.1. Methods of RCS Calculation
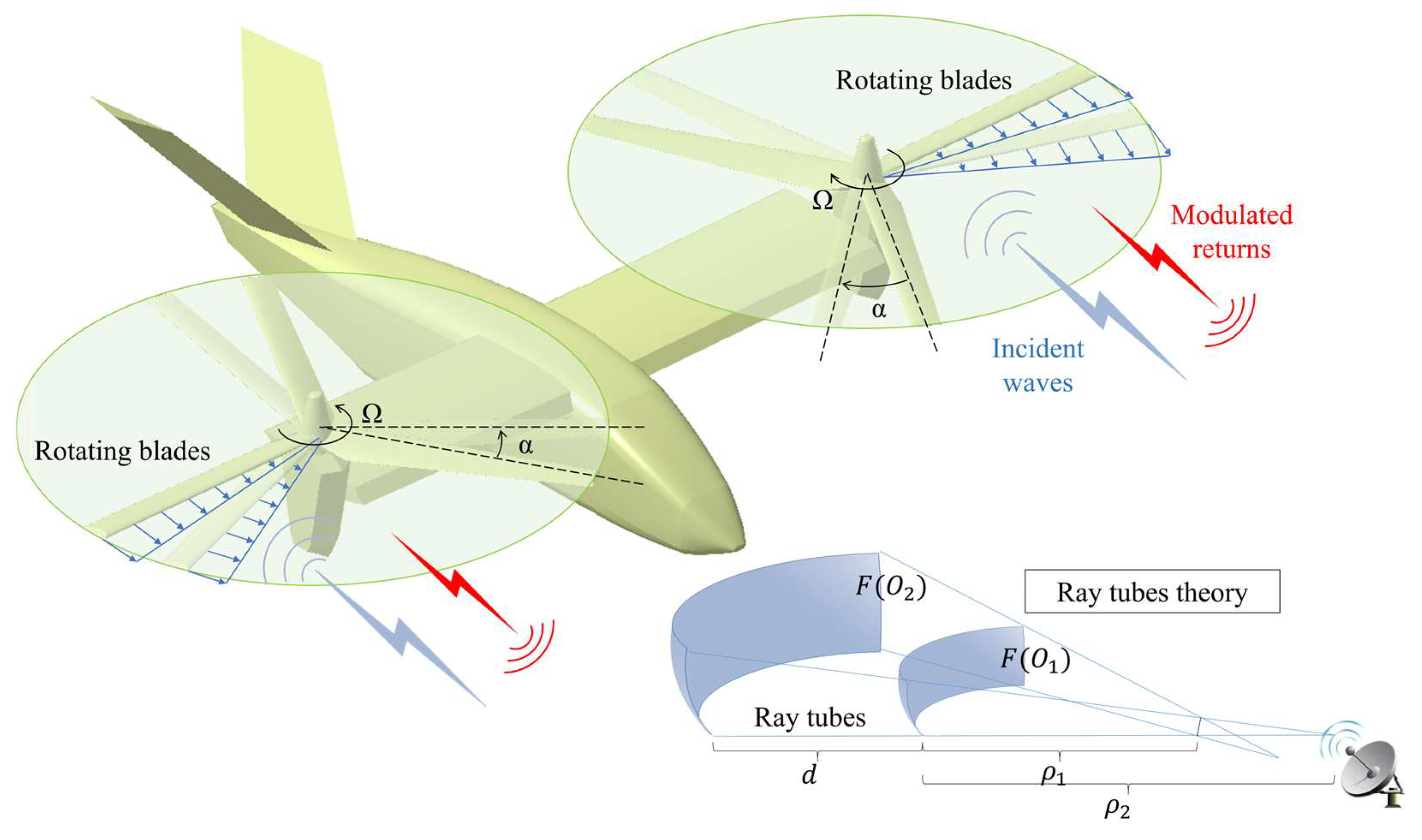
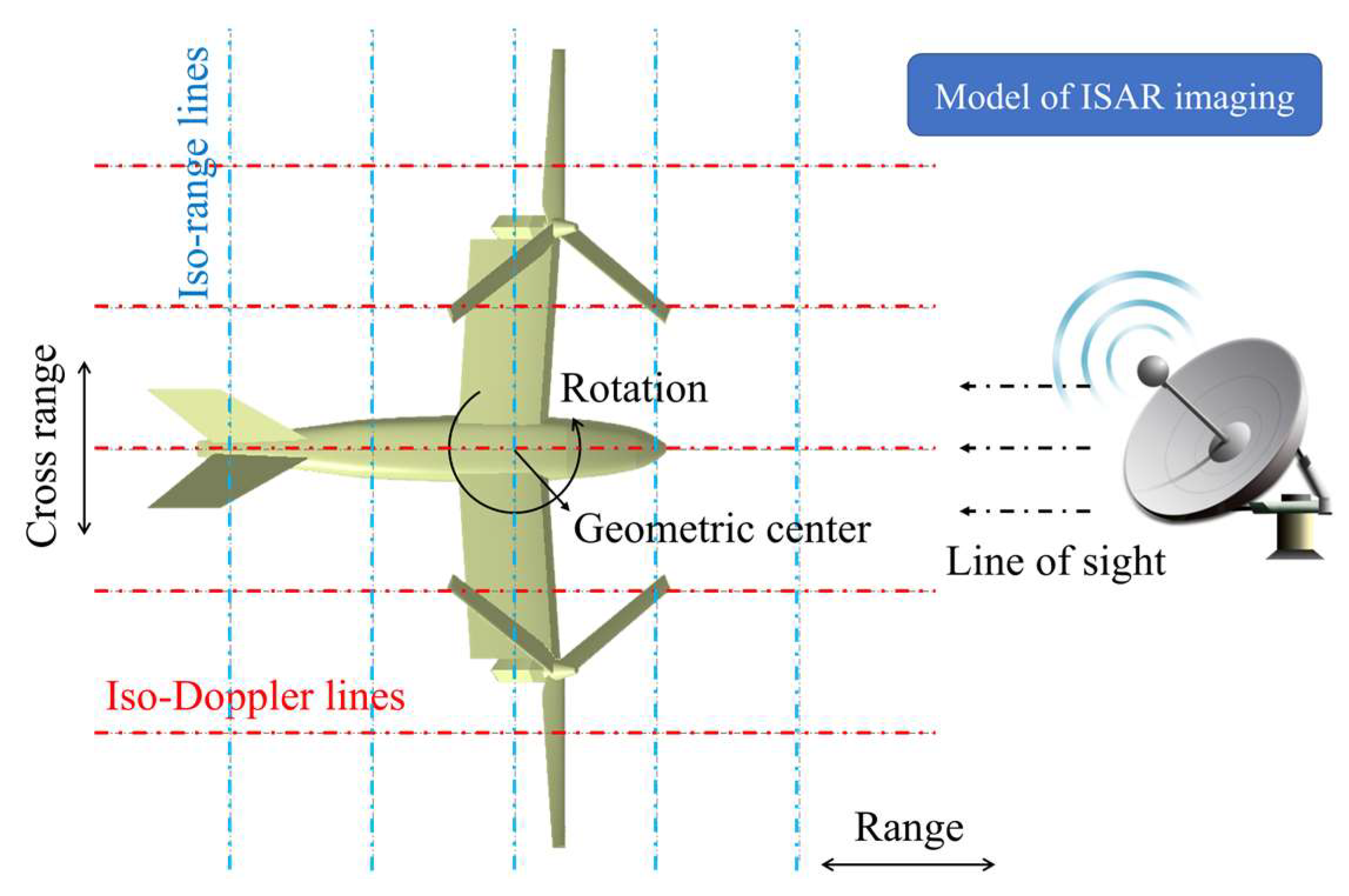
2.2. Principle of Micro-Doppler and ISAR Imaging
2.3. Dynamic Process Simulation
2.3.1. Principle of Quasi-Static
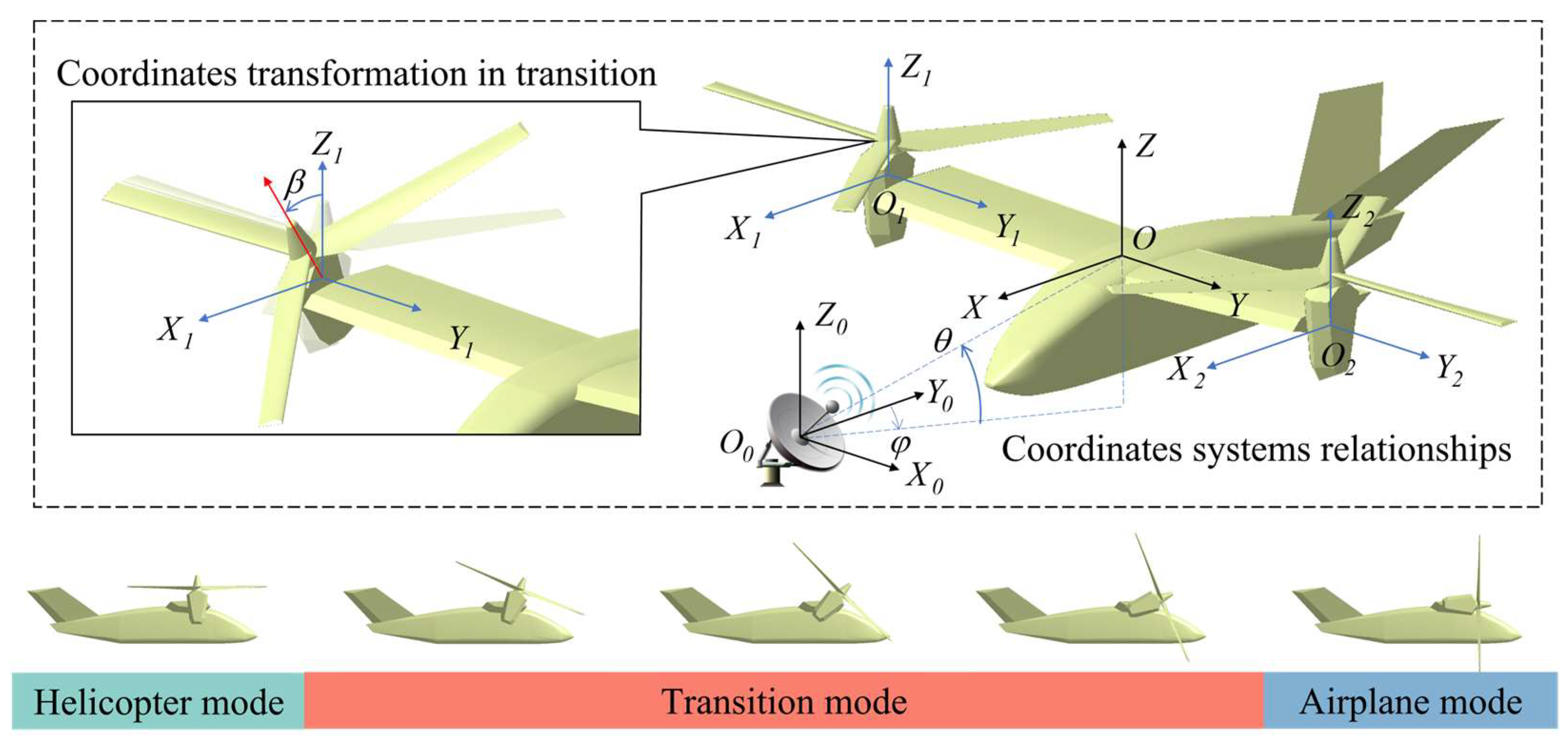
2.3.2. Dynamic Coordinates Transformation
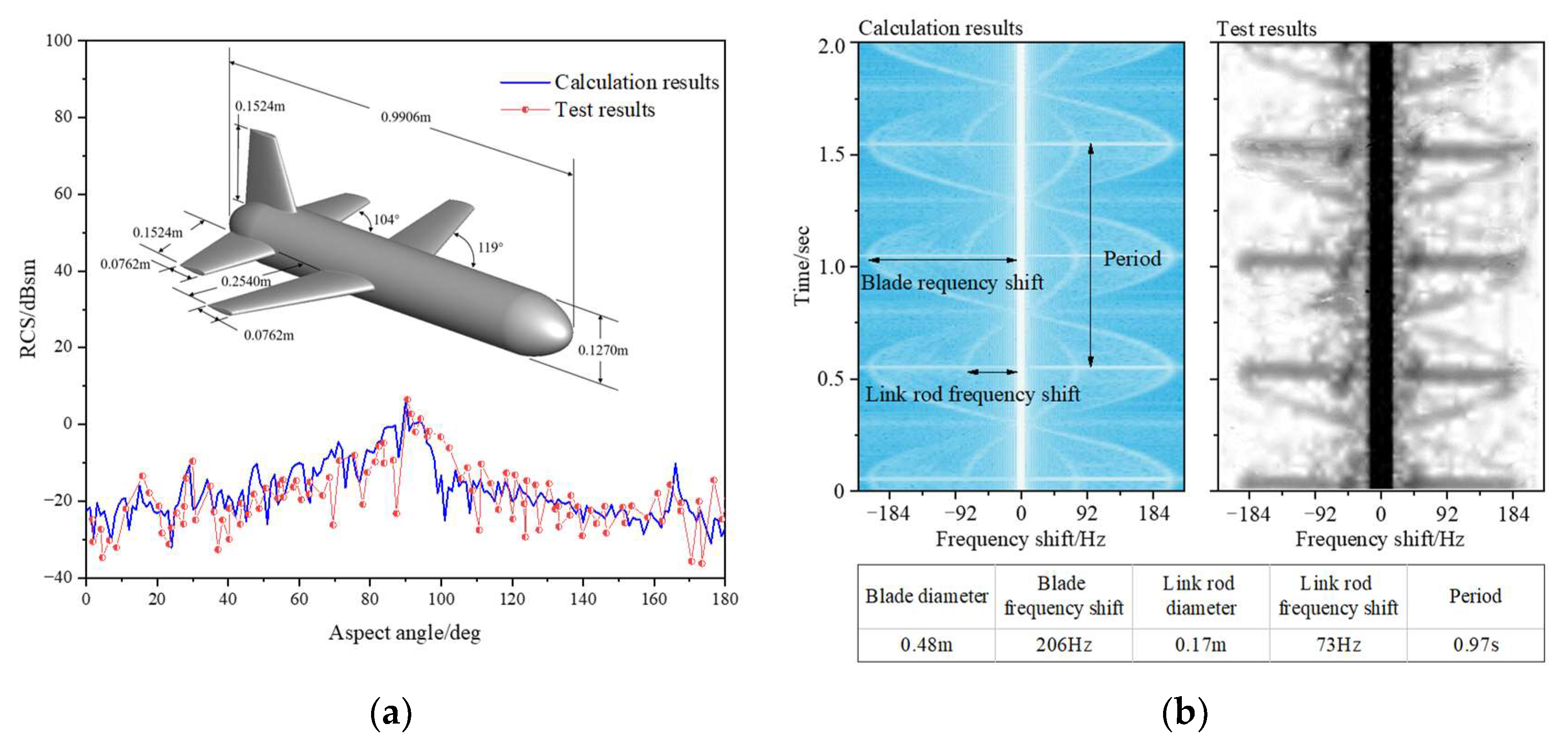
2.4. Method Verification
3. Results and Analyses
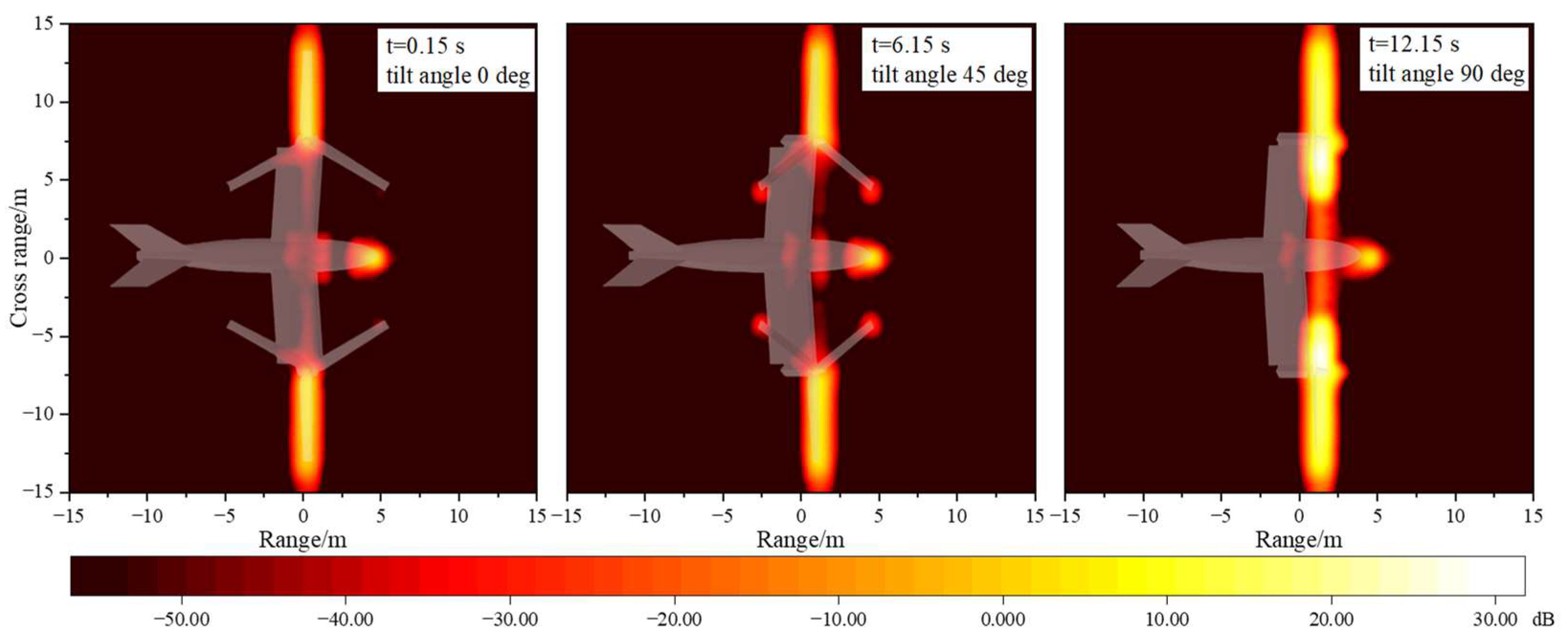
3.1. Multi-Mode Dynamic Electromagnetic Scattering
3.2. Effects of Pitch Angle
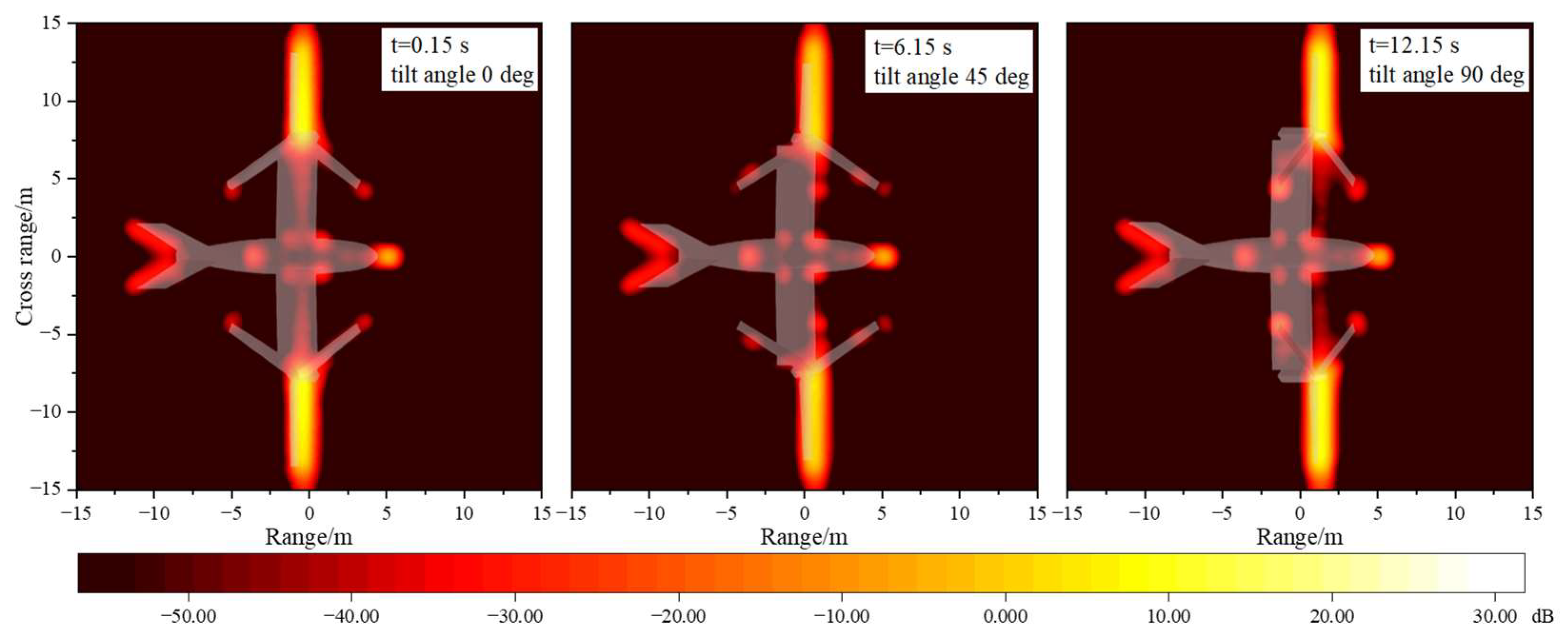
3.3. Effects of Azimuth Angle
4. Conclusions
- (1)
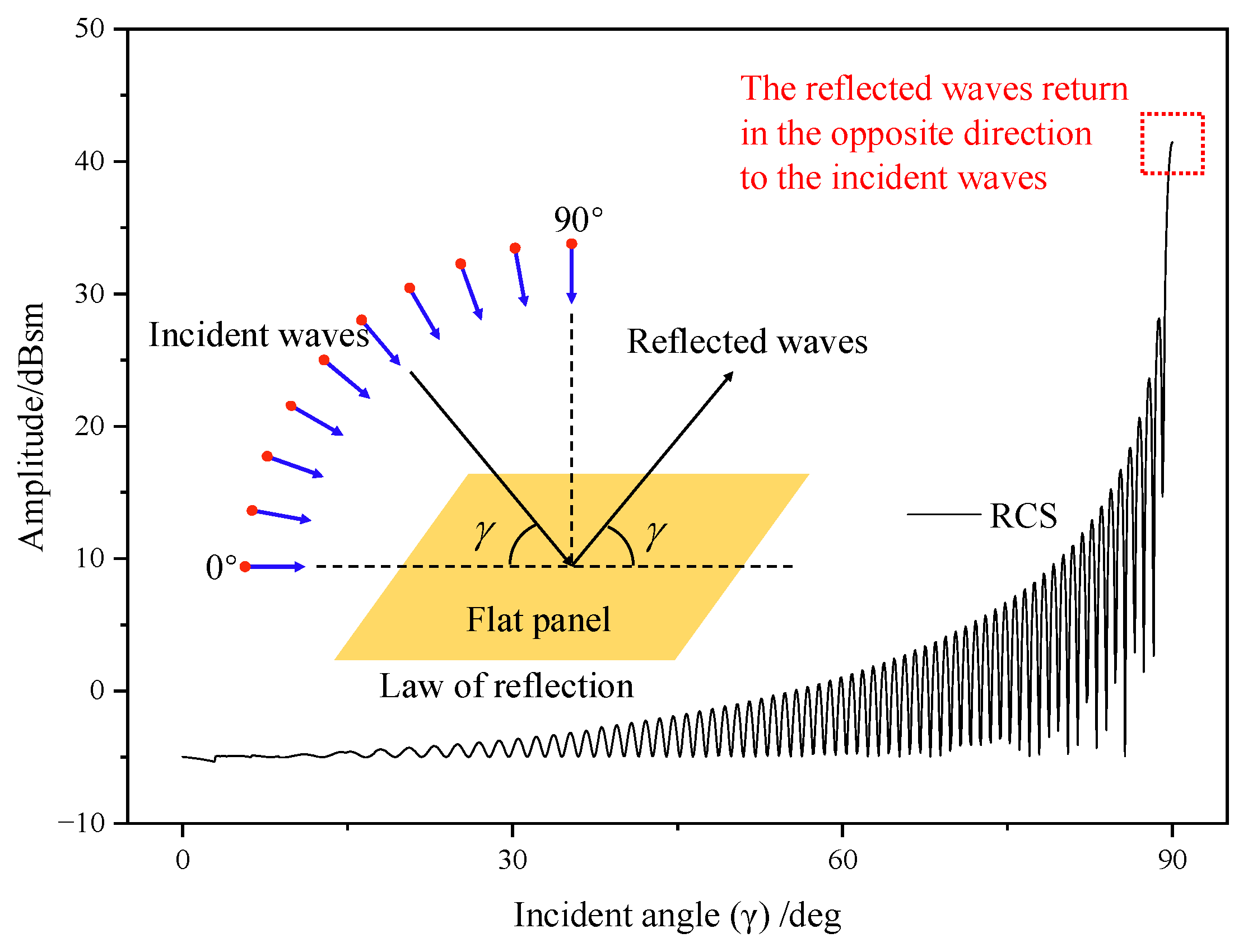
- Due to the rotation of the rotors, the dynamic RCS of the tilt-rotor aircraft in helicopter mode and airplane mode has obvious periodic characteristics. When the radar wave is incident from the front of the aircraft, the conversion from helicopter mode to airplane mode makes the rotor disk gradually perpendicular to the incident wave, resulting in an extremely strong specular reflection and a large increase in RCS, with an increase of 35.32 dB. In order to cope with the case, the rotor’s upper surface is suggested to be coated with wave-absorbing material to weaken the strong specular reflection. When the pitch angle or azimuth angle is not zero, the effect of the transition mode on the RCS growth is rapidly weakened.
- (2)
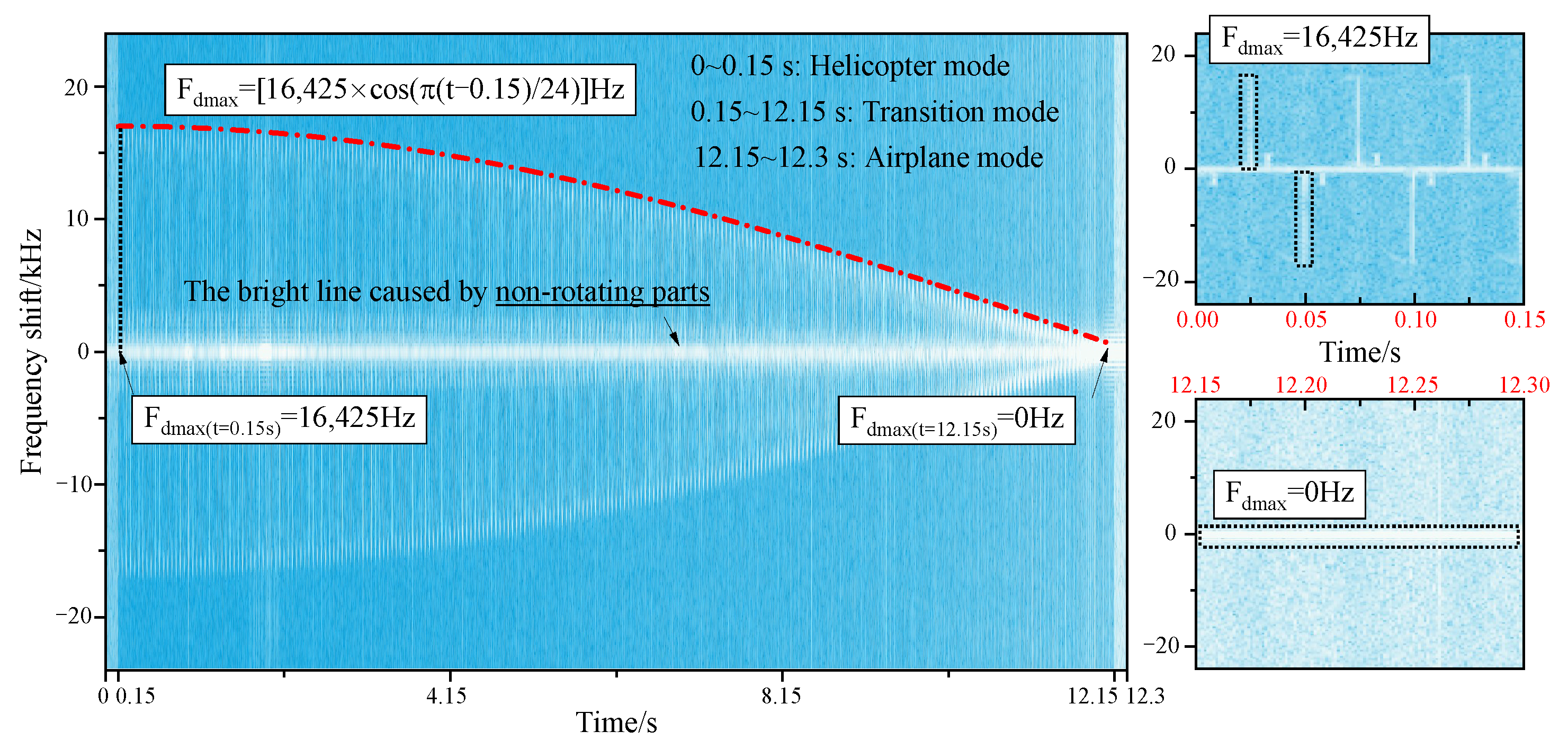
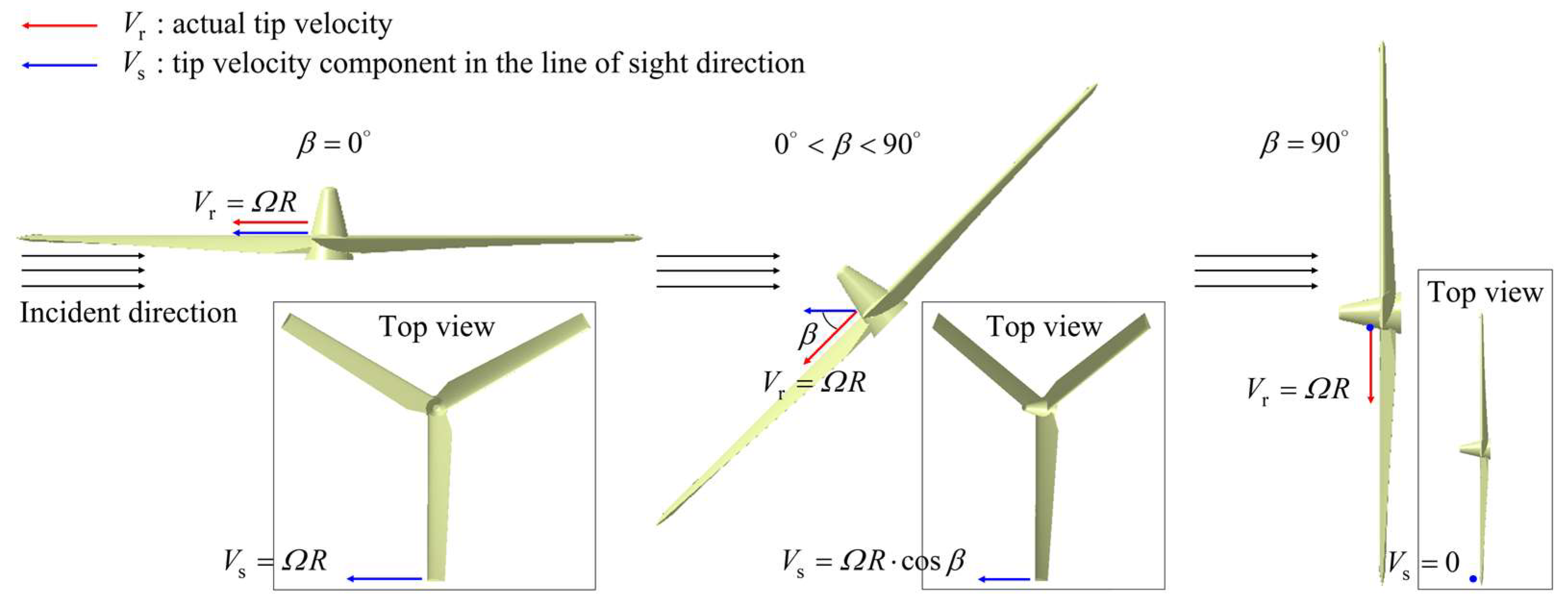
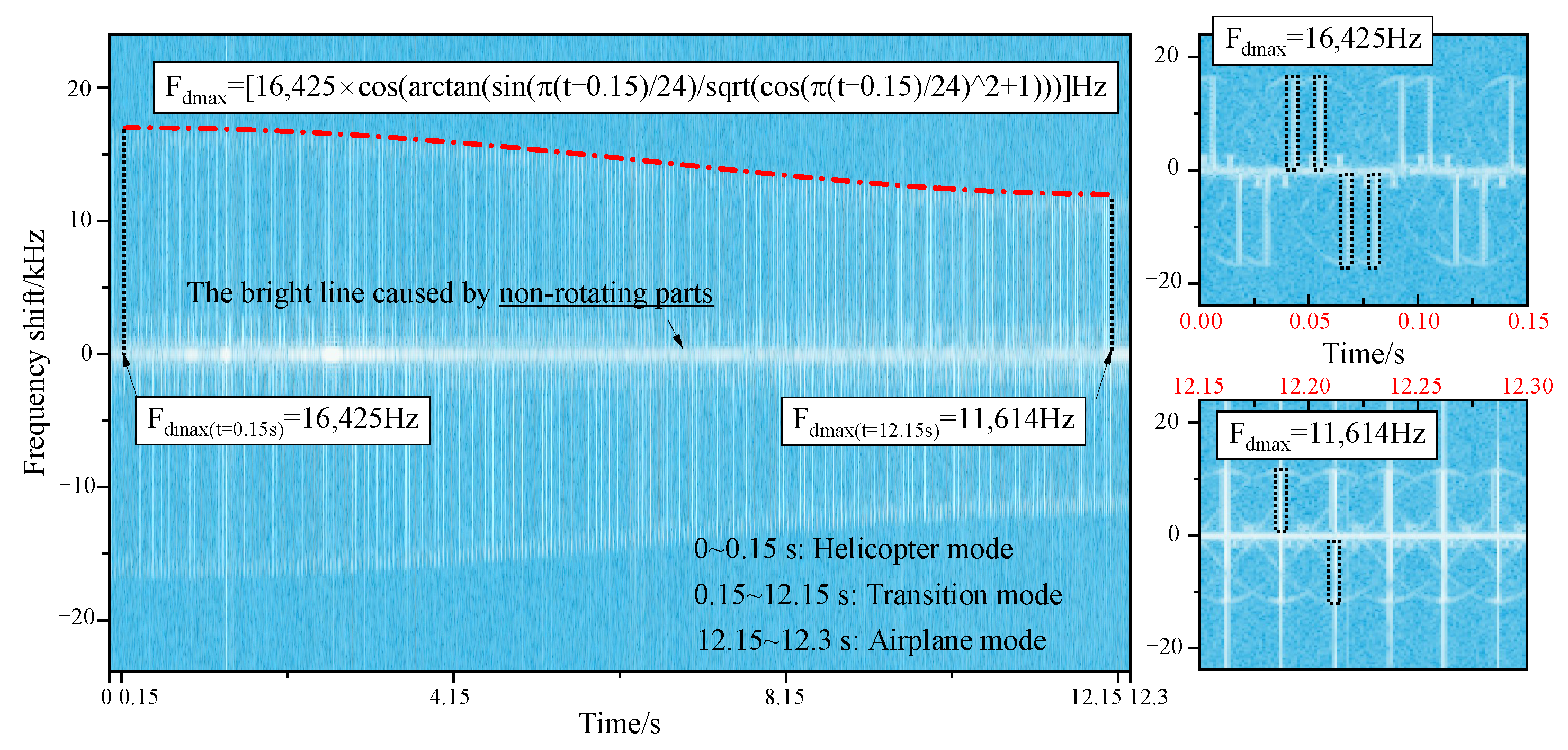
- When the forward or retreating blades are perpendicular to the incident direction of radar rays, the tilt-rotor aircraft has the maximum micro-Doppler frequency shift. In helicopter mode and airplane mode, the maximum micro-Doppler frequency shift remains constant. As the tilting proceeds, the angle between the rotor disk and the radar wave changes, which is related to the flight time, the tilt speed, and the wave’s incident direction. This angle has a definite function expression, and the maximum micro-Doppler frequency shift is proportional to the cosine of this angle. By acquiring real-time micro-Doppler signals from an airborne target and analyzing their changing patterns, it can be determined whether the target is a tilt-rotor aircraft. If so, the aircraft’s flight mode and speed are able to be rapidly identified according to the shift amplitude.
- (3)
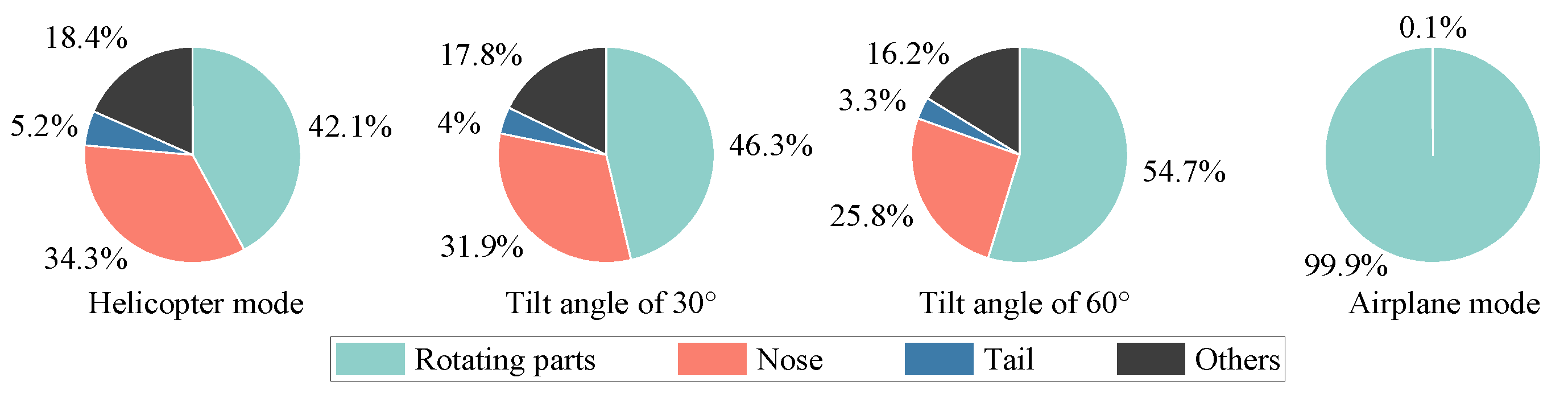
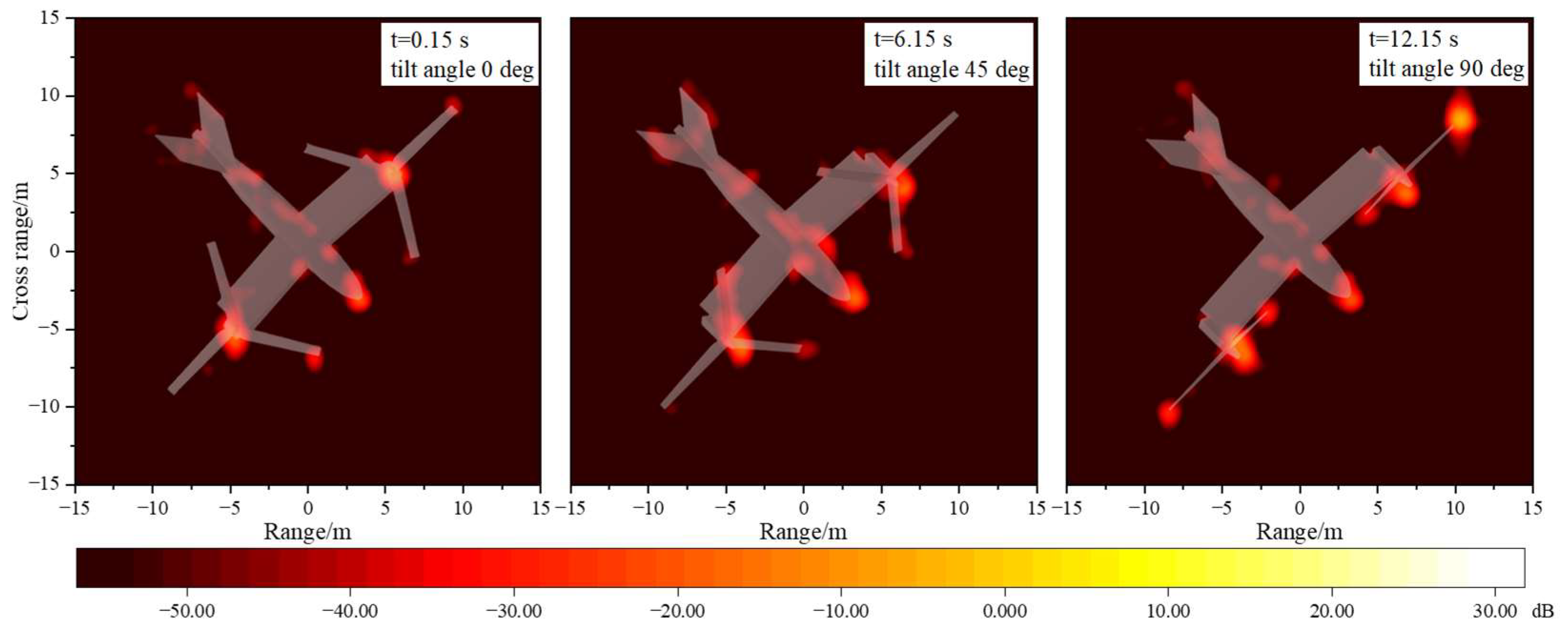
- The tilt-rotor aircraft has multiple important scattering sources. The surfaces of the rotors, the leading edge of the wings, and the nose show a planar scattering source distribution. While the blade tips, the wing–fuselage junctions, and the tail wings show a point-like distribution. In different flight modes and attitude angles, the importance of the above scattering sources is different. When the radar wave is incident from the front of the tilt-rotor aircraft, which flies in airplane mode, the upper surface of the rotor disk is the most significant strong scattering source, and the RCS reduction is needed in this area. Therefore, according to the flight mission requirements of the tilt-rotor aircraft, a reasonable analysis of the key scattering areas can provide effective help for the stealth design of the whole aircraft (e.g., blade tip sharpening, wing–fuselage integration fusion design, tail parallel swept design, and so on).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Z.M.; Li, X.P.; Dong, G.X. Wideband RCS reduction based on hybrid checkerboard metasurface. Sensors 2023, 23, 4054. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, A.; Tarkian, M.; Amadori, K.; Ölvander, J. Multidisciplinary optimization of unmanned aircraft considering radar signature, sensors, and trajectory constraints. J. Aircr. 2018, 55, 1629–1640. [Google Scholar] [CrossRef]
- Clemente, C.; Soraghan, J.J. GNSS-based passive bistatic radar for micro-Doppler analysis of helicopter rotor blades. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 491–500. [Google Scholar] [CrossRef]
- Taj, Z.U.D.; Bilal, A.; Awais, M.; Salamat, S.; Abbas, M.; Maqsood, A. Design exploration and optimization of aerodynamics and radar cross section for a fighter aircraft. Aerosp. Sci. Technol. 2023, 133, 108114. [Google Scholar] [CrossRef]
- Albani, M.; Carluccio, G.; Pathak, P.H. A uniform geometrical theory of diffraction for vertices formed by truncated curved wedges. IEEE Trans. Antennas Propag. 2015, 63, 3136–3143. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, L.X.; Chen, T.G.; Liu, W. Electromagnetic scattering of coated objects over sea surface based on SBR-SDFSM. J. Electromagn. Waves Appl. 2018, 32, 1079–1092. [Google Scholar] [CrossRef]
- Lorente-López, J.; Rodríguez, J.V.; Quesada-Pereira, F.; Juan-Llácer, L.; Rodríguez-Rodríguez, I. UTD-PO solution for E-plane radiation pattern calculation of rectangular horn antennas with rectangular-shaped corrugations. IEEE Access. 2023, 11, 17424–17429. [Google Scholar] [CrossRef]
- Aglar, M.J.; Lozano, L.; Moreno, J.; González, I.; Cátedra, F. An efficient hybrid technique in RCS predictions of complex targets at high frequencies. J. Comput. Phys. 2017, 345, 345–357. [Google Scholar]
- Bladel, J.V. Electromagnetic fields in the presence of rotating bodies. Proc. IEEE 1976, 64, 301–318. [Google Scholar] [CrossRef]
- Govdeli, Y.; Muzaffar, S.M.B.; Raj, R.; Elhadidi, B.; Kayacan, E. Unsteady aerodynamic modeling and control of pusher and tilt-rotor quadplane configurations. Aerosp. Sci. Technol. 2019, 94, 105421. [Google Scholar] [CrossRef]
- Zhang, H.L.; Wang, Z.F.; Teng, F.; Xia, P.Q. Dynamic strain measurement of rotor blades in helicopter flight using fiber bragg grating sensor. Sensors 2023, 23, 6692. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.Y.; Lee, J.I.; Seo, D.W. RCS estimation of drone motion using mesh-element rotation in MoM and micro-Doppler signatures. IEEE Trans. Antennas Propag. 2022, 70, 7344–7349. [Google Scholar] [CrossRef]
- Jiang, X.W.; Zhao, Q.J.; Zhao, G.Q.; Li, P. Integrated optimization analyses of aerodynamic/ stealth characteristics of helicopter rotor based on surrogate model. Chin. J. Aeronaut. 2015, 28, 737–748. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, J.; Lu, Y.; Zhang, Y. A complete automatic target recognition system of low altitude, small RCS and slow speed (LSS) targets based on multi-dimensional feature fusion. Sensors 2019, 19, 5048. [Google Scholar] [CrossRef] [PubMed]
- Sutherland, J.; Datta, A. Fabrication, testing, and 3D comprehensive analysis of swept-tip tiltrotor blades. J. Am. Helicopter Soc. 2023, 68, 1–17. [Google Scholar] [CrossRef]
- Cardoso, D.N.; Esteban, S.; Raffo, G.V. A new robust adaptive mixing control for trajectory tracking with improved forward flight of a tilt-rotor UAV. ISA Trans. 2021, 110, 86–104. [Google Scholar] [CrossRef]
- Stratton, J.A.; Chu, L.J. Diffraction theory of electromagnetic waves. Phys. Rev. 1939, 56, 99–107. [Google Scholar] [CrossRef]
- Kouyoumjian, R.G.; Pathak, P.H. A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface. Proc. IEEE 1974, 62, 1448–1461. [Google Scholar] [CrossRef]
- Michaeli, A. Equipment edge currents for arbitrary aspects of observation. IEEE Trans. Antennas Propag. 1984, 32, 252–258. [Google Scholar] [CrossRef]
- Youssef, N.N. Radar cross section of complex targets. Proc. IEEE 1989, 77, 722–734. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, Y.K.; Liu, F.L.; Huang, P.L.; Ji, J.Z. Experimental analysis on micro-Doppler characteristics of rotors. J. Beijing Univ. Aeronaut. Astronaut. 2014, 40, 916–920. (In Chinese) [Google Scholar]



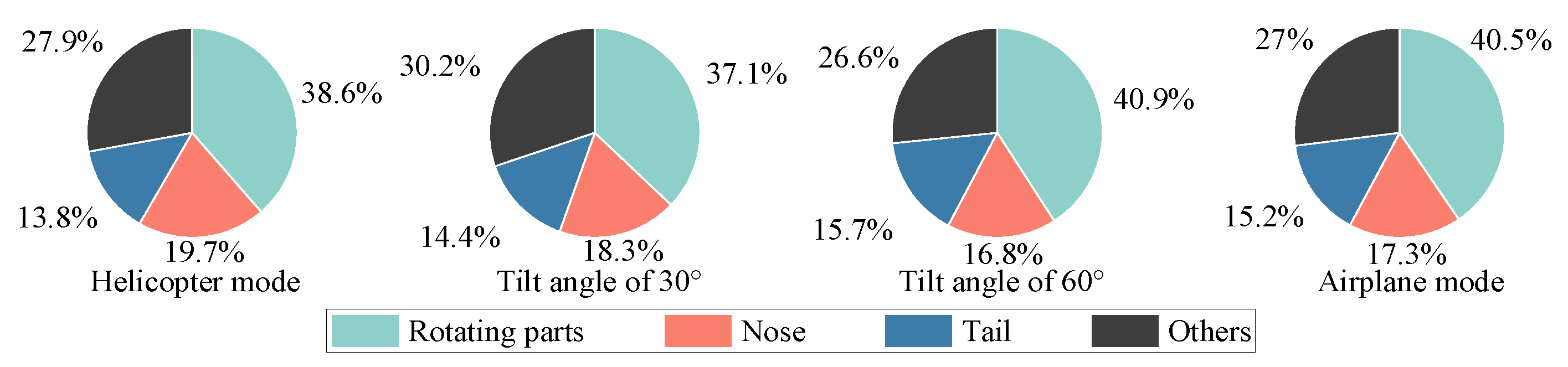


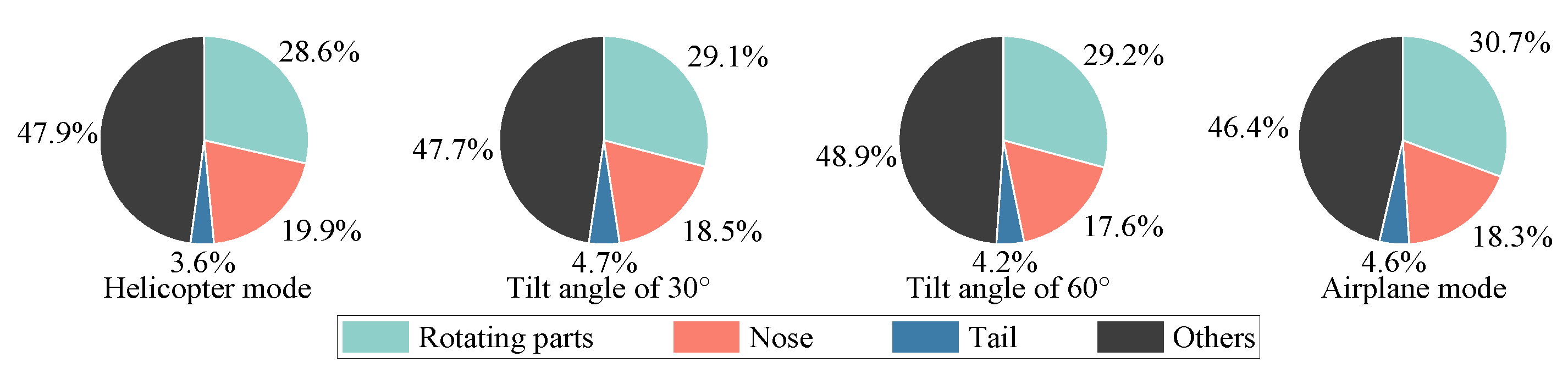
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Radius of rotors () | 5.9 m | Length of fuselage () | 17.25 m |
| Rotational speed () | 400 r/min | Width of fuselage () | 2.17 m |
| Wingspan () | 7.4 m | Height of tail wings () | 4.20 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, Z.; Yang, Y.; Jiang, X.; Zhao, Q.; Chen, X. Dynamic Electromagnetic Scattering Simulation of Tilt-Rotor Aircraft in Multiple Modes. Sensors 2023, 23, 7606. https://doi.org/10.3390/s23177606
Fei Z, Yang Y, Jiang X, Zhao Q, Chen X. Dynamic Electromagnetic Scattering Simulation of Tilt-Rotor Aircraft in Multiple Modes. Sensors. 2023; 23(17):7606. https://doi.org/10.3390/s23177606
Chicago/Turabian StyleFei, Zhongyang, Yan Yang, Xiangwen Jiang, Qijun Zhao, and Xi Chen. 2023. "Dynamic Electromagnetic Scattering Simulation of Tilt-Rotor Aircraft in Multiple Modes" Sensors 23, no. 17: 7606. https://doi.org/10.3390/s23177606
APA StyleFei, Z., Yang, Y., Jiang, X., Zhao, Q., & Chen, X. (2023). Dynamic Electromagnetic Scattering Simulation of Tilt-Rotor Aircraft in Multiple Modes. Sensors, 23(17), 7606. https://doi.org/10.3390/s23177606






