π-FBG Fiber Optic Acoustic Emission Sensor for the Crack Detection of Wind Turbine Blades
Abstract
:1. Introduction
2. FBG Acoustic Emission Detection System
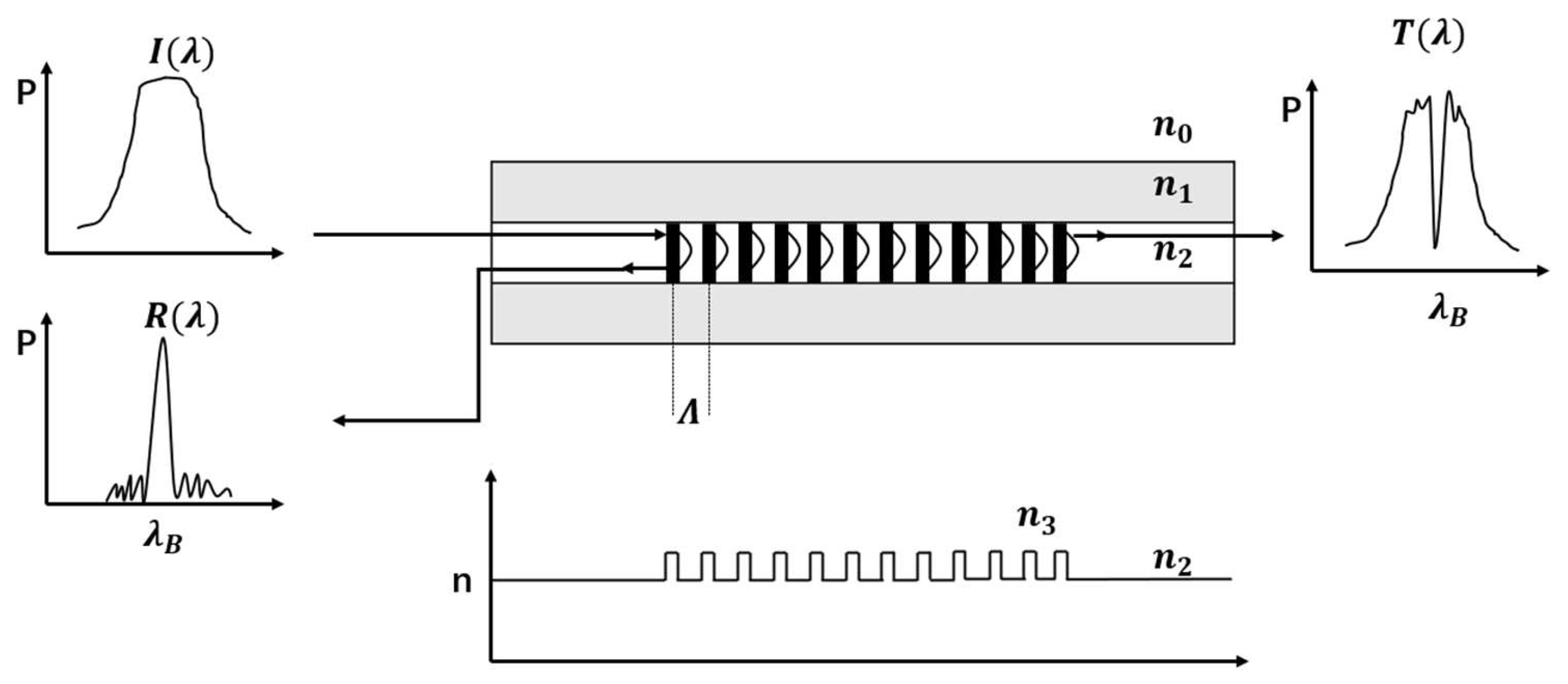
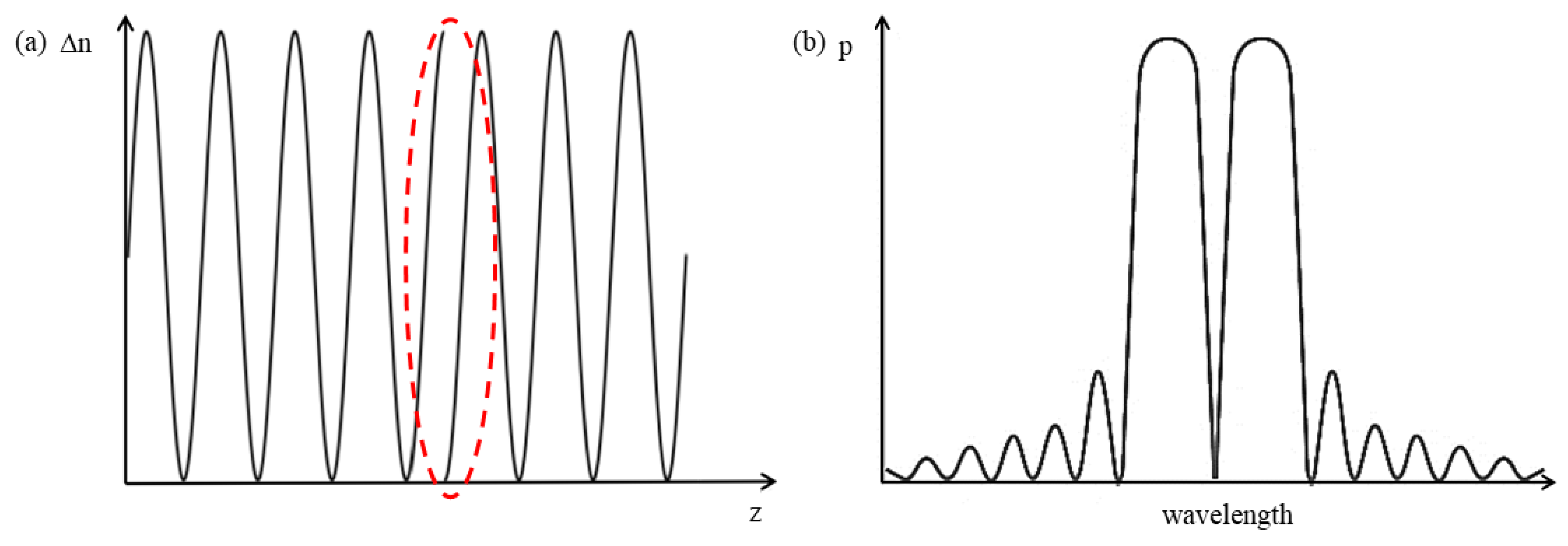
2.1. Fundamentals of FBG Acoustic Emission Detection
2.2. FBG Acoustic Emission Detection System
2.3. Experimental Device
2.4. System Testing
3. Signal Denoising
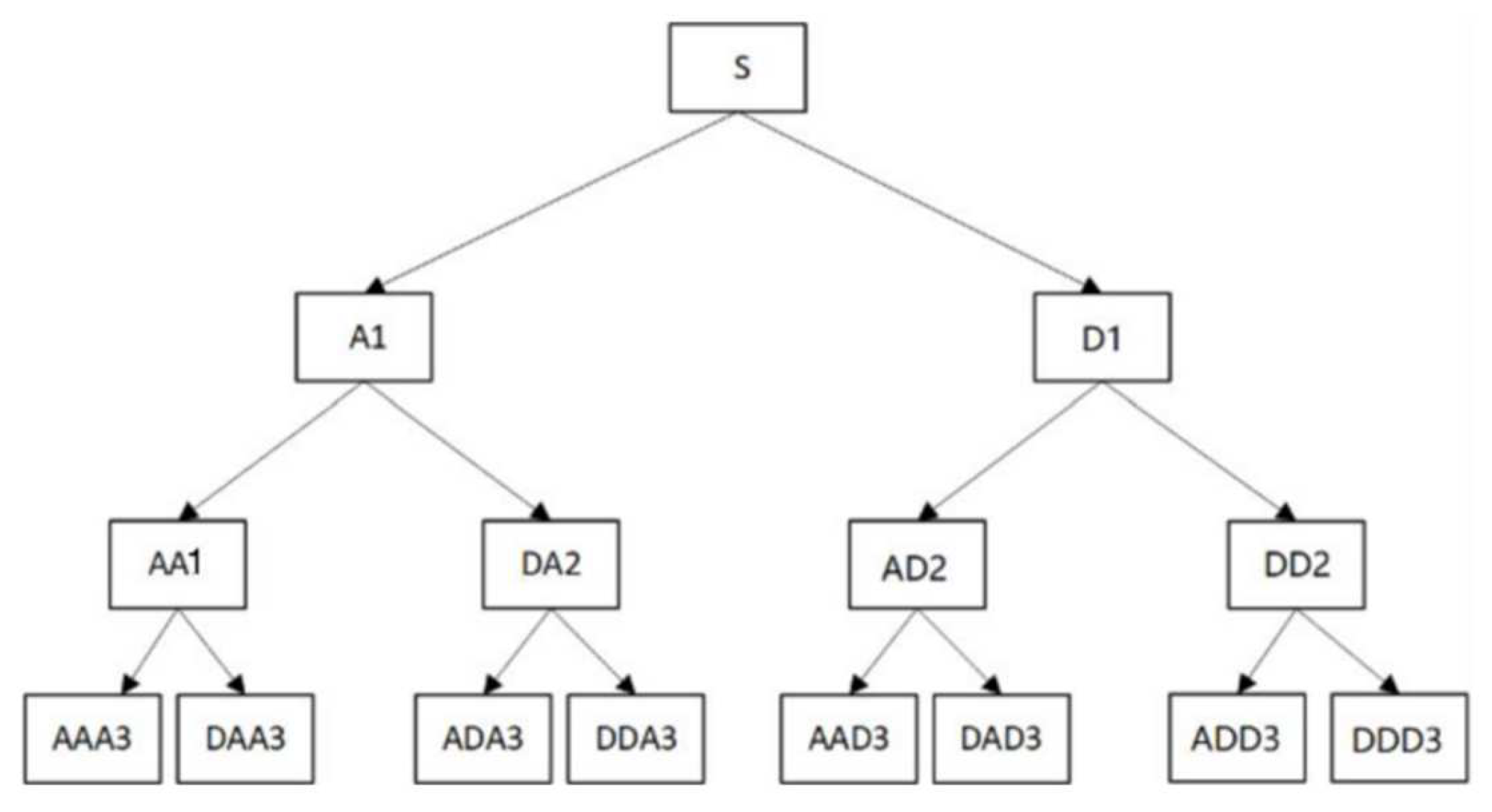
3.1. Wavelet Packet Decomposition
- Select a suitable wavelet basis function and determine the number of decomposition layers of the signal. For acoustic emission signals, wavelet basis function generally adopts Daubechies wavelets, Symlet wavelets, and Coiflet wavelets. The blade acoustic emission signal is generally a high-frequency burst signal, so a wavelet with high compactness, good orthogonality, and high vanishing distance should be chosen. When the number of decomposition layers is higher, the distortion of the reconstructed signal is bigger while the computation is increased, and when the number of layers is too small, the noise cannot be eliminated well.
- Calculate the wavelet packet coefficients of each layer after signal decomposition, and then determine the optimal signal decomposition path by minimizing a cost function, which is also called the optimal tree. In this paper, the minimum Shannon entropy criterion is adopted, and f is the original signal and is the wavelet packet coefficient after signal decomposition. The entropy calculation formula is
- 3.
- Select a suitable threshold for filtering the wavelet decomposition coefficients. The selection of threshold rules and functions determines the quality of noise reduction. Currently, commonly used threshold rules include sqtwolog rules, rigrsure rules, heursure rules, and minimaxi rules. In this paper, the minimaxi threshold rule is adopted. When the signal has only a small number of high-frequency parts in the noise range, the effect is better, and the loss of the original signal is small while denoising. It generates an extreme value with the goal of minimizing the mean square error, which can minimize the maximum mean square error. The threshold calculation expression is
- 4.
- Reconstruct the wavelet coefficients after processing.
3.2. Wavelet Packet Decomposition Combined with Empirical Modal Decomposition
- Use EMD to decompose the signal into IMF components and residuals.
- Calculate the correlation coefficient of each IMF component with the original signal, and select the IMF component with the larger correlation coefficient.
- Select the appropriate wavelet basis function to perform WPD noise reduction on the selected IMF components.
- Reconstruct the denoised IMF component.
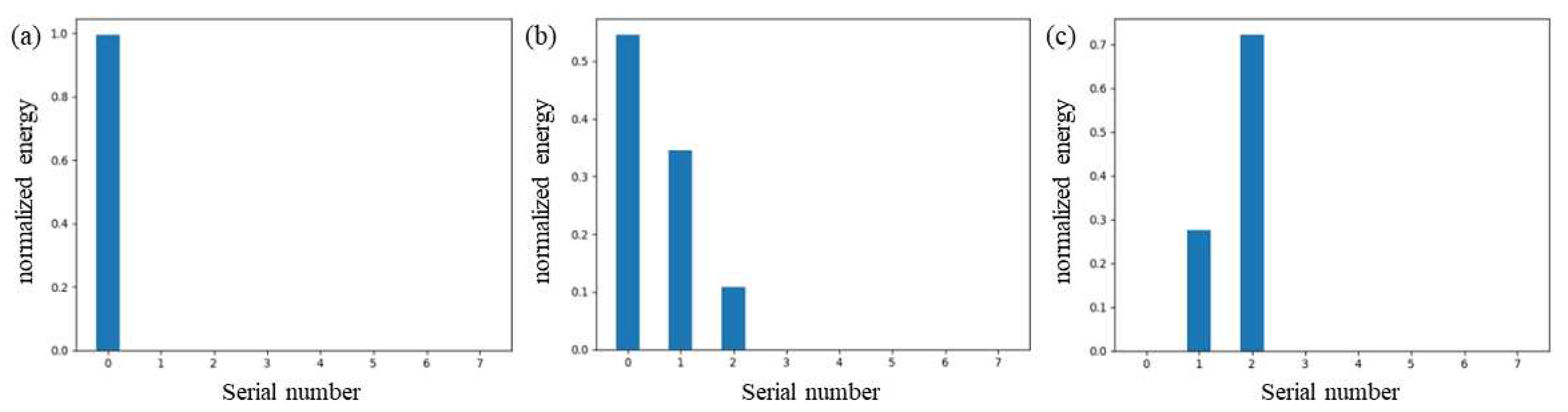
3.3. Noise Reduction Test
4. Wind Turbine Blade Damage Acoustic Emission Signal Characteristics
4.1. Wind Turbine Blade Structure
4.2. Wind Turbine Blade Damage Acoustic Signal
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Global Wind Energy Council. GWEC|Global Wind Report 2021; Global Wind Energy Council: Brussels, Belgium, 2021. [Google Scholar]
- Ribrant, J.; Bertling, M.L. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997–2005. IEEE Trans. Energy Convers 2007, 22, 167–173. [Google Scholar] [CrossRef]
- Zhang, D.; Qian, L.; Mao, B.; Huang, C.; Huang, B.; Si, Y. A data-driven design for fault detection ofwind turbines using random forests and XGBoost. IEEE Access 2018, 6, 21020–21031. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Tobias, A.M.; Pérez, J.M.P.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Marín, J.C.; Barroso, A.; París, F.; Cañas, J. Study of fatigue damage in wind turbine blades. Eng. Fail. Anal. 2009, 16, 656–668. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Luo, X. A two-stage data-driven approach for image-basedwind turbine blade crack inspections. IEEE ASME Trans. Mechatron. 2019, 24, 1271–1281. [Google Scholar] [CrossRef]
- Schubel, P.J.; Crossley, R.J.; Boateng, E.; Hutchinson, J. Review of structural health and cure monitoring techniques for large wind turbine blades. Renew. Energy 2013, 51, 113–123. [Google Scholar] [CrossRef]
- Lee, K.; Aihara, A.; Puntsagdash, G.; Kawaguchi, T.; Sakamoto, H.; Okuma, M. Feasibility study on a strain based deflection monitoring system for wind turbine blades. Mech. Syst. Signal Process. 2017, 82, 117–129. [Google Scholar] [CrossRef]
- Yan, Y.J.; Cheng, L.; Wu, Z.Y.; Yam, L.H. Development in vibration-based structural damage detection technique. Mech. Syst. Signal Process. 2007, 21, 2198–2211. [Google Scholar] [CrossRef]
- Dervilis, N.; Choi, M.; Taylor, S.; Barthorpe, R.; Park, G.; Farrar, C.; Worden, K. On damage diagnosis for a wind turbine blade using pattern recognition. J. Sound Vib. 2014, 333, 1833–1850. [Google Scholar] [CrossRef]
- Stokkeland, M.; Klausen, K.; Johansen, T.A. Autonomous visual navigation of unmanned aerial vehicle for wind turbine inspection. In Proceedings of the International Conference on Materials for Renewable Energy & Environment, Denver, CO, USA, 9–12 June 2015; pp. 998–1007. [Google Scholar]
- Nair, A.; Cai, C.S. Acoustic emission monitoring of bridges: Review and case studies. Eng. Struct. 2010, 32, 1704–1714. [Google Scholar] [CrossRef]
- Bouzid, G.Y.; Tian, K.; Cumanan, D. Moore: Structural health monitoring of wind turbine blades: Acoustic source localization using wireless sensor networks. J. Sens. 2015, 2015, 139695. [Google Scholar] [CrossRef]
- Yang, W.; Peng, Z.; Wei, K.; Tian, W. Structural health monitoring of composite wind turbine blades: Challenges, issues and potential solutions. IET Renew. Power Gener. 2017, 11, 411–416. [Google Scholar] [CrossRef]
- Gholizadeh, S. A review of non-destructive testing methods of composite materials. Procedia Struct. Integr. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- Jinachandran, S.; Rajan, G. Fibre Bragg Grating Based Acoustic Emission Measurement System for Structural Health Monitoring Applications. Materials 2021, 14, 897. [Google Scholar] [CrossRef]
- Perze, I.M.; Gui, H.; Udd, E. Acoustic emission detection using fiber Bragg gratings. Proc. SPIE 2001, 4328, 209–215. [Google Scholar]
- Vidakovic, M.; Mccague, C.; Armakolas, I.; Sun, T.; Carlton, S.J.; Grattan, K.T.V. Fiber Bragg grating⁃based cascaded acoustic sensors for potential marine structural condition monitoring. J. Light. Technol. 2016, 34, 4473–4478. [Google Scholar] [CrossRef]
- Shekar, P.V.R.; Latha, D.M.; Kumari, K.; Pisipati, V.G.K.M. Optimal parameters for fiber Bragg gratings for sensing applications: A spectral study. SN Appl. Sci. 2021, 3, 666. [Google Scholar] [CrossRef]
- Sai, Y.; Jiang, M.; Sui, Q.; Lu, S.; Jia, L. Multi-source acoustic emission localization technology research based on FBG sensing network and time reversal focusing imaging. Optik 2016, 127, 493–498. [Google Scholar] [CrossRef]
- Sharma, S.C.; Harsha, S.P.; Kankar, P.K. Fault diagnosis of rolling element bearing using cyclic autocorrelation and wavelet transform. Neurocomputing 2013, 110, 9–17. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]





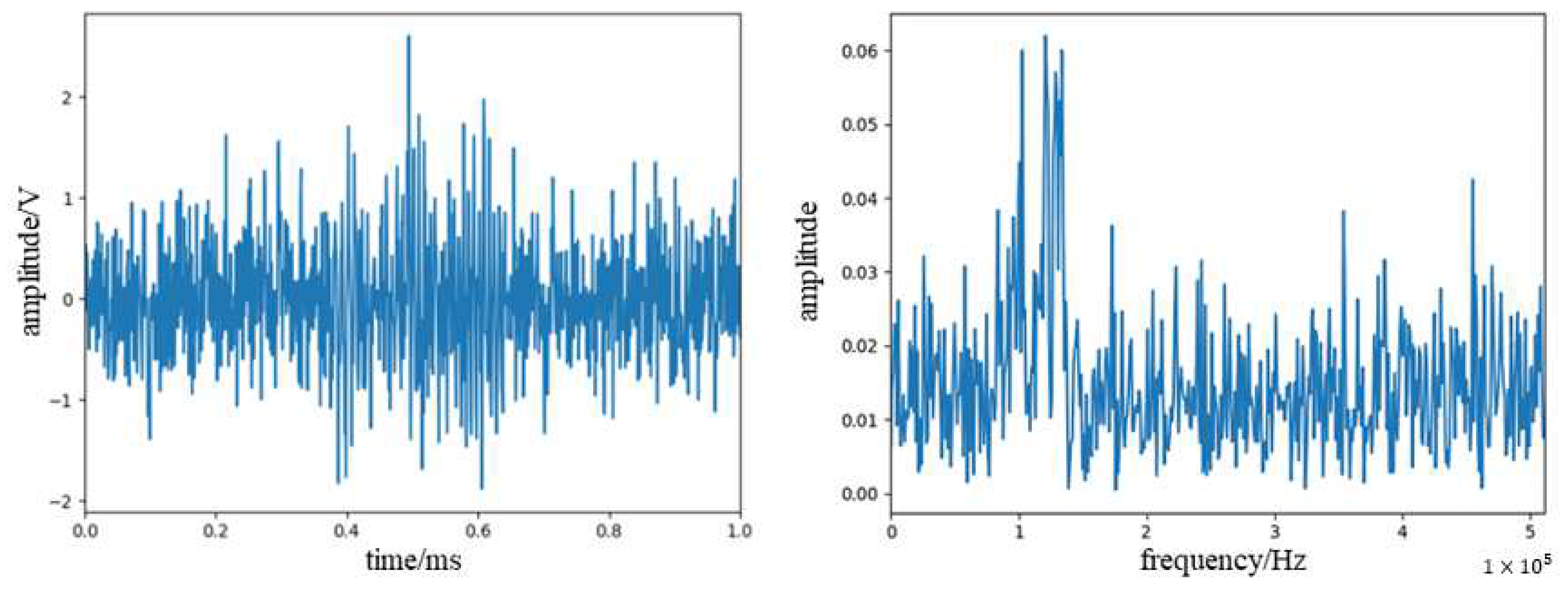
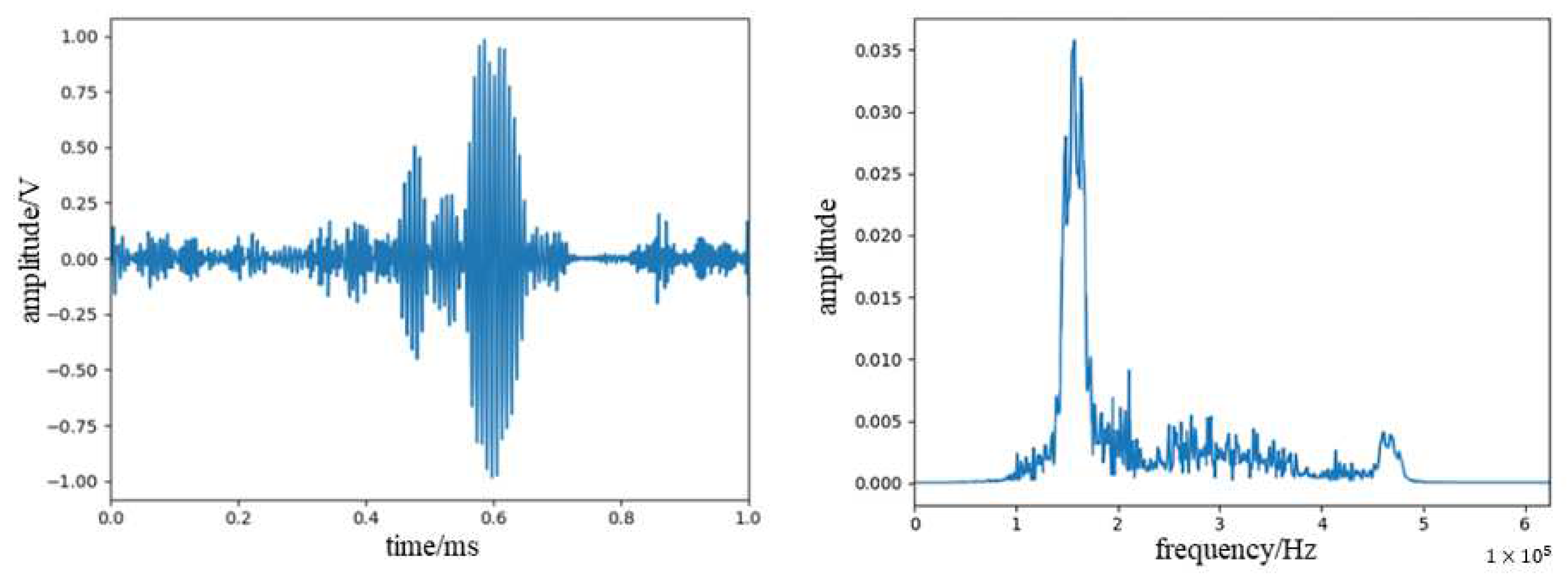
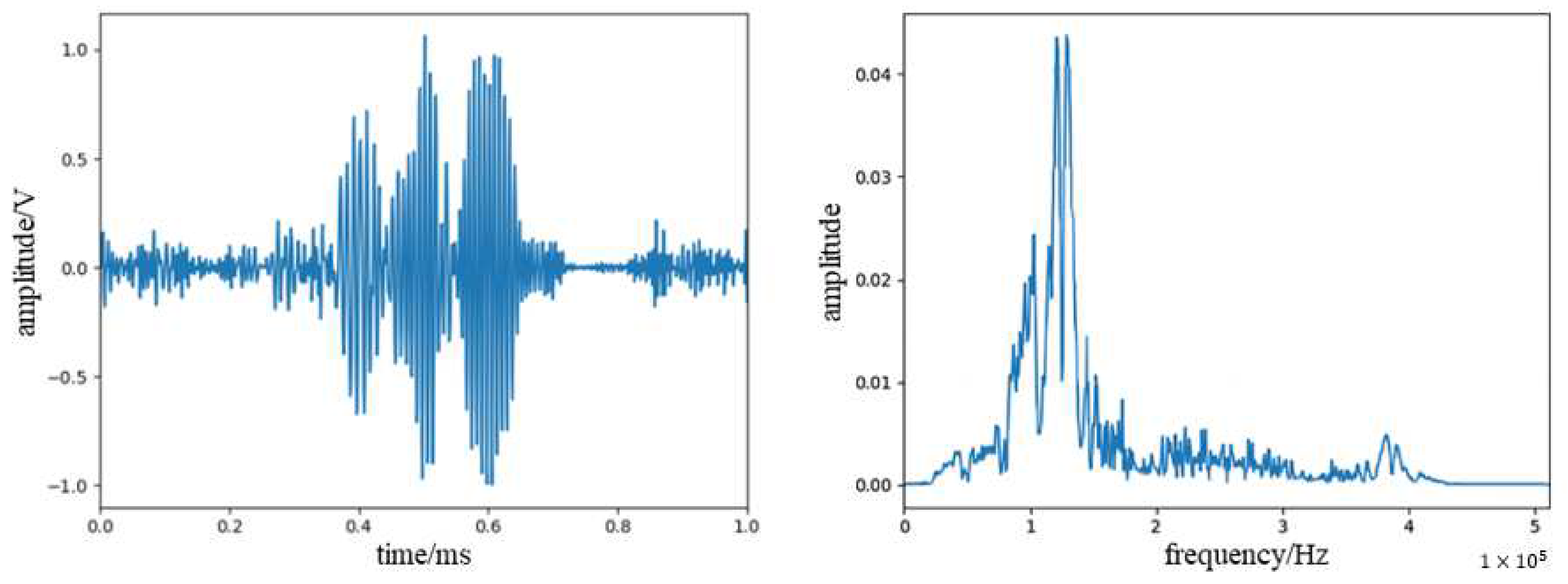


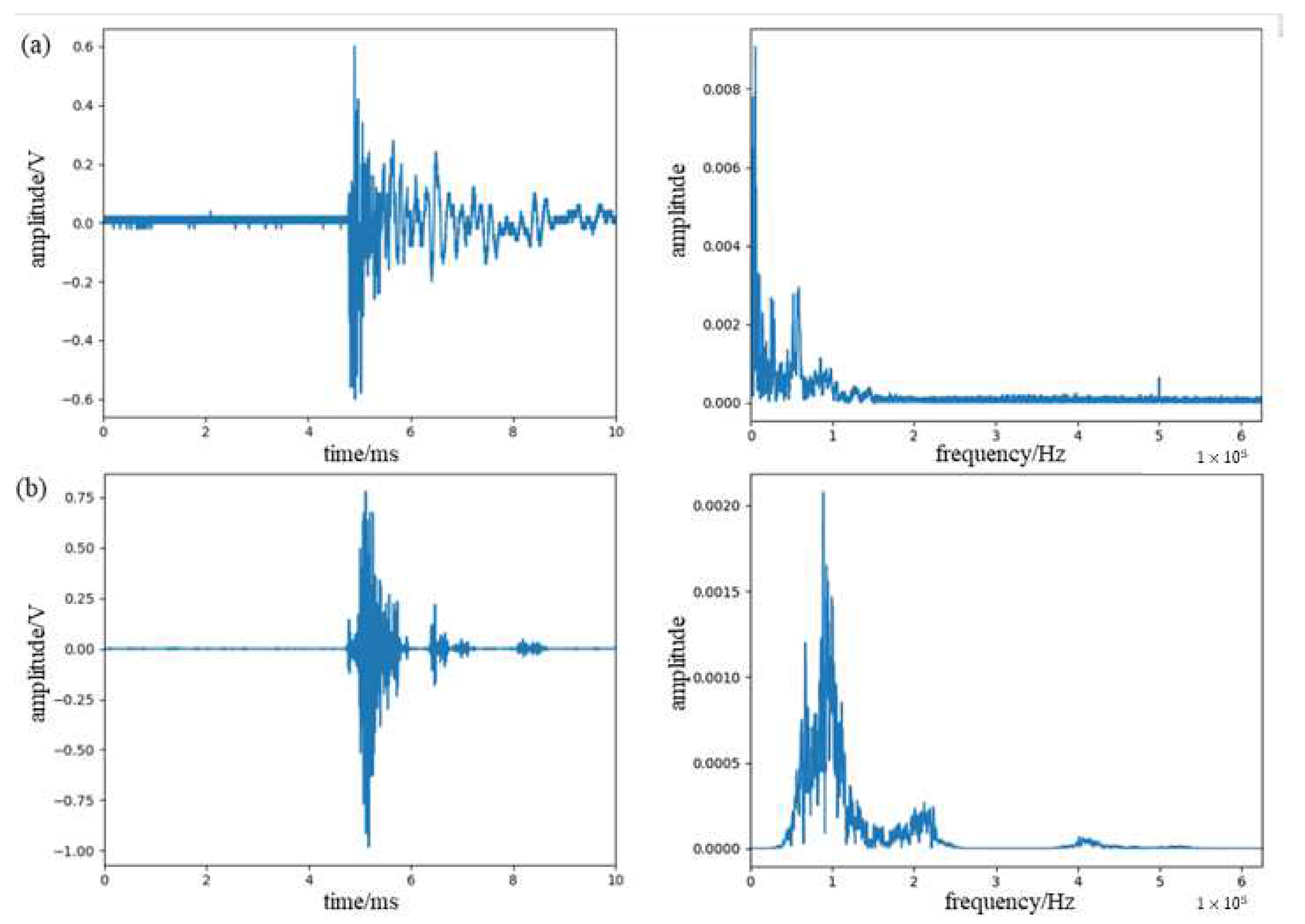

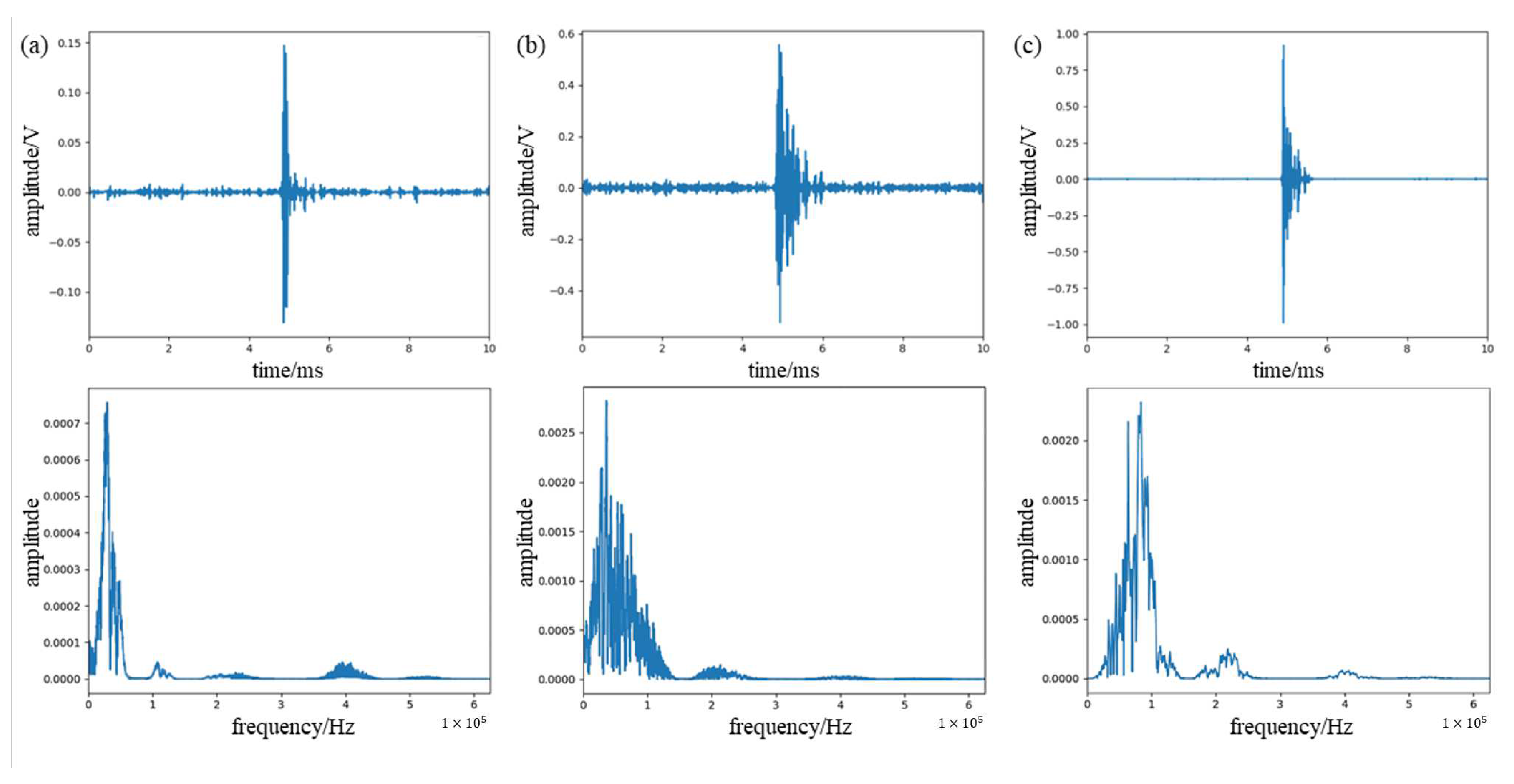
| Method | SNR (dB) | RMSE |
|---|---|---|
| WPD | 2.261 | 7.043 |
| WPD + EMD | 0.228 | 0.129 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Che, X.; Li, S.; Wang, G.; Liu, X. π-FBG Fiber Optic Acoustic Emission Sensor for the Crack Detection of Wind Turbine Blades. Sensors 2023, 23, 7821. https://doi.org/10.3390/s23187821
Yan Q, Che X, Li S, Wang G, Liu X. π-FBG Fiber Optic Acoustic Emission Sensor for the Crack Detection of Wind Turbine Blades. Sensors. 2023; 23(18):7821. https://doi.org/10.3390/s23187821
Chicago/Turabian StyleYan, Qi, Xingchen Che, Shen Li, Gensheng Wang, and Xiaoying Liu. 2023. "π-FBG Fiber Optic Acoustic Emission Sensor for the Crack Detection of Wind Turbine Blades" Sensors 23, no. 18: 7821. https://doi.org/10.3390/s23187821
APA StyleYan, Q., Che, X., Li, S., Wang, G., & Liu, X. (2023). π-FBG Fiber Optic Acoustic Emission Sensor for the Crack Detection of Wind Turbine Blades. Sensors, 23(18), 7821. https://doi.org/10.3390/s23187821






