Piezotronic Antimony Sulphoiodide/Polyvinylidene Composite for Strain-Sensing and Energy-Harvesting Applications
Abstract
:1. Introduction
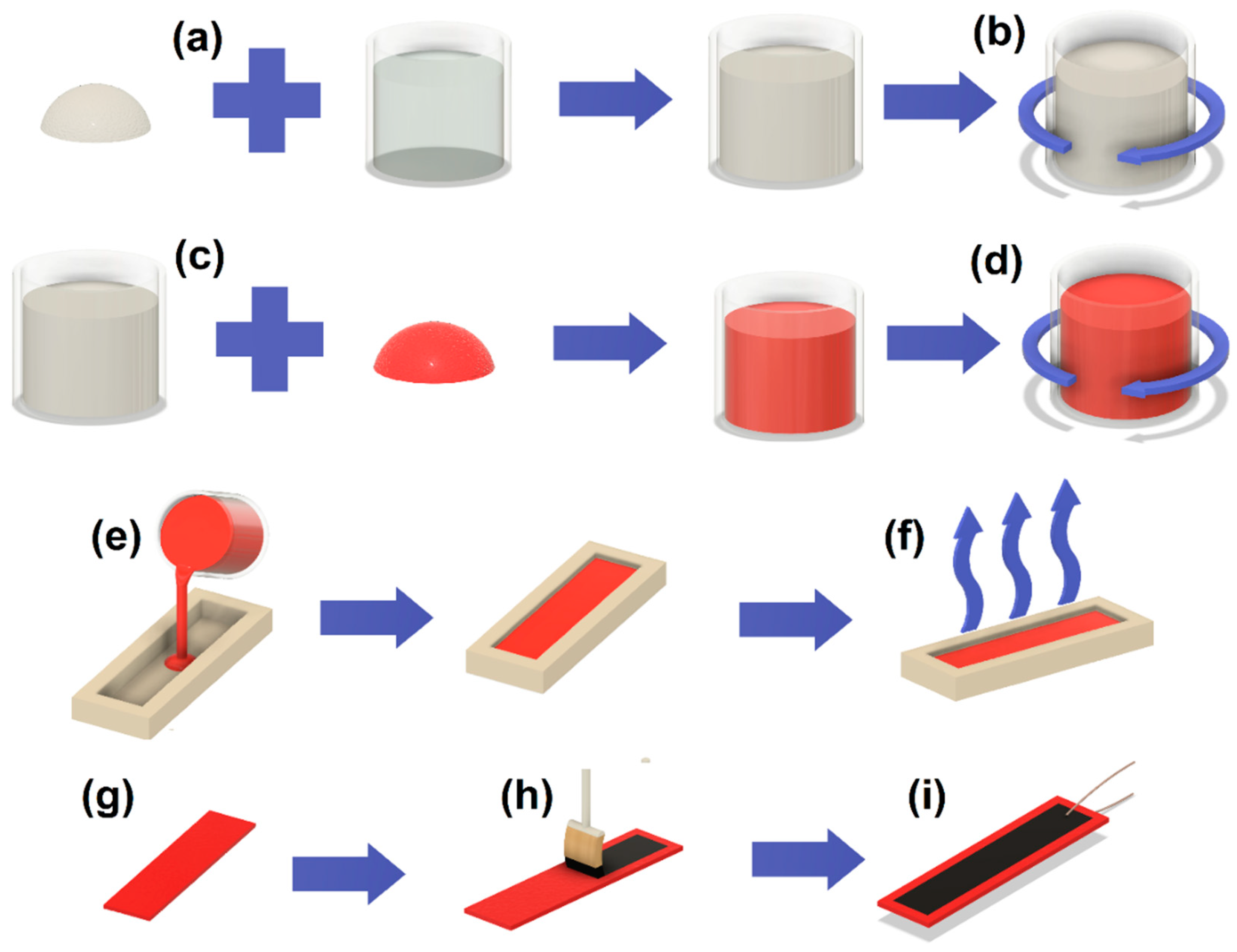
2. Sample Preparation
3. Testing and Measurement Procedures
4. Results and Discussion
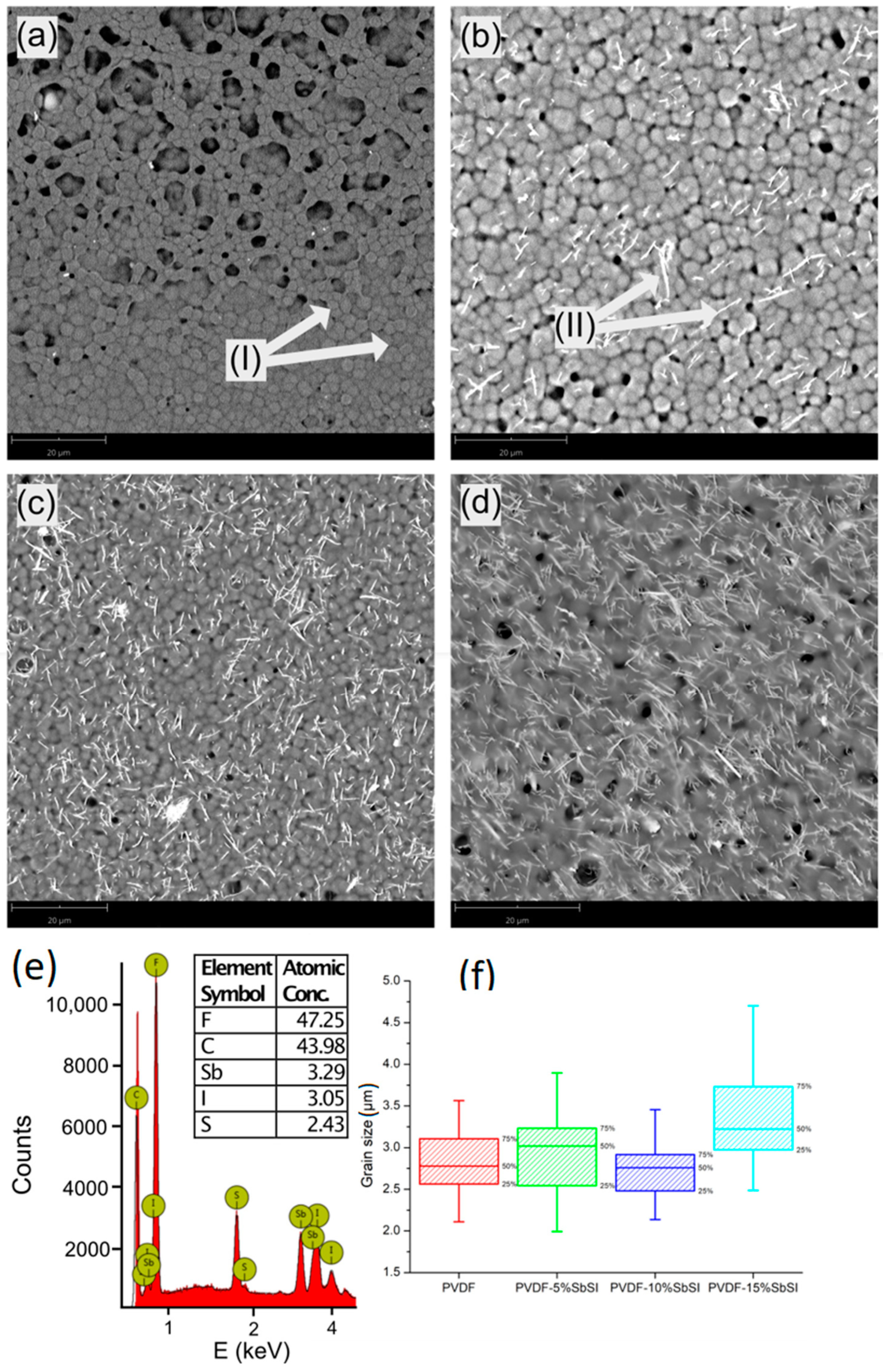
4.1. SEM Examination
4.2. Characterization of Samples under Static Deformation
4.3. Dynamic Strain Testing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pang, G.; Liu, H. Evaluation of a Low-cost MEMS Accelerometer for Distance Measurement. J. Intell. Robot. Syst. 2001, 30, 249–265. [Google Scholar] [CrossRef]
- Cao, L.; Kim, T.S.; Mantell, S.C.; Polla, D.L. Simulation and fabrication of piezoresistive membrane type MEMS strain sensors. Sens. Actuators A Phys. 2000, 80, 273–279. [Google Scholar] [CrossRef]
- Tze-Wei, Y.; Law, K.L.E.; Goldenberg, A. MEMS optical switches. IEEE Commun. Mag. 2001, 39, 158–163. [Google Scholar] [CrossRef]
- van Beek, J.T.M.; Puers, R. A review of MEMS oscillators for frequency reference and timing applications. J. Micromech. Microeng. 2012, 22, 013001. [Google Scholar] [CrossRef]
- Puers, R. Capacitive sensors: When and how to use them. Sens. Actuators A Phys. 1993, 37–38, 93–105. [Google Scholar] [CrossRef]
- Fiorillo, A.S.; Critello, C.D.; Pullano, S.A. Theory, technology and applications of piezoresistive sensors: A review. Sens. Actuators A Phys. 2018, 281, 156–175. [Google Scholar] [CrossRef]
- Hong, Y.; Wang, B.; Lin, W.; Jin, L.; Liu, S.; Luo, X.; Pan, J.; Wang, W.; Yang, Z. Highly anisotropic and flexible piezoceramic kirigami for preventing joint disorders. Sci. Adv. 2021, 7, eabf0795. [Google Scholar] [CrossRef]
- Jung, Y.H.; Hong, S.K.; Wang, H.S.; Han, J.H.; Pham, T.X.; Park, H.; Kim, J.; Kang, S.; Yoo, C.D.; Lee, K.J. Flexible Piezoelectric Acoustic Sensors and Machine Learning for Speech Processing. Adv. Mater. 2020, 32, 1904020. [Google Scholar] [CrossRef]
- Tressler, J.F.; Alkoy, S.; Newnham, R.E. Piezoelectric Sensors and Sensor Materials. J. Electroceramics 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Song, J.; Liu, J.; Xu, N.; Wang, Z.L. Piezoelectric Field Effect Transistor and Nanoforce Sensor Based on a Single ZnO Nanowire. Nano Lett. 2006, 6, 2768–2772. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L. Nanopiezotronics. Adv. Mater. 2007, 19, 889–892. [Google Scholar] [CrossRef]
- Wen, X.; Wu, W.; Ding, Y.; Wang, Z.L. Piezotronic Effect in Flexible Thin-film Based Devices. Adv. Mater. 2013, 25, 3371–3379. [Google Scholar] [CrossRef]
- Zhou, J.; Gu, Y.; Fei, P.; Mai, W.; Gao, Y.; Yang, R.; Bao, G.; Wang, Z.L. Flexible Piezotronic Strain Sensor. Nano Lett. 2008, 8, 3035–3040. [Google Scholar] [CrossRef]
- Zhang, Z.; Liao, Q.; Yan, X.; Wang, Z.L.; Wang, W.; Sun, X.; Lin, P.; Huang, Y.; Zhang, Y. Functional nanogenerators as vibration sensors enhanced by piezotronic effects. Nano Res. 2014, 7, 190–198. [Google Scholar] [CrossRef]
- Hu, G.; Zhang, Y.; Li, L.; Wang, Z.L. Piezotronic Transistor Based on Topological Insulators. ACS Nano 2018, 12, 779–785. [Google Scholar] [CrossRef]
- Lin, P.; Pan, C.; Wang, Z.L. Two-dimensional nanomaterials for novel piezotronics and piezophototronics. Mater. Today Nano 2018, 4, 17–31. [Google Scholar] [CrossRef]
- Peng, Y.; Que, M.; Tao, J.; Wang, X.; Lu, J.; Hu, G.; Wan, B.; Xu, Q.; Pan, C. Progress in piezotronic and piezo-phototronic effect of 2D materials. 2D Mater. 2018, 5, 042003. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Z.L. Piezotronic Nanowire-Based Resistive Switches As Programmable Electromechanical Memories. Nano Lett. 2011, 11, 2779–2785. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, G.; Zhao, J.; Zhang, H.; Yu, J.; Yang, X.; Zhang, Q.; Zhang, W.; Xu, S.; Sun, J.; et al. Piezotronic Graphene Artificial Sensory Synapse. Adv. Funct. Mater. 2019, 29, 1900959. [Google Scholar] [CrossRef]
- Jenkins, K.; Nguyen, V.; Zhu, R.; Yang, R. Piezotronic Effect: An Emerging Mechanism for Sensing Applications. Sensors 2015, 15, 22914–22940. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L. Piezotronic and Piezophototronic Effects. J. Phys. Chem. Lett. 2010, 1, 1388–1393. [Google Scholar] [CrossRef]
- Huang, C.T.; Song, J.; Lee, W.F.; Ding, Y.; Gao, Z.; Hao, Y.; Chen, L.J.; Wang, Z.L. GaN nanowire arrays for high-output nanogenerators. J. Am. Chem. Soc. 2010, 132, 4766–4771. [Google Scholar] [CrossRef]
- Kou, J.; Liu, Y.; Zhu, Y.; Zhai, J. Progress in piezotronics of transition-metal dichalcogenides. J. Phys. D Appl. Phys. 2018, 51, 493002. [Google Scholar] [CrossRef]
- Liu, X.; Shen, X.; Sa, B.; Zhang, Y.; Li, X.; Xue, H. Piezotronic-enhanced photocatalytic performance of heterostructured BaTiO3/SrTiO3 nanofibers. Nano Energy 2021, 89, 106391. [Google Scholar] [CrossRef]
- Mistewicz, K.; Nowak, M.; Stróż, D.; Guiseppi-Elie, A. Ferroelectric SbSI nanowires for ammonia detection at a low temperature. Talanta 2018, 189, 225–232. [Google Scholar] [CrossRef]
- Toroń, B.; Mistewicz, K.; Jesionek, M.; Kozioł, M.; Zubko, M.; Stróż, D. A new hybrid piezo/triboelectric SbSeI nanogenerator. Energy 2022, 238, 122048. [Google Scholar] [CrossRef]
- Mistewicz, K.; Das, T.K.; Nowacki, B.; Smalcerz, A.; Kim, H.J.; Hajra, S.; Godzierz, M.; Masiuchok, O. Bismuth sulfoiodide (BiSI) nanorods: Synthesis, characterization, and photodetector application. Sci. Rep. 2023, 13, 8800. [Google Scholar] [CrossRef] [PubMed]
- Jesionek, M.; Toroń, B.; Szperlich, P.; Biniaś, W.; Biniaś, D.; Rabiej, S.; Starczewska, A.; Nowak, M.; Kępińska, M.; Dec, J. Fabrication of a new PVDF/SbSI nanowire composite for smart wearable textile. Polymer 2019, 180, 121729. [Google Scholar] [CrossRef]
- Kozioł, M.; Toroń, B.; Szperlich, P.; Jesionek, M. Fabrication of a piezoelectric strain sensor based on SbSI nanowires as a structural element of a FRP laminate. Compos. Part Eng. 2019, 157, 58–65. [Google Scholar] [CrossRef]
- Grekov, A.; Danilova, S.; Zaks, P.; Kulieva, V.; Rubanov, L.; Syrkin, L.; Chekhunova, N.; Elgard, A. Piezoelectric Elements Made from Antimony Sulfoiodide Crystals; American Institute of Physics: Melville, NY, USA, 1974; Volume 19, pp. 393–394. [Google Scholar]
- Nowak, M.; Szperlich, P.; Bober, Ł.; Szala, J.; Moskal, G.; Stróż, D. Sonochemical preparation of SbSI gel. Ultrason. Sonochemistry 2008, 15, 709–716. [Google Scholar] [CrossRef]
- Mistewicz, K. Pyroelectric Nanogenerator Based on an SbSI/TiO2 Nanocomposite. Sensors 2022, 22, 69. [Google Scholar] [CrossRef] [PubMed]
- Tamilselvan, M.; Bhattacharyya, A.J. Antimony sulphoiodide (SbSI), a narrow band-gap non-oxide ternary semiconductor with efficient photocatalytic activity. RSC Adv. 2016, 6, 105980–105987. [Google Scholar] [CrossRef]
- Szperlich, P.; Toroń, B. An Ultrasonic Fabrication Method for Epoxy Resin/SbSI Nanowire Composites, and their Application in Nanosensors and Nanogenerators. Polymers 2019, 11, 479. [Google Scholar] [CrossRef] [PubMed]
- Toroń, B.; Szperlich, P.; Nowak, M.; Stróż, D.; Rzychoń, T. Novel piezoelectric paper based on SbSI nanowires. Cellulose 2018, 25, 7–15. [Google Scholar] [CrossRef]
- Toroń, B.; Szperlich, P.; Kozioł, M. SbSI Composites Based on Epoxy Resin and Cellulose for Energy Harvesting and Sensors—The Influence of SBSI Nanowires Conglomeration on Piezoelectric Properties. Materials 2020, 13, 902. [Google Scholar] [CrossRef]
- Nowak, M.; Nowrot, A.; Szperlich, P.; Jesionek, M.; Kępińska, M.; Starczewska, A.; Mistewicz, K.; Stróż, D.; Szala, J.; Rzychoń, T.; et al. Fabrication and characterization of SbSI gel for humidity sensors. Sens. Actuators A Phys. 2014, 210, 119–130. [Google Scholar] [CrossRef]
- Starczewska, A.; Solecka, B.; Nowak, M.; Szperlich, P. Dielectric properties of SbSI in the temperature range of 292–475 K. Acta Phys. Pol. A 2014, 126, 1125–1127. [Google Scholar] [CrossRef]
- Liu, S.; Han, Q.; Ma, N.; Li, C. Modulation of elastic wave propagation in piezoelectric laminated nanocomposite shells considering agglomeration effects. Acta Mech. 2022, 233, 5215–5239. [Google Scholar] [CrossRef]
- Li, C.; Han, Q. Semi-analytical wave characteristics analysis of graphene-reinforced piezoelectric polymer nanocomposite cylindrical shells. Int. J. Mech. Sci. 2020, 186, 105890. [Google Scholar] [CrossRef]
- Yaseen, H.M.; Park, S. Enhanced Power Generation by Piezoelectric P(VDF-TrFE)/rGO Nanocomposite Thin Film. Nanomaterials 2023, 13, 860. [Google Scholar] [CrossRef]
- Pullicino, E.; Zou, W.; Gresil, M.; Soutis, C. The Effect of Shear Mixing Speed and Time on the Mechanical Properties of GNP/Epoxy Composites. Appl. Compos. Mater. 2017, 24, 301–311. [Google Scholar] [CrossRef]
- Sharma, A.; Sukesh Babu, M.; Velmurugan, R.; Imai, T.; Sarathi, R. Impact of shear mixing time of epoxy-silica nanocomposites on its electrical and mechanical properties. Nano Express 2021, 2, 010031. [Google Scholar] [CrossRef]
- Nan, C.-W.; Jia, Q. Obtaining ultimate functionalities in nanocomposites: Design, control, and fabrication. MRS Bull. 2015, 40, 719–724. [Google Scholar] [CrossRef]
- Whiter, R.A.; Calahorra, Y.; Ou, C.; Kar-Narayan, S. Observation of Confinement-Induced Self-Poling Effects in Ferroelectric Polymer Nanowires Grown by Template Wetting. Macromol. Mater. Eng. 2016, 301, 1016–1025. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Qi, Y.; Gong, S.; Zhao, R.; Hongbin, Y.; Wu, Z.; Cui, D.; Wang, L.; Ma, C.; et al. Observation of room-temperature ferroelectricity in elemental Te nanowires. arXiv 2022, arXiv:2211.04066. [Google Scholar] [CrossRef]
- Yulfriska, N.; Darvina, Y.; Yulkifli, Y.; Ramli, R. Microstructure of magnetite—Polyvinylidene fluoride (Fe3O4/PVDF) nanocomposite prepared by spin coating method. J. Phys. Conf. Ser. 2019, 1185, 012025. [Google Scholar] [CrossRef]
- Pradel, K.C.; Wu, W.; Zhou, Y.; Wen, X.; Ding, Y.; Wang, Z.L. Piezotronic Effect in Solution-Grown p-Type ZnO Nanowires and Films. Nano Lett. 2013, 13, 2647–2653. [Google Scholar] [CrossRef]
- Wang, Z.L. Piezopotential gated nanowire devices: Piezotronics and piezo-phototronics. Nano Today 2010, 5, 540–552. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, J.; Wang, D.; Musavigharavi, P.; Stach, E.A.; Olsson, R., III; Jariwala, D. Aluminum scandium nitride-based metal–ferroelectric–metal diode memory devices with high on/off ratios. Appl. Phys. Lett. 2021, 118, 202901. [Google Scholar] [CrossRef]
- Salam, M.A.-E.; Elkomy, G.; Osman, H.; Nagy, M.; El-Sayed, F. Structure–electrical conductivity of polyvinylidene fluoride/graphite composites. J. Reinf. Plast. Compos. 2012, 31, 1342–1352. [Google Scholar] [CrossRef]
- Stassi, S.; Cauda, V.; Canavese, G.; Pirri, C.F. Flexible Tactile Sensing Based on Piezoresistive Composites: A Review. Sensors 2014, 14, 5296–5332. [Google Scholar] [CrossRef] [PubMed]
- Spanu, A.; Pinna, L.; Viola, F.; Seminara, L.; Valle, M.; Bonfiglio, A.; Cosseddu, P. A high-sensitivity tactile sensor based on piezoelectric polymer PVDF coupled to an ultra-low voltage organic transistor. Org. Electron. 2016, 36, 57–60. [Google Scholar] [CrossRef]
- Tang, X.; Pionteck, J.; Pötschke, P. Improved piezoresistive sensing behavior of poly(vinylidene fluoride)/carbon black composites by blending with a second polymer. Polymer 2023, 268, 125702. [Google Scholar] [CrossRef]
- Khatua, D.; Padhy, M.; Singh, R.K.; Choudhary, R.N.P.; Achary, P.G.R. Investigation of electrical and thermal properties of poly (vinylidene fluoride)/strontium hexaferrite polymer composites. J. Mater. Sci. Mater. Electron. 2020, 31, 22687–22698. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Y.; Chen, Z.; Guo, Y.; Wang, D.; Wertz, E.A.; Shi, J. Effect of strain on the Curie temperature and band structure of low-dimensional SbSI. Appl. Phys. Lett. 2018, 112, 183104. [Google Scholar] [CrossRef]
- Thakur, P.; Kool, A.; Hoque, N.A.; Bagchi, B.; Khatun, F.; Biswas, P.; Brahma, D.; Roy, S.; Banerjee, S.; Das, S. Superior performances of in situ synthesized ZnO/PVDF thin film based self-poled piezoelectric nanogenerator and self-charged photo-power bank with high durability. Nano Energy 2018, 44, 456–467. [Google Scholar] [CrossRef]
- Biswas, P.; Hoque, N.A.; Thakur, P.; Saikh, M.M.; Roy, S.; Khatun, F.; Bagchi, B.; Das, S. Highly Efficient and Durable Piezoelectric Nanogenerator and Photo-power cell Based on CTAB Modified Montmorillonite Incorporated PVDF Film. ACS Sustain. Chem. Eng. 2019, 7, 4801–4813. [Google Scholar] [CrossRef]
- Pabba, D.P.; Satthiyaraju, M.; Ramasdoss, A.; Sakthivel, P.; Chidhambaram, N.; Dhanabalan, S.; Abarzúa, C.V.; Morel, M.J.; Udayabhaskar, R.; Mangalaraja, R.V.; et al. MXene-Based Nanocomposites for Piezoelectric and Triboelectric Energy Harvesting Applications. Micromachines 2023, 14, 1273. [Google Scholar] [CrossRef]
- Horowitz, S.B.; Sheplak, M.; Cattafesta, L.N.; Nishida, T. A MEMS acoustic energy harvester. J. Micromech. Microeng. 2006, 16, S174. [Google Scholar] [CrossRef]
- Javadi, M.; Heidari, A.; Darbari, S. Realization of enhanced sound-driven CNT-based triboelectric nanogenerator, utilizing sonic array configuration. Curr. Appl. Phys. 2018, 18, 361–368. [Google Scholar] [CrossRef]
- Sun, K.H.; Kim, J.E.; Kim, J.; Song, K. Sound energy harvesting using a doubly coiled-up acoustic metamaterial cavity. Smart Mater. Struct. 2017, 26, 075011. [Google Scholar] [CrossRef]
- Li, B.; Laviage, A.J.; You, J.H.; Kim, Y.-J. Harvesting low-frequency acoustic energy using quarter-wavelength straight-tube acoustic resonator. Appl. Acoust. 2013, 74, 1271–1278. [Google Scholar] [CrossRef]







| Sample | Deflection, ⁰ | a, pA/V | b, pA | R, MΩ | ρ, GΩ·cm |
|---|---|---|---|---|---|
| Pure PVDF | 0 | 50.85 (24) | 4.80 (73) | 19.665 (30) | 393 (20) |
| 15 | 62.5 (11) | −4.7 (34) | 15.99 (29) | 319 (17) | |
| 30 | 61.7 (11) | −1.7 (34) | 16.21 (30) | 324 (18) | |
| 60 | 67.97 (98) | 9.6 (30) | 14.71 (21) | 294 (16) | |
| 5% wt. SbSI | 0 | 60.31 (31) | 3.60 (94) | 16.581 (85) | 331 (17) |
| 15 | 57.30 (51) | 0.5 (16) | 17.45 (16) | 349 (18) | |
| 30 | 56.87 (86) | −2.1 (26) | 17.58 (27) | 351 (19) | |
| 60 | 49.71 (40) | 2.5 (12) | 20.12 (16) | 402 (21) | |
| 10% wt. SbSI | 0 | 53.3 (33) | 0.8 (99) | 18.8 (12) | 375 (30) |
| 15 | 52.93 (58) | 0.4 (18) | 18.89 (21) | 378 (20) | |
| 30 | 43.46 (80) | −0.1 (24) | 23.01 (42) | 460 (25) | |
| 60 | 42.26 (61) | −2.1 (19) | 23.66 (34) | 473 (25) | |
| 15% wt. SbSI | 0 | 18.39 (10) | −1.98 (31) | 54.36 (30) | 1087 (56) |
| 15 | 7.75 (27) | −4.95 (81) | 128.9 (44) | 2577 (158) | |
| 30 | 5.83 (13) | −2.86 (38) | 171.5 (37) | 3429 (190) | |
| 60 | 4.81 (29) | −0.99 (87) | 208 (12) | 4155 (326) |
| Sample | a1, GΩ·cm | b1, GΩ·cm | c1 |
|---|---|---|---|
| Pure PVDF | 300 (18) | −92 (27) | 0.011 (38) |
| 5% wt. SbSI | 533.6 (84) | 205.1 (83) | 0.694 (61) |
| 10% wt. SbSI | 577 (29) | 218 (28) | 0.46 (20) |
| 15% wt. SbSI | 4504 (26) | 3417 (26) | 0.1110 (35) |
| Deflection, ⁰ | ρ0, GΩ·cm | a2, GΩ·cm | b2 |
|---|---|---|---|
| 0 | 363 (31) | 0.003 (39) | 0.012 (14) |
| 15 | 333 (14) | 0.019 (33) | 0.0128 (20) |
| 30 | 334 (12) | 0.22 (13) | 0.0157 (10) |
| 60 | 329 (51) | 0.24 (57) | 0.0155 (40) |
| f, Hz | Sample | Up-p, V | Up-pF, V/N | P, nW | PF, nW/N | PV, mW/m3 |
|---|---|---|---|---|---|---|
| 100 | Pure PVDF | 0.1148 (74) | 0.0163 (11) | 0.238 | 0.034 | 1.19 |
| 5% wt. SbSI | 0.0489 (23) | 0.00693 (32) | 0.0364 | 0.005 | 0.182 | |
| 10% wt. SbSI | 0.0853 (27) | 0.01209 (39) | 0.307 | 0.044 | 1.54 | |
| 15% wt. SbSI | 0.1705 (99) | 0.0242 (14) | 0.725 | 0.103 | 3.63 | |
| 200 | Pure PVDF | 0.1583 (44) | 0.01908 (53) | 0.553 | 0.067 | 2.76 |
| 5% wt. SbSI | 0.1203 (32) | 0.01450 (38) | 0.437 | 0.053 | 2.18 | |
| 10% wt. SbSI | 0.2232 (79) | 0.02690 (95) | 0.882 | 0.106 | 4.41 | |
| 15% wt. SbSI | 0.154 (11) | 0.0218 (15) | 1.27 | 0.153 | 6.33 | |
| 400 | Pure PVDF | 0.1501 (85) | 0.0187 (11) | 0.611 | 0.076 | 3.05 |
| 5% wt. SbSI | 0.099 (13) | 0.0123 (16) | 1.17 | 0.146 | 5.86 | |
| 10% wt. SbSI | 0.267 (22) | 0.0334 (28) | 3.43 | 0.429 | 17.2 | |
| 15% wt. SbSI | 0.176 (15) | 0.0220 (19) | 1.82 | 0.228 | 9.11 | |
| 1000 | Pure PVDF | 0.2156 (59) | 0.02696 (74) | 2.14 | 0.267 | 10.7 |
| 5% wt. SbSI | 0.089 (16) | 0.0112 (20) | 1.50 | 0.188 | 7.51 | |
| 10% wt. SbSI | 0.215 (21) | 0.0269 (27) | 6.71 | 0.838 | 33.5 | |
| 15% wt. SbSI | 0.140 (16) | 0.0174 (20) | 4.10 | 0.513 | 20.5 |
| Frequency, Hz | Sample | Up-p, V | P, nW | PV, mW/m3 |
|---|---|---|---|---|
| 100 | Pure PVDF | 0.1128 (39) | 0.516 | 2.58 |
| 5% wt. SbSI | 0.0537 (14) | 0.134 | 0.67 | |
| 10% wt. SbSI | 0.1697 (42) | 1.12 | 5.62 | |
| 15% wt. SbSI | 0.0910 (63) | 0.36 | 1.8 | |
| 200 | Pure PVDF | 0.207 (10) | 0.879 | 4.4 |
| 5% wt. SbSI | 0.1885 (59) | 0.704 | 3.52 | |
| 10% wt. SbSI | 0.1094 (34) | 0.446 | 2.23 | |
| 15% wt. SbSI | 0.1230 (66) | 1.08 | 5.4 | |
| 400 | Pure PVDF | 0.2118 (73) | 1.20 | 5.99 |
| 5% wt. SbSI | 0.0829 (33) | 0.099 | 0.50 | |
| 10% wt. SbSI | 0.1109 (44) | 0.532 | 2.66 | |
| 15% wt. SbSI | 0.1385 (78) | 1.26 | 6.32 | |
| 1000 | Pure PVDF | 0.210 (11) | 2.16 | 10.8 |
| 5% wt. SbSI | 0.1132 (33) | 0.831 | 4.16 | |
| 10% wt. SbSI | 0.3349 (66) | 6.44 | 32.2 | |
| 15% wt. SbSI | 0.169 (13) | 2.14 | 10.7 |
| Material | Common Factor | Device Size, cm3 | P, nW | PV, mW/m3 | Parameters | Ref. |
|---|---|---|---|---|---|---|
| PZT (MEMS) | Sound wave excitation | 2.5 | 0.006 | - | The sound pressure level of 149 dB, resonant frequency of 3.9 kHz | [60] |
| PDMS/CNT | Sound wave excitation | 6.9 | 40 | - | An acoustic wave of 4.24 kHz, with different power inputs to the speaker (80, 40, and 20 W) | [61] |
| PZT (metamaterial) | Sound wave excitation | 676 | 345 | - | The sound pressure level of 100 dB at 600 Hz of frequency | [62] |
| PVDF (beam array) | Sound wave excitation and PVDF material | 1500 | 2200 | - | The sound pressure level of 100 dB, frequencies of 146, 439, and 734 Hz | [63] |
| Epoxy/SbSI | Sound wave excitation and SbSI-based nanocomposite | 2 | 0.9 | 0.45 | An acoustic wave of 175 Hz frequency, sound pressure level of 90 dB | [34] |
| PVDF/SbSI (fibers) | PVDF material and SbSI-based nanocomposite | 0.005 | 0.017 | 3.46 | Mechanical vibrations of 50 Hz frequency | [28] |
| Cellulose/SbSI | Sound wave excitation and SbSI-based nanocomposite | 0.005 | 0.208 | 41.5 | An acoustic wave of 175 Hz frequency, sound pressure level of 90 dB | [35] |
| PVDF/SbSI | This paper | 0.2 | 6.71 | 33.5 | An acoustic sine wave of frequency 1 kHz, Force F = 8.3 N | This paper |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jała, J.; Nowacki, B.; Toroń, B. Piezotronic Antimony Sulphoiodide/Polyvinylidene Composite for Strain-Sensing and Energy-Harvesting Applications. Sensors 2023, 23, 7855. https://doi.org/10.3390/s23187855
Jała J, Nowacki B, Toroń B. Piezotronic Antimony Sulphoiodide/Polyvinylidene Composite for Strain-Sensing and Energy-Harvesting Applications. Sensors. 2023; 23(18):7855. https://doi.org/10.3390/s23187855
Chicago/Turabian StyleJała, Jakub, Bartłomiej Nowacki, and Bartłomiej Toroń. 2023. "Piezotronic Antimony Sulphoiodide/Polyvinylidene Composite for Strain-Sensing and Energy-Harvesting Applications" Sensors 23, no. 18: 7855. https://doi.org/10.3390/s23187855
APA StyleJała, J., Nowacki, B., & Toroń, B. (2023). Piezotronic Antimony Sulphoiodide/Polyvinylidene Composite for Strain-Sensing and Energy-Harvesting Applications. Sensors, 23(18), 7855. https://doi.org/10.3390/s23187855







