A Stream Function Smoothing Method for the Design of MRI Gradient Coils on Non-Developable Surfaces
Abstract
1. Introduction
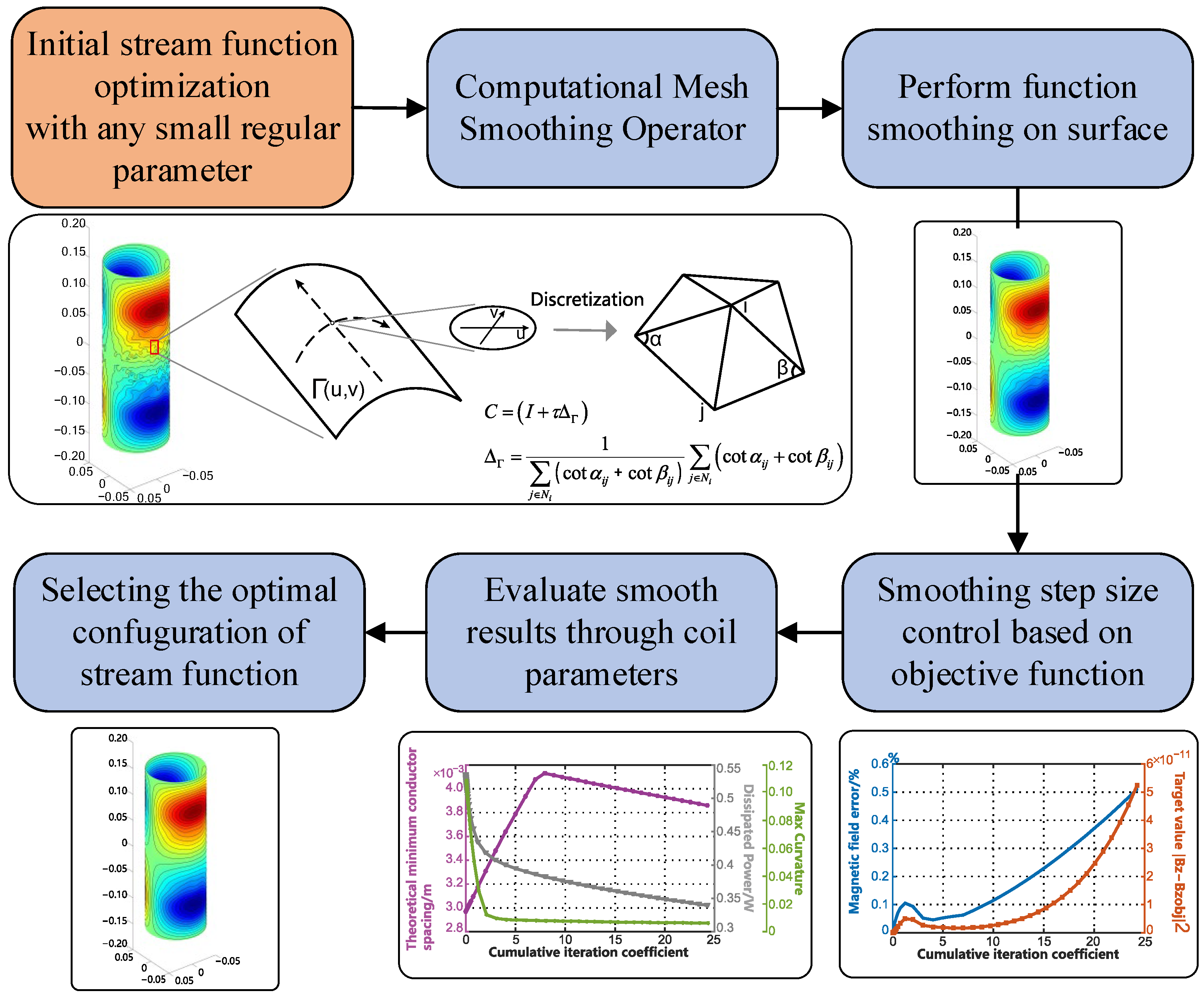
2. Methods
2.1. Previous Work
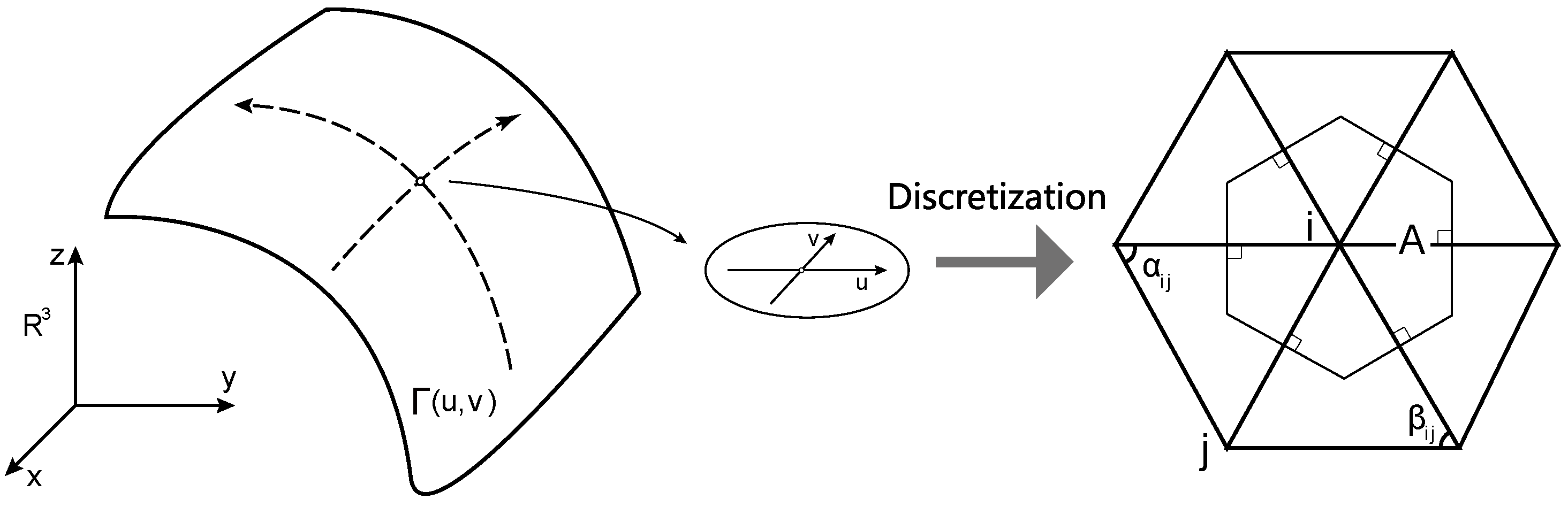
2.2. Smooth Function on a Surface
2.3. Smoothing Coefficients Based on the Objective Function Control
2.4. Controlling the Spacing between Contour Lines Based on the Tangential Gradient
2.5. Curvature Changes in Implicit Contour Expression
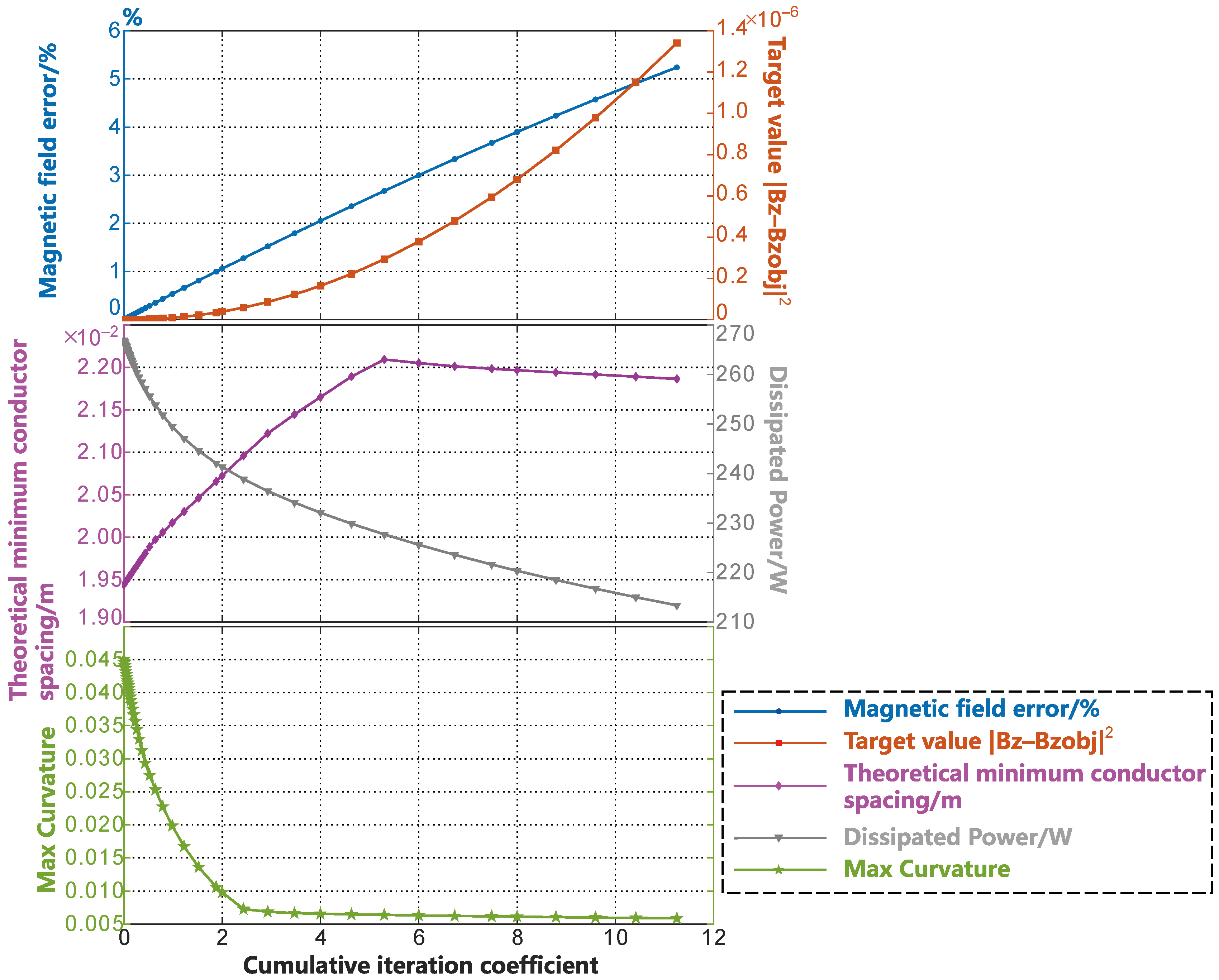
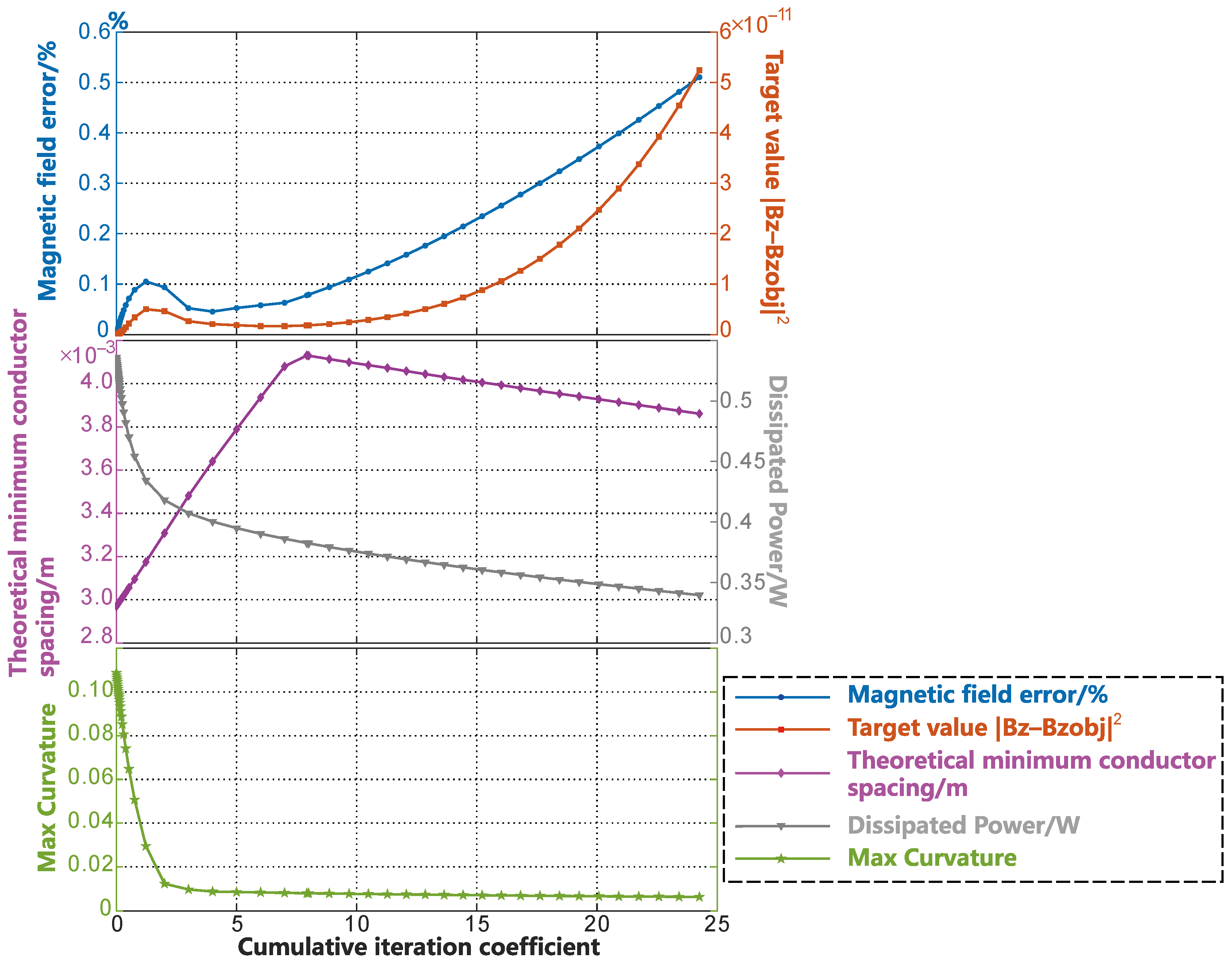
3. Numerical Example
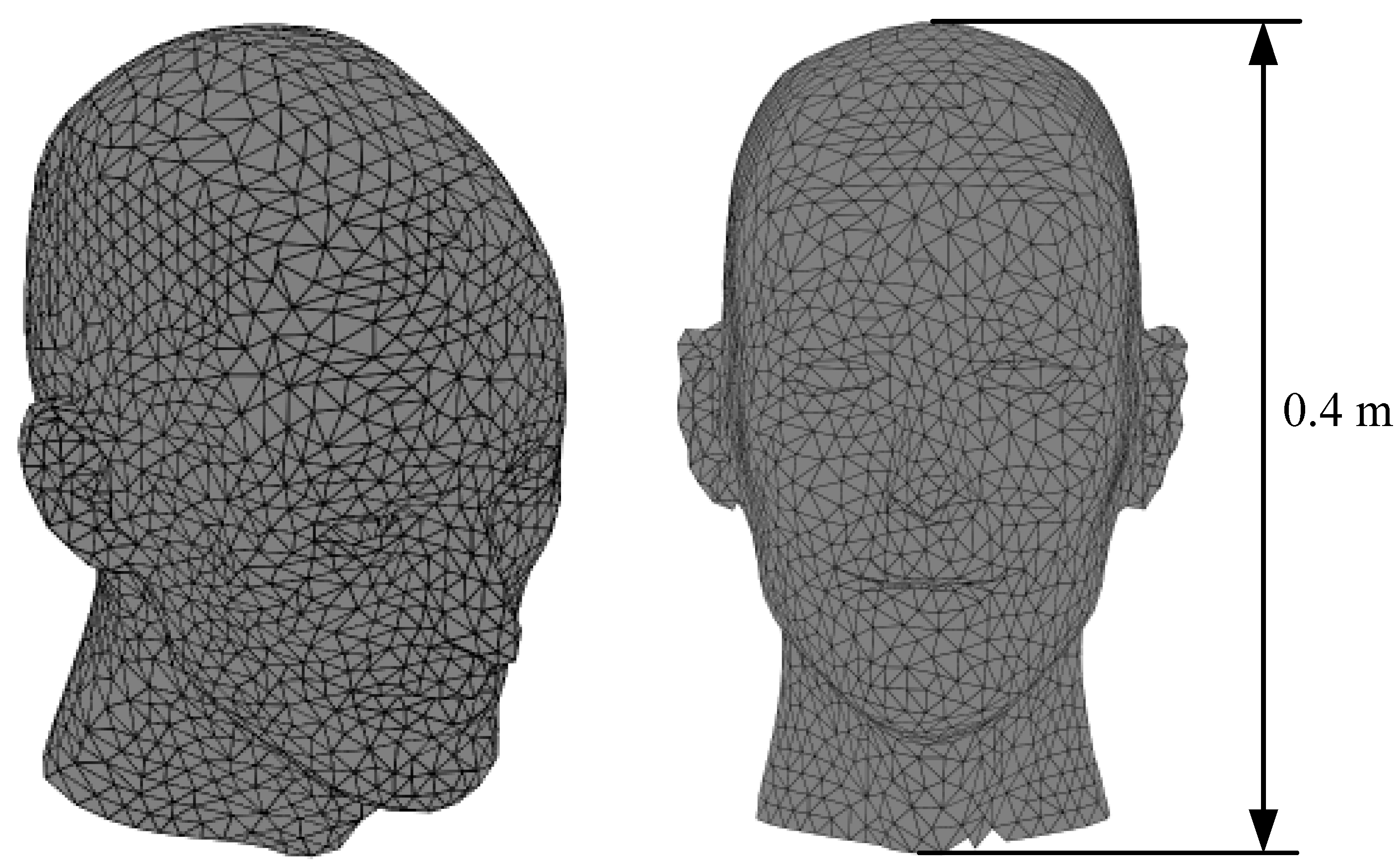
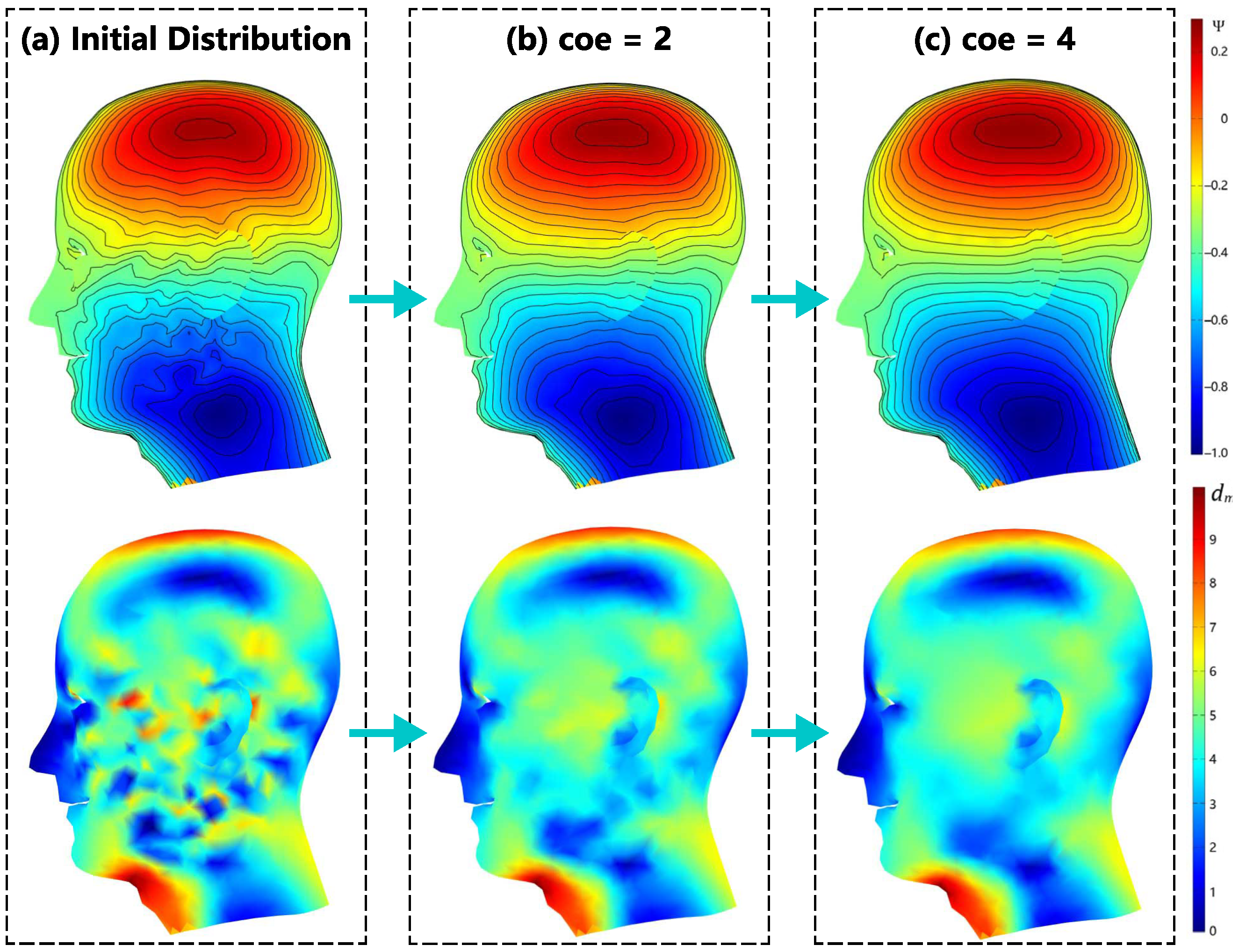
3.1. Undevelopable Human Head Surface Gradient Coil
3.1.1. X-Gradient Coil on an Undevelopable Surface
3.1.2. Y-Gradient Coil on Undevelopable Surface
3.2. Cylindrical Developable Surface Gradient Coil
3.2.1. Cylindrical Gradient Coil
3.2.2. Cylindrical Unfolded Gradient Coil
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hidalgo-Tobon, S.S. Theory of gradient coil design methods for magnetic resonance imaging. Concepts Magn. Reson. Part A 2010, 36A, 223–242. [Google Scholar] [CrossRef]
- Turner, R. Gradient coil design: A review of methods. Magn. Reson. Imaging 1993, 11, 903–920. [Google Scholar] [CrossRef] [PubMed]
- Jia, F.; Liu, Z.; Zaitsev, M.; Hennig, J.; Korvink, J.G. Design multiple-layer gradient coils using least-squares finite element method. Struct. Multidiscip. Optim. 2014, 49, 523–535. [Google Scholar] [CrossRef]
- Lemdiasov, R.A.; Ludwig, R. A stream function method for gradient coil design. Concepts Magn. Reson. Part B Magn. Reson. Eng. 2010, 26B, 67–80. [Google Scholar] [CrossRef]
- Tomasi, D. Stream function optimization for gradient coil design. Magn. Reson. Med. 2001, 45, 505–512. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Wang, L.; Wang, Q.-L.; Chen, L.-M.; Jia, F.; Liu, Z. Design of super-elliptical gradient coils based on multiple objective Pareto optimization method. Acta Phys. Sin. 2017, 66, 341–351. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Y.-H.; Jia, F.; Liu, Z.-Y. Design of gradient coils on super-elliptical cylindrical surfaces. Acta Phys. Sin. 2014, 63, 238301. [Google Scholar] [CrossRef]
- Gudino, N.; Littin, S. Advancements in Gradient System Performance for Clinical and Research MRI. J. Magn. Reson. Imaging 2023, 57, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Ren, H. Design Method of Magnetic Resonance System Gradient Coil on non-Developable Surface. Master’s Thesis, University of Chinese Academy of Sciences (Changchun Institute of Optics, Fine Mechanics and Physics), Changchun, China, 2019. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.I.A.K. Solutions of Ill-Posed Problems; Winston Publishing: Great Falls, MT, Canada, 1977. [Google Scholar]
- Engl, H.W.; Ramlau, R. Regularization of Inverse Problems; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Shou, G.; Ling, X.; Feng, L.; Zhu, M.; Yu, L.; Crozier, S. MRI Coil Design Using Boundary-Element Method with Regularization Technique: A Numerical Calculation Study. IEEE Trans. Magn. 2010, 46, 1052–1059. [Google Scholar] [CrossRef]
- Ren, H.; Pan, H.; Jia, F.; Korvink, J.G.; Liu, Z. Accurate surface normal representation to facilitate gradient coil optimization on curved surface. Magn. Reson. Lett. 2023, 3, 67–84. [Google Scholar] [CrossRef]
- Calvetti, D.; Morigi, S.; Reichel, L.; Sgallari, F. Tikhonov regularization and the L-curve for large discrete ill-posed problems. J. Comput. Appl. Math. 2000, 123, 423–446. [Google Scholar] [CrossRef]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996; Volume 375. [Google Scholar]
- Sigmund, O.; Petersson, J. Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- Desbrun, M.; Meyer, M.; Schröder, P.; Barr, A.H. Implicit fairing of irregular meshes using diffusion and curvature flow. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 8–13 August 1999; pp. 317–324. [Google Scholar]
- Kimmel, R. Intrinsic Scale Space for Images on Surfaces: The Geodesic Curvature Flow. Graph. Models Image Process. 1997, 59, 365–372. [Google Scholar] [CrossRef]
- Rosenberg, S. The Laplacian on a Riemannian Manifold: An Introduction to Analysis on Manifolds; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Bajaj, C.L.; Xu, G. Anisotropic diffusion of surfaces and functions on surfaces. ACM Trans. Graph. 2003, 22, 4–32. [Google Scholar] [CrossRef]
- Crane, K. Discrete differential geometry: An applied introduction. Not. AMS Commun. 2018, 1153–1159. [Google Scholar]
- Turner, R. Minimum inductance coils. J. Phys. E Sci. Instrum. 1988, 21, 948. [Google Scholar] [CrossRef]
- Chavhan, G.B. MRI Made Easy; JP Medical Ltd.: London, UK, 2013. [Google Scholar]
- Lee, D.T.; Schachter, B.J. Two algorithms for constructing a Delaunay triangulation. Int. J. Comput. Inf. Sci. 1980, 9, 219–242. [Google Scholar] [CrossRef]
- Li, H.; Zeng, W.; Morvan, J.M.; Chen, L.; Gu, X.D. Surface Meshing with Curvature Convergence. IEEE Trans. Vis. Comput. Graph. 2014, 20, 919–934. [Google Scholar] [CrossRef] [PubMed][Green Version]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Ren, H.; Zuo, T.; Liu, Z. A Stream Function Smoothing Method for the Design of MRI Gradient Coils on Non-Developable Surfaces. Sensors 2023, 23, 7912. https://doi.org/10.3390/s23187912
Yang B, Ren H, Zuo T, Liu Z. A Stream Function Smoothing Method for the Design of MRI Gradient Coils on Non-Developable Surfaces. Sensors. 2023; 23(18):7912. https://doi.org/10.3390/s23187912
Chicago/Turabian StyleYang, Bohan, Hao Ren, Tongxing Zuo, and Zhenyu Liu. 2023. "A Stream Function Smoothing Method for the Design of MRI Gradient Coils on Non-Developable Surfaces" Sensors 23, no. 18: 7912. https://doi.org/10.3390/s23187912
APA StyleYang, B., Ren, H., Zuo, T., & Liu, Z. (2023). A Stream Function Smoothing Method for the Design of MRI Gradient Coils on Non-Developable Surfaces. Sensors, 23(18), 7912. https://doi.org/10.3390/s23187912




