Delamination Detection and Localization in Vibrating Composite Plates and Shells Using the Inverse Finite Element Method
Abstract
:1. Introduction
2. Theoretical Framework
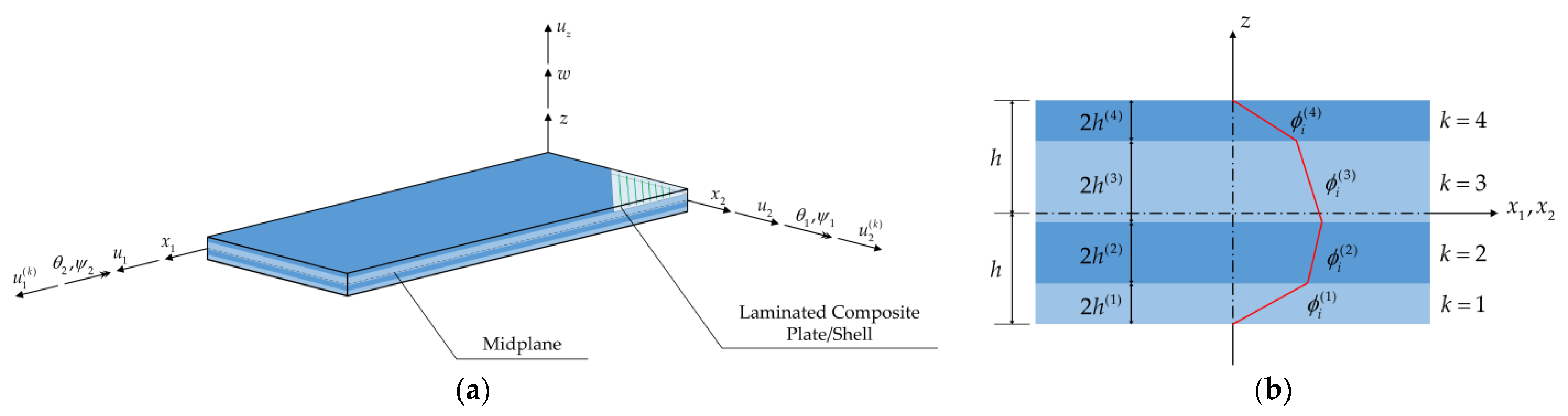
2.1. RZT and Derivatization of the iRZT4 Inverse Element
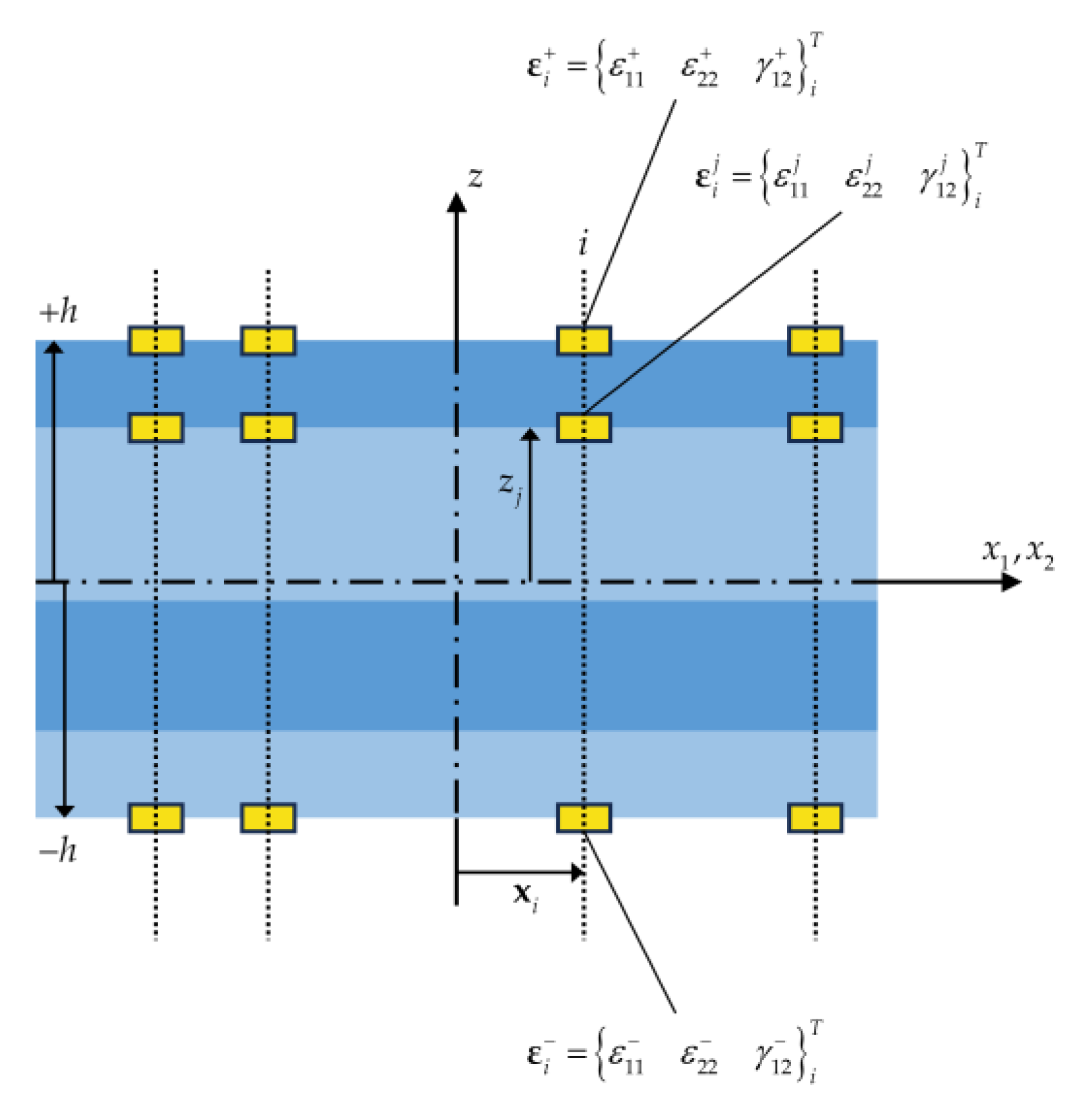
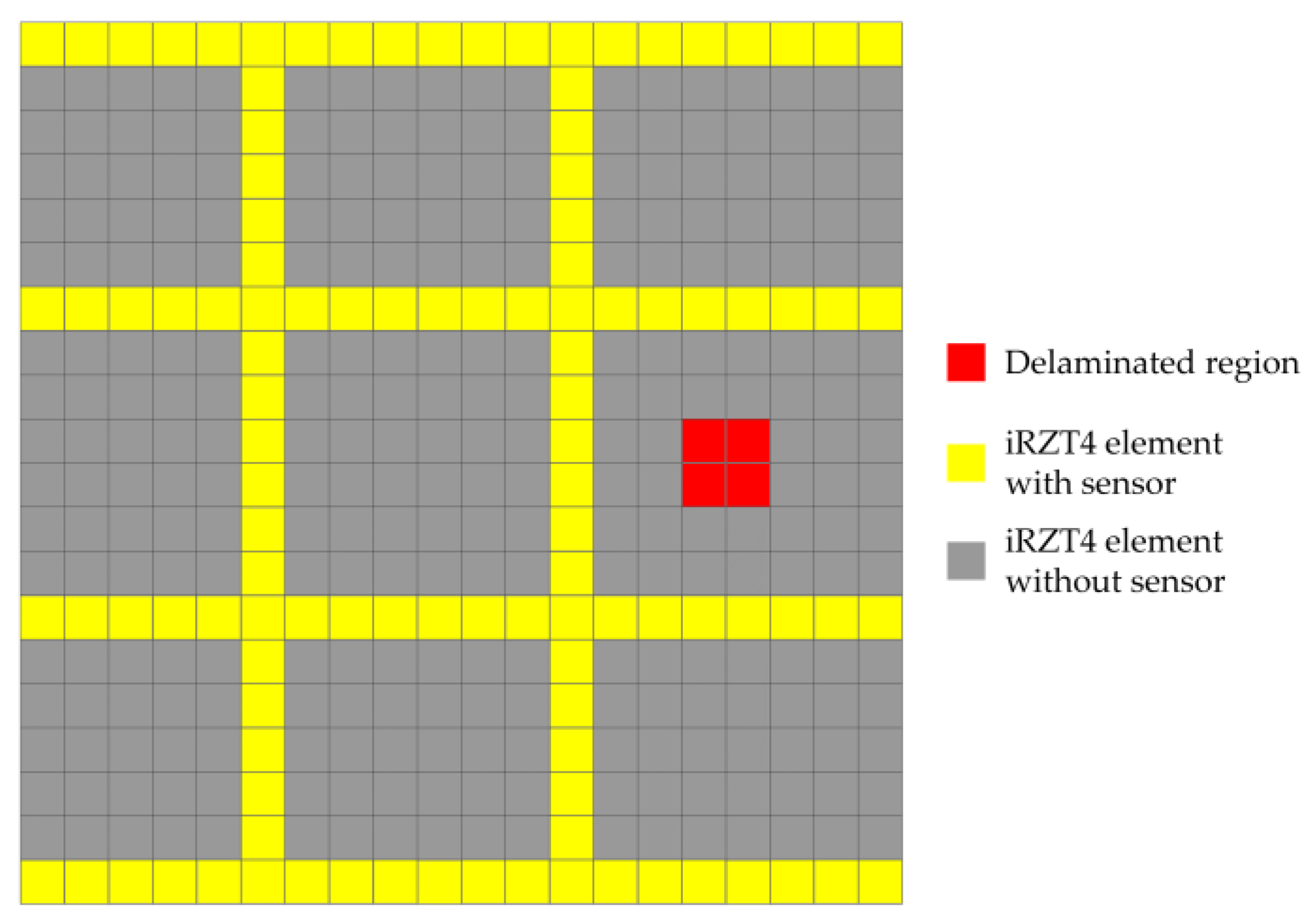
2.2. Damage Detection Toolbox Based on iFEM–RZT
3. Numerical Examples
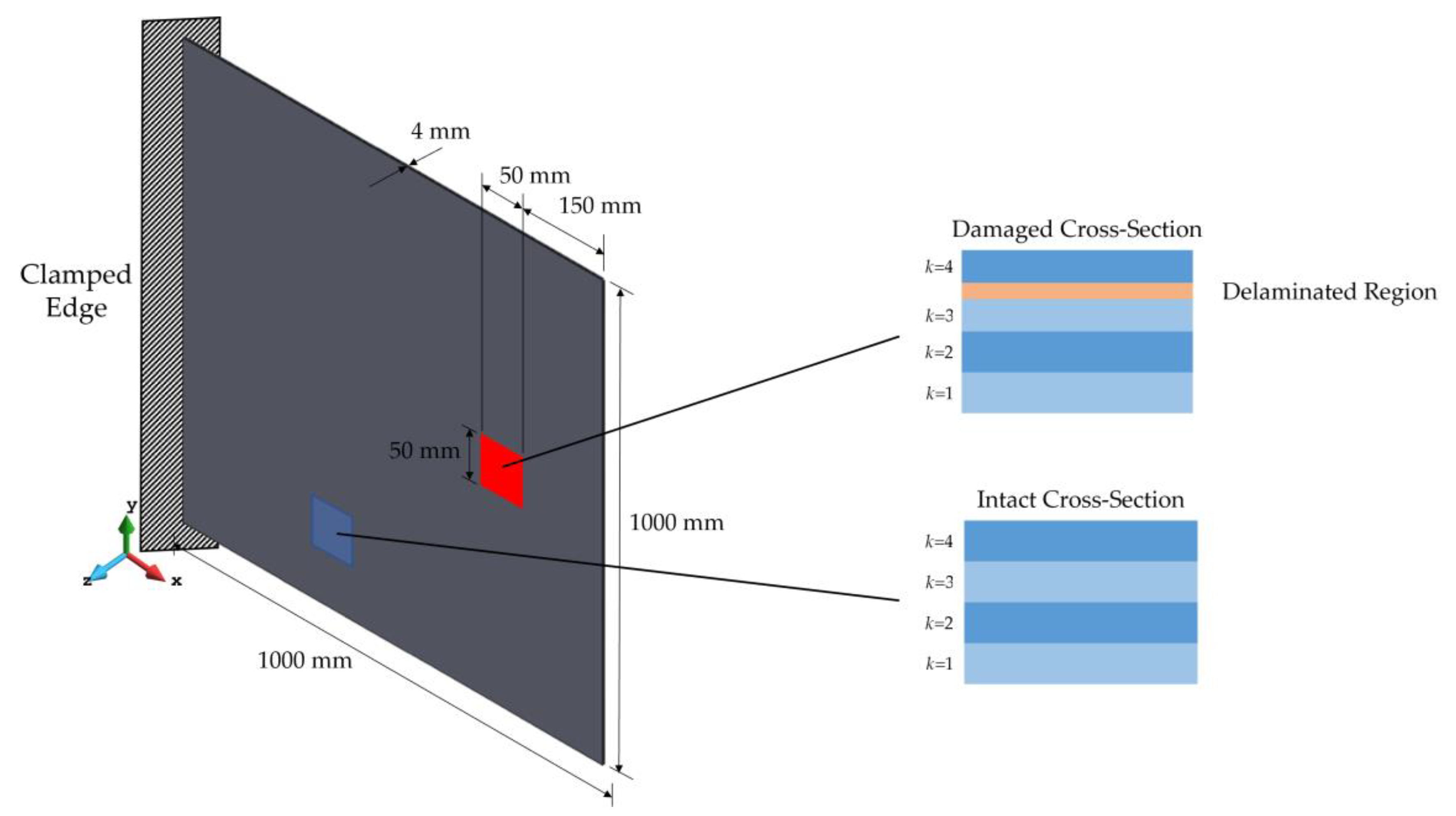
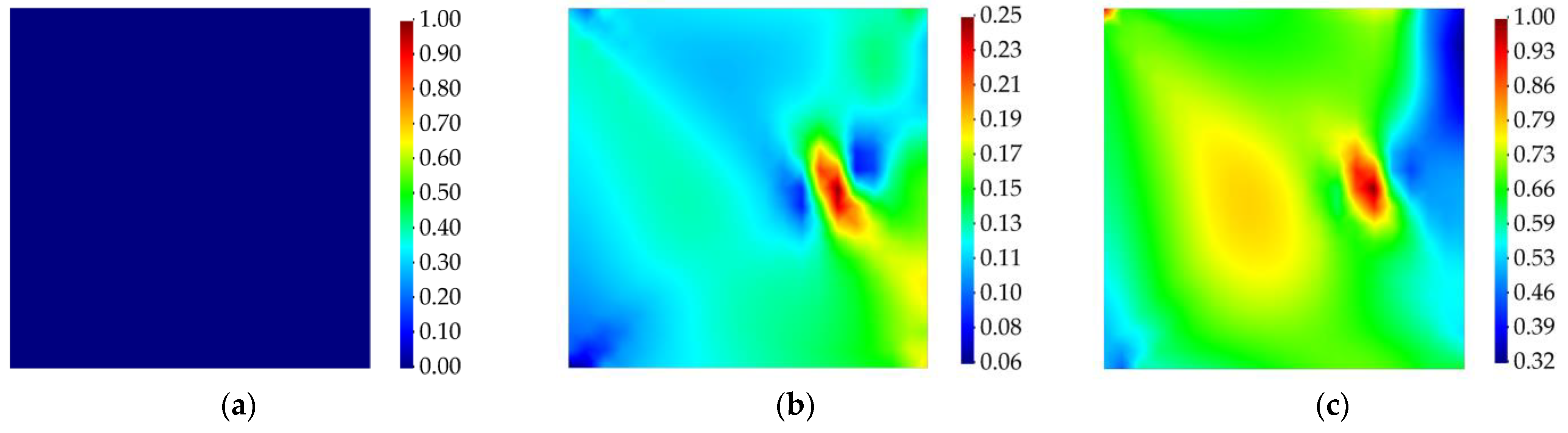
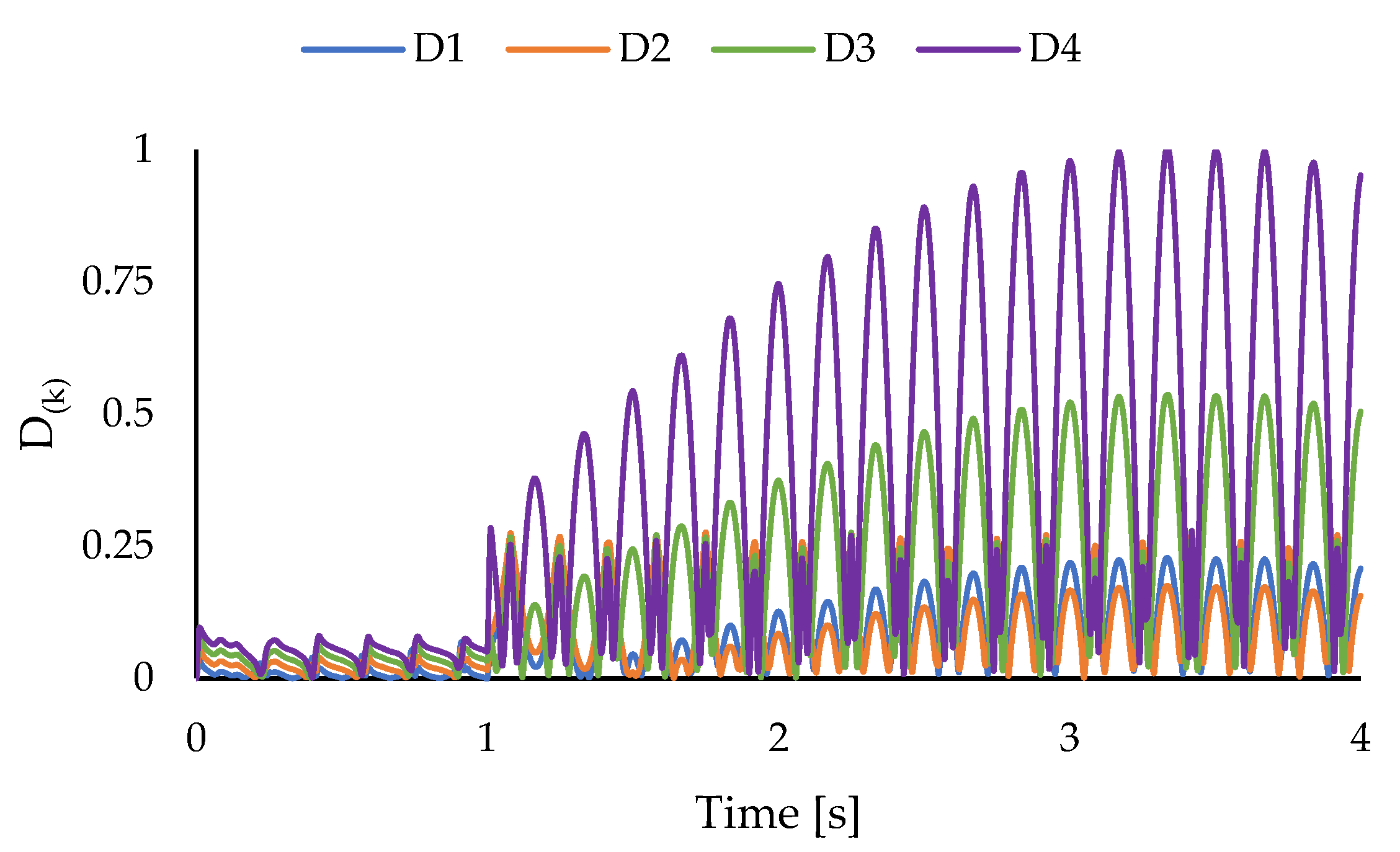
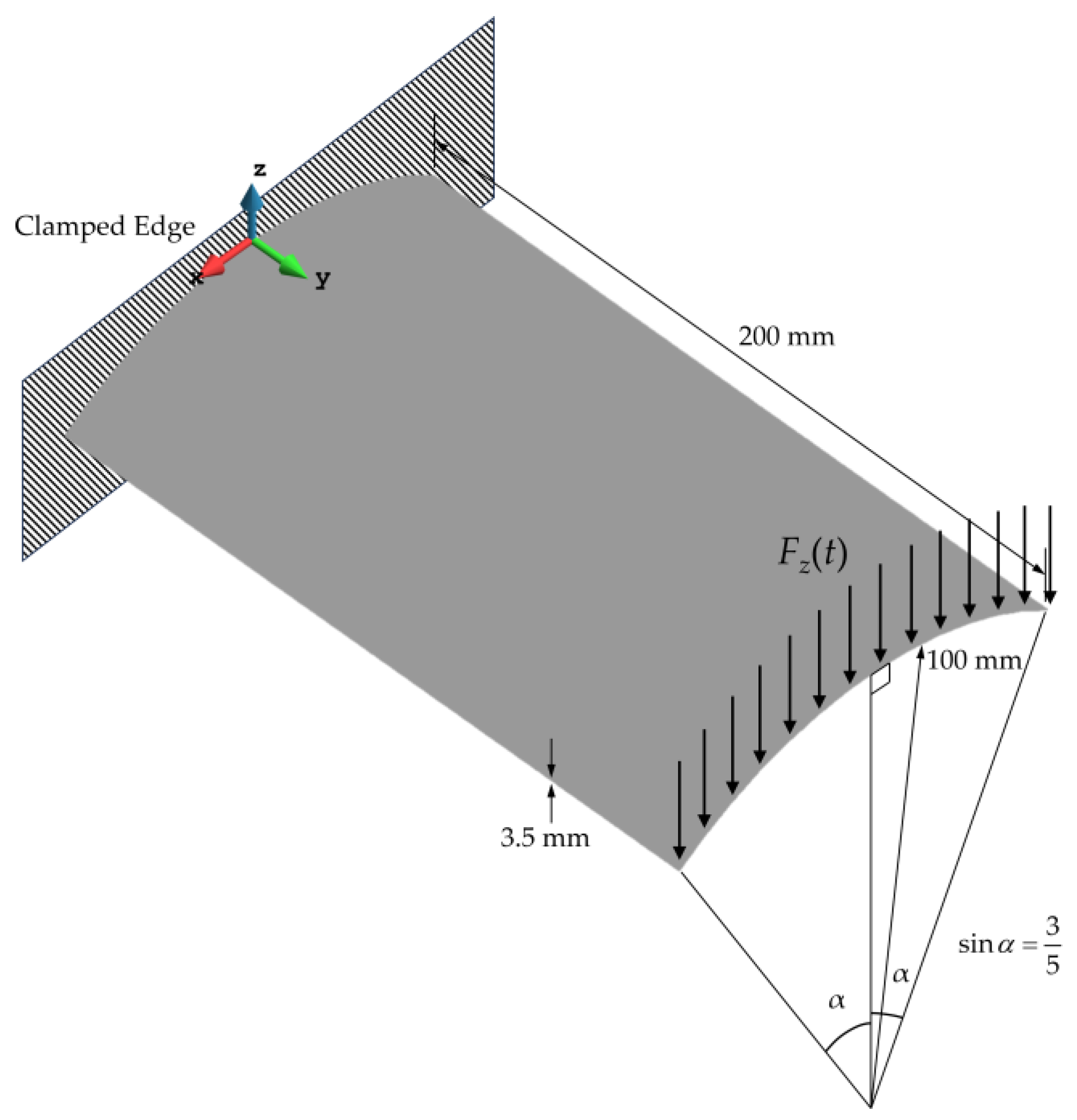
3.1. Cantilevered Plate Subject to Harmonic Load
- Cantilevered laminated composite plate subject to harmonic bending load;
- Cantilevered laminated composite plate subject to harmonic torsion load.
3.1.1. Cantilevered Laminated Composite Plate Subject to Harmonic Bending Load
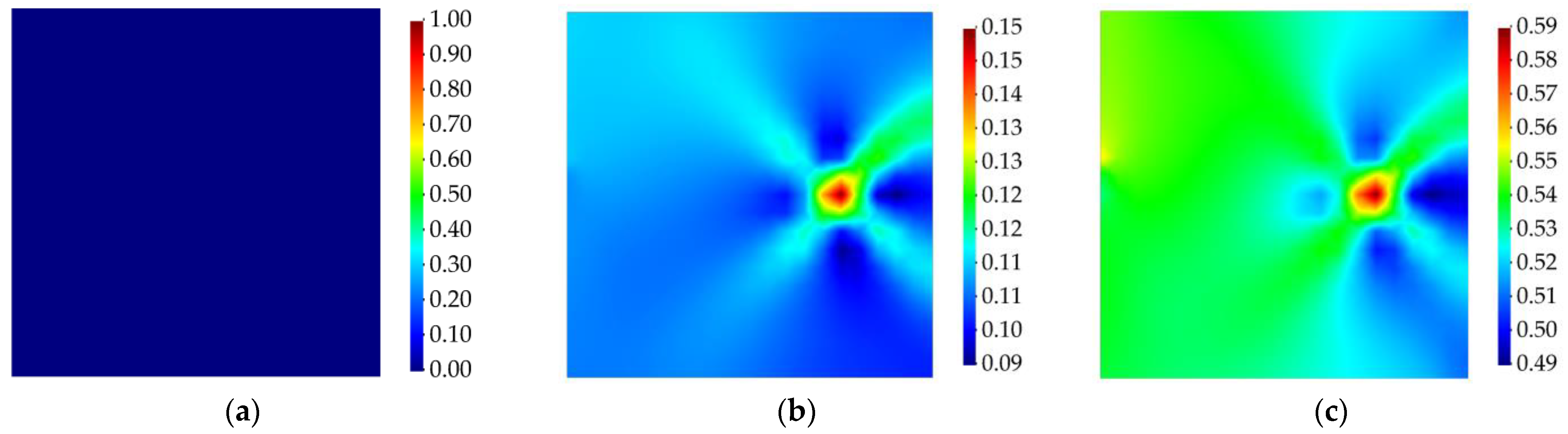
3.1.2. Cantilevered Laminated Composite Plate Subject to Harmonic Torsion Load
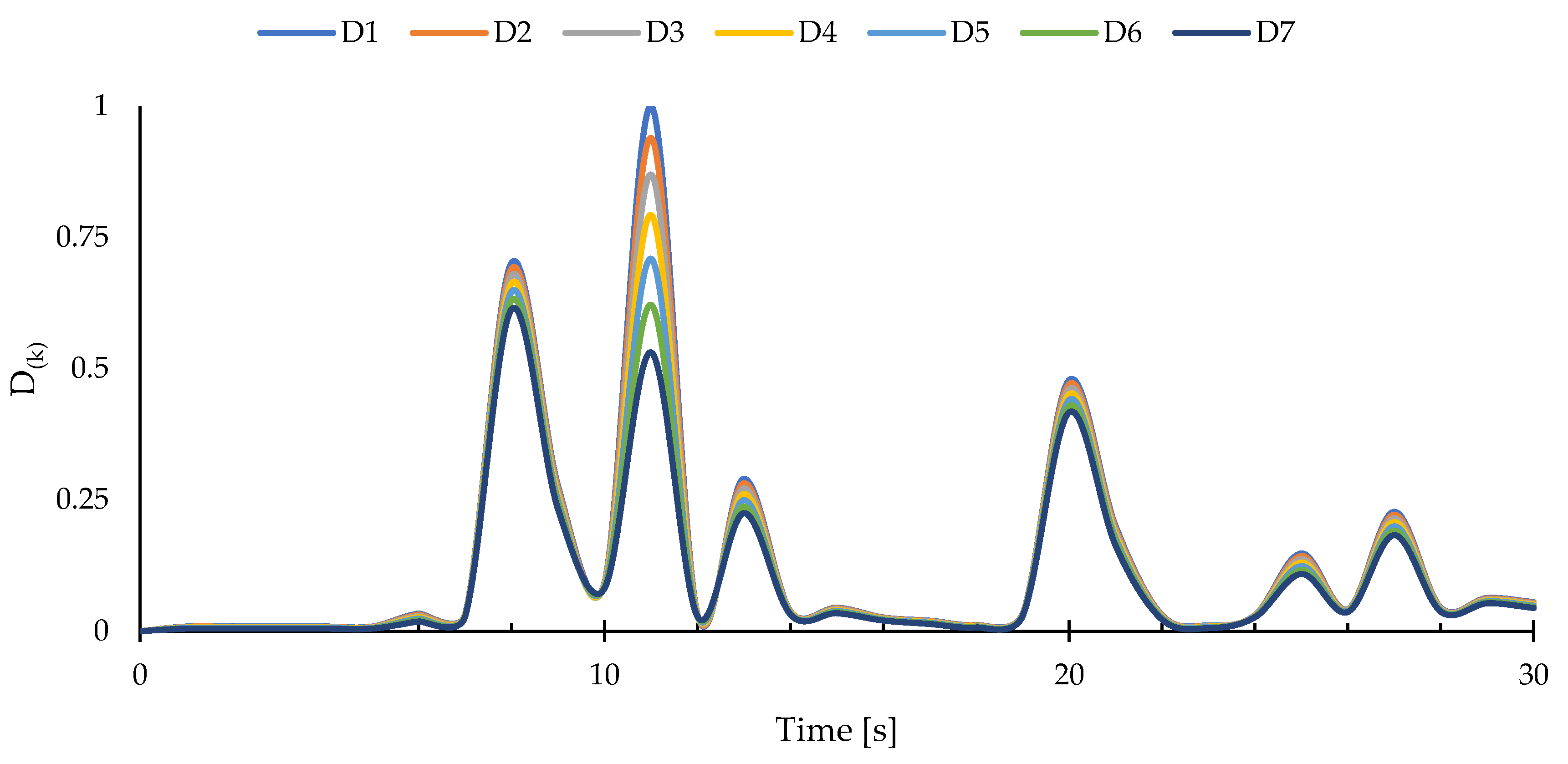
3.2. Cantilevered Curved Shell Subject to Random Bending Load
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
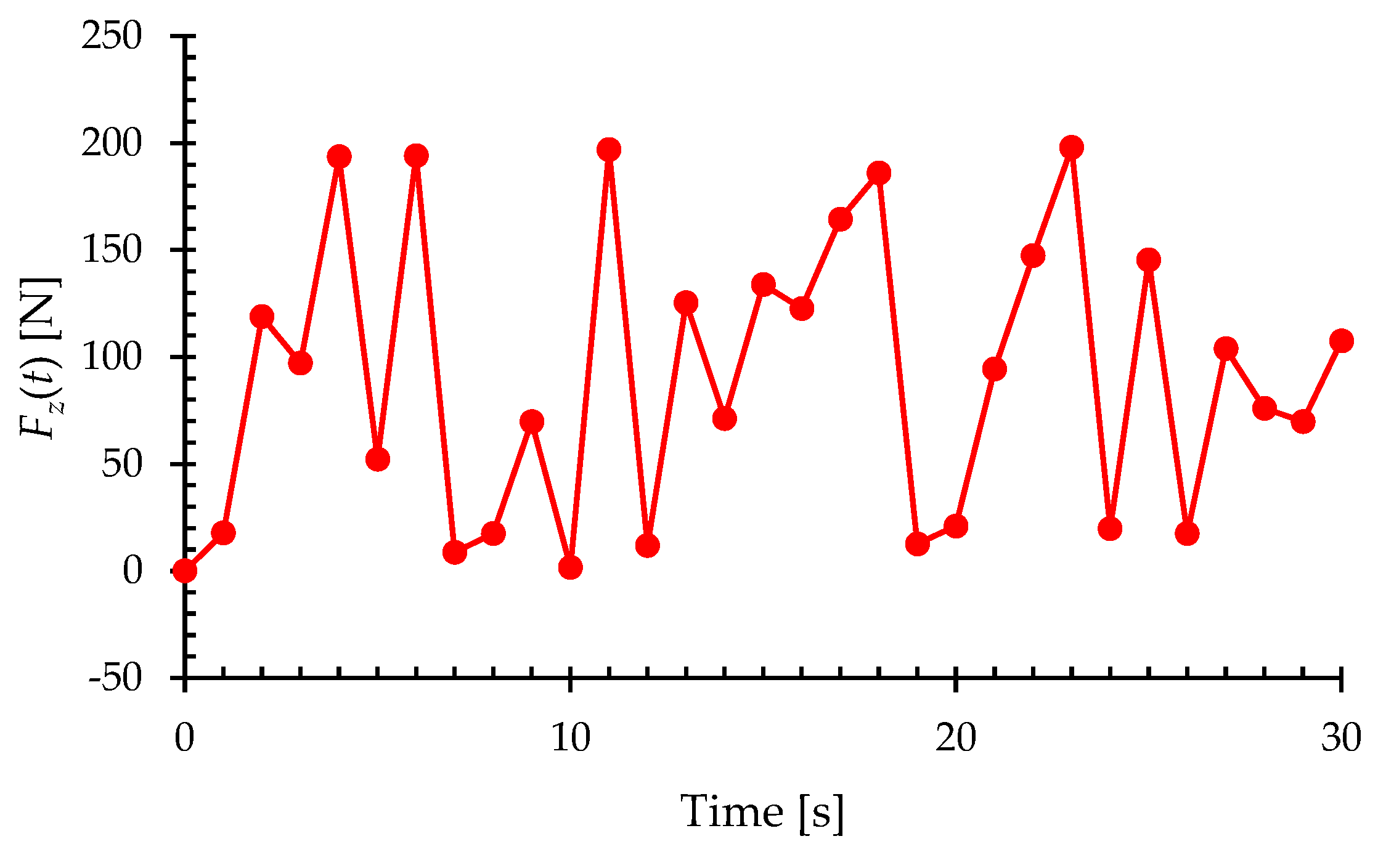
| Time [s] | Force [N] | Time [s] | Force [N] |
|---|---|---|---|
| 0 | 0.00 | 16 | 122.62 |
| 1 | 17.68 | 17 | 164.43 |
| 2 | 118.82 | 18 | 185.96 |
| 3 | 97.04 | 19 | 12.56 |
| 4 | 193.61 | 20 | 20.94 |
| 5 | 52.20 | 21 | 94.42 |
| 6 | 194.10 | 22 | 147.35 |
| 7 | 8.68 | 23 | 197.94 |
| 8 | 17.39 | 24 | 19.75 |
| 9 | 69.75 | 25 | 145.35 |
| 10 | 1.65 | 26 | 17.38 |
| 11 | 196.91 | 27 | 103.93 |
| 12 | 11.78 | 28 | 75.94 |
| 13 | 125.40 | 29 | 69.76 |
| 14 | 71.24 | 30 | 107.49 |
| 15 | 133.85 |
References
- Starnes, J.H.; Rhodes, M.D.; Williams, J.G. Effect of Impact Damage and Holes on the Compressive Strength of a Graphite/Epoxy Laminate. Nondestruct. Eval. Flaw Crit. Compos. Mater. 1979, 696, 145–171. [Google Scholar]
- Garg, A.C. Delamination—A Damage Mode in Composite Structures. Eng. Fract. Mech. 1988, 29, 557–584. [Google Scholar] [CrossRef]
- Scarponi, C.; Briotti, G. Ultrasonic Technique for the Evaluation of Delaminations on CFRP, GFRP, KFRP Composite Materials. Compos. Part B Eng. 2000, 31, 237–243. [Google Scholar] [CrossRef]
- Zhou, G.; Sim, L.M. Damage Detection and Assessment in Fibre-Reinforced Composite Structures with Embedded Fibre Optic Sensors-Review. Smart Mater. Struct. 2002, 11, 925–939. [Google Scholar] [CrossRef]
- Mitchell, M.R.; Link, R.E.; Arumugam, V.; Kumar, C.S.; Santulli, C.; Sarasini, F.; Stanley, A.J. A Global Method for the Identification of Failure Modes in Fiberglass Using Acoustic Emission. J. Test. Eval. 2011, 39, 103730. [Google Scholar] [CrossRef]
- Bakhtiary Davijani, A.A.; Hajikhani, M.; Ahmadi, M. Acoustic Emission Based on Sentry Function to Monitor the Initiation of Delamination in Composite Materials. Mater. Des. 2011, 32, 3059–3065. [Google Scholar] [CrossRef]
- Ataş, A.; Soutis, C. Subcritical Damage Mechanisms of Bolted Joints in CFRP Composite Laminates. Compos. Part B Eng. 2013, 54, 20–27. [Google Scholar] [CrossRef]
- Bull, D.J.; Spearing, S.M.; Sinclair, I.; Helfen, L. Three-Dimensional Assessment of Low Velocity Impact Damage in Particle Toughened Composite Laminates Using Micro-Focus X-ray Computed Tomography and Synchrotron Radiation Laminography. Compos. Part A Appl. Sci. Manuf. 2013, 52, 62–69. [Google Scholar] [CrossRef]
- Vavrik, D.; Jakubek, J.; Jandejsek, I.; Krejci, F.; Kumpova, I.; Zemlicka, J. Visualization of Delamination in Composite Materials Utilizing Advanced X-Ray Imaging Techniques. J. Inst. 2015, 10, C04012. [Google Scholar] [CrossRef]
- Ghadermazi, K.; Khozeimeh, M.A.; Taheri-Behrooz, F.; Safizadeh, M.S. Delamination Detection in Glass–Epoxy Composites Using Step-Phase Thermography (SPT). Infrared Phys. Technol. 2015, 72, 204–209. [Google Scholar] [CrossRef]
- Chrysafi, A.P.; Athanasopoulos, N.; Siakavellas, N.J. Damage Detection on Composite Materials with Active Thermography and Digital Image Processing. Int. J. Therm. Sci. 2017, 116, 242–253. [Google Scholar] [CrossRef]
- Szebényi, G.; Hliva, V. Detection of Delamination in Polymer Composites by Digital Image Correlation—Experimental Test. Polymers 2019, 11, 523. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Gorbatikh, L.; Fonteyn, S.; Van Hemelrijck, D.; Pyl, L.; Carrella-Payan, D.; Lomov, S.V. Digital Image Correlation Assisted Characterization of Mode I Fatigue Delamination in Composites. Compos. Struct. 2020, 253, 112746. [Google Scholar] [CrossRef]
- Ricci, F.; Monaco, E.; Boffa, N.D.; Maio, L.; Memmolo, V. Guided Waves for Structural Health Monitoring in Composites: A Review and Implementation Strategies. Prog. Aerosp. Sci. 2022, 129, 100790. [Google Scholar] [CrossRef]
- Capello, E. Workpiece Damping and Its Effect on Delamination Damage in Drilling Thin Composite Laminates. J. Mater. Process. Technol. 2004, 148, 186–195. [Google Scholar] [CrossRef]
- Mehbudi, P.; Baghlani, V.; Akbari, J.; Bushroa, A.R.; Mardi, N.A. Applying Ultrasonic Vibration to Decrease Drilling-Induced Delamination in GFRP Laminates. Procedia CIRP 2013, 6, 577–582. [Google Scholar] [CrossRef]
- Seif, M.A.; Khashaba, U.A.; Rojas-Oviedo, R. Measuring Delamination in Carbon/Epoxy Composites Using a Shadow Moiré Laser Based Imaging Technique. Compos. Struct. 2007, 79, 113–118. [Google Scholar] [CrossRef]
- De Albuquerque, V.H.C.; Tavares, J.M.R.S.; Durão, L.M.P. Evaluation of Delamination Damage on Composite Plates Using an Artificial Neural Network for the Radiographic Image Analysis. J. Compos. Mater. 2010, 44, 1139–1159. [Google Scholar] [CrossRef]
- Jia, Z.; Chen, C.; Wang, F.; Zhang, C. Analytical Study of Delamination Damage and Delamination-Free Drilling Method of CFRP Composite. J. Mater. Process. Technol. 2020, 282, 116665. [Google Scholar] [CrossRef]
- Jones, R. Damage Tolerance of Advanced Composite Materials-Compression. In Proceedings of the International Conference on the Role of Fracture Mechanics in Modern Technology, Fukuoka, Japan, 2–6 June 1986; pp. 653–663. [Google Scholar]
- Johnson, A.F.; Pickett, A.K.; Rozycki, P. Computational Methods for Predicting Impact Damage in Composite Structures. Compos. Sci. Technol. 2001, 61, 2183–2192. [Google Scholar] [CrossRef]
- Aymerich, F.; Staszewski, W.J. Impact Damage Detection in Composite Laminates Using Nonlinear Acoustics. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1084–1092. [Google Scholar] [CrossRef]
- Ratcliffe, C.P.; Bagaria, W.J. Vibration Technique for Locating Delamination in a Composite Beam. AIAA J. 1998, 36, 1074–1077. [Google Scholar] [CrossRef]
- Barman, S.K.; Jebieshia, T.R.; Tiwari, P.; Maiti, D.K.; Maity, D. Two-Stage Inverse Method to Detect Delamination in Composite Beam Using Vibration Responses. AIAA J. 2019, 57, 1312–1322. [Google Scholar] [CrossRef]
- Kessler, S.S.; Spearing, S.M.; Atalla, M.J.; Cesnik, C.E.S.; Soutis, C. Damage Detection in Composite Materials Using Frequency Response Methods. Compos. Part B Eng. 2002, 33, 87–95. [Google Scholar] [CrossRef]
- Zhang, Z.; Shankar, K.; Ray, T.; Morozov, E.V.; Tahtali, M. Vibration-Based Inverse Algorithms for Detection of Delamination in Composites. Compos. Struct. 2013, 102, 226–236. [Google Scholar] [CrossRef]
- Garcia, D.; Palazzetti, R.; Trendafilova, I.; Fiorini, C.; Zucchelli, A. Vibration-Based Delamination Diagnosis and Modelling for Composite Laminate Plates. Compos. Struct. 2015, 130, 155–162. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. A Least-Squares Variational Method for Full-Field Reconstruction of Elastic Deformations in Shear-Deformable Plates and Shells. Comput. Methods Appl. Mech. Eng. 2005, 194, 327–339. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M. Shape Sensing Methods: Review and Experimental Comparison on a Wing-Shaped Plate. Prog. Aerosp. Sci. 2018, 99, 14–26. [Google Scholar] [CrossRef]
- Ko, W.L.; Richards, W.L.; Tran, V. Displacement Theories for In-Flight Deformed Shape Predictions of Aerospace Structures 2007. Available online: https://ntrs.nasa.gov/citations/20070032936 (accessed on 2 September 2023).
- Pisoni, A.C.; Santolini, C.; Hauf, D.E.; Dubowsky, S. Displacements in a Vibrating Body by Strain Gauge Measurements. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=5a40a3f64a8ace0de82bb56886328813f0cdc7a9 (accessed on 2 September 2023).
- Bruno, R.; Toomarian, N.; Salama, M. Shape Estimation from Incomplete Measurements: A Neural-Net Approach. Smart Mater. Struct. 1994, 3, 92. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E.; Tessler, A.; Spangler, J.L. A Quadrilateral Inverse-Shell Element with Drilling Degrees of Freedom for Shape Sensing and Structural Health Monitoring. Eng. Sci. Technol. Int. J. 2016, 19, 1299–1313. [Google Scholar] [CrossRef]
- Papa, U.; Russo, S.; Lamboglia, A.; Del Core, G.; Iannuzzo, G. Health Structure Monitoring for the Design of an Innovative UAS Fixed Wing through Inverse Finite Element Method (iFEM). Aerosp. Sci. Technol. 2017, 69, 439–448. [Google Scholar] [CrossRef]
- Esposito, M.; Gherlone, M. Composite Wing Box Deformed-Shape Reconstruction Based on Measured Strains: Optimization and Comparison of Existing Approaches. Aerosp. Sci. Technol. 2020, 99, 105758. [Google Scholar] [CrossRef]
- Oboe, D.; Colombo, L.; Sbarufatti, C.; Giglio, M. Shape Sensing of a Complex Aeronautical Structure with Inverse Finite Element Method. Sensors 2021, 21, 1388. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Mattone, M.; Gherlone, M. Experimental Shape Sensing and Load Identification on a Stiffened Panel: A Comparative Study. Sensors 2022, 22, 1064. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Roy, R.; Surace, C.; Gherlone, M. Hybrid Shell-Beam Inverse Finite Element Method for the Shape Sensing of Stiffened Thin-Walled Structures: Formulation and Experimental Validation on a Composite Wing-Shaped Panel. Sensors 2023, 23, 5962. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Du, Z.; Tang, Y. Numerical Study on the Displacement Reconstruction of Subsea Pipelines Using the Improved Inverse Finite Element Method. Ocean Eng. 2022, 248, 110763. [Google Scholar] [CrossRef]
- Li, M.; Dirik, Y.; Oterkus, E.; Oterkus, S. Shape Sensing of NREL 5 MW Offshore Wind Turbine Blade Using iFEM Methodology. Ocean Eng. 2023, 273, 114036. [Google Scholar] [CrossRef]
- Savino, P. Shape sensing with inverse finite element method for slender structures. Struct. Eng. Mech. Int. J. 2019, 72, 217–227. [Google Scholar]
- Liu, M.; Zhang, X.; Song, H.; Zhou, S.; Zhou, Z.; Zhou, W. Inverse Finite Element Method for Reconstruction of Deformation in the Gantry Structure of Heavy-Duty Machine Tool Using FBG Sensors. Sensors 2018, 18, 2173. [Google Scholar] [CrossRef]
- Oboe, D.; Colombo, L.; Sbarufatti, C.; Giglio, M. Comparison of Strain Pre-Extrapolation Techniques for Shape and Strain Sensing by iFEM of a Composite Plate Subjected to Compression Buckling. Compos. Struct. 2021, 262, 113587. [Google Scholar] [CrossRef]
- Kefal, A.; Tabrizi, I.E.; Yildiz, M.; Tessler, A. A Smoothed iFEM Approach for Efficient Shape-Sensing Applications: Numerical and Experimental Validation on Composite Structures. Mech. Syst. Signal Process. 2021, 152, 107486. [Google Scholar] [CrossRef]
- Cerracchio, P.; Gherlone, M.; Di Sciuva, M.; Tessler, A. A Novel Approach for Displacement and Stress Monitoring of Sandwich Structures Based on the Inverse Finite Element Method. Compos. Struct. 2015, 127, 69–76. [Google Scholar] [CrossRef]
- Tessler, A.; Di Sciuva, M.; Gherlone, M. A Consistent Refinement of First-Order Shear Deformation Theory for Laminated Composite and Sandwich Plates Using Improved Zigzag Kinematics. J. Mech. Mater. Struct. 2010, 5, 341–367. [Google Scholar] [CrossRef]
- Kefal, A.; Tessler, A.; Oterkus, E. An Enhanced Inverse Finite Element Method for Displacement and Stress Monitoring of Multilayered Composite and Sandwich Structures. Compos. Struct. 2017, 179, 514–540. [Google Scholar] [CrossRef]
- Colombo, L.; Sbarufatti, C.; Giglio, M. Definition of a Load Adaptive Baseline by Inverse Finite Element Method for Structural Damage Identification. Mech. Syst. Signal Process. 2019, 120, 584–607. [Google Scholar] [CrossRef]
- Colombo, L.; Oboe, D.; Sbarufatti, C.; Cadini, F.; Russo, S.; Giglio, M. Shape Sensing and Damage Identification with iFEM on a Composite Structure Subjected to Impact Damage and Non-Trivial Boundary Conditions. Mech. Syst. Signal Process. 2021, 148, 107163. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.A.; Kefal, A.; Yildiz, M. A Comparative and Review Study on Shape and Stress Sensing of Flat/Curved Shell Geometries Using C0-Continuous Family of iFEM Elements. Sensors 2020, 20, 3808. [Google Scholar] [CrossRef]
- Li, M.; Wu, Z.; Yang, H.; Huang, H. Direct Damage Index Based on Inverse Finite Element Method for Structural Damage Identification. Ocean Eng. 2021, 221, 108545. [Google Scholar] [CrossRef]
- Li, M.; Jia, D.; Wu, Z.; Qiu, S.; He, W. Structural Damage Identification Using Strain Mode Differences by the iFEM Based on the Convolutional Neural Network (CNN). Mech. Syst. Signal Process. 2022, 165, 108289. [Google Scholar] [CrossRef]
- Li, T.; Cao, M.; Li, J.; Yang, L.; Xu, H.; Wu, Z. Structural Damage Identification Based on Integrated Utilization of Inverse Finite Element Method and Pseudo-Excitation Approach. Sensors 2021, 21, 606. [Google Scholar] [CrossRef]
- Kefal, A.; Diyaroglu, C.; Yildiz, M.; Oterkus, E. Coupling of Peridynamics and Inverse Finite Element Method for Shape Sensing and Crack Propagation Monitoring of Plate Structures. Comput. Methods Appl. Mech. Eng. 2022, 391, 114520. [Google Scholar] [CrossRef]
- Oboe, D.; Poloni, D.; Sbarufatti, C.; Giglio, M. Towards Automatic Crack Size Estimation with iFEM for Structural Health Monitoring. Sensors 2023, 23, 3406. [Google Scholar] [CrossRef]
- Roy, R.; Gherlone, M. Delamination and Skin-Spar Debond Detection in Composite Structures Using the Inverse Finite Element Method. Materials 2023, 16, 1969. [Google Scholar] [CrossRef] [PubMed]
- Ganjdoust, F.; Kefal, A.; Tessler, A. A Novel Delamination Damage Detection Strategy Based on Inverse Finite Element Method for Structural Health Monitoring of Composite Structures. Mech. Syst. Signal Process. 2023, 192, 110202. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.A.; Tabrizi, I.E.; Kefal, A.; Yildiz, M. A Combined Experimental/Numerical Study on Deformation Sensing of Sandwich Structures through Inverse Analysis of Pre-Extrapolated Strain Measurements. Measurement 2021, 185, 110031. [Google Scholar] [CrossRef]
- Chaboche, J.L. Continuum Damage Mechanics: Part I—General Concepts. J. Appl. Mech. 1988, 55, 59–64. [Google Scholar] [CrossRef]





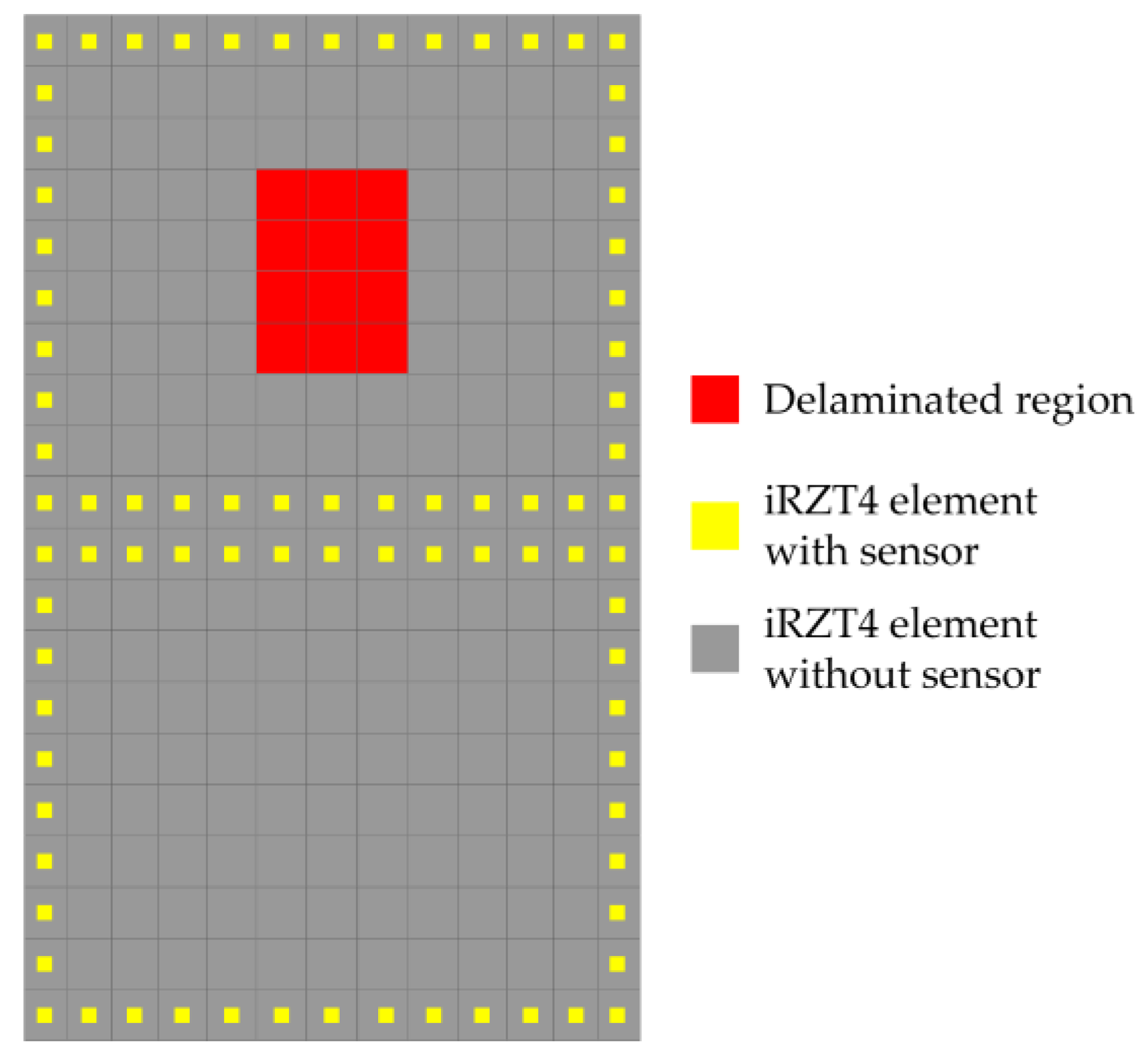



| Young’s Modulus [GPa] | Poisson’s Ratio | Shear Modulus [GPa] |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganjdoust, F.; Kefal, A.; Tessler, A. Delamination Detection and Localization in Vibrating Composite Plates and Shells Using the Inverse Finite Element Method. Sensors 2023, 23, 7926. https://doi.org/10.3390/s23187926
Ganjdoust F, Kefal A, Tessler A. Delamination Detection and Localization in Vibrating Composite Plates and Shells Using the Inverse Finite Element Method. Sensors. 2023; 23(18):7926. https://doi.org/10.3390/s23187926
Chicago/Turabian StyleGanjdoust, Faraz, Adnan Kefal, and Alexander Tessler. 2023. "Delamination Detection and Localization in Vibrating Composite Plates and Shells Using the Inverse Finite Element Method" Sensors 23, no. 18: 7926. https://doi.org/10.3390/s23187926
APA StyleGanjdoust, F., Kefal, A., & Tessler, A. (2023). Delamination Detection and Localization in Vibrating Composite Plates and Shells Using the Inverse Finite Element Method. Sensors, 23(18), 7926. https://doi.org/10.3390/s23187926







