Modelling Weather Precipitation Intensity on Surfaces in Motion with Application to Autonomous Vehicles
Abstract
:1. Introduction
2. Precipitation Flux Model
2.1. Model Description
2.2. Dimensional Analysis
3. Model Validation
3.1. Experimental Setup
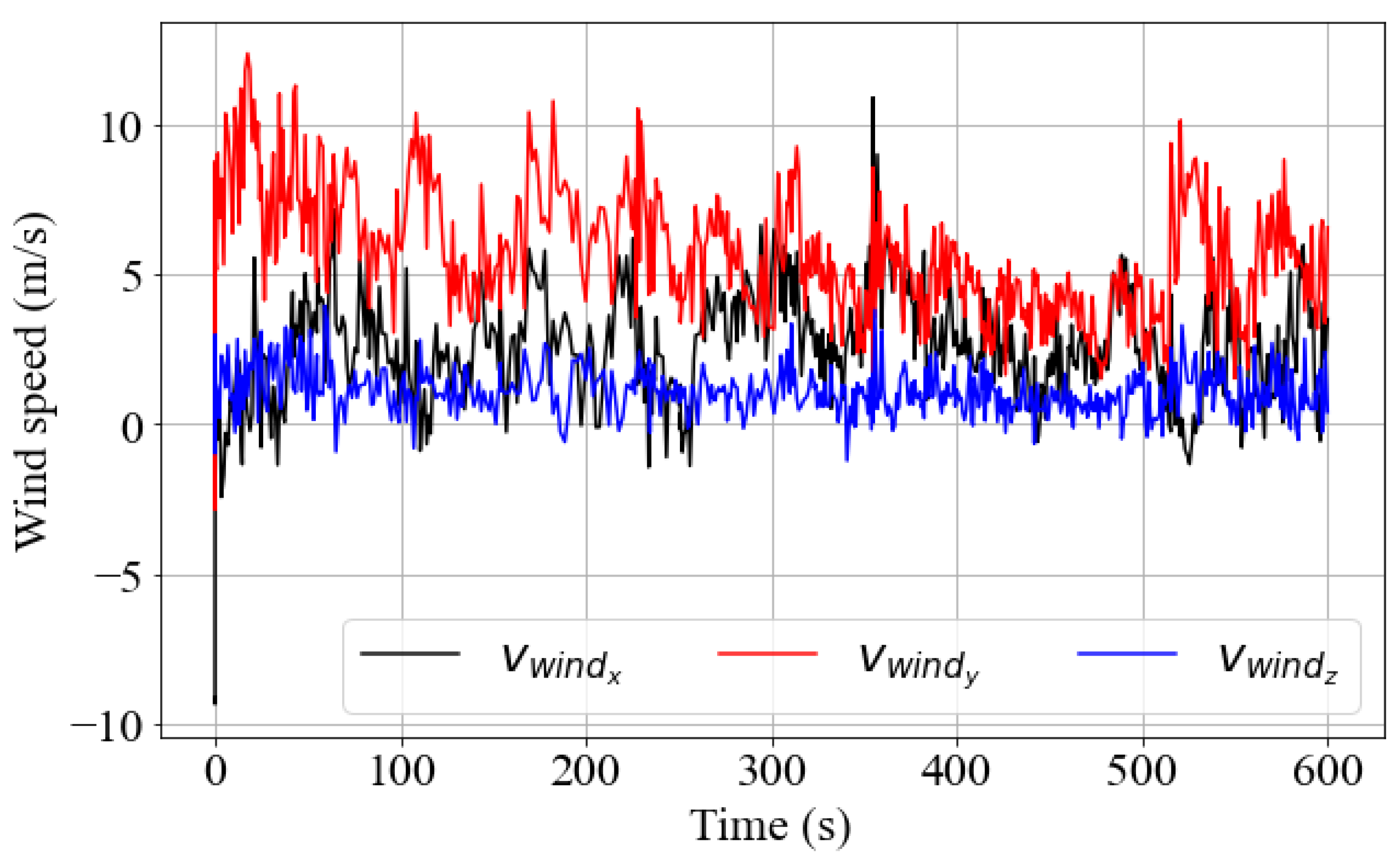
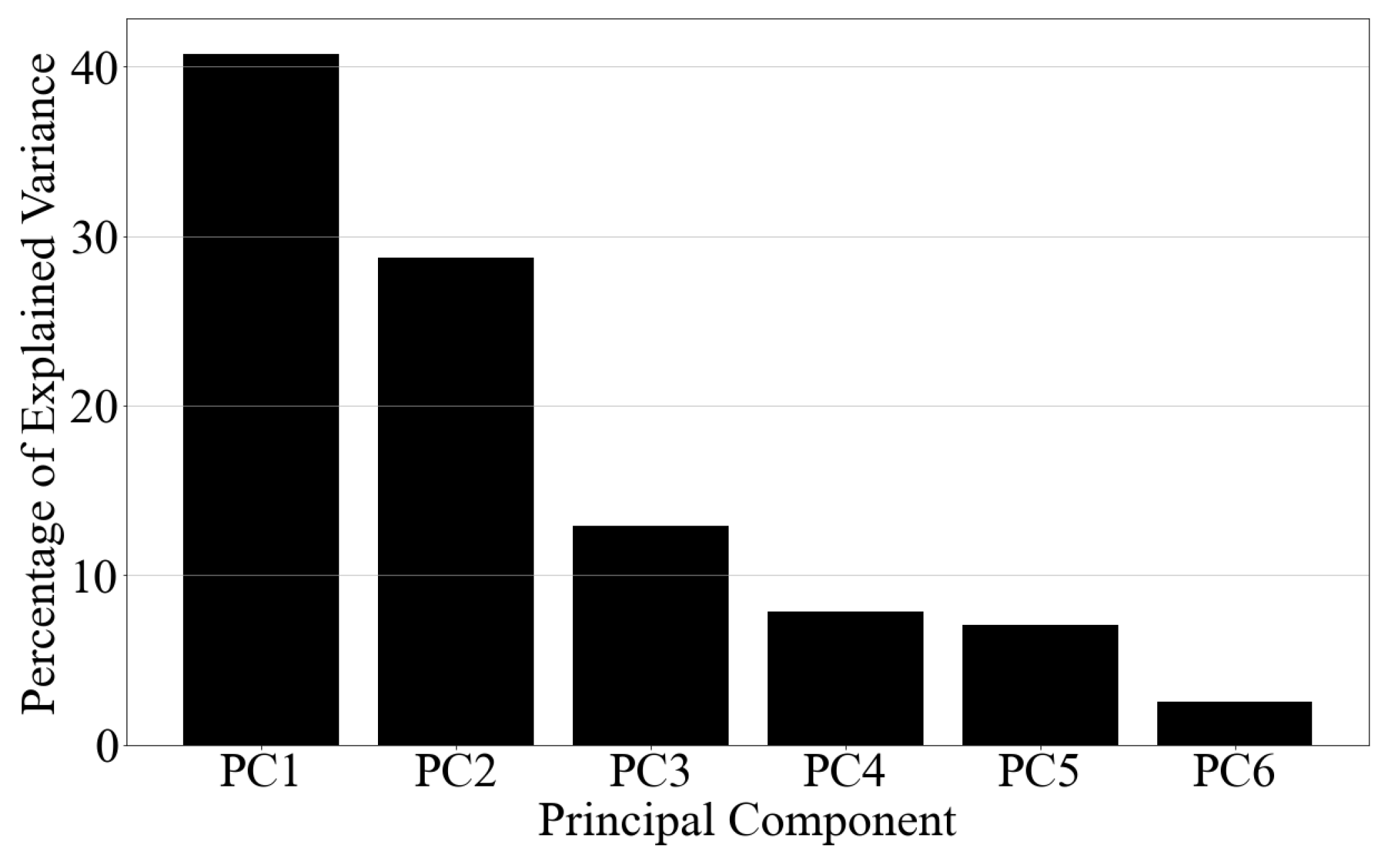
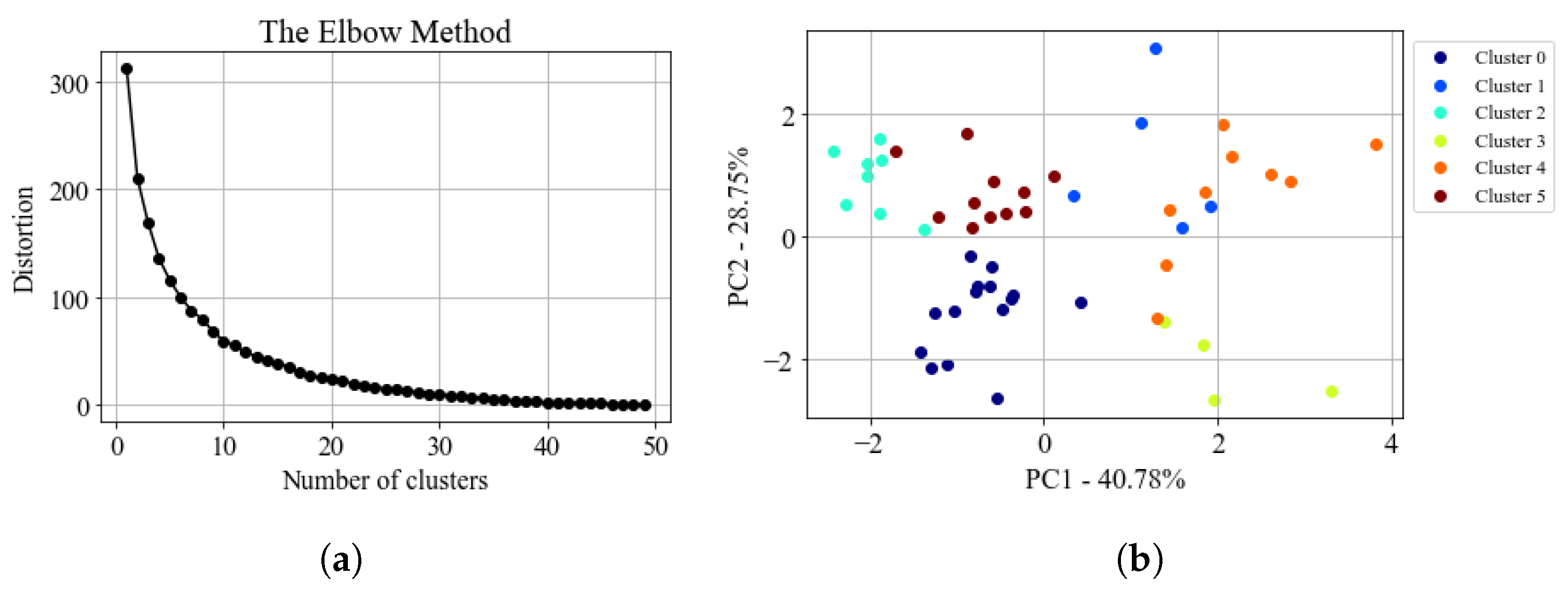
3.2. Data Processing
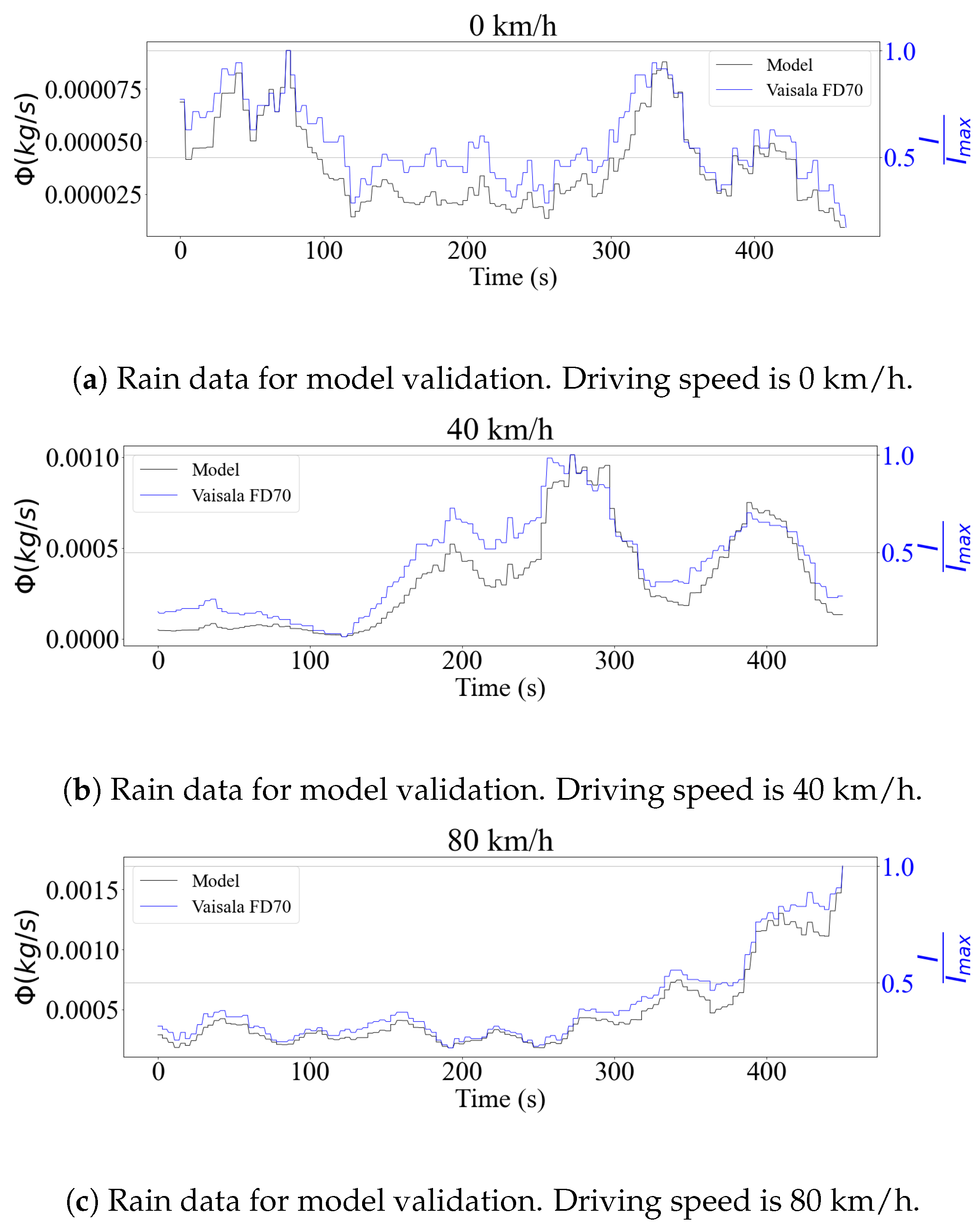
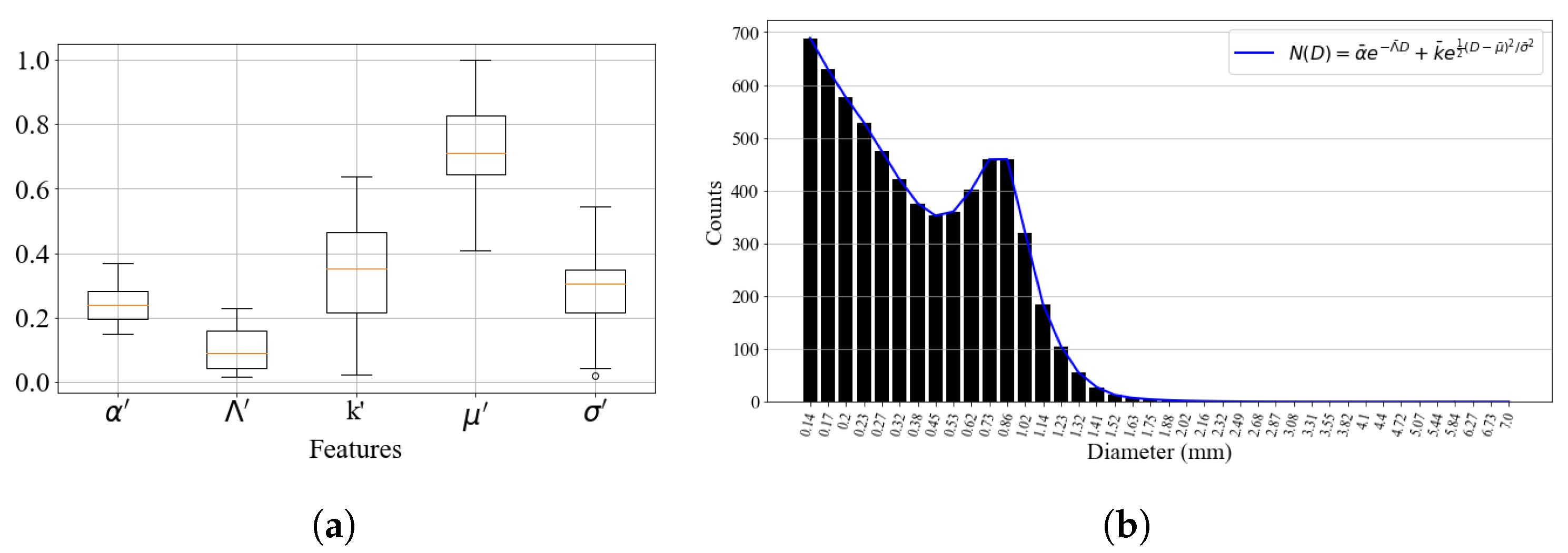
3.3. Validation Results
4. Evaluation of Perceived Precipitation
4.1. Simulation Parameters
4.2. Setting Realistic Parameters for Simulation
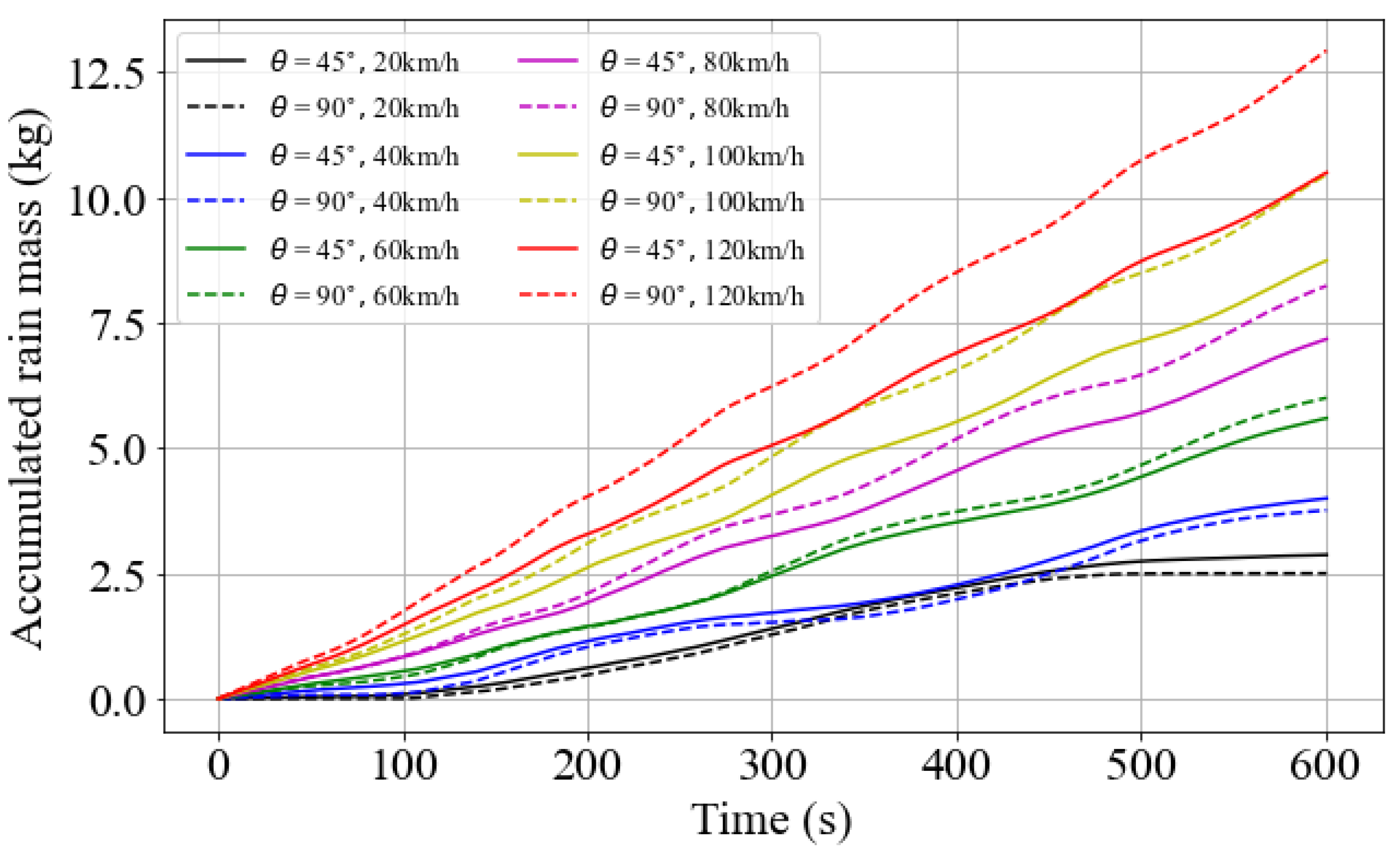
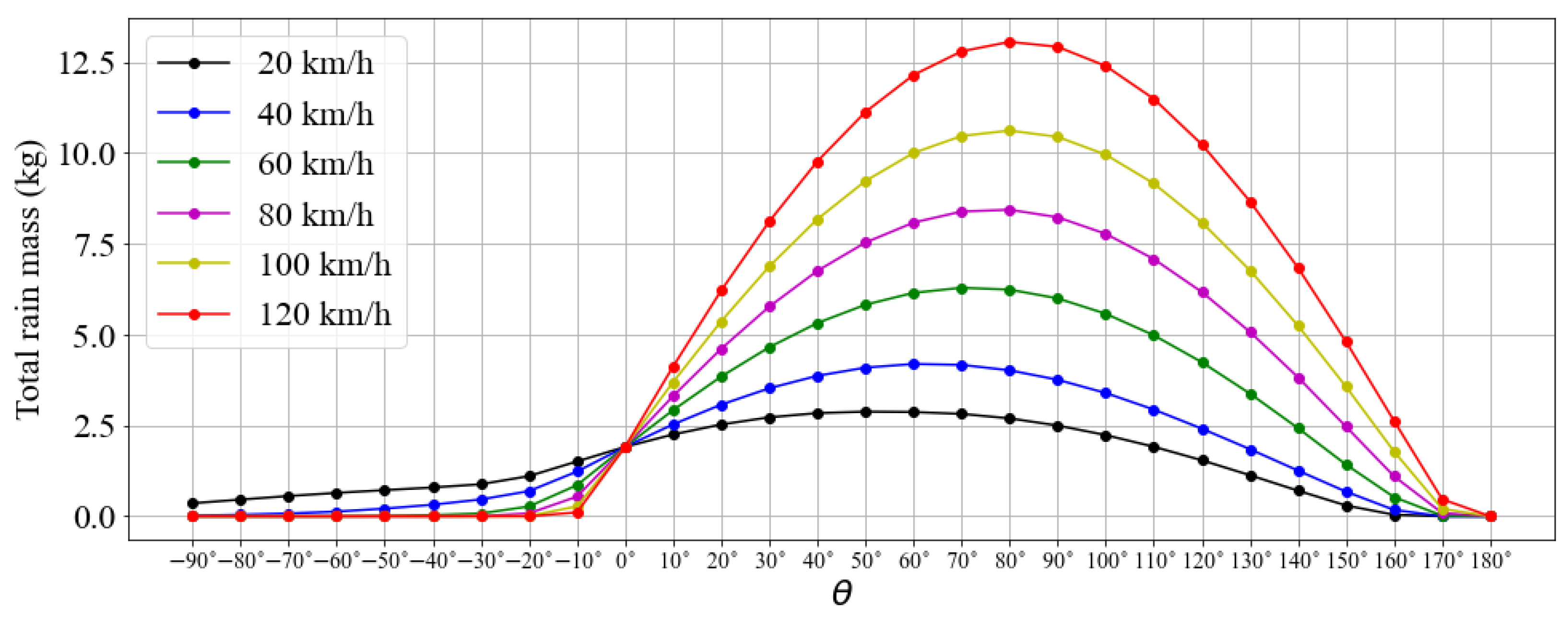
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Vargas, J.; Alsweiss, S.; Toker, O.; Razdan, R.; Santos, J. An Overview of Autonomous Vehicles Sensors and Their Vulnerability to Weather Conditions. Sensors 2021, 21, 5397. [Google Scholar] [CrossRef]
- Favarò, F.M.; Nader, N.; Eurich, S.O.; Tripp, M.; Varadaraju, N. Examining accident reports involving autonomous vehicles in California. PLoS ONE 2017, 12, e0184952. [Google Scholar] [CrossRef]
- Dixit, V.V.; Chand, S.; Nair, D.J. Autonomous Vehicles: Disengagements, Accidents and Reaction Times. PLoS ONE 2016, 11, e0168054. [Google Scholar] [CrossRef] [PubMed]
- Szénási, S.; Kertész, G.; Felde, I.; Nádai, L. Statistical accident analysis supporting the control of autonomous vehicles. J. Comput. Methods Sci. Eng. 2021, 21, 85–97. [Google Scholar] [CrossRef]
- Van Brummelen, J.; O’Brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Bertoldo, S.; Lucianaz, C.; Allegretti, M. 77 GHz automotive anti-collision radar used for meteorological purposes. In Proceedings of the 2017 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), Verona, Italy, 11–15 September 2017; pp. 49–52. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Hnewa, M.; Radha, H. Object Detection under Rainy Conditions for Autonomous Vehicles: A Review of State-of-the-Art and Emerging Techniques. IEEE Signal Process. Mag. 2021, 38, 53–67. [Google Scholar] [CrossRef]
- Dey, K.C.; Mishra, A.; Chowdhury, M. Potential of Intelligent Transportation Systems in Mitigating Adverse Weather Impacts on Road Mobility: A Review. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1107–1119. [Google Scholar] [CrossRef]
- Rabiei, E.; Haberlandt, U.; Sester, M.; Fitzner, D. Rainfall estimation using moving cars as rain gauges – laboratory experiments. Hydrol. Earth Syst. Sci. 2013, 17, 4701–4712. [Google Scholar] [CrossRef]
- Drobot, S.; Chapman, M.; Schuler, E.; Wiener, G.; Mahoney, W.; Pisano, P.; McKeever, B. Improving Road Weather Hazard Products with Vehicle Probe Data: Vehicle Data Translator Quality-Checking Procedures. Transp. Res. Rec. J. Transp. Res. Board 2010, 2169, 128–140. [Google Scholar] [CrossRef]
- Sziroczak, D.; Rohacs, D.; Rohacs, J. Review of using small UAV based meteorological measurements for road weather management. Prog. Aerosp. Sci. 2022, 134, 100859. [Google Scholar] [CrossRef]
- Neumann, P.P.; Bartholmai, M. Real-time wind estimation on a micro unmanned aerial vehicle using its inertial measurement unit. Sens. Actuators A Phys. 2015, 235, 300–310. [Google Scholar] [CrossRef]
- Palomaki, R.T.; Rose, N.T.; Bossche, M.v.d.; Sherman, T.J.; Wekker, S.F.J.D. Wind Estimation in the Lower Atmosphere Using Multirotor Aircraft. J. Atmos. Ocean. Technol. 2017, 34, 1183–1191. [Google Scholar] [CrossRef]
- Chilson, P.B.; Bell, T.M.; Brewster, K.A.; Britto Hupsel de Azevedo, G.; Carr, F.H.; Carson, K.; Doyle, W.; Fiebrich, C.A.; Greene, B.R.; Grimsley, J.L.; et al. Moving towards a Network of Autonomous UAS Atmospheric Profiling Stations for Observations in the Earth’s Lower Atmosphere: The 3D Mesonet Concept. Sensors 2019, 19, 2720. [Google Scholar] [CrossRef] [PubMed]
- Hangan, H.; Agelin-Chaab, M.; Gultepe, I.; Elfstrom, G.; Komar, J. Weather aerodynamic adaptation for autonomous vehicles: A tentative framework. Trans. Can. Soc. Mech. Eng. 2022, 47, 175–184. [Google Scholar] [CrossRef]
- Carvalho, M.; Hangan, H. Machine Learning Method for Road Vehicle Collected Data Analysis. J. Appl. Meteorol. Climatol. 2023, 62, 755–768. [Google Scholar] [CrossRef]
- Pao, W.Y.; Li, L.; Howorth, J.; Agelin-Chaab, M.; Roy, L.; Knutzen, J.; Baltazar y Jimenez, A.; Muenker, K. Wind Tunnel Testing Methodology for Autonomous Vehicle Optical Sensors in Adverse Weather Conditions. In Proceedings of the International Stuttgart Symposium, Stuttgart, Germany, 4–5 July 2023; Springer Fachmedien: Wiesbaden, Germany, 2023. [Google Scholar]
- Stern, S.A. An optimal speed for traversing a constant rain. Am. J. Phys. 1983, 51, 815–818. [Google Scholar] [CrossRef]
- Angelis, A.D. Is it really worth running in the rain? Eur. J. Phys. 1987, 8, 201–202. [Google Scholar] [CrossRef]
- Holden, J.J.; Belcher, S.E.; Horvath, A.; Pytharoulis, I. Raindrops keep falling on my head. Weather 1995, 50, 367–370. [Google Scholar] [CrossRef]
- Bailey, H. On Running in the Rain. Coll. Math. J. 2002, 33, 88–92. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T. Walking or running in the rain—A simple derivation of a general solution. Eur. J. Phys. 2011, 32, 355–361. [Google Scholar] [CrossRef]
- Bocci, F. Whether or not to run in the rain. Eur. J. Phys. 2012, 33, 1321–1332. [Google Scholar] [CrossRef]
- Davalos, D.; Chowdhury, J.; Hangan, H. Joint wind and ice hazard for transmission lines in mountainous terrain. J. Wind. Eng. Ind. Aerodyn. 2023, 232, 105276. [Google Scholar] [CrossRef]
- Makkonen, L. Estimation of wet snow accretion on structures. Cold Reg. Sci. Technol. 1989, 17, 83–88. [Google Scholar] [CrossRef]
- Makkonen, L. Modeling power line icing in freezing precipitation. Atmos. Res. 1998, 46, 131–142. [Google Scholar] [CrossRef]
- Mohammadian, B.; Namdari, N.; Abou Yassine, A.H.; Heil, J.; Rizvi, R.; Sojoudi, H. Interfacial phenomena in snow from its formation to accumulation and shedding. Adv. Colloid Interface Sci. 2021, 294, 102480. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.H. Dimensional Analysis and the Buckingham Pi Theorem. Am. J. Phys. 1972, 40, 1815–1822. [Google Scholar] [CrossRef]
- Curtis, W.D.; Logan, J.D.; Parker, W.A. Dimensional analysis and the pi theorem. Linear Algebra Its Appl. 1982, 47, 117–126. [Google Scholar] [CrossRef]
- Bakarji, J.; Callaham, J.; Brunton, S.L.; Kutz, J.N. Dimensionally consistent learning with Buckingham Pi. Nat. Comput. Sci. 2022, 2, 834–844. [Google Scholar] [CrossRef]
- Frasson, R.P.d.M.; da Cunha, L.K.; Krajewski, W.F. Assessment of the Thies optical disdrometer performance. Atmos. Res. 2011, 101, 237–255. [Google Scholar] [CrossRef]
- Acharya, R. Chapter 7—Tropospheric impairments: Measurements and mitigation. In Satellite Signal Propagation, Impairments and Mitigation; Acharya, R., Ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 195–245. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Cohen, I., Huang, Y., Chen, J., Benesty, J., Eds.; Springer Topics in Signal Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Kikuchi, K.; Kameda, T.; Higuchi, K.; Yamashita, A. A global classification of snow crystals, ice crystals, and solid precipitation based on observations from middle latitudes to polar regions. Atmos. Res. 2013, 132–133, 460–472. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Dadkhah, H.; Dabiri, H.; Bozzano, F.; Scarascia Mugnozza, G.; Mazzanti, P. Precipitation Time Series Analysis and Forecasting for Italian Regions. Eng. Proc. 2023, 39, 23. [Google Scholar] [CrossRef]
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Marshall, J.S. The distribution of raindrops with size. J. Meteor. 1948, 5, 165–166. [Google Scholar] [CrossRef]




| Model | Approach | Comments |
|---|---|---|
| Stern (1983) [19] | Drop strikes | The model assumes constant rainfall conditions Rainfall volume is not calculated |
| de Angelis (1987) [20] | Drop strikes | The model assumes constant rainfall conditions Rainfall volume is not calculated Misconception that it is always better to move fast in the rain |
| Holden et al. (1995) [21] | Rain flux | The simulations only consider vertical rain Experimental aspects are not considered |
| Bailey (2002) [22] | Rain flux | Introduces the concept of relative droplet velocity Different expression for upwind and downwind motion |
| Ehrmann and Blachowicz (2011) [23] | Rain flux | Simulations assume constant rainfall conditions Experimental aspects are not considered |
| Bocci (2012) [24] | Rain flux | It is based on equations from electromagnetism Simulations assume constant rainfall conditions Experimental aspects are not considered |
| Carvalho and Hangan (2023) | Rain flux | It is based on Bocci’s model Deals with the issue of particle flux Relies on experimental data for validation |
| Rain | Snow | ||||
|---|---|---|---|---|---|
| 0 km/h | 40 km/h | 80 km/h | 0 km/h | 30 km/h | 80 km/h |
| 0.95155 | 0.95422 | 0.99241 | 0.93424 | 0.91836 | 0.88894 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, M.; Hangan, H. Modelling Weather Precipitation Intensity on Surfaces in Motion with Application to Autonomous Vehicles. Sensors 2023, 23, 8034. https://doi.org/10.3390/s23198034
Carvalho M, Hangan H. Modelling Weather Precipitation Intensity on Surfaces in Motion with Application to Autonomous Vehicles. Sensors. 2023; 23(19):8034. https://doi.org/10.3390/s23198034
Chicago/Turabian StyleCarvalho, Mateus, and Horia Hangan. 2023. "Modelling Weather Precipitation Intensity on Surfaces in Motion with Application to Autonomous Vehicles" Sensors 23, no. 19: 8034. https://doi.org/10.3390/s23198034
APA StyleCarvalho, M., & Hangan, H. (2023). Modelling Weather Precipitation Intensity on Surfaces in Motion with Application to Autonomous Vehicles. Sensors, 23(19), 8034. https://doi.org/10.3390/s23198034






