Survey on Exact kNN Queries over High-Dimensional Data Space
Abstract
:1. Introduction
| Domains | Applications |
|---|---|
| Sensor Networks | intrusion detection systems [6,7], fault detection [8], fault identification [9], fault classification [10], fall prediction [11], indoor localisation [12,13], etc. |
| Robotics | arm movement recognition [14], human emotion classification [15,16], scan matching [17], object recognition [18], fast point cloud registration [19], etc. |
| Mining Industry | predict blast-induced ground vibration in open-pit coal mines [20], safety risk assessment and risk prediction in underground coal mines [21], classification of human activities [22], etc. |
| Recommendation Systems | recommending products, recommending media to users and showing targeted relevant advertisements to customers and many more [23,24,25] |
| Data Mining | pattern recognition [26,27,28,29], regression [30,31,32], outlier detection [33,34,35,36] |
| Machine Learning | text categorisation [37,38], question answering [39], text mining [40], face recognition [41,42], emotion recognition [43,44], image recognition [45,46], handwriting recognition [47,48] and credit card fraud detection [49] |
| Others | time series [50], economic forecasting and many more applications [51] |
- kNN queries in high-dimensional space are widely used and are becoming increasingly popular in various applications in recent years.
- In kNN Search, though many works have been proposed in the literature, there is no survey on exact kNN over high-dimensional data.
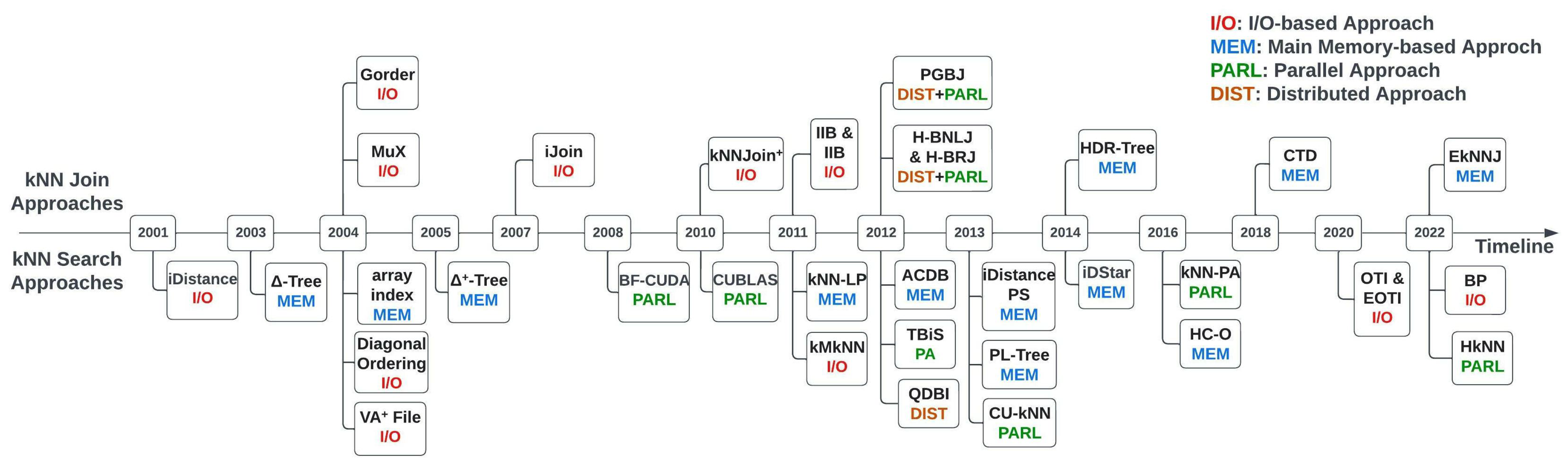
- We present a comprehensive overview of the kNN queries over high-dimensional data, which covers 20 kNN Search methods and 9 kNN Join methods. As per our knowledge, this is the first detailed study of the exact kNN approaches in high-dimensional data space.
- We systematically classify and compare existing strategies. For each approach, we explain in detail its method, basic features, as well as its strengths and weaknesses over other methods. As a result, we summed up the existing techniques.
- We discuss a number of open challenges as well as future research directions for resolving kNN query problems.
2. Background
2.1. Definitions
2.2. Related Work
3. Classification of kNN Queries
- Indexing Technique—index-based techniques speed up the kNN Search operation over HD datasets with an extra space cost of building certain data structures in advance. We discussed a few commonly used index structures such as R-trees, iDistance and so on in the below Indexing Technique section.
- Partitioning strategies—this partitions the whole dataset based on data-based and space-based partitioning. Using an appropriate partitioning strategy determines how well an approach will perform, which makes it an important computational parameter. The space-based approach does not require any knowledge of the actual dataset. It divides the entire data space into two or more partitions and is recursively applied to every newly generated region to further partition the space. On the other hand, a data-based approach adjusts the size and position of divisions based on the distribution of the data.
- Dimensionality reduction strategy—this is computationally intensive in terms of processing the HD dataset. Thus, various researchers used the DR strategy, which helps in reducing the dimensions in order to process them efficiently. It basically reduces the dimensionality by projecting the high-dimensional data to a low-dimensional space, which captures the majority of important information. Examples include PCA, iDistance, etc.
- Distance computation approach—when determining the kNN, the Distance Metric plays a very important role. So, to search for the k closest neighbour data points, we need to find the distance between the query point and all the other data points. Many computation approaches are available to find the similarity between points, but in our case, the majority of approaches use the Euclidean distance.
3.1. Indexing Technique
3.2. Partitioning Strategies
3.3. Dimensionality Reduction Strategy
3.4. Distance Computation Approach
3.5. Computing Paradigm
4. kNN Search
4.1. I/O Based
4.2. Main Memory
4.3. Parallel and Distributed
5. kNN Join Approaches
5.1. IO-Based
5.2. Memory-Based
5.3. Parallel and Distributed
6. Applications
6.1. Sensor Networks
6.2. Robotics
6.3. Mining Industry
6.4. Recommendation Systems
6.5. Data Mining
6.6. Machine Learning
7. Comparative Study
7.1. kNN Search Techniques
7.2. kNN Join Techniques
8. Conclusions
9. Challenges and Future Directions
- In the approaches that use a cluster-based partitioning strategy, finding the ideal number of clusters is always difficult because it mostly depends on the size of the dataset, the number of features and the distribution of the data points. So, we can take into account all these factors when designing an efficient approach. It will help to improve the performance.
- A clustering approach is used for partitioning, which provides indexes with better pruning power. So, considering the importance of effective search in high-dimensional space, research can be conducted on the quality of dataset clustering to distribute the data instances within clusters more reasonably.
- The structure of the relevant triangle has a big effect on how well a search method based on triangle inequality works. As a result, existing works use an efficient optimal triangle-inequality approach to select an optimal cluster centre from among all cluster centres that aid in the construction of a suitable triangle. In order to reduce space and time complexity further, the triangle’s composition can be optimised by creating a few promising reference points and using them to make optimum triangles.
- As per our survey, not a single parallel and distributed exact kNN Join approach for a high-dimensional dataset is available. Distributed parallel computing offers several problem-solving capabilities. Using it as a direction for research can improve the overall performance of kNN queries over high-dimensional data by a large amount. The approaches that are available support up to 20 dimensionalities only. So, there is room for further research in kNN Join over high-dimensional data based on parallel, distributed or hybrid Computing Paradigms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Andoni, A.; Indyk, P. Near-Optimal hashing algorithms for approximate nearest neighbour in high dimensions. Commun. ACM 2008, 51, 117–122. [Google Scholar] [CrossRef] [Green Version]
- Bawa, M.; Condie, T.; Ganesan, P. LSH forest: Self-tuning indexes for similarity search. In Proceedings of the 14th international conference on World Wide Web, Chiba, Japan, 10–14 May 2005; pp. 651–660. [Google Scholar]
- Lv, Q.; Josephson, W.; Wang, Z.; Charikar, M.; Li, K. Multi-probe LSH: Efficient indexing for high-dimensional similarity search. In Proceedings of the 33rd International Conference on Very Large Data Bases, Vienna, Austria, 23–27 September 2007; pp. 950–961. [Google Scholar]
- Jegou, H.; Douze, M.; Schmid, C. Product quantization for nearest neighbour search. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 117–128. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Pan, Z.; Li, R. A new cell-level search based non-exhaustive approximate nearest neighbour (ANN) search algorithm in the framework of product quantization. IEEE Access 2019, 7, 37059–37070. [Google Scholar] [CrossRef]
- Li, W.; Yi, P.; Wu, Y.; Pan, L.; Li, J. A new intrusion detection system based on kNN classification algorithm in wireless sensor network. J. Electr. Comput. Eng. 2014, 2014, 240217. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Zhao, H.; Fan, F.; Liu, G.; Xu, Q.; Nazir, S. An Enhanced Intrusion Detection Model Based on Improved kNN in WSNs. Sensors 2022, 22, 1407. [Google Scholar] [CrossRef]
- Yang, J.; Sun, Z.; Chen, Y. Fault detection using the clustering-kNN rule for gas sensor arrays. Sensors 2016, 16, 2069. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, G.Z.; Li, J.; Hu, Y.T.; Li, Y.; Du, Z.Y. Fault identification of chemical processes based on k NN variable contribution and CNN data reconstruction methods. Sensors 2019, 19, 929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, C.; Tham, C.K. Graphel: A graph-based ensemble learning method for distributed diagnostics and prognostics in the industrial internet of things. In Proceedings of the 2018 IEEE 24th International Conference on Parallel and Distributed Systems (ICPADS), Sentosa, Singapore, 11–13 December 2018; pp. 903–909. [Google Scholar]
- Liang, S.; Ning, Y.; Li, H.; Wang, L.; Mei, Z.; Ma, Y.; Zhao, G. Feature selection and predictors of falls with foot force sensors using kNN-based algorithms. Sensors 2015, 15, 29393–29407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dziubany, M.; Machhamer, R.; Laux, H.; Schmeink, A.; Gollmer, K.U.; Burger, G.; Dartmann, G. Machine learning based indoor localization using a representative k nearest-neighbour classifier on a low-cost IoT-hardware. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 2050–2054. [Google Scholar]
- Ferreira, D.; Souza, R.; Carvalho, C. Qa-knn: Indoor localization based on quartile analysis and the knn classifier for wireless networks. Sensors 2020, 20, 4714. [Google Scholar] [CrossRef]
- Al-Faiz, M.Z.; Ali, A.A.; Miry, A.H. A k nearest neighbour based algorithm for human arm movements recognition using EMG signals. In Proceedings of the 2010 1st International Conference on Energy, Power and Control (EPC-IQ), Basrah, Iraq, 30 November–2 December 2010; pp. 159–167. [Google Scholar]
- Shen, B.; Zhao, Y.; Li, G.; Zheng, W.; Qin, Y.; Yuan, B.; Rao, Y. V-tree: Efficient kNN Search on moving objects with road-network constraints. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017; pp. 609–620. [Google Scholar]
- Fiorini, L.; Mancioppi, G.; Semeraro, F.; Fujita, H.; Cavallo, F. Unsupervised emotional state classification through physiological parameters for social robotics applications. Knowl.-Based Syst. 2020, 190, 105217. [Google Scholar] [CrossRef]
- Markom, M.; Adom, A.; Shukor, S.A.; Rahim, N.A.; Tan, E.M.M.; Ilias, B. Improved kNN Scan Matching for Local Map Classification in Mobile Robot Localisation Application. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bogor, Indonesia, 2019; Volume 557, p. 012019. [Google Scholar]
- Pinto, A.M.; Rocha, L.F.; Moreira, A.P. Object recognition using laser range finder and machine learning techniques. Robot. Comput.-Integr. Manuf. 2013, 29, 12–22. [Google Scholar] [CrossRef]
- Xu, G.; Pang, Y.; Bai, Z.; Wang, Y.; Lu, Z. A fast point clouds registration algorithm for laser scanners. Appl. Sci. 2021, 11, 3426. [Google Scholar] [CrossRef]
- Zheng, B.; Zheng, K.; Xiao, X.; Su, H.; Yin, H.; Zhou, X.; Li, G. Keyword-aware continuous knn query on road networks. In Proceedings of the 2016 IEEE 32Nd international conference on data engineering (ICDE), Helsinki, Finland, 16–20 May 2016; pp. 871–882. [Google Scholar]
- Tripathy, D.; Parida, S.; Khandu, L. Safety risk assessment and risk prediction in underground coal mines using machine learning techniques. J. Inst. Eng. (India) Ser. D 2021, 102, 495–504. [Google Scholar] [CrossRef]
- Mohsen, S.; Elkaseer, A.; Scholz, S.G. Human activity recognition using K-nearest neighbour machine learning algorithm. In Proceedings of the International Conference on Sustainable Design and Manufacturing, Split, Croatia, 15–17 September 2021; pp. 304–313. [Google Scholar]
- Patro, S.G.K.; Mishra, B.K.; Panda, S.K.; Kumar, R.; Long, H.V.; Taniar, D.; Priyadarshini, I. A hybrid action-related K-nearest neighbour (HAR-kNN) approach for recommendation systems. IEEE Access 2020, 8, 90978–90991. [Google Scholar] [CrossRef]
- Subramaniyaswamy, V.; Logesh, R. Adaptive kNN based recommender system through mining of user preferences. Wirel. Pers. Commun. 2017, 97, 2229–2247. [Google Scholar] [CrossRef]
- Li, G.; Zhang, J. Music personalized recommendation system based on improved kNN algorithm. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018; pp. 777–781. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbour pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef] [Green Version]
- Pan, Z.; Wang, Y.; Ku, W. A new k harmonic nearest neighbour classifier based on the multi-local means. Expert Syst. Appl. 2017, 67, 115–125. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, Y.; Ku, W. A new general nearest neighbour classification based on the mutual neighbourhood information. Knowl.-Based Syst. 2017, 121, 142–152. [Google Scholar] [CrossRef]
- De Figueiredo, J.; Oliveira, F.; Esmi, E.; Freitas, L.; Schleicher, J.; Novais, A.; Sussner, P.; Green, S. Automatic detection and imaging of diffraction points using pattern recognition. Geophys. Prospect. 2013, 61, 368–379. [Google Scholar] [CrossRef]
- Nguyen, B.; Morell, C.; De Baets, B. Large-scale Distance Metric learning for k nearest neighbours regression. Neurocomputing 2016, 214, 805–814. [Google Scholar] [CrossRef]
- Song, Y.; Liang, J.; Lu, J.; Zhao, X. An efficient instance selection algorithm for k nearest neighbour regression. Neurocomputing 2017, 251, 26–34. [Google Scholar] [CrossRef]
- Stone, C.J. Consistent nonparametric regression. Ann. Stat. 1977, 5, 595–620. [Google Scholar] [CrossRef]
- Angiulli, F.; Basta, S.; Pizzuti, C. Distance-based detection and prediction of outliers. IEEE Trans. Knowl. Data Eng. 2005, 18, 145–160. [Google Scholar] [CrossRef]
- Ghoting, A.; Parthasarathy, S.; Otey, M.E. Fast mining of distance-based outliers in high-dimensional datasets. Data Min. Knowl. Discov. 2008, 16, 349–364. [Google Scholar] [CrossRef] [Green Version]
- Ning, J.; Chen, L.; Zhou, C.; Wen, Y. Parameter k search strategy in outlier detection. Pattern Recognit. Lett. 2018, 112, 56–62. [Google Scholar] [CrossRef]
- Ramaswamy, S.; Rastogi, R.; Shim, K. Efficient algorithms for mining outliers from large datasets. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 427–438. [Google Scholar]
- Li, B.; Yu, S.; Lu, Q. An improved k nearest neighbour algorithm for text categorization. arXiv 2003, arXiv:cs/0306099. [Google Scholar]
- Jiang, S.; Pang, G.; Wu, M.; Kuang, L. An improved K-nearest-neighbour algorithm for text categorization. Expert Syst. Appl. 2012, 39, 1503–1509. [Google Scholar] [CrossRef]
- Soares, J.N.; Cavalcante, H.G.; Maia, J.E. A Question Classification in Closed Domain Question-Answer Systems. Int. J. Appl. Inf. Syst. 2021, 12, 1–5. [Google Scholar]
- Bijalwan, V.; Kumar, V.; Kumari, P.; Pascual, J. kNN based machine learning approach for text and document mining. Int. J. Database Theory Appl. 2014, 7, 61–70. [Google Scholar] [CrossRef]
- Zhao, J.; Han, J.; Shao, L. Unconstrained face recognition using a set-to-set distance measure on deep learned features. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2679–2689. [Google Scholar] [CrossRef] [Green Version]
- Tofighi, A.; Khairdoost, N.; Monadjemi, S.A.; Jamshidi, K. A robust face recognition system in image and video. Int. J. Image, Graph. Signal Process. 2014, 6, 1. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Yin, Z.; Chen, P.; Nichele, S. Emotion recognition using multi-modal data and machine learning techniques: A tutorial and review. Inf. Fusion 2020, 59, 103–126. [Google Scholar] [CrossRef]
- Murugappan, M. Human emotion classification using wavelet transform and kNN. In Proceedings of the 2011 International Conference on Pattern Analysis and Intelligence Robotics, Kuala Lumpur, Malaysia, 28–29 June 2011; Volume 1, pp. 148–153. [Google Scholar]
- Guru, D.; Sharath, Y.; Manjunath, S. Texture features and kNN in classification of flower images. IJCA Spec. Issue RTIPPR (1) 2010, 21–29. [Google Scholar]
- Zawbaa, H.M.; Abbass, M.; Hazman, M.; Hassenian, A.E. Automatic fruit image recognition system based on shape and color features. In Proceedings of the International Conference on Advanced Machine Learning Technologies and Applications, Cairo, Egypt, 28–30 November 2014; pp. 278–290. [Google Scholar]
- Zanchettin, C.; Bezerra, B.L.D.; Azevedo, W.W. A kNN-SVM hybrid model for cursive handwriting recognition. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Hamid, N.A.; Sjarif, N.N.A. Handwritten recognition using SVM, kNN and neural network. arXiv 2017, arXiv:1702.00723. [Google Scholar]
- Akila, S.; Reddy, U.S. Cost-sensitive Risk Induced Bayesian Inference Bagging (RIBIB) for credit card fraud detection. J. Comput. Sci. 2018, 27, 247–254. [Google Scholar] [CrossRef]
- Lytridis, C.; Lekova, A.; Bazinas, C.; Manios, M.; Kaburlasos, V.G. WINkNN: Windowed intervals’ number kNN classifier for efficient time-series applications. Mathematics 2020, 8, 413. [Google Scholar] [CrossRef] [Green Version]
- Imandoust, S.B.; Bolandraftar, M. Application of k nearest neighbour (knn) approach for predicting economic events: Theoretical background. Int. J. Eng. Res. Appl. 2013, 3, 605–610. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming; Addison-Wesley: Reading, MA, USA, 1973; Volume 3. [Google Scholar]
- Böhm, C.; Krebs, F. Supporting KDD applications by the k nearest neighbour join. In Proceedings of the International Conference on Database and Expert Systems Applications, Prague, Czech Republic, 1–5 September 2003; pp. 504–516. [Google Scholar]
- Böhm, C.; Krebs, F. The k nearest neighbour join: Turbo charging the kdd process. Knowl. Inf. Syst. 2004, 6, 728–749. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k means clustering algorithm. J. R. Stat. Society. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar]
- Lu, W.; Shen, Y.; Chen, S.; Ooi, B.C. Efficient processing of k nearest neighbour joins using mapreduce. arXiv 2012, arXiv:1207.0141. [Google Scholar]
- Dasarathy, B.V. Nearest neighbour (NN) norms: NN pattern classification techniques. IEEE Comput. Soc. Tutor. 1991, 17, 441–458. [Google Scholar]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Wang, R. Efficient kNN classification with different numbers of nearest neighbours. IEEE Trans. Neural Networks Learn. Syst. 2017, 29, 1774–1785. [Google Scholar] [CrossRef]
- Guttman, A. R-trees: A dynamic index structure for spatial searching. In Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984; pp. 47–57. [Google Scholar]
- Beckmann, N.; Kriegel, H.P.; Schneider, R.; Seeger, B. The R*-tree: An efficient and robust access method for points and rectangles. In Proceedings of the 1990 ACM SIGMOD International Conference on Management of Data, Atlantic City, NJ, USA, 23–26 May 1990; pp. 322–331. [Google Scholar]
- Kamel, I.; Faloutsos, C. Hilbert R-tree: An Improved R-Tree Using Fractals. In Proceedings of the VLDB’94: Proceedings of the 20th International Conference on Very Large Data Bases, San Francisco, CA, USA, 12–15 September 1993. [Google Scholar]
- Arge, L.; Berg, M.d.; Haverkort, H.; Yi, K. The priority R-tree: A practically efficient and worst-case optimal R-tree. ACM Trans. Algorithms (TALG) 2008, 4, 1–30. [Google Scholar] [CrossRef]
- Sproull, R.F. Refinements to nearest-neighbour searching ink-dimensional trees. Algorithmica 1991, 6, 579–589. [Google Scholar] [CrossRef]
- Fukunaga, K.; Narendra, P.M. A branch and bound algorithm for computing k nearest neighbours. IEEE Trans. Comput. 1975, 100, 750–753. [Google Scholar] [CrossRef]
- Yianilos, P.N. Data structures and algorithms for nearest neighbour. In Proceedings of the fourth annual ACM-SIAM Symposium on Discrete algorithms, Austin, TX, USA, 25–27 January 1993; Volume 66, pp. 311–321. [Google Scholar]
- Bozkaya, T.; Ozsoyoglu, M. Distance-based indexing for high-dimensional metric spaces. In Proceedings of the 1997 ACM SIGMOD International Conference on Management of Data, Tucson, AR, USA, 11–15 May 1997; pp. 357–368. [Google Scholar]
- Li, Y.; Guo, L. An active learning based TCM-kNN algorithm for supervised network intrusion detection. Comput. Secur. 2007, 26, 459–467. [Google Scholar] [CrossRef]
- Shapoorifard, H.; Shamsinejad, P. Intrusion detection using a novel hybrid method incorporating an improved kNN. Int. J. Comput. Appl 2017, 173, 5–9. [Google Scholar] [CrossRef]
- Weber, R.; Schek, H.J.; Blott, S. A quantitative analysis and performance study for similarity-search methods in high-dimensional spaces. Proc. VLDB 1998, 98, 194–205. [Google Scholar]
- Beyer, K.; Goldstein, J.; Ramakrishnan, R.; Shaft, U. When is “nearest neighbour” meaningful? In Proceedings of the International Conference on Database Theory, Jerusalem, Israel, 10–12 January 1999; pp. 217–235. [Google Scholar]
- Kouiroukidis, N.; Evangelidis, G. The effects of dimensionality curse in high dimensional kNN Search. In Proceedings of the 2011 15th Panhellenic Conference on Informatics, Kastoria, Greece, 30 September–2 October 2011; pp. 41–45. [Google Scholar]
- Cui, B.; Ooi, B.C.; Su, J.; Tan, K.L. Contorting high dimensional data for efficient main memory kNN processing. In Proceedings of the 2003 ACM SIGMOD International Conference on Management of Data, San Diego, CA, USA, 9–12 June 2003; pp. 479–490. [Google Scholar]
- Garcia, V.; Debreuve, E.; Nielsen, F.; Barlaud, M. K-nearest neighbour search: Fast GPU-based implementations and application to high-dimensional feature matching. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 3757–3760. [Google Scholar]
- Yu, C.; Zhang, R.; Huang, Y.; Xiong, H. High-dimensional kNN Joins with incremental updates. Geoinformatica 2010, 14, 55–82. [Google Scholar] [CrossRef]
- Garcia, V.; Debreuve, E.; Barlaud, M. Fast k nearest neighbour search using GPU. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, AK, USA, 23–28 June 2008; pp. 1–6. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Chakrabarti, K.; Mehrotra, S. Local dimensionality reduction: A new approach to indexing high dimensional spaces. In Proceedings of the VLDB Conference, Cairo, Egypt, 10–14 September 2000. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Vidal, R.; Ma, Y.; Sastry, S.S. Principal component analysis. In Generalized Principal Component Analysis; Springer: New York, NY, USA, 2016; pp. 25–62. [Google Scholar]
- Ciaccia, P.; Patella, M.; Zezula, P. M-tree: An efficient access method for similarity search in metric spaces. Proc. Vldb 1997, 97, 426–435. [Google Scholar]
- Yang, C.; Yu, X.; Liu, Y. Continuous kNN Join processing for real-time recommendation. In Proceedings of the 2014 IEEE International Conference on Data Mining, Shenzhen, China, 14–17 December 2014; pp. 640–649. [Google Scholar]
- Kibriya, A.M.; Frank, E. An empirical comparison of exact nearest neighbour algorithms. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery, Berlin, Heidelberg, 17–21 September 2007; pp. 140–151. [Google Scholar]
- Bhatia, N. Survey of nearest neighbour techniques. arXiv 2010, arXiv:1007.0085. [Google Scholar]
- Abbasifard, M.R.; Ghahremani, B.; Naderi, H. A survey on nearest neighbour search methods. Int. J. Comput. Appl. 2014, 95, 39–52. [Google Scholar]
- Liu, T.; Moore, A.; Yang, K.; Gray, A. An investigation of practical approximate nearest neighbour algorithms. Adv. Neural Inf. Process. Syst. 2004, 17, 825–832. [Google Scholar]
- Li, W.; Zhang, Y.; Sun, Y.; Wang, W.; Li, M.; Zhang, W.; Lin, X. Approximate nearest neighbour search on high dimensional data—experiments, analyses and improvement. IEEE Trans. Knowl. Data Eng. 2019, 32, 1475–1488. [Google Scholar] [CrossRef]
- Song, G.; Rochas, J.; Huet, F.; Magoules, F. Solutions for processing k nearest neighbour joins for massive data on mapreduce. In Proceedings of the 2015 23rd Euromicro International Conference on Parallel, Distributed and Network-Based Processing, Turku, Finland, 4–6 March 2015; pp. 279–287. [Google Scholar]
- Song, G.; Rochas, J.; El Beze, L.; Huet, F.; Magoules, F. K nearest neighbour joins for big data on mapreduce: A theoretical and experimental analysis. IEEE Trans. Knowl. Data Eng. 2016, 28, 2376–2392. [Google Scholar] [CrossRef] [Green Version]
- Adomavicius, G.; Tuzhilin, A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE Trans. Knowl. Data Eng. 2005, 17, 734–749. [Google Scholar] [CrossRef]
- Boiman, O.; Shechtman, E.; Irani, M. In defense of nearest-neighbour based image classification. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Malkov, Y.; Ponomarenko, A.; Logvinov, A.; Krylov, V. Approximate nearest neighbour algorithm based on navigable small world graphs. Inf. Syst. 2014, 45, 61–68. [Google Scholar] [CrossRef]
- Iwasaki, M. Pruned bi-directed k nearest neighbour graph for proximity search. In Proceedings of the International Conference on Similarity Search and Applications, Tokyo, Japan, 24–26 October 2016; pp. 20–33. [Google Scholar]
- Malkov, Y.A.; Yashunin, D.A. Efficient and robust approximate nearest neighbour search using hierarchical navigable small world graphs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 824–836. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hajebi, K.; Abbasi-Yadkori, Y.; Shahbazi, H.; Zhang, H. Fast approximate nearest-neighbour search with k nearest neighbour graph. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 1312–1317. [Google Scholar]
- Zhang, Y.M.; Huang, K.; Geng, G.; Liu, C.L. Fast kNN graph construction with locality sensitive hashing. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Prague, Czech Republic, 23–27 September 2013; pp. 660–674. [Google Scholar]
- Zhao, W.L.; Yang, J.; Deng, C.H. Scalable nearest neighbour search based on kNN graph. arXiv 2017, arXiv:1701.08475. [Google Scholar]
- Yang, J.; Zhao, W.L.; Deng, C.H.; Wang, H.; Moon, S. Fast nearest neighbour search based on approximate k NN graph. In Proceedings of the International Conference on Internet Multimedia Computing and Service, Qingdao, China, 23–25 August 2017; pp. 327–338. [Google Scholar]
- Alshammari, M.; Stavrakakis, J.; Takatsuka, M. Refining a k nearest neighbour graph for a computationally efficient spectral clustering. Pattern Recognit. 2021, 114, 107869. [Google Scholar]
- Fu, C.; Xiang, C.; Wang, C.; Cai, D. Fast approximate nearest neighbour search with the navigating spreading-out graph. arXiv 2017, arXiv:1707.00143. [Google Scholar]
- Fu, C.; Cai, D. Efanna: An extremely fast approximate nearest neighbour search algorithm based on knn graph. arXiv 2016, arXiv:1609.07228. [Google Scholar]
- Harwood, B.; Drummond, T. Fanng: Fast approximate nearest neighbour graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5713–5722. [Google Scholar]
- Munoz, J.V.; Gonçalves, M.A.; Dias, Z.; Torres, R.d.S. Hierarchical clustering-based graphs for large scale approximate nearest neighbour search. Pattern Recognit. 2019, 96, 106970. [Google Scholar] [CrossRef]
- Fu, C.; Wang, C.; Cai, D. High dimensional similarity search with satellite system graph: Efficiency, scalability and unindexed query compatibility. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4139–4150. [Google Scholar] [CrossRef]
- Aumüller, M.; Bernhardsson, E.; Faithfull, A. ANN-Benchmarks: A benchmarking tool for approximate nearest neighbour algorithms. Inf. Syst. 2020, 87, 101374. [Google Scholar] [CrossRef]
- Shimomura, L.C.; Oyamada, R.S.; Vieira, M.R.; Kaster, D.S. A survey on graph-based methods for similarity searches in metric spaces. Inf. Syst. 2021, 95, 101507. [Google Scholar] [CrossRef]
- Wang, M.; Xu, X.; Yue, Q.; Wang, Y. A comprehensive survey and experimental comparison of graph-based approximate nearest neighbour search. arXiv 2021, arXiv:2101.12631. [Google Scholar]
- Ferhatosmanoglu, H.; Tuncel, E.; Agrawal, D.; El Abbadi, A. High dimensional nearest neighbour searching. Inf. Syst. 2006, 31, 512–540. [Google Scholar] [CrossRef]
- Yu, C.; Ooi, B.C.; Tan, K.L.; Jagadish, H. Indexing the distance: An efficient method to knn processing. Proc. Vldb 2001, 1, 421–430. [Google Scholar]
- Jagadish, H.V.; Ooi, B.C.; Tan, K.L.; Yu, C.; Zhang, R. iDistance: An adaptive B+-tree based indexing method for nearest neighbour search. ACM Trans. Database Syst. (TODS) 2005, 30, 364–397. [Google Scholar] [CrossRef]
- Hu, J.; Cui, B.; Shen, H. Diagonal ordering: A new approach to high-dimensional kNN processing. In Proceedings of the 15th Australasian database conference, Dunedin, New Zealand, 18–22 January 2004; Volume 27, pp. 39–47. [Google Scholar]
- Pan, Y.; Pan, Z.; Wang, Y.; Wang, W. A new fast search algorithm for exact k nearest neighbours based on optimal triangle-inequality-based check strategy. Knowl.-Based Syst. 2020, 189, 105088. [Google Scholar] [CrossRef]
- Song, Y.; Gu, Y.; Zhang, R.; Yu, G. Brepartition: Optimized high-dimensional kNN Search with bregman distances. IEEE Trans. Knowl. Data Eng. 2020, 34, 1053–1065. [Google Scholar] [CrossRef]
- Wang, J.; Lu, J.; Fang, Z.; Ge, T.; Chen, C. PL-Tree: An efficient indexing method for high-dimensional data. In Proceedings of the International Symposium on Spatial and Temporal Databases, Munich, Germany, 21–23 August 2013; pp. 183–200. [Google Scholar]
- Tang, B.; Yiu, M.L.; Hua, K.A. Exploit every bit: Effective caching for high-dimensional nearest neighbour search. IEEE Trans. Knowl. Data Eng. 2016, 28, 1175–1188. [Google Scholar] [CrossRef]
- Al Aghbari, Z.; Makinouchi, A. Linearization approach for efficient kNN Search of high-dimensional data. In Proceedings of the International Conference on Web-Age Information Management, Dalian, China, 15–17 July 2004; pp. 229–238. [Google Scholar]
- Cui, B.; Coi, B.C.; Su, J.; Tan, K.L. Indexing high-dimensional data for efficient in-memory similarity search. IEEE Trans. Knowl. Data Eng. 2005, 17, 339–353. [Google Scholar]
- Hong, H.; Juan, G.; Ben, W. An improved kNN algorithm based on adaptive cluster distance bounding for high dimensional indexing. In Proceedings of the 2012 Third Global Congress on Intelligent Systems, Wuhan, China, 6–8 November 2012; pp. 213–217. [Google Scholar]
- Schuh, M.A.; Wylie, T.; Banda, J.M.; Angryk, R.A. A comprehensive study of idistance partitioning strategies for knn queries and high-dimensional data indexing. In Proceedings of the British National Conference on Databases, Oxford, UK, 8–10 July 2013; pp. 238–252. [Google Scholar]
- Jian, L.; Wang, C.; Liu, Y.; Liang, S.; Yi, W.; Shi, Y. Parallel data mining techniques on graphics processing unit with compute unified device architecture (CUDA). J. Supercomput. 2013, 64, 942–967. [Google Scholar] [CrossRef]
- Sismanis, N.; Pitsianis, N.; Sun, X. Parallel search of k nearest neighbours with synchronous operations. In Proceedings of the 2012 IEEE Conference on High Performance Extreme Computing, Waltham, MA USA, 10–12 September 2012; pp. 1–6. [Google Scholar]
- Xiao, B.; Biros, G. Parallel algorithms for nearest neighbour search problems in high dimensions. SIAM J. Sci. Comput. 2016, 38, S667–S699. [Google Scholar] [CrossRef]
- Muhr, D.; Affenzeller, M. Hybrid (CPU/GPU) Exact Nearest Neighbours Search in High-Dimensional Spaces. In Proceedings of the IFIP International Conference on Artificial Intelligence Applications and Innovations, Crete, Greece, 17–20 June 2022; pp. 112–123. [Google Scholar]
- Qiao, B.; Ding, L.; Wei, Y.; Wang, X. A kNN Query Processing Algorithm over High-Dimensional Data Objects in P2P Systems. In Proceedings of the 2011 2nd International Congress on Computer Applications and Computational Science, Bali, Indonesia, 15–17 November 2012; 144, pp. 133–139. [Google Scholar]
- Xia, C.; Lu, H.; Ooi, B.C.; Hu, J. Gorder: An efficient method for kNN Join processing. In Proceedings of the Thirtieth International Conference on Very Large Data Bases, Toronto, Canada, 31 August–3 September 2004; Volume 30, pp. 756–767. [Google Scholar]
- Wang, J.; Lin, L.; Huang, T.; Wang, J.; He, Z. Efficient k nearest neighbour join algorithms for high dimensional sparse data. arXiv 2010, arXiv:1011.2807. [Google Scholar]
- Yu, C.; Cui, B.; Wang, S.; Su, J. Efficient index-based kNN Join processing for high-dimensional data. Inf. Softw. Technol. 2007, 49, 332–344. [Google Scholar] [CrossRef]
- Ukey, N.; Yang, Z.; Zhang, G.; Liu, B.; Li, B.; Zhang, W. Efficient kNN Join over Dynamic High-Dimensional Data. In Proceedings of the Australasian Database Conference, Sydney, NSW, Australia, 2–4 September 2022; pp. 63–75. [Google Scholar]
- Zhang, C.; Li, F.; Jestes, J. Efficient parallel kNN Joins for large data in MapReduce. In Proceedings of the 15th International Conference on Extending Database Technology, Berlin, Germany, 27–30 March 2012; pp. 38–49. [Google Scholar]
- Garcia, V.; Nielsen, F. Searching high-dimensional neighbours: Cpu-based tailored data-structures versus gpu-based brute-force method. In Proceedings of the International Conference on Computer Vision/Computer Graphics Collaboration Techniques and Applications, Rocquencourt, France, 4–6 May 2009; pp. 425–436. [Google Scholar]
- Bayer, R.; McCreight, E. Organization and maintenance of large ordered indexes. In Software Pioneers; Springer: Berlin/Heidelberg, Germany, 2002; pp. 245–262. [Google Scholar]
- Berchtold, S.; Böhm, C.; Kriegal, H.P. The pyramid-technique: Towards breaking the curse of dimensionality. In Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data, Washington, DC, USA, 1–4 June 1998; pp. 142–153. [Google Scholar]
- Al Aghbari, Z. Array-index: A plug&search K nearest neighbours method for high-dimensional data. Data Knowl. Eng. 2005, 52, 333–352. [Google Scholar]
- Cayton, L. Fast nearest neighbour retrieval for bregman divergences. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 112–119. [Google Scholar]
- Berchtold, S.; Keim, D.A.; Kriegel, H.P. The X-tree: An index structure for high-dimensional data. In Proceedings of the Very Large Data-Bases, Mumbai, India, 3–6 September 1996; pp. 28–39. [Google Scholar]
- Lin, K.I.; Jagadish, H.V.; Faloutsos, C. The TV-tree: An index structure for high-dimensional data. VLDB J. 1994, 3, 517–542. [Google Scholar] [CrossRef] [Green Version]
- Sellis, T.; Roussopoulos, N.; Faloutsos, C. The R+-Tree: A Dynamic Index for Multi-Dimensional Objects. In Proceedings of the 13th International Conference on Very Large Data Bases, San Francisco, CA, USA, 1–4 September 1987; pp. 507–518. [Google Scholar]
- Samet, H. The quadtree and related hierarchical data structures. ACM Comput. Surv. (CSUR) 1984, 16, 187–260. [Google Scholar] [CrossRef] [Green Version]
- Eldawy, A.; Mokbel, M.F. Spatialhadoop: A mapreduce framework for spatial data. In Proceedings of the 2015 IEEE 31st International Conference on Data Engineering, Seoul, Republic of Korea, 13–17 April 2015; pp. 1352–1363. [Google Scholar]
- Jolliffe, I.T. Principal component analysis: A beginner’s guide—I. Introduction and application. Weather 1990, 45, 375–382. [Google Scholar] [CrossRef]
- Jin, H.; Ooi, B.C.; Shen, H.T.; Yu, C.; Zhou, A.Y. An adaptive and efficient dimensionality reduction algorithm for high-dimensional indexing. In Proceedings of the Proceedings 19th International Conference on Data Engineering (Cat. No. 03CH37405), Bangalore, India, 5–8 March 2003; pp. 87–98. [Google Scholar]
- Mu, Y.; Yan, S. Non-metric locality-sensitive hashing. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; Volume 24, pp. 539–544. [Google Scholar]
- Zhang, Z.; Ooi, B.C.; Parthasarathy, S.; Tung, A.K. Similarity search on bregman divergence: Towards non-metric indexing. Proc. VLDB Endow. 2009, 2, 13–24. [Google Scholar] [CrossRef] [Green Version]
- Puzicha, J.; Buhmann, J.M.; Rubner, Y.; Tomasi, C. Empirical evaluation of dissimilarity measures for color and texture. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1165–1172. [Google Scholar]
- Perronnin, F.; Liu, Y.; Renders, J.M. A family of contextual measures of similarity between distributions with application to image retrieval. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2358–2365. [Google Scholar]
- Rasiwasia, N.; Moreno, P.J.; Vasconcelos, N. Bridging the gap: Query by semantic example. IEEE Trans. Multimed. 2007, 9, 923–938. [Google Scholar] [CrossRef] [Green Version]
- Gray, R.; Buzo, A.; Gray, A.; Matsuyama, Y. Distortion measures for speech processing. IEEE Trans. Acoust. Speech, Signal Process. 1980, 28, 367–376. [Google Scholar] [CrossRef]
- Vial, P.H.; Magron, P.; Oberlin, T.; Févotte, C. Phase retrieval with Bregman divergences and application to audio signal recovery. IEEE J. Sel. Top. Signal Process. 2021, 15, 51–64. [Google Scholar] [CrossRef]
- Kuang, Q.; Zhao, L. A practical GPU based kNN algorithm. In Proceedings of the 2009 International Symposium on Computer Science and Computational Technology (ISCSCI 2009), Huangshan, China, 26–28 December 2009; pp. 151–155. [Google Scholar]
- Al Aghbari, Z.; Al-Hamadi, A. Efficient kNN Search by linear projection of image clusters. Int. J. Intell. Syst. 2011, 26, 844–865. [Google Scholar] [CrossRef]
- Wang, X. A fast exact k nearest neighbours algorithm for high dimensional search using k means clustering and triangle inequality. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 1293–1299. [Google Scholar]
- Satish, N.; Harris, M.; Garland, M. Designing efficient sorting algorithms for manycore GPUs. In Proceedings of the 2009 IEEE International Symposium on Parallel & Distributed Processing, Rome, Italy, 23–29 May 2009; pp. 1–10. [Google Scholar]
- Chang, D.; Jones, N.A.; Li, D.; Ouyang, M.; Ragade, R.K. Compute pairwise Euclidean distances of data points with GPUs. In Proceedings of the iASTED international Symposium on Computational Biology and Bioinformatics, Orlando, FL, USA, 16–18 November 2008; pp. 278–283. [Google Scholar]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Almalawi, A.M.; Fahad, A.; Tari, Z.; Cheema, M.A.; Khalil, I. k NNVWC: An Efficient k-Nearest Neighbours Approach Based on Various-Widths Clustering. IEEE Trans. Knowl. Data Eng. 2015, 28, 68–81. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, X.; Wang, W.; Shi, B.; Pei, J. Using high dimensional indexes to support relevance feedback based interactive images retrieval. In Proceedings of the 32nd International Conference on Very Large Data Bases, Seoul, Republic of Korea, 12–15 September 2006; pp. 1211–1214. [Google Scholar]
- Shen, H.T.; Ooi, B.C.; Zhou, X. Towards effective indexing for very large video sequence database. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, ML, USA, 14–16 June 2005; pp. 730–741. [Google Scholar]
- Ilarri, S.; Mena, E.; Illarramendi, A. Location-dependent queries in mobile contexts: Distributed processing using mobile agents. IEEE Trans. Mob. Comput. 2006, 5, 1029–1043. [Google Scholar] [CrossRef]
- Doulkeridis, C.; Vlachou, A.; Kotidis, Y.; Vazirgiannis, M. Peer-to-peer similarity search in metric spaces. In Proceedings of the 33rd International Conference on Very Large Data Bases, Vienna, Austria, 23–27 September 2007; pp. 986–997. [Google Scholar]
- Qu, L.; Chen, Y.; Yang, X. iDistance based interactive visual surveillance retrieval algorithm. In Proceedings of the 2008 International Conference on Intelligent Computation Technology and Automation (ICICTA), Changsha, China, 20–22 October 2008; Volume 1, pp. 71–75. [Google Scholar]
- Schuh, M.A.; Wylie, T.; Angryk, R.A. Mitigating the curse of dimensionality for exact knn retrieval. In Proceedings of the Twenty-Seventh International Flairs Conference, Pensacola Beach, FL, USA, 21–23 May 2014. [Google Scholar]
- Schuh, M.A.; Wylie, T.; Angryk, R.A. Improving the performance of high-dimensional knn retrieval through localized dataspace segmentation and hybrid indexing. In Proceedings of the East European Conference on Advances in Databases and Information Systems, Genoa, Italy, 1–4 September 2013; pp. 344–357. [Google Scholar]
- Wylie, T.; Schuh, M.A.; Sheppard, J.W.; Angryk, R.A. Cluster analysis for optimal indexing. In Proceedings of the Twenty-Sixth International FLAIRS Conference, St. Pete Beach, FL, USA, 22–24 May 2013. [Google Scholar]
- Boytsov, L.; Naidan, B. Learning to prune in metric and non-metric spaces. Adv. Neural Inf. Process. Syst. 2013, 26. [Google Scholar]
- Weber, R.; Blott, S. An Approximation Based Data Structure for Similarity Search; Technical Report; Citeseer: Princeton, NJ, USA, 1997. [Google Scholar]
- Batcher, K.E. Sorting networks and their applications. In Proceedings of the Spring Joint Computer Conference, Atlantic City, NJ, USA 30 April–2 May 1968; pp. 307–314. [Google Scholar]
- Liu, B.; Lee, W.C.; Lee, D.L. Supporting complex multi-dimensional queries in P2P systems. In Proceedings of the 25th IEEE International Conference on Distributed Computing Systems (ICDCS’05), Columbus, OH, USA, 6–10 June 2005; pp. 155–164. [Google Scholar]
- Li, M.; Lee, W.C.; Sivasubramaniam, A.; Zhao, J. Supporting K nearest neighbours query on high-dimensional data in P2P systems. Front. Comput. Sci. China 2008, 2, 234–247. [Google Scholar] [CrossRef]
- Jagadish, H.V.; Ooi, B.C.; Vu, Q.H.; Zhang, R.; Zhou, A. Vbi-tree: A peer-to-peer framework for supporting multi-dimensional indexing schemes. In Proceedings of the 22nd International Conference on Data Engineering (ICDE’06), Atlanta, GA, USA, 3–7 April 2006; p. 34. [Google Scholar]
- Clarke, L.; Glendinning, I.; Hempel, R. The MPI message passing interface standard. In Programming Environments for Massively Parallel Distributed Systems; Springer: Basel, Switzerland, 25–29 April 1994; pp. 213–218. [Google Scholar]
- Dagum, L.; Menon, R. OpenMP: An industry standard API for shared-memory programming. IEEE Comput. Sci. Eng. 1998, 5, 46–55. [Google Scholar] [CrossRef] [Green Version]
- Luebke, D.; Harris, M. General-purpose computation on graphics hardware. In Proceedings of the Workshop, Singapore, 16–18 June 2004; Volume 33, p. 6. [Google Scholar]
- Corral, A.; Manolopoulos, Y.; Theodoridis, Y.; Vassilakopoulos, M. Closest pair queries in spatial databases. ACM SIGMOD Rec. 2000, 29, 189–200. [Google Scholar] [CrossRef]
- Brinkhoff, T.; Kriegel, H.P.; Seeger, B. Efficient processing of spatial joins using R-trees. ACM SIGMOD Rec. 1993, 22, 237–246. [Google Scholar] [CrossRef] [Green Version]
- Hjaltason, G.R.; Samet, H. Incremental distance join algorithms for spatial databases. In Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data, Washington, DC, USA, 1–4 June 1998; pp. 237–248. [Google Scholar]
- Koudas, N.; Sevcik, K.C. High dimensional similarity joins: Algorithms and performance evaluation. IEEE Trans. Knowl. Data Eng. 2000, 12, 3–18. [Google Scholar] [CrossRef]
- Böhm, C.; Braunmüller, B.; Krebs, F.; Kriegel, H.P. Epsilon grid order: An algorithm for the similarity join on massive high-dimensional data. ACM SIGMOD Rec. 2001, 30, 379–388. [Google Scholar] [CrossRef]
- Kahveci, T.; Lang, C.A.; Singh, A.K. Joining massive high-dimensional datasets. In Proceedings of the Proceedings 19th International Conference on Data Engineering (Cat. No. 03CH37405), Bangalore, India, 5–8 March 2003; pp. 265–276. [Google Scholar]
- Shim, K.; Srikant, R.; Agrawal, R. High-dimensional similarity joins. IEEE Trans. Knowl. Data Eng. 2002, 14, 156–171. [Google Scholar] [CrossRef]
- Corral, A.; D’Ermiliis, A.; Manolopoulos, Y.; Vassilakopoulos, M. VA-files vs R*-trees in distance join queries. In Proceedings of the East European Conference on Advances in Databases and Information Systems, Tallinn, Estonia, 12–15 September 2005; pp. 153–166. [Google Scholar]
- Achlioptas, D. Database-friendly random projections. In Proceedings of the twentieth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, Barbara, CA, USA, 21–23 May 2001; pp. 274–281. [Google Scholar]
- Nálepa, F.; Batko, M.; Zezula, P. Continuous Time-Dependent kNN Join by Binary Sketches. In Proceedings of the 22nd International Database Engineering &Applications Symposium, Villa San Giovanni, Italy, 18–20 June 2018; pp. 64–73. [Google Scholar]
- Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Selma, C.; Bril El Haouzi, H.; Thomas, P.; Gaudreault, J.; Morin, M. An iterative closest point method for measuring the level of similarity of 3D log scans in wood industry. In Service Orientation in Holonic and Multi-Agent Manufacturing, Proceedings of the 7th International Workshop on Service Orientation in Holonic and Multi-Agent Manufacturing (SOHOMA’17), Nantes, France, 19–20 October 2017; Springer: Berlin/Heidelberg, Germany, 2018; pp. 433–444. [Google Scholar]
- Chabanet, S.; Thomas, P.; El-Haouzi, H.B.; Morin, M.; Gaudreault, J. A knn approach based on icp metrics for 3d scans matching: An application to the sawing process. IFAC-PapersOnLine 2021, 54, 396–401. [Google Scholar] [CrossRef]
- Sakurai, Y.; Yoshikawa, M.; Uemura, S.; Kojima, H. The A-tree: An index structure for high-dimensional spaces using relative approximation. Proc. VLDB 2000, 2000, 5–16. [Google Scholar]
- Ooi, B.C.; Tan, K.L.; Yu, C.; Bressan, S. Indexing the edges—A simple and yet efficient approach to high-dimensional indexing. In Proceedings of the Nineteenth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, Dallas, TX, USA, 15–18 May 2000; pp. 166–174. [Google Scholar]
- Arya, S.; Mount, D.M.; Netanyahu, N.S.; Silverman, R.; Wu, A.Y. An optimal algorithm for approximate nearest neighbour searching fixed dimensions. J. ACM (JACM) 1998, 45, 891–923. [Google Scholar] [CrossRef]
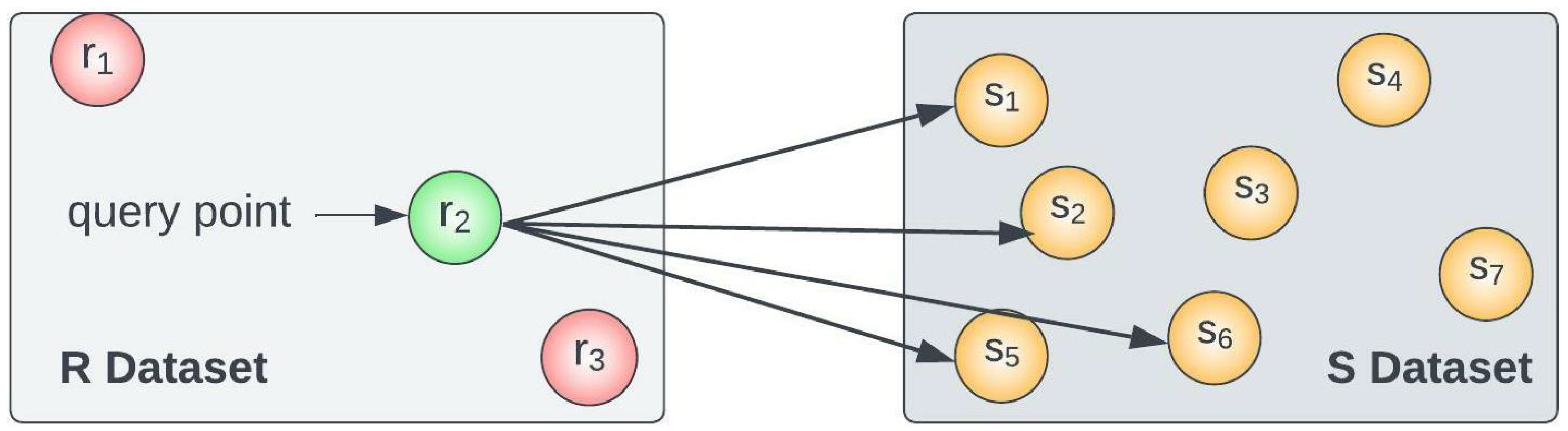
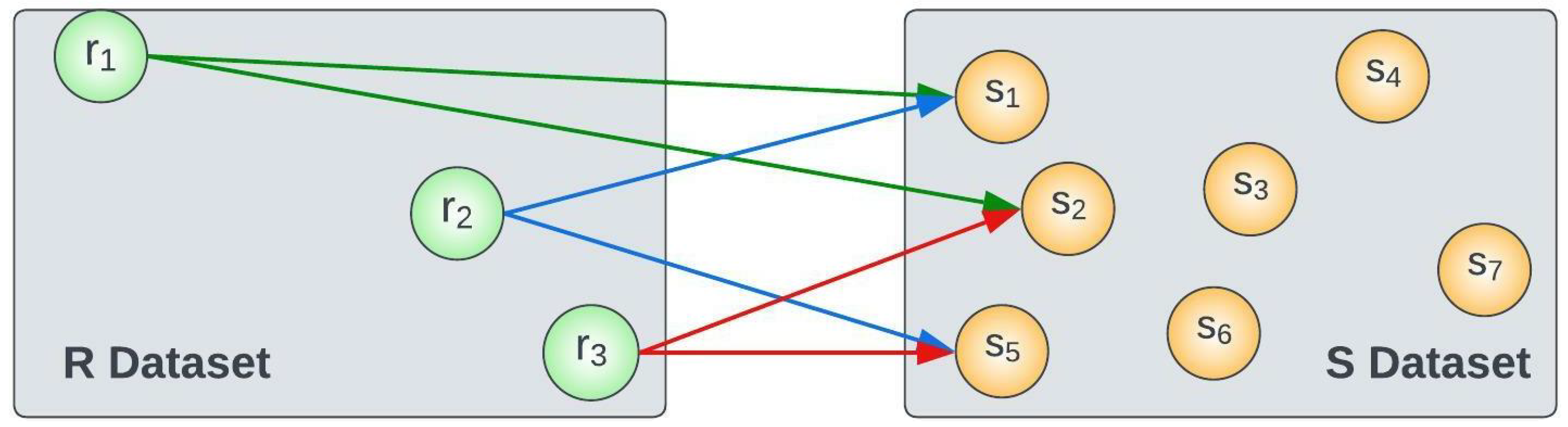

| Symbols | Definitions |
|---|---|
| Datasets | |
| Data points of R and S dataset | |
| k | number of nearest neighbours |
| Euclidean distance function | |
| Dimensionality of original dataset | |
| q | Query data point |
| d-dimensional space |
| Comp. Para. | Part Strat. | Indexing Technique | Techniques | Dim. Reduction Approach | App. | Synth. Dim. | Real. Dim. | Dyn. Data | Dist. Mt. | Time. Comp. |
|---|---|---|---|---|---|---|---|---|---|---|
| I/O | Space | VA-file | VA-file [109] | KLT | Both | N/A | Mod. | No | L2 | O(log n) * |
| Data | B-tree | iDistance [110,111] | iDistance | Exact | Mod. | Mod. | Yes | L2 | O(log n) * | |
| Diagonal Ordering [112] | PCA | Exact | Mod. | Mod. | No | L2 | O(log n) * | |||
| N/A | OTI & EOTI [113] | N/A | Exact | N/A | High+ | No | L2 | O(n) | ||
| BB-trees | BP [114] | PCCP | Both | High | High | No | Breg. dist. | O(nlogn) * | ||
| MEM. | Space | R-tree | PL-Tree [115] | CPF | Exact | Mod. | Mod. | Yes | L2 | O(log n) * |
| Hash-based | HC-O [116] | N/A | Both | N/A | High+ | No | L2 | O(n) | ||
| Data | -tree | -tree [74] | PCA | Exact | Moerate | Mod. | Yes | L2 | O(n) * | |
| 1D array | Array-index [117] | array-index | Exact | Mod. | N/A | No | L2 | O(log n) * | ||
| -tree | -tree [74,118] | PCA | Exact | Mod. | Mod. | Yes | L2 | O(n) * | ||
| ACDB | ACDB [119] | N/A | Exact | N/A | Mod. | No | L2 | O(nlogn) * | ||
| B-tree | iDistance-PS [120] | iDistance | Exact | Mod. | High | No | L2 | O(n) * | ||
| iDStar [115] | iDistance | Exact | High+ | High | No | L2 | O(n) * | |||
| PARL. | Space | N/A | CU-kNN [121] | 1D reduct | Exact | Mod. | Mod. | No | L2 | O(n) * |
| TBiS [122] | N/A | Exact | N/A | High | No | L2 | O(log n) | |||
| Randomised k dim. tree | kNN-PA [123] | N/A | Both | High+ | High+ | No | L2 | O(nlogn) * | ||
| Data | N/A | HkNN [124] | N/A | Exact | High+ | N/A | No | L2 | O(n) * | |
| No Part | N/A | BF-CUDA [77] | N/A | Exact | Mod. | Mod. | No | L2 | O(n) * | |
| CUBLAS [75] | N/A | Exact | High | High | No | L2 | O(log n) * | |||
| DISTR. | Space | Quad-trees | QDBI [125] | N/A | Exact | Mod. | N/A | No | L2 | O(log n) * |
| Comp. Para. | Part Strat. | Indexing Technique | Techniques | Dim. Reduct App. | App. | Synth. Dim. | Real. Dim. | Dyn. Data | Dist. Mt. | Time Comp. |
|---|---|---|---|---|---|---|---|---|---|---|
| I/O | Space | R-Tree | MuX [53,54] | N/A | Exact | Mod. | Mod. | No | L2 | O(nlogn) |
| N/A | Gorder [126] | PCA | Exact | Mod. | Mod. | No | L2 | O(n) * | ||
| inverted index | IIB & IIIB [127] | N/A | Exact | High+ | Mod. | No | L2 | O(nlogn) * | ||
| Data | iDistance | iJoin [128] | PCA | Exact | Mod. | Mod. | No | L2 | O(nlogn) * | |
| kNNJoin [76] | iDistance | Exact | Mod. | Mod. | Yes | L2 | O(nlogn) * | |||
| MEM. | Data | HDR-Tree | HDR-Tree [83] | PCA | Both | High | High | Yes | L2 | O(nlogn) |
| EkNN [129] | PCA | Exact | N/A | High+ | Yes | L2 | O(nlogn) * | |||
| DISTR. & PARL. | Space | R-Tree | H-BNLJ & H-BRJ [130] | N/A | Both | Mod. | Mod. | No | L2 | O(n) * |
| Data | N/A | PGBJ [58] | N/A | Both | Mod. | Mod. | No | L2 | O(nlogn) * |
| Sr No. | Techniques | Merits | Demerits |
|---|---|---|---|
| 1. | iDistance [110,111] | 1. Support online query answering 2. Robust and adaptive to different data distributions 3. It can be integrated into DBMS cost-effectively | 1. It has a wide search region 2. Lossy transformation leads to false drops 3. When dim. increases, pruning efficiency decreases |
| 2. | -tree [74] | 1. Provides an optimised index structure 2. Reduce the search space and speed up the kNN query in the main memory environment | 1. Effective for correlated dataset 2. Entire tree must be rebuilt on a recurring basis |
| 3. | array-index [117] | 1. Minimal disk access 2. It is simple and compact, yet faster | 1. Not considered real-life dataset for experiments |
| 4. | Diagonal Ordering [112] | 1. It avoids unnecessary distance computation 2. It can effectively adapt to varied data distributions 3. Supports online query answering | 1. Experimental study was performed on a 30D dataset only, which doesn’t guarantee to outperform a very high-dimensional dataset |
| 5. | VA-file [109] | 1. Prevents excessively uneven data distribution across the clusters 2. Useful for kNN Search in non-uniform datasets | 1. For better search results, consider approximation 2. The performance degrades as dim. increases 3. Do not consider the cache and query workload |
| 6. | -tree [74,118] | 1. It helps to minimise the computational cost and cache misses 2. Outperforms iDistance, Pyramid tree, etc. | 1. It cannot stop a tree-rebuilding process 2. With varying datasets, the optimum values of parameters (like clusters) might also differ |
| 7. | BF-CUDA [77] | 1. Supports fast, parallel kNN Search | 1. Unable to scale to a very large dataset |
| 8. | CUBLAS [75] | 1. It provides a significant speedup and outperforms the ANN C++ library | 1. The performance gets impacted by the cost of data movement 2. It can be ineffective for large-scale environments |
| 9. | ACDB [119] | 1. Using the triangle inequality, CPU cost was effectively minimised and provided better performance | 1. The initial center pivots and k value both have a significant impact on the cluster method |
| 10. | TBiS [122] | 1. Offers simple data and programme structures, synchronous concurrency and optimal data localisation | 1. With an increasing number of data items and k value, the performance dramatically degrades |
| 11. | QDBI [125] | 1. Good scalability and search performance | 1. Experiments not performed on a real dataset 2. Not much focused on high-dimensional dataset |
| 12. | iDistance-PS [120] | 1. Enhancements to the filtering power of iDistance 2. Provides efficient kNN querying | 1. The problem of dimensionality is significantly worse in space-based approaches |
| 13. | PL-Tree [115] | 1. It can scale well with dimensionality and data size. Also supports efficient point queries & range queries | 1. Perform experiments using 12D dim. only 2. iDistance outperforms PL-Tree for point queries |
| 14. | CU-kNN [121] | 1. Provides high-performance 2. It improves core issues with CUDA-based data mining algorithms | 1. Suffers from big data scalability 2. Data movement and the cost is an issue |
| 15. | iDStar [115] | 1. It performs better in high-dimensional, tightly clustered dataspaces | 1. Less pruning power for scattered clusters 2. Not much effective for dimensionality above 256 |
| 16. | kNN-PA [123] | 1. It is scalable and allows kNN Searches for any HD datasets over thousands of cores | 1. Not designed for continuous point updates 2. Ineffective in a distributed-memory environment |
| 17. | HC-O [116] | 1. It speeds up the candidate refining process during the kNN Search 2. It is a fundamental method that works for both exact and approximate kNN Search techniques | 1. In the workload, they presume a stable distribution of queries 2. The tightness of the distance bounds and the histogram affects the pruning power |
| 18. | OTI and EOTI [113] | 1. Lower complexity and faster search algorithm 2. It reduces costly distance computation | 1. OTI suffers from large space and time complexity 2. The process of constructing triangles can be improved for better efficiency |
| 19. | BP [114] | 1. It is the first high-dimensional non-metric Bregman divergence that provides a better kNN Search 2. Performance improvements in CPU time & IO cost | 1. Does not effectively support massive data updates 2. By transforming Bregman distance to L2, more effective solutions can be implemented |
| 20. | HkNN [124] | 1. Effectively split work between the CPU and GPU 2. It provides a hybrid approach for the kNN Search 3. Effectiveness grows linearly with increasing dim. | 1. Compared results using only brute-force tech. 2. There is scope to examine various optimised k selection approaches and distance kernels |
| Sr No. | Techniques | Merits | Demerits |
|---|---|---|---|
| 1. | MuX [53,54] | 1. Designed to reduce the I/O and CPU costs | 1. Performance degrades with an increased dim. 2. High memory overhead |
| 2. | Gorder [126] | 1. Reduce random access 2. Prunes the unpromising block blocks | 1. It requires significantly more computation 2. Designed for static data |
| 3. | iJoin [128] | 1. Adaptive and dynamic | 1. Very costly for dynamic data |
| 4. | IIB and IIIB [127] | 1. Effective for the sparse dataset | 1. It may not be feasible for correlated datasets. Algorithms’ effectiveness can be optimised |
| 5. | kNNJoin [76] | 1. It supports efficient searching and dynamic updates | 1. Unable to meet the real-time requirements 2. High distance computation cost & node overlap |
| 6. | H-BNLJ and H-BRJ [130] | 1. Easy to implement | 1. Slower and unable to scale well 2. Communication overhead is very high |
| 7. | PGBJ [58] | 1. Increasing the k value does not affect the communication overhead 2. Disk usage is very low | 1. Inefficient for high-dimensional data 2. Pivot selection significantly affects performance 3. time-consuming operations for big datasets |
| 8. | HDR-tree [83] | 1. Searches for affected users are made efficient 2. It is effective for high-dimensional data | 1. Lack of Support for Deletions 2. Lack of Support for Batch Updates |
| 9. | EkNNJ [129] | 1. Efficient dynamic update, batch and lazy update 2. Provide optimised deletion | 1. Does not support fully dynamic HD kNN Join 2. Scope for deletion optimisation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ukey, N.; Yang, Z.; Li, B.; Zhang, G.; Hu, Y.; Zhang, W. Survey on Exact kNN Queries over High-Dimensional Data Space. Sensors 2023, 23, 629. https://doi.org/10.3390/s23020629
Ukey N, Yang Z, Li B, Zhang G, Hu Y, Zhang W. Survey on Exact kNN Queries over High-Dimensional Data Space. Sensors. 2023; 23(2):629. https://doi.org/10.3390/s23020629
Chicago/Turabian StyleUkey, Nimish, Zhengyi Yang, Binghao Li, Guangjian Zhang, Yiheng Hu, and Wenjie Zhang. 2023. "Survey on Exact kNN Queries over High-Dimensional Data Space" Sensors 23, no. 2: 629. https://doi.org/10.3390/s23020629
APA StyleUkey, N., Yang, Z., Li, B., Zhang, G., Hu, Y., & Zhang, W. (2023). Survey on Exact kNN Queries over High-Dimensional Data Space. Sensors, 23(2), 629. https://doi.org/10.3390/s23020629









