1. Introduction
Anti-counterfeiting techniques can prevent or identify counterfeits to a certain extent, and traditional techniques can be classified into the following categories: visual anti-counterfeiting, electronic identification anti-counterfeiting, electronic code anti-counterfeiting, and texture anti-counterfeiting. Visual anti-counterfeiting mainly uses laser holography [
1,
2,
3,
4], special inks [
5,
6,
7,
8], temperature changes [
9,
10], security lines [
11], chemical substances [
12], and so on. They have special materials or unique formulations that not only cost a lot but also lose security once their information is leaked. Electronic identification anti-counterfeiting [
13] commonly includes radio frequency, magnetic recording, integrated circuit cards, etc. These techniques work in conjunction with data management systems but they are not as generalizable as relying on specialized devices and are limited in application scenarios and scope. Based on the uniqueness of texture, all digital images of texture anti-counterfeiting marks [
14,
15] are obtained by high-definition photography, and then a database is established to upload, number, and save them. Consumers take photos with their mobile phones and retrieve the corresponding images saved in a database for human-eye comparison, but there is a lack of objective and intelligent means of identification. Traditional techniques suffer from various problems, such as excessive cost, poor user experience, and poor objectivity.
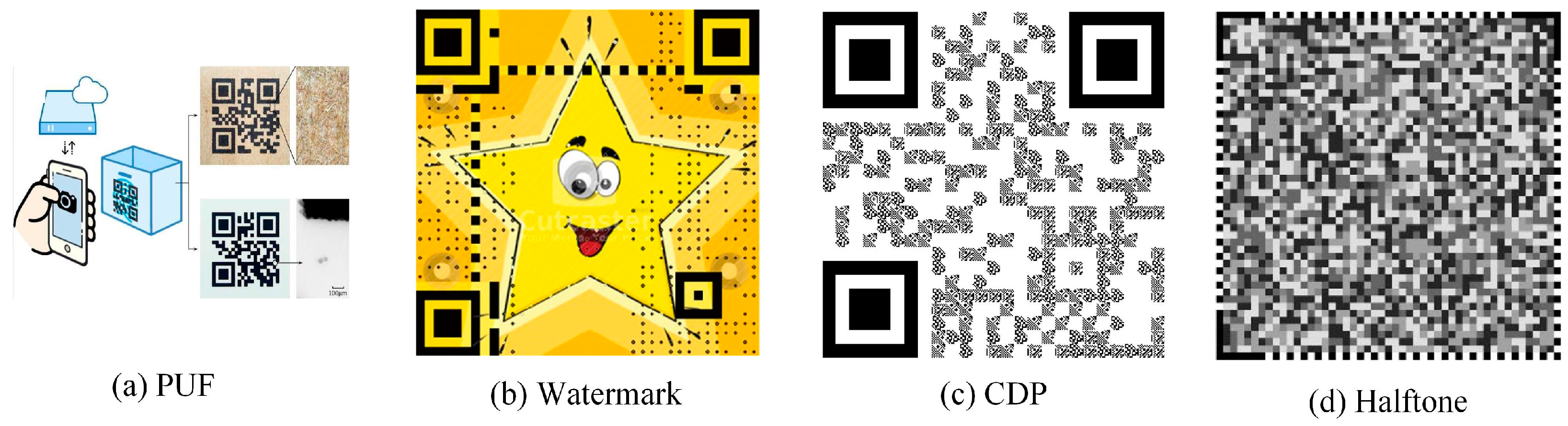
Different degrees of random toner adsorption occur in a digital graphic during printing, ensuring its physical non-replicability. The special design of the graphic can further amplify the distortion phenomenon, which can be identified by the algorithm. QR codes are widely used due to their strong coding ability and large information capacity. As QR codes are composed of a large number of black and white blocks, they are insensitive to the noise and distortion generated during printing. Therefore, the fusion of anti-counterfeiting graphics with QR codes is gaining increasing attention. At present, the fusion can be summarized as physical unclonable function (PUF) [
16,
17,
18,
19], watermark [
20,
21,
22,
23], copy detection pattern (CDP) [
24,
25,
26,
27,
28], and halftone [
29,
30,
31,
32]. Although the above methods can achieve certain anti-counterfeiting effects, there are still some aspects that can be improved.
For example, [
16] utilizes natural texture features and printing micro-features, then calculates the feature similarity between the code to be tested and the sample code through the feature extraction algorithm; however, this requires high-precision printing and capturing equipment. The authors in [
20] adopt the improved discrete wavelet transform and singular value decomposition algorithm to hide the digital watermark in the 2D code. In [
21], the researchers embed specific random micro-textures into a 2D code and then convert them into a security layer. Any degradation process due to counterfeiting will change the statistics of the micro-textures and thus achieve anti-counterfeiting. However, watermarking algorithms can show some robustness to relatively low-intensity attacks, while for high-intensity attacks, the watermarking information is altered or significantly lost. A new 2LQR code is proposed in [
24] to replace the black block of the QR code with a black and white module of the same size with anti-copy ability. This system includes public and private storage levels; the public level ensures that the decoding program can decode, and the private level uses the sensitivity of the module to the print capture process to distinguish real from fake codes. However, this code would attract visual errors, where it is easy for the naked eye to find the specific structure of the module, while also requiring precision in the capture device, which is not conducive to commercial generalization. The authors in [
29] propose a two-dimensional code anti-replication scheme based on the spectral and spatial bar code channel model. Two sets of spectral and spatial features are extracted from the channel model and identified in a cascaded combination. However, the feature extraction process of this method is relatively complicated. In [
30], the researchers add a double security authentication to the position of embedded information and then reduce the interval distance through fourth-order modulation. In this way, it is easier to create differences after printing and capturing, thus achieving the anti-replication effect.
Figure 1 shows some representative anti-counterfeiting patterns.
To address the above issues, this paper designs a texture-hidden QR code, based on the codec mechanism of QR codes, using Gaussian distribution and information-hiding technology. The licensee generates a digital image of the code and then uses an officially authorized printer to legally print the authentic product and paste it on the goods or documents for circulation. The forger does not have access to the original code digital image, so the process involves scanning, reprinting, and pasting the fake product or document on top of the original. Users upload codes by taking photos on their mobile phones, which can be used to verify authenticity. The code has abundant texture details and specific frequency characteristics which improve the anti-replication capability while maintaining the generality of the QR codes. An efficient quality assessment algorithm is also proposed to address possible blur in the authentication processing. The proposed method describes the DFT low-frequency region of a code and computes and compares its magnitude and azimuthal features to determine the presence and degree of blur. Finally, this paper proposes a dual feature detection algorithm that includes both a decodability analysis and DFT spectral features. Specially designed anti-counterfeiting textures will show different diffusion patterns after printing. The details of fake codes will be glued together in large quantities, the code points will be destroyed, and the decoding will fail. To ensure accuracy, this paper calculates the spectral similarity between the tested code and the sample code and further compares the eigenvalues in four feature regions. The contributions of this paper are as follows.
- (1)
This paper designs a texture-hidden anti-counterfeiting QR code to solve the problem of the easily illegally copied QR code.
- (2)
An effective quality assessment algorithm is proposed to judge the type and degree of blur.
- (3)
The proposed dual-feature detection algorithm is shown to cope with different forgery means, capture devices, and attack scenarios.
The paper is structured as follows:
Section 2 introduces the design process of anti-counterfeiting QR codes,
Section 3 describes the quality assessment algorithm and the dual feature detection algorithm for the code,
Section 4 presents the experimental effects in detail, and
Section 5 concludes the paper.
2. The Design of Anti-Counterfeiting QR Codes
During the printing process of a digital pattern, the toner will be scattered randomly. Genuine codes only need to be printed once, while forged codes need to be printed at least twice, which can cause severe distortion. Realizing the above mechanism, this paper designs a texture-hidden QR code based on Gaussian distribution and information hiding to achieve an anti-copying effect. The code generation process is shown in
Figure 2 and consists of three stages. The first stage is the generation process of an anti-counterfeiting texture. Random patterns generated from the Gaussian distribution function exhibit strong texture properties. Bilinear interpolation is used so that its gray level variation is moderately continuous, with more irregular gray level differences. Halftone operations are then performed by using error diffusion to bring the frequency of the digital code closer to the frequency sampled from the scanning and printing devices, and to improve signal aliasing during replication. The second stage is the refined process of the QR code. The semantic decoding process of QR codes first detects the position detection region and then detects the black and white code blocks. In this paper, the code points outside the position detection region and the calibration region are reduced, which does not affect the decoding. The third stage is the fusion of the above specially designed texture and the refined QR code at the code points. The anti-counterfeit code visually implements the information hiding of code points and has specific frequency characteristics, thus improving the anti-copy capability while maintaining the commonality of the QR code.
Step 1: Generate Gaussian random textures
A random matrix is built from a Gaussian random generation function and visualized as a fine random texture pattern. The pattern and its enlarged detail are shown in
Figure 3. Random patterns have the characteristics of a strong texture, and at the same time, have differences in each part, which increase the difficulty of counterfeiting. If the random variable
follows a Gaussian distribution with expected value
and standard deviation
, its probability density function is:
where
determines the location of the distribution;
determines the magnitude of the distribution; and
is reconstructed into the matrix
.
Step 2: Use bilinear interpolation operation
Bilinear interpolation is to perform linear interpolation in both directions separately. Interpolation has the effect of low-pass filtering which can be anti-aliasing and effectively reduce some of the visual distortions caused by image scaling.
Figure 4 shows the bilinear interpolated texture pattern and its enlarged detail. It can be seen that continuously varying grayscale levels are formed between pixels in the image details, with smooth patterns and increased low-frequency information. Bilinear interpolation takes the distance to the last four pixels as a reference weight and computes the integrated score by linearly interpolating it twice to obtain the pixel value of the current point. It can be expressed as follows:
where
,
,
, and
are the known points, and
,
,
, and
are values of proportion; the closer points are more important.
Step 3: Adopt halftone treatment
Since the printing device can only print black and white, the continuous gray tone image must be processed into a binary halftone image in the printing process, and the unit coverage area of small black and white dots that human eyes cannot distinguish is used to simulate the gray level change of the image so that the binary image looks as close as possible to the original image. In this paper, the error diffusion method proposed by [
33] is adopted for the halftone processing of texture images, that is, every pixel in the image and its neighboring pixels are processed, and the error (the difference between the actual output and the original image) generated on a pixel is dispersed to the surrounding pixels in a certain proportion. After the above operation,
is obtained.
Figure 5 shows the texture pattern and its enlarged detail after the halftone treatment.
Step 4: Refine QR code
Figure 6 shows the QR code generated based on the Zxing open-source code and its refined code. First, the horizontal pixel values of the location detection area of the QR code are calculated and divided by the corresponding ratio (1:1:3:1:1) to obtain the minimum component module size. Then, the position and size of the calibration pattern are calculated according to the ratio characteristics of 1:1:1:1:1. Finally, the areas of the QR code are refined, except for the location detection area and calibration pattern, as follows:
where
represents the value of the original QR code and
is the reduced local pixel size.
Step 5: Combine texture patterns and refined QR code
Figure 7 shows the combined anti-counterfeiting texture code and its details. The code points in the code data region are minor and nearly integrated into the anti-counterfeiting background. Since the position detection area is complete and the original QR code has a maximum error correction capability of 30%, the semantics of the anti-counterfeiting code can still be decoded by the code scanning device. The position detection area, calibration area, and black and white code points of the refined QR code are unchanged, while the rest of the code is replaced with Gaussian random texture patterns. The formula for this is as follows:
5. Conclusions
In this paper, a texture-hidden anti-counterfeiting QR code and a related authentication scheme for mobile devices are proposed. The authentication scheme includes a quality assessment algorithm and dual feature detection. In the test of quality assessment algorithms, the proposed algorithm is compared with several current common algorithms without reference and the superiority of the proposed algorithm is verified. In the authenticity test, the proposed dual feature method is compared with various texture and corner methods. The proposed method achieves an accuracy, precision, and recall of up to 100%, and it also performs well on attacked datasets with reduction and cut. In the following research work, it is necessary to expand the data set (attacks of various physical sizes, higher forgery technologies, and complex application scenarios) to more comprehensively evaluate the practicality of the codes and authentication schemes to achieve convenient pre-sale anti-counterfeit measures.
The dataset used in this paper is obtained by smartphones shooting under indoor conditions, but the collection of 2D codes will also encounter some abnormal conditions, such as insufficient illumination, severe shaking, etc. How to efficiently recover codes and authenticate them is a problem that requires further work. In addition, with multiple forgery devices available, how to authenticate codes using only genuine samples is an important research direction.