1. Introduction and Backgrounds
In a mature autonomous driving system, the environment perception module is equivalent to human eyes and ears, while the decision-planning module is equivalent to the human brain.
Most traditional decision-planning modules have a layered and hierarchical architecture, where the content is transferred layer by layer. Such a structure makes it easier to decompose complex tasks; thus, it is convenient to detect problems with the specific module. In addition, relying heavily on prior knowledge and formulae, traditional methods have strong interpretability. Owing to their good performance in terms of accuracy and interpretability, the traditional decision-planning modules are the mainstream system of autonomous driving technology at present. It is indeed established that the cascade structure in traditional approaches also brings drawbacks in the aspects of instantaneity and reliability. First, data computation and transmission through different layers hinder the instantaneity and flexibility of the modules. Second, the operation of traditional modules requires all elements in it to operate under normal condition, or it will be out of order, i.e., the system of traditional decision-planning modules is vulnerable and unreliable.
The adaptive cruise control (ACC) method has been widely applied in most traditional vehicle-following practices. In order to maintain a relatively stable distance with the target vehicle, the speed of the ego vehicle changes along with the target one on the straight road. As described in [
1], the paper used the SMPC method, and a conditional linear Gaussian model was proposed and trained with actual measurements to estimate the probability distribution of the future speed of the preceding vehicle. Then, the paper built the relevant driving scenarios in the single lane in the CarMaker, applied the control strategy in the simulation scene, and verified it. Ioannou et al. modeled the ACC system as a hybrid system with constant acceleration, smooth acceleration, and a linear state feedback controller in [
2]. Kitazono et al. in [
3] adopted an adaptive neural network scheme to solve the traffic stability problem in convoys. In addition, there are also many other different strategies used to adjust the distance between the ego and target vehicles, with the utilization of the ACC system. In [
4], Choi et al. used a fixed distance strategy and a sliding mode control method to control the speed and distance between two vehicles.
There are two main traditional obstacle avoidance methods, including reference line fitting methods and artificial potential field methods. As for the reference line fitting method, the rationale of trajectory planning is widely adopted to generate a cluster of alternative trajectories, with the consideration of vehicle dynamics and the general vehicle attitudes. Then, these trajectories are sorted on the basis of cost value, and a collision-free obstacle avoidance trajectory with the least cost is finally obtained after collision detection. Finally, the trajectory tracking control algorithm is used to control the ego vehicle to avoid the obstacles. The artificial potential field method is a virtual force method, and its basic idea is to regard the vehicle’s motion in the surrounding environment as the motion of the vehicle in the artificially established virtual position. The target point generates gravity, which guides the vehicle toward the target point, and the obstacles generate repulsion to avoid a collision between the ego vehicle and the obstacles. Under the combined force of gravity and repulsion, the ego vehicle moves along the direction of the potential field decline, resulting in an optimal path without collision. To avoid the local minimum, Ref. [
5] proposed a virtual potential field detection circle model with an adjustable radius. The “minimum trap” formed by the obstacle repulsion field had been detected by the model in advance, whose success rate in obstacle avoidance has reached 90% or more. In [
6], the obstacle avoidance function was introduced into the path planning layer, and the trajectory tracking layer transformed the linear time-varying MPC optimization problem into a quadratic programming problem, which has realized the path emergency obstacle avoidance and tracking.
Recently, some optimization methods based on traditional obstacle avoidance have been proposed and have achieved good results. In [
7], a personalized motion planning and tracking control framework was proposed to prevent collisions between autonomous vehicles and obstacles ahead. The simulation results showed that the proposed framework could improve the corresponding driving performance according to the individualized needs of different passengers. The author in [
8] improved an algorithm integrating path pruning, smoothing, and optimization with geometric collision detection based on the rapidly exploring random trees (RRT) algorithm. The simulation indicated that the vehicle could successfully track the path efficiently and reach the destination safely. An improved heuristic Bi-RRT algorithm, specialized for an unknown dynamic environment, was put forward by [
9] for obstacle avoidance. Thence, the related experiments have verified the good performance of such an algorithm in differentiable coherence path generation, ensuring both ride comfort and stability of the vehicle.
Today, with the continuous development of artificial intelligence technology, more industries have entered the digital deepening and intelligent extension stage. The essence of digitization is data, while the foundation of intelligence is artificial intelligence technology. In the current stage of autonomous driving, technology based on data-driven methods has been fully developed. Until now, data-driven methods have not only played a part in the perception and positioning of autonomous driving technology, but have also imposed increasing influences in decision-making planning and autonomous driving control technology.
Reinforcement learning is a machine learning method, often used to deal with sequential decision-making issues. Since the reinforcement learning method is trained through trial and error in the training process, the method strongly depends on the simulation environment. For the autonomous driving decision-planning module based on the reinforcement learning method, the system’s input can be raw perceptual data, such as pixel data from an RGBD camera or lidar points cloud data. Refs. [
10,
11,
12,
13] presented some model-free deep reinforcement learning methods for autonomous driving. For those data with high dimensions, a convolutional neural network for dimensionality reduction is necessary before being passed into the reinforcement learning network. Being mature, the external perception and recognition technology based on cameras and lidars make accurate data accessible, including the ego surrounding environment status information, target vehicle status information, and self-vehicle status information. Moreover, developers can directly obtain a list of relevant objects from the simulation platform.
Recently, reinforcement learning algorithms have been increasingly utilized to deal with complex sequential decision-making and control problems. In the following field of vehicles, the literature [
14] applied the policy gradient algorithm in reinforcement learning to train the CACC longitudinal controller to eliminate the errors of car following. However, the exploitation of the discrete control variable and more straight-forward environmental reward rules caused the repeated oscillations of the control quantities during the simulation. Ref. [
15] proposed a potential game-combined multi-agent deep deterministic policy gradient (MADDPG) approach to optimize multiple UAVs’ trajectories. Ref. [
16] put forward a method that combined imitation learning with reinforcement learning enabling the agent to achieve a higher success rate in urban autonomous driving navigation scenarios. The literature [
17] designed an autonomous driving system using the Q network and A* algorithm. For an unknown rough terrain scenario, Ref. [
18] constructed a deep reinforcement learning method for safe local planning of a ground vehicle. However, the above-mentioned algorithms were still restricted within the longitudinal control on straight roads, but seldom addressed the issues related to the turning part of intersections.
Similarly, in the obstacle avoidance part of the high-precision map, obstacle avoidance methods are all based on reinforcement learning methods. The literature [
19] investigated the dual-target behavior of trajectory tracking and obstacle avoidance based on waypoints through augmenting the agent’s observation vector by the reward trade-off parameter, thus enabling the agent to adapt to changes in its reward function. In [
20], the author proposed a deep Q-network-based method for collision-free decisions. The DQN-aided algorithm was introduced for determining the trajectory and velocity of the AV by receiving real-time traffic information from the base stations. In [
21], they presented a novel learning-based control algorithm for ASV systems with collision avoidance. The proposed control algorithm combined a conventional control method with deep reinforcement learning to provide a closed-loop stability guarantee, uncertainty compensation, and collision avoidance. The scholars in [
22] proposed an interpretable decision-making framework for autonomous vehicles at highway on-ramps adopting a latent space actor–critic-based method with asymmetric inputs. When constructing the simulation scene, the ego vehicle and the obstacle are usually simplified as a circle or a mass point, where the circle center is the center of the vehicle, and the radius is the safety distance. In this case, the interaction between the vehicle’s polys (i.e., the attitude requirements of the vehicle) has been ignored, especially when passing through a narrow passable area. Hence, such methods did not make full use of the advantages of reinforcement learning. Meanwhile, the reinforcement learning method requires the input dimension of the object list to be unified. Such requirements have imposed more challenges to the scene where the external obstacles are not fixed.
Based on the above-mentioned problems ignored in previous studies on autonomous driving related to reinforcement learning, this paper conducts related research using the CARLA simulation platform. CARLA is an open-source autonomous driving simulation platform based on the UE4 engine’s rendering, which provides users with the Python API interface, which can build rich driving scenes, and rich map elements can be obtained. In addition, the CARLA platform can also import self-built OpenDRIVE map files and OpenSCENARIO autonomous driving scene files, which can be customized according to the users’ own needs.
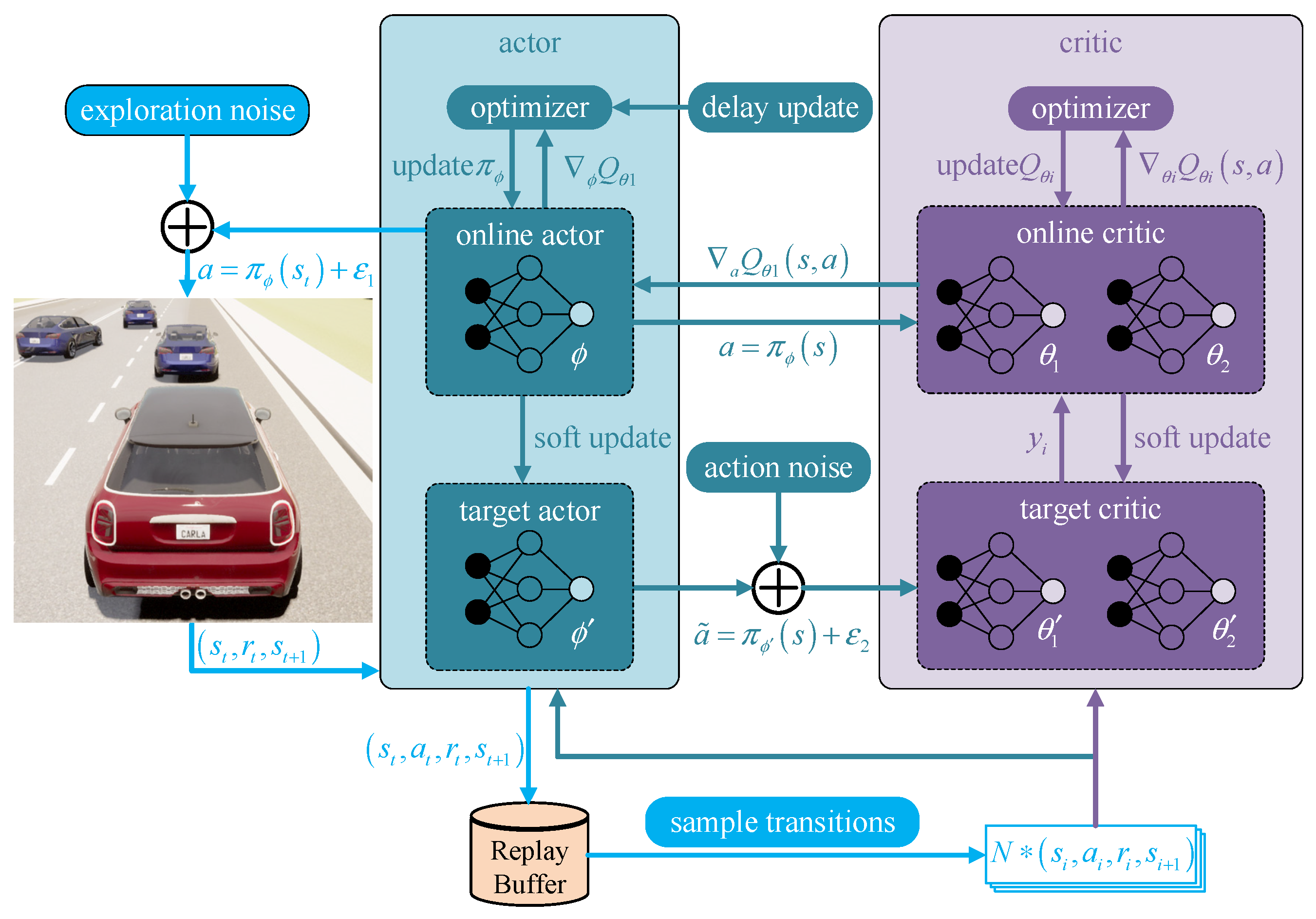
In this paper, the factor of the braker is not taken into consideration in the CARLA simulation platform, while only two control quantities are required in the controlled vehicle, i.e., the steering wheel angle and the accelerator pedal strength. Previous studies on autonomous driving technology based on reinforcement learning usually discretize both control quantities, with the utilization of the reinforcement learning model based on the DQN method for training. From a human driver’s perspective, when driving a vehicle, the steering wheel angle and the brake pedal’s position can take any value within the limit range. In other words, the input variables are continuous. To give full play to the characteristics of the neural network model and get closer to the level of human driver operation, the reinforcement learning basic model in this paper adopts the twin delayed deep deterministic policy gradient network framework that can generate actions in a continuous space. Additionally, this method will be referred to as TD3 for short. To sum up, the relevant scenarios of car following and obstacle avoidance in this paper are all carried out using the CARLA simulation platform, and the TD3 method is used as the calculation benchmark. The main contributions of this article are as follows:
A car-following model method based on reinforcement learning is proposed, which combines the relevant map elements in the map and the Frenet coordinate system, and can follow the car stably on straights, intersections, and curves.
We propose an external obstacle state input algorithm that can be adaptive to the ego vehicle’s speed. Additionally, this algorithm can represent the shape and pose of a random number of obstacles.
An obstacle avoidance method using reinforcement learning under map constraints is designed based on the improved obstacle input method. This method can still perform well when passing through narrow passable areas.
The rest of this paper is organized as follows. In
Section 2, a reinforcement learning-based target tracking model is presented, and this model can have perfect curve passing performance.
Section 3 mainly introduces a multi-obstacle representation method. Finally,
Section 4 concludes the paper.
3. Obstacle Avoidance Using Deep Reinforcement Learning Approach
3.1. Improved Obstacle Representation
For the obstacle avoidance, owing to the fact that the number of external obstacles is not fixed, some researchers have adopted the rasterization processing method to rasterize the observation range. A rectangle grid or a sectorial grid is used to encode obstacles to determine the location and size of the obstacles. Moreover, the obstacle information is dimensionally reduced to address the issue that the input dimension is not fixed. For rasterization methods, a question that needs to be considered is the accuracy of the grid. The smaller the grid size, the higher the accuracy of its representation, and the larger the input dimension of the reinforcement learning neural network, which is more inconducive to episode training. However, if the grid size is enlarged, the accuracy will be worsened and the passable area will be shrunk, making it more difficult for the vehicle to get through the passable narrow area in complex obstacle avoidance scenarios. In a way, the grid map method will hinder the performance of the vehicle when passing through the narrow areas.
The perceptual information that the ego vehicle receives at a certain moment is unknown globally, and the perceptual results constantly change from time to time. In the case of uncertain external obstacles, taking the external obstacle input as the research object, it is difficult for us to utilize the fixed-dimensional data input to represent the obstacle information. Inspired by this limitation, it is thought that the shape of the ego vehicle is determined, and the ego vehicle’s position, attitude, and speed information can also be accurately obtained through the simulation platform or sensors. Suppose that a polygon is fixed on the vehicle body coordinate system. The polygon follows the movement of the vehicle, and the shape can change according to the speed of the vehicle. When the speed of the vehicle is slow, the polygon range is small. The extent of the polygon also expands in accordance with the increase in the vehicle’s speed. When the ego vehicle is driving in an obstacle avoidance scene, the state function of the obstacle input part only considers the part that enters the polygonal area. For the reinforcement learning neural network, this method can screen and sort out the complex obstacle scenes with unfixed numbers and the location distribution, but only a part of external obstacles within a certain range will be quantitatively calculated.
The improved state input of the self-vehicle obstacle avoidance process is shown in
Figure 10. The input is divided into two areas, the sectorial area with the center of the ego vehicle as the dot and the extended rectangular area of the ego vehicle in the forward direction. The angle of the sector is determined by the maximum slip angle of the front wheels on both sides of the vehicle, while the width of the extended rectangular area depends on the bounding box length of the vehicle. Both areas take the center line of the vehicle’s forward direction as the axis. Among them, the sectorial area is divided by a group of equally angularly spaced line segments with the length of the sector radius. After encountering obstacles and lane boundary lines within the fan-shaped range, the corresponding inner-sector line segments will intersect with them. The data of line segments intersecting with the obstacles and lane boundary lines are stored as a list to represent the obstacle status within the sector. Similarly, the rectangular extension area of the yellow part is also divided by a cluster of equally spaced line segments. When obstacles and lane boundary lines are encountered and intersected with each other, the intersecting data of different interval line segments and obstacles are stored in a list to represent the status of obstacles in a rectangular area. The specific algorithm is shown in Algorithm 2:
| Algorithm 2. Obstacle input representation algorithm |
| Initialize the sectorial and rectangular areas according to the maximum slip angle of the front wheel, the size of the ego vehicle frame, and the speed of the ego vehicle. |
| Obtain the number and of the sectors and rectangles, and determine the angular interval of the sector and the distance interval of the rectangle . |
| Combine multiple obstacle vehicles and lane boundaries into one obstacle set. |
| Initialize the sector area representation , and the rectangle area representation within the extended area , in which represents the radius of the sector and represents the length of the rectangle. |
| # Calculate sector representation. |
| For in cycles do: |
| if The current line segment intersects the set of obstacles: |
| Confirm the intersection of the current line segment and the obstacle, and calculate the distance from the intersection to the origin, and update the corresponding |
| else: |
| The current corresponding section is not updated |
| end for |
| for in cycles do: |
| if The current line segment intersects the set of obstacles: |
| Confirm the intersection of the current line segment and the obstacle, and calculate the distance from the intersection to the corresponding horizontal reference line of the vehicle, and update the corresponding . |
| else: |
| The current corresponding section is not updated. |
| end for |
| Normalize the updated and . |
In the actual training process, the number of divisions of sectors and rectangles is set in advance by the parameter file, and the intervals are the same size, so the characterization of sectors and rectangles can be simplified as follows:
As mentioned above, the lengths of the sectorial area and the rectangular area in the process are proportional to the speed of the ego vehicle:
To represent the obstacle state at different ego vehicle speeds and calculate the reward function in the relevant state more accurately, the representation list in the region needs to be normalized, and the elements in
and
can be expressed as follows:
Take
Figure 10 as an example; the number of segmented rectangular areas is 10. After the algorithm and various optimizations, the representations in the sectorial area and the rectangular area are shown as
On the left side and right side of the sectorial area, there is an intersection with the obstacle, and the simplified distance from the intersection to the center of the vehicle is as above. If the area near the center of the sectorial symmetry axis has no intersection with the obstacle, the corresponding state list element is 1. In the rectangular area, there is no intersection between the rectangular area and the obstacle in the current round, so the elements of the state list are all 1. From the current scene graph and this representation, it can be directly inferred in the current round that the ego vehicle can go straight forward from the current attitude.
3.2. Corresponding Reward Function Design
The sectorial areas and rectangular areas mentioned above are all forward detection areas during the driving process of the ego vehicle. The obstacles or lane boundaries in the detection area might affect the driving state of the ego vehicle in the following process. According to the schematic diagram of the obstacle avoidance scene and the corresponding state representation of obstacles and lane boundaries, it is found that the larger the element value, the farther the direction is from the obstacle or the lane boundary. When the element value is 1, it means that within the current detection range, there are no obstacles or lane boundaries in this direction. For the obstacles and lane boundaries within the detection range, the closer they are to the ego vehicle, the greater the possibility that the ego vehicle will collide with the obstacles or exceed the lane boundary; the closer the obstacles or lane boundary is to the forward direction of the ego vehicle, the higher the possibility that the ego vehicle will collide with an obstacle or exceed the lane boundary.
In order to describe the reward function of obstacles at different positions at each moment relative to the ego vehicle, the state bias vector and weight vector can be introduced.
represents the sectorial state bias vector and
represents the rectangle state bias vector. The role of bias vectors is to make the state vectors symmetrically distributed. During the calculation process of reward function in this part, the two-state bias vectors and the obstacle and lane boundary state functions are superimposed to generate new state vectors. The inner product of the new state vectors and the weight vectors obtained by this part of the operation are used as the benchmarks for the reward function of the obstacle and lane boundary parts, as described in the following formula,
Among them,
is the weight vector of the sectorial area mentioned above. With the weight values, the closer to the center, the greater the weight, which means that the obstacle or boundary distance corresponding to the position has a greater impact on the driving of the ego vehicle. To obtain a large reward value, the ego vehicle tends to approach the driving state in which there are no obstacles and boundaries in the forward direction as much as possible. Similarly, the reward function in the rectangular area is as follows:
represents the weight vector of the rectangular area mentioned above. Different from
,
represents the weight vector of the ego vehicle’s forward direction. As long as an external obstacle appears anywhere within the area, the vehicle will collide with the obstacle or exceed the lane boundary if it continues to go straight forward. Therefore, the weight of this area does now show much difference. There is little difference between the weights in this area.
In this obstacle representation method, the detection range is designed for different numbers of obstacles, and the input state of obstacles is unified, which is convenient to generate more complex data in the training process. Additionally, this method is used to unify the obstacle vehicles that need to be considered at each moment and the lane boundary lines on both sides into an obstacle set, which simplifies the separate discussion of obstacles and lane boundary modules in the obstacle avoidance process. This part of the reward replaces the reward section
and
, and the rest is the same as the previous section, which can be described as follows,
3.3. Simulation Results and Analysis
In the training process of the improved obstacle avoidance method, we enhance the environment complexity in the training process of the reinforcement learning neural network, which is embodied as follows: We have increased the randomness of the obstacle position and the randomness of the obstacle vehicle direction. In the obstacle environment of each episode, the scene of two vehicles side by side often occurs, resulting in a narrow traversable area at this location, and higher requirements for the attitudes of passing vehicles near this location. As shown in
Figure 11, in these scenarios, under the model of the obstacle input state and reward function designed with the traditional method, the success rate of the ego vehicle passing through the area is low.
In order to compare with traditional classical methods, we also add the trajectory of the lattice planner into the same scenario. The lattice planner is a graph-based approach to the path planning issue that reduces the search space into a uniform discretization of vertices corresponding to positions and headings. It generates multiple obstacle avoidance trajectories, and then selects the most suitable one according to the cost ranking. The algorithm has good performance in both real vehicle and simulated obstacle avoidance scenes.
The trajectory comparison of the three obstacle avoidance methods is presented in
Figure 11. The dark blue rectangle is obstacle vehicles on the road, and they are distributed in a random state within a specific range. The cyan one refers to the driving trajectory of the ego vehicle frame using the multi-obstacle input method, and the black points are the center locations of the ego vehicle during the whole episode. The green points represent the final trajectory points generated by the lattice planner. The red rectangle is the bounding trajectories of the ego vehicle using the reinforcement learning method with the traditional obstacle representation method. Specifically, in the first obstacle scene in the series, the side-by-side vehicles appear next to the first vehicle. Although the three obstacle avoidance methods all have passed the obstacle field in the simulation verification, the driving trajectories in the narrow area are slightly different. Similar to the traditional method lattice planner, the trajectory using the obstacle avoidance method with the obstacle state representation in
Section 3 is smoother when passing through narrow areas, and the obstacle avoidance effect is more stable when compared with the ordinary obstacle avoidance method. It can be seen from the obstacle scenes in the series diagram that the ego vehicle, based on the common obstacle avoidance RL method, collided with obstacle vehicles. However, the obstacle avoidance method in
Section 3 can still pass in a relatively stable state even though the traversable area is narrow.
Table 1 displays the statistics of the obstacle avoidance performance parameters of three methods. It is found that both our work and the lattice planner have better performance, but the lattice planner consumes a longer time per step and is more unstable. Although the common RL algorithm takes the shortest time and is relatively stable, it has limited ability of passing through complex obstacles. Our improved algorithm has the best and most stable passing performance, taking a relatively short time with the highest success rate.
From the results and obstacle avoidance trajectories of the above three obstacle avoidance methods, it can be seen that the improved multi-obstacle environment state and reward function design method can uniformly process the external obstacles with random numbers and attitudes so that the ego vehicle can better pass obstacle areas in complex obstacle scenarios.