Design Methodology for a Magnetic Levitation System Based on a New Multi-Objective Optimization Algorithm
Abstract
:1. Introduction
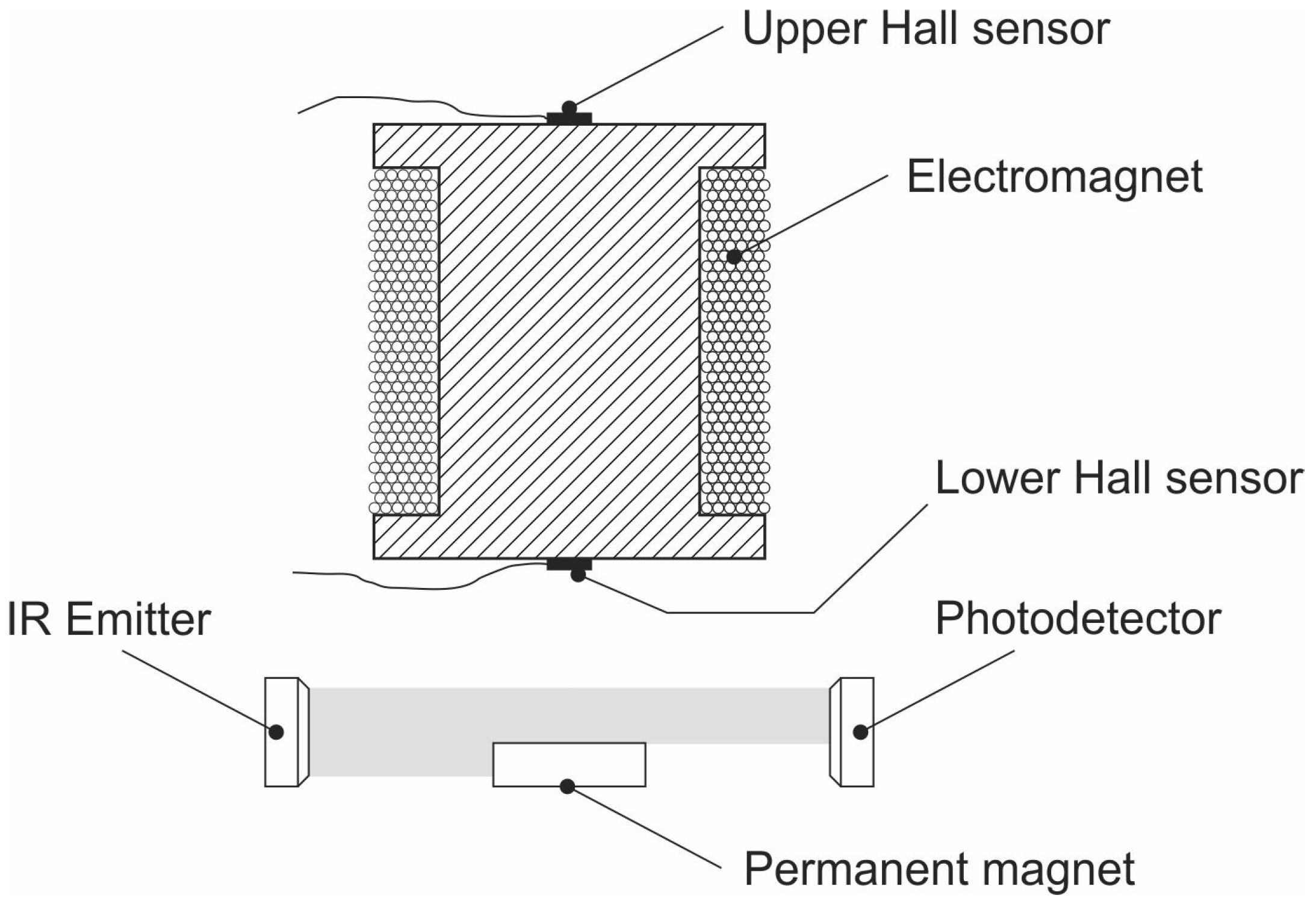
2. Materials and Methods: The Magnetic Levitation System
2.1. Object
2.1.1. Determination of the Magnetic Force
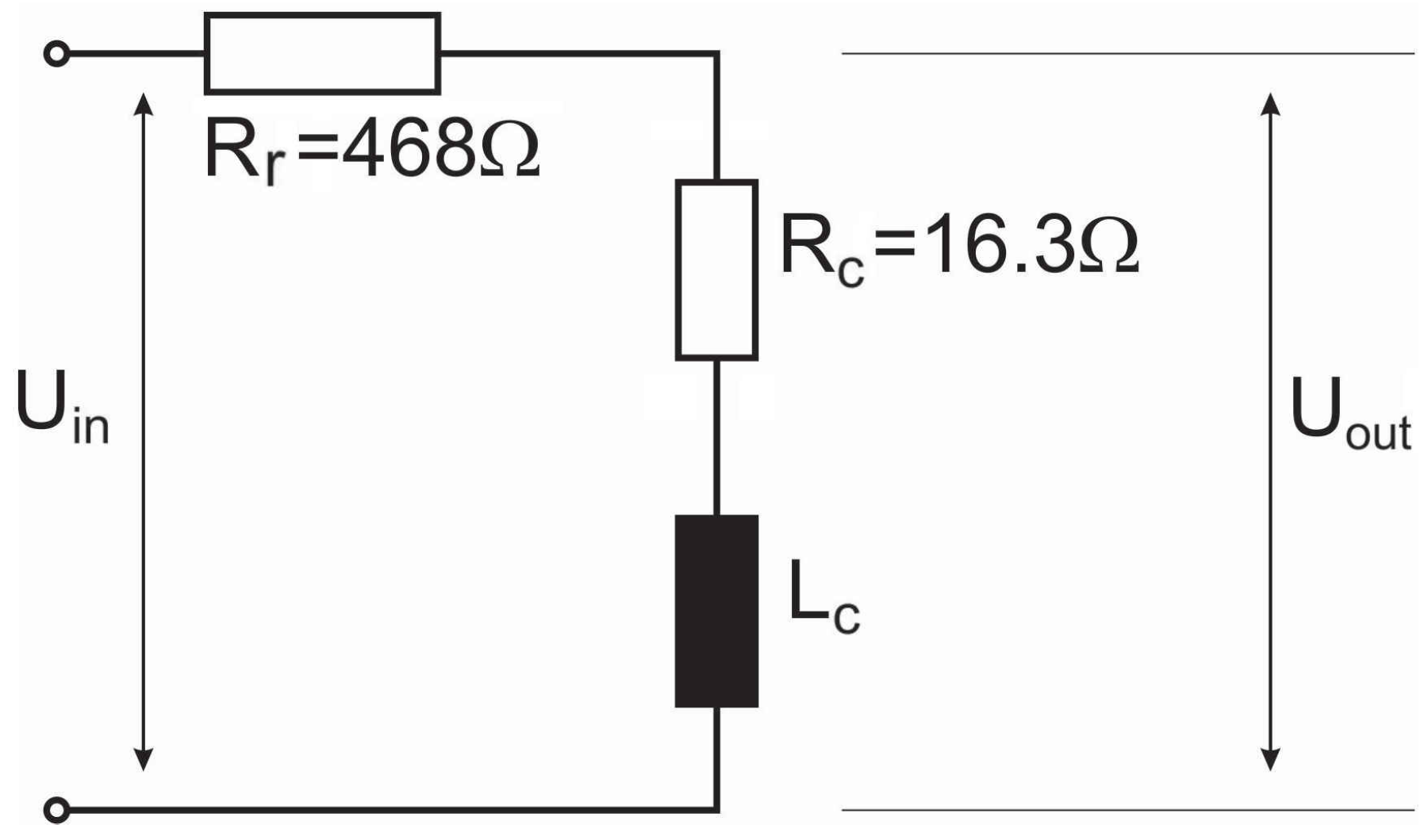
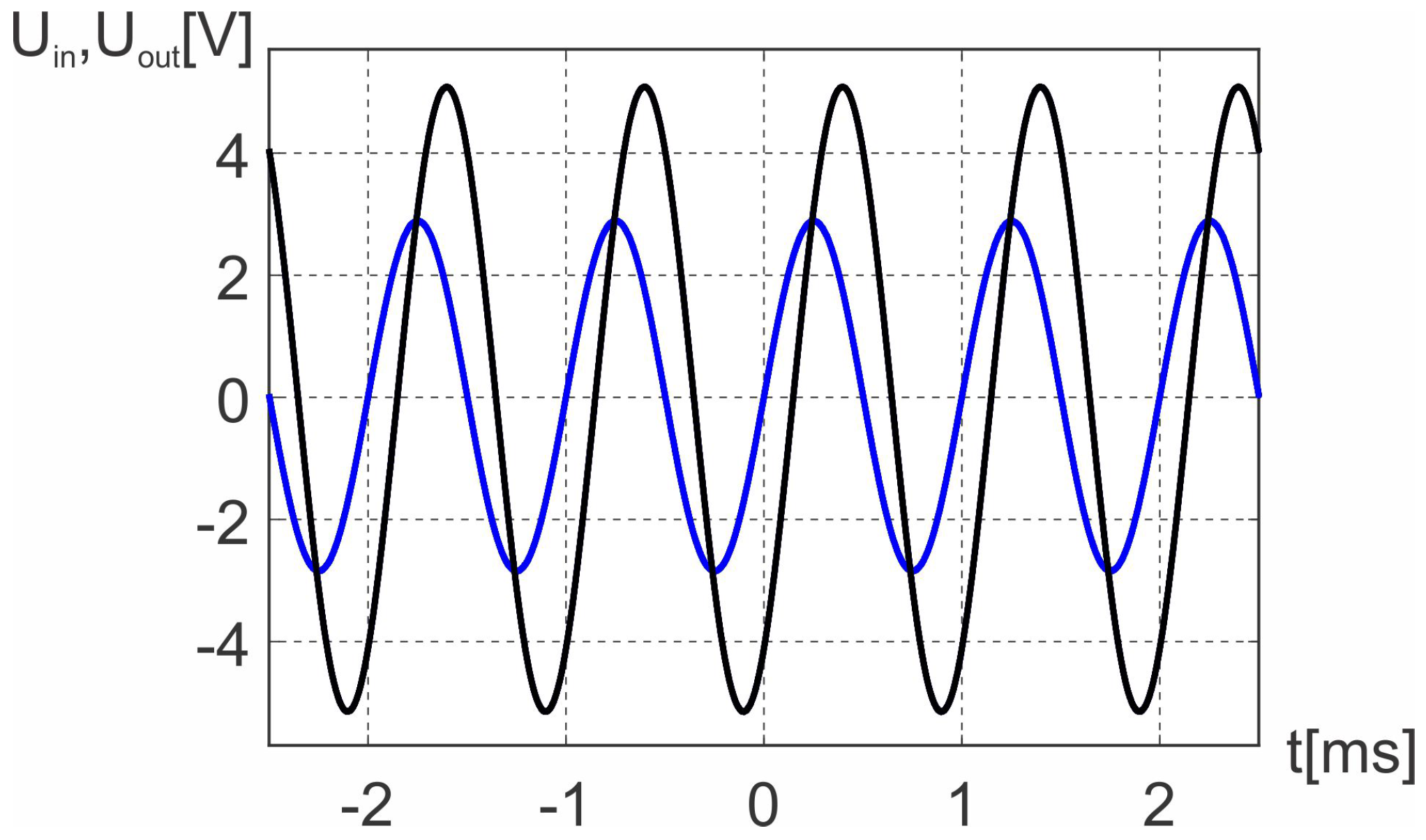
2.1.2. Experimental Determination of Coil Resistance and Inductance
2.1.3. The Transfer Function of the Object
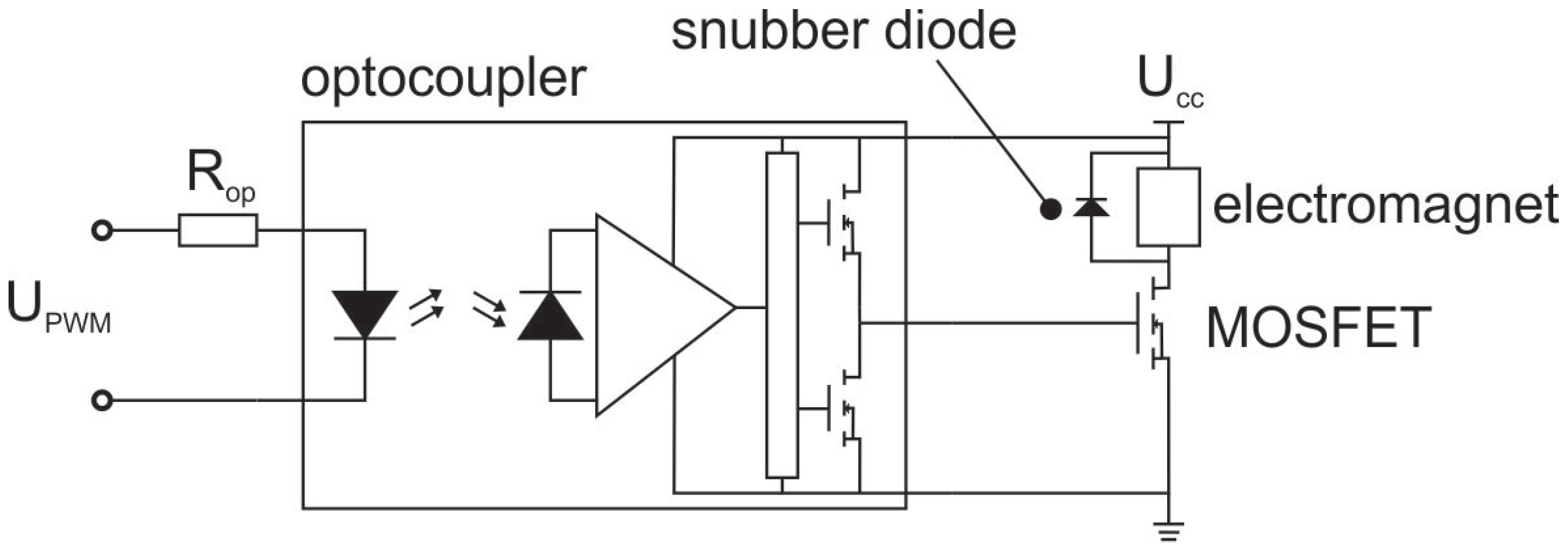
2.2. Actuator
2.3. Sensor
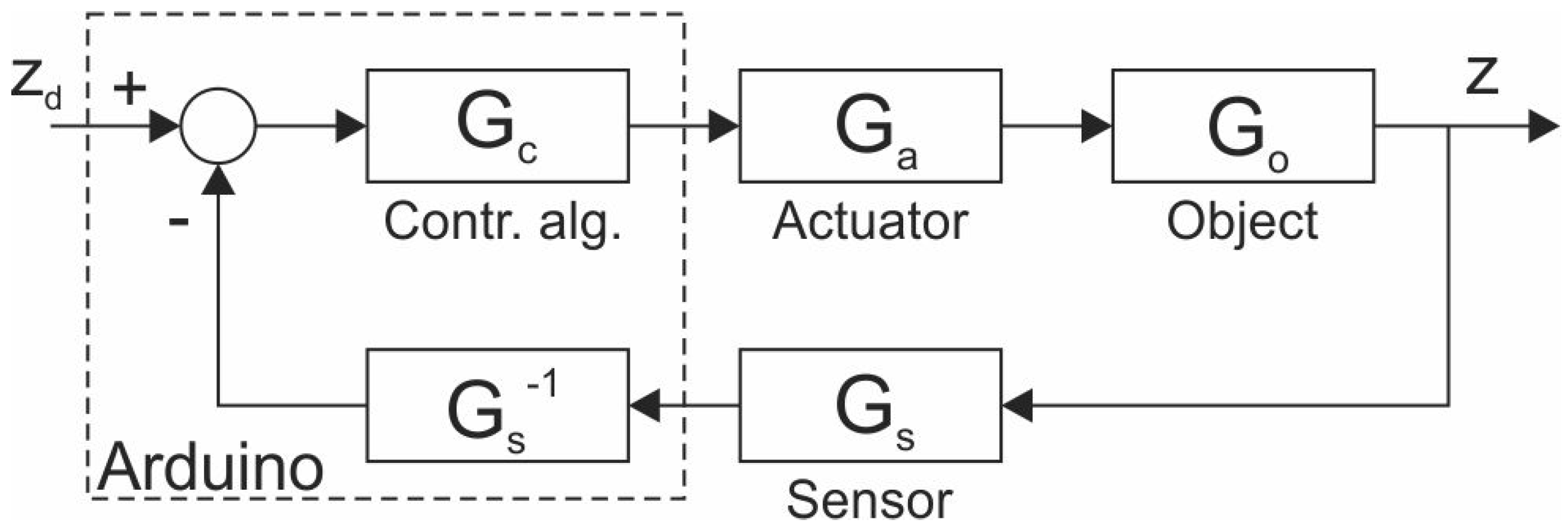
2.4. Controller
3. Materials and Methods: The Developed Algorithm
3.1. Problem Statement
3.2. Description of the Algorithm
- Let M be the number of simulations we would like to perform with a given transfer function.
- Assume , and to be the limits of the controller parameters, thenwhere and are uniformly distributed random numbers. This algorithm can scan any region of parameter space of interest, however for the initial search it is safe to assume that The upper limit, however, requires more attention since the equipment at hand may not handle too large values of the controller parameters. For example, in our case the upper limit of the electrical current in the coil was around 1A, or, in terms of voltage—. It is easy to calculate the upper limits with the inverse Laplace transform of the expressionwhere is the height (difference) a magnet needs to move up by. By substituting the in the resulting expression of , one may find whether the modeled response would correspond to that of a real plant.
- t– current time that the algorithm uses for calculations. Starts from zero;
- —the value of the step response signal at the current time t;
- —the value of the step response signal’s derivative at the current time t;
- —the time step. This value changes as the algorithm progresses, depending on the step response. You can safely start with a very low value as the algorithm quickly finds the suitable time step for your process. For example, if one can ignore the changes occurring on the time scale of 1 ns, then the initial value can be ns.
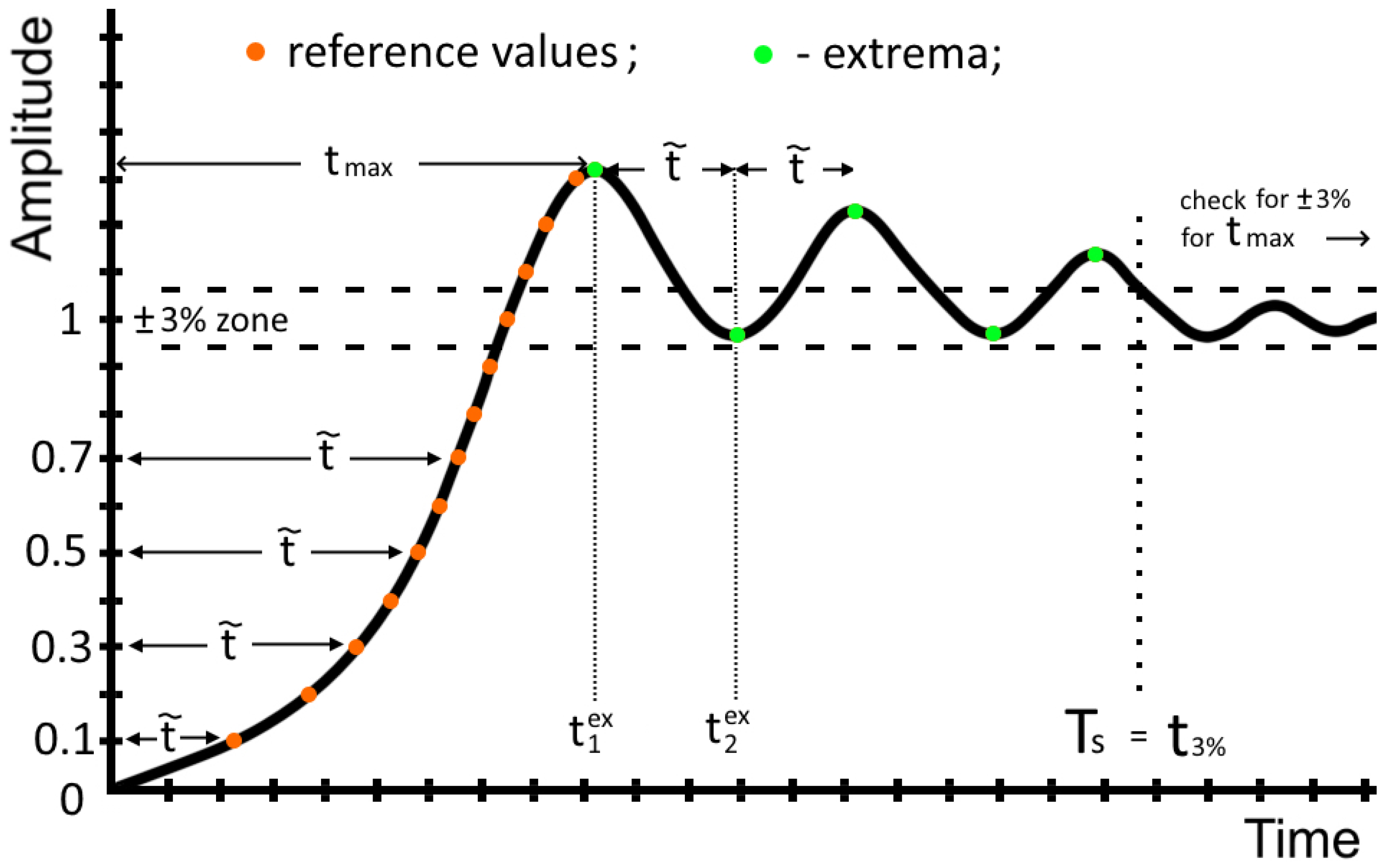
- —key parameter, the current recorded reference time. The two mechanisms for when this value changes are described later;
- —how many decimal amplitude values the signal has crossed. An auxiliary counter needed for the first mechanism for detecting ;
- —an auxiliary counter needed for the second mechanism for detecting . Number of local extremums;
- —the minimum out of all recorded reference times . Needed for the calculation of the time step . This parameter helps the algorithm to distinguish the possible rapid oscillations (see Figure 12);
- —a positive integer regulating how fine do we divide the shortest reference time to calculate the . Increase this parameter for additional accuracy;
- —the largest reference time used as a verification for determining the settling time ;
- —the time of a local extremum;
- —the amplitude of a local extremum;
- —the time when the signal reached the range;
- —the settling time of the current curve;
- —percentage overshoot;
- —the amplitude difference between neighboring oscillations;
- —largest amplitude between neighboring oscillations. This helps to understand the scale of oscillations of the signal. If the number of local extremums then this value is not defined.
| Algorithm 1 Processing of the given signal. Using the following algorithm, we gather large statistical data |
|
4. Results and Discussion
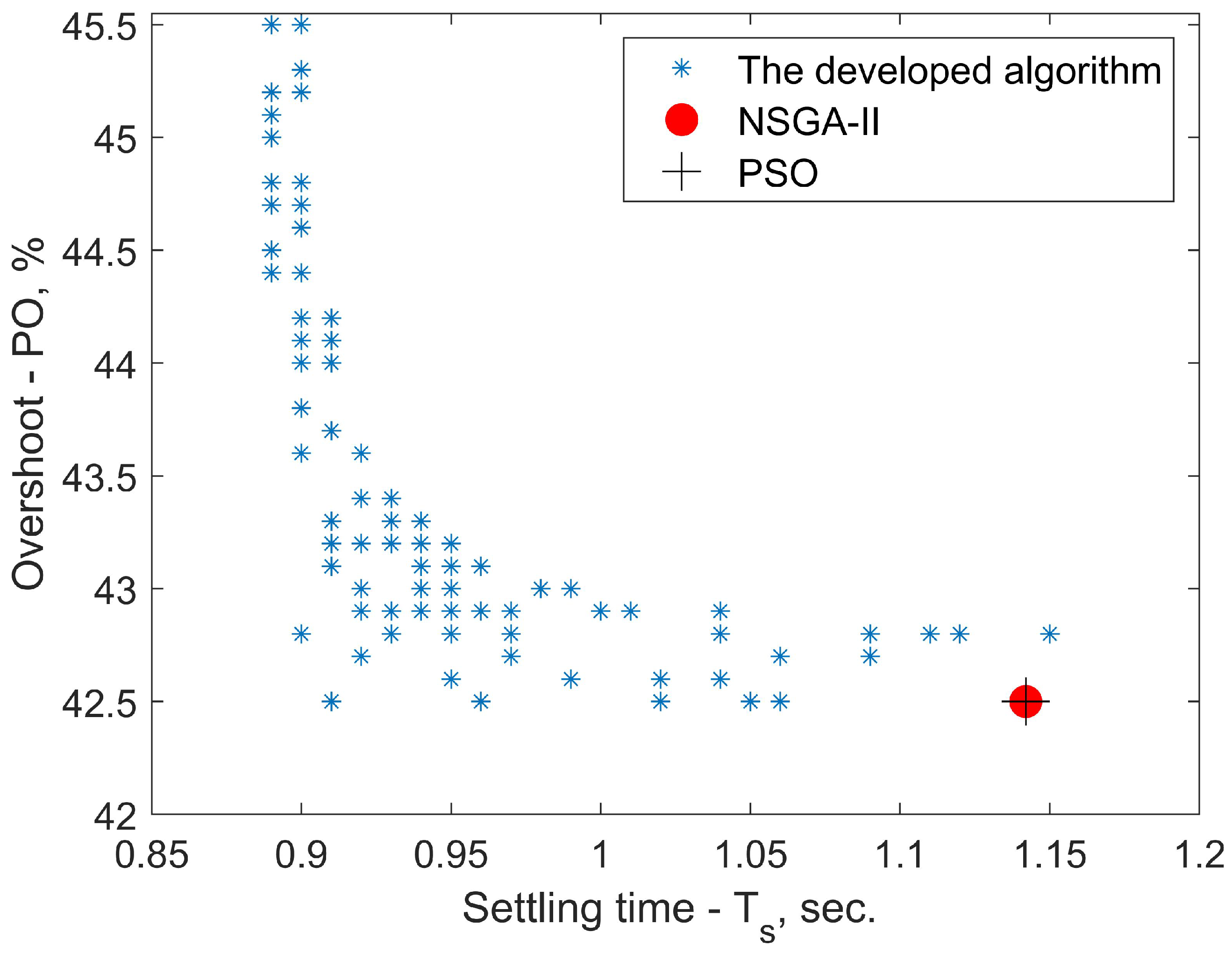
4.1. Multi-Objective Optimization
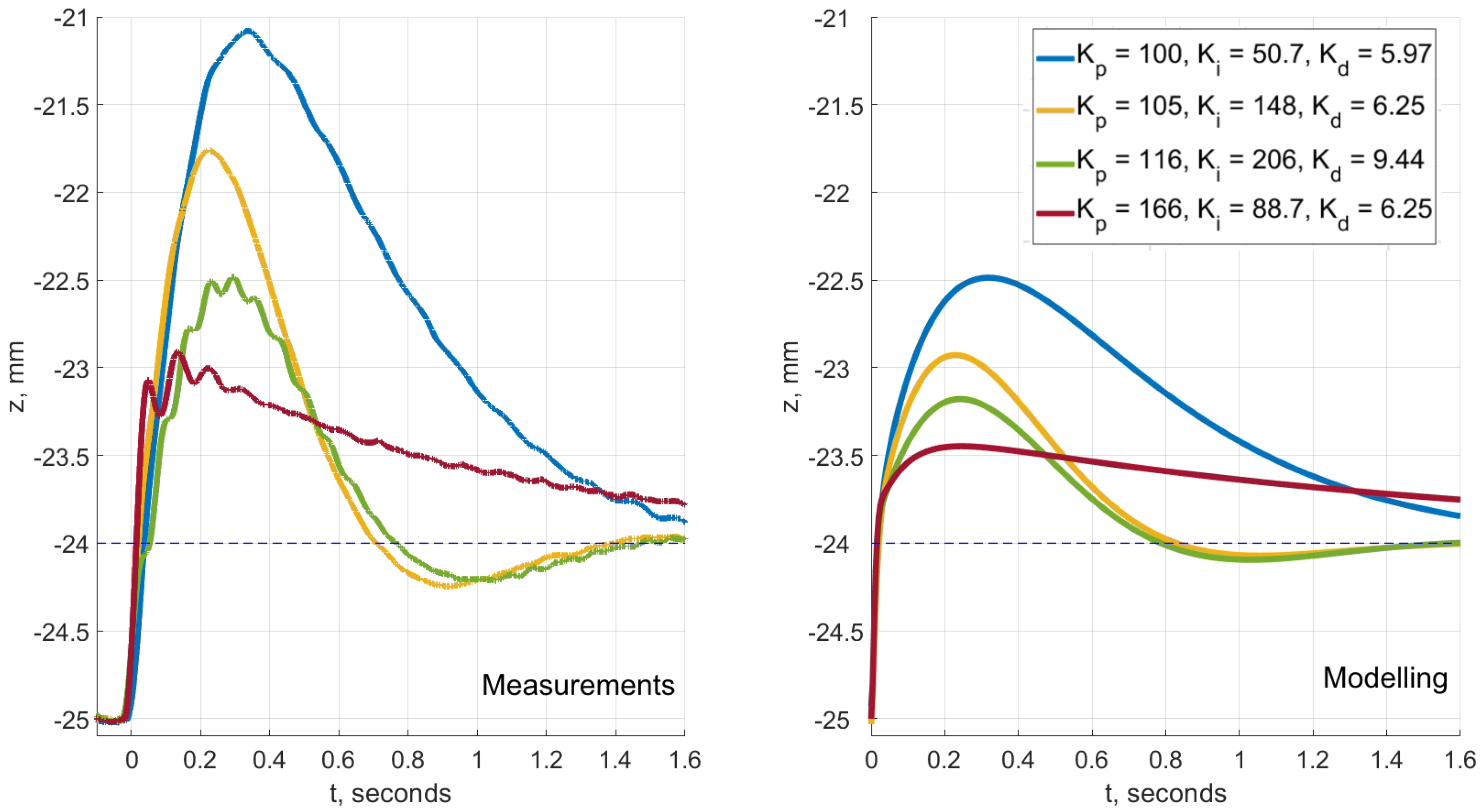
4.2. Experimental Verification
4.3. The Multi-Objective Problem for Optimal Coil Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Astrom, K.J.; Hagglund, T. Advanced PID Control; ISA-The Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 2006. [Google Scholar]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control. Syst. Technol. 2005, 13, 559–576. [Google Scholar] [CrossRef] [Green Version]
- Astolfi, A. Model reduction by moment matching for nonlinear systems. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancún, Mexico, 9–11 December 2008; pp. 4873–4878. [Google Scholar] [CrossRef]
- Shrivastava, N.; Varshney, P. Comparative analysis of order reduction techniques. In Proceedings of the 2016 Second International Innovative Applications of Computational Intelligence on Power, Energy and Controls with their Impact on Humanity (CIPECH), Ghaziabad, India, 18–19 November 2016; pp. 46–50. [Google Scholar] [CrossRef]
- Doetsch, G. Introduction to the Theory and Application of the Laplace Transformation; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Cohen, A. Numerical Methods for Laplace Transform Inversion; Numerical Methods and Algorithms; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Davies, B.; Martin, B. Numerical inversion of the Laplace transform: A survey and comparison of methods. J. Comput. Phys. 1979, 33, 1–32. [Google Scholar] [CrossRef]
- Hosono, T. Numerical inversion of Laplace transform and some applications to wave optics. Radio Sci. 1981, 16, 1015–1019. [Google Scholar] [CrossRef]
- Yan, L. Development and application of the maglev transportation system. IEEE Trans. Appl. Supercond. 2008, 18, 92–99. [Google Scholar]
- Wai, R.J.; Lee, J.D.; Chuang, K.L. Real-time PID control strategy for maglev transportation system via particle swarm optimization. IEEE Trans. Ind. Electron. 2010, 58, 629–646. [Google Scholar] [CrossRef]
- Peijnenburg, A.; Vermeulen, J.; Van Eijk, J. Magnetic levitation systems compared to conventional bearing systems. Microelectron. Eng. 2006, 83, 1372–1375. [Google Scholar] [CrossRef]
- Fang, J.; Le, Y.; Sun, J.; Wang, K. Analysis and design of passive magnetic bearing and damping system for high-speed compressor. IEEE Trans. Magn. 2012, 48, 2528–2537. [Google Scholar] [CrossRef]
- Barry, N.; Casey, R. Elihu Thomson’s jumping ring in a levitated closed-loop control experiment. IEEE Trans. Educ. 1999, 42, 72–80. [Google Scholar] [CrossRef]
- Boudali, H.; Williams, R.; Giras, T. A Simulink simulation framework of a MagLev model. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2003, 217, 227–236. [Google Scholar] [CrossRef]
- Berkelman, P.; Dzadovsky, M. Magnetic levitation over large translation and rotation ranges in all directions. IEEE/ASME Trans. Mechatronics 2011, 18, 44–52. [Google Scholar] [CrossRef]
- Yaseen, M.H.; Abd, H.J. Modeling and control for a magnetic levitation system based on SIMLAB platform in real time. Results Phys. 2018, 8, 153–159. [Google Scholar] [CrossRef]
- Chopade, A.S.; Khubalkar, S.W.; Junghare, A.; Aware, M.; Das, S. Design and implementation of digital fractional order PID controller using optimal pole-zero approximation method for magnetic levitation system. IEEE/CAA J. Autom. Sin. 2016, 5, 977–989. [Google Scholar] [CrossRef]
- Morales, R.; Sira-Ramírez, H. Trajectory tracking for the magnetic ball levitation system via exact feedforward linearisation and GPI control. Int. J. Control 2010, 83, 1155–1166. [Google Scholar] [CrossRef]
- Awelewa, A.A.; Samuel, I.A.; Abdulkareem, A.; Iyiola, S.O. An Undergraduate Control Tutorial on Root Locus-Based Magnetic Levitation System Stabilization. Int. J. Eng. Comput. Sci. 2013, 13, 22–30. [Google Scholar]
- Hurley, W.G.; Wolfle, W.H. Electromagnetic design of a magnetic suspension system. IEEE Trans. Educ. 1997, 40, 124–130. [Google Scholar] [CrossRef]
- Oguchi, K.; Tomigashi, Y. Digital control for a magnetic suspension system as an undergraduate project. Int. J. Electr. Eng. Educ. 1990, 27, 226–236. [Google Scholar] [CrossRef]
- Wei, W.; Xue, W.; Li, D. On disturbance rejection in magnetic levitation. Control Eng. Pract. 2019, 82, 24–35. [Google Scholar] [CrossRef]
- Salim, T.T.; Karsli, V.M. Control of single axis magnetic levitation system using fuzzy logic control. Int. J. Adv. Comput. Sci. Appl. 2013, 4, 83–88. [Google Scholar]
- Al-Muthairi, N.; Zribi, M. Sliding mode control of a magnetic levitation system. Math. Probl. Eng. 2004, 2004, 93–107. [Google Scholar] [CrossRef] [Green Version]
- Kuo, C.L.; Li, T.H.S.; Guo, N.R. Design of a novel fuzzy sliding-mode control for magnetic ball levitation system. J. Intell. Robot. Syst. 2005, 42, 295–316. [Google Scholar] [CrossRef]
- Oliveira, V.A.; Tognetti, E.S.; Siqueira, D. Robust controllers enhanced with design and implementation processes. IEEE Trans. Educ. 2006, 49, 370–382. [Google Scholar] [CrossRef]
- de Jesús Rubio, J.; Zhang, L.; Lughofer, E.; Cruz, P.; Alsaedi, A.; Hayat, T. Modeling and control with neural networks for a magnetic levitation system. Neurocomputing 2017, 227, 113–121. [Google Scholar] [CrossRef]
- Hajjaji, A.E.; Ouladsine, M. Modeling and nonlinear control of magnetic levitation systems. IEEE Trans. Ind. Electron. 2001, 48, 831–838. [Google Scholar] [CrossRef] [Green Version]
- Morales, R.; Feliu, V.; Sira-Ramirez, H. Nonlinear control for magnetic levitation systems based on fast online algebraic identification of the input gain. IEEE Trans. Control Syst. Technol. 2011, 19, 757–771. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.J. Real-Time Implementation of the Prescribed Performance Tracking Control for Magnetic Levitation Systems. Sensors 2022, 22, 9132. [Google Scholar] [CrossRef] [PubMed]
- Maximov, S.; Gonzalez-Montañez, F.; Escarela-Perez, R.; Olivares-Galvan, J.C.; Ascencion-Mestiza, H. Analytical Analysis of Magnetic Levitation Systems with Harmonic Voltage Input. Actuators 2020, 9, 82. [Google Scholar] [CrossRef]
- Tipler, P.A.; Mosca, G. Physics for Scientists and Engineers, 6th ed.; W. H. Freeman and Company: New York, NY, USA, 2008. [Google Scholar]
- Serway, R.A.; Jewett, J.W. Physics for Scientists and Engineers with Modern Physics, 9th ed.; Brooks/Cole: Salt Lake City, UT, USA, 2014. [Google Scholar]
- de Queiroz, A.C.M. Mutual Inductance and Inductance Calculations by Maxwell’s Method. 2014. Available online: http://www.coe.ufrj.br/~acmq/programs (accessed on 7 March 2020).
- Galvão, R.K.H.; Yoneyama, T.; Araújo, F.M.U.; Machado, R.G. A simple technique for identifying a linearized model for a didactic magnetic levitation system. IEEE Trans. Educ. 2003, 46, 22–25. [Google Scholar] [CrossRef]
- Lin, C.M.; Lin, M.H.; Chen, C.W. SoPC-based adaptive PID control system design for magnetic levitation system. IEEE Syst. J. 2011, 5, 278–287. [Google Scholar] [CrossRef]
- Zhang, Y.; Xian, B.; Ma, S. Continuous robust tracking control for magnetic levitation system with unidirectional input constraint. IEEE Trans. Ind. Electron. 2015, 62, 5971–5980. [Google Scholar] [CrossRef]
- Bächle, T.; Hentzelt, S.; Graichen, K. Nonlinear model predictive control of a magnetic levitation system. Control Eng. Pract. 2013, 21, 1250–1258. [Google Scholar] [CrossRef]
- Folea, S.; Muresan, C.I.; De Keyser, R.; Ionescu, C.M. Theoretical analysis and experimental validation of a simplified fractional order controller for a magnetic levitation system. IEEE Trans. Control Syst. Technol. 2015, 24, 756–763. [Google Scholar] [CrossRef]
- Lundberg, K.H.; Lilienkamp, K.A.; Marsden, G. Low-cost magnetic levitation project kits. IEEE Control Syst. Mag. 2004, 24, 65–69. [Google Scholar]
- Chalupa, P.; Maly, M.; Novák, J. Nonlinear Simulink Model Of Magnetic Levitation Laboratory Plant. In Proceedings of the ECMS, Regensburg, Germany, 31 May–3 June 2016; pp. 293–299. [Google Scholar]
- Chalupa, P.; Novák, J.; Malỳ, M. Modelling and model predictive control of magnetic levitation laboratory plant. In Proceedings of the 31st European Conference on Modelling and Simulation, ECMS 2017, Budapest, Hungary, 23–26 May 2017; European Council for Modelling and Simulation: Caserta, Italy, 2017. [Google Scholar]
- da Silva, L.R.; Flesch, R.C.C.; Normey-Rico, J.E. Controlling industrial dead-time systems: When to use a PID or an advanced controller. ISA Trans. 2020, 99, 339–350. [Google Scholar] [CrossRef]
- Sánchez, J.; Guinaldo, M.; Visioli, A.; Dormido, S. Identification of process transfer function parameters in event-based PI control loops. ISA Trans. 2018, 75, 157–171. [Google Scholar] [CrossRef] [PubMed]
- Balaguer, P.; Alfaro, V.; Arrieta, O. Second order inverse response process identification from transient step response. ISA Trans. 2011, 50, 231–238. [Google Scholar] [CrossRef]
- Ozsoy, M.; Sims, N.D.; Ozturk, E. Robotically assisted active vibration control in milling: A feasibility study. Mech. Syst. Signal Process. 2022, 177, 109152. [Google Scholar] [CrossRef]
- Chen, J.; Ma, D.; Xu, Y.; Chen, J. Delay Robustness of PID Control of Second-Order Systems: Pseudoconcavity, Exact Delay Margin, and Performance Tradeoff. IEEE Trans. Autom. Control 2022, 67, 1194–1209. [Google Scholar] [CrossRef]
- Mercorelli, P.; Lehmann, K.; Liu, S. Robust flatness based control of an electromagnetic linear actuator using adaptive PID controller. In Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat. No.03CH37475), Maui, HI, USA, 9–12 December 2003; Volume 4, pp. 3790–3795. [Google Scholar] [CrossRef]
- Mercorelli, P. An Antisaturating Adaptive Preaction and a Slide Surface to Achieve Soft Landing Control for Electromagnetic Actuators. IEEE/ASME Trans. Mechatronics 2012, 17, 76–85. [Google Scholar] [CrossRef]
- Zhao, C.; Guo, L. Control of Nonlinear Uncertain Systems by Extended PID. IEEE Trans. Autom. Control 2021, 66, 3840–3847. [Google Scholar] [CrossRef]
- Babajamali, Z.; Khabaz, M.K.; Aghadavoudi, F.; Farhatnia, F.; Eftekhari, S.A.; Toghraie, D. Pareto multi-objective optimization of tandem cold rolling settings for reductions and inter stand tensions using NSGA-II. ISA Trans. 2022, 130, 399–408. [Google Scholar] [CrossRef]
- Yusoff, Y.; Ngadiman, M.S.; Zain, A.M. Overview of NSGA-II for Optimizing Machining Process Parameters. Procedia Eng. 2011, 15, 3978–3983. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Mathworks. Global Optimization Toolbox User’s Guide; Mathworks: Natick, MA, USA, 2018. [Google Scholar]
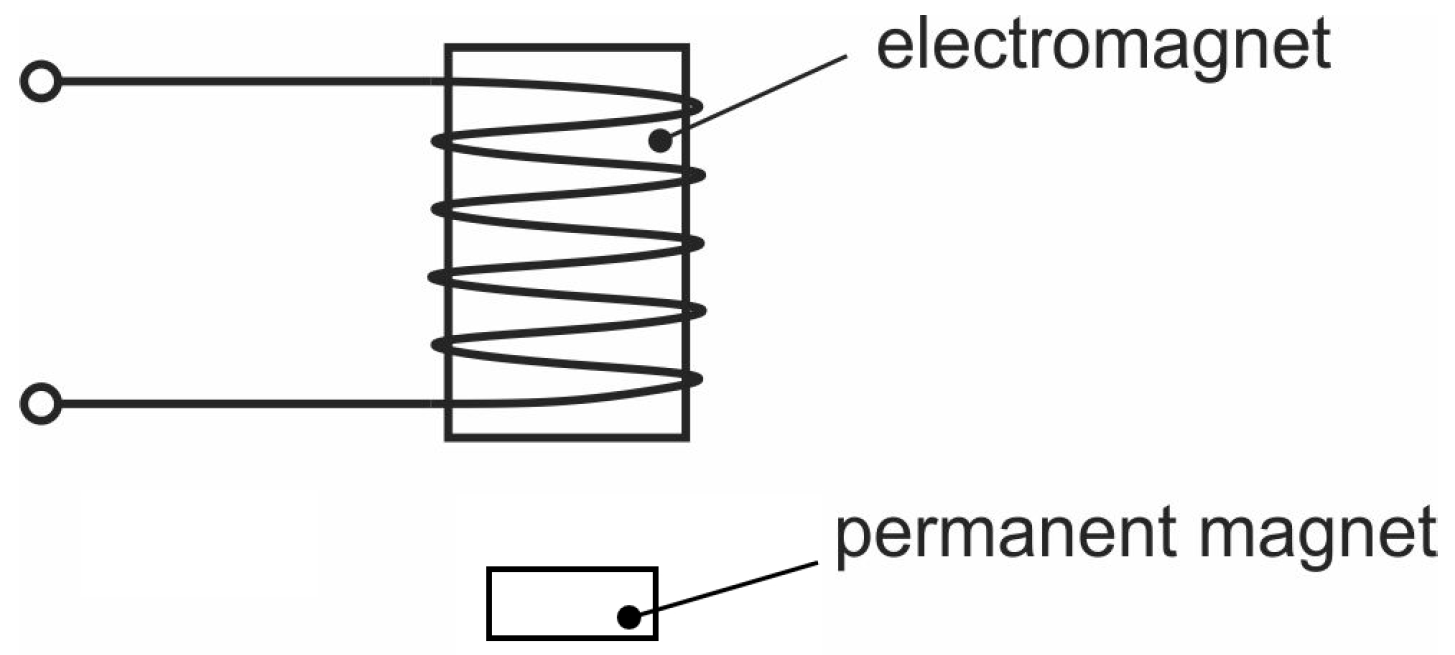




| i A | 0 A | 0.2 A | 0.4 A | 0.6 A | 0.8 A | 1.0 A |
|---|---|---|---|---|---|---|
| mm | 0 mN | 52.0 mN | 101.0 mN | 151.1 mN | 200.1 mN | 250.2 mN |
| mm | 0 mN | 32.4 mN | 63.8 mN | 94.2 mN | 126.5 mN | 156.0 mN |
| mm | 0 mN | 23.5 mN | 45.1 mN | 65.7 mN | 86.3 mN | 106.9 mN |
| mm | 0 mN | 14.7 mN | 28.4 mN | 42.2 mN | 54.9 mN | 68.7 mN |
| mm | 0 mN | 9.8 mN | 18.6 mN | 28.4 mN | 38.3 mN | 48.1 mN |
| mm | 0 mN | 6.9 mN | 13.7 mN | 20.6 mN | 27.5 mN | 33.4 mN |
| Function | ||||
|---|---|---|---|---|
| SSE | 0.0026 | 0.017 | 0.022 |
| z [mm] | [V] |
|---|---|
| 3.32 | |
| 1.20 | |
| 0.504 | |
| 0.219 | |
| 0.135 | |
| 0.072 |
| (s) | k | PO | (s) | ||||
|---|---|---|---|---|---|---|---|
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 223 | 875 | 9.58 | 0.49 | 1 | — | 61.3 | 0.0026 |
| 534 | 938 | 6.75 | 0.74 | 3 | 0.59 | 80.7 | 0.0032 |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 85.1 | 171 | 3.67 | 1.41 | 4 | 2.7 | 129 | 0.0047 |
| 224 | 391 | 8.15 | 0.26 | 1 | — | 63.5 | 0.0030 |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reznichenko, I.; Podržaj, P. Design Methodology for a Magnetic Levitation System Based on a New Multi-Objective Optimization Algorithm. Sensors 2023, 23, 979. https://doi.org/10.3390/s23020979
Reznichenko I, Podržaj P. Design Methodology for a Magnetic Levitation System Based on a New Multi-Objective Optimization Algorithm. Sensors. 2023; 23(2):979. https://doi.org/10.3390/s23020979
Chicago/Turabian StyleReznichenko, Igor, and Primož Podržaj. 2023. "Design Methodology for a Magnetic Levitation System Based on a New Multi-Objective Optimization Algorithm" Sensors 23, no. 2: 979. https://doi.org/10.3390/s23020979






