Electron Temperature Measurements Using a Two-Filter Soft X-ray Array in VEST
Abstract
:1. Introduction
2. Design of the Two-Filter Soft X-ray Array
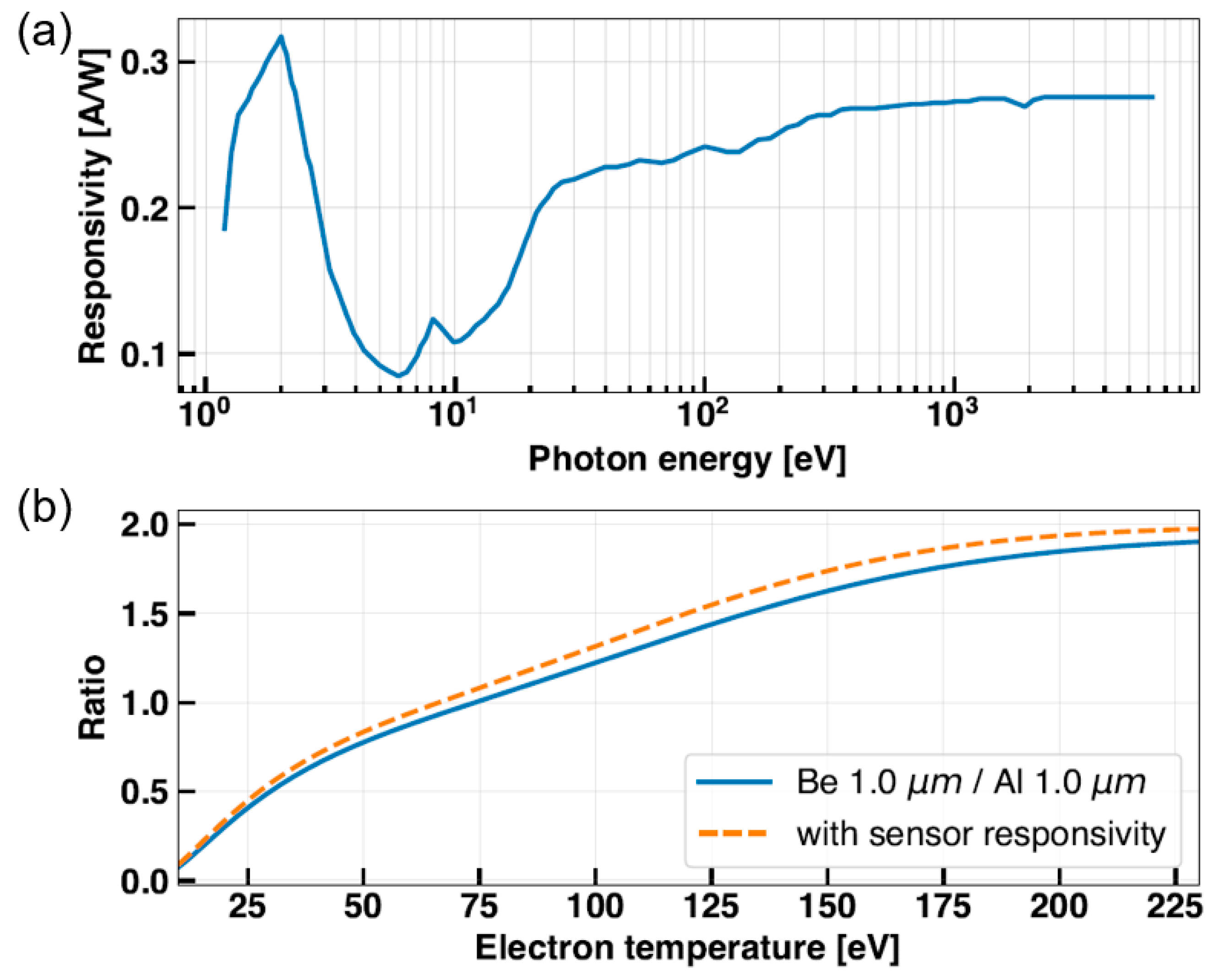
2.1. Selection of Soft X-ray Filters
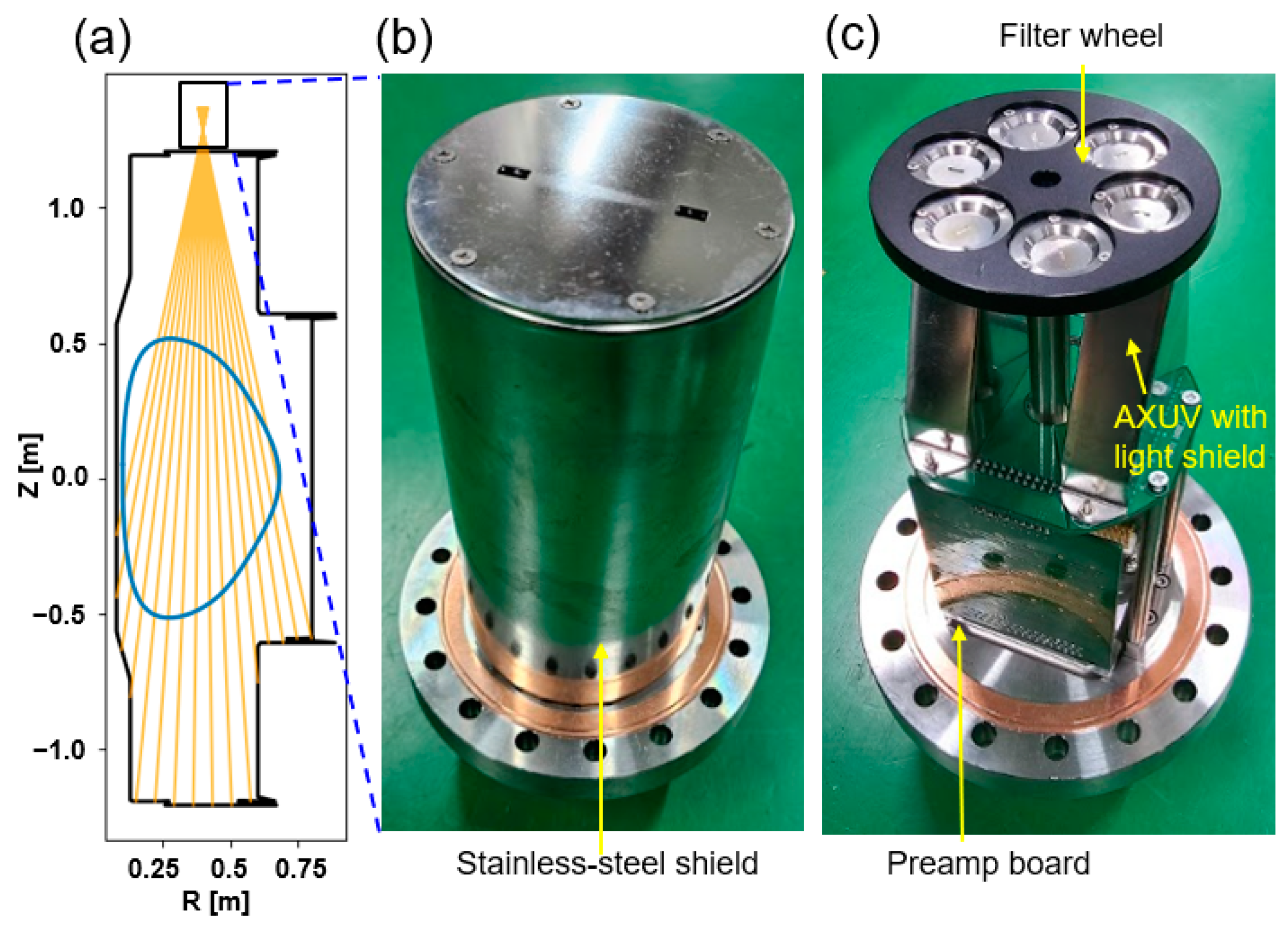
2.2. Pinhole Camera
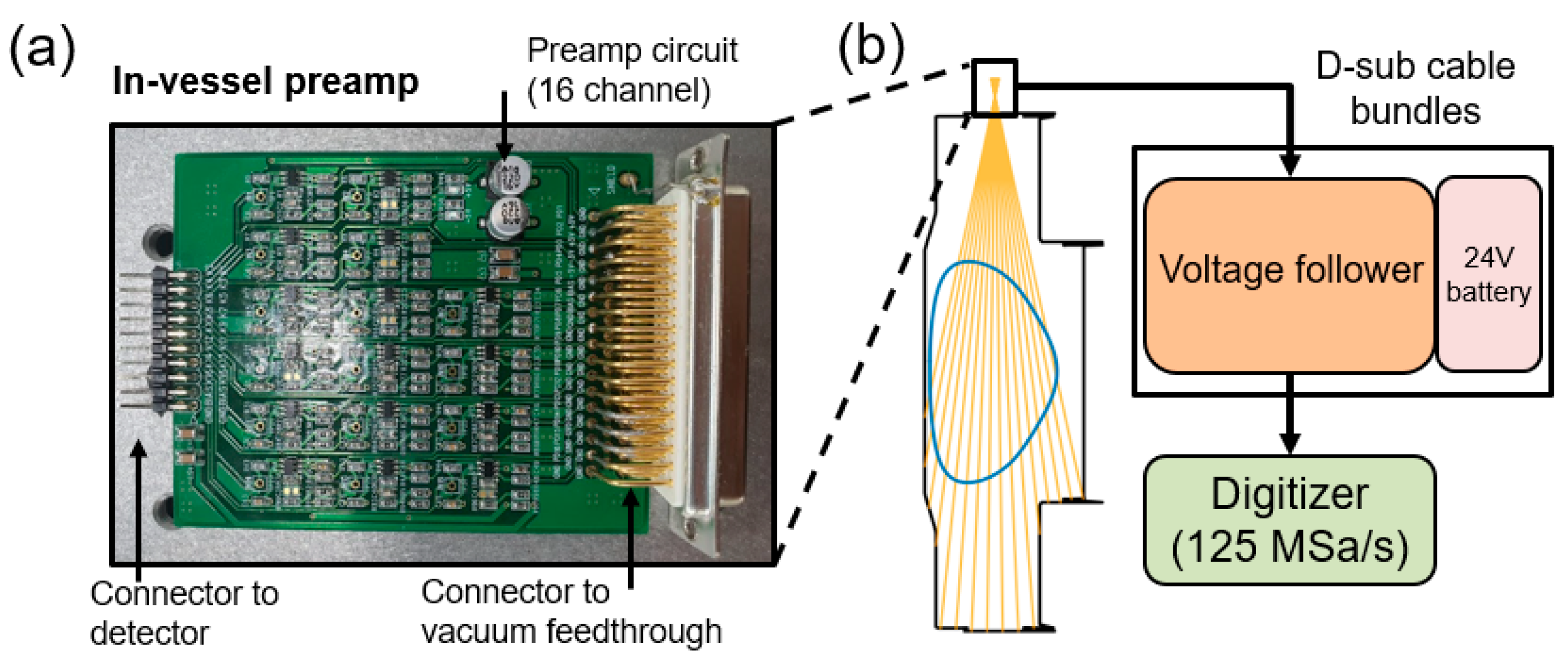
2.3. Electronics and Data Acquisition
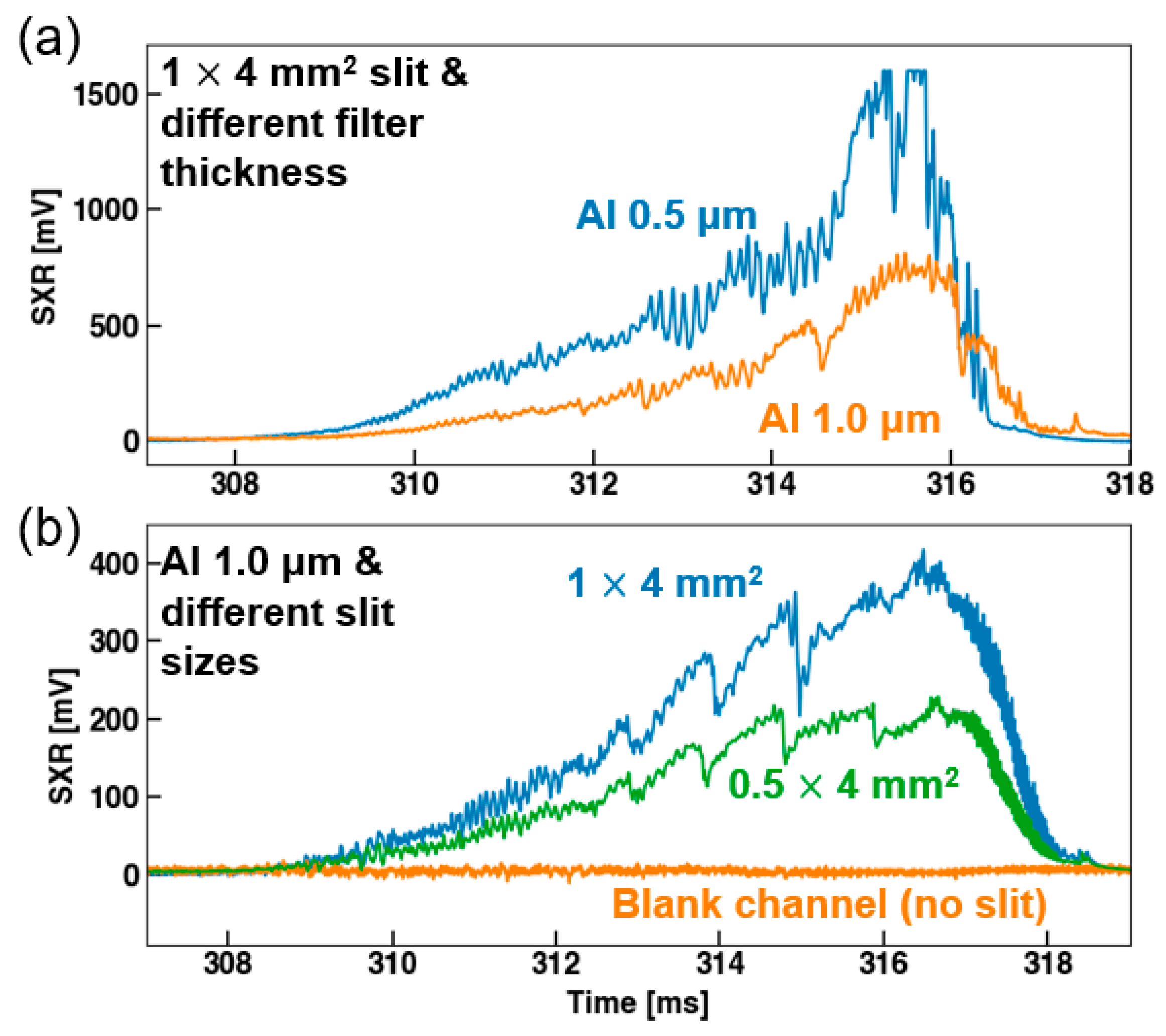
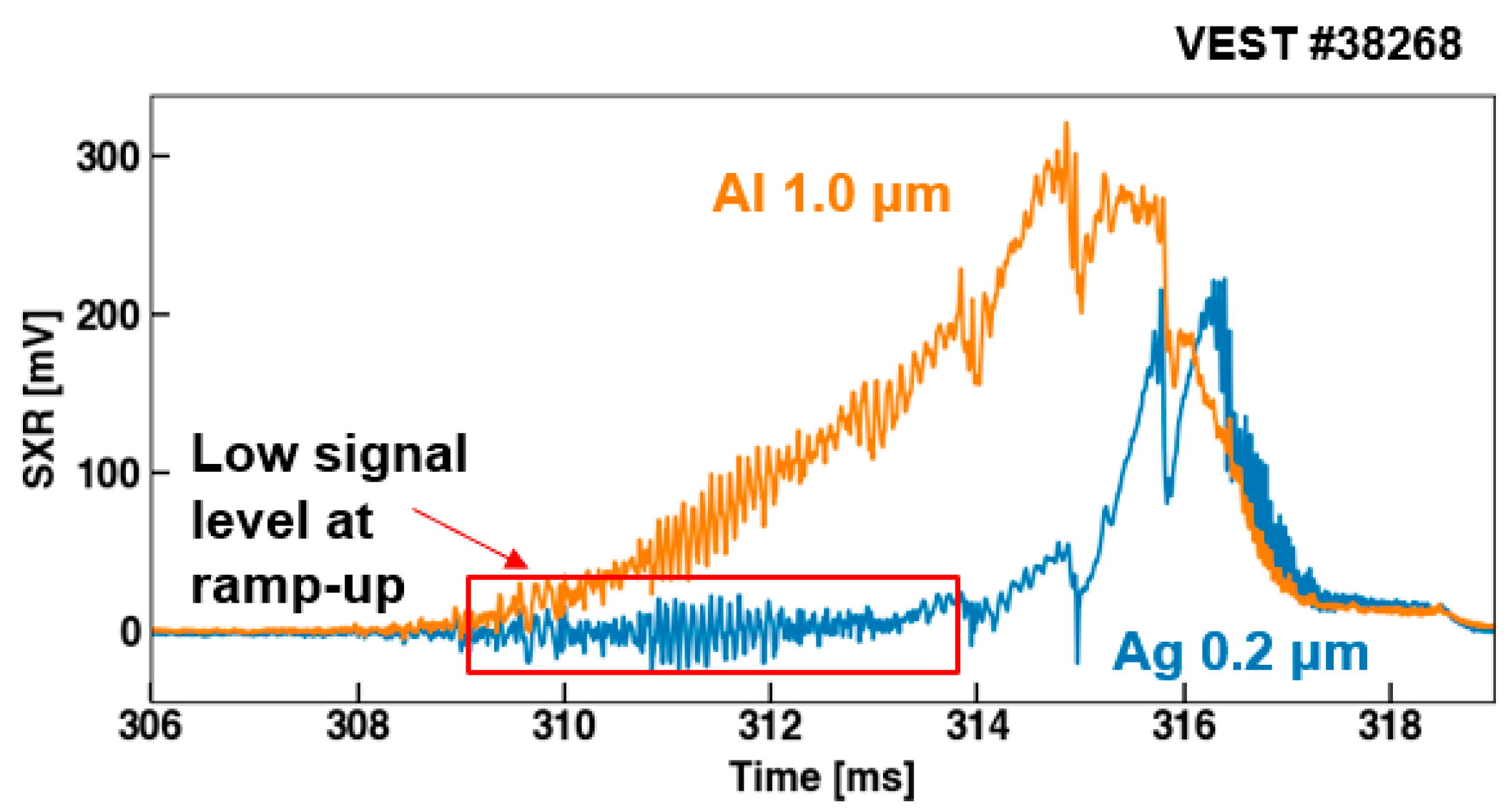
3. Experimental SXR Measurements
4. Initial Electron Temperature Estimation
4.1. Ratio Comparison of Be/Al Filter Sets
4.2. Consideration of Error Contribution from Impurity Line Emissions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Delgado-Aparicio, L.F.; Stutman, D.; Tritz, K.; Finkenthal, M.; Bell, R.; Gates, D.; Kaita, R.; LeBlanc, B.; Maingi, R.; Yuh, H.; et al. A ‘Multi-Colour’ SXR Diagnostic for Time and Space-Resolved Measurements of Electron Temperature, MHD Activity and Particle Transport in MCF Plasmas. Plasma Phys. Control. Fusion 2007, 49, 1245–1257. [Google Scholar] [CrossRef]
- White, A.E.; Schmitz, L.; McKee, G.R.; Holland, C.; Peebles, W.A.; Carter, T.A.; Shafer, M.W.; Austin, M.E.; Burrell, K.H.; Candy, J.; et al. Measurements of Core Electron Temperature and Density Fluctuations in DIII-D and Comparison to Nonlinear Gyrokinetic Simulations. Phys. Plasmas 2008, 15, 056116. [Google Scholar] [CrossRef]
- Turri, G.; Udintsev, V.S.; Sauter, O.; Goodman, T.P.; Fable, E. MHD as Trigger of Electron Temperature Oscillations in ECCD Discharges in TCV. Plasma Phys. Control. Fusion 2008, 50, 065010. [Google Scholar] [CrossRef]
- Sertoli, M.; Horváth, L.; Pokol, G.I.; Igochine, V.; Barrera, L. Characterization of Saturated MHD Instabilities through 2D Electron Temperature Profile Reconstruction from 1D ECE Measurements. Nucl. Fusion 2013, 53, 053015. [Google Scholar] [CrossRef]
- Choi, M.J.; Park, H.K.; Yun, G.S.; Lee, W.; Luhmann, N.C.; Lee, K.D.; Ko, W.-H.; Park, Y.-S.; Park, B.H.; In, Y. 2D/3D Electron Temperature Fluctuations near Explosive MHD Instabilities Accompanied by Minor and Major Disruptions. Nucl. Fusion 2016, 56, 066013. [Google Scholar] [CrossRef]
- Chung, K.J.; An, Y.H.; Jung, B.K.; Lee, H.Y.; Sung, C.; Na, Y.S.; Hahm, T.S.; Hwang, Y.S. Design Features and Commissioning of the Versatile Experiment Spherical Torus (VEST) at Seoul National University. Plasma Sci. Technol. 2013, 15, 244–251. [Google Scholar] [CrossRef]
- Kim, Y.-G.; Kim, D.; Lee, J.-H.; Yoo, M.-G.; Lee, H.; Kim, S.; Lee, C.-Y.; Kim, Y.; Hwang, Y.S.; Na, Y.-S. Development of Thomson Scattering System on VEST. Fusion Eng. Des. 2019, 143, 130–136. [Google Scholar] [CrossRef]
- Xu, P.; Lin, S.Y.; Hu, L.Q.; Duan, Y.M.; Zhang, J.Z.; Chen, K.Y.; Zhong, G.Q. First Results Obtained from the Soft X-ray Pulse Height Analyzer on Experimental Advanced Superconducting Tokamak. Rev. Sci. Instrum. 2010, 81, 063501. [Google Scholar] [CrossRef]
- Huang, X.L.; Zhang, Y.P.; Zhu, Y.B.; Li, X.; He, L.; Li, Y.X.; Zhou, J.; Cheng, S.K.; Yang, Y.M.; Bai, R.H.; et al. Toroidal Soft X-ray Array on the EXL-50 Spherical Tokamak. Rev. Sci. Instrum. 2021, 92, 053501. [Google Scholar] [CrossRef]
- Purohit, S.; Joisa, Y.S.; Raval, J.V.; Ghosh, J.; Tanna, R.; Shukla, B.K.; Bhatt, S.B. Silicon Drift Detector Based X-ray Spectroscopy Diagnostic System for the Study of Non-Thermal Electrons at Aditya Tokamak. Rev. Sci. Instrum. 2014, 85, 11E419. [Google Scholar] [CrossRef]
- Kubkowska, M.; Czarnecka, A.; Figacz, W.; Jabłoński, S.; Kaczmarczyk, J.; Krawczyk, N.; Ryć, L.; Biedermann, C.; Koenig, R.; Thomsen, H.; et al. Laboratory Tests of the Pulse Height Analysis System for Wendelstein 7-X. J. Inst. 2015, 10, P10016. [Google Scholar] [CrossRef]
- Shi, Y.; Chen, Z.; Wan, B.; Lv, B.; Hu, L.; Lin, S.; Hu, Q.; Qian, J.; Liu, H.; Liu, S.; et al. Soft X-ray Pulse Height Analyzer in the HT-7 Tokamak. Rev. Sci. Instrum. 2004, 75, 4930–4933. [Google Scholar] [CrossRef]
- Xiang, J.; Takeda, S.; Cai, Y.; Tanabe, H.; Cao, Q.; Tanaka, H.; Ono, Y. Double-Filter High-Resolution Soft X-ray Tomographic Diagnostic for Investigating Electron Acceleration in TS-6 Reconnection Merging Experiments. Rev. Sci. Instrum. 2021, 92, 083504. [Google Scholar] [CrossRef]
- McGarry, M.B.; Franz, P.; Den Hartog, D.J.; Goetz, J.A.; Thomas, M.A.; Reyfman, M.; Kumar, S.T.A. High-Performance Double-Filter Soft X-ray Diagnostic for Measurement of Electron Temperature Structure and Dynamics. Rev. Sci. Instrum. 2012, 83, 10E129. [Google Scholar] [CrossRef]
- Delgado-Aparicio, L.F.; Stutman, D.; Tritz, K.; Finkenthal, M.; Bell, R.; Hosea, J.; Kaita, R.; LeBlanc, B.; Roquemore, L.; Wilson, J.R. Fast Electron Temperature Measurements Using a “Multicolor” Optical Soft X-ray Array. J. Appl. Phys. 2007, 102, 073304. [Google Scholar] [CrossRef]
- Svoboda, J.; Imrisek, M.; Mikszuta-Michalik, K.; Mlynar, J.; Ficker, O.; Bilkova, P.; Weinzettl, V.; Jaulmes, F.; Hron, M.; Panek, R. Conceptual Design of Tomographic Soft X-ray Detectors for COMPASS-U Tokamak. Fusion Eng. Des. 2021, 168, 112656. [Google Scholar] [CrossRef]
- Lee, S.H.; Jang, J.; Hong, J.; Pacella, D.; Romano, A.; Gabellieri, L.; Jang, S.; Kim, J.; Choe, W. Installation of Soft X-ray Array Diagnostics and Its Application to Tomography Reconstruction Using Synthetic KSTAR X-ray Images. Rev. Sci. Instrum. 2014, 85, 11E827. [Google Scholar] [CrossRef]
- Bando, T.; Ohdachi, S.; Suzuki, Y. Developments of Scintillator-Based Soft X-ray Diagnostic in LHD with CsI:Tl and P47 Scintillators. Rev. Sci. Instrum. 2016, 87, 11E317. [Google Scholar] [CrossRef]
- Bernert, M.; Eich, T.; Burckhart, A.; Fuchs, J.C.; Giannone, L.; Kallenbach, A.; McDermott, R.M.; Sieglin, B.; ASDEX Upgrade Team. Application of AXUV Diode Detectors at ASDEX Upgrade. Rev. Sci. Instrum. 2014, 85, 033503. [Google Scholar] [CrossRef]
- Kim, S.; Jang, J.Y.; Kim, Y.; Hwang, Y.S. Acceleration of Ion Rotation during Internal Reconnection Events in the Versatile Experiment Spherical Torus (VEST). Nucl. Fusion 2021, 61, 126011. [Google Scholar] [CrossRef]
- Xiao, C.; Franz, P.; Chapman, B.E.; Craig, D.; Ding, W.X.; Gadani, G.; Marrelli, L.; Martin, P.; Pasqualotto, R.; Spizzo, G.; et al. Soft-X-ray Emission, Plasma Equilibrium, and Fluctuation Studies on Madison Symmetric Torus. Rev. Sci. Instrum. 2003, 74, 2157–2160. [Google Scholar] [CrossRef]
- Chung, H.-K.; Chen, M.H.; Morgan, W.L.; Ralchenko, Y.; Lee, R.W. FLYCHK: Generalized Population Kinetics and Spectral Model for Rapid Spectroscopic Analysis for All Elements. High Energy Density Phys. 2005, 1, 3–12. [Google Scholar] [CrossRef]
- Yang, J.; Hong, S.H.; Kim, D.; Jang, J.; Kim, J.Y.; Jung, E.C.; Kim, Y.; Hwang, Y.S. Effect of Boronization in VEST: Achieving 0.1 MA Discharge. Fusion Eng. Des. 2018, 137, 358–361. [Google Scholar] [CrossRef]
- Ralchenko, Y.; Kramida, A. Development of NIST Atomic Databases and Online Tools. Atoms 2020, 8, 56. [Google Scholar] [CrossRef] [PubMed]
- Herfindal, J.L.; Dawson, J.D.; Ennis, D.A.; Hartwell, G.J.; Loch, S.D.; Maurer, D.A. Design and Initial Operation of a Two-Color Soft X-ray Camera System on the Compact Toroidal Hybrid Experiment. Rev. Sci. Instrum. 2014, 85, 11D850. [Google Scholar] [CrossRef]
- Morimoto, S.; Okamoto, S.; Yanagi, N.; Iiyoshi, A.; Uo, K. Effects of Light Impurities on Electron Temperature Measured by Soft X-ray Filter Method. Jpn. J. Appl. Phys. 1986, 25, 120. [Google Scholar] [CrossRef]
- Nishimura, K.; Sanpei, A.; Tanaka, H.; Ishii, G.; Kodera, R.; Ueba, R.; Himura, H.; Masamune, S.; Ohdachi, S.; Mizuguchi, N. 2D Electron Temperature Diagnostic Using Soft X-ray Imaging Technique. Rev. Sci. Instrum. 2014, 85, 033502. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.W.; Lim, S.; Jeong, W.; Kim, S.; Kim, J.H.; Hwang, Y.S.; Sung, C. Electron Temperature Measurements Using a Two-Filter Soft X-ray Array in VEST. Sensors 2023, 23, 8357. https://doi.org/10.3390/s23208357
Lee MW, Lim S, Jeong W, Kim S, Kim JH, Hwang YS, Sung C. Electron Temperature Measurements Using a Two-Filter Soft X-ray Array in VEST. Sensors. 2023; 23(20):8357. https://doi.org/10.3390/s23208357
Chicago/Turabian StyleLee, M. W., S. Lim, W. Jeong, S. Kim, J. H. Kim, Y. S. Hwang, and C. Sung. 2023. "Electron Temperature Measurements Using a Two-Filter Soft X-ray Array in VEST" Sensors 23, no. 20: 8357. https://doi.org/10.3390/s23208357
APA StyleLee, M. W., Lim, S., Jeong, W., Kim, S., Kim, J. H., Hwang, Y. S., & Sung, C. (2023). Electron Temperature Measurements Using a Two-Filter Soft X-ray Array in VEST. Sensors, 23(20), 8357. https://doi.org/10.3390/s23208357





