Resistive Sensing of Seed Cotton Moisture Regain Based on Pressure Compensation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
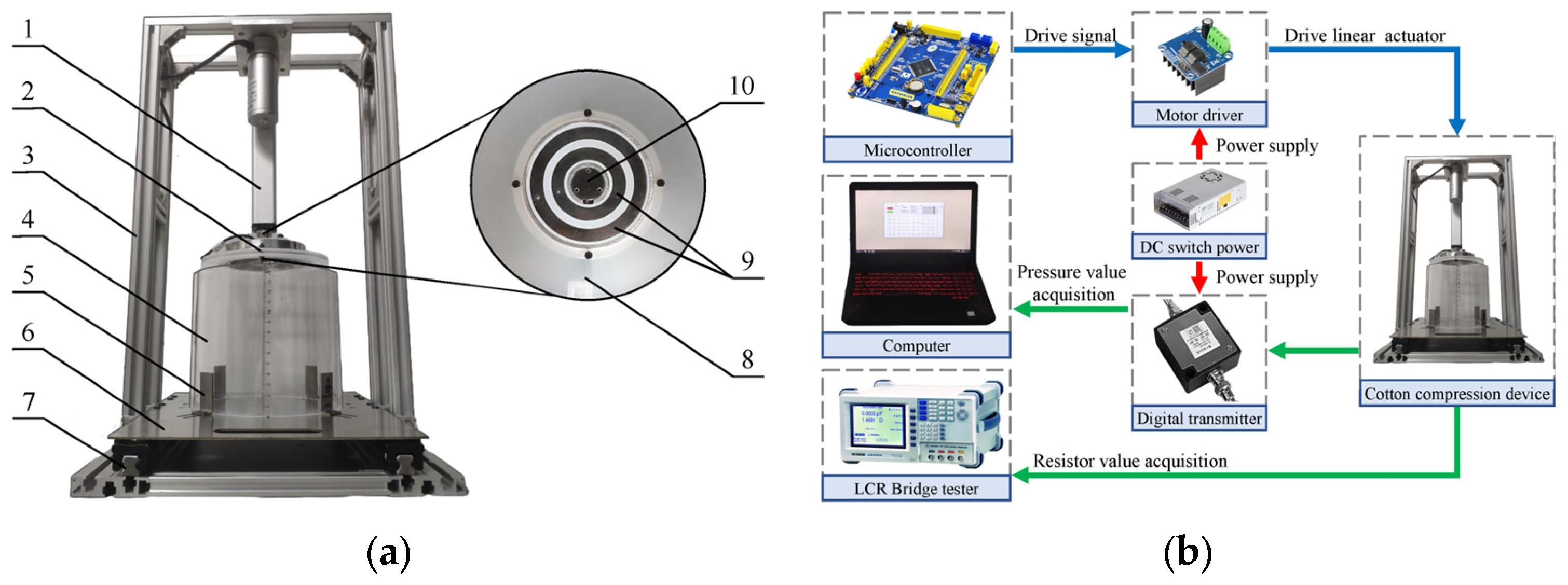
2.2. Data Acquisition
2.3. Experiment Methods
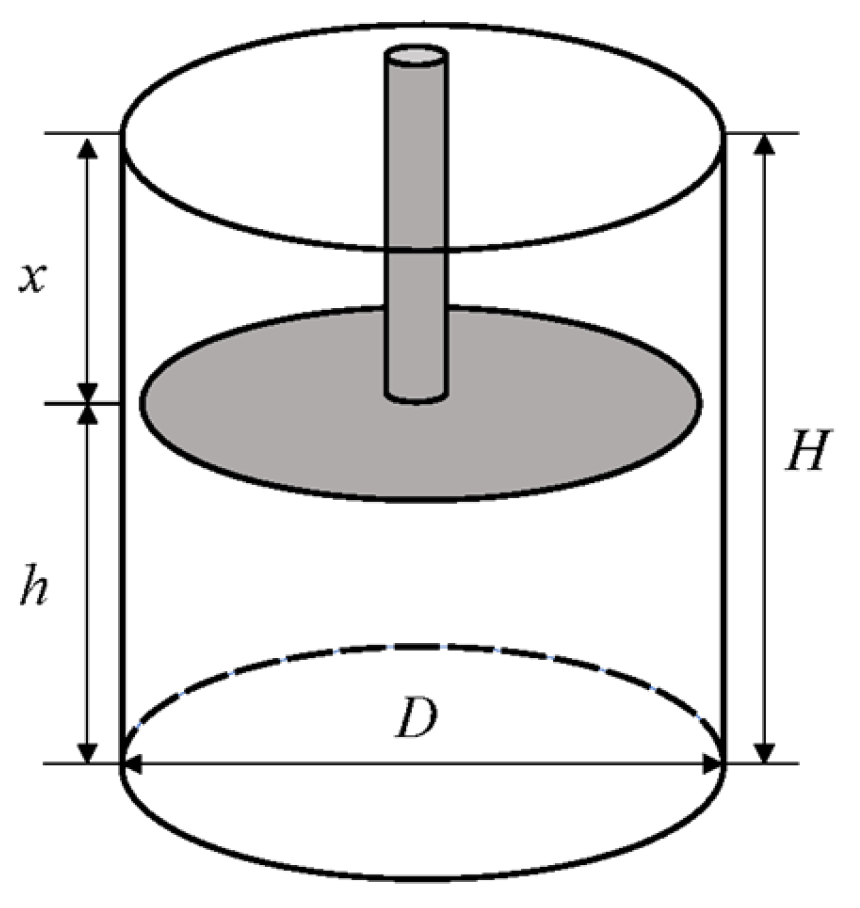
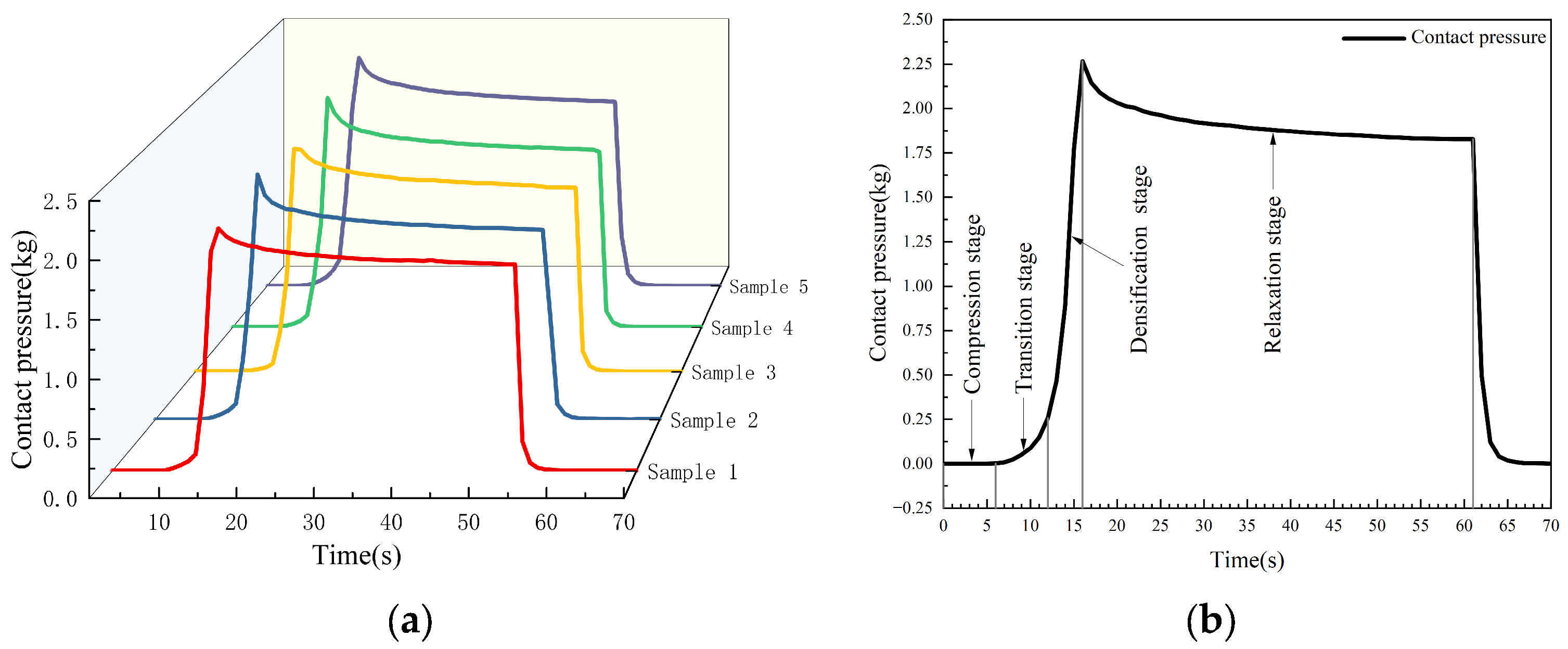
2.3.1. Seed Cotton Densification Experiment
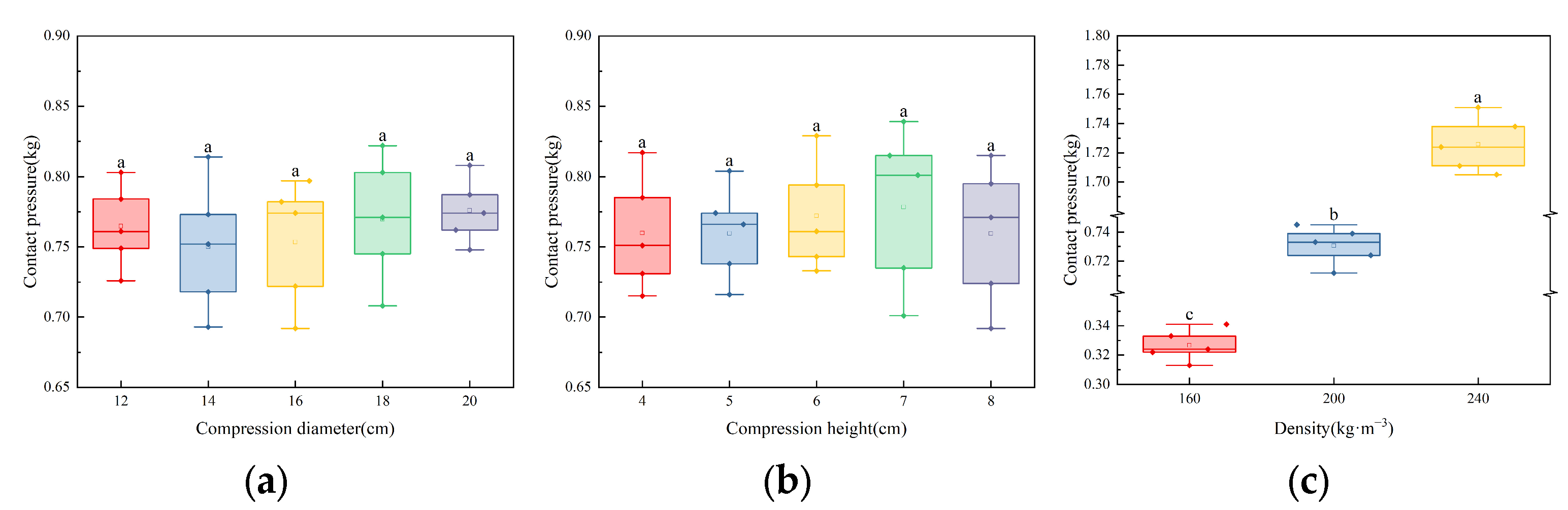
2.3.2. Factors Influencing Contact Pressure
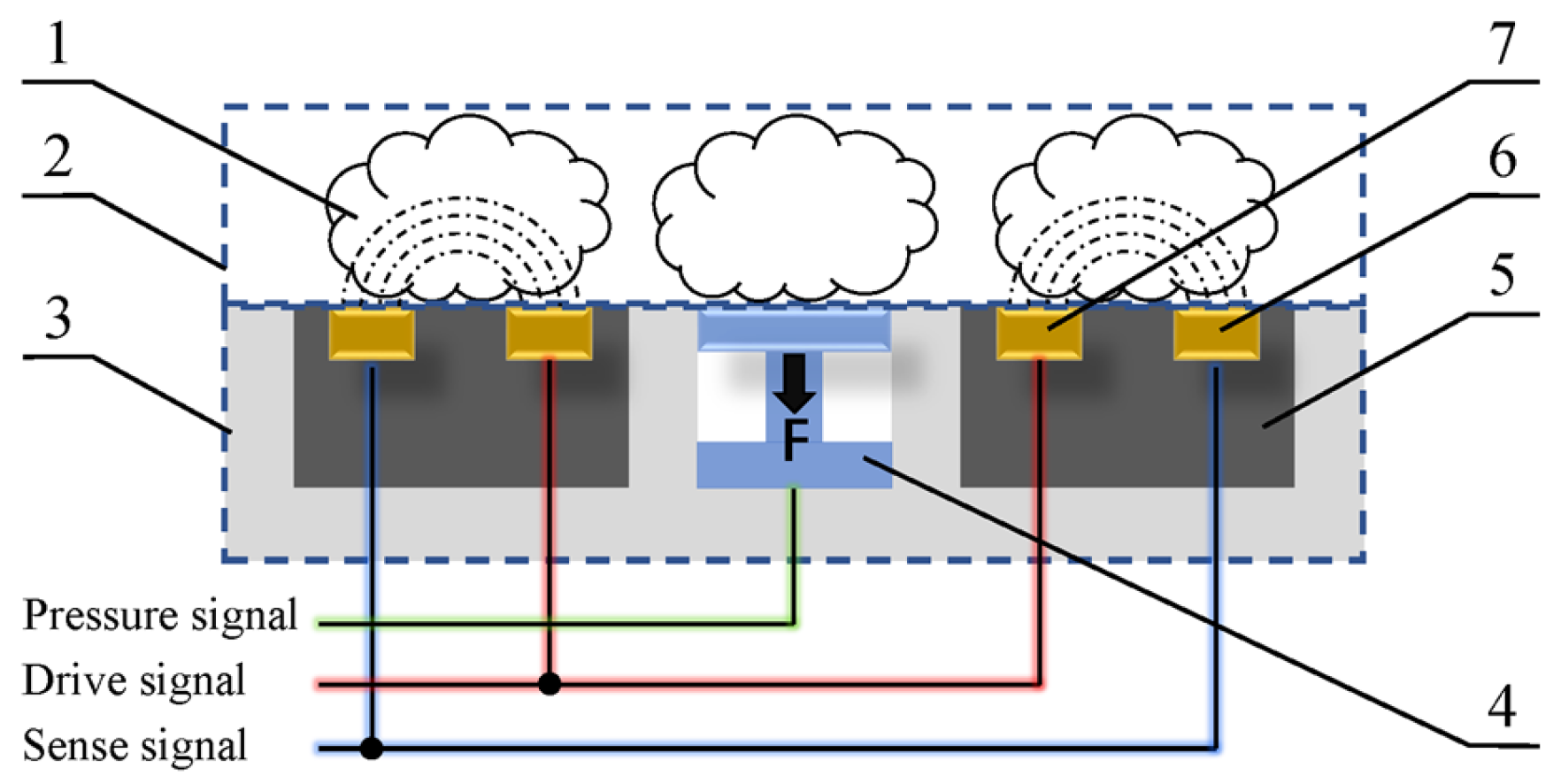
2.3.3. Influencing Factors of Conductivity
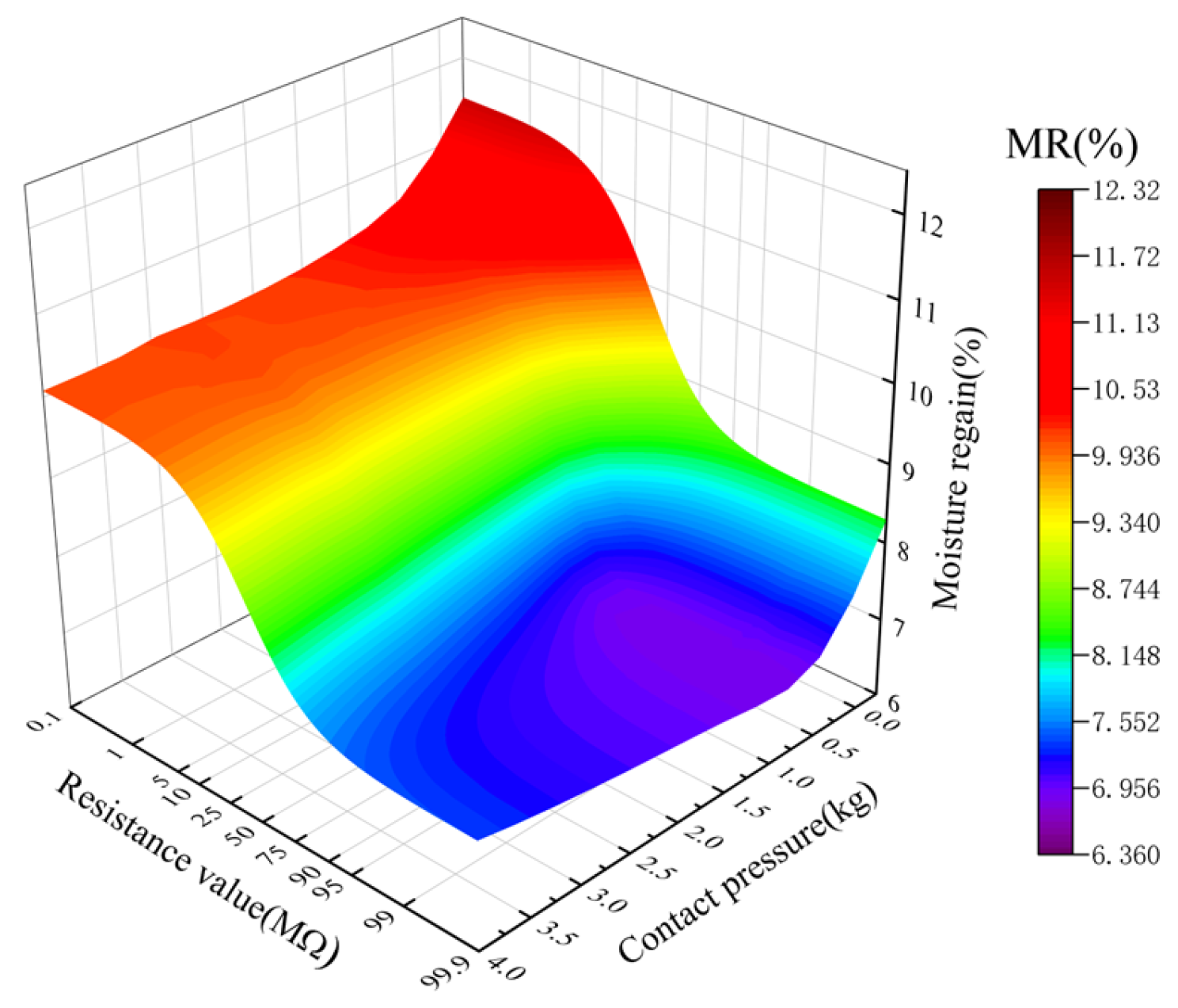
2.3.4. The MR Measurement Model
2.4. Data Processing
3. Results and Discussion
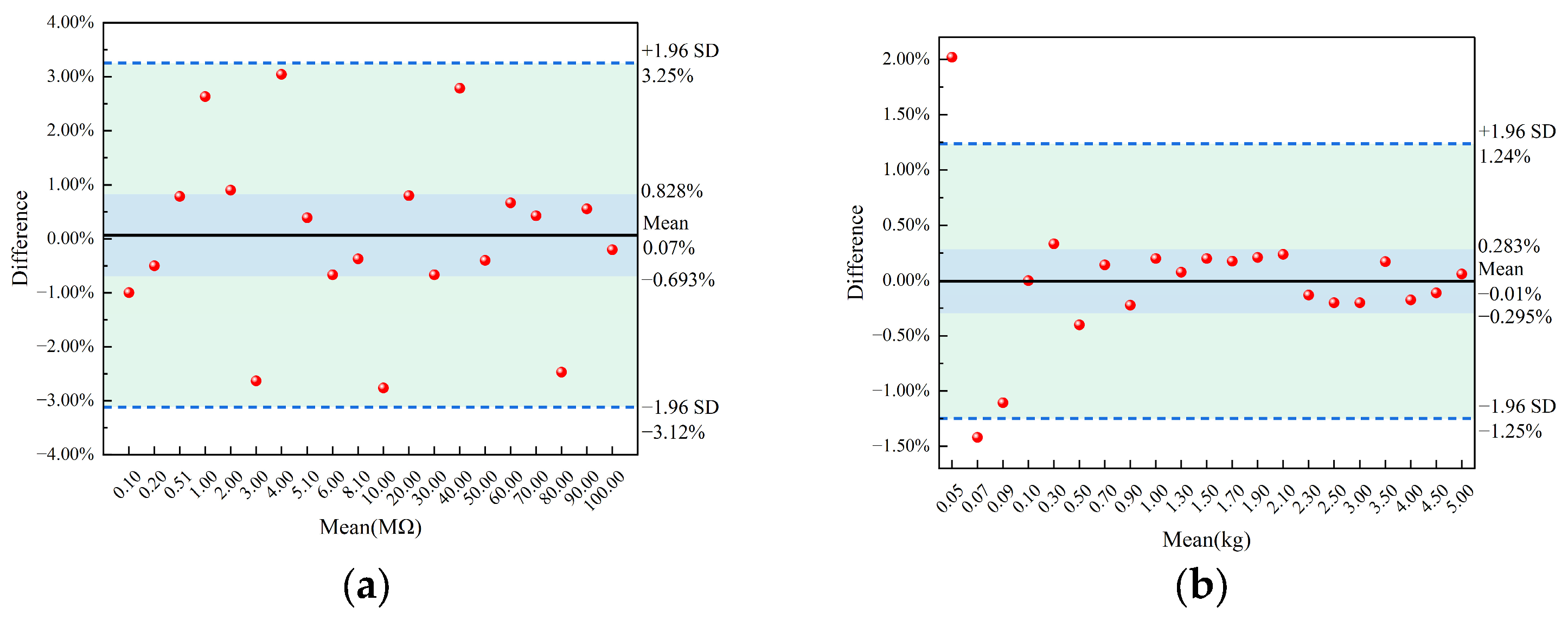
3.1. Equipment Calibration
3.2. Mechanical Analysis of Seed Cotton Compression
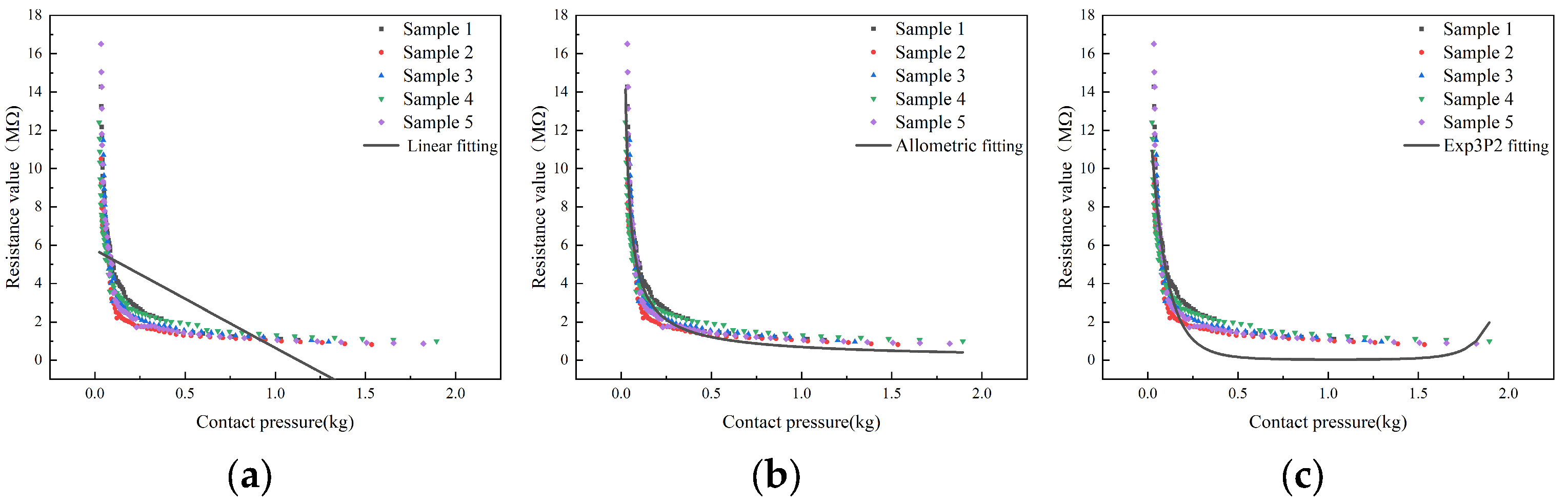
3.3. Analysis of Influencing Factors of Contact Pressure
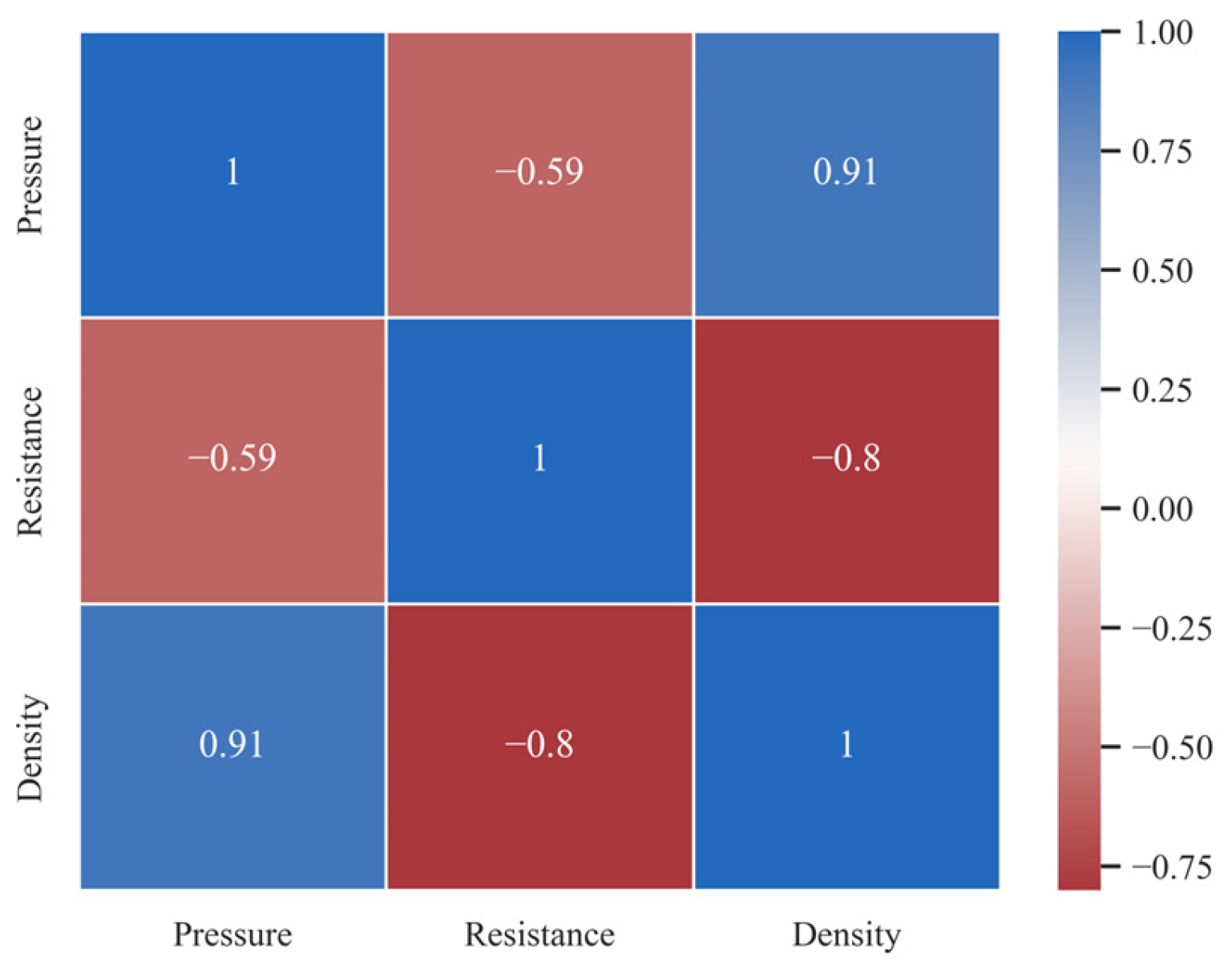
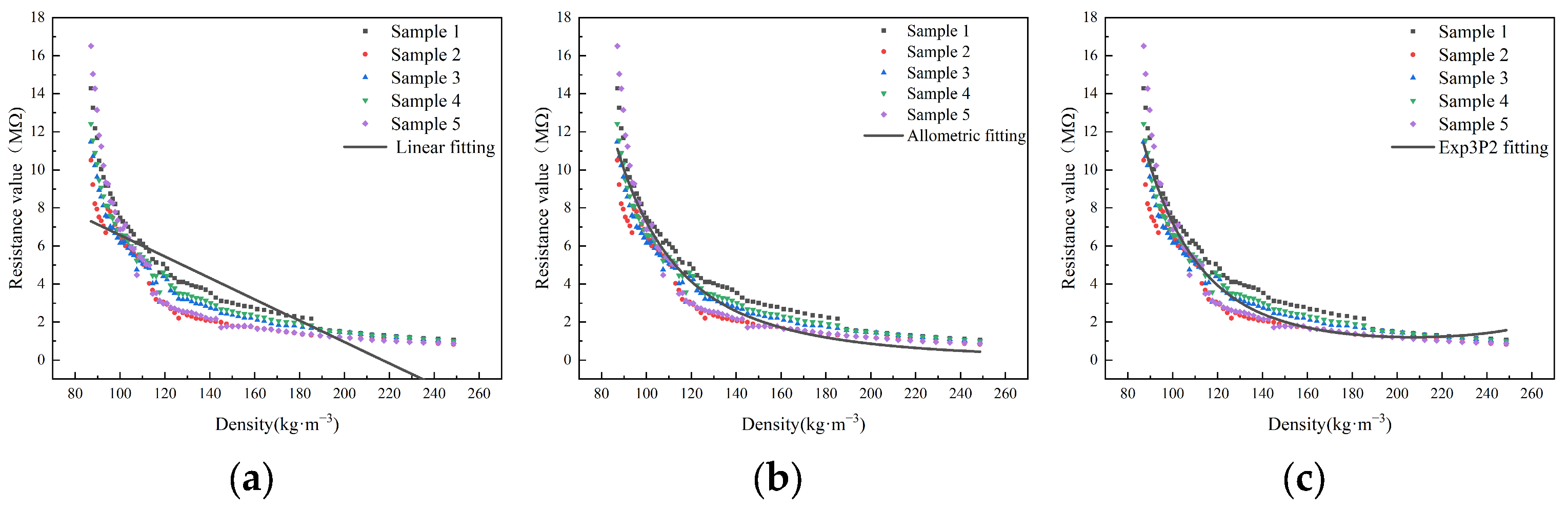
3.4. Analysis of Influencing Factors of Conductivity
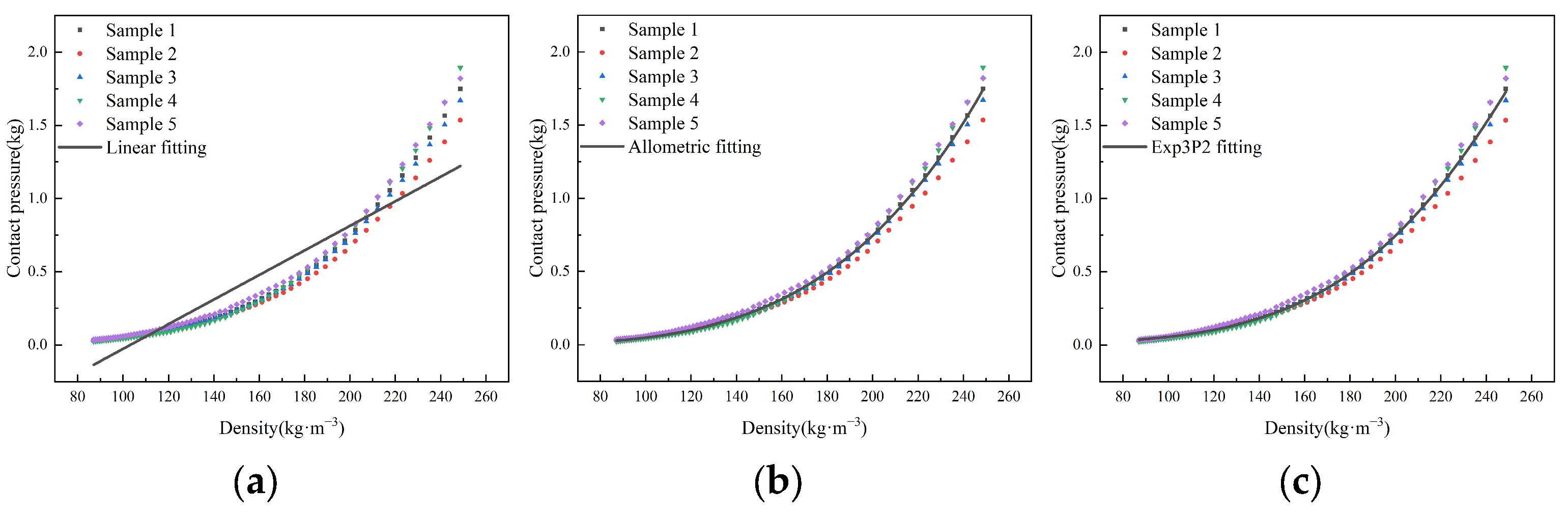
3.5. Model Performance Comparison and Validation
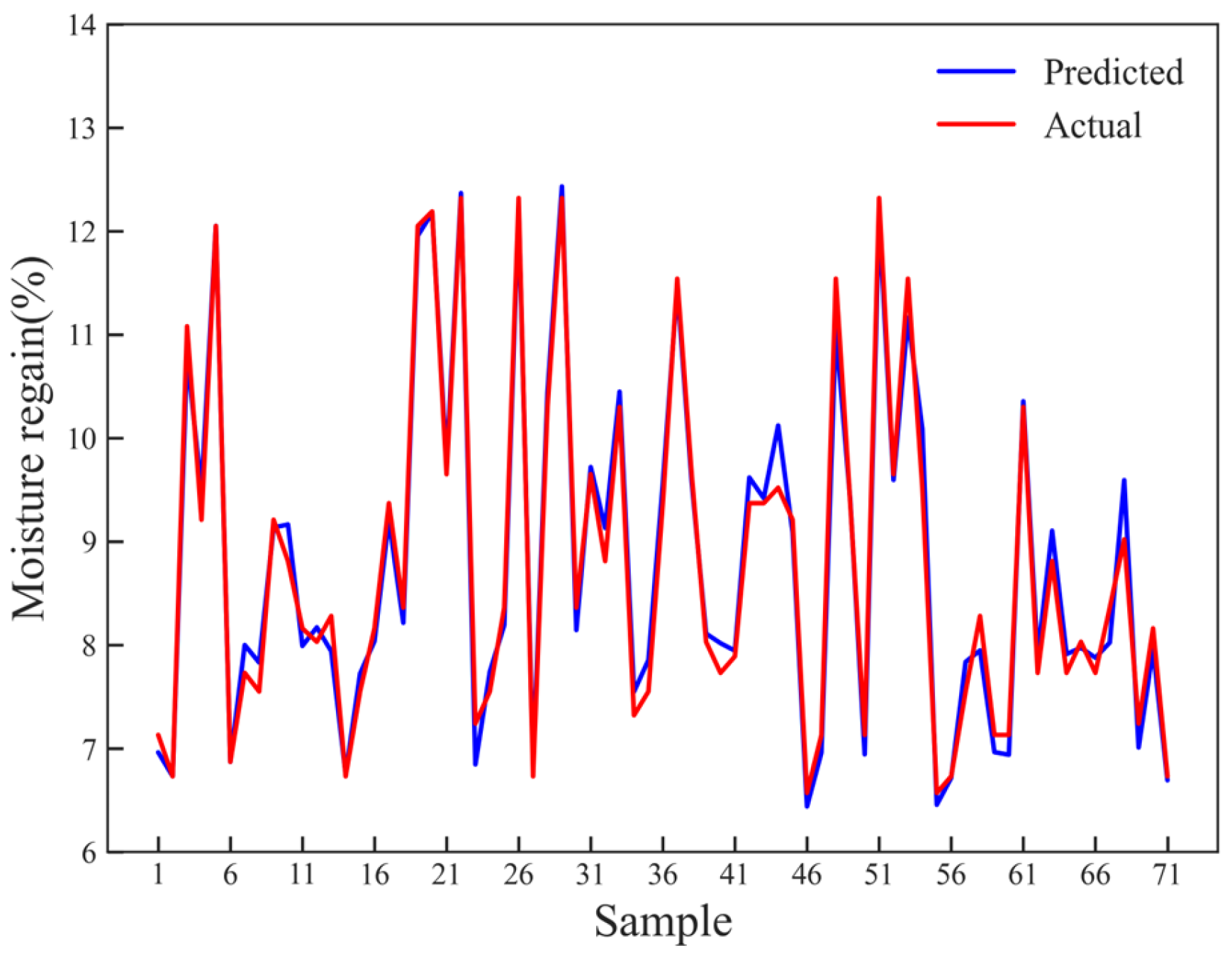
3.6. Performance Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tausif, M.; Jabbar, A.; Naeem, M.S.; Basit, A.; Ahmad, F.; Cassidy, T. Cotton in the New Millennium: Advances, Economics, Perceptions and Problems. Text. Prog. 2018, 50, 1–66. [Google Scholar] [CrossRef]
- El-Yamani, A.; Marey, S.; Sayed-Ahmed, I. Influence of Mechanical Harvesting Process on Productivity and Quality of Cotton Fiber. J. Soil Sci. Agric. Eng. 2017, 8, 301–306. [Google Scholar] [CrossRef]
- Delhom, C.D.; Rodgers, J.E., III. Cotton moisture—Its importance, measurements and impacts. In Proceedings of the Bremen International Cotton Conference, Bremen, Germany, 16–18 March 2016; pp. 1–7. [Google Scholar]
- Van der Sluijs, M.; Long, R. The Effect of Seed Cotton Moisture during Harvesting on—Part 1—Fiber Quality. Text. Res. J. 2016, 86, 1925–1936. [Google Scholar] [CrossRef]
- Van Der Sluijs, M.H.; Delhom, C. The Effect of Seed Cotton Moisture during Harvesting on: Part 2 Yarn and Fabric Quality. Text. Res. J. 2017, 87, 1841–1847. [Google Scholar] [CrossRef]
- Zang, L. Research and application of in-car seed cotton rewetting rate detection device. China Cotton Process. 2018, 9–11. [Google Scholar]
- Murphy, E.J.; Walker, A.C. Electrical Conduction in Textiles. I The Dependence of the Resistivity* of Cotton, Silk and Wool on Relative Humidity and Moisture Content. J. Phys. Chem. 1928, 32, 1761–1786. [Google Scholar] [CrossRef]
- Jia, G.; Chen, M.; Yao, M.; Lu, S. Effect of Various Factors on Resistance Measurements of Fiber Bales Using Parallel Electrodes. J. Electrost. 2010, 68, 465–468. [Google Scholar] [CrossRef]
- Sang, X.; Qin, J.; Xia, B. Design of Cotton Moisture Regain Detection System Based on RC Transient Effect. China Cotton Process. 2014, 27–29. [Google Scholar] [CrossRef]
- Akahira, T. Effect of Humidity on the Electrical Resistance of Fibrous Insulating Materials. J. Inst. Electr. Eng. Jpn. 1923, 43, 719–746. [Google Scholar]
- Byler, R.K. Resistivity of Cotton Lint for Moisture Sensing. Trans. ASAE 1998, 41, 877–882. [Google Scholar] [CrossRef]
- Zheng, Y.; Ding, T.; Li, Y. Design of a New Cotton Moisture Online Automatic Measurement Instrument Based on Resistance Measurement Principle. Instrum. Tech. Sens. 2002, 21–22+28. [Google Scholar] [CrossRef]
- Wang, M.; Li, C.; Kan, Z.; Wang, L.; Zhao, Y. Current status of measurement methods for cotton rewetting rate. Jiangsu Agric. Sci. 2014, 42, 268–270. [Google Scholar] [CrossRef]
- Zhang, R.; Chang, J.; Han, C.; Chen, M.; Zhang, J. Rapid Detection System for Seed Cotton Quality. Chinese Patent CN202111602368.1, 10 May 2022. [Google Scholar]
- GB/T 6102.2-2012; Test Method for Moisture Regain in Raw Cotton—Electrical Resistance Meter. Standardization Administration of China, Standards Press of China: Beijing, China, 2012.
- Kawakita, K.; Lüdde, K.-H. Some Considerations on Powder Compression Equations. Powder Technol. 1971, 4, 61–68. [Google Scholar] [CrossRef]
- Faborode, M.O.; O’Callaghan, J.R. Theoretical Analysis of the Compression of Fibrous Agricultural Materials. J. Agric. Eng. Res. 1986, 35, 175–191. [Google Scholar] [CrossRef]
- Yang, M.; Li, X.; Yang, H. Study on the Compression Process of Forage Grass. Trans. CSAE 1996, 60–64. [Google Scholar]
- Wang, H.; He, D.; Zhang, X. Experimental Study on the Compressibility of Corn Stalks. J. Inn. Mong. Agric. Univ. (Nat. Sci. Ed.) 2014, 35, 88–90. [Google Scholar]
- Kong, F.; Wu, T.; Chen, C.; Sun, Y.; Xie, Q.; Shi, L. Compression, Stress Relaxation Characteristics and Model Construction of Seed Cotton. Trans. CSAE 2021, 37, 53–60. [Google Scholar]
- Ren, Y.; Deng, M.; Zhang, L.; Yang, Y.; Gao, H.; Li, Y. Analysis of Sliding Friction of Different Density Raw Cotton. Xinjiang Agric. Mech. 2021, 29–31+34. [Google Scholar] [CrossRef]
- Guo, H.; Gao, G.; Zhou, W.; Liu, J.; Hao, L. Design of Load and Bale Density Monitoring and Control System for a Wheeled Self-Propelled Square Baler. J. ASABE 2022, 65, 599–608. [Google Scholar] [CrossRef]
- Li, H.; Zhuang, Q.; Xu, Y. Influence of Fabric Structural Parameters on the Conductivity of Polypyrrole Conductive Fabrics. J. Donghua Univ. (Nat. Sci. Ed.) 2015, 41, 37–42. [Google Scholar]
- Li, Y.; Zhao, H.; Guo, J.; Yao, Y.; Xing, C.; Liu, Z. Breeding and Cultivation Techniques of Early Maturing Cotton Xinluzao 80. Agric. Sci. Technol. Commun. 2018, 309–310. [Google Scholar]
- GB/T 6102.1-2006; Test Method for Moisture Regain in Raw Cotton by Oven Drying. Standardization Administration of China, Standards Press of China: Beijing, China, 2006.
- Walker, A.C.; Quell, M.H. 15—Influence of Ash Constituents on the Electrical Conduction of Cotton. J. Text. Inst. Trans. 1933, 24, T123–T130. [Google Scholar] [CrossRef]
- Hearle, J.W.S. 11—The Electrical Resistance of Textile Materials: I. The Influence of Moisture Content. J. Text. Inst. Trans. 1953, 44, T117–T143. [Google Scholar] [CrossRef]
- Wattonville, J.D. 7760 Cotton Picker. In Proceedings of the 2008 Providence, Providence, RI, USA, 29 June–2 July 2008; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2008. [Google Scholar]



| Relative Humidity (%) | Temperature (°C) | |||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | |
| 60 | 7.38% | 7.29% | 7.18% | 7.06% | 6.92% | 6.78% | 6.62% | 6.41% |
| 70 | 8.44% | 8.36% | 8.26% | 8.14% | 8.00% | 7.84% | 7.66% | 7.42% |
| 80 | 10.33% | 10.18% | 10.01% | 9.82% | 9.61% | 9.38% | 9.13% | 8.85% |
| 90 | 12.68% | 12.57% | 12.37% | 12.14% | 11.88% | 11.6% | 11.31% | 11.03% |
| Category | Expression | Model Parameter | R2 | RMSE | ||
|---|---|---|---|---|---|---|
| a | b | c | ||||
| Linear function | y = a + bx | −8.660 × 10−1 | 8.390 × 10−3 | - | 0.865 | 0.147 |
| Allometric function | y = axb | 7.508 × 10−10 | 3.909 | - | 0.993 | 0.033 |
| Exp3P2 function | −6.618 | 4.300 × 10−2 | −5.759 × 10−5 | 0.993 | 0.032 | |
| Category | Expression | Model Parameter | R2 | RMSE | ||
|---|---|---|---|---|---|---|
| a | b | c | ||||
| Linear function | y = a + bx | 5.617 × 10−2 | 1.218 × 10 | - | 0.641 | 1.869 |
| Allometric function | y = axb | 1.004 × 10−7 | −3.071 | - | 0.921 | 0.875 |
| Exp3P2 function | 6.846 | −6.400 × 10−2 | 1.547 × 10−4 | 0.929 | 0.830 | |
| Category | Expression | Model Parameter | R2 | RMSE | ||
|---|---|---|---|---|---|---|
| a | b | c | ||||
| Linear function | y = a + bx | 5.761 | −5.110 | - | 0.354 | 2.508 |
| Allometric function | y = axb | 6.960 × 10−1 | −8.070 × 10−1 | - | 0.893 | 1.021 |
| Exp3P2 function | 2.669 | −1.171 × 10 | 5.627 | 0.829 | 1.291 | |
| Algorithm Model | Model Performance Evaluation Indicators | |
|---|---|---|
| R2 | RMSE | |
| SVR | 0.974 | 0.296% |
| RF | 0.977 | 0.261% |
| BPNN | 0.986 | 0.204% |
| Group | Oven Method (%) | Experimental Platform (%) * | RMSE (%) | CV (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ1 | ρ2 | ρ3 | ρ4 | ρ5 | ρ6 | ρ7 | ρ8 | ρ9 | ρ10 | ρ11 | Mean | ||||
| 1 | 5.94 | 5.94 | 5.95 | 5.85 | 5.74 | 5.81 | 5.77 | 6.02 | 6.36 | 6.20 | 6.03 | 6.42 | 6.01 | 0.23 | 3.66 |
| 2 | 6.88 | 6.54 | 6.82 | 6.68 | 6.76 | 6.63 | 7.05 | 7.18 | 7.09 | 7.20 | 7.15 | 7.16 | 6.93 | 0.24 | 3.43 |
| 3 | 7.96 | 7.95 | 7.88 | 8.13 | 8.11 | 8.08 | 8.14 | 7.94 | 7.93 | 7.73 | 8.02 | 8.08 | 8.00 | 0.13 | 1.51 |
| 4 | 9.39 | 9.21 | 9.16 | 9.26 | 9.52 | 9.66 | 9.72 | 9.69 | 9.54 | 9.64 | 9.39 | 9.45 | 9.48 | 0.21 | 2.01 |
| 5 | 10.51 | 10.40 | 10.47 | 10.46 | 10.42 | 10.28 | 10.26 | 10.39 | 10.55 | 10.73 | 10.83 | 10.86 | 10.51 | 0.20 | 1.88 |
| 6 | 11.77 | 11.86 | 11.80 | 11.78 | 11.67 | 11.59 | 11.51 | 11.65 | 11.68 | 11.63 | 11.57 | 11.72 | 11.68 | 0.23 | 0.86 |
| Mean | 0.20 | 2.22 | |||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, L.; Zhang, R.; Duan, H.; Chang, J.; Zeng, Z.; Qian, Y.; Hong, M. Resistive Sensing of Seed Cotton Moisture Regain Based on Pressure Compensation. Sensors 2023, 23, 8421. https://doi.org/10.3390/s23208421
Fang L, Zhang R, Duan H, Chang J, Zeng Z, Qian Y, Hong M. Resistive Sensing of Seed Cotton Moisture Regain Based on Pressure Compensation. Sensors. 2023; 23(20):8421. https://doi.org/10.3390/s23208421
Chicago/Turabian StyleFang, Liang, Ruoyu Zhang, Hongwei Duan, Jinqiang Chang, Zhaoquan Zeng, Yifu Qian, and Mianzhe Hong. 2023. "Resistive Sensing of Seed Cotton Moisture Regain Based on Pressure Compensation" Sensors 23, no. 20: 8421. https://doi.org/10.3390/s23208421
APA StyleFang, L., Zhang, R., Duan, H., Chang, J., Zeng, Z., Qian, Y., & Hong, M. (2023). Resistive Sensing of Seed Cotton Moisture Regain Based on Pressure Compensation. Sensors, 23(20), 8421. https://doi.org/10.3390/s23208421






