A Generative Adversarial Network to Synthesize 3D Magnetohydrodynamic Distortions for Electrocardiogram Analyses Applied to Cardiac Magnetic Resonance Imaging
Abstract
:1. Introduction
2. Related Works
2.1. MHD Distortion Models
2.2. Data Augmentation and Synthesis Techniques
2.2.1. Transformation Methods
2.2.2. Pattern-Mixing Methods
2.2.3. Decomposition Methods
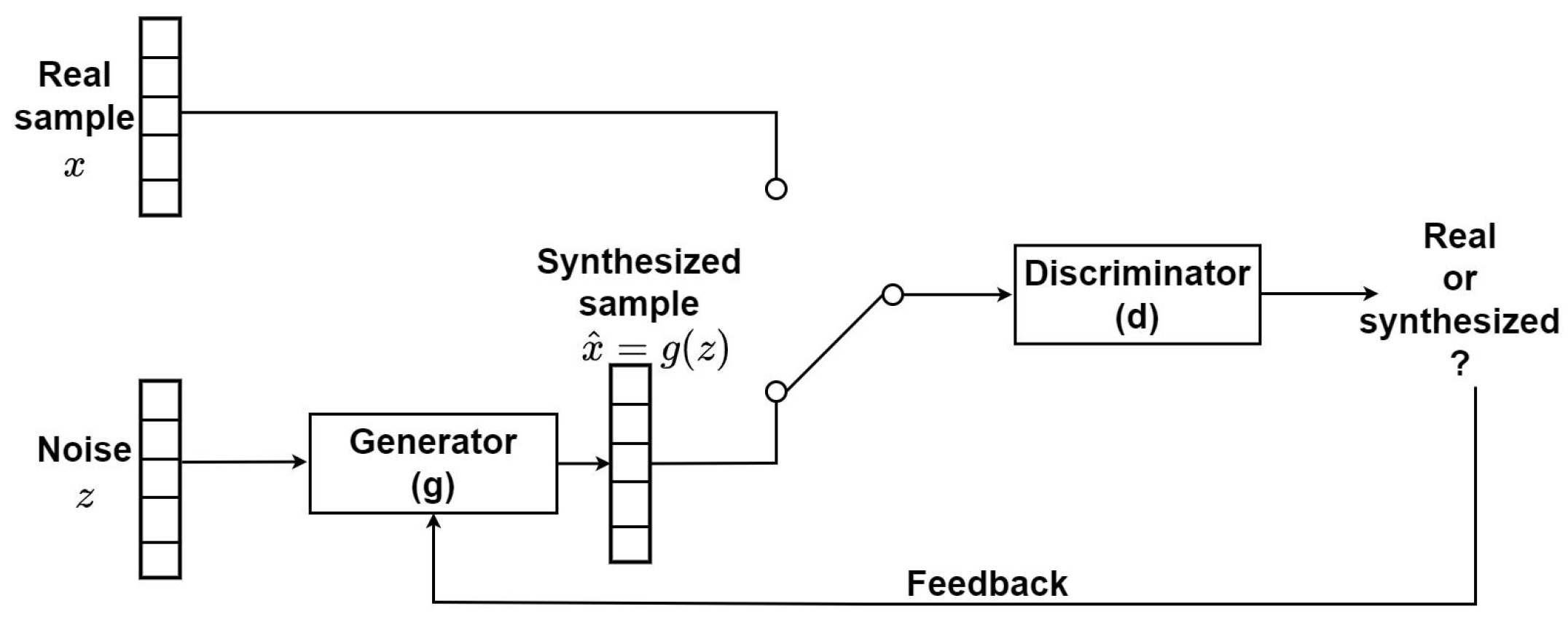
2.3. Generative Methods and Deep Generative Models
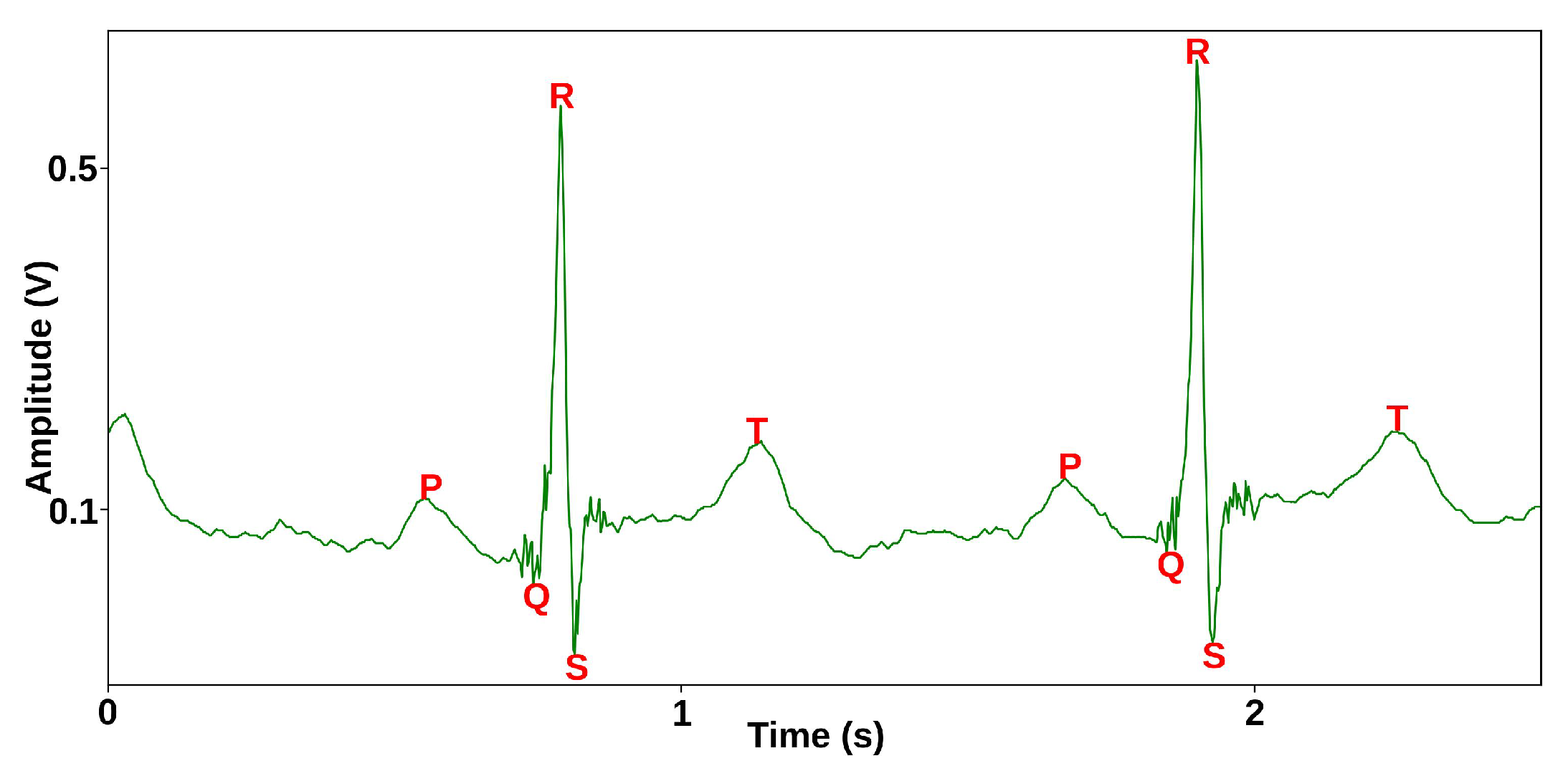
3. Materials and Methods
3.1. Datasets
3.1.1. INCART
3.1.2. Getemed
3.1.3. Schiller
3.1.4. Siemens
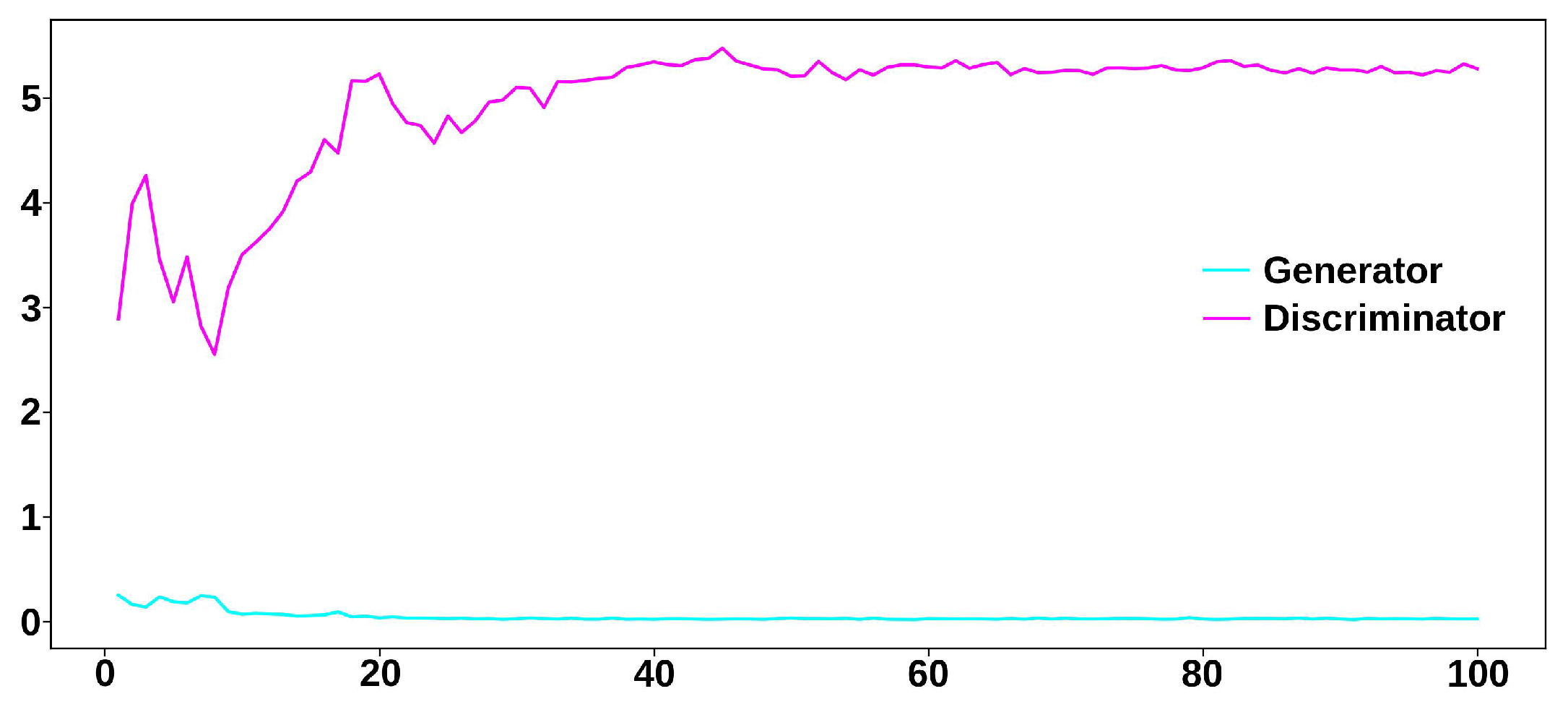
3.2. Data Synthesis Pipeline
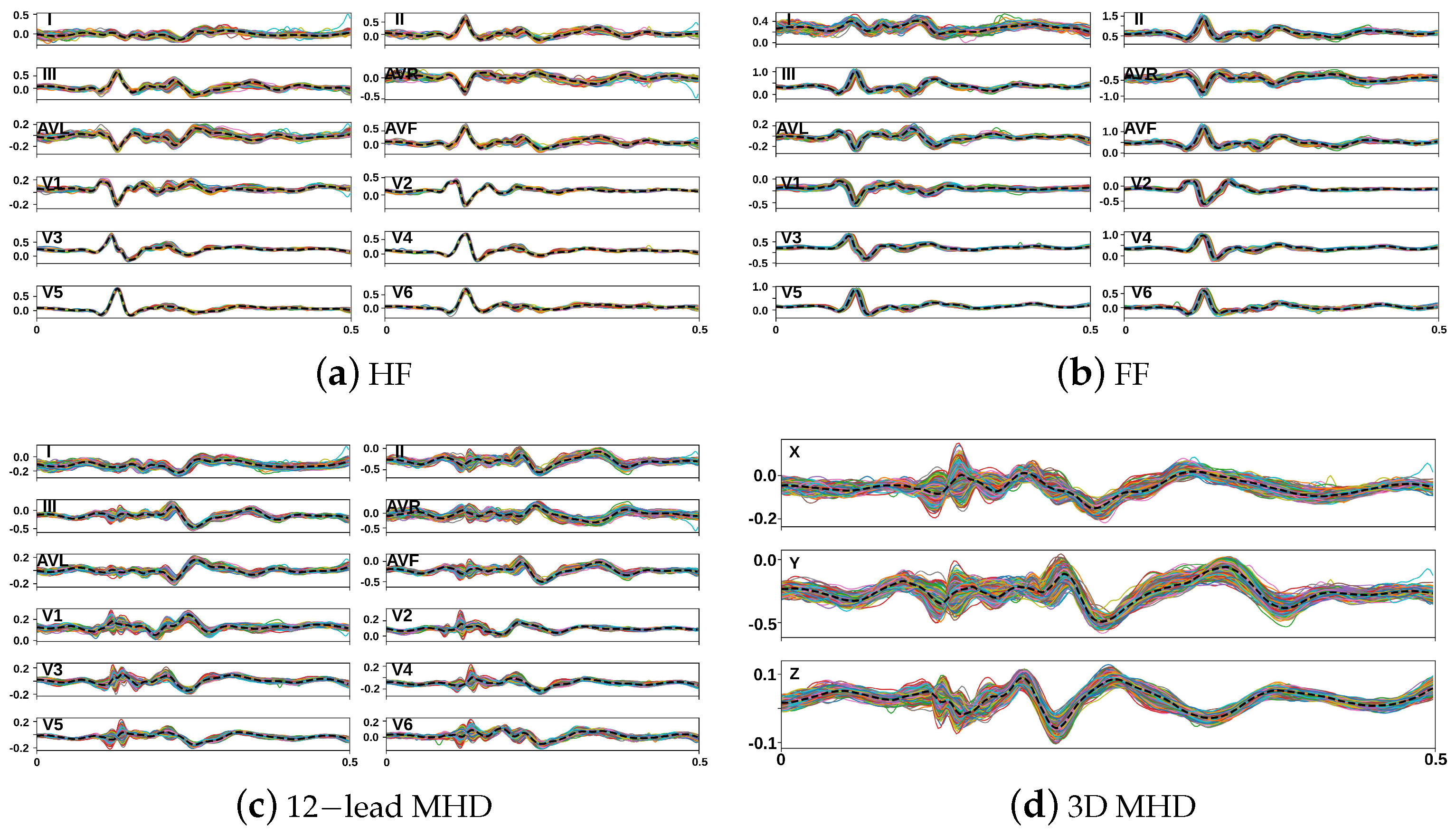
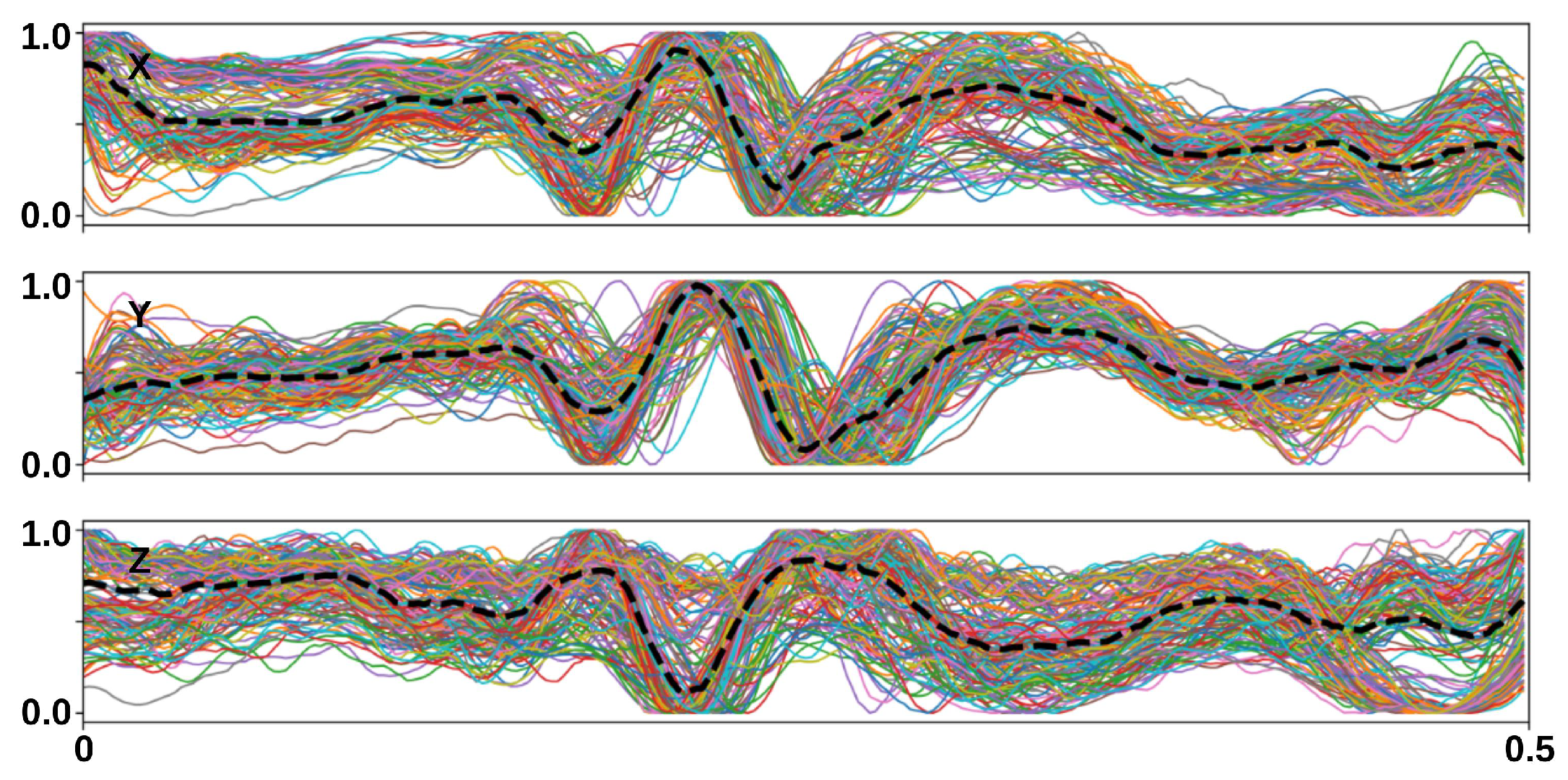
3.2.1. MHD Distortion Input Database Preparation
3.2.2. Synthesis of Realistic MHD Distortion Templates and ECG Dataset Augmentation
3.3. Evaluation Metrics
3.3.1. Similarity Metrics
- l is a list of index pairs , with and .
- and .
- For all , is related to as follows:
- ∘
- .
- ∘
- .
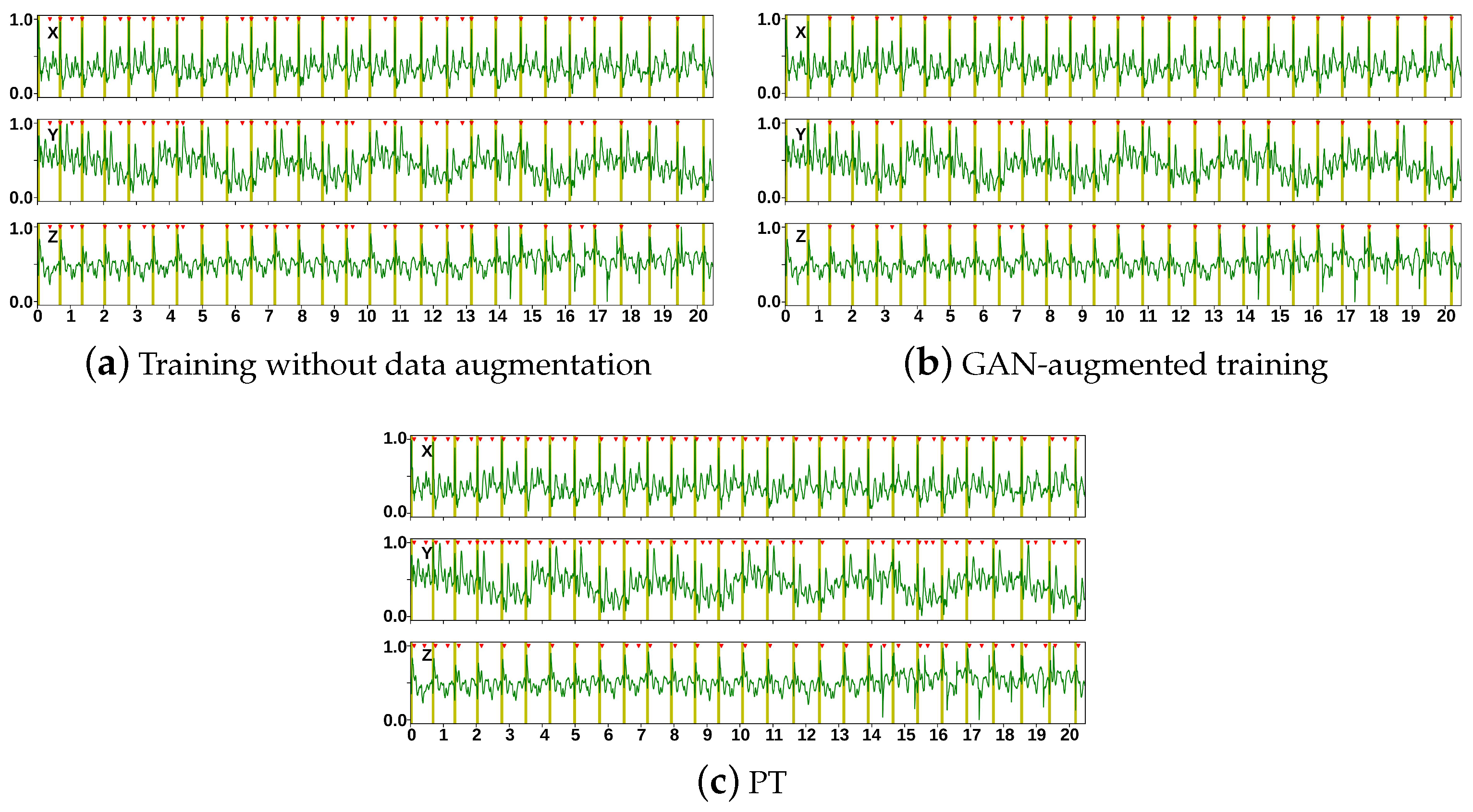
3.3.2. Accuracy of a DL-Based R-Peak Detector Trained Using Augmented Data
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BLSTM | Bidirectional long short-term memory |
| CNN | Convolutional neural network |
| DGM | Deep generative models |
| DL | Deep learning |
| DTW | Dynamic time warping |
| ECG | Electrocardiogram |
| GAN | Generative adversarial network |
| HF | Head first |
| FF | Feet first |
| FN | False negative |
| FP | False positive |
| LSTM | Long short-term memory |
| MHD | Magnetohydrodynamic |
| MMD | Maximum mean discrepancy |
| MRI | Magnetic resonance imaging |
| RNN | Recurrent neural network |
| TP | True positive |
| VAE | Variational autoencoder |
| VCG | Vectorcardiogram |
References
- Dogan, H.; Dogan, R.O. A comprehensive review of computer-based Techniques for R-peaks/QRS complex detection in ECG signal. Arch. Comput. Methods Eng. 2023, 30, 3703–3721. [Google Scholar] [CrossRef]
- Oster, J.; Clifford, G.D. Acquisition of electrocardiogram signals during magnetic resonance imaging. Physiol. Meas. 2017, 38, R119–R142. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Liu, C.; Jiang, X.; Zhang, Z.; Zhang, Y.; Li, J.; Wei, S. Performance analysis of ten common QRS detectors on different ECG application cases. J. Healthc. Eng. 2018, 2018, 9050812. [Google Scholar] [CrossRef] [PubMed]
- Husain, K.; Mohd Zahid, M.S.; Ul Hassan, S.; Hasbullah, S.; Mandala, S. Advances of ECG Sensors from Hardware, Software and Format Interoperability Perspectives. Electronics 2021, 10, 105. [Google Scholar] [CrossRef]
- Merdjanovska, E.; Rashkovska, A. Comprehensive survey of computational ECG analysis: Databases, methods and applications. Expert Syst. Appl. 2022, 203, 117206. [Google Scholar] [CrossRef]
- Petmezas, G.; Stefanopoulos, L.; Kilintzis, V.; Tzavelis, A.; Rogers, J.A.; Katsaggelos, A.K.; Maglaveras, N. State-of-the-art deep Learning Methods on electrocardiogram data: Systematic review. JMIR Med. Inform. 2022, 10, 38454. [Google Scholar] [CrossRef]
- Mehri, M.; Calmon, G.; Odille, F.; Oster, J. A deep learning architecture using 3D vectorcardiogram to detect R-peaks in ECG with enhanced precision. Sensors 2023, 23, 2288. [Google Scholar] [CrossRef]
- Krug, J.; Schmidt, M.; Rose, G.; Friebe, M. A database of electrocardiogram signals acquired in different magnetic resonance imaging scanners. In Proceedings of the Computing in Cardiology, Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar]
- Mehri, M.; Aublin, P.; Calmon, G.; Odille, F.; Oster, J. A data augmentation framework to improve R-peak detection in ECG recorded in MRI scanners. In Proceedings of the International Society for Magnetic Resonance in Medicine Annual Meeting & Exhibition, Toronto, ON, Canada, 3–8 June 2023. [Google Scholar]
- Influence of the MHD Effect on 12-Lead and 3-Lead ECGs Recorded in 1T to 7T MRI Scanners. 2021. Available online: https://physionet.org/content/mhd-effect-ecg-mri/1.0.0/ (accessed on 25 May 2023).
- Oster, J.; Llinares, R.; Payne, S.; Tse, Z.T.H.; Schmidt, E.J.; Clifford, G.D. Comparison of three artificial models of the magnetohydrodynamic effect on the electrocardiogram. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1400–1417. [Google Scholar] [CrossRef]
- Aublin, P.G.; Felblinger, J.; Oster, J. Hermite based parametric representation of magnetohydrodynamic effect for the generation of synthetic ECG signals during magnetic resonance imaging. In Proceedings of the Computers in Cardiology, Atlanta, GA, USA, 1–4 October 2023. [Google Scholar]
- Tenforde, T.S. Magnetically induced electric fields and currents in the circulatory system. Prog. Biophys. Mol. Biol. 2005, 87, 279–288. [Google Scholar] [CrossRef]
- Abi-Abdallah, D.; Robin, V.; Drochon, A.; Fokapu, O. Alterations in human ECG due to the Magnetohydrodynamic effect: A method for accurate R-peak detection in the presence of high MHD artifacts. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 1842–1845. [Google Scholar]
- Martin, V.; Drochon, A.; Fokapu, O.; Gerbeau, J.F. Magnetohemodynamics in the aorta and electrocardiograms. Phys. Med. Biol. 2012, 57, 3177–3195. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Zhang, K.; Fung, K.M.; Thai, T.C.; Moore, K.; Mannel, R.S.; Liu, H.; Zheng, B.; Qiu, Y. Recent advances and clinical applications of deep learning in medical image analysis. Med. Image Anal. 2022, 79, 102444. [Google Scholar] [CrossRef] [PubMed]
- Behrad, F.; Saniee Abadeh, M. An overview of deep learning methods for multimodal medical data mining. Expert Syst. Appl. 2022, 200, 117006. [Google Scholar] [CrossRef]
- McDuff, D.; Curran, T.; Kadambi, A. Synthetic Data in Healthcare. arXiv 2023, arXiv:2304.03243. [Google Scholar]
- Moradi, R.; Berangi, R.; Minaei, B. A survey of regularization strategies for deep models. Artif. Intell. Rev. 2020, 53, 3947–3986. [Google Scholar] [CrossRef]
- Iwana, B.K.; Uchida, S. An empirical survey of data augmentation for time series classification with neural networks. PLoS ONE 2021, 16, e0254841. [Google Scholar] [CrossRef]
- Iglesias, G.; Talavera, E.; González-Prieto, Á.; Mozo, A.; Gómez-Canaval, S. Data augmentation techniques in time series domain: A survey and taxonomy. Neural Comput. Appl. 2023, 35, 10123–10145. [Google Scholar] [CrossRef]
- Raghu, A.; Shanmugam, D.; Pomerantsev, E.; Guttag, J.V.; Stultz, C.M. Data augmentation for electrocardiograms. In Proceedings of the Conference on Health, Inference, and Learning, Virtual, 7–8 April 2022; pp. 282–310. [Google Scholar]
- Zahid, M.U.; Kiranyaz, S.; Ince, T.; Devecioglu, O.C.; Chowdhury, M.E.; Khandakar, A.; Tahir, A.; Gabbouj, M. Robust R-peak detection in low-quality Holter ECGs using 1D convolutional neural network. IEEE Trans. Biomed. Eng. 2021, 69, 119–128. [Google Scholar] [CrossRef]
- Soler, A.I.R.; Arini, P.D.; Caracciolo, S.F.; Ingallina, F.; Bonomini, M.P. Evaluation of a Gaussian mixture model for generating synthetic ECG signals during an angioplasty procedure. In Proceedings of the Artificial Intelligence in Neuroscience: Affective Analysis and Health Applications, Tenerife, Spain, 31 May–3 June 2022; pp. 567–575. [Google Scholar]
- Sankaran, K.; Holmes, S.P. Generative models: An interdisciplinary perspective. Annu. Rev. Stat. Its Appl. 2022, 10, 325–352. [Google Scholar] [CrossRef]
- Bandara, K.; Hewamalage, H.; Liu, Y.H.; Kang, Y.; Bergmeir, C. Improving the accuracy of global forecasting models using time series data augmentation. Pattern Recognit. 2021, 120, 108148. [Google Scholar] [CrossRef]
- Que, W.; Han, C.; Zhao, X.; Shi, L. An ECG generative model of myocardial infarction. Comput. Methods Programs Biomed. 2022, 225, 107062. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, Y.; Shang, J.; Xiao, C.; Sun, J. Opportunities and challenges of deep learning methods for electrocardiogram data: A systematic review. Comput. Biol. Med. 2020, 122, 103801. [Google Scholar] [CrossRef] [PubMed]
- Brophy, E.; Wang, Z.; She, Q.; Ward, T. Generative adversarial networks in time series: A systematic literature review. ACM Comput. Surv. 2023, 55, 1–31. [Google Scholar] [CrossRef]
- Wen, Q.; Sun, L.; Yang, F.; Song, X.; Gao, J.; Wang, X.; Xu, H. Time series data augmentation for deep learning: A survey. In Proceedings of the International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 19–27 August 2021; pp. 4653–4660. [Google Scholar]
- Haradal, S.; Hayashi, H.; Uchida, S. Biosignal Data Augmentation Based on Generative Adversarial Networks. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society, Honolulu, HI, USA, 18–21 July 2018; pp. 368–371. [Google Scholar]
- Wang, P.; Hou, B.; Shao, S.; Yan, R. ECG Arrhythmias detection using auxiliary classifier generative adversarial network and residual network. IEEE Access 2019, 7, 100910–100922. [Google Scholar] [CrossRef]
- Hatamian, F.N.; Ravikumar, N.; Vesal, S.; Kemeth, F.P.; Struck, M.; Maier, A. The effect of data augmentation on classification of atrial fibrillation in short single-lead ECG signals using deep neural networks. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 4–8 May 2020; pp. 1264–1268. [Google Scholar]
- Lan, T.; Hu, Q.; Liu, X.; He, K.; Yang, C. Arrhythmias classification using short-time Fourier transform and GAN based data augmentation. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society, Montreal, QC, Canada, 20–24 July 2020; pp. 308–311. [Google Scholar]
- Golany, T.; Freedman, D.; Radinsky, K. SimGANs: Simulator-based generative adversarial networks for ECG synthesis to improve deep ECG classification. In Proceedings of the International Conference on Machine Learning, Virtual Event, 13–18 July 2020; pp. 3597–3606. [Google Scholar]
- Ma, S.; Cui, J.; Xiao, W.; Liu, L. Deep learning-based data augmentation and model fusion for automatic arrhythmia identification and classification algorithms. Comput. Intell. Neurosci. 2022, 2022, 1577778. [Google Scholar] [CrossRef]
- Rahman, M.M.; Rivolta, M.W.; Badilini, F.; Sassi, R. A Systematic Survey of Data Augmentation of ECG Signals for AI Applications. Sensors 2023, 23, 5237. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Babaeizadeh, S. Synthesis of standard 12-lead electrocardiograms using two-dimensional generative adversarial networks. J. Electrocardiol. 2021, 69, 6–14. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Xu, Y.; Chen, P.; Zhang, J.; Zhang, Y. Generative adversarial network with transformer generator for boosting ECG classification. Biomed. Signal Process. Control. 2023, 80, 104276. [Google Scholar] [CrossRef]
- Adib, E.; Afghah, F.; Prevost, J.J. Synthetic ECG signal generation using generative neural networks. arXiv 2021, arXiv:2112.03268. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, 215–220. [Google Scholar] [CrossRef]
- St Petersburg INCART 12-Lead Arrhythmia Dataset. Available online: https://physionet.org/content/incartdb/1.0.0/ (accessed on 25 May 2023).
- Reyna, M.A.; Alday, E.A.P.; Gu, A.; Liu, C.; Seyedi, S.; Rad, A.B.; Elola, A.; Li, Q.; Sharma, A.; Clifford, G.D. Classification of 12-lead ECGs: The PhysioNet/Computing in Cardiology Challenge 2020. In Proceedings of the 2020 Computing in Cardiology, Rimini, Italy, 13–16 September 2020; pp. 1–4. [Google Scholar]
- Dos Reis, J.E.; Soullié, P.; Oster, J.; Soler, E.P.; Petitmangin, G.; Felblinger, J.; Odille, F. Reconstruction of the 12-lead ECG using a novel MR-compatible ECG sensor network. Magn. Reson. Med. 2019, 82, 1929–1945. [Google Scholar] [CrossRef]
- Kors, J.A.; van Herpen, G.; Sittig, A.C.; van Bemmel, J. Reconstruction of the Frank vectorcardiogram from standard electrocardiographic leads: Diagnostic comparison of different methods. Eur. Heart J. 1990, 11, 1083–1092. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Delaney, A.M.; Brophy, E.; Ward, T.E. Synthesis of realistic ECG using generative adversarial networks. arXiv 2019, arXiv:1909.09150. [Google Scholar]
- Zhu, F.; Ye, F.; Fu, Y.; Liu, Q.; Shen, B. Electrocardiogram generation with a bidirectional LSTM-CNN generative adversarial network. Sci. Rep. 2019, 9, 6734. [Google Scholar] [CrossRef] [PubMed]
- Chia, J.M.; Fischer, S.E.; Wickline, S.; Lorenz, C.H. Performance of QRS detection for cardiac magnetic resonance imaging with a novel vectorcardiographic triggering method. J. Magn. Reson. Imaging 2000, 12, 678–688. [Google Scholar] [CrossRef]
- Gregory, T.S.; Oshinski, J.N.; Tse, Z.T.H. ECG Electrode Placements for Magnetohydrodynamic Voltage Suppression. J. Imaging 2018, 4, 94. [Google Scholar] [CrossRef]

| Layer | Output Shape | # of Parameters | |
|---|---|---|---|
| Discriminator | Conv1D | (32, 250, 32) | 1568 |
| LeakyReLU | (32, 250, 32) | 0 | |
| Conv1D | (32, 250, 64) | 32,832 | |
| LeakyReLU | (32, 250, 64) | 0 | |
| MaxPooling1D | (32, 125, 64) | 0 | |
| Conv1D | (32, 125, 128) | 131,200 | |
| LeakyReLU | (32, 125, 128) | 0 | |
| Conv1D | (32, 125, 256) | 524,544 | |
| LeakyReLU | (32, 125, 256) | 0 | |
| MaxPooling1D | (32, 62, 256) | 0 | |
| Flatten | (32, 15872) | 0 | |
| Dense | (32, 1) | 15,873 | |
| Generator | Dense | (32, 1, 250) | 62,750 |
| Reshape | (32, 250, 1) | 0 | |
| Bidirectional | (32, 250, 24) | 4992 | |
| Dropout | (32, 250, 24) | 0 | |
| Dense | (32, 250, 3) | 75 |
| MMD | DTW | |
|---|---|---|
| X | 0.85 | 121.27 |
| Y | 0.56 | 155.66 |
| Z | 0.97 | 104.78 |
| 0.79 ± 0.28 | 127.24 ± 35.97 |
| Dataset | Method | # of R-Peaks | TPs | FPs | FNs | P (%) | R (%) | F1 (%) |
|---|---|---|---|---|---|---|---|---|
| Getemed | w/o | 887 | 865 | 402 | 22 | 68.27 | 97.52 | 80.31 |
| GAN | 872 | 65 | 15 | 93.06 | 98.31 | 95.61 | ||
| PT | 817 | 560 | 70 | 64.37 | 92.11 | 74.41 | ||
| Schiller | w/o | 69 | 67 | 1 | 2 | 98.72 | 96.08 | 97.26 |
| GAN | 67 | 0 | 2 | 100.00 | 96.08 | 97.92 | ||
| PT | 68 | 1 | 1 | 98.49 | 98.69 | 98.54 | ||
| Siemens | w/o | 51 | 46 | 2 | 5 | 91.67 | 88.68 | 89.88 |
| GAN | 51 | 0 | 0 | 100.00 | 100.00 | 100.00 | ||
| PT | 49 | 16 | 2 | 74.91 | 92.59 | 81.72 |
| Method | P (%) | R (%) | F1 (%) |
|---|---|---|---|
| w/o | 68.27 | 97.52 | 80.31 |
| GAN | 93.06 | 98.31 | 95.61 |
| VAE | 81.78 | 87.03 | 84.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehri, M.; Calmon, G.; Odille, F.; Oster, J.; Lalande, A. A Generative Adversarial Network to Synthesize 3D Magnetohydrodynamic Distortions for Electrocardiogram Analyses Applied to Cardiac Magnetic Resonance Imaging. Sensors 2023, 23, 8691. https://doi.org/10.3390/s23218691
Mehri M, Calmon G, Odille F, Oster J, Lalande A. A Generative Adversarial Network to Synthesize 3D Magnetohydrodynamic Distortions for Electrocardiogram Analyses Applied to Cardiac Magnetic Resonance Imaging. Sensors. 2023; 23(21):8691. https://doi.org/10.3390/s23218691
Chicago/Turabian StyleMehri, Maroua, Guillaume Calmon, Freddy Odille, Julien Oster, and Alain Lalande. 2023. "A Generative Adversarial Network to Synthesize 3D Magnetohydrodynamic Distortions for Electrocardiogram Analyses Applied to Cardiac Magnetic Resonance Imaging" Sensors 23, no. 21: 8691. https://doi.org/10.3390/s23218691
APA StyleMehri, M., Calmon, G., Odille, F., Oster, J., & Lalande, A. (2023). A Generative Adversarial Network to Synthesize 3D Magnetohydrodynamic Distortions for Electrocardiogram Analyses Applied to Cardiac Magnetic Resonance Imaging. Sensors, 23(21), 8691. https://doi.org/10.3390/s23218691







