Learning Compliant Box-in-Box Insertion through Haptic-Based Robotic Teleoperation
Abstract
:1. Introduction
2. Related Works
3. Methodology
3.1. Demonstration Phase
3.1.1. Teleoperation Control
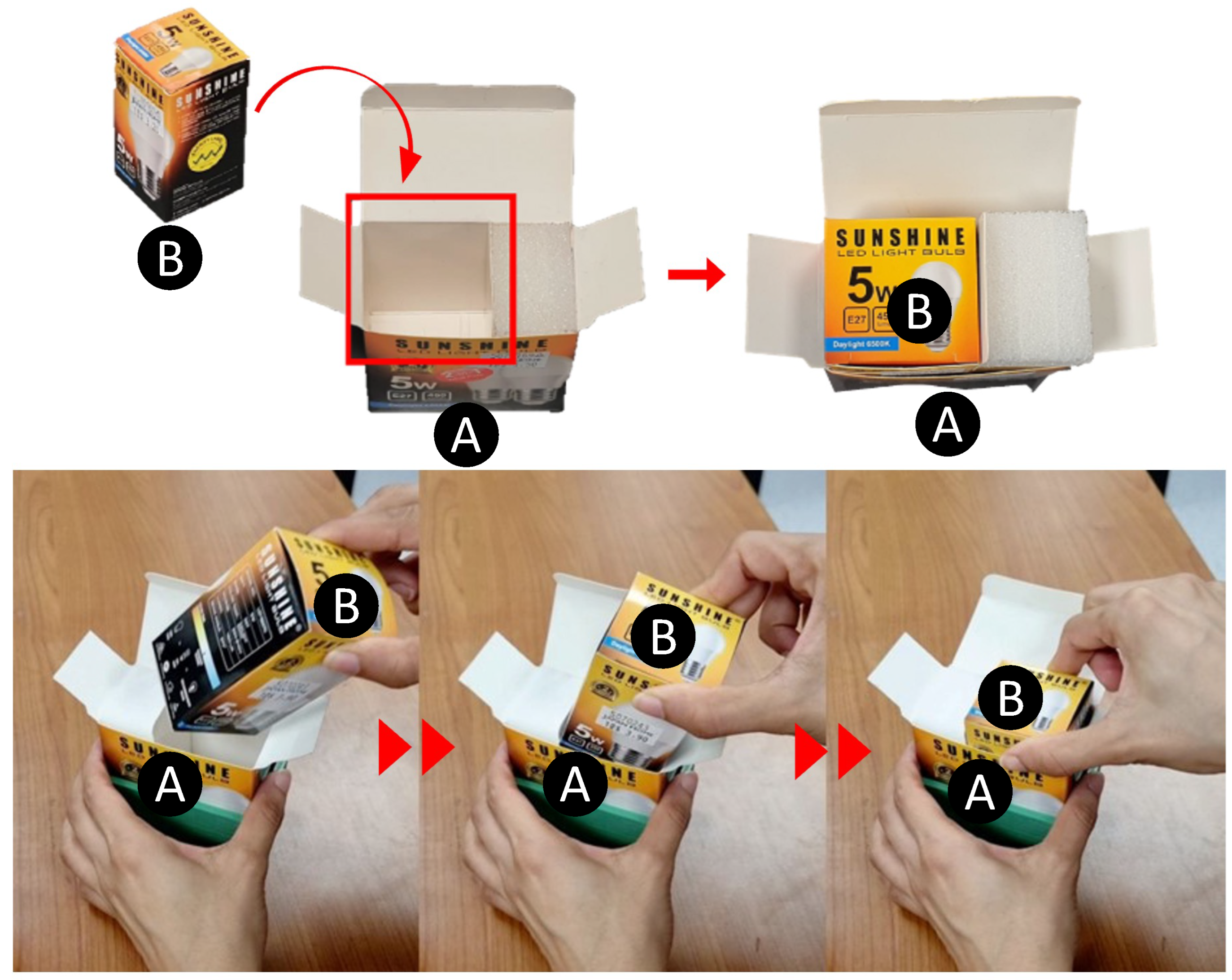
3.1.2. Task Demonstration
3.2. Learning Phase
3.2.1. K-Means Clustering
3.2.2. Expectation Maximisation (EM)
3.2.3. Gaussian Mixture Regression (GMR)
3.3. Generalisation Phase
- Note: This work does not address the problem of generalisation for varying object orientations.
Trajectory Generalisation Using Barycentric Coordinates
4. Experimental Validation
| Quantity Name | Symbol | Value and Units |
|---|---|---|
| Stiffness for joint i | 15 Nm/rad | |
| Joint 1 damping for master | 3.3132 Ns | |
| Joint 2 damping for master | 3.4284 Ns | |
| Joint 3 damping for master | 3.1245 Ns | |
| Joint 4 damping for master | 3.2895 Ns | |
| Joint 5 damping for master | 2.836 Ns | |
| Joint 6 damping for master | 2.8579 Ns | |
| Joint 7 damping for master | 7.6092 Ns | |
| Pick time | ≈11 s | |
| Place time | ≈25 s | |
| Insert time | ≈34 s | |
| Retract time | ≈40 s | |
| Full form | Acronym | |
| Learning from Demonstration | LfD | |
| Gaussian Mixture Model | GMM | |
| Gaussian Mixture Regression | GMR | |
| Expectation Maximisation | EM | |
| Internet Protocol Suite | TCP/IP | |
4.1. Task Demonstration
4.2. Learning Autonomous Insertion with GMM and GMR
4.3. Generalisation and Repeatability Test
4.4. Discussion
5. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Expectation Maximisation
Appendix B. Gaussian Mixture Regression
References
- Whitney, D.E. Mechanical Assemblies: Their Design, Manufacture, and Role in Product Development; Oxford University Press: New York, NY, USA, 2004; Volume 1. [Google Scholar]
- Xu, J.; Hou, Z.; Liu, Z.; Qiao, H. Compare contact model-based control and contact model-free learning: A survey of robotic peg-in-hole assembly strategies. arXiv 2019, arXiv:1904.05240. [Google Scholar]
- Chin, K.S.; Ratnam, M.M.; Mandava, R. Force-guided robot in automated assembly of mobile phone. Assem. Autom. 2003, 23, 75–86. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J.; Zhao, W.; Liu, H.; Wang, G. Multiple peg-in-hole compliant assembly based on a learning-accelerated deep deterministic policy gradient strategy. Ind. Robot. Int. J. Robot. Res. Appl. 2021, 49, 54–64. [Google Scholar] [CrossRef]
- Song, R.; Li, F.; Fu, T.; Zhao, J. A robotic automatic assembly system based on vision. Appl. Sci. 2020, 10, 1157. [Google Scholar] [CrossRef]
- Navarro-Alarcon, D.; Liu, Y.H.; Romero, J.G.; Li, P. On the visual deformation servoing of compliant objects: Uncalibrated control methods and experiments. Int. J. Robot. Res. 2014, 33, 1462–1480. [Google Scholar] [CrossRef]
- Kazemi, M.; Valois, J.S.; Bagnell, J.A.; Pollard, N. Human-inspired force compliant grasping primitives. Auton. Robot. 2014, 37, 209–225. [Google Scholar] [CrossRef]
- Hogan, N. The mechanics of multi-joint posture and movement control. Biol. Cybern. 1985, 52, 315–331. [Google Scholar] [CrossRef]
- Mason, M.T. Compliance and force control for computer controlled manipulators. IEEE Trans. Syst. Man Cybern. 1981, 11, 418–432. [Google Scholar] [CrossRef]
- Xing, D.; Liu, X.; Liu, F.; Xu, D. Efficient insertion strategy for precision assembly with uncertainties using a passive mechanism. IEEE Trans. Ind. Inform. 2020, 17, 1263–1273. [Google Scholar] [CrossRef]
- Wermelinger, M.; Johns, R.; Gramazio, F.; Kohler, M.; Hutter, M. Grasping and Object Reorientation for Autonomous Construction of Stone Structures. IEEE Robot. Autom. Lett. 2021, 6, 5105–5112. [Google Scholar] [CrossRef]
- Wang, T.; Joo, H.J.; Song, S.; Hu, W.; Keplinger, C.; Sitti, M. A versatile jellyfish-like robotic platform for effective underwater propulsion and manipulation. Sci. Adv. 2023, 9, eadg0292. [Google Scholar] [CrossRef]
- Zhai, Y.; Boer, A.D.; Yan, J.; Shih, B.; Faber, M.; Speros, J.; Gupta, R.; Tolley, M.T. Desktop fabrication of monolithic soft robotic devices with embedded fluidic control circuits. Sci. Robot. 2023, 8, adg3792. [Google Scholar] [CrossRef] [PubMed]
- Argall, B.D.; Chernova, S.; Veloso, M.; Browning, B. A survey of robot learning from demonstration. Robot. Auton. Syst. 2009, 57, 469–483. [Google Scholar] [CrossRef]
- Polverini, M.P.; Zanchettin, A.M.; Rocco, P. A constraint-based programming approach for robotic assembly skills implementation. Robot. Comput. Integr. Manuf. 2019, 59, 69–81. [Google Scholar] [CrossRef]
- Kyrarini, M.; Haseeb, M.A.; Ristić-Durrant, D.; Gräser, A. Robot learning of industrial assembly task via human demonstrations. Auton. Robot. 2019, 43, 239–257. [Google Scholar] [CrossRef]
- Havoutis, I.; Calinon, S. Learning assistive teleoperation behaviors from demonstration. In Proceedings of the 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 23–27 October 2016; pp. 258–263. [Google Scholar] [CrossRef]
- Pervez, A.; Ali, A.; Ryu, J.H.; Lee, D. Novel learning from demonstration approach for repetitive teleoperation tasks. In Proceedings of the 2017 IEEE World Haptics Conference (WHC), Munich, Germany, 6–9 June 2017; pp. 60–65. [Google Scholar] [CrossRef]
- Huang, B.; Ye, M.; Lee, S.L.; Yang, G.Z. A Vision-Guided Multi-Robot Cooperation Framework for Learning-by-Demonstration and Task Reproduction. 2017. Available online: http://xxx.lanl.gov/abs/1706.00508 (accessed on 29 September 2023).
- Lin, L.; Yang, Y.; Song, Y.; Nemec, B.; Ude, A.; Rytz, J.; Buch, A.; Krüger, N.; Savarimuthu, T. Peg-in-Hole assembly under uncertain pose estimation. In Proceedings of the Proceeding of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 2842–2847. [Google Scholar] [CrossRef]
- Sabbaghi, E.; Bahrami, M.; Ghidary, S.S. Learning of gestures by imitation using a monocular vision system on a humanoid robot. In Proceedings of the 2014 Second RSI/ISM International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 15–17 October 2014; pp. 588–594. [Google Scholar] [CrossRef]
- Calinon, S.; Guenter, F.; Billard, A. On learning, representing, and generalizing a task in a humanoid robot. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2007, 37, 286–298. [Google Scholar] [CrossRef] [PubMed]
- Calinon, S.; Sauser, E.L.; Billard, A.G.; Caldwell, D.G. Evaluation of a probabilistic approach to learn and reproduce gestures by imitation. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 2671–2676. [Google Scholar]
- Lee, S.H.; Suh, I.H.; Calinon, S.; Johansson, R. Autonomous framework for segmenting robot trajectories of manipulation task. Auton. Robot. 2015, 38, 107–141. [Google Scholar] [CrossRef]
- Brown, J.C.; Smaragdis, P. Hidden Markov and Gaussian mixture models for automatic call classification. J. Acoust. Soc. Am. 2009, 125, EL221–EL224. [Google Scholar] [CrossRef]
- Meier, F.; Schaal, S. A probabilistic representation for dynamic movement primitives. arXiv 2016, arXiv:1612.05932. [Google Scholar]
- Ghalamzan E, A.M.; Paxton, C.; Hager, G.D.; Bascetta, L. An incremental approach to learning generalizable robot tasks from human demonstration. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5616–5621. [Google Scholar] [CrossRef]
- Luo, J.; Solowjow, E.; Wen, C.; Ojea, J.A.; Agogino, A.M. Deep reinforcement learning for robotic assembly of mixed deformable and rigid objects. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2062–2069. [Google Scholar]
- Chi, R.; Li, H.; Shen, D.; Hou, Z.; Huang, B. Enhanced P-Type Control: Indirect Adaptive Learning From Set-Point Updates. IEEE Trans. Autom. Control 2023, 68, 1600–1613. [Google Scholar] [CrossRef]
- Roman, R.C.; Precup, R.E.; Petriu, E.M. Hybrid data-driven fuzzy active disturbance rejection control for tower crane systems. Eur. J. Control 2021, 58, 373–387. [Google Scholar] [CrossRef]
- Elguea-Aguinaco, Í.; Serrano-Muñoz, A.; Chrysostomou, D.; Inziarte-Hidalgo, I.; Bøgh, S.; Arana-Arexolaleiba, N. A review on reinforcement learning for contact-rich robotic manipulation tasks. Robot. Comput.-Integr. Manuf. 2023, 81, 102517. [Google Scholar] [CrossRef]
- Luo, J.; Yang, C.; Li, Q.; Wang, M. A Task Learning Mechanism for the Telerobots. Int. J. Humanoid Robot. 2019, 16, 1950009. [Google Scholar] [CrossRef]
- Calinon, S.; Billard, A. A framework integrating statistical and social cues to teach a humanoid robot new skills. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Workshop on Social Interaction with Intelligent Indoor Robots, Pasadena, CA, USA, 23–27 May 2008. number CONF. [Google Scholar]
- Hormann, K.; Sukumar, N. Generalized Barycentric Coordinates in Computer Graphics and Computational Mechanics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Caccavale, R.; Saveriano, M.; Finzi, A.; Lee, D. Kinesthetic teaching and attentional supervision of structured tasks in human–robot interaction. Auton. Robot. 2019, 43, 1291–1307. [Google Scholar] [CrossRef]
- Kuchenbecker, K.J.; Niemeyer, G. Induced master motion in force-reflecting teleoperation. J. Dyn. Sys. Meas. Control 2006, 128, 800–810. [Google Scholar] [CrossRef]
- Niemeyer, G.; Preusche, C.; Stramigioli, S.; Lee, D. Telerobotics. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1085–1108. [Google Scholar]
- Das, H.; Zak, H.; Kim, W.S.; Bejczy, A.K.; Schenker, P.S. Operator performance with alternative manual control modes in teleoperation. Presence Teleoperators Virtual Environ. 1992, 1, 201–218. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Force Control; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Luh, J.; Fisher, W.; Paul, R. Joint torque control by a direct feedback for industrial robots. IEEE Trans. Autom. Control 1983, 28, 153–161. [Google Scholar] [CrossRef]
- Kana, S.; Gurnani, J.; Ramanathan, V.; Turlapati, S.H.; Ariffin, M.Z.; Campolo, D. Fast kinematic re-calibration for industrial robot arms. Sensors 2022, 22, 2295. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern recognition. Mach. Learn. 2006, 128, 9. [Google Scholar]
- Waldron, S. Affine generalised barycentric coordinates. Jaen J. Approx. 2011, 3, 209–226. [Google Scholar]
- Calinon, S. A tutorial on task-parameterized movement learning and retrieval. Intell. Serv. Robot. 2015, 9, 1–29. [Google Scholar] [CrossRef]
- Huang, Y.; Silverio, J.; Rozo, L.; Caldwell, D.G. Generalized Task-Parameterized Skill Learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018. [Google Scholar] [CrossRef]
- Whitney, D.E. Quasi-Static Assembly of Compliantly Supported Rigid Parts. J. Dyn. Syst. Meas. Control 1982, 104, 65–77. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, H.; Pham, D.T.; Wang, Y.; Qu, M.; Lim, J.; Su, S. Peg–hole disassembly using active compliance. R. Soc. Open Sci. 2019, 6, 190476. [Google Scholar] [CrossRef] [PubMed]
- Beltran-Hernandez, C.C.; Petit, D.; Ramirez-Alpizar, I.G.; Harada, K. Variable Compliance Control for Robotic Peg-in-Hole Assembly: A Deep-Reinforcement-Learning Approach. Appl. Sci. 2020, 10, 6923. [Google Scholar] [CrossRef]
- Suomalainen, M.; Kyrki, V. Learning 6-D compliant motion primitives from demonstration. arXiv 2018, arXiv:1809.01561. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kana, S.; Gurnani, J.; Ramanathan, V.; Ariffin, M.Z.; Turlapati, S.H.; Campolo, D. Learning Compliant Box-in-Box Insertion through Haptic-Based Robotic Teleoperation. Sensors 2023, 23, 8721. https://doi.org/10.3390/s23218721
Kana S, Gurnani J, Ramanathan V, Ariffin MZ, Turlapati SH, Campolo D. Learning Compliant Box-in-Box Insertion through Haptic-Based Robotic Teleoperation. Sensors. 2023; 23(21):8721. https://doi.org/10.3390/s23218721
Chicago/Turabian StyleKana, Sreekanth, Juhi Gurnani, Vishal Ramanathan, Mohammad Zaidi Ariffin, Sri Harsha Turlapati, and Domenico Campolo. 2023. "Learning Compliant Box-in-Box Insertion through Haptic-Based Robotic Teleoperation" Sensors 23, no. 21: 8721. https://doi.org/10.3390/s23218721
APA StyleKana, S., Gurnani, J., Ramanathan, V., Ariffin, M. Z., Turlapati, S. H., & Campolo, D. (2023). Learning Compliant Box-in-Box Insertion through Haptic-Based Robotic Teleoperation. Sensors, 23(21), 8721. https://doi.org/10.3390/s23218721






