Damage Identification of Railway Bridges through Temporal Autoregressive Modeling
Abstract
:1. Introduction
2. Theoretical Framework
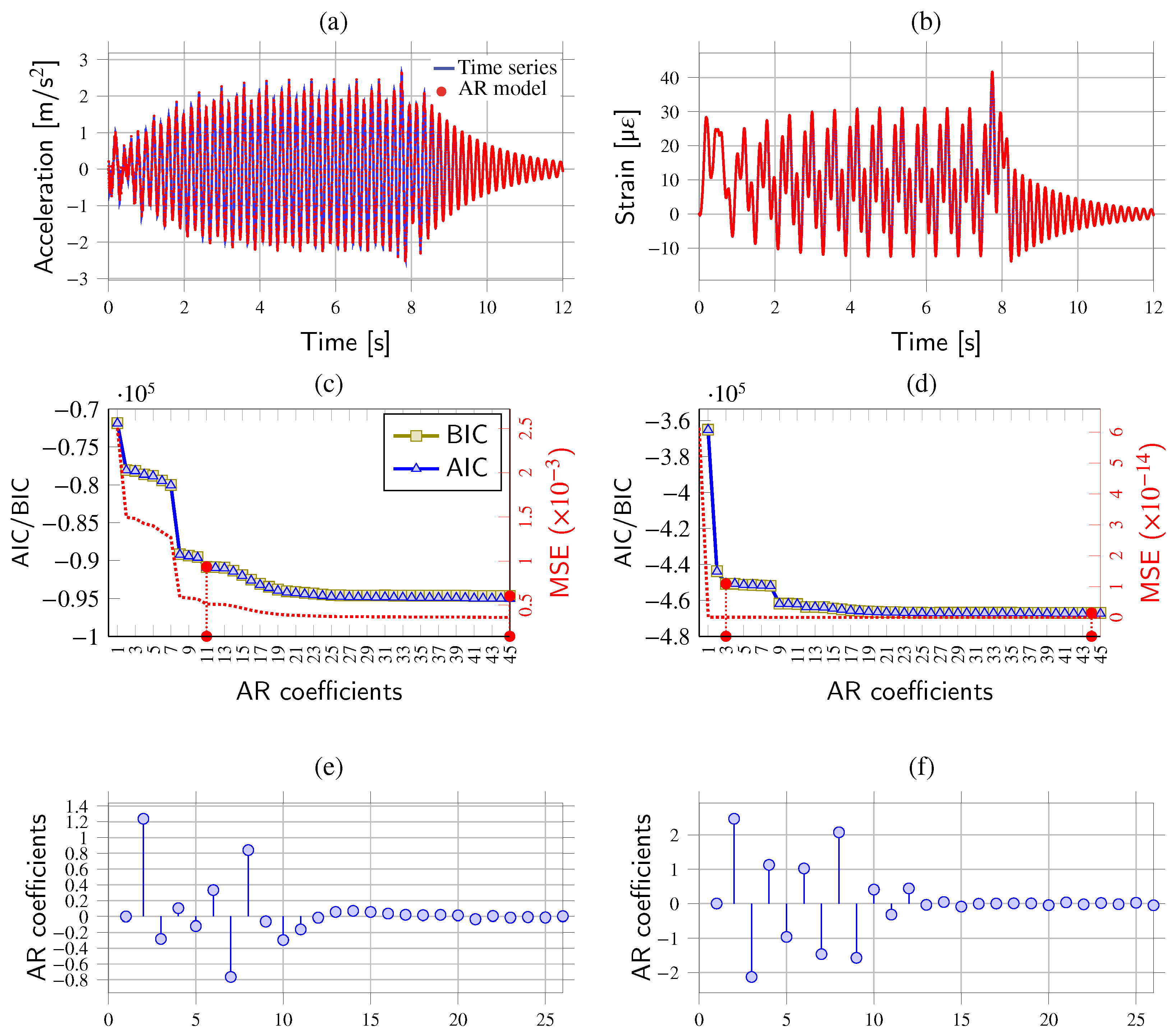
2.1. Feature Extraction: Autoregressive Modeling
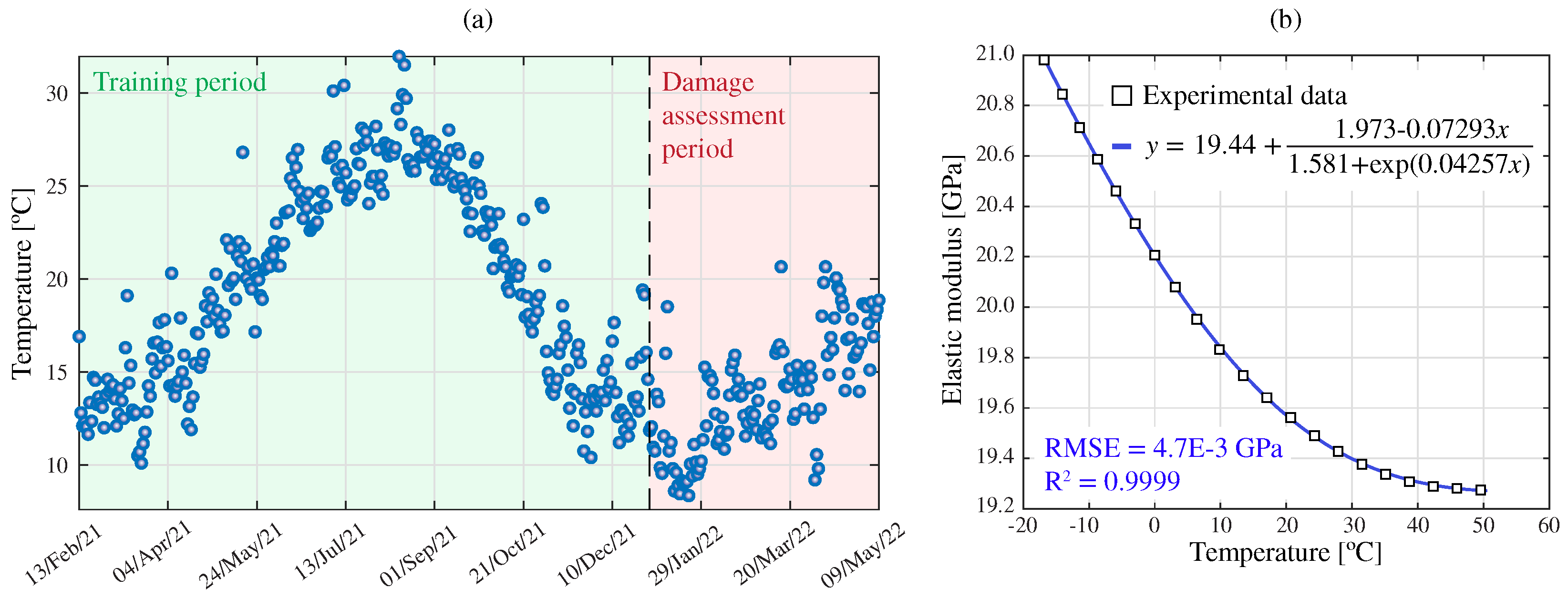
2.2. Elimination of Operational/Environmental Effects and Anomaly Detection
2.2.1. Data Clustering Using DBSCAN
- For each as-yet unlabeled data point p within the training period , consider the points located within a region of radius as per the Euclidean distance (-neighborhood).
- If at least points (including p) fall within the distance from p, a new cluster C is defined. Subsequently, p is designated as a core point of C, while the remaining points are marked as directly reachable from p. If this condition is not met, p is labeled as a noise point.
- The cluster C is expanded to encompass all points indirectly reachable from p. A point q is considered reachable if there exists a path of directly reachable points between p and q.
- If point q is not directly connected to any other point, it is identified as a border point.
- Once all paths originating from p terminate at a border point, the next unlabeled point is processed until none remain.
2.2.2. Cluster-Based Data Normalization Using PCA
2.2.3. Novelty Analysis Using Sensor-Based Control Charts
3. Numerical Results and Discussion
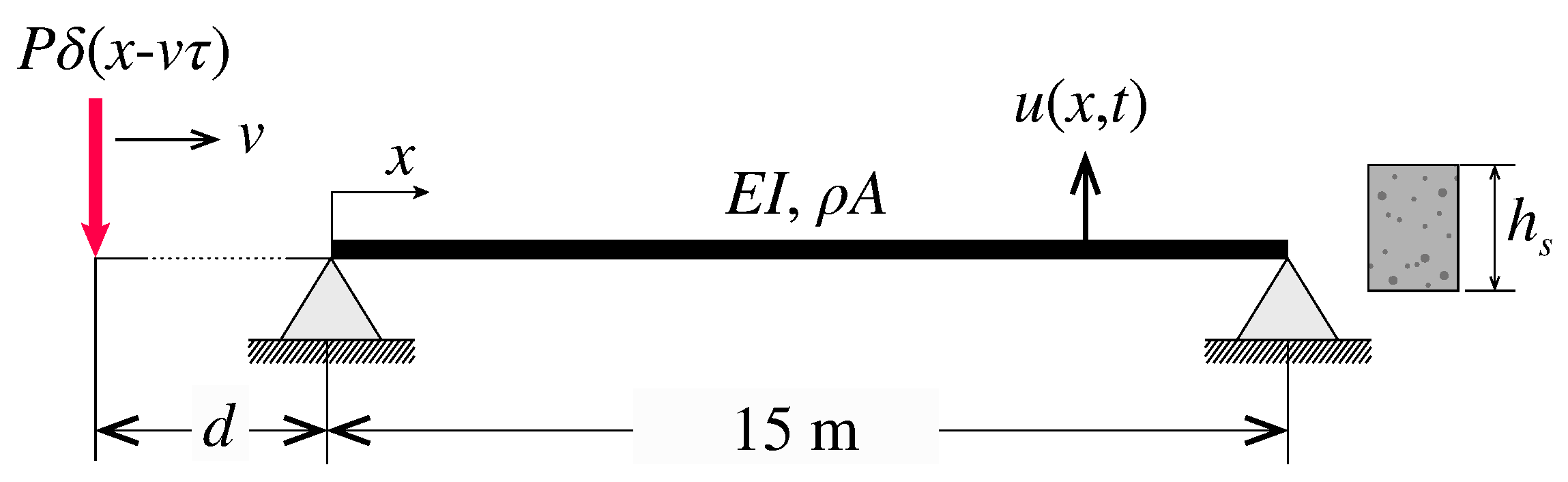
3.1. Case Study I: Simply Supported Bridge
3.2. Case Study II: The Mascarat Bridge
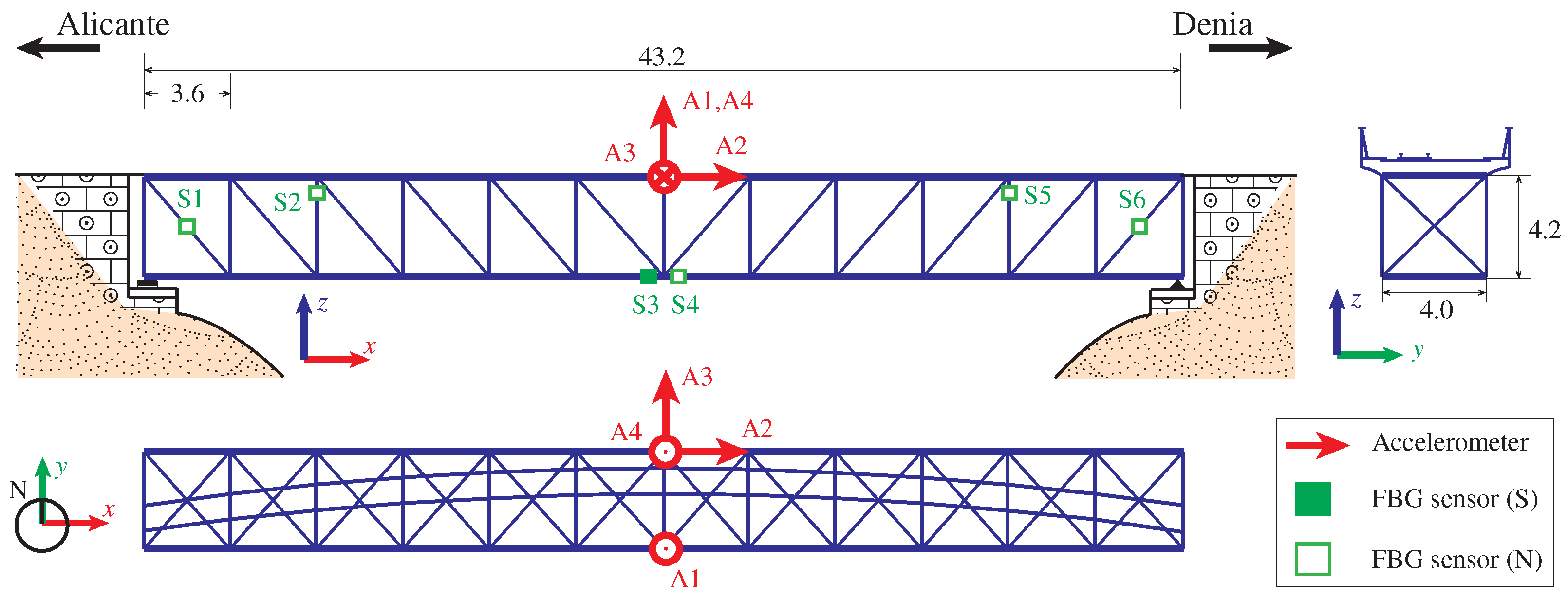
3.2.1. Description of the Structure
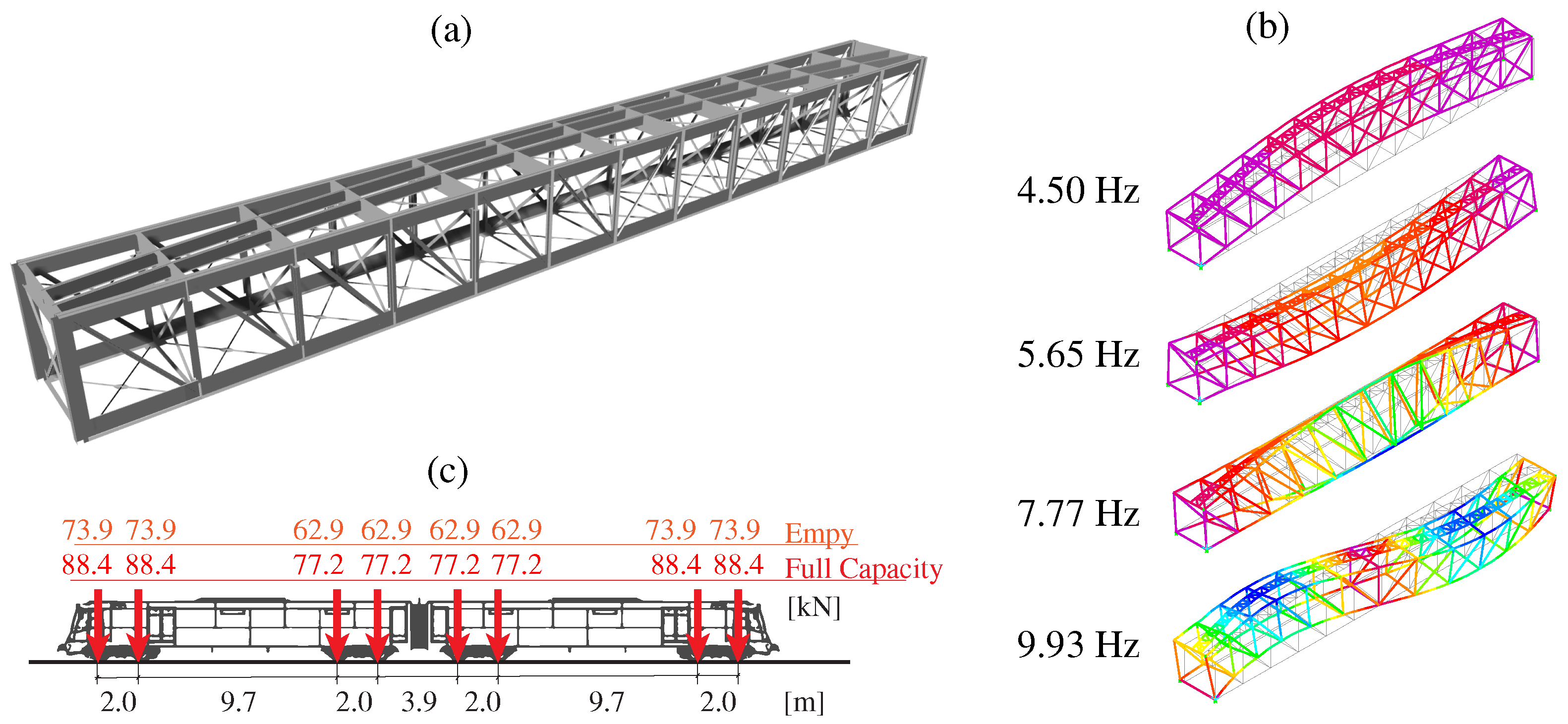
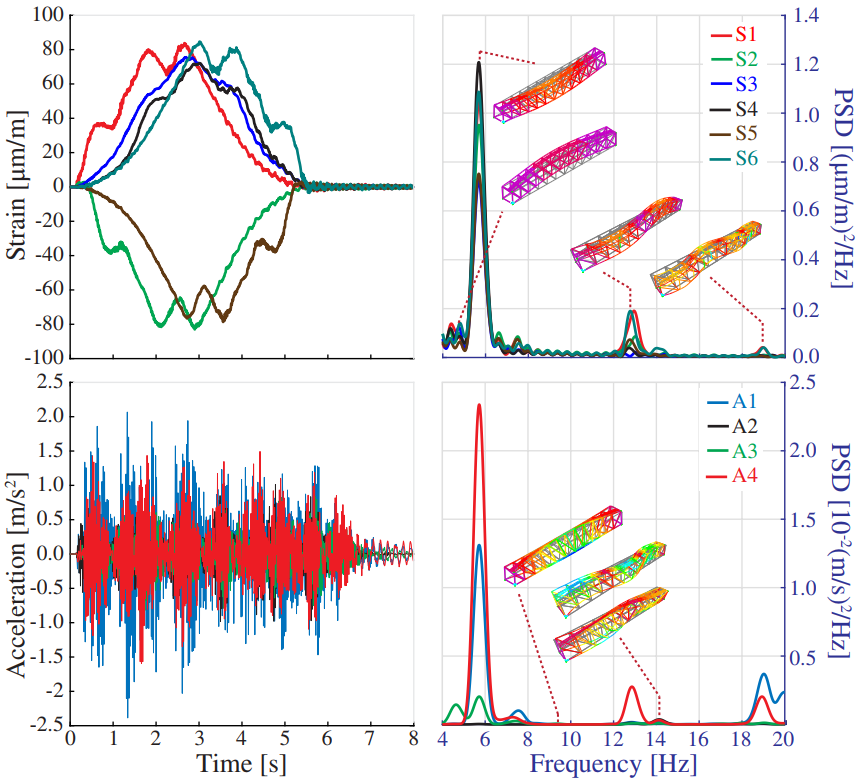
3.2.2. Finite Element Model and Experimental Validation
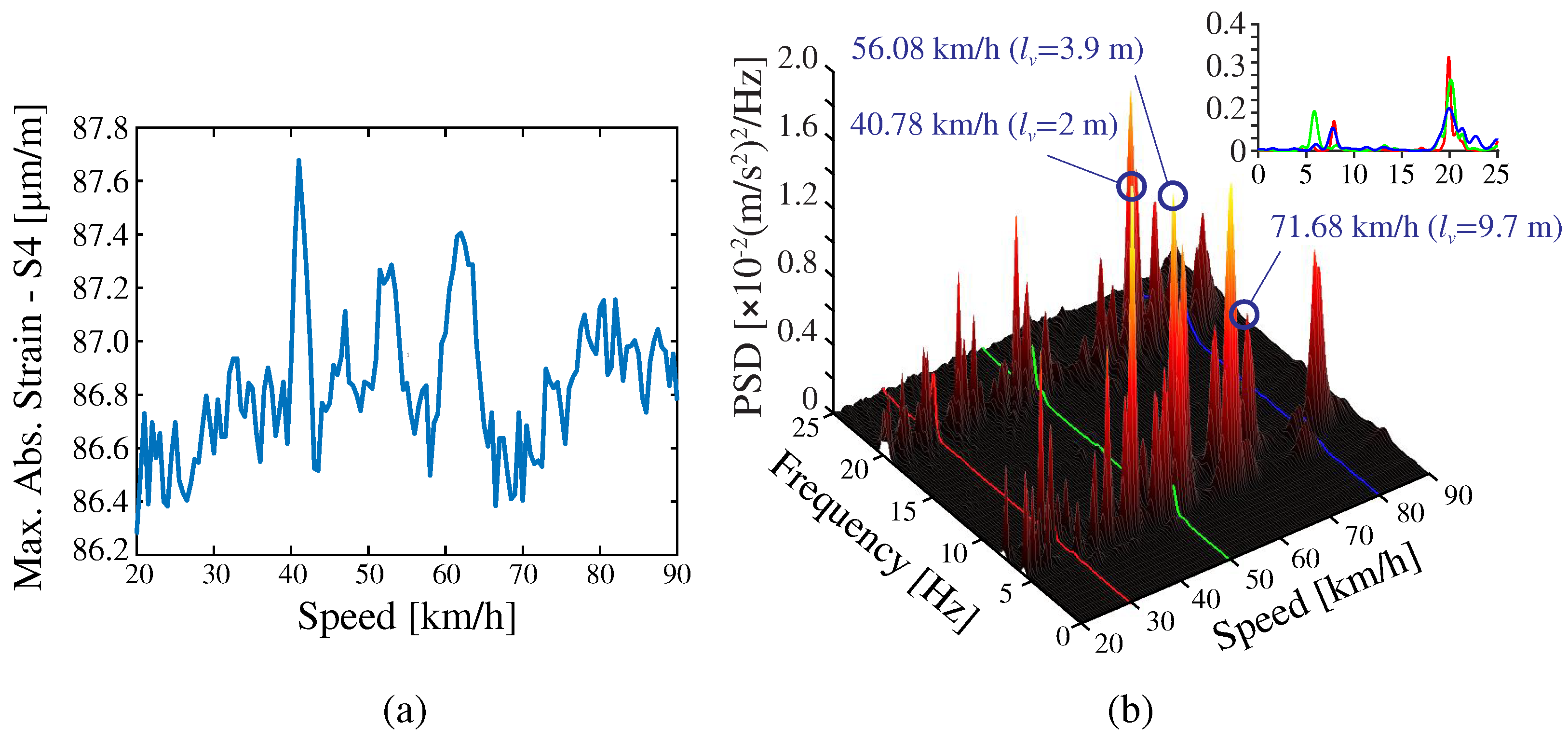
3.2.3. Damage Identification Results
4. Conclusions
- The presented SHM approach leverages continuous extraction of sensor-level AR coefficients, offering an easily implementable solution with minimal computational burden and expert intervention.
- Strain recordings under moving train load conditions are considerably less affected by high-oscillating components compared to acceleration data. This allows more compact AR models to be generated with AR coefficients less affected by operational factors (train speed and weight).
- To unveil the presence of damage, it is of pivotal importance to eliminate the effects of EOCs. To this end, the two-step statistical pattern recognition approach combining DBSCAN and PCA has shown proficiency in minimizing EOC-driven variance in the time series of continuously extracted AR coefficients.
- The proposed SHM approach provides a set of sensor-based control charts, offering great potential for damage detection, quantification, and localization. The latter can be achieved by interpreting radar graphs of the data points violating in-control upper control limits.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Closed-Form Solution of the Moving Load Problem for Simply Supported Beams
References
- European Comission. Directorate-General for Mobility and Transport. In White Paper on Transport: Roadmap to a Single European Transport Area: Towards a Competitive and Resource-Efficient Transport System; Publications office of the European Union: Luxembourg, 2011. [Google Scholar]
- Paulsson, B.; Olofsson, J.; Hedlund, H.; Bell, B.; Täljsten, B.; Elfgren, L. Sustainable Bridges–Results from a European Integrated Research Project. In Proceedings of the IABSE Symposium Report; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 2010; Volume 97, pp. 17–24. [Google Scholar]
- Monitoring, R.M. Seventh monitoring report on the development of the rail market under Article 15 (4) of Directive 2012/34/EU of the European Parliament and of the Council. COM 2021, 5. [Google Scholar]
- Kienzler, C.; Lotz, C.; Stern, S. Using Analytics to Get European Rail Maintenance on Track; McKinsey & Company: New York, NY, USA, 2020. [Google Scholar]
- HAQ, G.; Ortega Hortelano, A.; Tsakalidis, A.; Gkoumas, K.; Pekár, F.; Balen, M.; Grosso, M.; Marques Dos Santos, F. Research and Innovation in Bridge Maintenance, Inspection and Monitoring: A European Perspective Based on the Transport Research and Innovation Monitoring and Information System (TRIMIS): Study; EU Publications: Luxembourg, 2019.
- Cawley, P. Structural health monitoring: Closing the gap between research and industrial deployment. Struct. Health Monit. 2018, 17, 1225–1244. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Caredda, G.; Porcu, M.C.; Buitrago, M.; Bertolesi, E.; Adam, J.M. Analysing local failure scenarios to assess the robustness of steel truss-type bridges. Eng. Struct. 2022, 262, 114341. [Google Scholar] [CrossRef]
- López, S.; Makoond, N.; Sánchez-Rodríguez, A.; Adam, J.M.; Riveiro, B. Learning from failure propagation in steel truss bridges. Eng. Fail. Anal. 2023, 152, 107488. [Google Scholar] [CrossRef]
- García-Macías, E.; Ubertini, F. Integrated SHM systems: Damage detection through unsupervised learning and data fusion. In Structural Health Monitoring Based on Data Science Techniques; Springer: Berlin/Heidelberg, Germany, 2021; pp. 247–268. [Google Scholar]
- Ierimonti, L.; Cavalagli, N.; Venanzi, I.; García-Macías, E.; Ubertini, F. A transfer Bayesian learning methodology for structural health monitoring of monumental structures. Eng. Struct. 2021, 247, 113089. [Google Scholar] [CrossRef]
- Torres, B.; Poveda, P.; Ivorra, S.; Estevan, L. Long-term static and dynamic monitoring to failure scenarios assessment in steel truss railway bridges: A case study. Eng. Fail. Anal. 2023, 152, 107435. [Google Scholar] [CrossRef]
- Tokognon, C.A.; Gao, B.; Tian, G.Y.; Yan, Y. Structural health monitoring framework based on Internet of Things: A survey. IEEE Internet Things J. 2017, 4, 619–635. [Google Scholar] [CrossRef]
- Lan, Y.; Zhang, Y.; Lin, W. Diagnosis algorithms for indirect bridge health monitoring via an optimized AdaBoost-linear SVM. Eng. Struct. 2023, 275, 115239. [Google Scholar] [CrossRef]
- Lan, Y.; Li, Z.; Koski, K.; Fülöp, L.; Tirkkonen, T.; Lin, W. Bridge frequency identification in city bus monitoring: A coherence-PPI algorithm. Eng. Struct. 2023, 296, 116913. [Google Scholar] [CrossRef]
- Vagnoli, M.; Remenyte-Prescott, R.; Andrews, J. Railway bridge structural health monitoring and fault detection: State-of-the-art methods and future challenges. Struct. Health Monit. 2018, 17, 971–1007. [Google Scholar] [CrossRef]
- Castillo-Mingorance, J.M.; Sol-Sánchez, M.; Moreno-Navarro, F.; Rubio-Gámez, M.C. A critical review of sensors for the continuous monitoring of smart and sustainable railway infrastructures. Sustainability 2020, 12, 9428. [Google Scholar] [CrossRef]
- He, Z.; Li, W.; Salehi, H.; Zhang, H.; Zhou, H.; Jiao, P. Integrated structural health monitoring in bridge engineering. Autom. Constr. 2022, 136, 104168. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A Systematic Review of Advanced Sensor Technologies for Non-Destructive Testing and Structural Health Monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Wu, G.; Yang, C.; He, Y. Damage identification method for continuous girder bridges based on spatially-distributed long-gauge strain sensing under moving loads. Mech. Syst. Signal Process. 2018, 104, 415–435. [Google Scholar] [CrossRef]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D.K. Fibre Bragg gratings in structural health monitoring—Present status and applications. Sens. Actuators A Phys. 2008, 147, 150–164. [Google Scholar] [CrossRef]
- Glisic, B. Concise historic overview of strain sensors used in the monitoring of civil structures: The first one hundred years. Sensors 2022, 22, 2397. [Google Scholar] [CrossRef]
- Du, C.; Dutta, S.; Kurup, P.; Yu, T.; Wang, X. A review of railway infrastructure monitoring using fiber optic sensors. Sens. Actuators A Phys. 2020, 303, 111728. [Google Scholar] [CrossRef]
- Sasy Chan, Y.W.; Wang, H.P.; Xiang, P. Optical fiber sensors for monitoring railway infrastructures: A review towards smart concept. Symmetry 2021, 13, 2251. [Google Scholar] [CrossRef]
- Svendsen, B.T.; Frøseth, G.T.; Øiseth, O.; Rønnquist, A. A data-based structural health monitoring approach for damage detection in steel bridges using experimental data. J. Civ. Struct. Health Monit. 2022, 12, 101–115. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Magalhães, F.; Cunha, Á. Explaining operational modal analysis with data from an arch bridge. Mech. Syst. Signal Process. 2011, 25, 1431–1450. [Google Scholar] [CrossRef]
- García-Macías, E.; Ubertini, F. Automated operational modal analysis and ambient noise deconvolution interferometry for the full structural identification of historic towers: A case study of the Sciri Tower in Perugia, Italy. Eng. Struct. 2020, 215, 110615. [Google Scholar] [CrossRef]
- Tomassini, E.; García-Macías, E.; Reynders, E.; Ubertini, F. Model-assisted clustering for automated operational modal analysis of partially continuous multi-span bridges. Mech. Syst. Signal Process. 2023, 200, 110587. [Google Scholar] [CrossRef]
- Vestroni, F.; Capecchi, D. Damage detection in beam structures based on frequency measurements. J. Eng. Mech. 2000, 126, 761–768. [Google Scholar] [CrossRef]
- Giglioni, V.; García-Macías, E.; Venanzi, I.; Ierimonti, L.; Ubertini, F. The use of receiver operating characteristic curves and precision-versus-recall curves as performance metrics in unsupervised structural damage classification under changing environment. Eng. Struct. 2021, 246, 113029. [Google Scholar] [CrossRef]
- Santos, J.P.; Crémona, C.; Orcesi, A.D.; Silveira, P. Multivariate statistical analysis for early damage detection. Eng. Struct. 2013, 56, 273–285. [Google Scholar] [CrossRef]
- Wang, X.; Makis, V. Autoregressive model-based gear shaft fault diagnosis using the Kolmogorov–Smirnov test. J. Sound Vib. 2009, 327, 413–423. [Google Scholar] [CrossRef]
- Morgan, J.; Tatar, J. Calculation of the residual sum of squares for all possible regressions. Technometrics 1972, 14, 317–325. [Google Scholar] [CrossRef]
- Cantero, D.; Ülker-Kaustell, M.; Karoumi, R. Time–frequency analysis of railway bridge response in forced vibration. Mech. Syst. Signal Process. 2016, 76, 518–530. [Google Scholar] [CrossRef]
- Gonzalez, I.; Karoumi, R. Analysis of the annual variations in the dynamic behavior of a ballasted railway bridge using Hilbert transform. Eng. Struct. 2014, 60, 126–132. [Google Scholar] [CrossRef]
- Matsuoka, K.; Tokunaga, M.; Kaito, K. Bayesian estimation of instantaneous frequency reduction on cracked concrete railway bridges under high-speed train passage. Mech. Syst. Signal Process. 2021, 161, 107944. [Google Scholar] [CrossRef]
- Tronci, E.M.; Beigi, H.; Feng, M.Q.; Betti, R. A transfer learning SHM strategy for bridges enriched by the use of speaker recognition x-vectors. J. Civ. Struct. Health Monit. 2022, 12, 1285–1298. [Google Scholar] [CrossRef]
- Zhang, C.; Mousavi, A.A.; Masri, S.F.; Gholipour, G.; Yan, K.; Li, X. Vibration feature extraction using signal processing techniques for structural health monitoring: A review. Mech. Syst. Signal Process. 2022, 177, 109175. [Google Scholar] [CrossRef]
- Datteo, A.; Busca, G.; Quattromani, G.; Cigada, A. On the use of AR models for SHM: A global sensitivity and uncertainty analysis framework. Reliab. Eng. Syst. Saf. 2018, 170, 99–115. [Google Scholar] [CrossRef]
- Yao, R.; Pakzad, S.N. Autoregressive statistical pattern recognition algorithms for damage detection in civil structures. Mech. Syst. Signal Process. 2012, 31, 355–368. [Google Scholar] [CrossRef]
- Meixedo, A.; Santos, J.; Ribeiro, D.; Calçada, R.; Todd, M.D. Online unsupervised detection of structural changes using train–induced dynamic responses. Mech. Syst. Signal Process. 2022, 165, 108268. [Google Scholar] [CrossRef]
- Wang, X.; Zhuo, Y.; Li, S. Damage detection of high-speed railway box girder using train-induced dynamic responses. Sustainability 2023, 15, 8552. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Liu, A.; Wang, L.; Bornn, L.; Farrar, C. Robust structural health monitoring under environmental and operational uncertainty with switching state-space autoregressive models. Struct. Health Monit. 2019, 18, 435–453. [Google Scholar] [CrossRef]
- Al-Smadi, A.; Wilkes, D.M. Robust and accurate ARX and ARMA model order estimation of non-Gaussian processes. IEEE Trans. Signal Process. 2002, 50, 759–763. [Google Scholar] [CrossRef]
- Psaradakis, Z.; Spagnolo, N. On the determination of the number of regimes in Markov-switching autoregressive models. J. Time Ser. Anal. 2003, 24, 237–252. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: Berlin/Heidelberg, Germany, 1998; pp. 199–213. [Google Scholar]
- Gorgin, R.; Luo, Y.; Wu, Z. Environmental and operational conditions effects on Lamb wave based structural health monitoring systems: A review. Ultrasonics 2020, 105, 106114. [Google Scholar] [CrossRef] [PubMed]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. (TODS) 2017, 42, 1–21. [Google Scholar] [CrossRef]
- García-Macías, E.; Ubertini, F. Least Angle Regression for early-stage identification of earthquake-induced damage in a monumental masonry palace: Palazzo dei Consoli. Eng. Struct. 2022, 259, 114119. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis for Special Types of Data; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Yan, A.M.; Kerschen, G.; De Boe, P.; Golinval, J.C. Structural damage diagnosis under varying environmental conditions—Part I: A linear analysis. Mech. Syst. Signal Process. 2005, 19, 847–864. [Google Scholar] [CrossRef]
- Ribeiro, D.; Leite, J.; Meixedo, A.; Pinto, N.; Calçada, R.; Todd, M. Statistical methodologies for removing the operational effects from the dynamic responses of a high-rise telecommunications tower. Struct. Control Health Monit. 2021, 28, e2700. [Google Scholar] [CrossRef]
- Hotelling, H. Multivariate quality control-illustrated by the air testing of sample bombsights. In Techniques of Statistical Analysis; McGraw Hill: New York, NY, USA, 1947. [Google Scholar]
- Yue, N.; Aliabadi, M. Hierarchical approach for uncertainty quantification and reliability assessment of guided wave-based structural health monitoring. Struct. Health Monit. 2021, 20, 2274–2299. [Google Scholar] [CrossRef]
- Instrucción de Acciones a Considerar en Puentes de Ferrocarril (IAPF) [Instruction on Actions to Be Considered in the Project of Railway Bridges]; Standard, Ministerio de Fomento: Marid, Spain, 2007.
- García-Macías, E.; Ruccolo, A.; Zanini, M.A.; Pellegrino, C.; Gentile, C.; Ubertini, F.; Mannella, P. P3P: A software suite for autonomous SHM of bridge networks. J. Civ. Struct. Health Monit. 2022. [Google Scholar] [CrossRef]
- Arvidsson, T.; Karoumi, R. Train–bridge interaction–a review and discussion of key model parameters. Int. J. Rail Transp. 2014, 2, 147–186. [Google Scholar] [CrossRef]
- Cantero, D.; Arvidsson, T.; OBrien, E.; Karoumi, R. Train–track–bridge modelling and review of parameters. Struct. Infrastruct. Eng. 2016, 12, 1051–1064. [Google Scholar] [CrossRef]
- Meruane, V.; Heylen, W. Structural damage assessment under varying temperature conditions. Struct. Health Monit. 2012, 11, 345–357. [Google Scholar] [CrossRef]







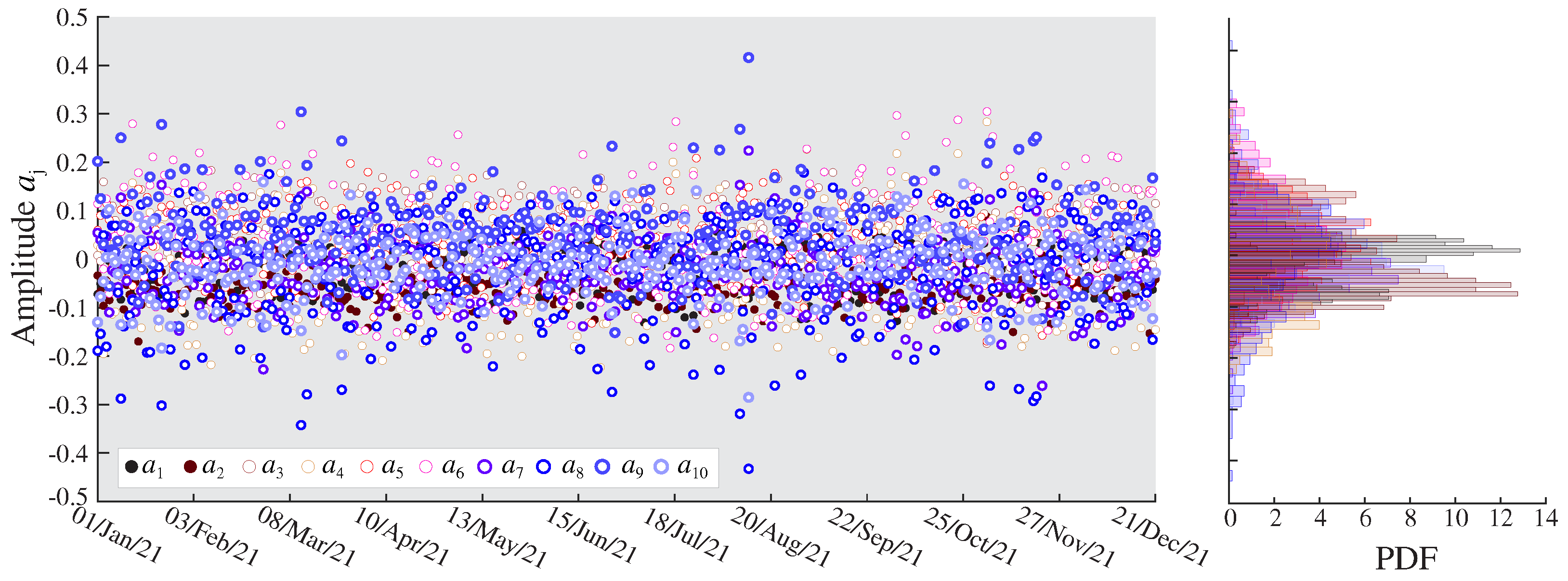
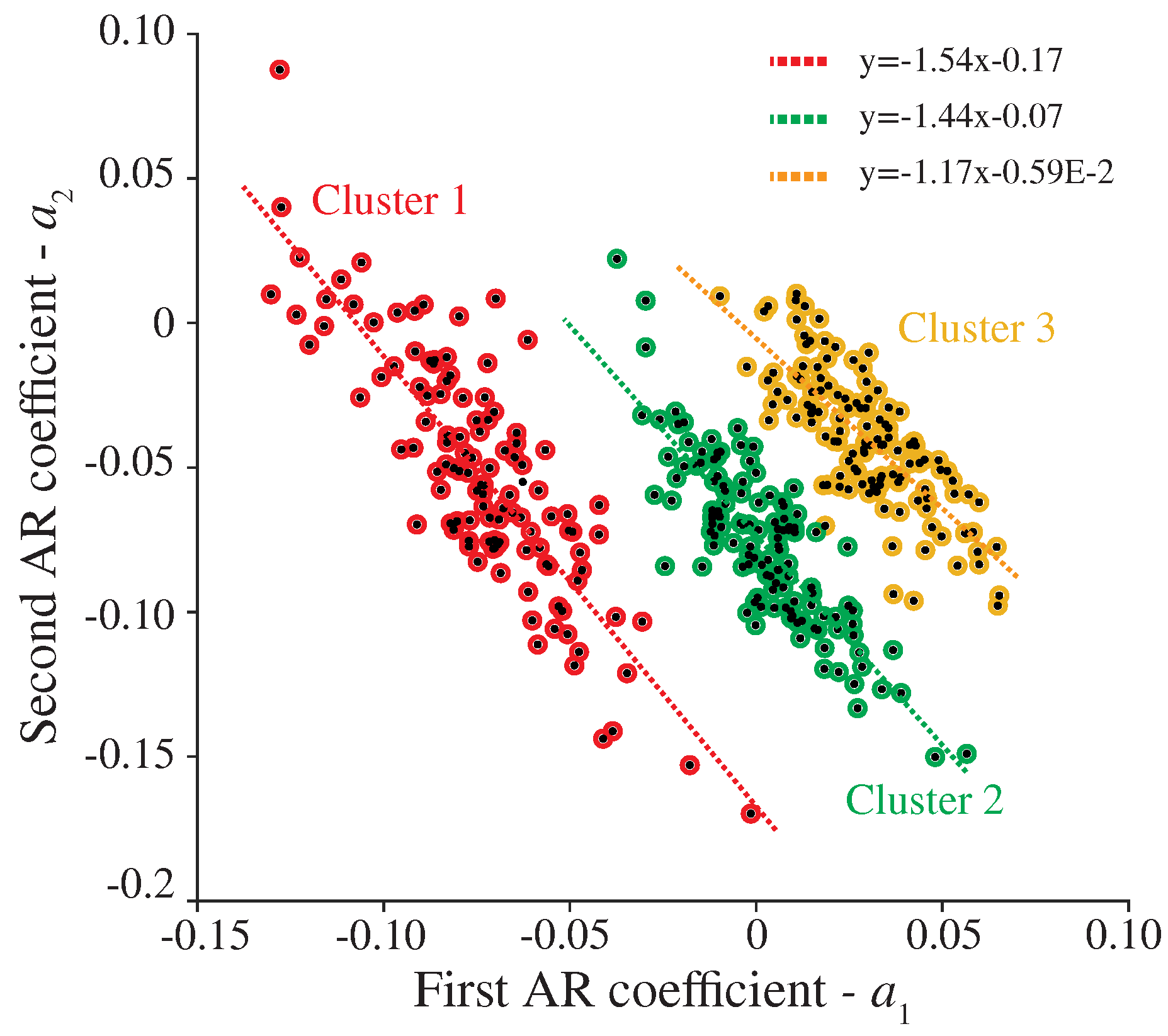
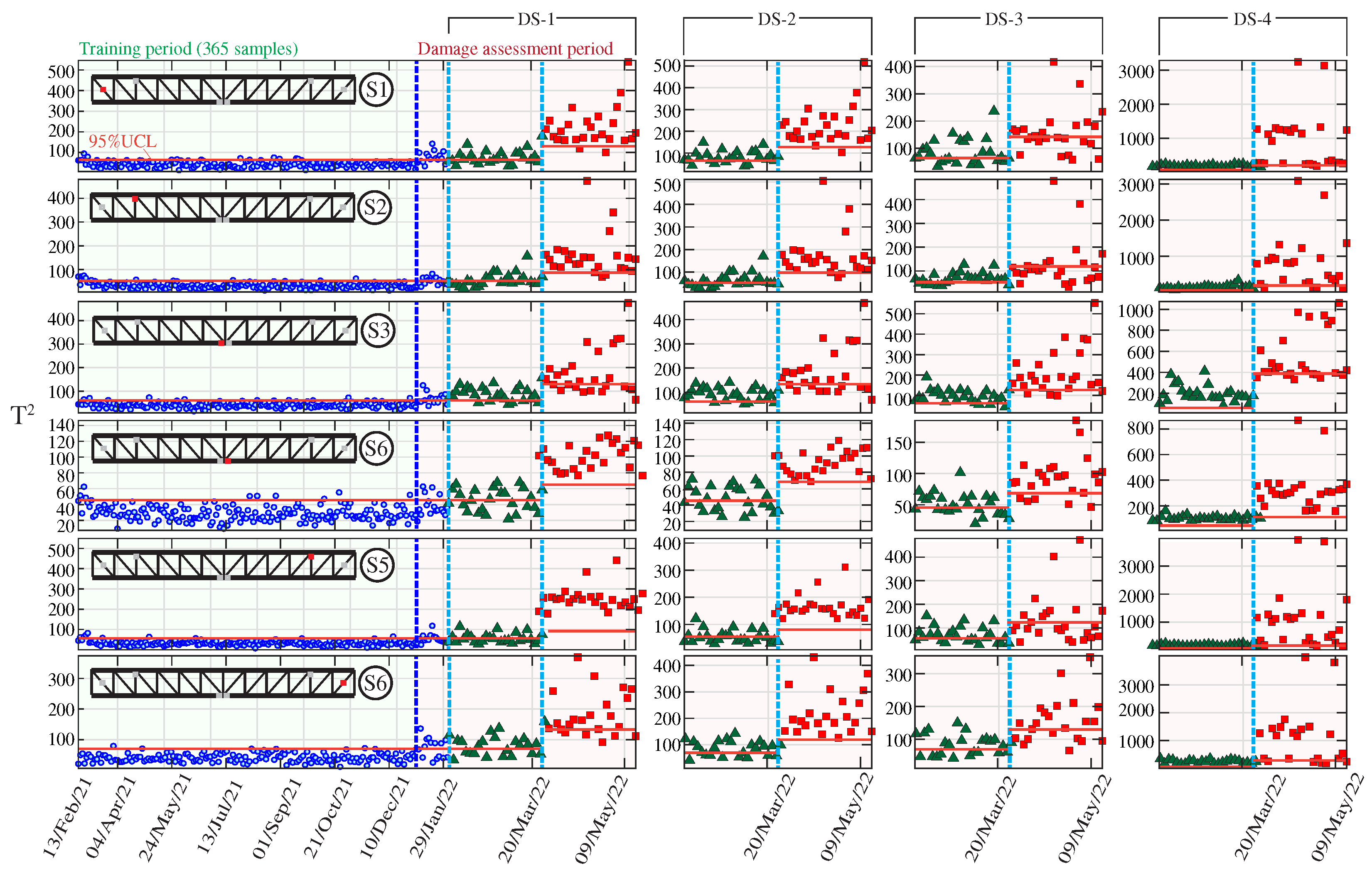

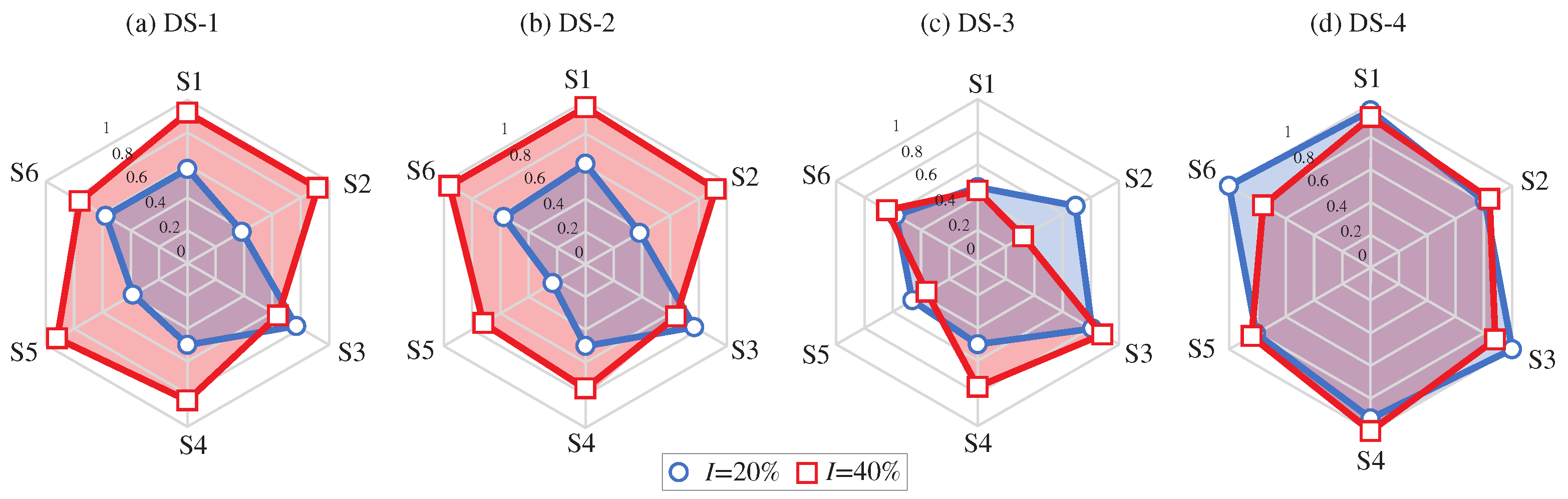
| Elements | Description |
|---|---|
| Connections | T-section formed by a 360 × 12 wing and a 560 × 11 web joined by 2 L 90 × 12. The upper and lower chords are reinforced by two 360 × 13 plates located on the wing in the central area of the bridge |
| Diagonals | L-type angles with widths between 80 and 120 mm and variable thickness |
| End uprights | L-type angle brackets with 70.9 × 90.7 mm dimensions and reinforcement plates of dimensions 360 × 90 mm, 160 × 90 mm and 150 × 11 mm |
| Remaining uprights | L-type angle brackets with 70 mm height and variable thickness, rein-forced with two 9 × 160 mm plates |
| Rafters | Double-T cross-sections with 450 × 9 mm and 70 × 9 mm flanges |
| Joists | Double-T cross-sections with 700 × 9 mm webs and 90 × 12 mm flanges |
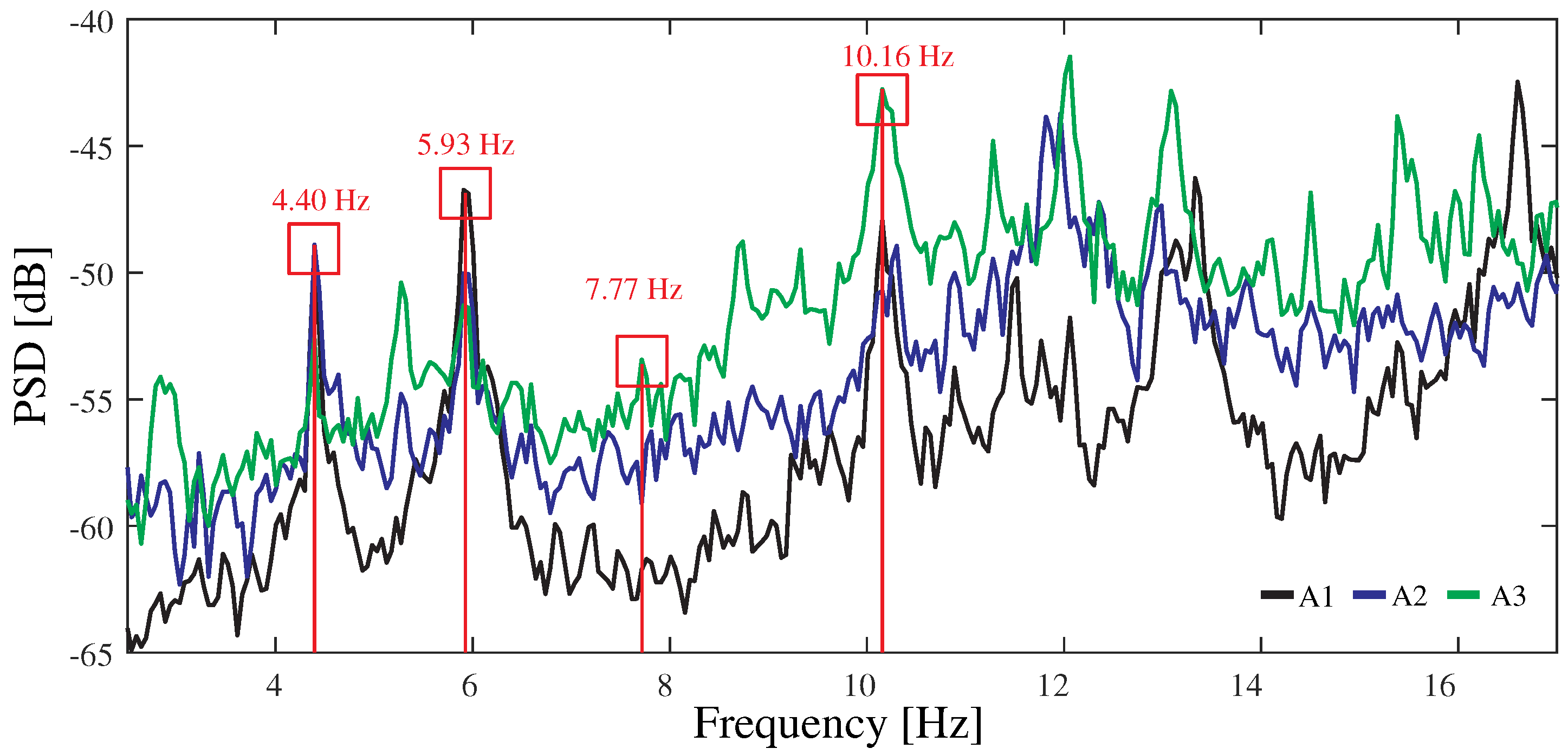
| DS-1 ( [%]) | DS-2 ( [%]) | DS-3 ( [%]) | DS-4 ( [%]) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Experim. | DS-0 | % | % | % | % | % | % | % | % |
| 4.40 | 4.49 | −0.50 | −1.20 | −0.49 | −1.17 | −0.18 | −1.21 | −0.23 | −1.32 |
| 5.93 | 5.65 | −0.67 | −1.62 | −0.26 | −0.65 | −0.53 | −2.10 | 0.04 | −0.72 |
| 7.77 | 7.77 | −0.02 | −0.06 | 0.00 | −0.01 | 0.38 | 0.27 | 0.85 | 0.81 |
| 10.16 | 9.93 | −0.13 | −0.36 | −0.12 | −0.33 | −0.05 | −0.20 | 0.01 | −0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anastasia, S.; García-Macías, E.; Ubertini, F.; Gattulli, V.; Ivorra, S. Damage Identification of Railway Bridges through Temporal Autoregressive Modeling. Sensors 2023, 23, 8830. https://doi.org/10.3390/s23218830
Anastasia S, García-Macías E, Ubertini F, Gattulli V, Ivorra S. Damage Identification of Railway Bridges through Temporal Autoregressive Modeling. Sensors. 2023; 23(21):8830. https://doi.org/10.3390/s23218830
Chicago/Turabian StyleAnastasia, Stefano, Enrique García-Macías, Filippo Ubertini, Vincenzo Gattulli, and Salvador Ivorra. 2023. "Damage Identification of Railway Bridges through Temporal Autoregressive Modeling" Sensors 23, no. 21: 8830. https://doi.org/10.3390/s23218830
APA StyleAnastasia, S., García-Macías, E., Ubertini, F., Gattulli, V., & Ivorra, S. (2023). Damage Identification of Railway Bridges through Temporal Autoregressive Modeling. Sensors, 23(21), 8830. https://doi.org/10.3390/s23218830








