Observing Liquid Sloshing Based on a Multi-Degree-of-Freedom Pendulum Model and Free Surface Fluctuation Sensor
Abstract
:1. Introduction
2. Spectral Analysis of Sloshing Liquid
2.1. CFD Modeling of Liquid Sloshing
2.2. Spectral Analysis of Liquid Sloshing
3. Multi-Degree-of-Freedom Pendulum Model
3.1. Generalized Pendulum Model
3.2. Spectral Analysis of Models
3.3. Pendulum Models with 2DOF
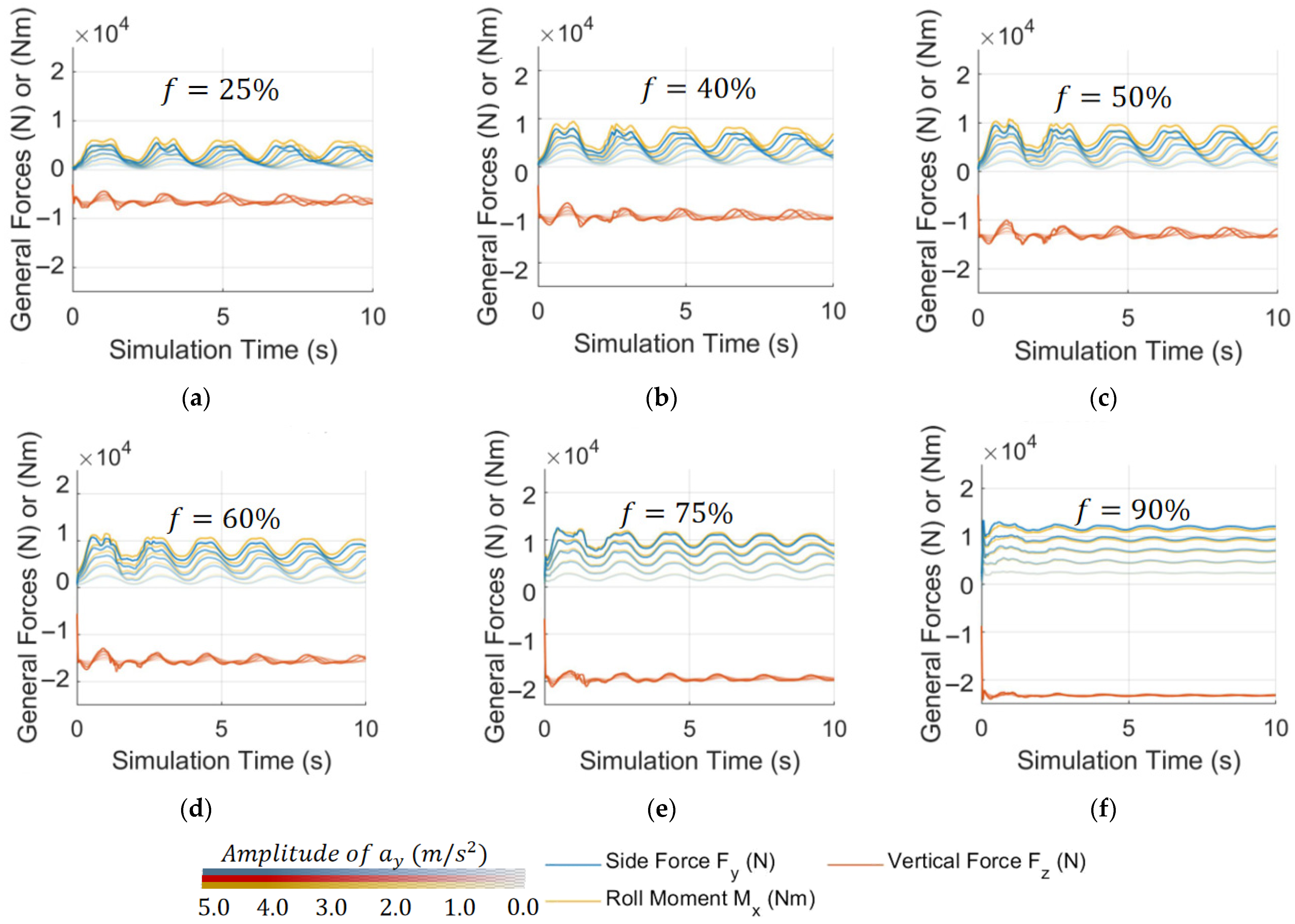
4. Simulation Analysis of Pendulum Models
4.1. Parameter Fitting for Pendulum Models
4.2. Map Analysis of Pendulum Models
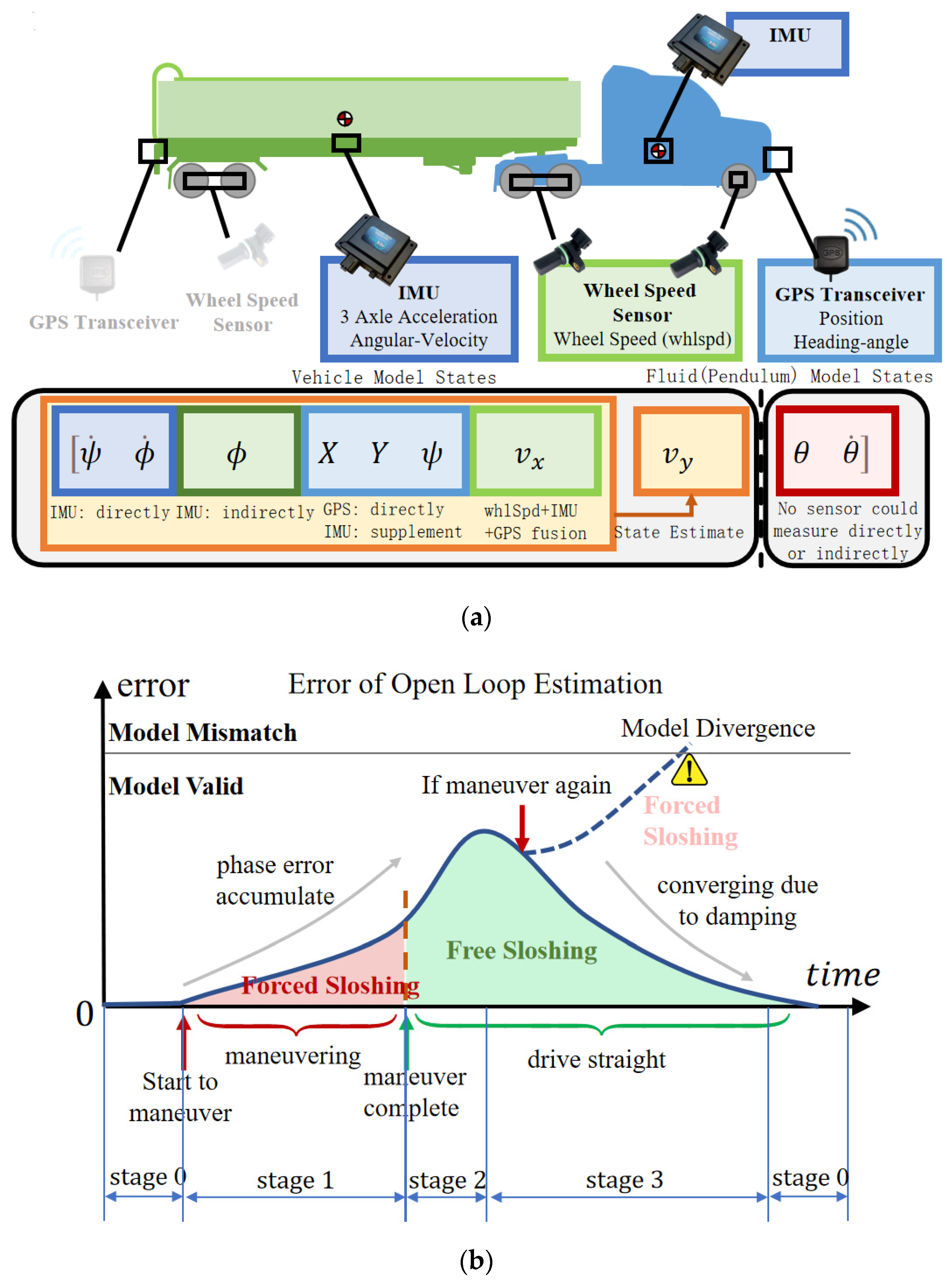
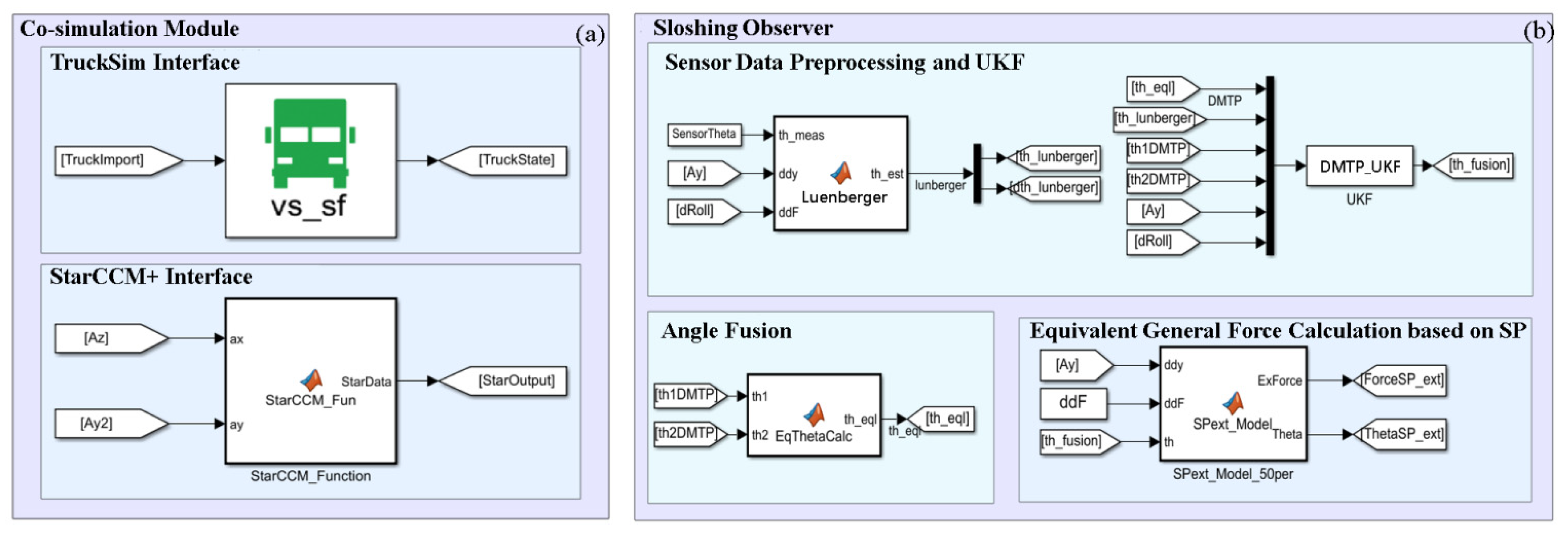
5. Sloshing Observer Design
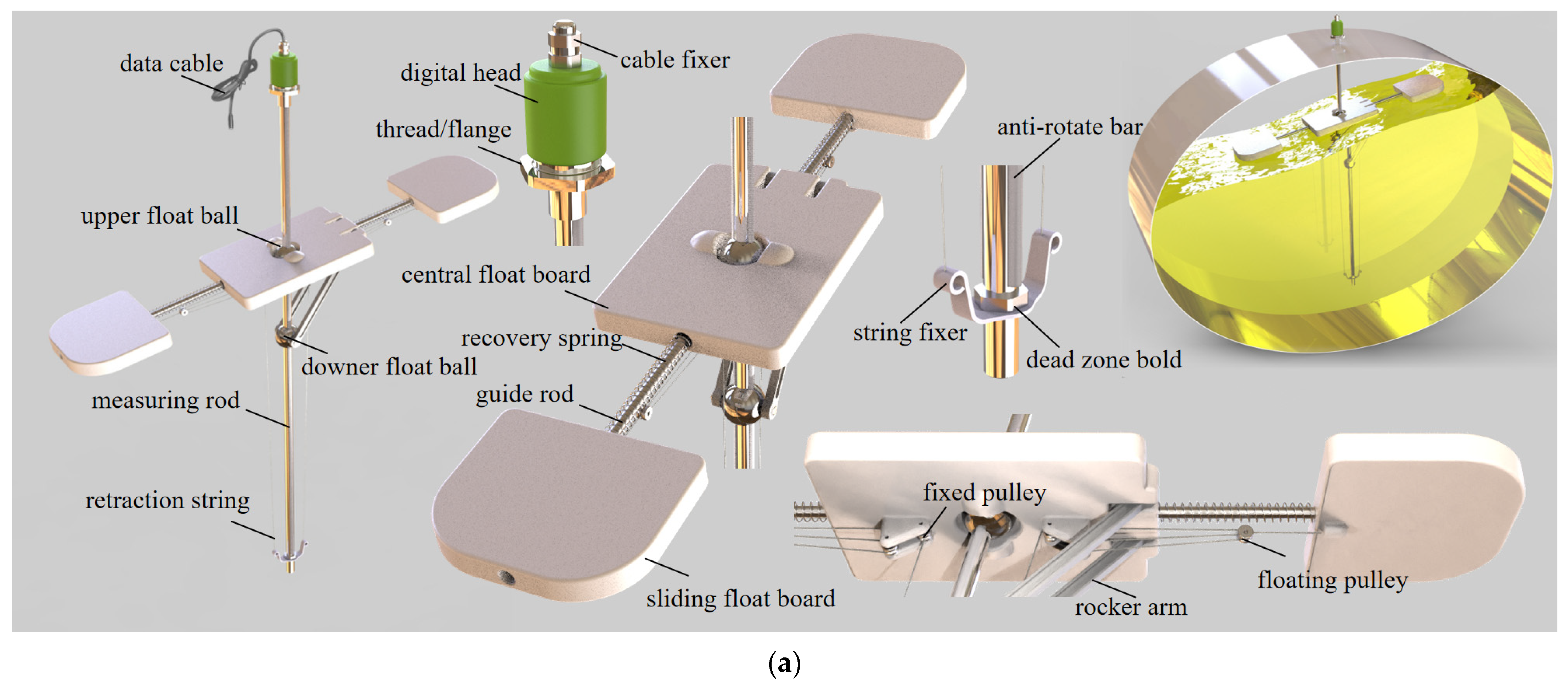
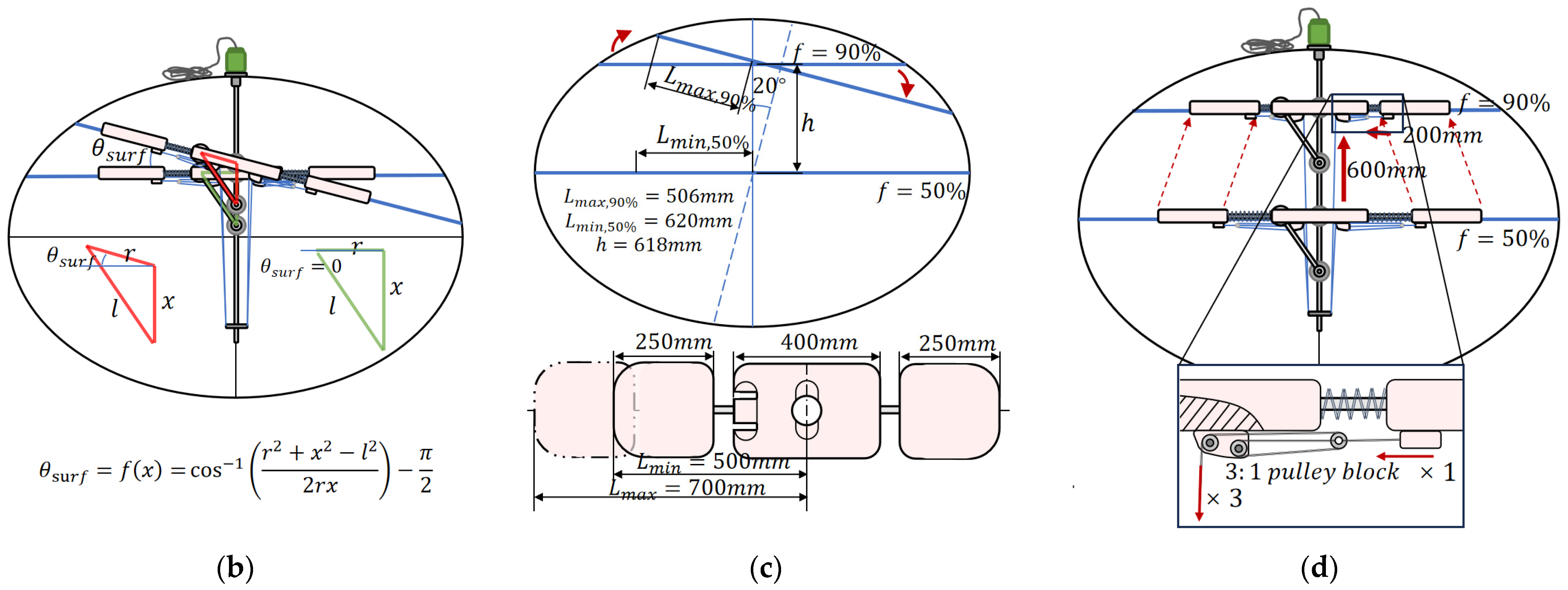
5.1. Free Surface Fluctuation Sensor Design
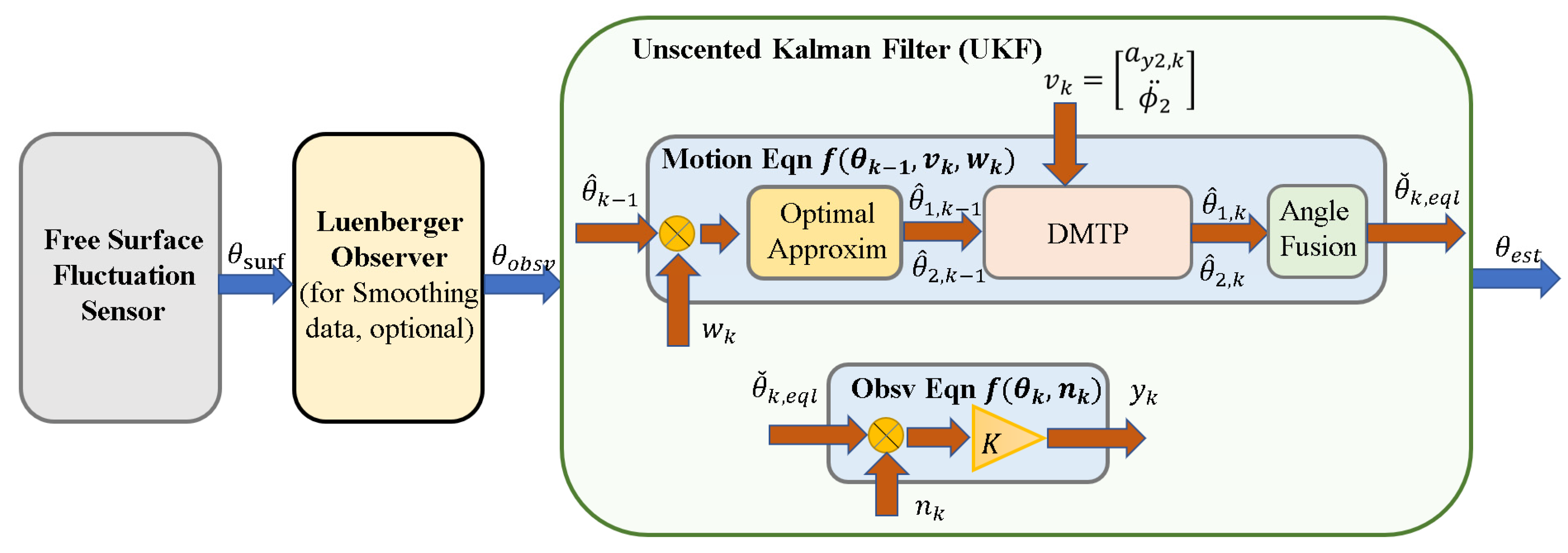
5.2. Observer Based on DMTP and Senser Data
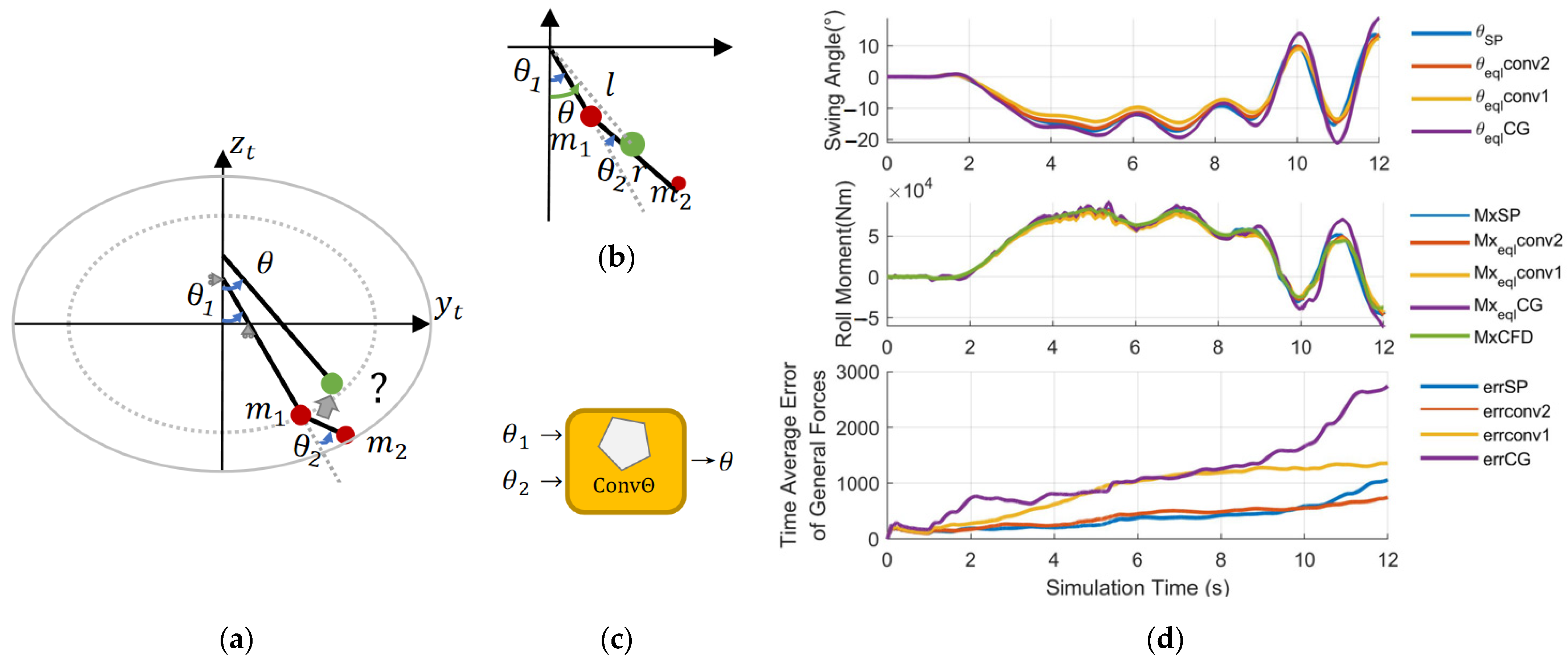
5.2.1. Fusion of Angles of DMTP to Linearized SP
5.2.2. Angle Decomposition and UKF Construction
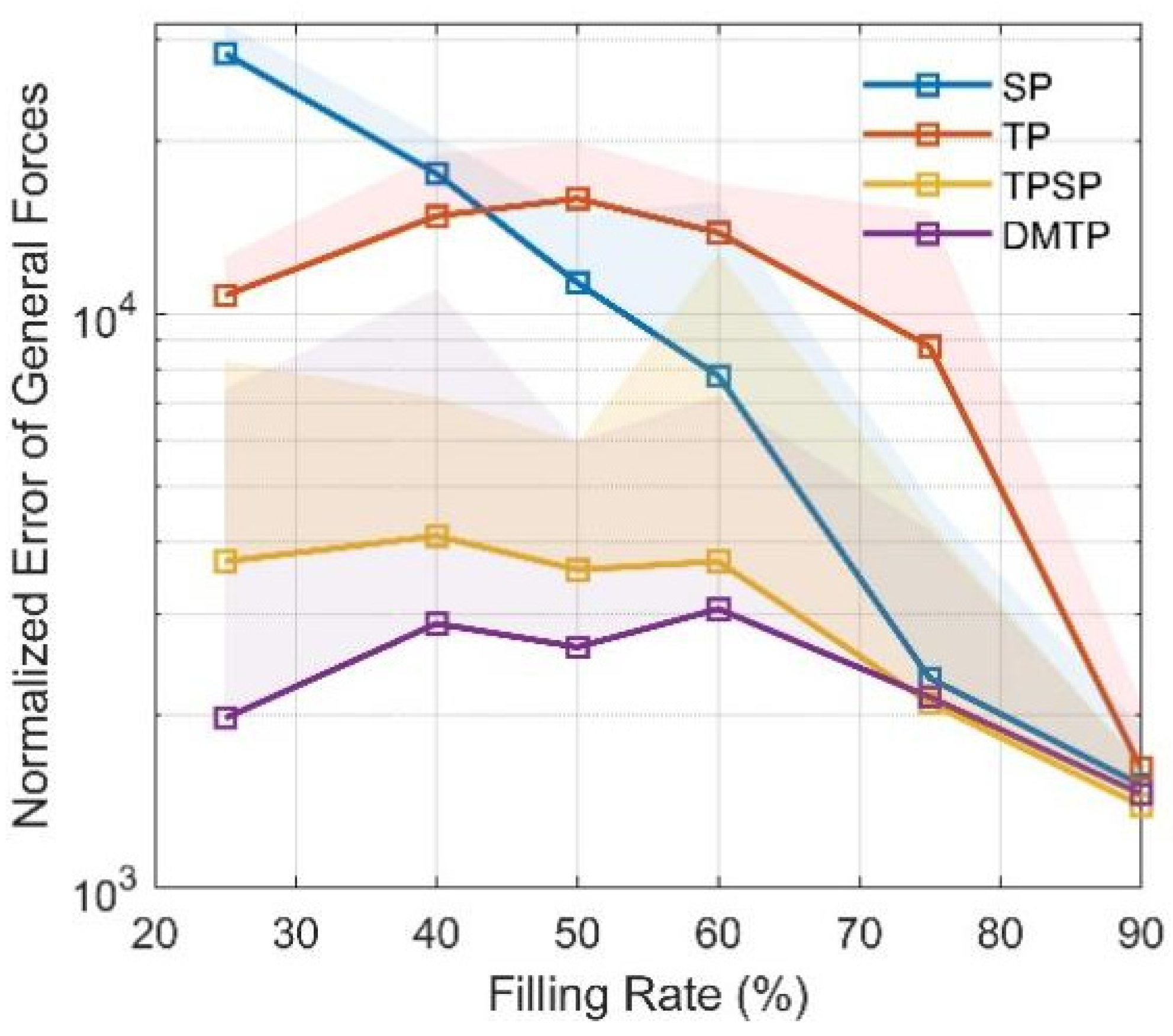
6. Simulation and Analysis of Sloshing Observation
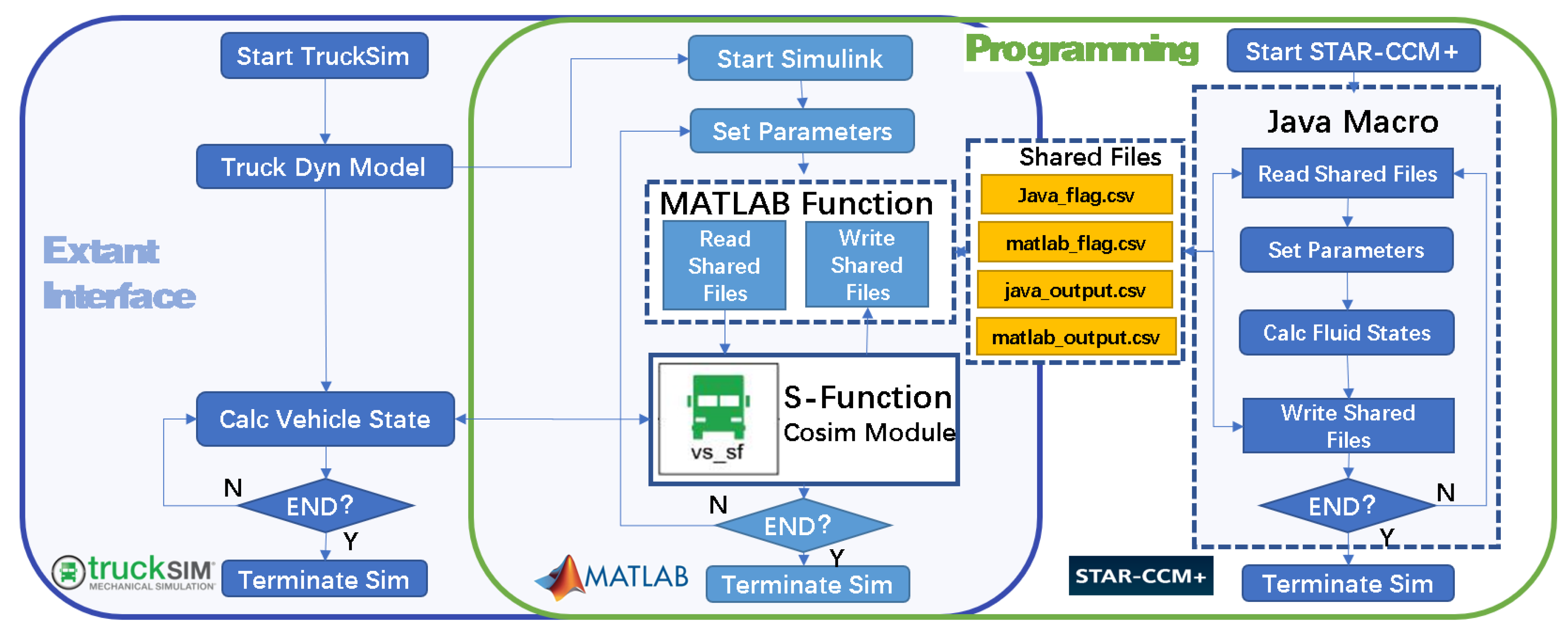
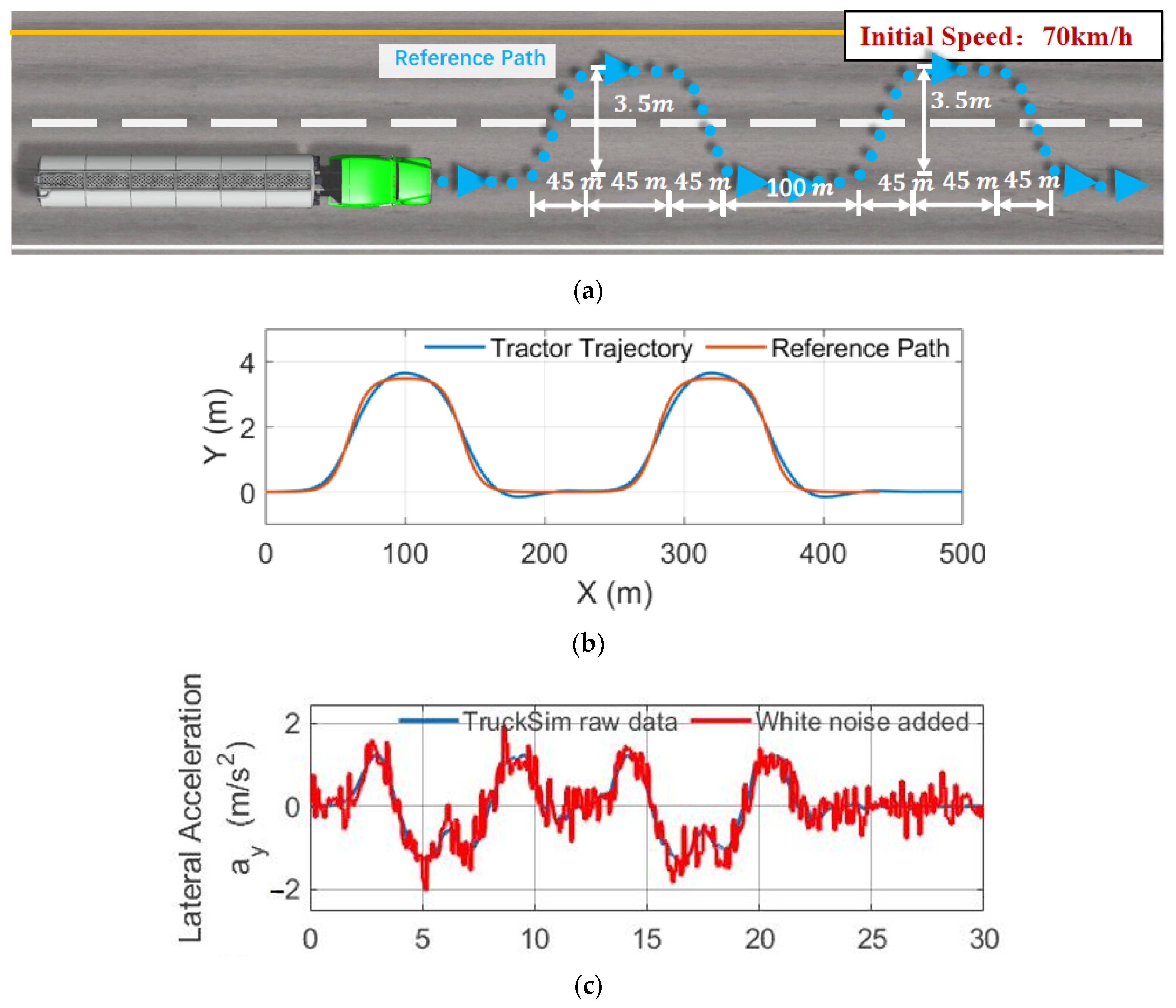
6.1. Simulation Model
6.2. Acquisition of Fluctuation Sensor Data
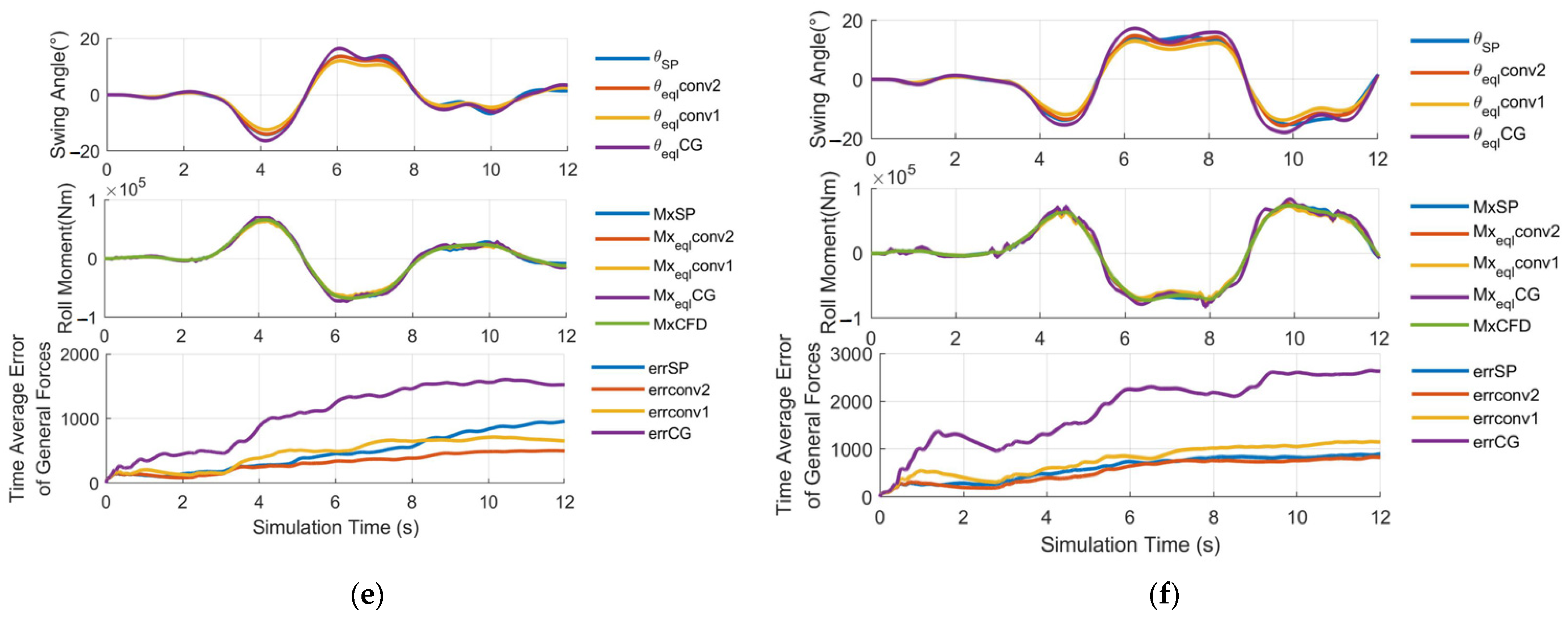
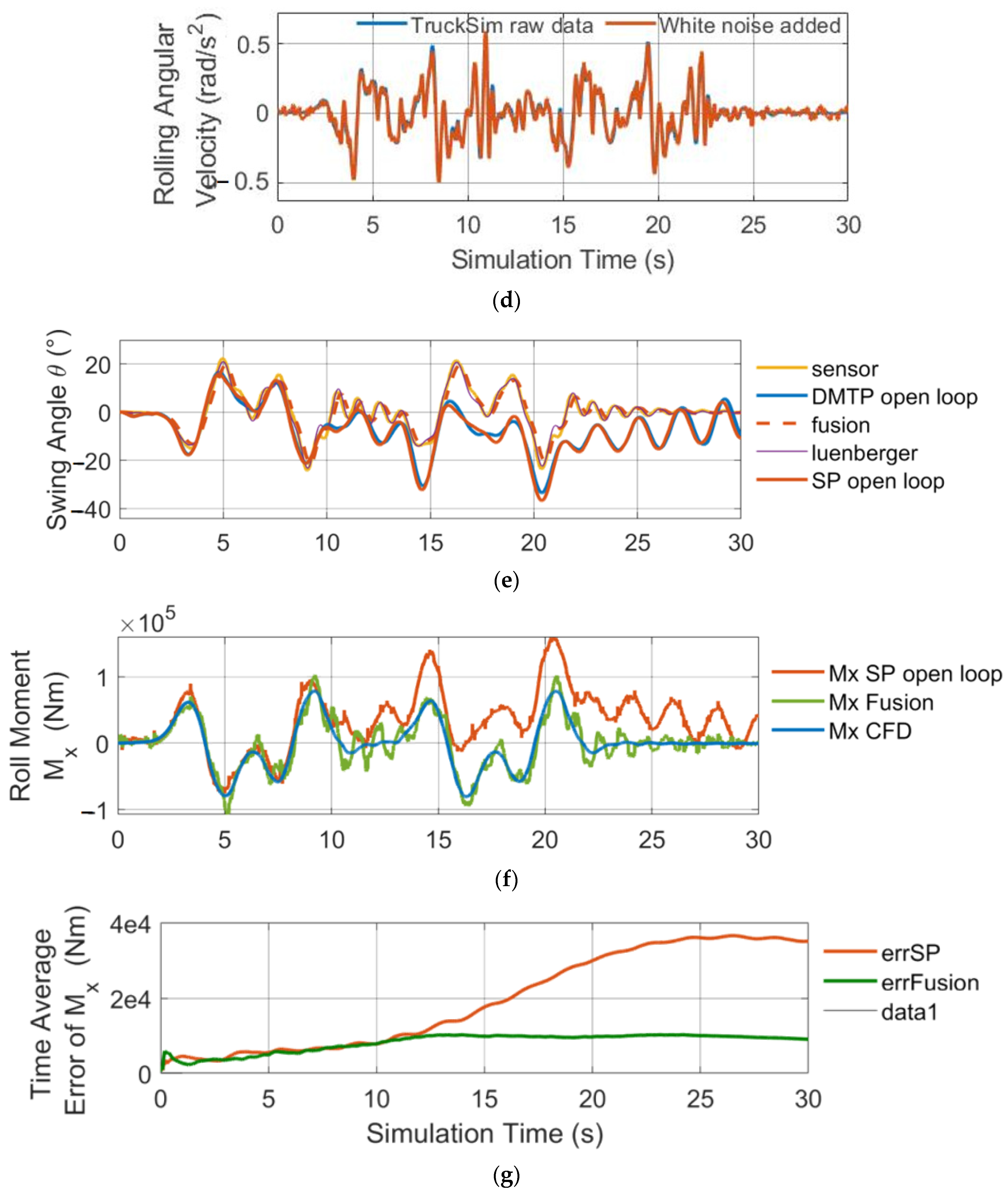
6.3. Results Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
Appendix B.1. Decomposition of the Angle from Linearized SP to DMTP
Appendix B.2. Construction of UKF
References
- Transportation Committee of China Railway Enterprise Management Association, Transport of Dangerous Goods by Railway Tank Vehicles, 1st ed.; China Railway Publishing House: Beijing, China, 2014; pp. 71–72.
- GB18564, 1-2006; Road Transport of Liquid Dangerous Goods Tank Vehicles Part 1: Technical Requirements for Metal Atmospheric Tank Bodies; Standardization Administration of China (SAC): Beijing, China, 2006.
- TSG R0005-2011, 5-2011; Supervision Regulations for Safety Technology of Mobile Pressure Vessels; Standardization Administration of China (SAC): Beijing, China, 2011.
- Wu, Z.; Sun, M. Statistic analysis and countermeasure study on 200 road transportation accidents of dangerous chemicals. J. Saf. Sci. Technol. 2006, 2, 3–8. [Google Scholar]
- Jia, X.; Zhang, Z.; Jiang, D. Research Status of Influence of Liquid Sloshing in Tank on Rollover Stability of Semi-loaded Tank Truck. Automob. Appl. Technol. 2022, 47, 193–196. [Google Scholar]
- Huang, Y.; Deng, G.; Zhang, X. Analysis of Instant Liquid Shock Effect of Non-Full-Filled Tank in Course of Turning. Chem. Mach. 2017, 44, 558–563. [Google Scholar]
- Chen, Y.; Rakheja, S.; Shangguan, W. Modified design and safety analysis of tank cross section based on roll stability. J. Vib. Shock 2016, 35, 146–151. [Google Scholar]
- Wang, X.; Chen, Q.; Wang, J. Analysis on the Influence of Lateral Acceleration on Lateral Stability of Non-Full-Load Liquid Tanker. J. Anhui Polytech. Univ. 2022, 37, 10–24. [Google Scholar]
- He, L.; Liu, Q. A Quasi-static Equivalent Mechanical Model for Roll Stability of Partially-filled Tanker Trucks. Mech. Eng. 2020, 42, 294–299. [Google Scholar]
- Wang, Z.; Liu, Y. Dynamics of Liquid-Filled Systems, 1st ed.; Science Press: Beijing, China, 2002. [Google Scholar]
- Xu, X.; Zhu, C.; Cai, H. Study on the driving stability of lane change for semi-trailer liquid tanker based on simulation platform. Exp. Technol. Manag. 2022, 39, 96–100. [Google Scholar]
- Zhao, W.; Ling, J.; Zong, C. Development of Anti-rollover Control Strategy for Liquid Tank Semi-trailer. Automot. Eng. 2019, 41, 50–56. [Google Scholar]
- Zhao, W.; Feng, R.; Zong, C. Anti-rollover control strategy of tank trucks based on equivalent sloshing model. J. Jilin Univ. (Eng. Technol. Ed.) 2018, 48, 30–35. [Google Scholar]
- Yu, D.; Li, X.; Liu, H.; Zheng, X.; Xu, Y. Research on Roll Stability Model of Partially-filled Tankers. J. Hunan Univ. (Nat. Sci.) 2016, 43, 40–44. [Google Scholar]
- Contreras, G.M.; Serrano, E.F.; Ramón, B. Stability of tanker trucks using the Davies method. J. Appl. Eng. Sci. 2022, 20, 602–609. [Google Scholar]
- Yu, D.; Chu, J. Study on roll-stability model optimization for partially filled tanker trucks. Adv. Mech. Eng. 2019, 11, 1687814019837805. [Google Scholar] [CrossRef]
- Salem, M.I. Rollover Stability of Partially Filled Heavy-Duty Elliptical Tankers Using Trammel Pendulums to Simulate Fluid Sloshing. Ph.D. Thesis, West Virginia University, Morgantown, WV, USA, 2000. [Google Scholar]
- Ren, Y.; Li, X.; Zheng, X.; Wang, J. Accurate Dynamics Modeling and Roll Stability of Tank Vehicle. J. Shanghai Jiao Tong Univ. 2020, 54, 312–321. [Google Scholar]
- Wan, Y. Study on Vehicle-Liquid Coupling Dynamic Characteristics and Anti-Rollover Control Method for Tank Vehicles. Ph.D. Thesis, Department of College of Automobile Engineering of Jilin University, Changchun, China, 2018. [Google Scholar]
- Yu, Z.; Cheng, X.; Li, J.; Li, S. Simulation analysis of lateral stability for liquid tank truck based on model predictive control (MPC). J. Chang. Univ. Technol. 2018, 39, 224–232. [Google Scholar]
- Yu, Z.; Li, J.; Cheng, X.; Dai, F.; Li, S. Simulation on the optimal control of the stability of liquid tank truck. Oil Gas Storage Transp. 2019, 38, 885–891. [Google Scholar]
- Matthew, A.; Mucino, V.H.; Gautam, M.; Salem, M. A Finite Element Modeling Approach for Stability Analysis of Partially Filled Tanker Trucks. SAE Trans. 1999, 108, 452–460. [Google Scholar]
- Mao, H.; Li, B.; Bei, S.; Ding, Y.; Quan, Z. Research on Roll Stability of Liquid Tanker Based on Fluid-solid Coupling. J. Jiangsu Univ. Technol. 2021, 27, 56–67. [Google Scholar]
- Li, J.; Yu, Z.; Cheng, X.; Dai, F.; Li, S. Simulation of stability control of tank trucks under vehicle-liquid coupling response. Oil Gas Storage Transp. 2020, 39, 188–194. [Google Scholar]
- Liu, K.; Kang, N. Simulation of liquid sloshing in braking process of tank truck. J. Beijing Univ. Aeronaut. Astronaut. 2009, 35, 799–803. [Google Scholar]
- Liu, K.; Kang, N. Simulation of liquid sloshing in turning process of tank truck. J. Beijing Univ. Aeronaut. Astronaut. 2009, 35, 1403–1407. [Google Scholar]
- Tang, Y.; Liu, Y.; Chen, C.; Chen, Z.; He, Y.; Zheng, M. Numerical study of liquid sloshing in 3D LNG tanks with unequal baffle height allocation schemes. Ocean. Eng. 2021, 234, 109181. [Google Scholar] [CrossRef]
- Ganuga, R.S.; Viswanathan, H.; Sonar, S.; Awasthi, A. Fluid-Structure Interaction Modelling of Internal Structures in a Sloshing Tank Subjected to Resonance. Int. J. Fluid Mech. Res. 2014, 41, 145–168. [Google Scholar] [CrossRef]
- Jadon, V.; Agawane, G.; Baghel, A.; Balide, V.; Banerjee, R.; Getta, A.; Viswanathan, H.; Awasthi, A. An Experimental and Multiphysics Based Numerical Study to Predict Automotive Fuel Tank Sloshing Noise; SAE Technical Paper Series; SAE: Warrendale, PA, USA, 2014. [Google Scholar] [CrossRef]
- Zheng, X.; You, Y.; Ma, Q.; Khayyer, A.; Shao, S. A Comparative Study on Violent Sloshing with Complex Baffles Using the ISPH Method. Appl. Sci. 2018, 8, 904. [Google Scholar] [CrossRef]
- Guagliumi, L.; Berti, A.; Monti, E.; Carricato, M. A Simple Model-Based Method for Sloshing Estimation in Liquid Transfer in Automatic Machines. IEEE Access 2021, 9, 129347–129357. [Google Scholar] [CrossRef]
- Di Leva, R.; Carricato, M.; Gattringer, H.; Müller, A. Sloshing dynamics estimation for liquid-filled containers performing 3-dimensional motions: Modeling and experimental validation. Multibody Syst. Dyn. 2022, 56, 153–171. [Google Scholar] [CrossRef]
- Tosun, U.; Aghazadeh, R.; Sert, C.; Özer, M.B. Tracking free surface and estimating sloshing force using image processing. Exp. Therm. Fluid Sci. 2017, 88, 423–433. [Google Scholar] [CrossRef]
- Arshad, S.M.N.; Ayaz, Y.; Ali, S.; Ansari, A.R.; Nawaz, R. Experimental Study on Slosh Dynamics Estimation in a Partially Filled Liquid Container Using a Low-Cost Measurement System. IEEE Sens. J. 2022, 22, 16212–16222. [Google Scholar] [CrossRef]
- Yang, X.; Xing, Y.; Wu, X.; Zhang, K. Multi-mass trammel pendulum model of fluid lateral sloshing for tank vehicle. J. Traffic Transp. Eng. 2018, 18, 140–151. [Google Scholar]
- Wu, X.; Yang, X.; Song, J. Study on Liquid Lateral Sloshing Model of Tank Vehicle. Agric. Equip. Veh. Eng. 2018, 56, 7–15. [Google Scholar]
- Zhang, B.; Zong, C.; Wang, H.; Zheng, H. State Estimation of Heavy Tractor Semitrailers Based on Adaptive Kalman Filter. Automob. Technol. 2012, 442, 1–4. [Google Scholar]
- Yu, Z. Research on Dynamics Stability Multi-Objective Control Based on Model Predictive Control for Heavy Duty Semi-Trailer. Ph.D. Thesis, Department of College of Automobile Engineering of Jilin University, Changchun, China, 2015. [Google Scholar]
- Feng, R. Research on Key Parameters Estimation and Anti-Rollover Control of Liquid-filled Tractor-Semitrailer. Master’s Thesis, Department of College of Automobile Engineering of Jilin University, Changchun, China, 2018. [Google Scholar]
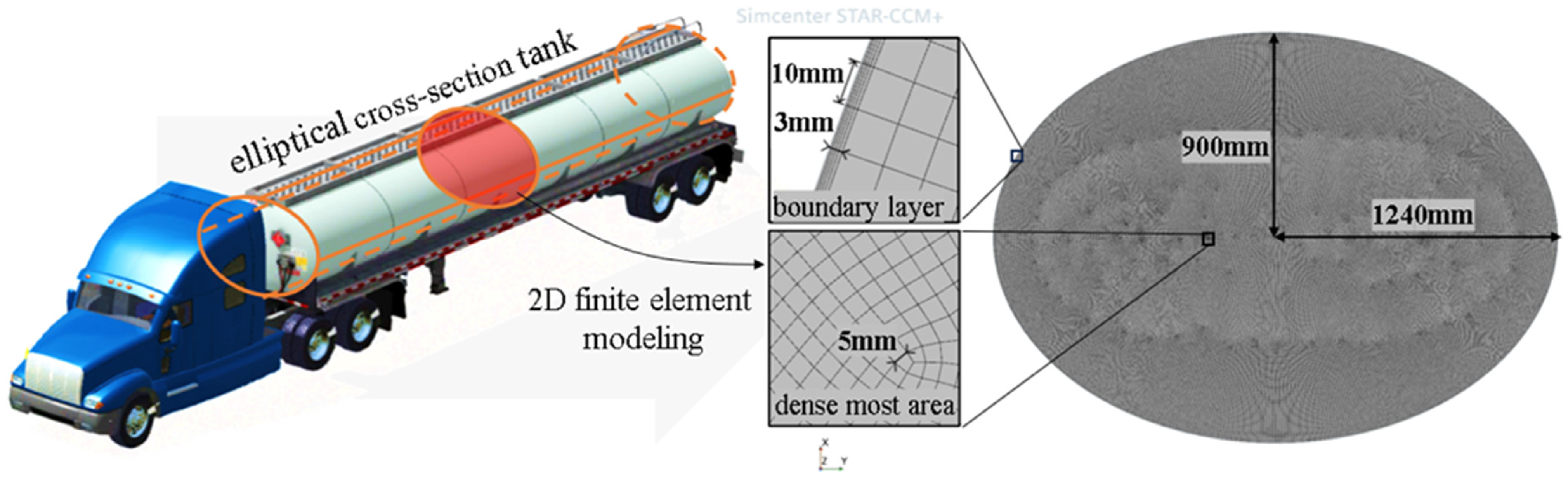
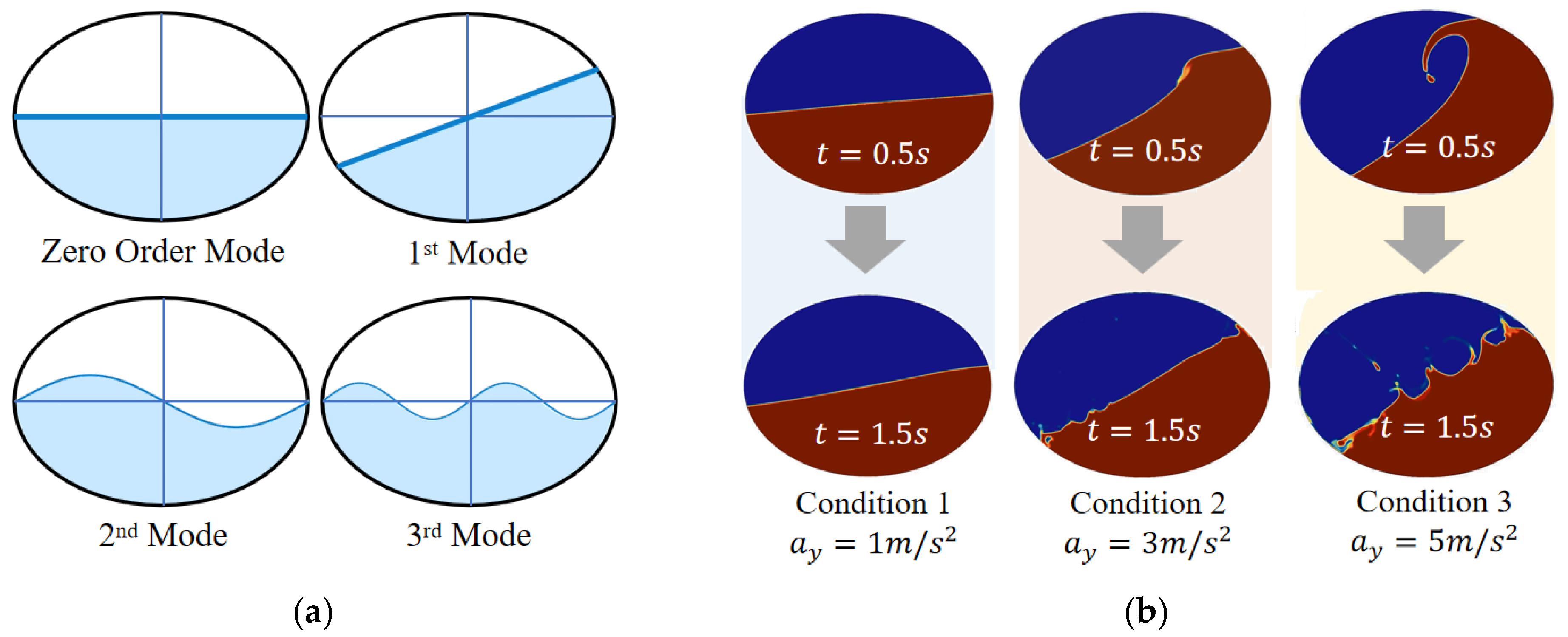

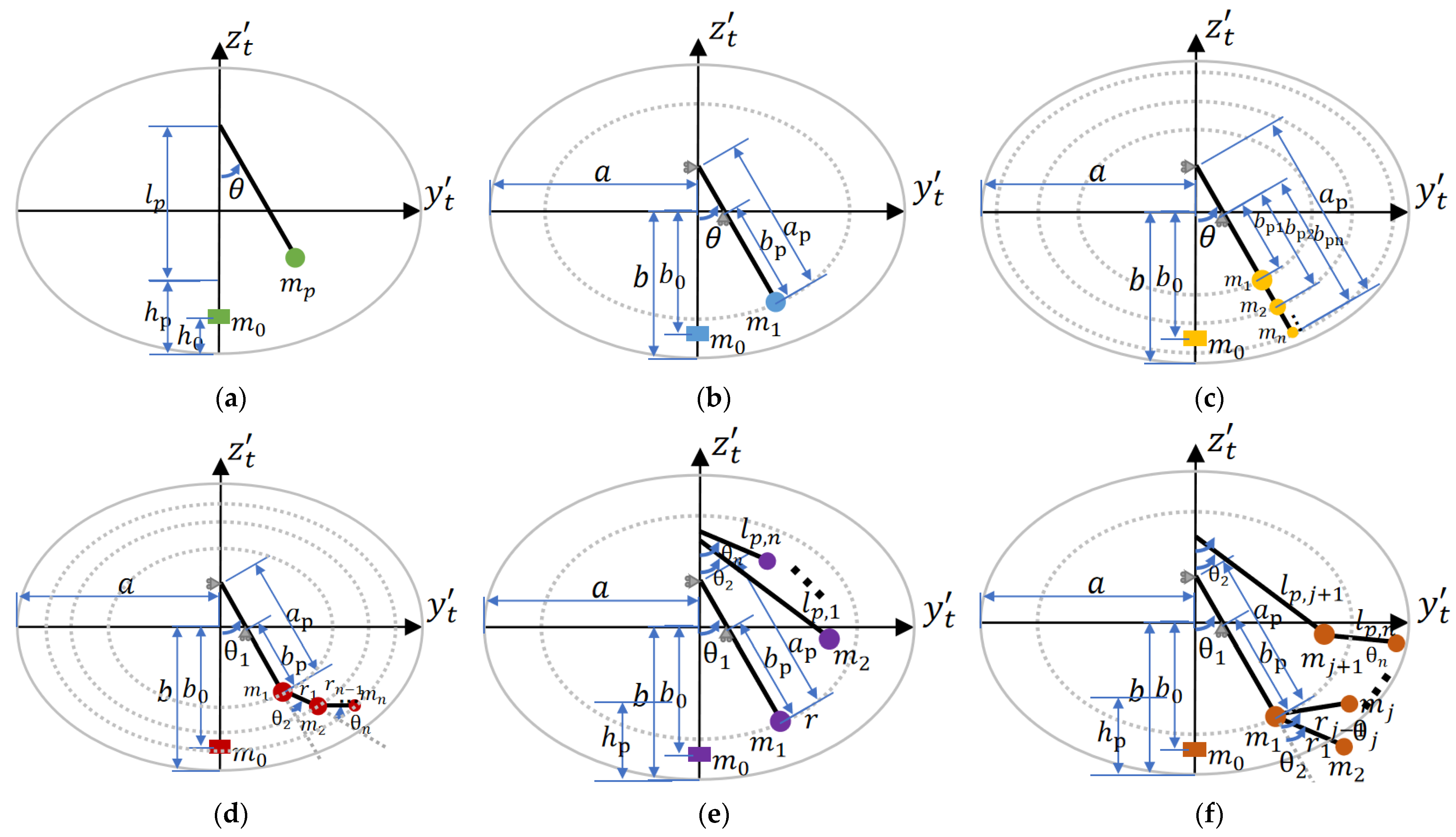
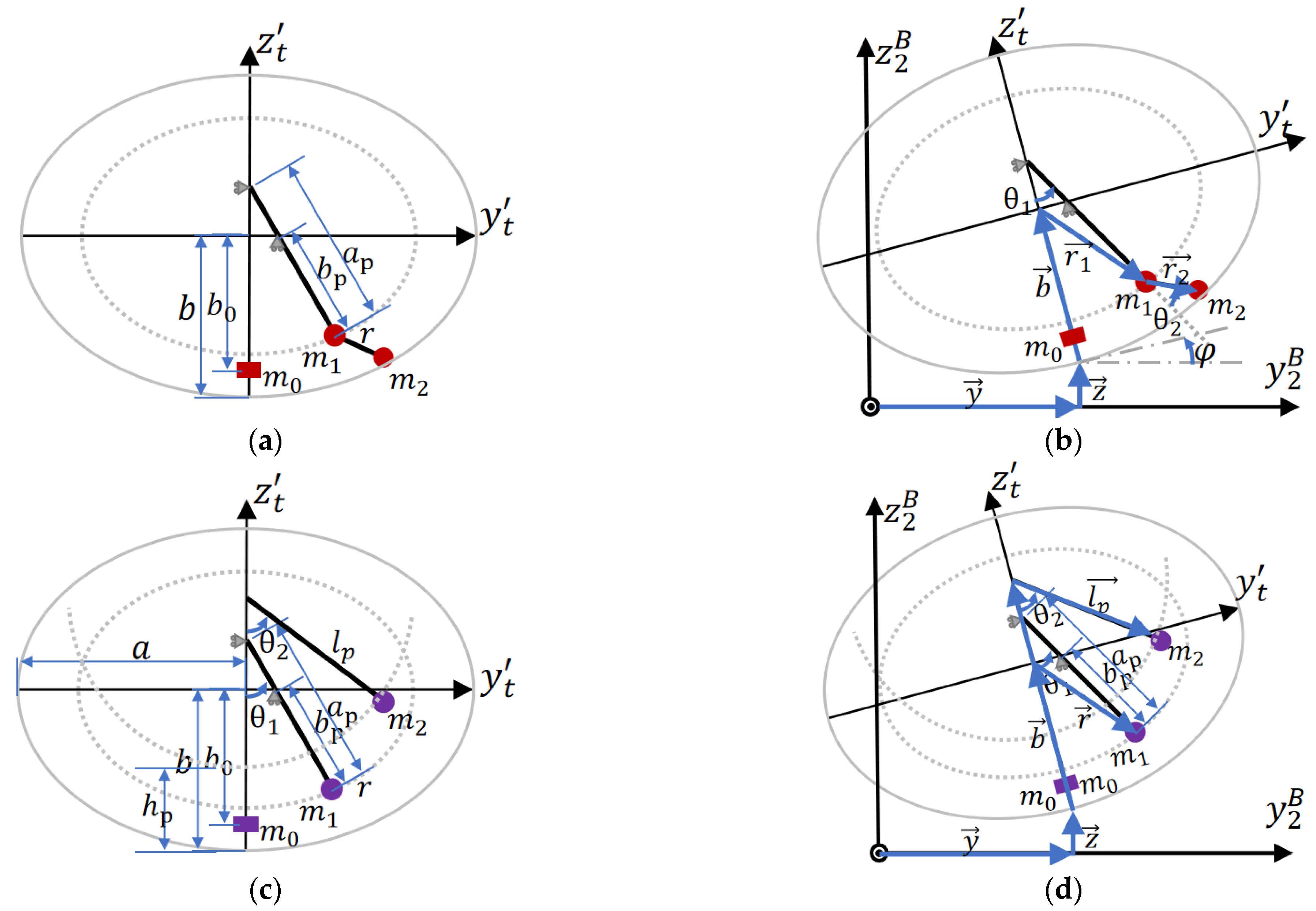


| Euler Phase Name | Phase | Material | Dynamic Viscosity | Density (Constant) |
|---|---|---|---|---|
| Gasoline | Liquid | C8H17(Gasoline) | 5.0272 × 10−4 | 751 |
| Air | Gas | Air | 1.85508 × 10−5 | 1.18415 |
| Model | Settings |
|---|---|
| Wall distance | Implicit tree |
| Multiphase interaction | Phase interaction between phases |
| Euler phases | See Table 1 |
| Mixture | Dynamic viscosity: Volume-weighted mixture |
| Adaptive time step | Time step provider: Free-surface CFL condition |
| Volume of fluid, VOF | HRIC → HRIC gradient smoothing |
| Dimension | Two-dimensional |
| Flow regime | Segregated flow |
| Turbulent Model | turbulence Realizable k- two-layer model Reynolds-averaged Navier–Stokes two-layer full y+ wall treatment |
| Gravity | Yes |
| Slosh Mode | 0 Order | Surface Incline | First | Second | Third | Higher Order | ∞ |
|---|---|---|---|---|---|---|---|
| Model Name | |||||||
| Rigid body | √ | ||||||
| QS | √ | √ | |||||
| Linearized SP | √ | √ | √ | ||||
| SP/TP | √ | √ | √ | √ | √ | ||
| Multi-DOF Pendulum | √ | √ | √ | √ | √ | √ | |
| FVM-CFD | √ | √ | √ | √ | √ | √ | |
| Real liquid | √ | √ | √ | √ | √ | √ | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, X.; Zhang, Y.; Gao, B. Observing Liquid Sloshing Based on a Multi-Degree-of-Freedom Pendulum Model and Free Surface Fluctuation Sensor. Sensors 2023, 23, 8831. https://doi.org/10.3390/s23218831
Qi X, Zhang Y, Gao B. Observing Liquid Sloshing Based on a Multi-Degree-of-Freedom Pendulum Model and Free Surface Fluctuation Sensor. Sensors. 2023; 23(21):8831. https://doi.org/10.3390/s23218831
Chicago/Turabian StyleQi, Xiaojing, Yingchao Zhang, and Bolin Gao. 2023. "Observing Liquid Sloshing Based on a Multi-Degree-of-Freedom Pendulum Model and Free Surface Fluctuation Sensor" Sensors 23, no. 21: 8831. https://doi.org/10.3390/s23218831
APA StyleQi, X., Zhang, Y., & Gao, B. (2023). Observing Liquid Sloshing Based on a Multi-Degree-of-Freedom Pendulum Model and Free Surface Fluctuation Sensor. Sensors, 23(21), 8831. https://doi.org/10.3390/s23218831








