Method Comparison for Simulating Non-Gaussian Beams and Diffraction for Precision Interferometry
Abstract
:1. Introduction
2. Wavefront Decomposition Methods
2.1. Properties and Individual Test of the Mode Expansion Method
2.1.1. MEM: Method Description
2.1.2. Error Definitions for the MEM
2.1.3. MEM Settings
2.1.4. Example: MEM Performance for a Clipped Gaussian Beam
2.2. Properties and Individual Test of the Gaussian Beam Decomposition
2.2.1. GBD: Method Description
2.2.2. GBDs and Their Errors
2.2.3. GBD Settings
2.2.4. Example: GBD Performance for a Clipped Gaussian Beam
Example 1: Comparing Different Grid Sizes
Example 2: Comparing Grid Shapes
3. Fair Comparison
- Criteria for a fair comparison
- Computational effort of the MEM and GBD
4. Method Comparison
4.1. Non-Clipped Gaussian Beams and Clipped Gaussian Beams in Free Space
4.1.1. Non-Clipped Gaussian Beams
Circular Gaussian Beam
General Astigmatic Gaussian Beam
4.1.2. Clipped Gaussian Beam
4.2. Aberrated Wavefronts
4.3. Reflection from Optical Components
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hecht, E. Optics, 4th ed.; Optics 4th edition by Eugene Hecht Reading; Addison Wesley Longman Inc.: Reading, MA, USA, 2001. [Google Scholar]
- Ghatak, A. Optics; Tata Mcgraw Hill Publishing Company: New York, NY, USA, 1989. [Google Scholar]
- Saleh, B.E.A.; Teich, M.C. Fourier Optics. In Fundamentals of Photonics; Wiley: Hoboken, NJ, USA, 1991; p. 127. [Google Scholar]
- Siegman, A. Lasers; University Science Books; Miller/Scheier Associates: Palo Alto, CA, USA, 1986. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Prince, T.A.; Binetruy, P.; Centrella, J.; Finn, L.S.; Team, L. LISA: Probing the Universe with Gravitational Waves; American Institute of Physics: New York, NY, USA, 2006. [Google Scholar]
- Hu, W.R.; Wu, Y.L. The Taiji Program in Space for gravitational wave physics and the nature of gravity. Natl. Sci. Rev. 2017, 4, 2. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser interferometer space antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Sasso, C.; Mana, G.; Mottini, S. Coupling of wavefront errors and pointing jitter in the LISA interferometer: Misalignment of the interfering wavefronts. Class. Quantum Gravity 2018, 35, 245002. [Google Scholar] [CrossRef]
- Sasso, C.; Mana, G.; Mottini, S. Coupling of wavefront errors and jitter in the LISA interferometer: Far-field propagation. Class. Quantum Gravity 2018, 35, 185013. [Google Scholar] [CrossRef]
- Tröbs, M.; Schuster, S.; Lieser, M.; Zwetz, M.; Chwalla, M.; Danzmann, K.; Barránco, G.F.; Fitzsimons, E.; Gerberding, O.; Heinzel, G.; et al. Reducing tilt-to-length coupling for the LISA test mass interferometer. Class. Quantum Gravity 2018, 35, 105001. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z.; Li, Y.; Fang, C.; Liu, H.; Gao, H. Method to remove tilt-to-length coupling caused by interference of flat-top beam and gaussian beam. Appl. Sci. 2019, 9, 4112. [Google Scholar] [CrossRef]
- Hartig, M.S.; Schuster, S.; Wanner, G. Geometric tilt-to-length coupling in precision interferometry: Mechanisms and analytical descriptions. J. Opt. 2022, 24, 065601. [Google Scholar] [CrossRef]
- Hartig, M.S.; Schuster, S.; Heinzel, G.; Wanner, G. Non-geometric tilt-to-length coupling in precision interferometry: Mechanisms and analytical descriptions. J. Opt. 2023, 25, 055601. [Google Scholar] [CrossRef]
- Saleh, B.E.A.; Teich, M.C. Ray Optics. In Fundamentals of Photonics; Wiley: Hoboken, NJ, USA, 1991; pp. 26–31. [Google Scholar]
- Goubau, G.; Schwering, F. On the guided propagation of electromagnetic wave beams. IRE Trans. Antennas Propag. 1961, 9, 248–256. [Google Scholar] [CrossRef]
- Tanaka, K.; Yoshida, K.; Taguchi, M. Analytical and experimental investigations of the diffraction field of a Gaussian beam through a sequence of apertures: Applicability of the beam mode expansion method. Appl. Opt. 1988, 27, 1310–1312. [Google Scholar] [CrossRef]
- Petrović, N.; Rakić, A. Modeling diffraction in free-space optical interconnects by the mode expansion method. Appl. Opt. 2003, 42, 5308. [Google Scholar] [CrossRef]
- Snyder, J.J. Modeling laser beam diffraction and propagation by the mode-expansion method. Appl. Opt. 2007, 46, 5056. [Google Scholar] [CrossRef] [PubMed]
- Freise, A.; Strain, K. Interferometer Techniques for Gravitational-Wave Detection. Living Rev. Relativ. 2010, 13, 1. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, F.; Mehrany, K. Optimum waist of localized basis functions in truncated series employed in some optical applications. Appl. Opt. 2010, 49, 1210. [Google Scholar] [CrossRef] [PubMed]
- Borghi, R.; Gori, F.; Santarsiero, M. Optimization of Laguerre-Gauss truncated series. Opt. Commun. 1996, 125, 197–203. [Google Scholar] [CrossRef]
- Mahon, R.J.; Murphy, J.A. Simulated propagation of ultrashort pulses modulated by low-Fresnel-number lenses using truncated series expansions. Appl. Opt. 2014, 53, 5701–5711. [Google Scholar] [CrossRef]
- Xiao, Y.; Tang, X.; Wan, C.; Qin, Y.; Peng, H.; Hu, C.; Qin, B. Laguerre-Gaussian mode expansion for arbitrary optical fields using a subspace projection method. Opt. Lett. 2019, 44, 1615–1618. [Google Scholar] [CrossRef]
- Liu, Y.; Lü, B. Truncated Hermite–Gauss series expansion and its application. Opt. Int. J. Light Electron Opt. 2006. [Google Scholar] [CrossRef]
- Popov, M.M. A new method of computation of wave fields using Gaussian beams. Wave Motion 1982, 4, 85–97. [Google Scholar] [CrossRef]
- Greynolds, A.W. Fat rays revisited: A synthesis of physical and geometrical optics with Gaubetalets. In Proceedings of the International Optical Design Conference, Kohala Coast, HI, USA, 22–26 June 2014. [Google Scholar]
- Greynolds, A.W. Propagation of Generally Astigmatic Gaussian Beams Along Skew Ray Paths. In Proceedings of the 29th Annual Technical Symposium, San Diego, CA, USA, 20–23 August 1985. [Google Scholar]
- Narayananl, G. Gaussian Beam Analysis of Relay Optics for the SEQUOIA Focal Plane Array. In Proceedings of the 15th International Symposium on Space Terahert Technology, Northampton, MA, USA, 27–29 April 2004; Volume 8. [Google Scholar]
- Ashcraft, J.N.; Douglas, E.S. An open-source Gaussian beamlet decomposition tool for modeling astronomical telescopes. In Proceedings of the Modeling, Systems Engineering, and Project Management for Astronomy IX; SPIE: Bellingham, WA USA, 2020; Volume 11450, pp. 354–366. [Google Scholar]
- White, B.; Norris, A.; Bayliss, A.; Burridge, R. Some remarks on the Gaussian beam summation method. Geophys. J. Int. 1987, 89, 579–636. [Google Scholar] [CrossRef]
- Leye, P.O.; Khenchaf, A.; Pouliguen, P. The Gaussian beam summation and the Gaussian launching methods in scattering problem. J. Electromagn. Anal. Appl. 2016, 8, 219. [Google Scholar] [CrossRef]
- Spies, M. Modeling of transducer fields in inhomogeneous anisotropic materials using Gaussian beam superposition. NDT E Int. 2000, 33, 155–162. [Google Scholar] [CrossRef]
- Alonso, M.; Forbes, G. Stable aggregates of flexible elements give a stronger link between rays and waves. Opt. Express 2002, 10, 728–739. [Google Scholar] [CrossRef]
- Kong, H.B.; Cho, D.J. Design and analysis of infrared diffractive optical systems using beam synthesis propagation. Korean J. Opt. Photonics 2013, 24, 189–195. [Google Scholar] [CrossRef]
- Tanushev, N.M.; Engquist, B.; Tsai, R. Gaussian beam decomposition of high frequency wave fields. J. Comput. Phys. 2009, 228, 8856–8871. [Google Scholar] [CrossRef]
- Şahin, E.; Onural, L. Calculation of the scalar diffraction field from curved surfaces by decomposing the three-dimensional field into a sum of Gaussian beams. J. Opt. Soc. Am. A 2013, 30, 527–536. [Google Scholar] [CrossRef]
- Worku, N.; Gross, H. Vectorial field propagation through high NA objectives using polarized Gaussian beam decomposition. In Proceedings of the Optical Trapping and Optical Micromanipulation XIV; Dholakia, K., Spalding, G.C., Eds.; International Society for Optics and Photonics; SPIE: Bellingham, WA USA, 2017; Volume 10347, p. 103470W. [Google Scholar] [CrossRef]
- Worku, N.G.; Ralf, H.; Herbert, G. Decomposition of a field with smooth wavefront into a set of Gaussian beams with non-zero curvatures. J. Opt. Soc. Am. A 2018, 35, 1091–1102. [Google Scholar] [CrossRef]
- Worku, N.G.; Gross, H. Propagation of truncated Gaussian beams and their application in modeling sharp-edge diffraction. J. Opt. Soc. Am. A 2019, 36, 859. [Google Scholar] [CrossRef]
- Rong, Y.; Shan-jun, M.; Bai-da, L. Application of Laguerre-Gauss truncated series expansion. High Power Laser Part. Beams 2006, 18, 931–934. [Google Scholar]
- Harvey, J.E.; Irvin, R.G.; Pfisterer, R.N. Modeling physical optics phenomena by complex ray tracing. Opt. Eng. 2015, 54, 035105. [Google Scholar] [CrossRef]
- Kimel, I.; Elias, L. Relations between Hermite and Laguerre Gaussian modes. IEEE J. Quantum Electron. 1993, 29, 2562–2567. [Google Scholar] [CrossRef]
- O’Neil, A.T.; Courtial, J. Mode transformations in terms of the constituent Hermite–Gaussian or Laguerre–Gaussian modes and the variable-phase mode converter. Opt. Commun. 2000, 181, 35–45. [Google Scholar] [CrossRef]
- Mahrdt, C. Laser Link Acquisition for the GRACE Follow-On Laser Ranging Interferometer. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany, 2014. [Google Scholar]
- Campbell, C. Fresnel Diffraction Of Gaussian Laser Beams By Circular Apertures. Opt. Eng. 1987, 26, 270–275. [Google Scholar] [CrossRef]
- Tanaka, K.; Saga, N.; Mizokami, H. Field spread of a diffracted Gaussian beam through a circular aperture. Appl. Opt. 1985, 24, 1102. [Google Scholar] [CrossRef]
- Drège, E.M.; Skinner, N.G.; Byrne, D.M. Analytical far-field divergence angle of a truncated Gaussian beam. Appl. Opt. 2000, 39, 4918–4925. [Google Scholar] [CrossRef] [PubMed]
- Carter, W.H. Spot size and divergence for Hermite Gaussian beams of any order. Appl. Opt. 1980, 19, 1027–1029. [Google Scholar] [CrossRef] [PubMed]
- Wanner, G.; Heinzel, G.; Kochkina, E.; Mahrdt, C.; Sheard, B.S.; Schuster, S.; Danzmann, K. Methods for simulating the readout of lengths and angles in laser interferometers with Gaussian beams. Opt. Commun. 2012, 285, 4831–4839. [Google Scholar] [CrossRef]
- Kochkina, E. Stigmatic and Astigmatic Gaussian Beams in Fundamental Mode. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany, 2015. [Google Scholar]
- Mahajan, V.N. Zernike Circle Polynomials and Optical Aberrations of Systems with Circular Pupils. Appl. Opt. 1994, 33, 8121–8124. [Google Scholar] [CrossRef]
- Masalehdan, H.; Lotfi, E.; Lotfi, A.; Jamshidi-Ghaleh, K. Modeling of Zernike Optical Aberrations by MTF and PSF. In Proceedings of the Biomedical Optics and 3-D Imaging; Optica Publishing Group: Washington, DC, USA, 2010; p. JMA98. [Google Scholar] [CrossRef]
- Vera-Daz, F.A.; Doble, N. The Human Eye and Adaptive Optics; InTech: London, UK, 2012. [Google Scholar]
- Born, M.; Wolf, E.; Bhatia, A.B.; Clemmow, P.C.; Gabor, D.; Stokes, A.R.; Taylor, A.M.; Wayman, P.A.; Wilcock, W.L. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Goodman, J.; Sutton, P. Introduction to Fourier Optics. Quantum Semiclass. Opt.-J. Eur. Opt. Soc. Part B 1996, 8, 1095. [Google Scholar] [CrossRef]
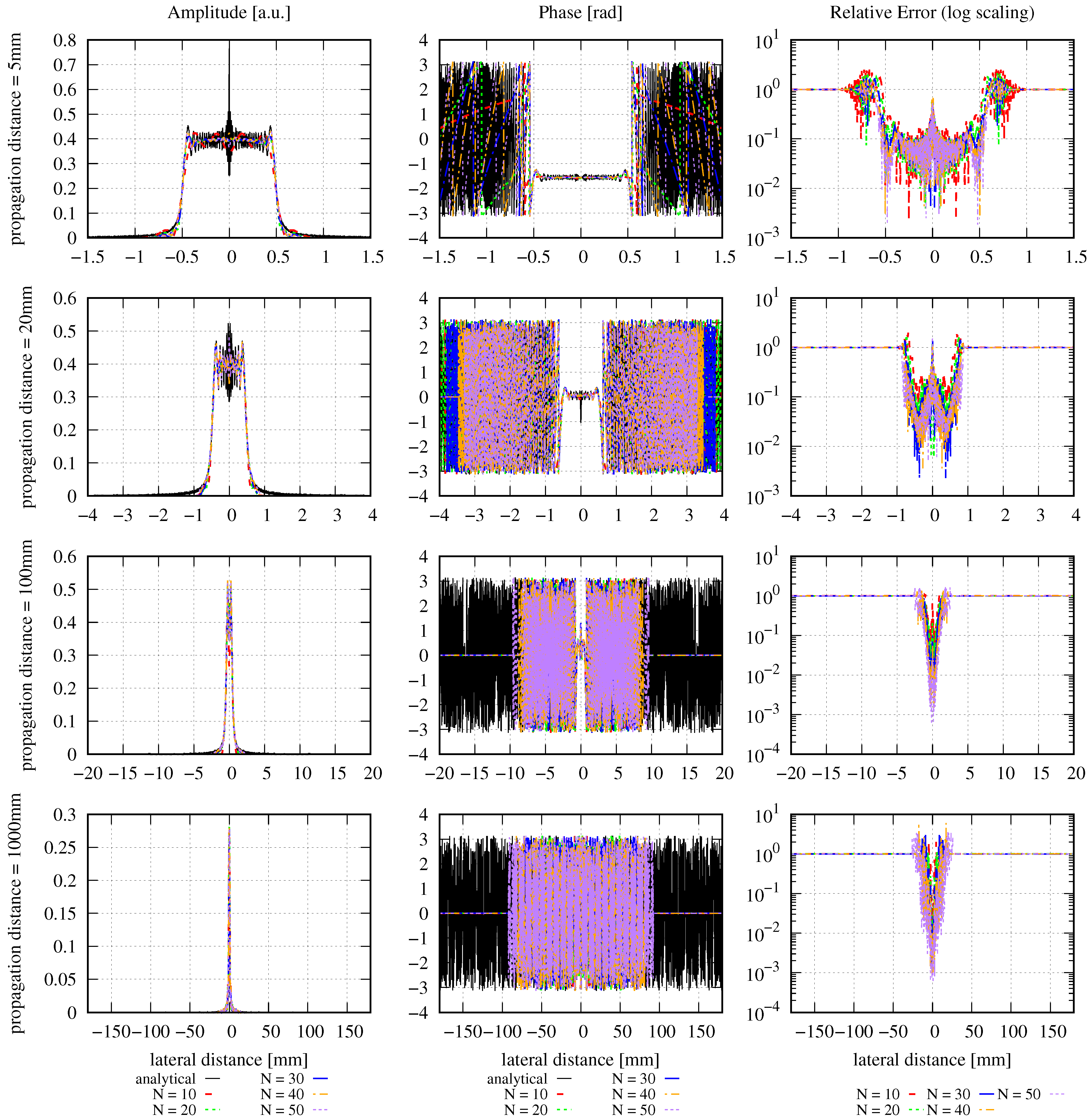


















| Parameter | Description | Value |
|---|---|---|
| wavelength | 1064 nm | |
| beam power | 1 W | |
| beam waist | 2 mm | |
| distance from the waist | 0 mm | |
| aperture radius | mm | |
| N | mode order of the MEM | 10, 20, 30, 40, 50 |
| waist of the modes used in the MEM | mm, mm, mm, mm, mm | |
| d | propagation distance | 5 mm, 20 mm, 100 mm, 1000 mm |
| X | number of sampling points | 3001 |
| Propagation Distance (mm) | Mode Order | NMSE | DNMSE (for Larger Lateral Ranges) | DNMSE (for Smaller Lateral Ranges) | The Summed Relative Error (for Larger Lateral Ranges) | The Summed Relative Error (for Smaller Lateral Ranges) |
|---|---|---|---|---|---|---|
| 10 | 0.0527 | 0.0519 | 0.0436 | 13.6 | 0.964 | |
| 20 | 0.0275 | 0.0268 | 0.021 | 12.8 | 0.731 | |
| 5 | 30 | 0.0186 | 0.0178 | 0.0116 | 12.5 | 0.486 |
| 40 | 0.0139 | 0.0132 | 0.0077 | 12.3 | 0.344 | |
| 50 | 0.0112 | 0.0105 | 0.0057 | 12.2 | 0.247 | |
| 10 | 0.0527 | 0.0517 | 0.0444 | 99.1 | 2.54 | |
| 20 | 0.0275 | 0.0265 | 0.0192 | 98.3 | 1.75 | |
| 20 | 30 | 0.0186 | 0.0175 | 0.0101 | 97.7 | 1.12 |
| 40 | 0.0139 | 0.013 | 0.0057 | 97.1 | 0.535 | |
| 50 | 0.0112 | 0.0102 | 0.0042 | 96.5 | 0.463 | |
| 10 | 0.0527 | 0.0517 | 0.0323 | 2.51 | 5.11 | |
| 20 | 0.0275 | 0.0265 | 0.0083 | 2.51 | 2.46 | |
| 100 | 30 | 0.0186 | 0.0175 | 0.0035 | 2.5 | 2.28 |
| 40 | 0.0139 | 0.013 | 2.5 | 1.22 | ||
| 50 | 0.0112 | 0.0103 | 2.49 | 0.538 | ||
| 10 | 0.0527 | 0.0516 | 0.0051 | 2.04 | 28.4 | |
| 20 | 0.0275 | 0.0264 | 2.03 | 8.48 | ||
| 1000 | 30 | 0.0186 | 0.0174 | 2.03 | 4.56 | |
| 40 | 0.0139 | 0.0129 | 2.03 | 2.77 | ||
| 50 | 0.0112 | 0.0102 | 2.02 | 1.68 |
| Parameter | Description | Value |
|---|---|---|
| wavelength | 1064 nm | |
| beam power | 1 W | |
| beam waist | 2 mm | |
| distance from the waist | 0 | |
| aperture radius | mm | |
| G | grid size of the GBD | , , , |
| L | window size of the GBD | mm |
| waist scaling factor of the GBD | 1.5 | |
| grid beam waist of the GBD | 11.2 m, 5.6 m, 2.2 m, 1.1 m | |
| grid shape | grid shape of the GBD | square |
| d | propagation distance | 5 mm, 20 mm, 100 mm, 1000 mm |
| X | the number of sampling points | 3001 |
| Propagation Distance (mm) | Grid Size | DNMSE (for Larger Ranges) | DNMSE (for Smaller Ranges) | The Summed Relative Error (for Larger Ranges) | The Summed Relative Error (for Smaller Ranges) |
|---|---|---|---|---|---|
| 5 | 0.0158 | 0.0134 | 11.83 | 0.471 | |
| 0.0196 | 2.57 | 15.7 | 0.189 | ||
| 1.95 | 5.84 | 12.0 | 0.0886 | ||
| 3.69 | 5.84 | 5.72 | 0.0304 | ||
| 20 | 0.0126 | 6.78 | 96.2 | 0.967 | |
| 5.38 | 8.57 | 97.6 | 0.381 | ||
| 1.20 | 6.92 | 81.81 | 0.111 | ||
| 1.93 | 5.98 | 40.54 | 0.0253 | ||
| 100 | 9.80 | 8.39 | 2.49 | 1.15 | |
| 5.26 | 9.53 | 2.59 | 0.273 | ||
| 1.22 | 1.50 | 2.89 | 0.040 | ||
| 1.94 | 6.82 | 1.45 | 0.0251 | ||
| 1000 | 9.87 | 4.64 | 2.08 | 2.38 | |
| 5.14 | 8.25 | 2.32 | 1.55 | ||
| 1.10 | 1.40 | 3.33 | 0.141 | ||
| 1.47 | 7.55 | 1.37 | 0.0780 |
| Propagation Distance (mm) | Grid Shape | DNMSE | The Summed Relative Error |
|---|---|---|---|
| 5 | square | 5.84 | 0.0886 |
| hexagonal | 2.41 | 0.0603 | |
| 20 | square | 6.92 | 0.111 |
| hexagonal | 3.12 | 0.0641 | |
| 100 | square | 1.50 | 0.0396 |
| hexagonal | 3.82 | 0.0583 | |
| 1000 | square | 1.40 | 0.141 |
| hexagonal | 2.50 | 0.167 |
| Parameter | Description | Value |
|---|---|---|
| wavelength | 1064 nm | |
| beam power | 1 W | |
| beam waist | 1 mm | |
| distance from the waist | 0 mm | |
| aperture radius | 4 mm | |
| N | mode order of the MEM | 50 |
| waist of the modes used in the MEM | mm | |
| G | grid size of the GBD | 400 × 400 |
| L | window size of the GBD | 8 mm |
| waist scaling factor of the GBD | 10/3 | |
| grid beam waist of the GBD | mm | |
| grid shape | grid shape of the GBD | square |
| d | propagation distance | , , , 3 Gm |
| X | number of sampling points | 3001 |
| Propagation Distance | Method | DNMSE | The Summed Relative Error |
|---|---|---|---|
| mm | MEM | 1.31 | 5.00 |
| GBD | 1.38 | 7.06 | |
| m | MEM | 4.16 | 0.0011 |
| GBD | 1.02 | 0.0019 | |
| km | MEM | 5.11 | 371 |
| GBD | 1.02 | 518 | |
| 3 Gm | MEM | 1.35 | 3.89 |
| GBD | 1.02 | 2.23 |
| Parameter | Description | Value |
|---|---|---|
| wavelength | 1064 nm | |
| beam power | 1 W | |
| beam waist in plane | 1 mm | |
| distance from the waist in plane | 0 mm | |
| beam waist in plane | 2 mm | |
| distance from the waist in plane | 0 mm | |
| tilt angle | 0.1 + 0.2i | |
| aperture radius | 8 mm | |
| N | mode order of the MEM | 50 |
| waist of the modes used in the MEM | mm | |
| G | grid size of the GBD | 300 × 300 |
| L | window size of the GBD | 16 mm |
| waist scaling factor of the GBD | 10/3 | |
| grid beam waist of the GBD | mm | |
| grid shape | grid shape of the GBD | square |
| d | propagation distance | , , |
| X | number of sampling points |
| Propagation Distance | Method | DNMSE | The Summed Relative Error |
|---|---|---|---|
| mm | MEM | 6.25 | 1.96 |
| GBD | 6.79 | 0.005 | |
| m | MEM | 2.34 | 3.57 |
| GBD | 4.74 | 2.63 | |
| 295 m | MEM | 1.11 | 0.465 |
| GBD | 4.75 | 0.629 |
| Parameter | Description | Value |
|---|---|---|
| wavelength | 1064 nm | |
| beam power | 1 W | |
| beam waist | 2 mm | |
| distance from the waist | 0 mm | |
| aperture radius | mm | |
| N | mode order of the MEM | 50 |
| waist of the modes used in the MEM | mm | |
| G | grid size of the GBD | 400 × 400 |
| L | window size of the GBD | mm |
| waist scaling factor of the GBD | 3/2 | |
| grid beam waist of the GBD | mm | |
| grid shape | grid shape of the GBD | square |
| d | propagation distance | 5 mm, 100 mm, 1000 mm, 3 Gm |
| X | number of sampling points | 3001 |
| Propagation Distance | Method | Discretized NMSE | The Summed Relative Error |
|---|---|---|---|
| 5 mm | MEM | 0.0057 | 0.247 |
| GBD | 0.132 | ||
| 100 mm | MEM | 0.538 | |
| GBD | 0.086 | ||
| 1000 mm | MEM | 1.68 | |
| GBD | 0.328 | ||
| 3 Gm (2 times spot size) | MEM | 8.77 | |
| GBD | 3.06 | ||
| 3 Gm ( 400 m) | MEM | 4.34 | |
| GBD | 2.52 |
| Parameter | Description | Value |
|---|---|---|
| wavelength | 1064 nm | |
| beam power | 1 W | |
| beam waist | 1 mm | |
| distance from the waist | 0 | |
| aperture radius | 1 mm | |
| N | mode order of the MEM | 50 |
| waist of the modes used in the MEM | mm | |
| G | grid size of the GBD | |
| L | window size of the GBD | 3 mm |
| waist scaling factor of the GBD | 8/3 | |
| grid beam waist of the GBD | mm | |
| grid shape | grid shape of the GBD | square |
| coefficient of Zernike polynomials | 10 | |
| d | propagation distance | 5 km |
| X | number of sampling points | = 40,401 |
| Parameter | Description | Value |
|---|---|---|
| wavelength | 1064 nm | |
| beam power | 1 W | |
| beam waist | 1 mm | |
| distance from the waist | 0 | |
| aperture radius | 4 mm | |
| N | mode order of the MEM | 50 |
| waist of the modes used in the MEM | mm | |
| G | grid size of the GBD | 400 × 400 |
| L | window size of the GBD | 8 mm |
| waist scaling factor of the GBD | 10/3 | |
| waist of the grid beam used in the GBD | mm | |
| grid shape | grid shape of the GBD | square |
| C | curvatures of the mirror | 0 mm, mm, mm, mm |
| size | the diameter of the mirror | 1 cm × 1 cm |
| X | number of sampling points | 3001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Tao, Y.; Weber, K.; Kaune, T.; Schuster, S.; Hao, Z.; Wanner, G. Method Comparison for Simulating Non-Gaussian Beams and Diffraction for Precision Interferometry. Sensors 2023, 23, 9024. https://doi.org/10.3390/s23229024
Zhao M, Tao Y, Weber K, Kaune T, Schuster S, Hao Z, Wanner G. Method Comparison for Simulating Non-Gaussian Beams and Diffraction for Precision Interferometry. Sensors. 2023; 23(22):9024. https://doi.org/10.3390/s23229024
Chicago/Turabian StyleZhao, Mengyuan, Yazheng Tao, Kevin Weber, Tim Kaune, Sönke Schuster, Zhenxiang Hao, and Gudrun Wanner. 2023. "Method Comparison for Simulating Non-Gaussian Beams and Diffraction for Precision Interferometry" Sensors 23, no. 22: 9024. https://doi.org/10.3390/s23229024
APA StyleZhao, M., Tao, Y., Weber, K., Kaune, T., Schuster, S., Hao, Z., & Wanner, G. (2023). Method Comparison for Simulating Non-Gaussian Beams and Diffraction for Precision Interferometry. Sensors, 23(22), 9024. https://doi.org/10.3390/s23229024





