Lightweight RepVGG-Based Cross-Modality Data Prediction Method for Solid Rocket Motors
Abstract
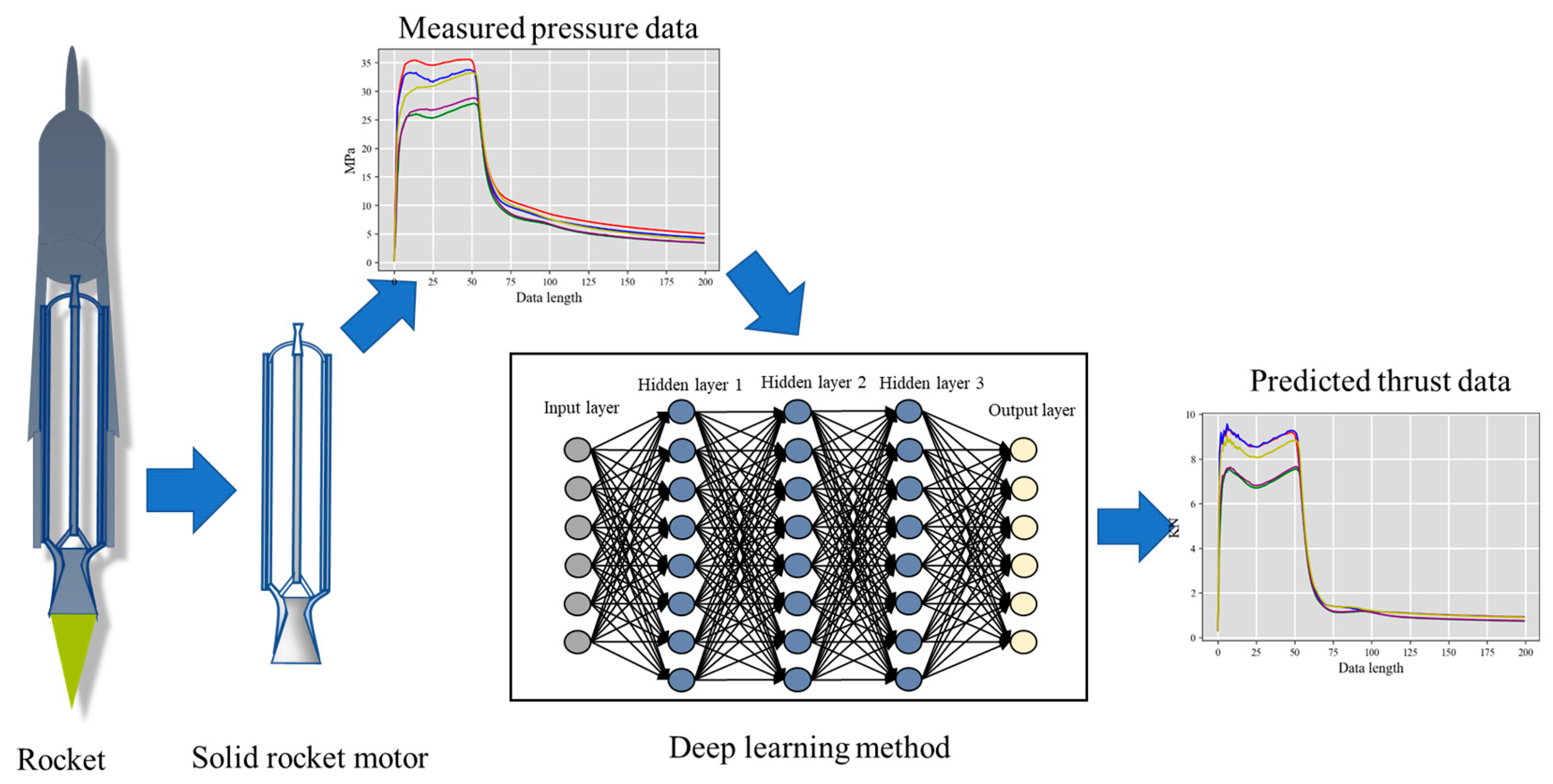
:1. Introduction
2. Deep Learning Method
2.1. Network Model Architecture
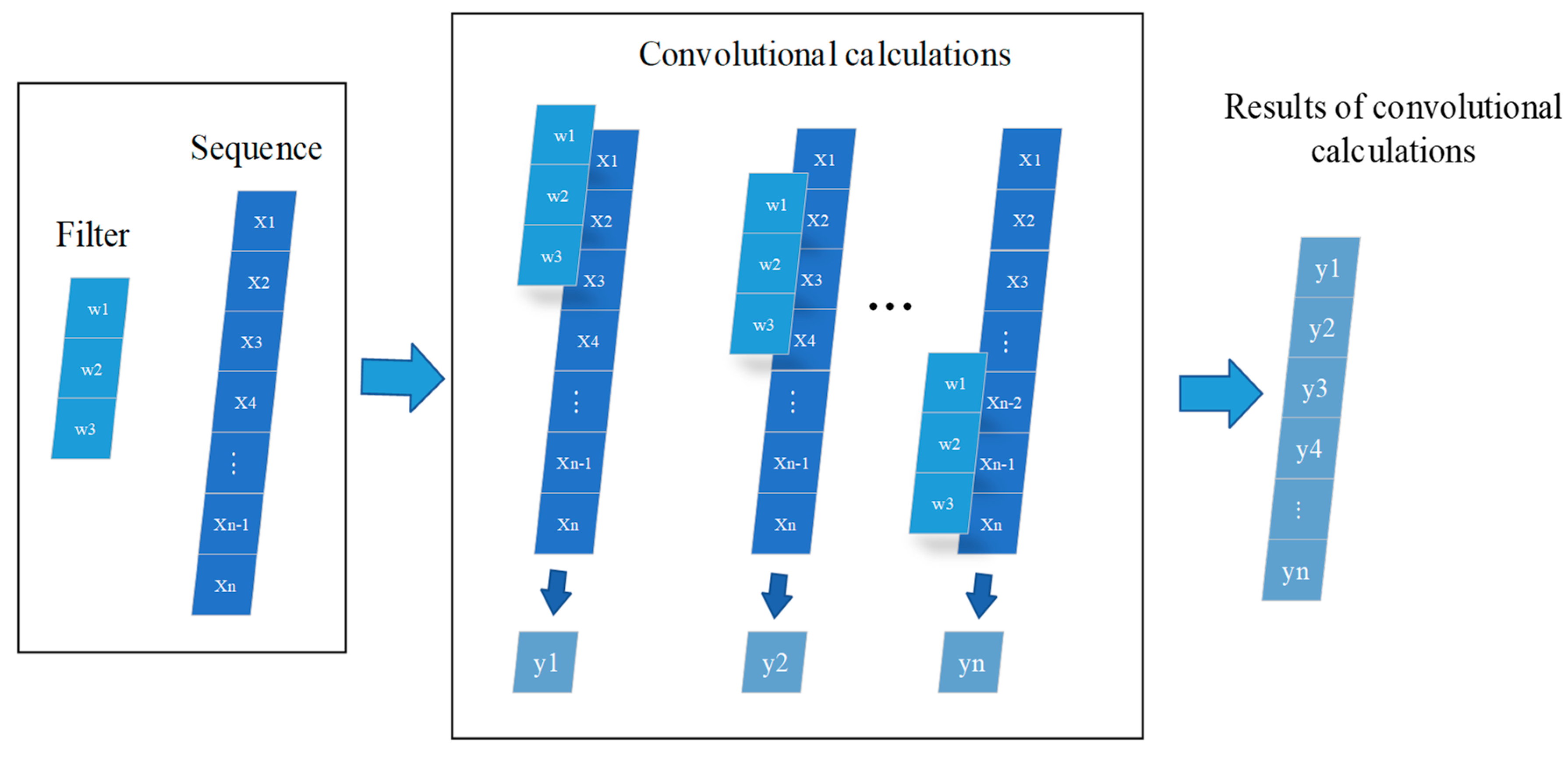
2.2. Convolutional Neural Network
2.3. RepVGG Network
2.4. Dropout
2.5. Cross-Modality Data Prediction Workflow
3. Simulation Research
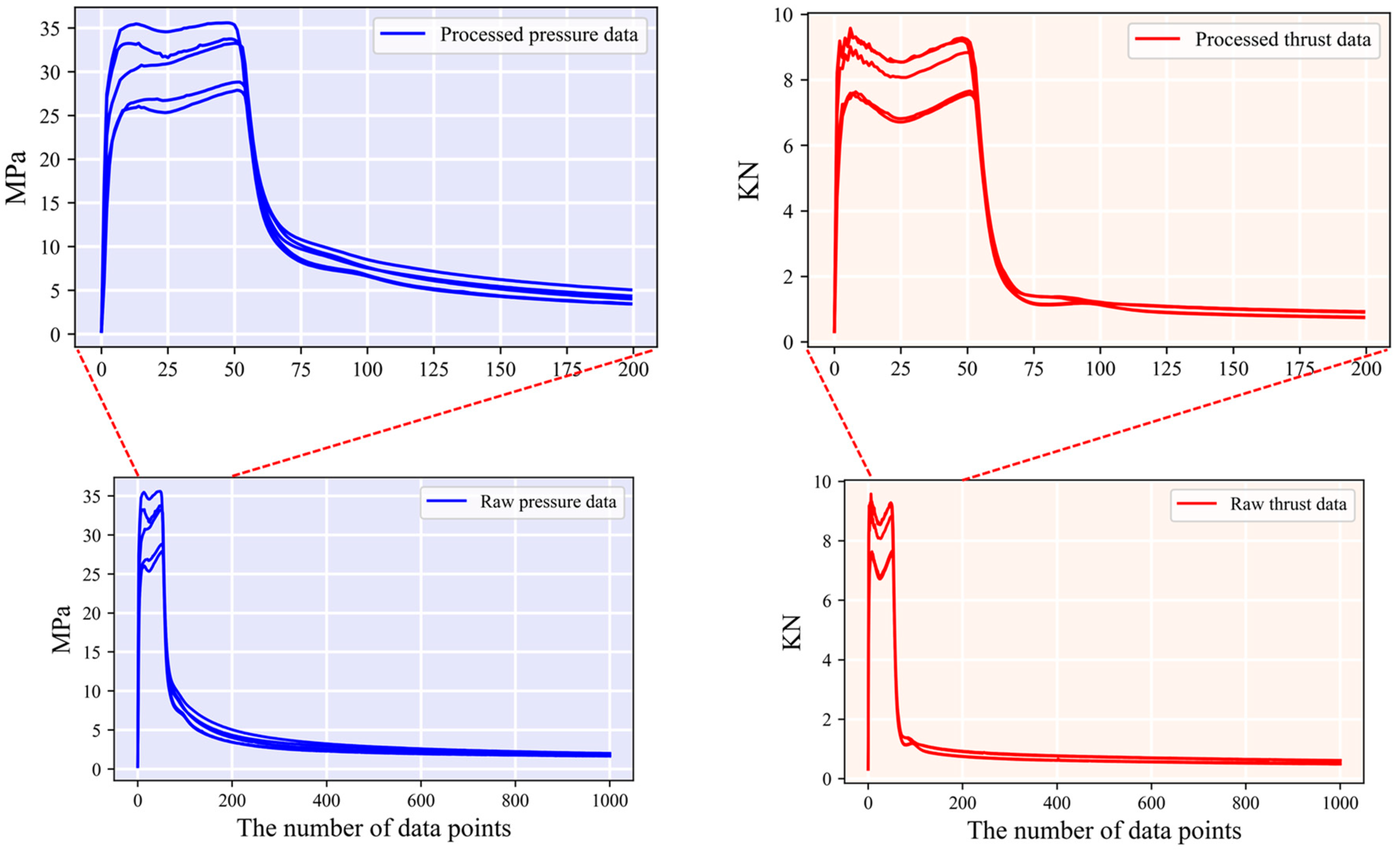
3.1. Data Preparation
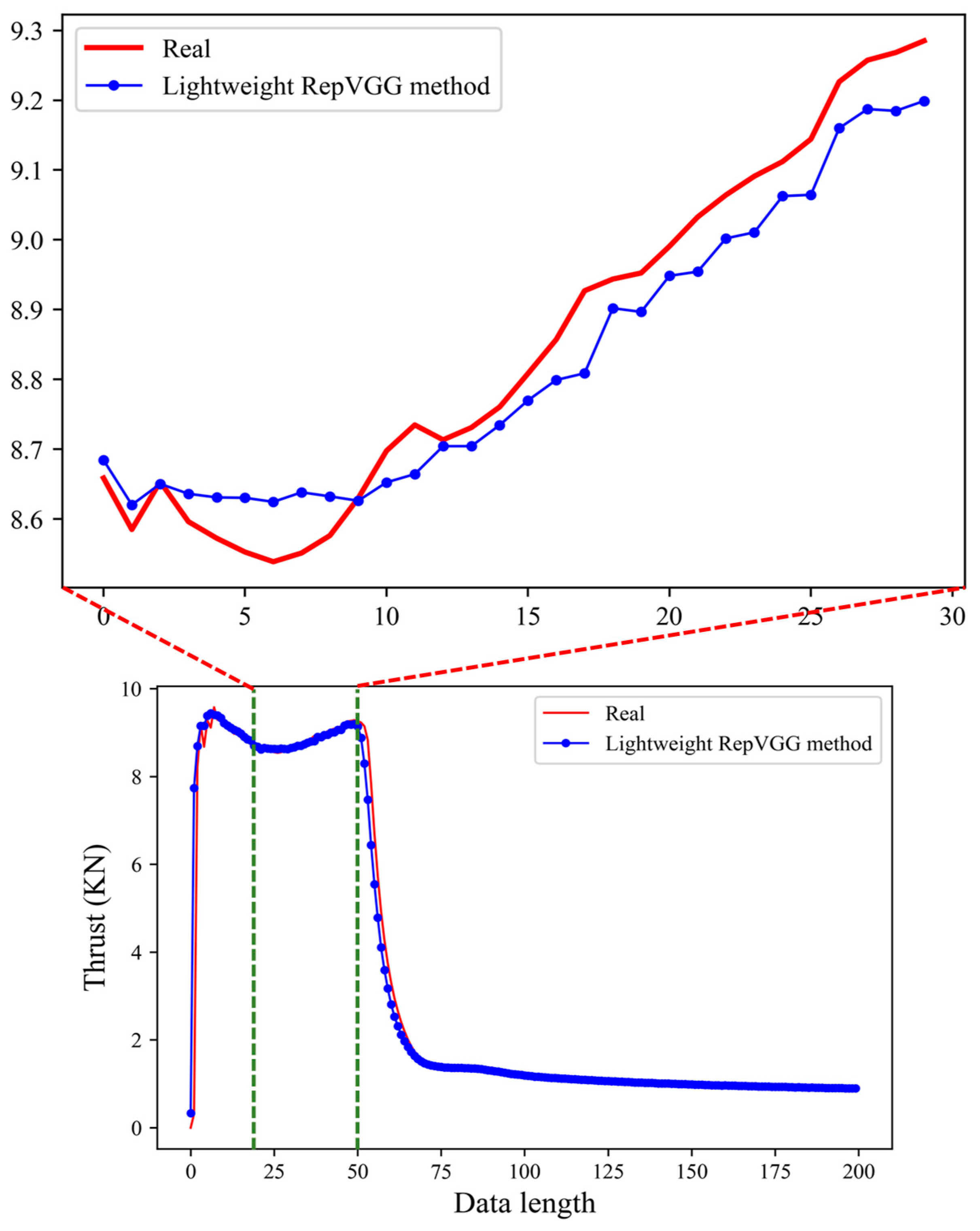
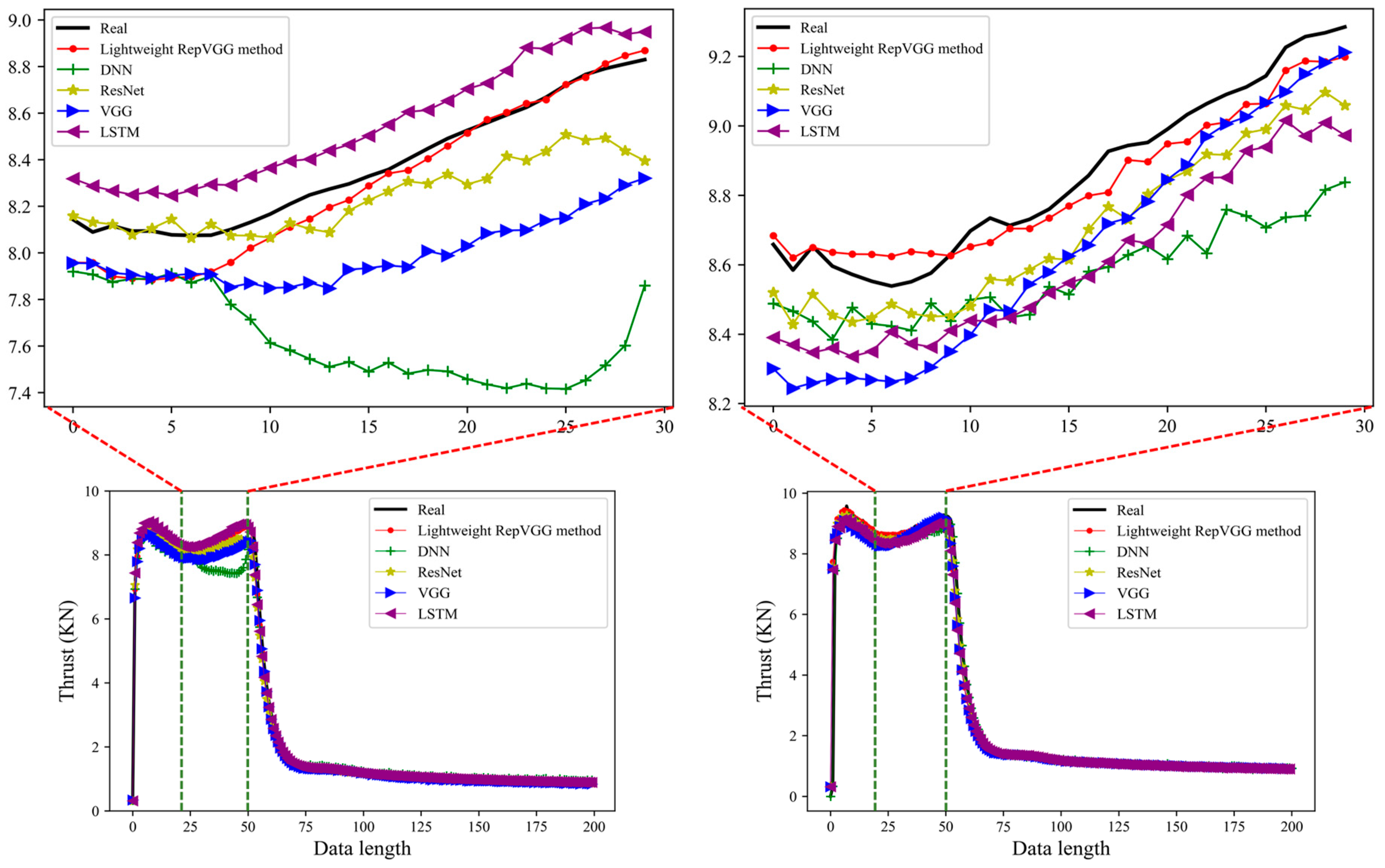
3.2. Simulation Prediction Results
3.3. Simulation Comparison and Analysis
3.3.1. Comparing Network Methods
3.3.2. Analysis of Comparative Results
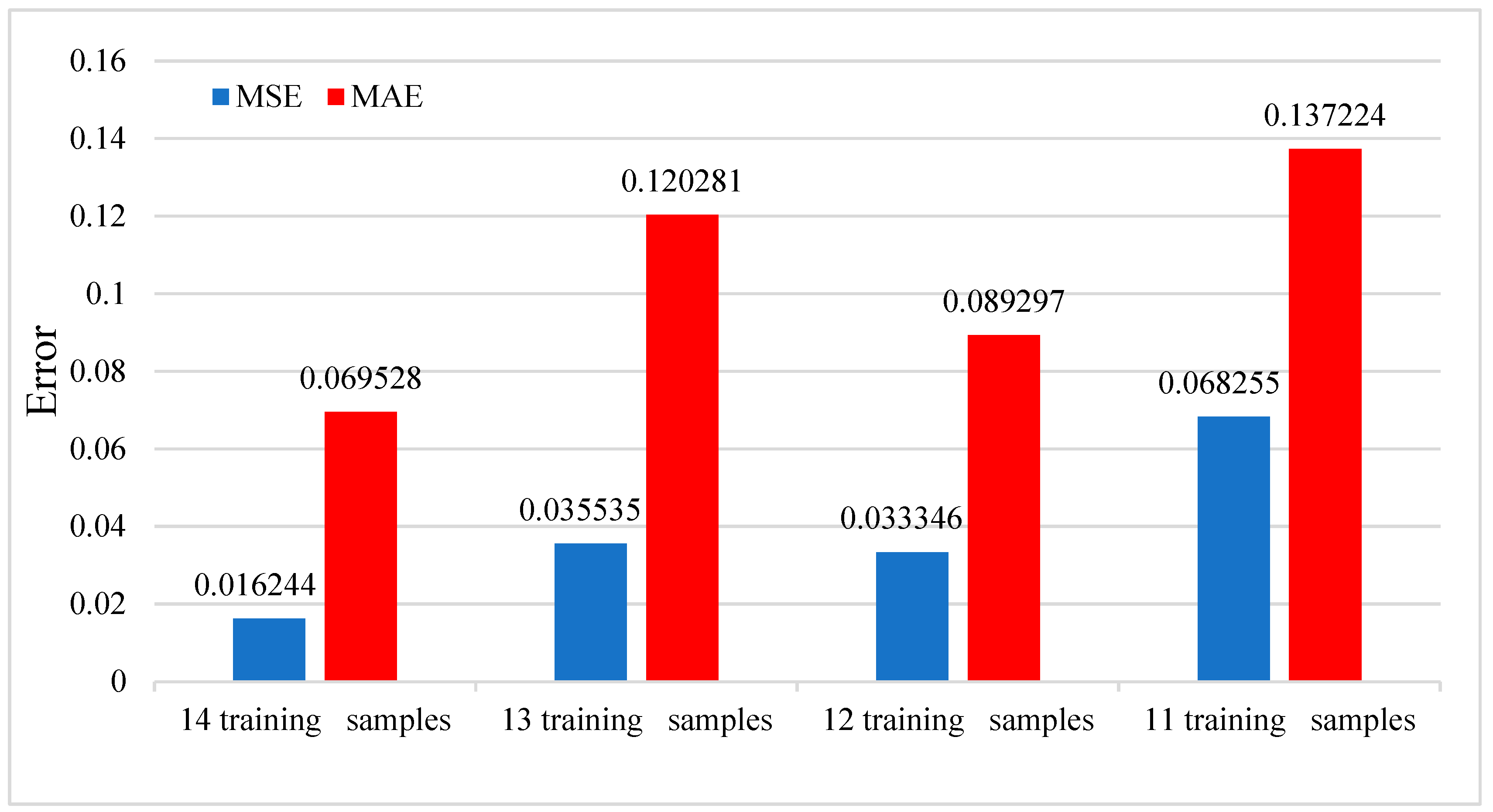
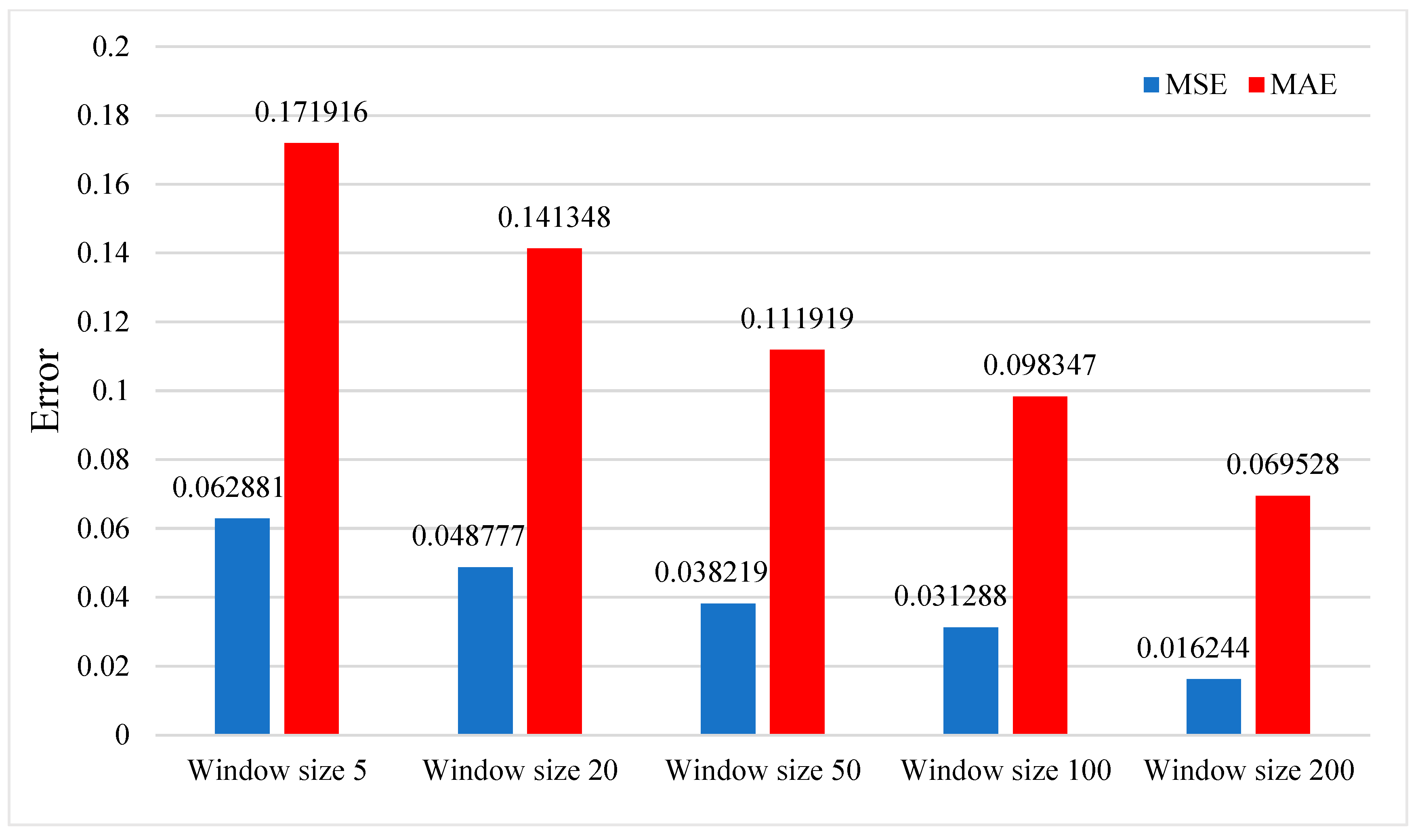
3.3.3. Effects of the Number of Training Samples and Window Size
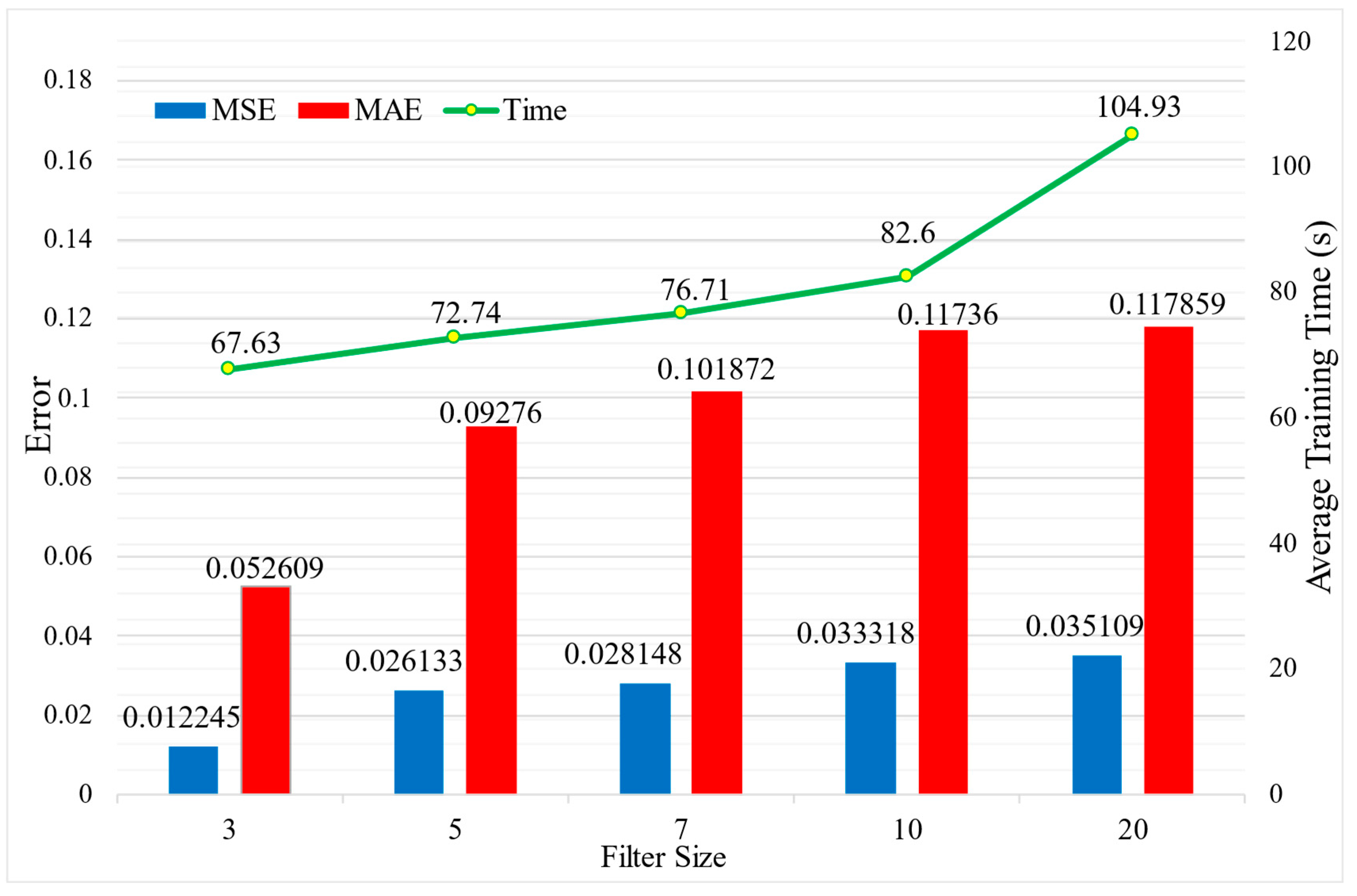
3.3.4. Effects of Number of Blocks and Filter Sizes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aliyu, B.; Osheku, C.; Oyedeji, E.; Adetoro, M.; Okon, A.; Idoko, C. Validating a novel theoretical expression for burn time and average thrust in solid rocket motor design. Adv. Res. 2015, 5, 1–11. [Google Scholar] [CrossRef]
- Naumann, K.; Stadler, L. Double-pulse solid rocket motor technology—Applications and technical solutions. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010; p. 6754. [Google Scholar]
- Davenas, A. Solid Rocket Propulsion Technology; Pergamon: Oxford, UK, 2012. [Google Scholar]
- Yan, D.; Wei, Z.; Xie, K.; Wang, N. Simulation of thrust control by fluidic injection and pintle in a solid rocket motor. Aerosp. Sci. Technol. 2020, 99, 105711. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, D.; Wang, W.; Okolo, P.N.; Zhang, W. Solid rocket motor design employing an efficient performance matching approach. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 4052–4065. [Google Scholar]
- Horne, W.; Burnside, N.; Panda, J.; Brodell, C. Measurements of unsteady pressures near the plume of a solid rocket motor. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, FL, USA, 11–13 May 2009; p. 3323. [Google Scholar]
- Açık, S. Internal Ballistic Design Optimization of a Solid Rocket Motor. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2010. [Google Scholar]
- Kamran, A.; Liang, G. An integrated approach for optimization of solid rocket motor. Aerosp. Sci. Technol. 2012, 17, 50–64. [Google Scholar] [CrossRef]
- Flora, J.; Auxillia, D.J. Sensor failure management in liquid rocket engine using artificial neural network. J. Sci. Ind. Res. 2020, 79, 1024–1027. [Google Scholar]
- O’Shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Sun, L.; Miller, T.C. Defect diagnosis in solid rocket motors using sensors and deep learning networks. AIAA J. 2021, 59, 276–281. [Google Scholar] [CrossRef]
- He, W.; Li, C.; Nie, X.; Wei, X.; Li, Y.; Li, Y.; Luo, S. Recognition and detection of aero-engine blade damage based on improved cascade mask r-cnn. Appl. Opt. 2021, 60, 5124–5133. [Google Scholar] [CrossRef]
- Tsutsumi, S.; Hirabayashi, M.; Sato, D.; Kawatsu, K.; Sato, M.; Kimura, T.; Hashimoto, T.; Abe, M. Data-driven fault detection in a reusable rocket engine using bivariate time-series analysis. Acta Astronaut. 2021, 179, 685–694. [Google Scholar] [CrossRef]
- Park, S.Y. Application of deep neural networks method to the fault diagnosis during the startup transient of a liquid-propellant rocket engine. Acta Astronaut. 2021, 177, 714–730. [Google Scholar] [CrossRef]
- Dai, J.; Li, T.; Xuan, Z.; Feng, Z. Automated defect analysis system for industrial computerized tomography images of solid rocket motor grains based on yolo-v4 model. Electronics 2022, 11, 3215. [Google Scholar] [CrossRef]
- Li, L.; Ren, J.; Wang, P.; Lü, Z.; Li, X.; Sun, M. An adaptive false-color enhancement algorithm for super-8-bit high grayscale x-ray defect image of solid rocket engine shell. Mech. Syst. Signal Process. 2022, 179, 109398. [Google Scholar] [CrossRef]
- Gamdha, D.; Unnikrishnakurup, S.; Rose, K.J.; Surekha, M.; Purushothaman, P.; Ghose, B.; Balasubramaniam, K. Automated defect recognition on X-ray radiographs of solid propellant using deep learning based on convolutional neural networks. J. Nondestruct. Eval. 2021, 40, 18. [Google Scholar] [CrossRef]
- Hoffmann, L.F.S.; Bizarria, F.C.P.; Bizarria, J.W.P. Detection of liner surface defects in solid rocket motors using multilayer perceptron neural networks. Polym. Test. 2020, 88, 106559. [Google Scholar] [CrossRef]
- Guo, X.; Yang, Y.; Han, X. Classification and inspection of debonding defects in solid rocket motor shells using machine learning algorithms. J. Nanoelectron. Optoelectron. 2021, 16, 1082–1089. [Google Scholar] [CrossRef]
- Williams, A.; Himschoot, A.; Saafir, M.; Gatlin, M.; Pendleton, D.; Alvord, D.A. A machine learning approach for solid rocket motor data analysis and virtual sensor development. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Online, 24–28 August 2020; p. 3935. [Google Scholar]
- Lv, H.; Chen, J.; Wang, J.; Yuan, J.; Liu, Z. A supervised framework for recognition of liquid rocket engine health state under steady-state process without fault samples. IEEE Trans. Instrum. Meas. 2021, 70, 3518610. [Google Scholar] [CrossRef]
- Zavoli, A.; Zolla, P.M.; Federici, L.; Migliorino, M.T.; Bianchi, D. Machine learning techniques for flight performance prediction of hybrid rocket engines. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Online, 9–11 August 2021; p. 3506. [Google Scholar]
- Li, X.; Yu, S.; Lei, Y.; Li, N.; Yang, B. Intelligent machinery fault diagnosis with event-based camera. IEEE Trans. Ind. Inform. 2023, 1–10. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X. Data privacy preserving federated transfer learning in machinery fault diagnostics using prior distributions. Struct. Health Monit. 2022, 21, 1329–1344. [Google Scholar] [CrossRef]
- Dhaked, D.K.; Dadhich, S.; Birla, D. Power output forecasting of solar photovoltaic plant using LSTM. Green Energy Intell. Transp. 2023, 2, 100113. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, J.; Chen, H.; Chen, J.; Li, Y.; Xu, J.; Deng, W. Intelligent diagnosis using continuous wavelet transform and gauss convolutional deep belief network. IEEE Trans. Reliab. 2022, 72, 692–702. [Google Scholar] [CrossRef]
- Li, H.; Lv, Y.; Yuan, R.; Dang, Z.; Cai, Z.; An, B. Fault diagnosis of planetary gears based on intrinsic feature extraction and deep transfer learning. Meas. Sci. Technol. 2022, 34, 014009. [Google Scholar] [CrossRef]
- Li, M.; Zhang, W.; Hu, B.; Kang, J.; Wang, Y.; Lu, S. Automatic assessment of depression and anxiety through encoding pupil-wave from hci in vr scenes. ACM Trans. Multimed. Comput. Commun. Appl. 2023, 20, 1–22. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R. Intelligent fault diagnosis for planetary gearbox using transferable deep q network under variable conditions with small training data. J. Dyn. Monit. Diagn. 2023, 2, 30–41. [Google Scholar]
- Han, S.; Feng, Z. Deep residual joint transfer strategy for cross-condition fault diagnosis of rolling bearings. J. Dyn. Monit. Diagn. 2023, 2, 51–60. [Google Scholar]
- Peng, D.; Wang, H.; Desmet, W.; Gryllias, K. RMA-CNN: A residual mixed-domain attention cnn for bearings fault diagnosis and its time-frequency domain interpretability. J. Dyn. Monit. Diagn. 2023, 2, 115–132. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, M.; Feng, G.; Xu, Y.; Zhen, D.; Gu, F. A novel deep model with meta-learning for rolling bearing few-shot fault diagnosis. J. Dyn. Monit. Diagn. 2023, 2, 1–22. [Google Scholar] [CrossRef]
- Li, X.; Zhang, C.; Li, X.; Zhang, W. Federated transfer learning in fault diagnosis under data privacy with target self-adaptation. J. Manuf. Syst. 2023, 68, 523–535. [Google Scholar] [CrossRef]
- Zhang, M.; Yan, C.; Dai, W.; Xiang, X.; Low, K.H. Tactical conflict resolution in urban airspace for unmanned aerial vehicles operations using attention-based deep reinforcement learning. Green Energy Intell. Transp. 2023, 2, 100107. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, L.; Yang, Z.; Zhao, S.; He, Y.; Wang, X.; Wang, H. Battery soh estimation method based on gradual decreasing current, double correlation analysis and gru. Green Energy Intell. Transp. 2023, 2, 100108. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, X.; Ma, N.; Han, J.; Ding, G.; Sun, J. Repvgg: Making vgg-style convnets great again. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 13733–13742. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Orbekk, E. Thrust vector model and solid rocket motor firing validations. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; p. 5055. [Google Scholar]
- Wei, X.; He, G.-q.; Li, J.; Zhou, Z.-F. The analysis on the rising section of experimental pressure in variable thrust pintle solid rocket motor. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; p. 4604. [Google Scholar]
- Wei, X.; Li, J.; He, G. Influence of structural parameters on the performance of vortex valve variable-thrust solid rocket motor. Int. J. Turbo Jet-Engines 2017, 34, 1–9. [Google Scholar] [CrossRef]
- Miikkulainen, R.; Liang, J.; Meyerson, E.; Rawal, A.; Fink, D.; Francon, O.; Raju, B.; Shahrzad, H.; Navruzyan, A.; Duffy, N.; et al. Evolving Deep Neural Networks. In Artificial Intelligence in the Age of Neural Networks and Brain Computing; Elsevier: Amsterdam, The Netherlands, 2019; pp. 293–312. [Google Scholar]
- Graves, A.; Graves, A. Long Short-Term Memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Liu, S.; Deng, W. Very deep convolutional neural network based image classification using small training sample size. In Proceedings of the 2015 3rd IAPR Asian Conference on Pattern Recognition (ACPR), Kuala Lumpur, Malaysia, 3–6 November 2015; pp. 730–734. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Zheng, S.; Wang, X.; Xu, M.; Li, X. Lightweight RepVGG-Based Cross-Modality Data Prediction Method for Solid Rocket Motors. Sensors 2023, 23, 9165. https://doi.org/10.3390/s23229165
Yang H, Zheng S, Wang X, Xu M, Li X. Lightweight RepVGG-Based Cross-Modality Data Prediction Method for Solid Rocket Motors. Sensors. 2023; 23(22):9165. https://doi.org/10.3390/s23229165
Chicago/Turabian StyleYang, Huixin, Shangshang Zheng, Xu Wang, Mingze Xu, and Xiang Li. 2023. "Lightweight RepVGG-Based Cross-Modality Data Prediction Method for Solid Rocket Motors" Sensors 23, no. 22: 9165. https://doi.org/10.3390/s23229165
APA StyleYang, H., Zheng, S., Wang, X., Xu, M., & Li, X. (2023). Lightweight RepVGG-Based Cross-Modality Data Prediction Method for Solid Rocket Motors. Sensors, 23(22), 9165. https://doi.org/10.3390/s23229165





