Exploration and Gas Source Localization in Advection–Diffusion Processes with Potential-Field-Controlled Robotic Swarms †
Abstract
:1. Introduction
Notation
2. Methods
2.1. Process Model
2.2. Measurements
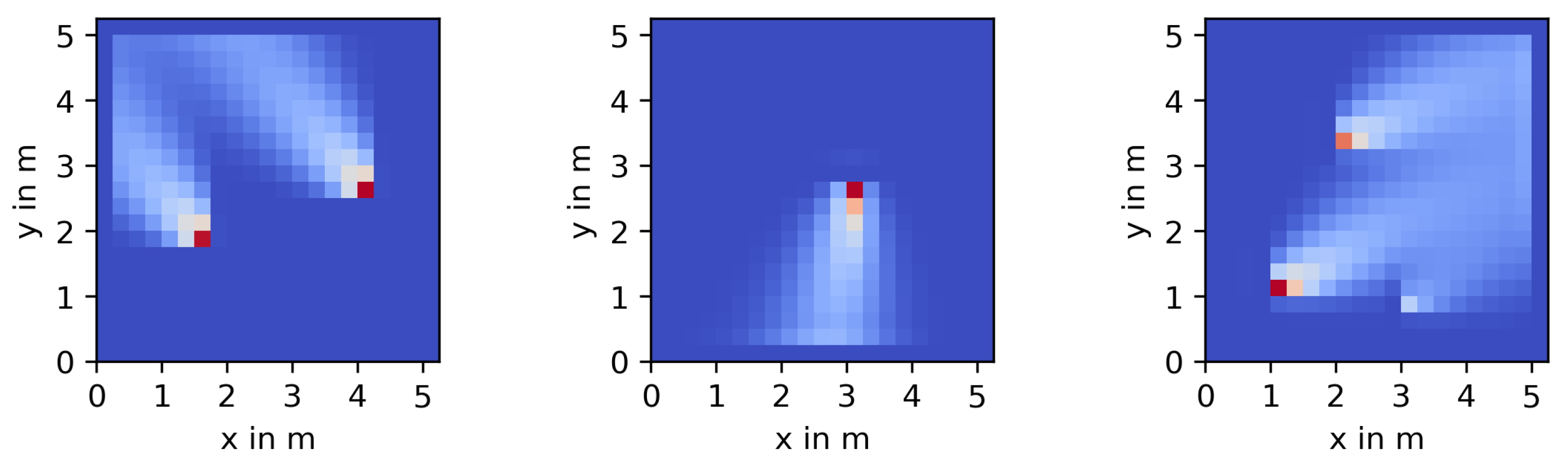
2.3. Bayesian Estimation of Process Parameters
- High variance of a particular cell would indicate little information about the concentration at this particular location;
- Low variance would indicate high information content, and thus changes in this particular element will have a strong impact on the deviations of the cost function from the MAP optimum.
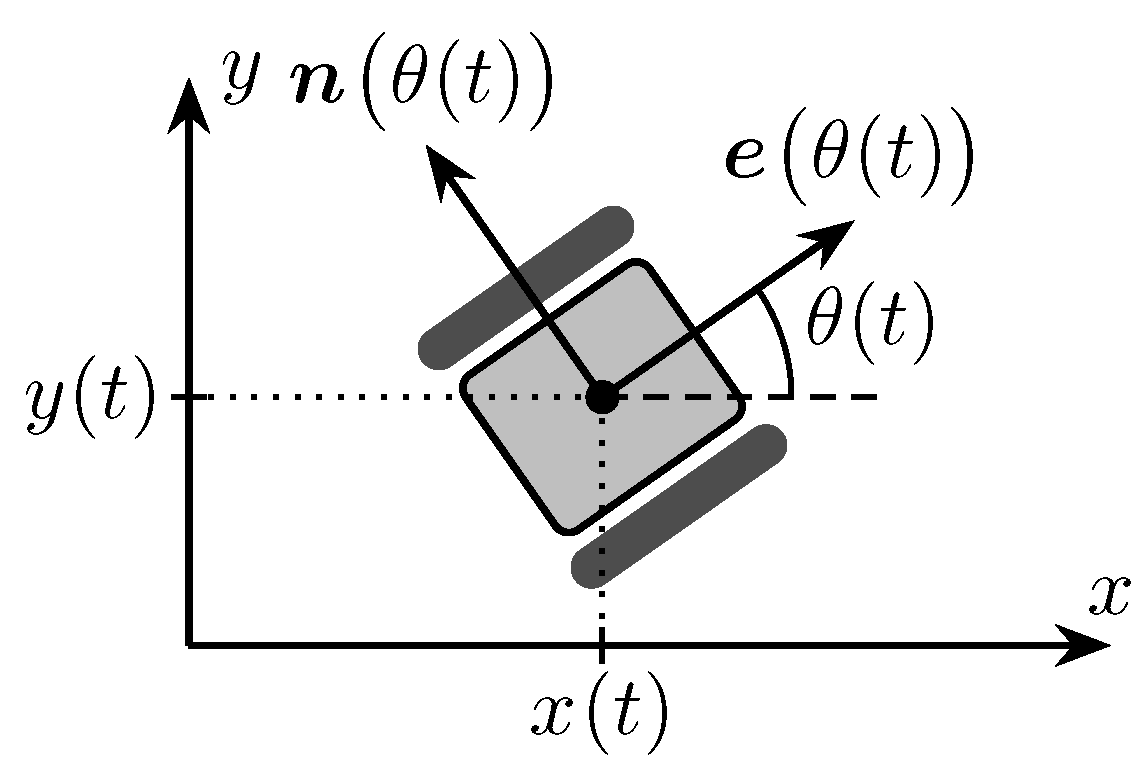
2.4. Robot Model
2.5. Potential Field Control
2.5.1. Repulsive Potential
2.5.2. Attractive Potential
2.5.3. Control Laws
2.5.4. Measurement Acquisition
3. Simulations
3.1. Simulation Parameters
3.2. Performance Metrics
- Wrong number of sources (too many, too few);
- Sources at the wrong location;
- Wrong source release rates (intensities).
- The reconstructed value is the largest of any of the in the local surroundings of , i.e., .
- is at least 5 times larger than the smallest value of within ,i.e., for .
- 1.
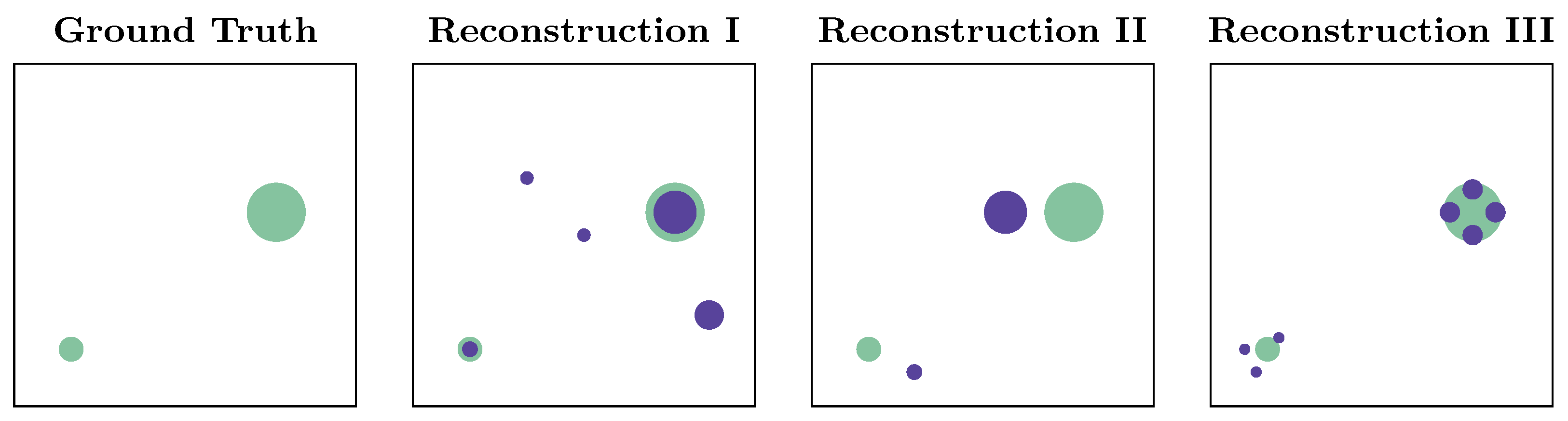
- Our first performance metric is the time step when the two sets are exactly identical for the first time. This time we denote as . This metric can be calculated for each simulation run, and we can evaluate its statistics when running multiple simulations.
- 2.
- As a second metric, we consider the time step when the reconstruction is “nearly exact” for the first time compared to the ground truth. We define “nearly exact” to mean any source distribution that (I) has the correct number of source candidates, and (II) all source candidates are very close to their correct location, i.e., the average euclidean distance between and its true position is less than 2 grid cells. The first time of the “nearly exact” reconstruction we denote as .
- 3.
- Our third metric takes into account that the reconstruction may hit upon the correct solution early on, then diverge from it temporarily, before it finally settles back into the correct distribution. So, we can define a time when the reconstruction is “wrong” for the last time. The time when the set of estimated source is last not exactly the ground truth is denoted as .
- 4.
- Similar to , we can also define the last time when the reconstruction is not “nearly exact”, where “nearly exact” is defined as in point two. This time we denote as . In general, the following inequalities hold:
- 5.
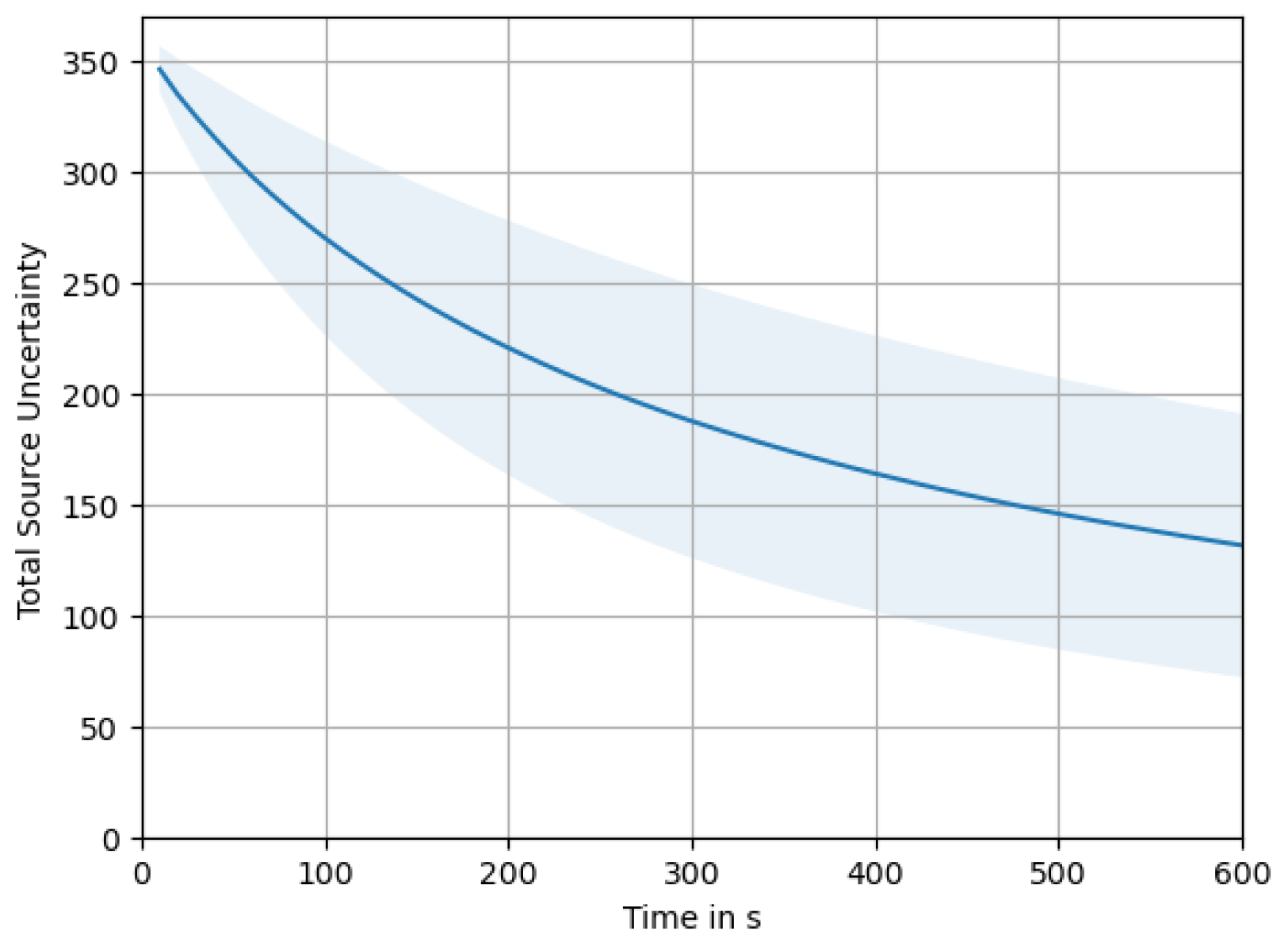
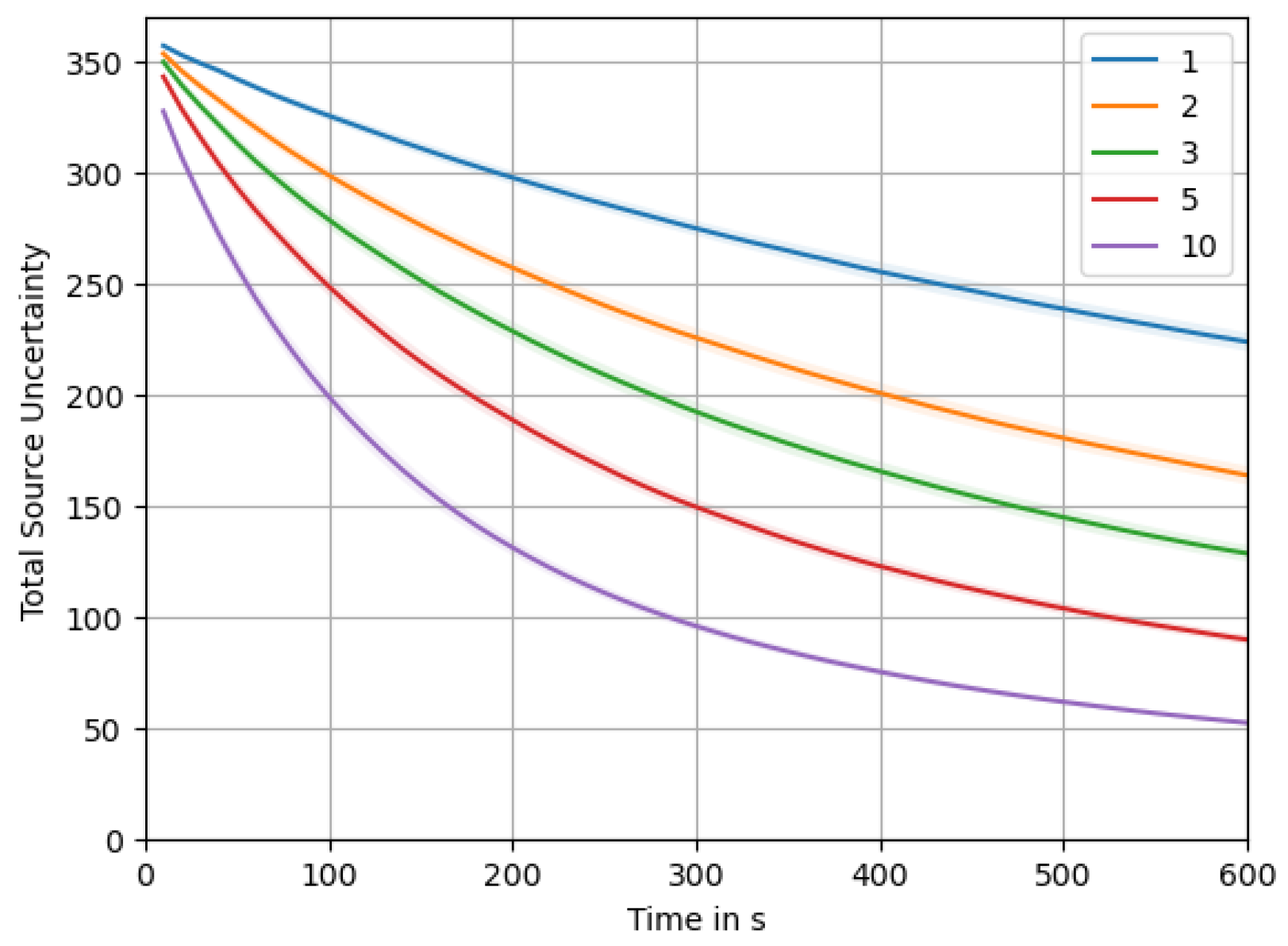
- Last, we will have a look at the total source uncertainty, , over time. This metric expresses the sum of source uncertainties at all locations, giving us a measure of the total amount of remaining uncertainty in the system. In contrast to the other metrics, this can be calculated without knowing the true source distribution, even online during an experiment.
3.3. Source Distributions
- 1.
- Sources must be at least 10% away from the edges.
- 2.
- Sources must be at least 20% away from each other.
3.4. Wind Models
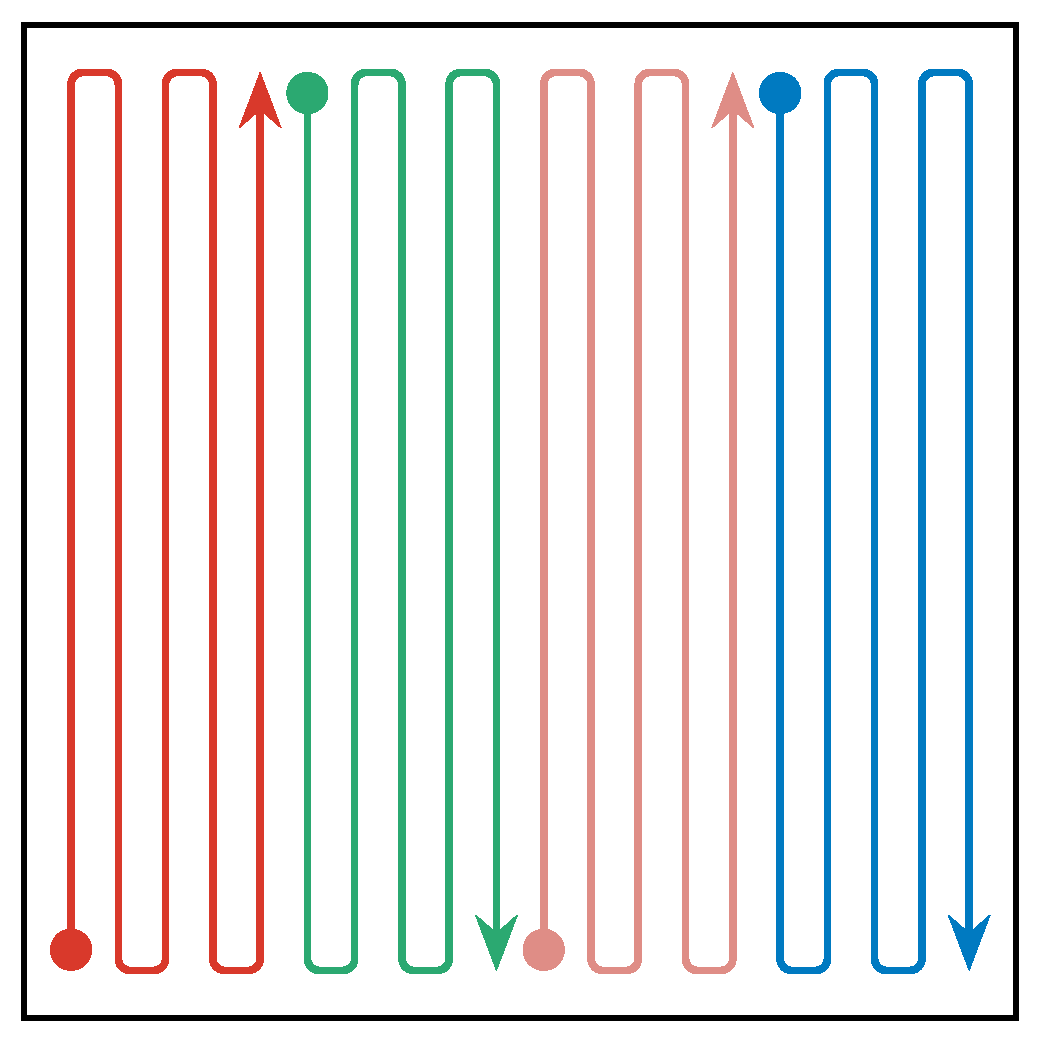
3.5. Benchmarks
4. Results and Discussion
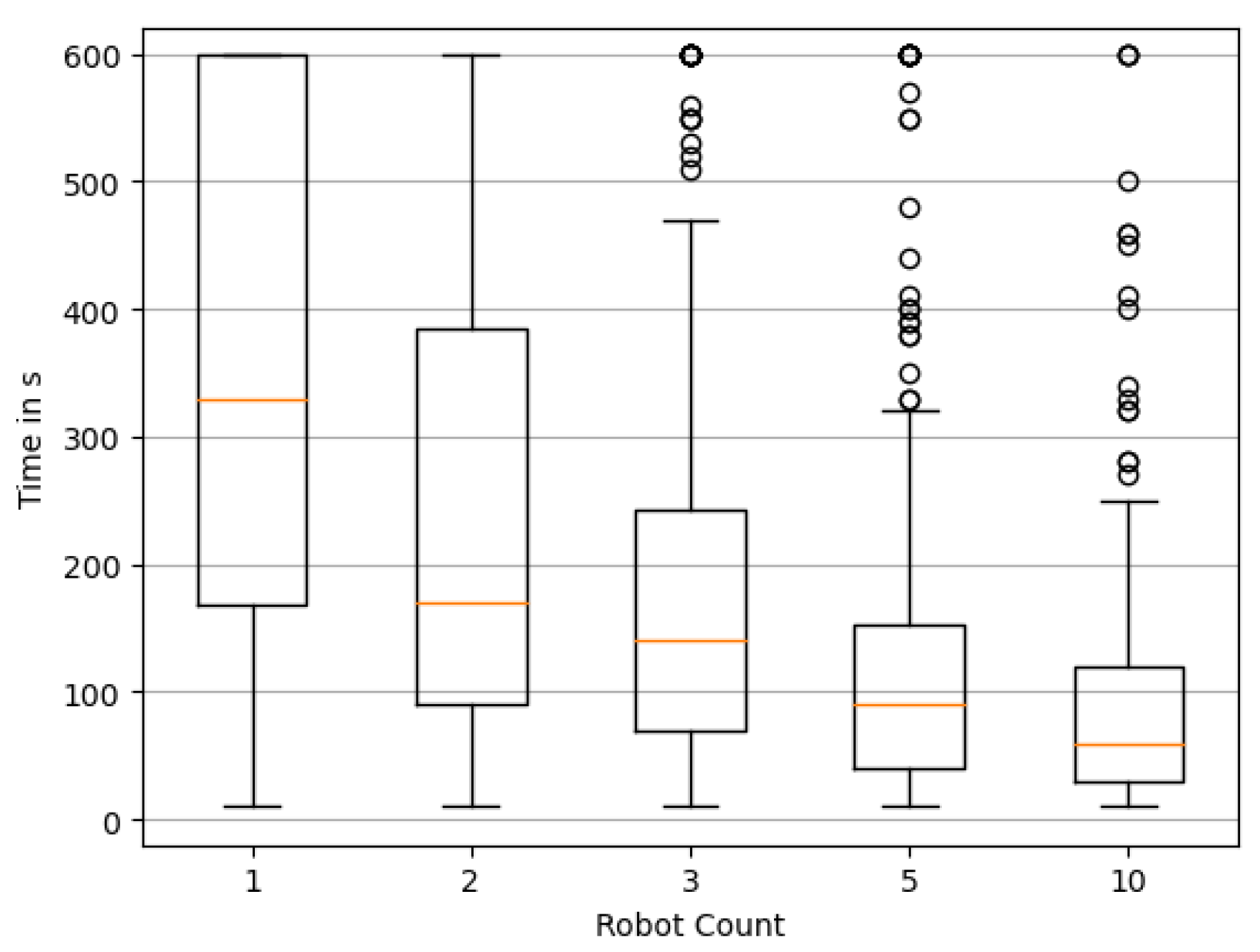
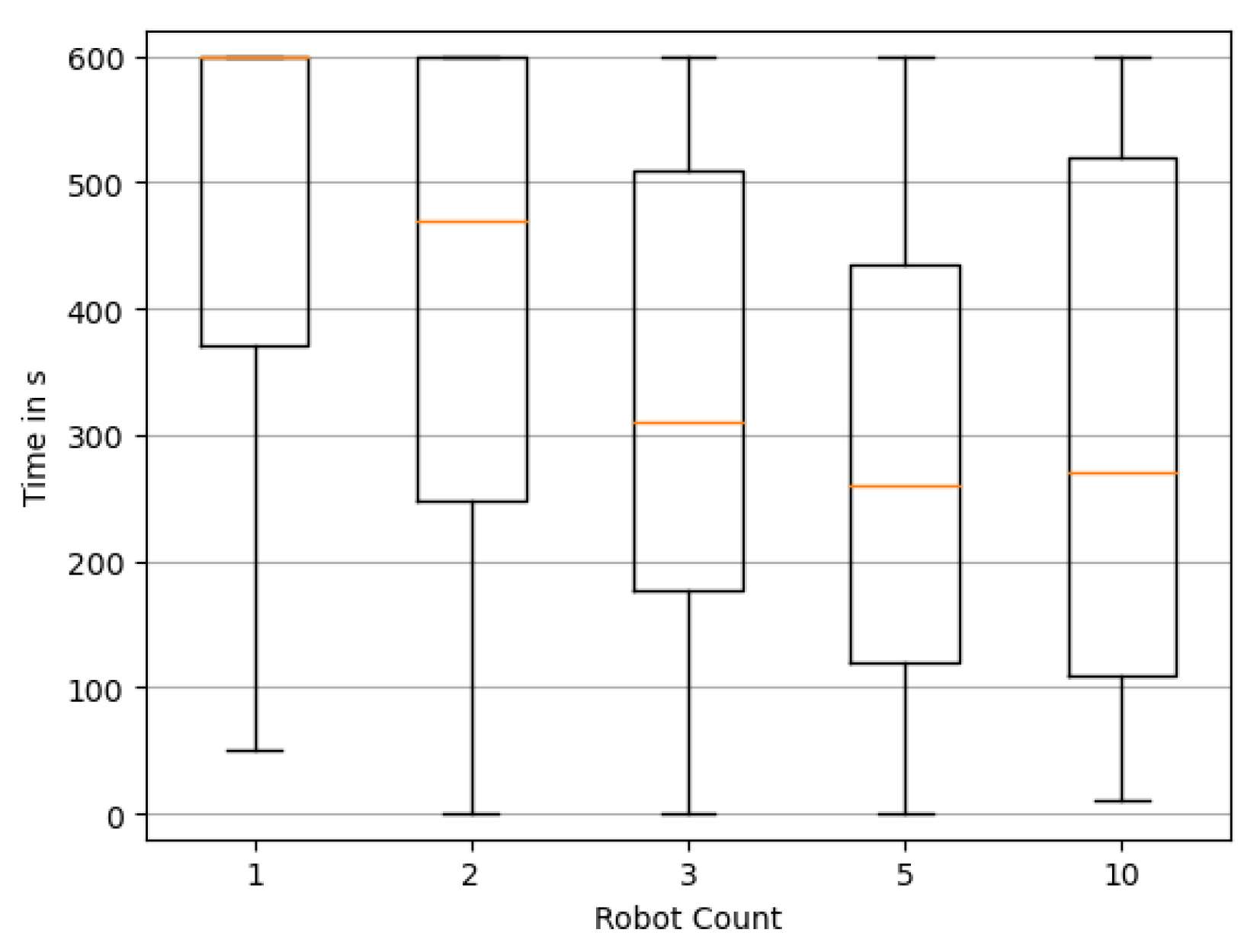
4.1. Evaluation of Swarm Size
4.2. Our Approach vs. Meander
4.3. Our Approach vs. Random Walk
4.4. Fluctuating vs. Static Wind
4.5. Rate of Information Gathering vs. Size of the Explored Areal
4.6. Performance of the Estimator
4.7. Performance of the Potential Field Control
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Distributions of the Time Required to Reconstruct the Source Locations Exactly
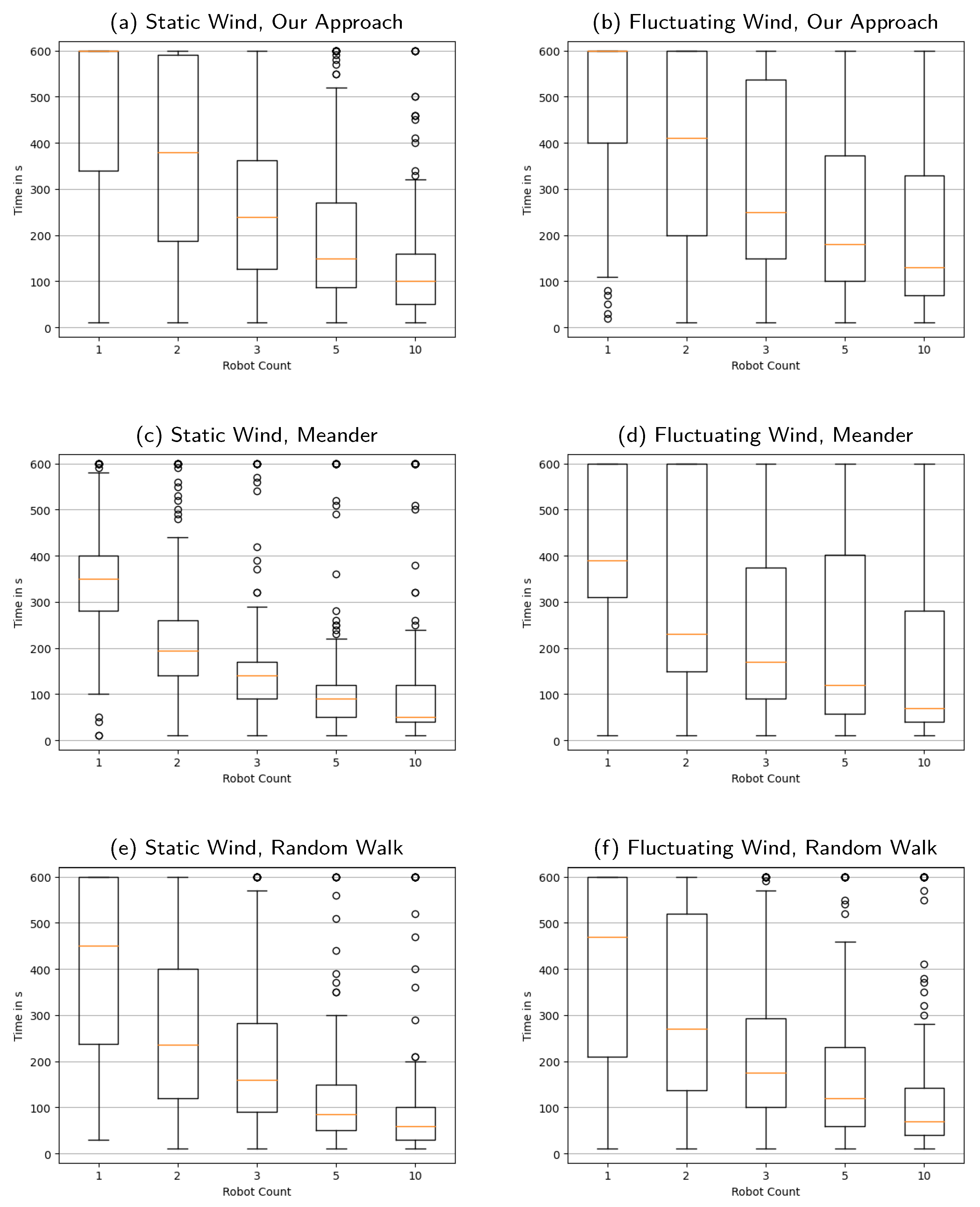
Appendix B. Distribution of the Time Required to Reconstruct the Source Locations Nearly Exactly

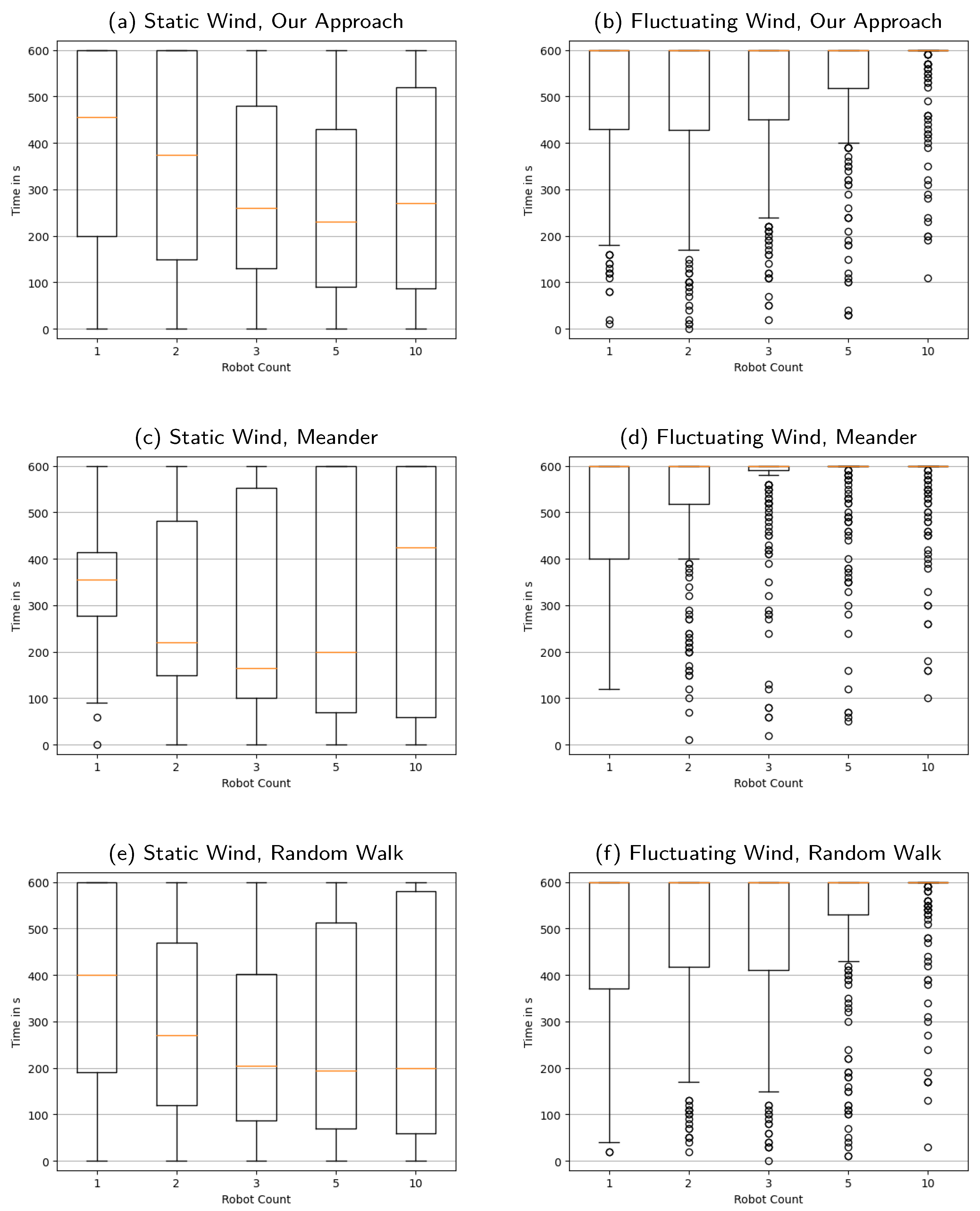
Appendix C. Distribution of the Time Required until the Last Reconstruction of Source Locations Is Not Exactly Correct

Appendix D. Distribution of the Time Required until the Last Reconstruction of Source Locations Is Not Nearly Exact
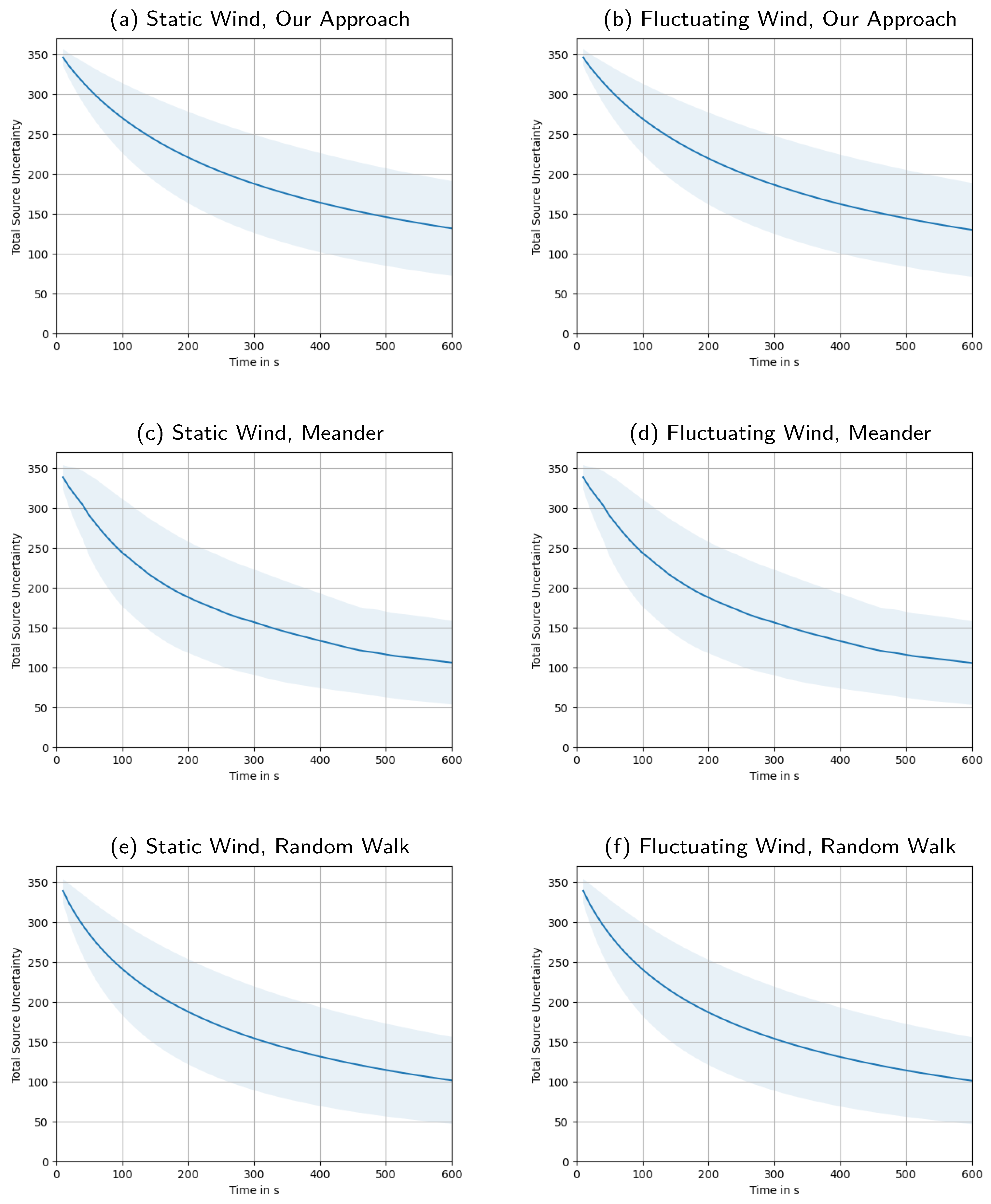
Appendix E. Total Source Uncertainty over Time, Averaged over All Swarm Sizes
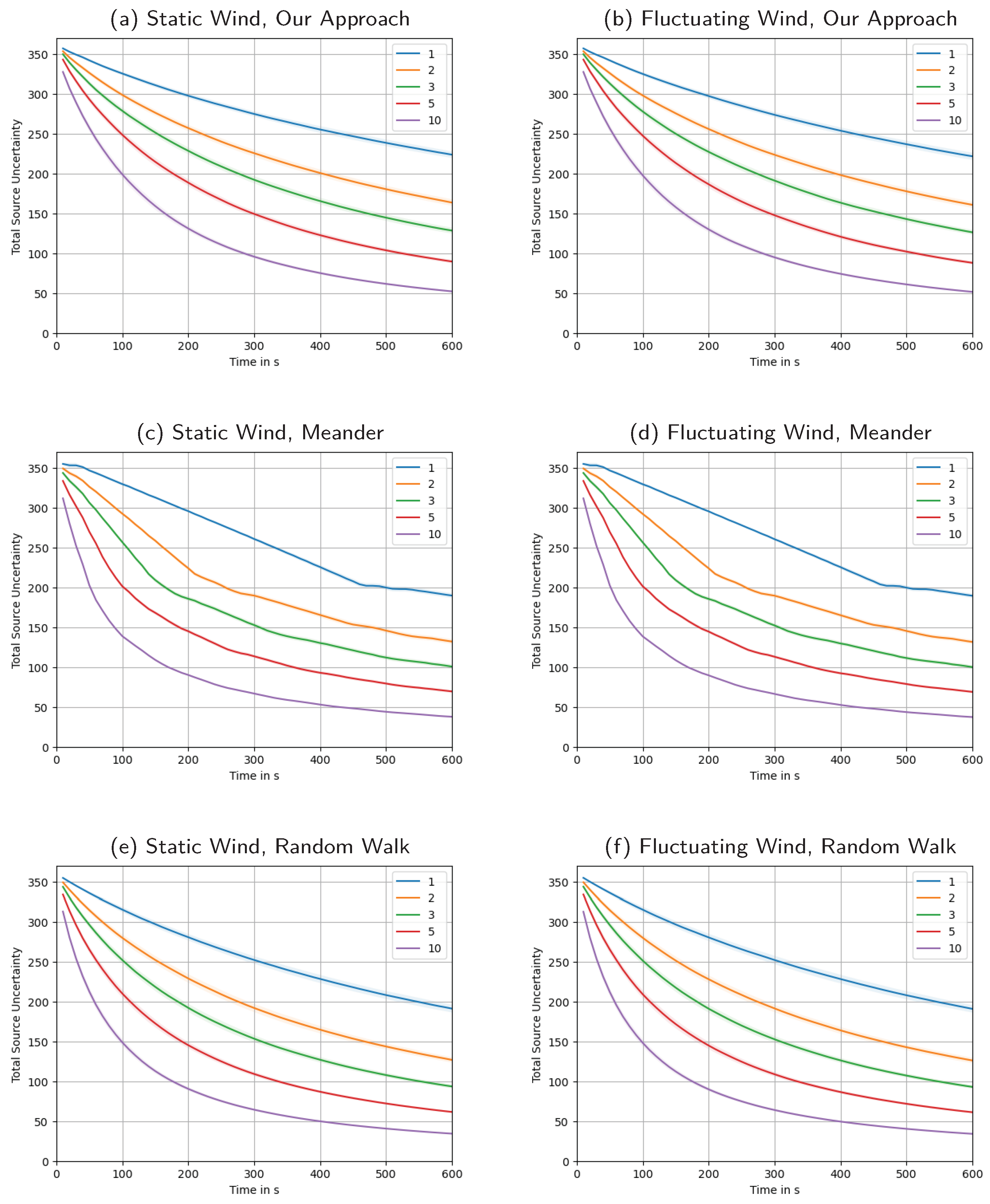
Appendix F. Total Source Uncertainty over Time, Averages Broken Down for Different Swarm Sizes
References
- Francis, A.; Li, S.; Griffiths, C.; Sienz, J. Gas source localization and mapping with mobile robots: A review. J. Field Robot. 2022, 39, 1341–1373. [Google Scholar] [CrossRef]
- Marjovi, A.; Marques, L. Optimal Swarm Formation for Odor Plume Finding. IEEE Trans. Cybern. 2014, 44, 2302–2315. [Google Scholar] [CrossRef] [PubMed]
- Neumann, P.P.; Hirschberger, P.; Bartholmai, M. Flying Ant Robot–Aerial Chemical Trail Detection and Localization. In Proceedings of the 2021 IEEE Sensors, Sydney, Australia, 31 October–3 November 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Soares, J.M.; Aguiar, A.P.; Pascoal, A.M.; Martinoli, A. A distributed formation-based odor source localization algorithm—Design, implementation, and wind tunnel evaluation. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1830–1836. [Google Scholar] [CrossRef]
- Wiedemann, T.; Schaab, M.; Gomez, J.M.; Shutin, D.; Scheibe, M.; Lilienthal, A.J. Gas Source Localization Based on Binary Sensing with a UAV. In Proceedings of the 2022 IEEE International Symposium on Olfaction and Electronic Nose (ISOEN), Aveiro, Portugal, 29 May–1 June 2022; pp. 1–3. [Google Scholar] [CrossRef]
- Ishida, H.; Wada, Y.; Matsukura, H. Chemical sensing in robotic applications: A review. IEEE Sens. J. 2012, 12, 3163–3173. [Google Scholar] [CrossRef]
- Lilienthal, A.; Duckett, T. Experimental analysis of gas-sensitive Braitenberg vehicles. Adv. Robot. 2004, 18, 817–834. [Google Scholar] [CrossRef]
- Rutkowski, A.; Edwards, S.; Willis, M.; Quinn, R.; Causey, G. A robotic platform for testing moth-inspired plume tracking strategies. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004, ICRA ’04, New Orleans, LA, USA, 26 April–1 May; 2004; Volume 4, pp. 3319–3324. [Google Scholar] [CrossRef]
- Chen, X.-x.; Huang, J. Odor source localization algorithms on mobile robots: A review and future outlook. Robot. Auton. Syst. 2019, 112, 123–136. [Google Scholar] [CrossRef]
- Marjovi, A.; Marques, L. Multi-robot odor distribution mapping in realistic time-variant conditions. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3720–3727. [Google Scholar] [CrossRef]
- Jing, T.; Meng, Q.H.; Ishida, H. Recent Progress and Trend of Robot Odor Source Localization. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 938–953. [Google Scholar] [CrossRef]
- Hutchinson, M.; Oh, H.; Chen, W.H. A review of source term estimation methods for atmospheric dispersion events using static or mobile sensors. Inf. Fusion 2017, 36, 130–148. [Google Scholar] [CrossRef]
- Wiedemann, T.; Manss, C.; Shutin, D. Multi-agent exploration of spatial dynamical processes under sparsity constraints. Auton. Agents Multi-Agent Syst. 2018, 32, 134–162. [Google Scholar] [CrossRef]
- Vergassola, M.; Villermaux, E.; Shraiman, B.I. ’Infotaxis’ as a strategy for searching without gradients. Nature 2007, 445, 406–409. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.Y.; Wang, J.Y.; Meng, Q.H. An Infotaxis-based Odor Source Searching Strategy for a Mobile Robot Equipped with a TDLAS Gas Sensor. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 4492–4497. [Google Scholar] [CrossRef]
- Hutchinson, M.; Oh, H.; Chen, W.H. Entrotaxis as a strategy for autonomous search and source reconstruction in turbulent conditions. Inf. Fusion 2018, 42, 179–189. [Google Scholar] [CrossRef]
- Hinsen, P.; Wiedemann, T.; Shutin, D. Potential Field Based Swarm Exploration of Processes Governed by Partial Differential Equations. In Proceedings of the ROBOT2022: Fifth Iberian Robotics Conference, Zaragoza, Spain, 23–25 November 2022; Tardioli, D., Matellán, V., Heredia, G., Silva, M.F., Marques, L., Eds.; Springer: Cham, Switzerland, 2022; pp. 117–129. [Google Scholar]
- Schwab, A.; Littek, F.; Lunze, J. Experimental Evaluation of a Novel Approach to Cooperative Control of Multiple Robots with Artificial Potential Fields. In Proceedings of the 2021 European Control Conference (ECC), Delft, The Netherlands, 29 June–2 July 2021. [Google Scholar] [CrossRef]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. Intl. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Koditschek, D. Robot Planning and Control Via Potential Functions. In The Robotics Review; MIT Press: Cambridge, MA, USA, 1989; pp. 349–367. [Google Scholar]
- Neumann, P.; Asadi, S.; Lilienthal, A.; Bartholmai, M.; Schiller, J. Autonomous Gas-Sensitive Microdrone: Wind Vector Estimation and Gas Distribution Mapping. IEEE Robot. Autom. Mag. 2012, 19, 50–61. [Google Scholar] [CrossRef]
- Strang, G. Computational Science and Engineering; Wellesley-Cambridge Press: Wellesley, MA, USA, 2007. [Google Scholar]
- Pérez Guerrero, J.; Pimentel, L.; Skaggs, T.; van Genuchten, M. Analytical solution of the advection–diffusion transport equation using a change-of-variable and integral transform technique. Int. J. Heat Mass Transf. 2009, 52, 3297–3304. [Google Scholar] [CrossRef]
- Wiedemann, T.; Lilienthal, A.J.; Shutin, D. Analysis of model mismatch effects for a model-based gas source localization strategy incorporating advection knowledge. Sensors 2019, 19, 520. [Google Scholar] [CrossRef] [PubMed]
- Rimon, E.; Koditschek, D. Exact robot navigation using artificial potential functions. IEEE Trans. Robot. Autom. 1992, 8, 501–518. [Google Scholar] [CrossRef]
- Bibbona, E.; Panfilo, G.; Tavella, P. The Ornstein–Uhlenbeck process as a model of a low pass filtered white noise. Metrologia 2008, 45, S117. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hinsen, P.; Wiedemann, T.; Shutin, D.; Lilienthal, A.J. Exploration and Gas Source Localization in Advection–Diffusion Processes with Potential-Field-Controlled Robotic Swarms. Sensors 2023, 23, 9232. https://doi.org/10.3390/s23229232
Hinsen P, Wiedemann T, Shutin D, Lilienthal AJ. Exploration and Gas Source Localization in Advection–Diffusion Processes with Potential-Field-Controlled Robotic Swarms. Sensors. 2023; 23(22):9232. https://doi.org/10.3390/s23229232
Chicago/Turabian StyleHinsen, Patrick, Thomas Wiedemann, Dmitriy Shutin, and Achim J. Lilienthal. 2023. "Exploration and Gas Source Localization in Advection–Diffusion Processes with Potential-Field-Controlled Robotic Swarms" Sensors 23, no. 22: 9232. https://doi.org/10.3390/s23229232
APA StyleHinsen, P., Wiedemann, T., Shutin, D., & Lilienthal, A. J. (2023). Exploration and Gas Source Localization in Advection–Diffusion Processes with Potential-Field-Controlled Robotic Swarms. Sensors, 23(22), 9232. https://doi.org/10.3390/s23229232





