Binary Neural Networks in FPGAs: Architectures, Tool Flows and Hardware Comparisons
Abstract
:1. Introduction
- (1)
- It covers a wide spectrum of AI-enabling technologies for BNNs by summarizing more existing works published up until early 2023.
- (2)
- BNN architectures, models and principles within the main categories of techniques are analyzed and discussed.
- (3)
- It covers the mainstream tool flows for machine learning to FPGAs. It introduces the key design and principle of each tool and also summarizes the workflow of each tool flow.
- (4)
- Identifying current challenges and future directions for BNNs in resource-limited devices, the paper also offers some comparisons of BNN architectures and benchmarking results to give insights into FPGA implementation.
2. Survey of Tool Flows for Machine Learning (ML) to FPGAs
2.1. Resources on Boards
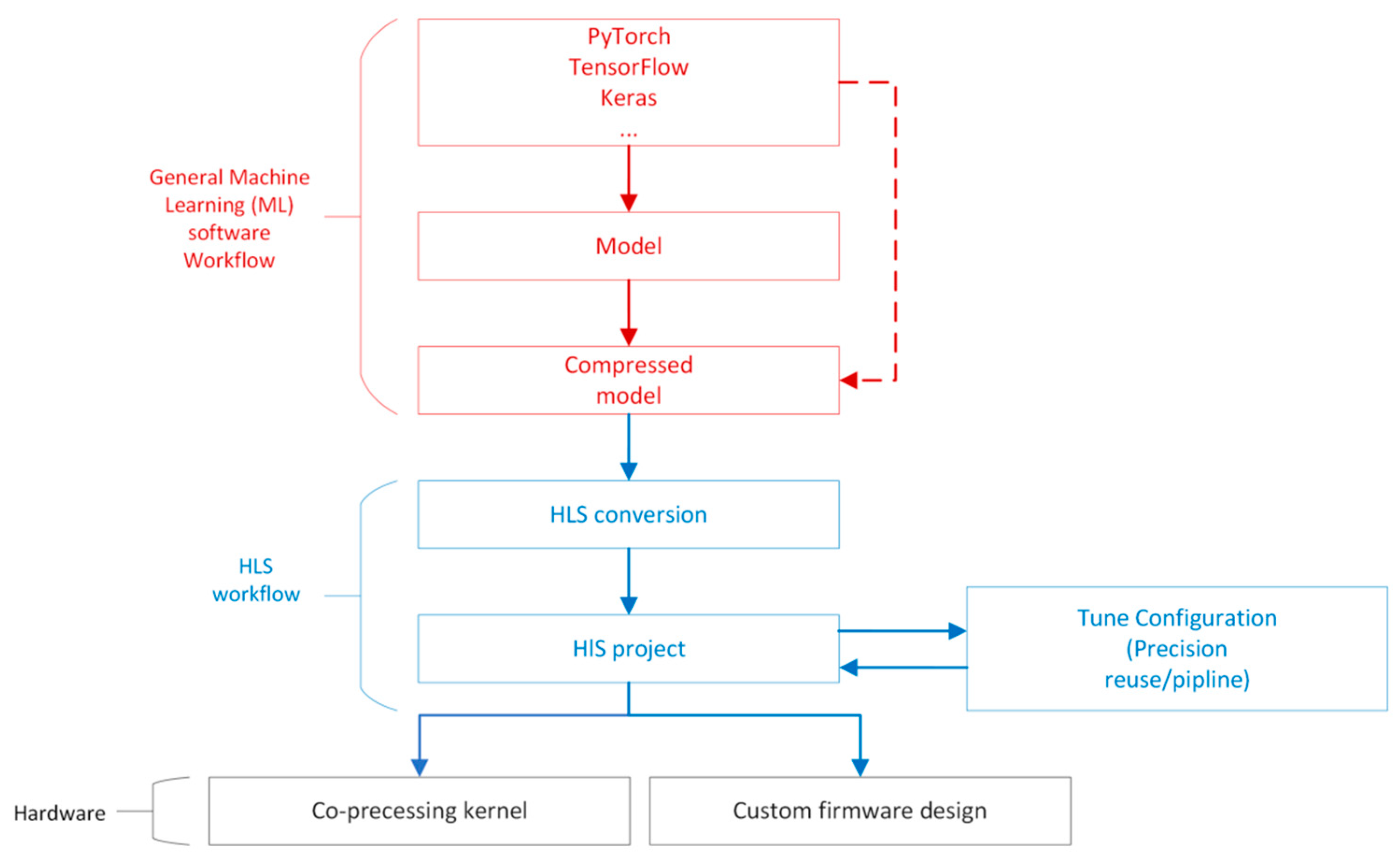
2.2. HLS4ML
- (1)
- Training the model and then undertaking compression (pruning and quantization) using a deep learning framework (Keras, TensorFlow or pytorch).
- (2)
- The HLS4ML package will convert the model to an HLS project and generate an Intellectual Property (IP) module.
- (3)
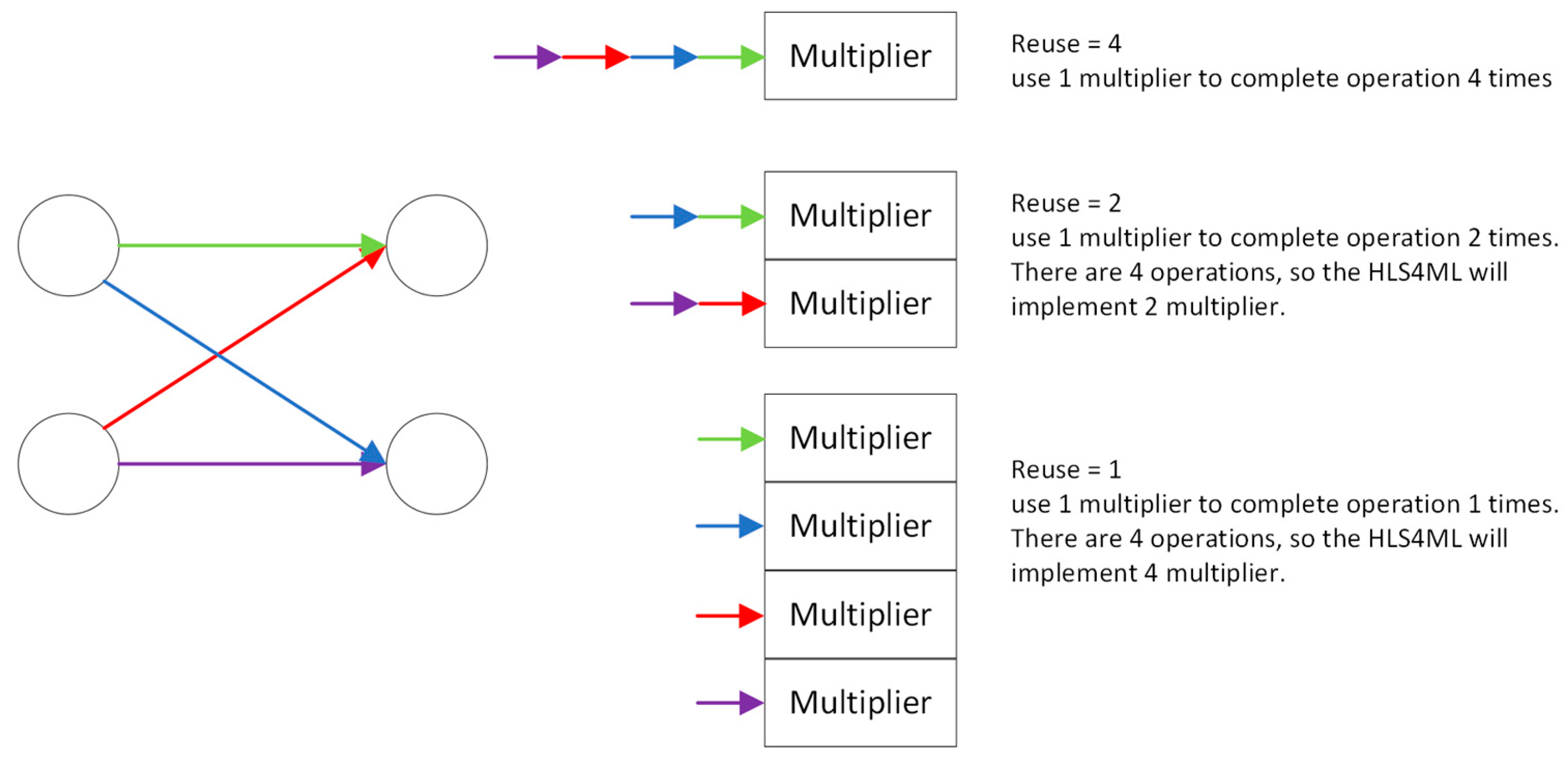
- Each layer and activation can be implemented as a separate configurable module which contains computational modeling of each layer. Configurations include clock period, IO type, bitwidth, reuse factor, and so on.
- (4)
- In Vivado, importing the IP generated by HLS4ML and then connecting to the PS (Processing System) and analyzing the resource cost, e.g., DSP, LUT, BRAM, and so on.
- (5)
- Synthesis and deployment in an FPGA.
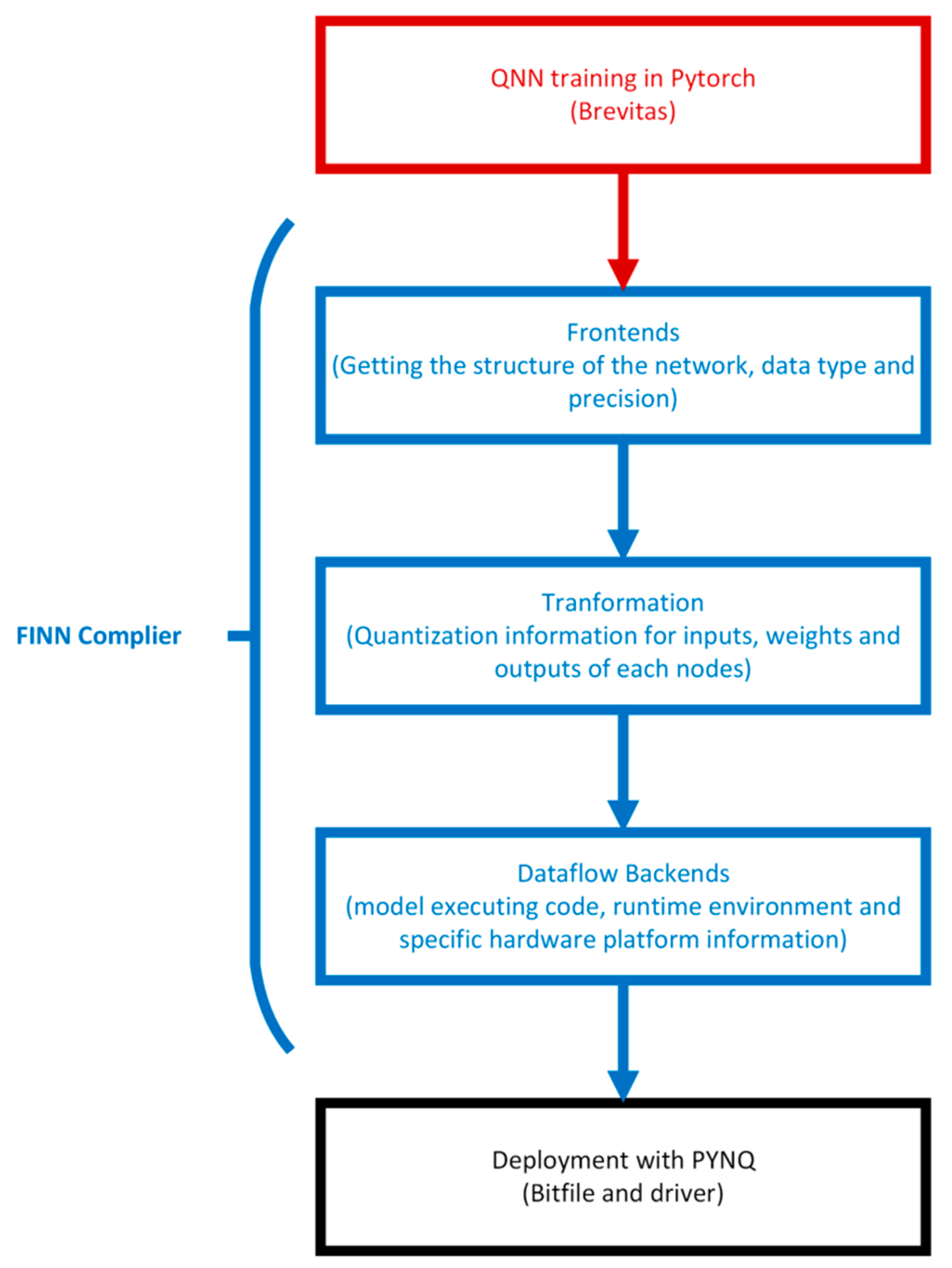
2.3. FINN
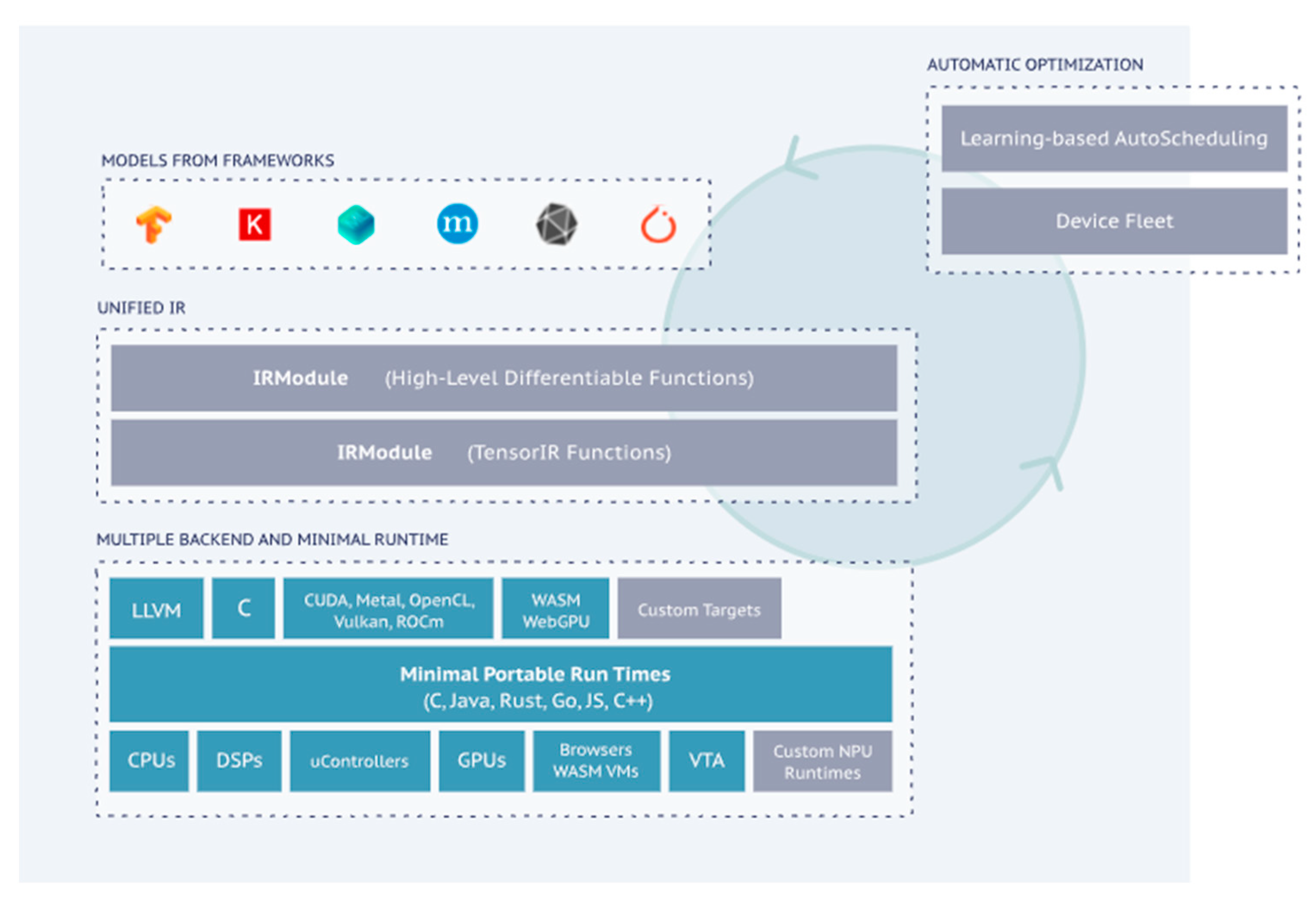
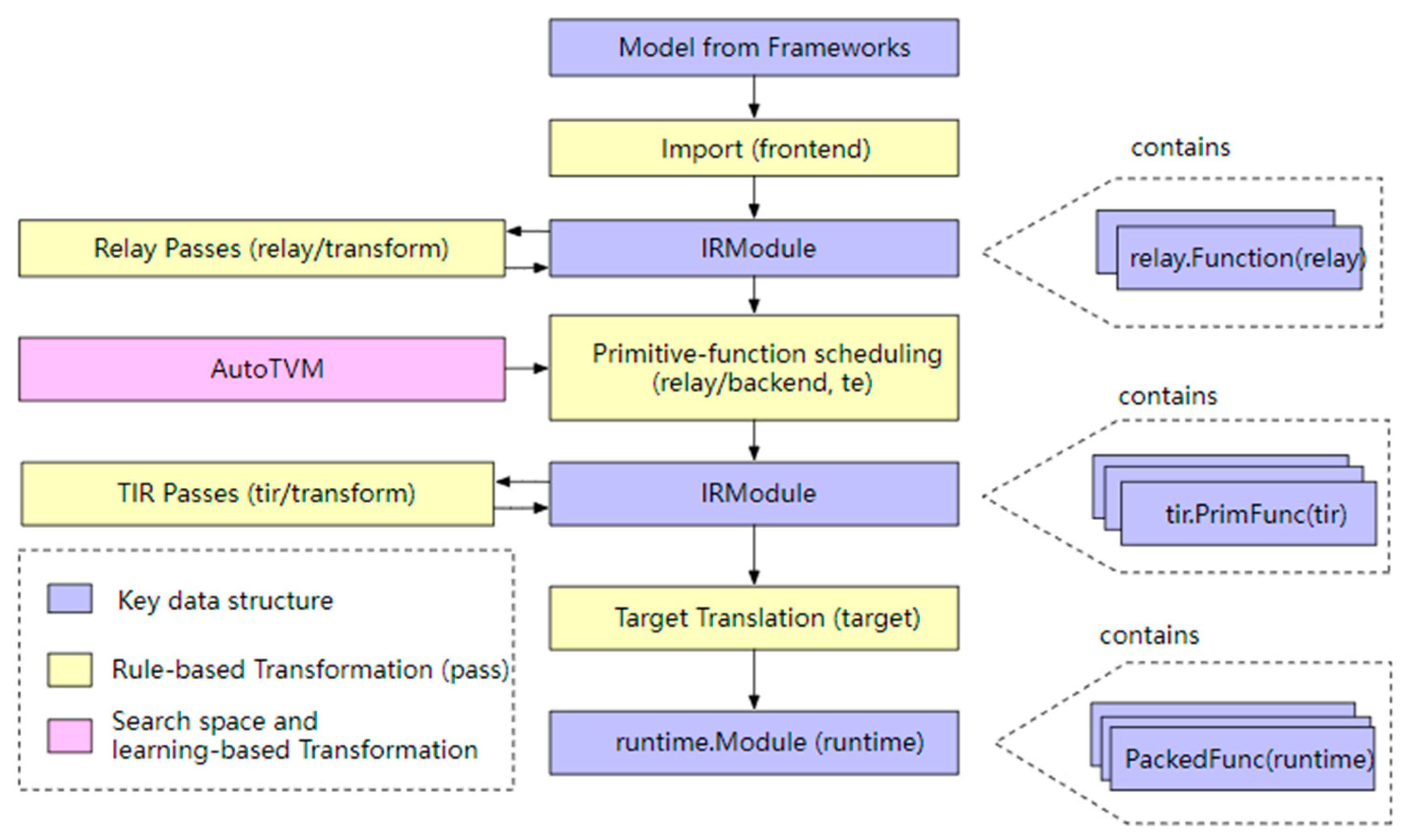
2.4. TVM/VTA
- (1)
- A model from a framework: a model exported from PyTorch, MXNet, etc.
- (2)
- The IR Module (Relay): the intermediate representation (IR) in the level of the TVM graph.
- (3)
- The tensor-level IR (TIR) for TVM, which contains specific scheduling details (loop nesting, parallelism, instruction sets, etc.) for each operator corresponding to the network layer.
- (4)
- The Runtime Module is the lowest-level IR of the TVM compilation stack, directly interfacing with the runtime to run on the target device.
2.5. Optimization
2.5.1. HLS4ML (Optimization for Arbitrary Precision Neural Networks)
- (1)
- Compression: Inspired by [53,54], L1 regularization was added as an additional penalty term to the loss function, L, to obtain a sparse model. L1 regularization has been proven to be a powerful way to generate a sparse weight matrix, which can, in turn, be used for feature selection [55]. The loss function can be expressed as:where is the original loss function, the term after the plus sign is L1 regularization and is the regularization factor. The authors’ experiments indicate that after seven iterations, in a three-hidden-layer model, they achieved a compression rate of nearly 70%.
- (2)
- Quantization: Optimization in terms of quantization is not specialized for BNNs, but it is worth mentioning. HLS4ML adopts fixed-point arithmetic to achieve lower resource costs and latency than floating-point arithmetic.
- (3)
- Parallelization: As described in Section 2.2, the reuse factor is a key optimization for back-end hardware that affects the parallelism of data flow in hardware. Users can choose the corresponding degree of parallelism based on the number of DSPs their platform has in order to achieve the shortest latency and higher resource utilization.
2.5.2. FINN (Special Optimization for BNNs)
- (1)
- XNOR and popcount replace the binary dot product and summation to avoid signed arithmetic. According to experimental results that were implemented by Vivado HLS, compared with signed-accumulate, popcount-accumulate only required nearly half the number of LUTs and FFs.
- (2)
- Converging batch normalization [56] and activation as threshold. Normally, a BNN will insert batch normalization between convolutional or fully connected layers and sign functions. A special threshold activation was designed that allowed the computation of activation using unsigned inputs and avoided batch normalization, which requires the utilization of large amounts of hardware resources during inferences. Experiments indicate that using a 16-bit dot product as input, regular batch normalization with sign activation needs 2 DSPs, 55 FFs and 40 LUTs, but the threshold activation only requires 6 LUTs.
- (3)
- Boolean OR for max pooling. Regularly, the pooling layer will perform before batch normalization and the activation function, which means that the pooling layer will have to deal with non-binarized values. FINN shows that the same outputs can be achieved by max pooling that is performed after activation functions without retrain networks. It further optimized the utilization of hardware resources during inference because max pooling is only performed with binarized values.
2.5.3. TVM/VTA (An Automatic Tool Chain for Various Platforms)
3. Survey of BNN Architectures
3.1. Binarized Neural Networks (BNNs)
3.2. XNOR-Net
3.3. DoReFa-Net
3.4. Bi-Real-Net
3.5. XNOR-Net++
3.6. BinaryDenseNet
- (1)
- The design philosophy of the BNN structure should be based on maximizing information retention.
- (2)
- Compact network structures may not be suitable for BNNs because compact neural network structures are designed to reduce redundancy, whereas BNNs aim to increase the transfer of information.
- (3)
- A bottleneck structure [59] should be avoided as much as possible. A bottleneck structure first decreases the number of channels and then increases them, which may lead to irreversible information loss in BNNs.
- (4)
- The downsampling layer should maintain full precision.
- (5)
- The shortcut structure preserves information and is friendly to BNNs.
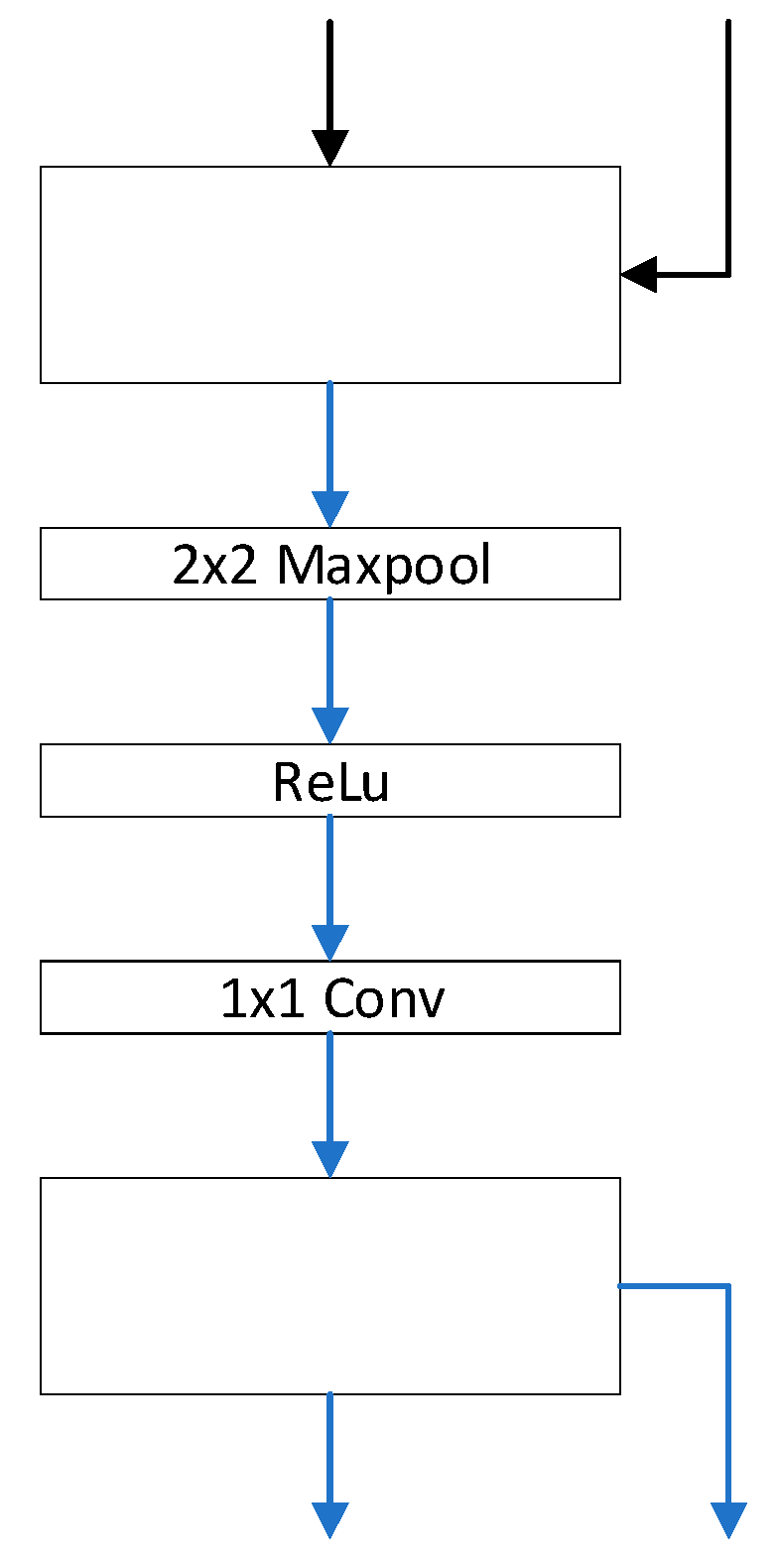
- (6)
- The order of operations to change the shortcut between blocks is Maxpool-ReLU-1x1Conv. The structure presents as Figure 11.
3.7. ReActNet
3.8. IR-Net
- (1)
- Zero mean to maximize the information entropy of the obtained binarized weights;
- (2)
- Unit norm, which makes the full-precision weights involved in binarization more spread out.
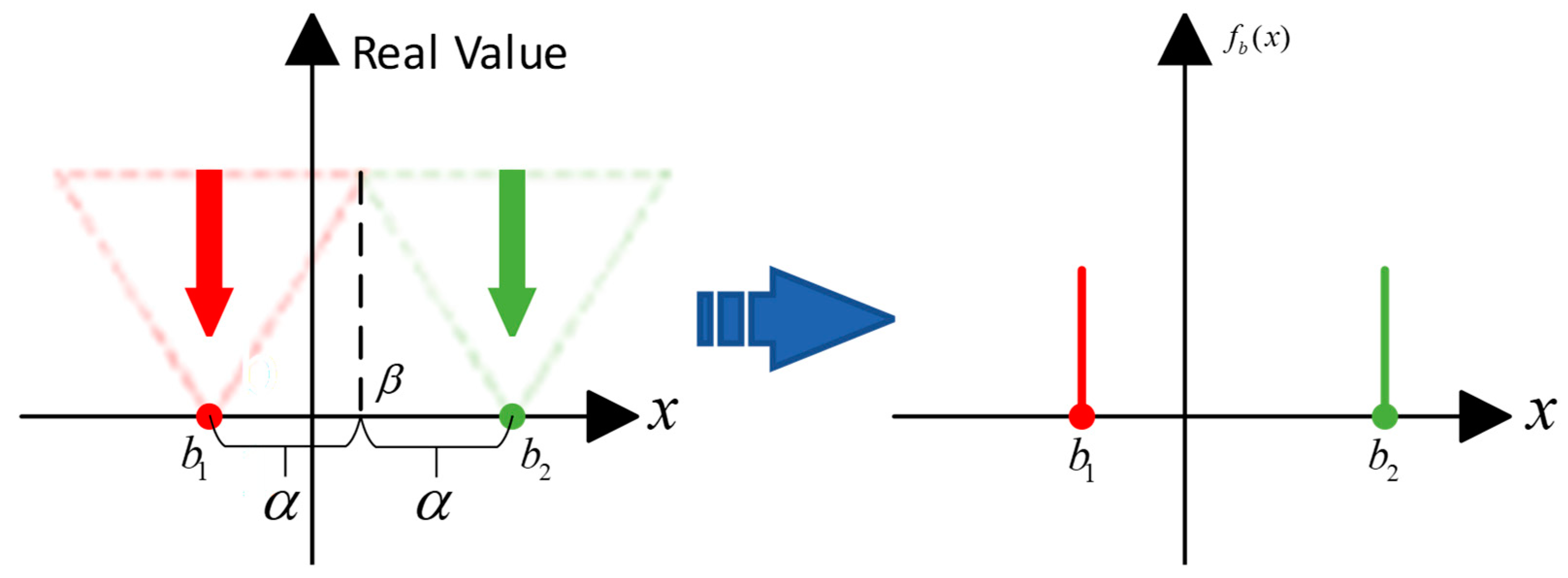
3.9. AdaBin
3.10. DyBNN
3.11. Binarized Ghost Module (BGM)
3.12. IE-Net
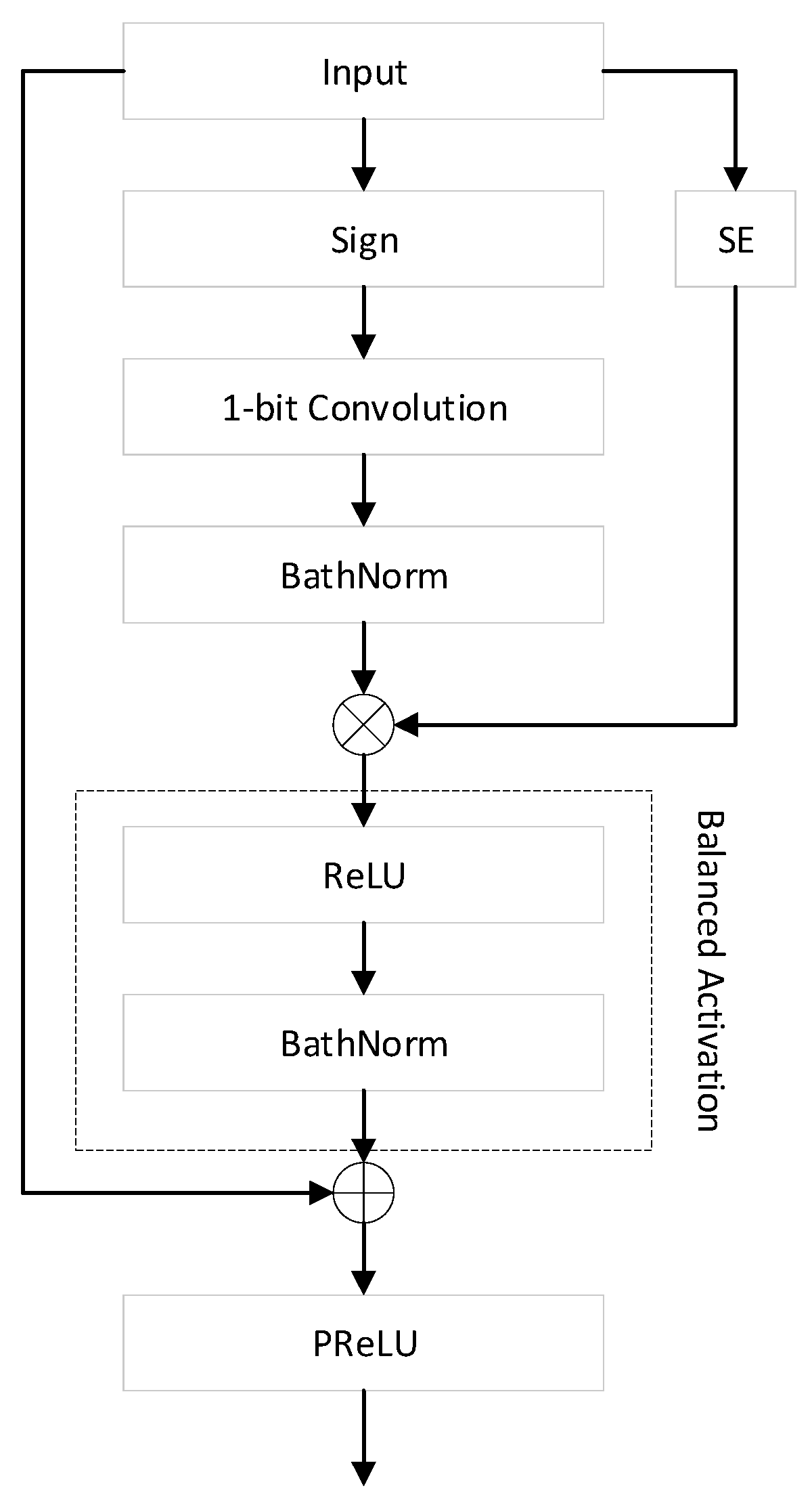
3.13. RB-Net
4. Applications of BNN and FPGA Implementation
5. Comparison of BNN Architectures for FPGA Implementation
5.1. MNIST
5.2. CIFAR10
6. Challenges and Future Directions
6.1. Online Training
6.2. Various Applications
6.3. Generalizability
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Dong, Y.; Liu, Q.; Du, B.; Zhang, L. Weighted Feature Fusion of Convolutional Neural Network and Graph Attention Network for Hyperspectral Image Classification. IEEE Trans. Image Process. 2022, 31, 1559–1572. [Google Scholar] [CrossRef] [PubMed]
- Amudhan, A.N.; Sudheer, A.P. Lightweight and Computationally Faster Hypermetropic Convolutional Neural Network for Small Size Object Detection. Image Vis. Comput. 2022, 119, 104396. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, F.; Lou, L.; Cheng, P.; Huang, Y. Real-Time Detection of Full-Scale Forest Fire Smoke Based on Deep Convolution Neural Network. Remote Sens. 2022, 14, 536. [Google Scholar] [CrossRef]
- Zhao, Z.; Bao, Z.; Zhao, Y.; Zhang, Z.; Cummins, N.; Ren, Z.; Schuller, B. Exploring Deep Spectrum Representations via Attention-Based Recurrent and Convolutional Neural Networks for Speech Emotion Recognition. IEEE Access 2019, 7, 97515–97525. [Google Scholar] [CrossRef]
- Issa, D.; Fatih Demirci, M.; Yazici, A. Speech Emotion Recognition with Deep Convolutional Neural Networks. Biomed. Signal Process. Control. 2020, 59, 101894. [Google Scholar] [CrossRef]
- Bardou, D.; Zhang, K.; Ahmad, S.M. Lung Sounds Classification Using Convolutional Neural Networks. Artif. Intell. Med. 2018, 88, 58–69. [Google Scholar] [CrossRef] [PubMed]
- Qin, H.; Gong, R.; Liu, X.; Bai, X.; Song, J.; Sebe, N. Binary Neural Networks: A Survey. Pattern Recognit. 2020, 105, 107281. [Google Scholar] [CrossRef]
- Courbariaux, M.; Bengio, Y.; David, J.-P. BinaryConnect: Training Deep Neural Networks with Binary Weights during Propagations. arXiv 2016, arXiv:1511.00363. [Google Scholar]
- Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1. arXiv 2016, arXiv:1602.02830. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. DoReFa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients. arXiv 2018, arXiv:1606.06160. [Google Scholar]
- Liu, Z.; Wu, B.; Luo, W.; Yang, X.; Liu, W.; Cheng, K.-T. Bi-Real Net: Enhancing the Performance of 1-Bit CNNs with Improved Representational Capability and Advanced Training Algorithm. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 722–737. [Google Scholar]
- Bethge, J.; Yang, H.; Bornstein, M.; Meinel, C. BinaryDenseNet: Developing an Architecture for Binary Neural Networks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1951–1960. [Google Scholar]
- Liu, Z.; Shen, Z.; Savvides, M.; Cheng, K.-T. ReActNet: Towards Precise Binary Neural Network with Generalized Activation Functions. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–18 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Springer International Publishing: Cham, Germany, 2020; pp. 143–159. [Google Scholar]
- Tu, Z.; Chen, X.; Ren, P.; Wang, Y. AdaBin: Improving Binary Neural Networks with Adaptive Binary Sets. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Germany, 2022; pp. 379–395. [Google Scholar]
- Zhang, J.; Su, Z.; Feng, Y.; Lu, X.; Pietikäinen, M.; Liu, L. Dynamic Binary Neural Network by Learning Channel-Wise Thresholds. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 1885–1889. [Google Scholar]
- Ding, R.; Liu, H.; Zhou, X. IE-Net: Information-Enhanced Binary Neural Networks for Accurate Classification. Electronics 2022, 11, 937. [Google Scholar] [CrossRef]
- Qin, H.; Gong, R.; Liu, X.; Shen, M.; Wei, Z.; Yu, F.; Song, J. Forward and Backward Information Retention for Accurate Binary Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: Seattle, WA, USA, 2020; pp. 2247–2256. [Google Scholar]
- Sun, R.; Zou, W.; Zhan, Y. “Ghost” and Attention in Binary Neural Network. IEEE Access 2022, 10, 60550–60557. [Google Scholar] [CrossRef]
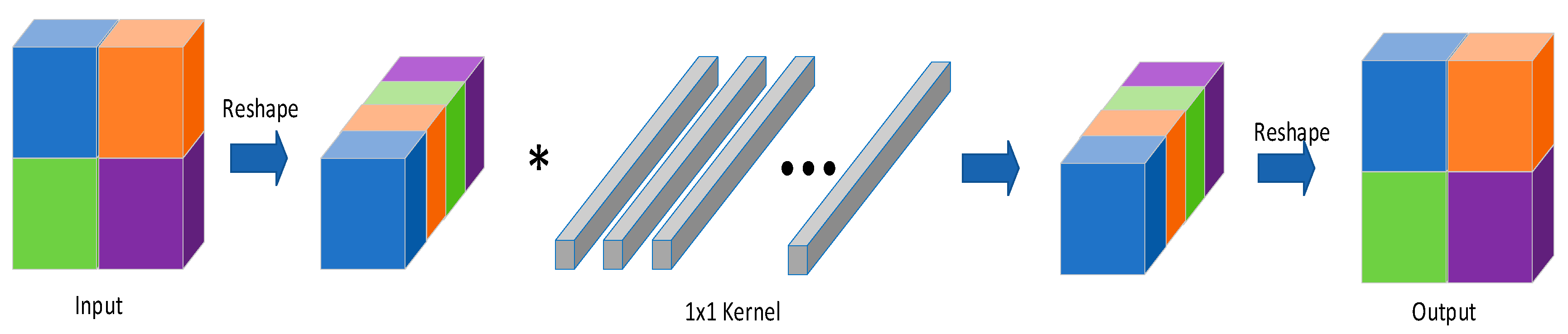
- Liu, C.; Ding, W.; Chen, P.; Zhuang, B.; Wang, Y.; Zhao, Y.; Zhang, B.; Han, Y. RB-Net: Training Highly Accurate and Efficient Binary Neural Networks with Reshaped Point-Wise Convolution and Balanced Activation. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 6414–6424. [Google Scholar] [CrossRef]
- Yuan, C.; Agaian, S.S. A Comprehensive Review of Binary Neural Network. Artif. Intell. Rev. 2023, 56, 1–65. [Google Scholar] [CrossRef]
- Sayed, R.; Azmi, H.; Shawkey, H.; Khalil, A.H.; Refky, M. A Systematic Literature Review on Binary Neural Networks. IEEE Access 2023, 11, 27546–27578. [Google Scholar] [CrossRef]
- Simons, T.; Lee, D.-J. A Review of Binarized Neural Networks. Electronics 2019, 8, 661. [Google Scholar] [CrossRef]
- Huang, C.-H. An FPGA-Based Hardware/Software Design Using Binarized Neural Networks for Agricultural Applications: A Case Study. IEEE Access 2021, 9, 26523–26531. [Google Scholar] [CrossRef]
- Fasfous, N.; Vemparala, M.-R.; Frickenstein, A.; Frickenstein, L.; Badawy, M.; Stechele, W. BinaryCoP: Binary Neural Network-Based COVID-19 Face-Mask Wear and Positioning Predictor on Edge Devices. In Proceedings of the 2021 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Portland, OR, USA, 17–21 June 2021; pp. 108–115. [Google Scholar]
- Penkovsky, B.; Bocquet, M.; Hirtzlin, T.; Klein, J.-O.; Nowak, E.; Vianello, E.; Portal, J.-M.; Querlioz, D. In-Memory Resistive RAM Implementation of Binarized Neural Networks for Medical Applications. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 690–695. [Google Scholar]
- Zhang, R.; Chung, A.C.S. MedQ: Lossless Ultra-Low-Bit Neural Network Quantization for Medical Image Segmentation. Med. Image Anal. 2021, 73, 102200. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Wu, D.; Zhou, Y.; Li, B.; Wang, W.; Meng, D. Binary Neural Network Hashing for Image Retrieval. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Montréal, QC, Canada, 11–15 July 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 1318–1327. [Google Scholar]
- Kung, J.; Zhang, D.; van der Wal, G.; Chai, S.; Mukhopadhyay, S. Efficient Object Detection Using Embedded Binarized Neural Networks. J. Sign. Process. Syst. 2018, 90, 877–890. [Google Scholar] [CrossRef]
- Bulat, A.; Tzimiropoulos, G. Binarized Convolutional Landmark Localizers for Human Pose Estimation and Face Alignment with Limited Resources. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 3726–3734. [Google Scholar]
- Sun, S.; Yin, Y.; Wang, X.; Xu, D.; Wu, W.; Gu, Q. Fast Object Detection Based on Binary Deep Convolution Neural Networks. CAAI Trans. Intell. Technol. 2018, 3, 191–197. [Google Scholar] [CrossRef]
- Leng, C.; Li, H.; Zhu, S.; Jin, R. Extremely Low Bit Neural Network: Squeeze the Last Bit Out with ADMM 2017. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Kim, H.; Choi, K. The Implementation of a Power Efficient BCNN-Based Object Detection Acceleration on a Xilinx FPGA-SoC. In Proceedings of the 2019 International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Atlanta, GA, USA, 14–17 July 2019; pp. 240–243. [Google Scholar]
- Zhuang, B.; Shen, C.; Tan, M.; Chen, P.; Liu, L.; Reid, I. Structured Binary Neural Networks for Image Recognition. Int. J. Comput. Vis. 2022, 130, 2081–2102. [Google Scholar] [CrossRef]
- Frickenstein, A.; Vemparala, M.-R.; Mayr, J.; Nagaraja, N.-S.; Unger, C.; Tombari, F.; Stechele, W. Binary DAD-Net: Binarized Driveable Area Detection Network for Autonomous Driving. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2295–2301. [Google Scholar]
- Qin, H.; Cai, Z.; Zhang, M.; Ding, Y.; Zhao, H.; Yi, S.; Liu, X.; Su, H. BiPointNet: Binary Neural Network for Point Clouds. arXiv 2021, arXiv:2010.05501. [Google Scholar]
- Aarrestad, T.; Loncar, V.; Ghielmetti, N.; Pierini, M.; Summers, S.; Ngadiuba, J.; Petersson, C.; Linander, H.; Iiyama, Y.; Guglielmo, G.D.; et al. Fast Convolutional Neural Networks on FPGAs with Hls4ml. Mach. Learn. Sci. Technol. 2021, 2, 045015. [Google Scholar] [CrossRef]
- Umuroglu, Y.; Fraser, N.J.; Gambardella, G.; Blott, M.; Leong, P.; Jahre, M.; Vissers, K. FINN: A Framework for Fast, Scalable Binarized Neural Network Inference. In Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22 February 2017; pp. 65–74. [Google Scholar]
- Blott, M.; Preusser, T.; Fraser, N.; Gambardella, G.; O’Brien, K.; Umuroglu, Y. FINN-R: An End-to-End Deep-Learning Framework for Fast Exploration of Quantized Neural Networks. ACM Trans. Reconfigurable Technol. Syst. 2018, 11, 1–23. [Google Scholar] [CrossRef]
- Chen, T.; Moreau, T.; Jiang, Z.; Zheng, L.; Yan, E.; Shen, H.; Cowan, M.; Wang, L.; Hu, Y.; Ceze, L.; et al. {TVM}: An Automated {End-to-End} Optimizing Compiler for Deep Learning. In 13th USENIX Symposium on Operating Systems Design and Implementation (OSDI 18); USENIX: Berkeley, CA, USA, 2018; pp. 578–594. [Google Scholar]
- Coelho, C.N., Jr.; Kuusela, A.; Li, S.; Zhuang, H.; Aarrestad, T.; Loncar, V.; Ngadiuba, J.; Pierini, M.; Pol, A.A.; Summers, S. Automatic Heterogeneous Quantization of Deep Neural Networks for Low-Latency Inference on the Edge for Particle Detectors. Nat. Mach. Intell. 2021, 3, 675–686. [Google Scholar] [CrossRef]
- Ngadiuba, J.; Loncar, V.; Pierini, M.; Summers, S.; Guglielmo, G.D.; Duarte, J.; Harris, P.; Rankin, D.; Jindariani, S.; Liu, M.; et al. Compressing Deep Neural Networks on FPGAs to Binary and Ternary Precision with Hls4ml. Mach. Learn. Sci. Technol. 2020, 2, 015001. [Google Scholar] [CrossRef]
- Duarte, J.; Han, S.; Harris, P.; Jindariani, S.; Kreinar, E.; Kreis, B.; Ngadiuba, J.; Pierini, M.; Rivera, R.; Tran, N.; et al. Fast Inference of Deep Neural Networks in FPGAs for Particle Physics. J. Inst. 2018, 13, P07027. [Google Scholar] [CrossRef]
- Deng, L. The MNIST Database of Handwritten Digit Images for Machine Learning Research [Best of the Web]. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
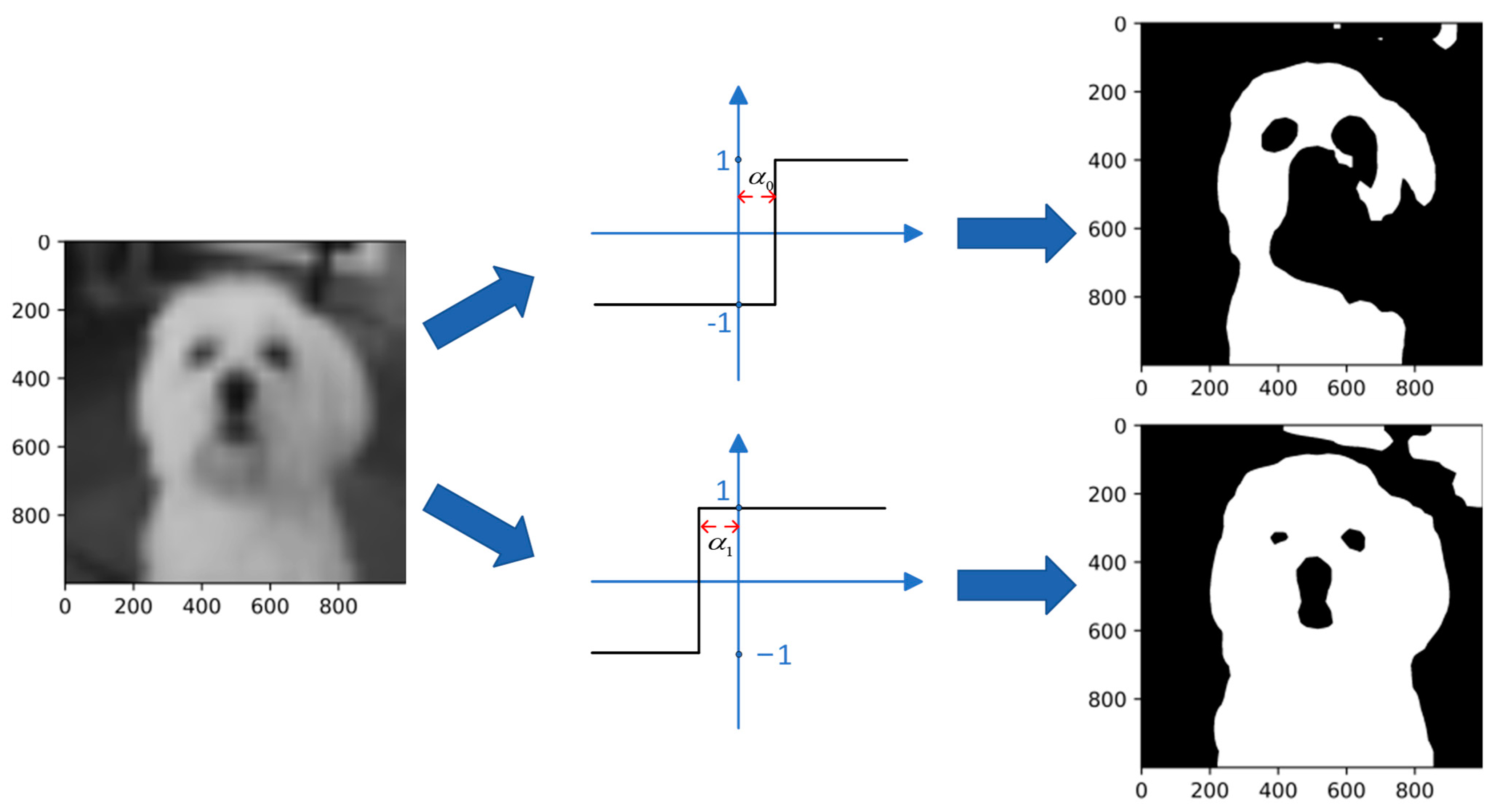
- Ghielmetti, N.; Loncar, V.; Pierini, M.; Roed, M.; Summers, S.; Aarrestad, T.; Petersson, C.; Linander, H.; Ngadiuba, J.; Lin, K.; et al. Real-Time Semantic Segmentation on FPGAs for Autonomous Vehicles with Hls4ml. Mach. Learn. Sci. Technol. 2022, 3, 045011. [Google Scholar] [CrossRef]
- Paszke, A.; Chaurasia, A.; Kim, S.; Culurciello, E. ENet: A Deep Neural Network Architecture for Real-Time Semantic Segmentation. arXiv 2016, arXiv:1606.02147. [Google Scholar]
- Preußer, T.B. Generic and Universal Parallel Matrix Summation with a Flexible Compression Goal for Xilinx FPGAs. In Proceedings of the 2017 27th International Conference on Field Programmable Logic and Applications (FPL), Ghent, Belgium, 4–8 September 2017; pp. 1–7. [Google Scholar]
- Umuroglu, Y.; Jahre, M. Streamlined Deployment for Quantized Neural Networks. arXiv 2018, arXiv:1709.04060. [Google Scholar]
- Apache TVM. Available online: https://tvm.apache.org/ (accessed on 19 August 2023).
- Moreau, T.; Chen, T.; Vega, L.; Roesch, J.; Yan, E.; Zheng, L.; Fromm, J.; Jiang, Z.; Ceze, L.; Guestrin, C.; et al. A Hardware–Software Blueprint for Flexible Deep Learning Specialization. IEEE Micro 2019, 39, 8–16. [Google Scholar] [CrossRef]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. arXiv 2015, arXiv:151000149. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning Both Weights and Connections for Efficient Neural Networks. Adv. Neural Inf. Process. Syst. 2015, 28, 2–9. [Google Scholar]
- Ng, A.Y. Feature Selection, L1 vs. L2 Regularization, and Rotational Invariance. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; Association for Computing Machinery: New York, NY, USA, 2004; p. 78. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Chen, T.; Zheng, L.; Yan, E.; Jiang, Z.; Moreau, T.; Ceze, L.; Guestrin, C.; Krishnamurthy, A. Learning to Optimize Tensor Programs. arXiv 2019, arXiv:1805.08166. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. Available online: https://arxiv.org/abs/1512.03385v1 (accessed on 11 August 2023).
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014, arXiv:1409.4842. [Google Scholar]
- Bulat, A.; Tzimiropoulos, G. XNOR-Net++: Improved Binary Neural Networks. arXiv 2019, arXiv:1909.13863. [Google Scholar]
- Bethge, J.; Bartz, C.; Yang, H.; Chen, Y.; Meinel, C. MeliusNet: Can Binary Neural Networks Achieve MobileNet-Level Accuracy? arXiv 2020, arXiv:2001.05936v2. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Han, K.; Wang, Y.; Tian, Q.; Guo, J.; Xu, C.; Xu, C. GhostNet: More Features from Cheap Operations. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1577–1586. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Liu, Y.; Shao, Z.; Teng, Y.; Hoffmann, N. NAM: Normalization-Based Attention Module. arXiv 2021, arXiv:2111.12419. [Google Scholar]
- Bengio, Y.; Léonard, N.; Courville, A. Estimating or Propagating Gradients through Stochastic Neurons for Conditional Computation. arXiv 2013, arXiv:1308.3432. [Google Scholar]
- Martinez, B.; Yang, J.; Bulat, A.; Tzimiropoulos, G. Training Binary Neural Networks with Real-to-Binary Convolutions. arXiv 2020, arXiv:2003.11535. [Google Scholar]
- Xin, J.; Wang, N.; Jiang, X.; Li, J.; Huang, H.; Gao, X. Binarized Neural Network for Single Image Super Resolution. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Germany, 2020; Volume 12349, pp. 91–107. ISBN 978-3-030-58547-1. [Google Scholar]
- Hirtzlin, T.; Bocquet, M.; Penkovsky, B.; Klein, J.-O.; Nowak, E.; Vianello, E.; Portal, J.-M.; Querlioz, D. Digital Biologically Plausible Implementation of Binarized Neural Networks with Differential Hafnium Oxide Resistive Memory Arrays. Front. Neurosci. 2019, 13, 1383. [Google Scholar] [CrossRef] [PubMed]
- Brahma, K.; Kumar, V.; Samir, A.E.; Chandrakasan, A.P.; Eldar, Y.C. Efficient Binary Cnn for Medical Image Segmentation. In Proceedings of the 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), Nice, France, 13–16 April 2021; pp. 817–821. [Google Scholar]
- Tong, L.; Chen, Y.; Xu, T.; Kang, Y. Fault Diagnosis for Modular Multilevel Converter (MMC) Based on Deep Learning: An Edge Implementation Using Binary Neural Network. IEEE J. Emerg. Sel. Top. Power Electron. 2022. [Google Scholar] [CrossRef]
- Cladera, F.; Bisulco, A.; Kepple, D.; Isler, V.; Lee, D.D. On-Device Event Filtering with Binary Neural Networks for Pedestrian Detection Using Neuromorphic Vision Sensors. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 3084–3088. [Google Scholar]
- Mani, V.R.S.; Saravanaselvan, A.; Arumugam, N. Performance Comparison of CNN, QNN and BNN Deep Neural Networks for Real-Time Object Detection Using ZYNQ FPGA Node. Microelectron. J. 2022, 119, 105319. [Google Scholar] [CrossRef]
- Vita, A.D.; Pau, D.; Benedetto, L.D.; Rubino, A.; Pétrot, F.; Licciardo, G.D. Low Power Tiny Binary Neural Network with Improved Accuracy in Human Recognition Systems. In Proceedings of the 2020 23rd Euromicro Conference on Digital System Design (DSD), Kranj, Slovenia, 26–28 August 2020; pp. 309–315. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Yu, S.; Li, Z.; Chen, P.-Y.; Wu, H.; Gao, B.; Wang, D.; Wu, W.; Qian, H. Binary Neural Network with 16 Mb RRAM Macro Chip for Classification and Online Training. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 16.2.1–16.2.4. [Google Scholar]
- Vorabbi, L.; Maltoni, D.; Santi, S. On-Device Learning with Binary Neural Networks. arXiv 2023, arXiv:2308.15308. [Google Scholar]




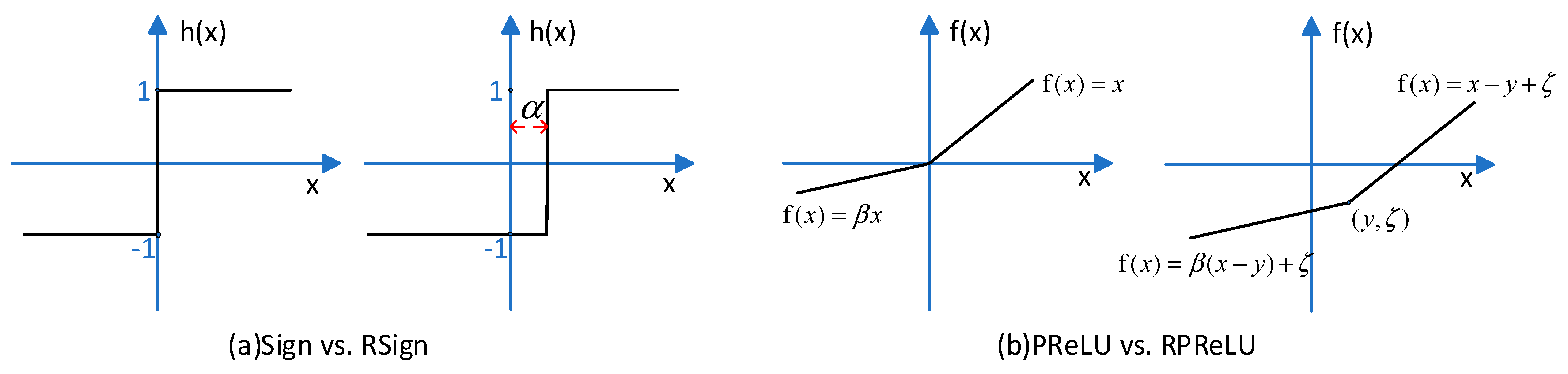



| Method | Architecture | Top-1 Accuracy (%) | Top-5 Accuracy (%) | ) | ) | ) |
|---|---|---|---|---|---|---|
| BWM [12] | AlexNet | 56.8 | 79.4 | 1.70 | 1.20 | 1.47 |
| ResNet-18 [59] | 60.8 | 83.0 | - | - | - | |
| GoogLeNet [60] | 65.5 | 86.1 | - | - | - | |
| XNOR [12] | AlexNet | 44.2 | 69.2 | - | - | - |
| ResNet-18 | 51.2 | 73.2 | 1.70 | 1.33 | 1.60 | |
| Bi-Real-Net [14] | ResNet-18 | 56.4 | 79.5 | 1.68 | 1.39 | 1.63 |
| ResNet-34 | 69.2 | 83.9 | 3.53 | 1.39 | 1.93 | |
| XNOR++ [61] | ResNet-18 () | 57.1 | 79.9 | 1.695 | 1.33 | 1.60 |
| BinaryDenseNet [15] | BinaryDenseNet28 | 60.7 | 82.4 | - | - | 2.58 |
| BinaryDenseNet37 | 62.5 | 83.9 | - | - | 2.71 | |
| BinaryDenseNet37-dilated | 63.7 | 84.7 | - | - | 2.20 | |
| MeliusNet [62] | MeliusnetC | 64.1 | - | 5.47 | 1.29 | 2.14 |
| Meliusnet42 | 69.2 | - | 9.69 | 1.74 | 3.25 | |
| Meliusnet59 | 71.0 | - | 18.3 | 2.45 | 5.32 | |
| ReActNet [16] | ReActNet-A(based on MobileNet-v1 [63]) | 69.4 | - | 4.82 | 0.12 | 0.87 |
| ReActNet-B(based on MobileNet-v1) | 70.1 | - | 4.69 | 0.44 | 1.63 | |
| ReActNet-C(based on MobileNet-v1) | 71.4 | - | 4.69 | 1.40 | 2.14 | |
| IR-Net | ResNet-18 | 58.1 | 80.0 | 1.68 | 1.40 | 1.67 |
| ResNet-34 | 62.9 | 84.1s | 1.93 | |||
| AdaBin [17] | AlexNet | 53.9 | 77.6 | - | - | - |
| ResNet-18 | 63.1 | 84.3 | 1.69 | 1.410 | 1.67 | |
| ReActNet | 66.4 | 86.5 | - | - | - | |
| ResNet-34 | 66.4 | 86.6 | - | - | - | |
| DyBNN [18] | ResNet-18 | 67.4 | 87.4 | - | - | - |
| MobileNet-v1 | 71.2 | 89.8 | - | - | - | |
| BGM [21] | ReActNet-B(based on MobileNet-v1) | 71.4 | - | - | - | - |
| IE-Net | ResNet-18 | 61.4 | 83.0 | - | 1.63 | - |
| ResNet-34 | 64.6 | 85.2 | - | 1.93 | - | |
| RB-Net | ResNet-18 | 66.8 | 87.1 | - | 0.52 | - |
| ResNet-34 | 70.2 | 89.2 | - | 0.71 | - |
| PYNQ-Z2 | Z7P | |
|---|---|---|
| (XC7Z020CLG400-1) | (XCZU7EV-2FFVC1156-MPSoC) | |
| System Logic Units | 13.3 K | 504 K |
| DSPs | 220 | 1728 |
| LUTs | 5.3 K | 230.4 K |
| LUTRAM | 1.74 K | 101.76 K |
| FF | 10.64 K | 460.8 K |
| Block RAM (BRAM) | 140 | 312 |
| Model | Board | Quantization Method | Accuracy | LUTs (Utilization) | LUTRAM | FF | BRAM | On-Chip Power (W) |
|---|---|---|---|---|---|---|---|---|
| MLP-4 | Z7P | BNN (non-scaling) | 88% ± 1% | 14,222 (6%) | 1707 (1.6%) | 22,853 (5%) | 13.5 (4%) | 3.556 |
| MLP-4 | PYNQ-Z2 | BNN (non-scaling) | 88% ± 1% | 11,579 (22%) | 1197 (6%) | 17,981 (16%) | 14.5 (10%) | 1.598 |
| CNV-4 | Z7P | BNN (non-scaling) | 92% ± 1% | 21,417 (9%) | 3734 (4%) | 29,899 (7%) | 14 (5%) | 3.721 |
| CNV-4 | PYNQ-Z2 | BNN (non-scaling) | 92% ± 1% | 18,773 (35%) | 2198 (12%) | 24,925 (23%) | 42(30%) | 1.808 |
| Model | Board | Quantization Method | Accuracy | BRAM-18K (Utilization) | DSP48E | FF | LUT | Reuse Factor | Latency (ms) [min, max] |
|---|---|---|---|---|---|---|---|---|---|
| CNV-4 | Z7P | Baseline (non-binarized) | 98% ± 1% | 83 (13%) | 3734 (216%) | 57,520 (12%) | 178,939 (77%) | 128 | - |
| CNV-4 | Z7P | BNN (non-scaling) | 76% ± 1% | 103 (16%) | 81 (4%) | 41,158 (8%) | 61,108 (26%) | 64 | [0.217, 0.219] |
| CNV-4 | Z7P | XNOR-Net | 82% ± 1% | 103 (16%) | 81 (4%) | 41,047 (8%) | 61,172 (26%) | 64 | [0.217, 0.219] |
| CNV-4 | Z7P | XNOR-Net (integer shifting scaling factor) | 83% ± 1% | 296(16%) | 502 (4%) | 58,587 (8%) | 83,152 (26%) | 8 | [0.164, 0.166] |
| CNV-4 | Z7P | XNOR-Net (integer shifting scaling factor) | 83% ± 1% | 181 (29%) | 251 (14%) | 46,028 (9%) | 72,021 (31%) | 16 | [0.170, 0.172] |
| CNV-4 | Z7P | XNOR-Net (integer shifting scaling factor) | 83% ± 1% | 139 (22%) | 161 (9%) | 43,170 (9%) | 64,916 (28%) | 32 | [0.186, 0.188] |
| CNV-4 | Z7P | XNOR-Net (integer shifting scaling factor) | 83% ± 1% | 103 (16%) | 81 (4%) | 41,045 (8%) | 61,048 (26%) | 64 | [0.217, 0.219] |
| Model | Board (Tool) | Quantization Method | Accuracy | LUTs (Utilization) | LUT RAM | FF | BRAM | On-Chip Power (W) | Time (s/Picture) |
|---|---|---|---|---|---|---|---|---|---|
| CNV-8 VGG-small | Z7P | BNN | 78% ± 2% | 41,713 (21%) | 3755 (4%) | 53,280 (12%) | 194 (62%) | 4.473 | 0.35 |
| CNV-8 VGG-small (half the number of channels) | Z7P | BNN | 75% ± 2% | 27,179 (12%) | 2653 (3%) | 32,359 (7%) | 77 (25%) | 3.901 | 0.16 |
| CNV-8 VGG-small (half the number of channels) | PYNQ-Z2 | BNN | 75% ± 2% | 25,318 (48%) | 2285 (13%) | 31,608 (29%) | 90 (64%) | 1.955 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Seng, K.P.; Ang, L.M.; Smith, J. Binary Neural Networks in FPGAs: Architectures, Tool Flows and Hardware Comparisons. Sensors 2023, 23, 9254. https://doi.org/10.3390/s23229254
Su Y, Seng KP, Ang LM, Smith J. Binary Neural Networks in FPGAs: Architectures, Tool Flows and Hardware Comparisons. Sensors. 2023; 23(22):9254. https://doi.org/10.3390/s23229254
Chicago/Turabian StyleSu, Yuanxin, Kah Phooi Seng, Li Minn Ang, and Jeremy Smith. 2023. "Binary Neural Networks in FPGAs: Architectures, Tool Flows and Hardware Comparisons" Sensors 23, no. 22: 9254. https://doi.org/10.3390/s23229254
APA StyleSu, Y., Seng, K. P., Ang, L. M., & Smith, J. (2023). Binary Neural Networks in FPGAs: Architectures, Tool Flows and Hardware Comparisons. Sensors, 23(22), 9254. https://doi.org/10.3390/s23229254







