Dynamic Condition Adversarial Adaptation for Fault Diagnosis of Wind Turbine Gearbox
Abstract
:1. Introduction
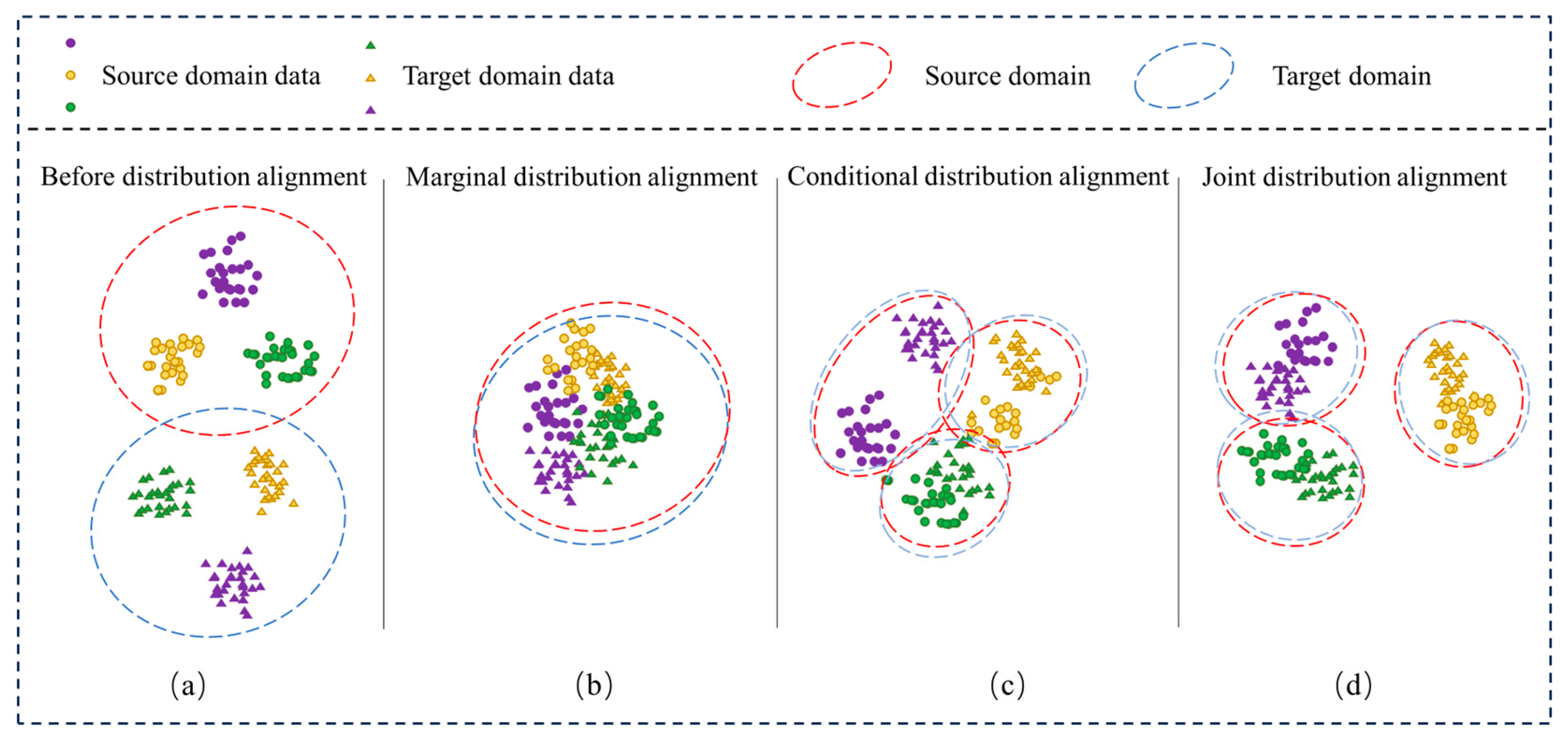
- The DCAA method jointly adjusts the marginal and conditional distributions between two different domains. By introducing dynamic weighting factors, it dynamically measures the relative importance of marginal and conditional alignment, enhancing the accuracy of feature distribution alignment.
- The method employs information entropy as a metric to assess the reliability of classifier predictions. It prioritizes using data with high confidence for domain adaptation training, thereby improving the fault diagnosis accuracy under complex working conditions.
- Through a series of experiments, the effectiveness of DCAA is demonstrated in both WT gearbox and bearing fault diagnosis scenarios. Furthermore, the method’s superiority is validated by comparing it with other domain adaptation approaches.
2. Related Work
2.1. Problem Description
2.2. Conditional Adversarial Domain Adaptation
3. Proposed Method
3.1. Subsection
3.2. Optimization Strategy
3.2.1. Classifier G
3.2.2. Domain Discriminator D1
3.2.3. Conditional Domain Discriminator D2
3.2.4. Dynamic Weight Factor
- (a)
- Information entropy weight ω1: The information entropy weight factor ω1 is used in the model to dynamically adjust the training weights of the classifier and discriminator. It is introduced to handle cases where certain training data may have high classification error due to noise or other factors. These data can negatively impact the alignment of classes in the domain discriminator and result in suboptimal transfer performance. The information entropy is calculated as the sum of the negative log likelihood of the classifier’s predicted probabilities for each class., i.e.,
- (b)
- Cross-entropy weight ω2: In this part, the cross-entropy weight ω2 is introduced to dynamically balance the relative importance of domain alignment and class alignment. When the feature marginal distributions between domains are far apart, domain alignment is prioritized to reduce the marginal distribution distance. On the other hand, when the feature marginal distributions are close, class alignment is prioritized to reduce the conditional distribution distance. By dynamically adjusting the weight, the convergence speed and class alignment performance of the model can be improved. The specific method is as follows.
3.2.5. Strategy
3.3. Optimization Algorithm
| Algorithm 1: Training process of CDAA |
| #pre-train feature extractor F and classifier G |
| Input: source domain data and labels, F, G |
| for i in [0, epoch1] do: |
| The classification loss is computed using Equation (4). |
| Model parameters are updated utilizing Equation (16). |
| end |
| Return: pre-trained F, G. |
| #pre-train Domain Discriminator D1 and Conditional Domain Discriminator D2. |
| Input: source domain data, target domain data, D1, D2. |
| for i in [0, epoch1] do: |
| The domain losses for D1 and D2 are computed using Equations (5) and (6), respectively. |
| Parameters of D1 and D2 are updated using Equations (16) and (17), respectively. |
| end |
| Return: pre-trained D1, D2. |
| # Adversarial training |
| Input: source domain data and labels, target domain data, pre-trained F, G, D1 and D2. |
| for i in [0, epoch2] do: |
| Parameters are optimized using Equation (15) to achieve the optimization objective outlined in Equation (13). |
| Parameters are optimized using Equations (17) and (18) to achieve the optimization objective outlined in Equation (14). |
| end |
| Output: fault diagnosis model. |
| where ‘epoch1′ and ‘epoch2′, respectively, denote the epochs for pre-training and training. |
4. Experiments
4.1. Dataset Description
4.2. Parameter Settings and Results
- (1)
- Experiment 1: The feature extractor is a 2D convolutional neural network with a kernel size of 5 × 5 and a pooling layer size of 2 × 2. A total of 150 epochs were set for training, with an initial learning rate of 0.001. The mini-batch size was set to 128, with 64 samples from the source domain and 64 samples from the target domain. In the training process, only the classifier was trained for the first five epochs. To eliminate the impact of randomness, the results were averaged over 20 experiments. To ensure fairness in the experiments, the same hyperparameters were set for the comparison models, and they were trained for the same number of epochs. The baseline in this study is a convolutional neural network with the same feature extractor, trained only on the source domain data. We evaluate and compare the performance of various models using the accuracy. Accuracy is defined as the ratio of the number of correctly classified samples to the total number of samples in the test set.
- (2)
- Experiment 2: The model parameters remain unchanged, and each batch size is set to 64, containing 32 samples from both the source and target domains. During the training process, the classifier is exclusively trained for the first 15 epochs, and the total number of epochs is set to 150. The baseline remains consistent with the previous experiments. There are a total of 12 transfer tasks based on the four operating conditions, and the results are shown in Table 3.
- (3)
- Results Analysis: Indeed, the experimental results clearly demonstrate that while convolutional neural networks (CNNs) have the ability to learn deep features, they struggle with domain shift in transfer tasks, resulting in the lowest accuracy among the tested models.
4.3. Visualization Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, T.D.; Yu, G.; Gao, M.; Zhao, L.L.; Bai, C.; Yang, W.Q. Fault Diagnosis Methods Based on Machine Learning and its Applications for Wind Turbines: A Review. IEEE Access 2021, 9, 147481–147511. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.Y.; Gao, L.; Zhang, Y.Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Lei, Y.G.; Yang, B.; Jiang, X.W.; Jia, F.; Li, N.P.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 39. [Google Scholar] [CrossRef]
- Wang, H.W.; Sun, W.L.; He, L.; Zhou, J.X. Intelligent Fault Diagnosis Method for Gear Transmission Systems Based on Improved Multi-Scale Reverse Dispersion Entropy and Swarm Decomposition. IEEE Trans. Instrum. Meas. 2022, 71, 13. [Google Scholar] [CrossRef]
- Xiao, W.; Ye, Z.; Wang, S.Y. Fault Diagnosis of Wind Turbine Based on Convolution Neural Network Algorithm. Comput. Intell. Neurosci. 2022, 2022, 10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.H.; Zhu, Y.Z.; Zhang, C.J.; Yu, P.; Li, Q.A. Abnormality Detection Method for Wind Turbine Bearings Based on CNN-LSTM. Energies 2023, 16, 3291. [Google Scholar] [CrossRef]
- Afridi, Y.S.; Hasan, L.; Ullah, R.; Ahmad, Z.; Kim, J.M. LSTM-Based Condition Monitoring and Fault Prognostics of Rolling Element Bearings Using Raw Vibrational Data. Machines 2023, 11, 531. [Google Scholar] [CrossRef]
- Liu, J.Y.; Wang, X.S.; Wu, S.J.; Wan, L.; Xie, F.Q. Wind turbine fault detection based on deep residual networks. Expert Syst. Appl. 2023, 213, 13. [Google Scholar] [CrossRef]
- Durbhaka, G.K.; Selvaraj, B.; Mittal, M.; Saba, T.; Rehman, A.; Goyal, L.M. Swarm-LSTM: Condition Monitoring of Gearbox Fault Diagnosis Based on Hybrid LSTM Deep Neural Network Optimized by Swarm Intelligence Algorithms. Comput. Mater. Contin. 2021, 66, 2041–2059. [Google Scholar] [CrossRef]
- Huang, D.J.; Zhang, W.A.; Guo, F.H.; Liu, W.J.; Shi, X.M. Wavelet Packet Decomposition-Based Multiscale CNN for Fault Diagnosis of Wind Turbine Gearbox. IEEE Trans. Cybern. 2023, 53, 443–453. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, W.Y.; Wang, X.; Gu, H. A novel wind turbine fault diagnosis method based on compressed sensing and DTL-CNN. Renew. Energy 2022, 194, 249–258. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.G.; Xing, S.B.; Yan, T.; Li, N.P. Deep Convolutional Transfer Learning Network: A New Method for Intelligent Fault Diagnosis of Machines with Unlabeled Data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.Q. Multi-Layer domain adaptation method for rolling bearing fault diagnosis. Signal Process. 2019, 157, 180–197. [Google Scholar] [CrossRef]
- Wu, Z.H.; Jiang, H.K.; Zhao, K.; Li, X.Q. An adaptive deep transfer learning method for bearing fault diagnosis. Measurement 2020, 151, 14. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Xu, N.X.; Ding, Q. Deep Learning-Based Machinery Fault Diagnostics with Domain Adaptation across Sensors at Different Places. IEEE Trans. Ind. Electron. 2020, 67, 6785–6794. [Google Scholar] [CrossRef]
- Cheng, C.; Zhou, B.T.; Ma, G.J.; Wu, D.R.; Yuan, Y. Wasserstein distance based deep adversarial transfer learning for intelligent fault diagnosis with unlabeled or insufficient labeled data. Neurocomputing 2020, 409, 35–45. [Google Scholar] [CrossRef]
- Kim, M.; Ko, J.U.; Lee, J.; Youn, B.D.; Jung, J.H.; Sun, K.H. A Domain Adaptation with Semantic Clustering (DASC) method for fault diagnosis of rotating machinery. ISA Trans. 2022, 120, 372–382. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.H.; Peng, G.L.; Chen, Y.H.; Zhang, Z.J. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Wu, H.; Li, J.M.; Zhang, Q.Y.; Tao, J.X.; Meng, Z. Intelligent fault diagnosis of rolling bearings under varying operating conditions based on domain-adversarial neural network and attention mechanism. ISA Trans. 2022, 130, 477–489. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.N.; Liang, B.; Cheng, Y.; Meng, D.S.; Yang, J.; Zhang, T. Deep Model Based Domain Adaptation for Fault Diagnosis. IEEE Trans. Ind. Electron. 2017, 64, 2296–2305. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Wang, L.Z.; Peng, G.L.; Li, S.J. WDA: An Improved Wasserstein Distance-Based Transfer Learning Fault Diagnosis Method. Sensors 2021, 21, 19. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Yang, W.G.; Jiang, D.X. A novel adversarial learning framework in deep convolutional neural network for intelligent diagnosis of mechanical faults. Knowl.-Based Syst. 2019, 165, 474–487. [Google Scholar] [CrossRef]
- Yu, C.H.; Wang, J.D.; Chen, Y.Q.; Huang, M.Y. Transfer Learning with Dynamic Adversarial Adaptation Network. In Proceedings of the 19th IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 778–786. [Google Scholar]
- Li, D.D.; Zhao, Y.; Zhao, Y. A dynamic-model-based fault diagnosis method for a wind turbine planetary gearbox using a deep learning network. Prot. Control Mod. Power Syst. 2022, 7, 14. [Google Scholar] [CrossRef]
- Wan, L.J.; Li, Y.Y.; Chen, K.Y.; Gong, K.; Li, C.Y. A novel deep convolution multi-adversarial domain adaptation model for rolling bearing fault diagnosis. Measurement 2022, 191, 17. [Google Scholar] [CrossRef]
- Tao, H.F.; Qiu, J.R.; Chen, Y.Y.; Stojanovic, V.; Cheng, L. Unsupervised cross-domain rolling bearing fault diagnosis based on time-frequency information fusion. J. Frankl. Inst. Eng. Appl. Math. 2023, 360, 1454–1477. [Google Scholar] [CrossRef]
- Tian, Q.; Zhu, Y.N.; Sun, H.Y.; Chen, S.C.; Yin, H.J. Unsupervised Domain Adaptation through Dynamically Aligning Both the Feature and Label Spaces. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 8562–8573. [Google Scholar] [CrossRef]
- Chen, R.X.; Zhu, Y.Q.; Yang, L.X.; Hu, X.L.; Chen, G.R. Adaptation Regularization Based on Transfer Learning for Fault Diagnosis of Rotating Machinery Under Multiple Operating Conditions. IEEE Sens. J. 2022, 22, 10655–10662. [Google Scholar] [CrossRef]
- Tian, M.; Su, X.M.; Chen, C.Z.; Luo, Y.Q.; Sun, X.M. Bearing fault diagnosis of wind turbines based on dynamic multi-adversarial adaptive network. J. Mech. Sci. Technol. 2023, 37, 1637–1651. [Google Scholar] [CrossRef]
- Shen, Y.J.; Chen, B.; Guo, F.H.; Meng, W.C.; Yu, L. A Modified Deep Convolutional Subdomain Adaptive Network Method for Fault Diagnosis of Wind Turbine Systems. IEEE Trans. Instrum. Meas. 2022, 71, 10. [Google Scholar] [CrossRef]
- Xia, B.J.; Wang, K.; Xu, A.D.; Zeng, P.; Yang, N.; Li, B.Y. Intelligent Fault Diagnosis for Bearings of Industrial Robot Joints Under Varying Working Conditions Based on Deep Adversarial Domain Adaptation. IEEE Trans. Instrum. Meas. 2022, 71, 13. [Google Scholar] [CrossRef]
- An, Y.Y.; Zhang, K.; Chai, Y.; Liu, Q.; Huang, X.H. Domain adaptation network base on contrastive learning for bearings fault diagnosis under variable working conditions. Expert Syst. Appl. 2023, 212, 9. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2016, 17, 35. [Google Scholar]
- Long, M.S.; Cao, Z.J.; Wang, J.M.; Jordan, M.I. Conditional Adversarial Domain Adaptation. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Sun, B.C.; Saenko, K. Deep CORAL: Correlation Alignment for Deep Domain Adaptation. In Proceedings of the 14th European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; Springer International Publishing Ag: Amsterdam, The Netherlands, 2016; pp. 443–450. [Google Scholar]
- Chen, Z.Y.; He, G.L.; Li, J.P.; Liao, Y.X.; Gryllias, K.; Li, W.H. Domain Adversarial Transfer Network for Cross-Domain Fault Diagnosis of Rotary Machinery. IEEE Trans. Instrum. Meas. 2020, 69, 8702–8712. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly accurate machine fault diagnosis using deep transfer learning. IEEE Trans. Ind. Inform. 2018, 15, 2446–2455. [Google Scholar] [CrossRef]








| Layer Type | Kernel Size | Stride | Output Size |
|---|---|---|---|
| Input | / | / | (3,128,128) |
| Conv | (5,5) | 1 | (6,124,124) |
| Polling | (2,2) | 2 | (6,62,62) |
| Dropout (p = 0.5) | / | / | (6,62,62) |
| Conv | (5,5) | 1 | (36,58,58) |
| Polling | (2,2) | 2 | (36,29,29) |
| Dropout (p = 0.5) | / | / | (36,29,29) |
| Conv | (3,3) | 2 | (256,14,14) |
| Polling | (2,2) | 2 | (256,7,7) |
| FC | / | / | (720,1) |
| Classifier | / | / | (num class, 1) |
| Transfer Task | Fault Diagnosis Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| Baseline | DANN | CDAN | CORAL | DATN | CDAA | |
| 20-0~30-2 | 67.14 ± 1.94 | 82.68 ± 1.52 | 84.49 ± 3.66 | 71.99 ± 6.67 | 87.32 ± 3.44 | 93.66 ± 2.99 |
| 30-2~20-0 | 66.27 ± 2.97 | 78.89 ± 1.25 | 80.78 ± 2.06 | 70.52 ± 1.61 | 86.43 ± 1.30 | 91.23 ± 2.66 |
| Average | 66.71 | 80.79 | 82.64 | 71.19 | 86.48 | 92.56 |
| Transfer Task | Fault Diagnosis Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| Baseline | DANN | CDAN | CORAL | DATN | CDAA | |
| 0~1 | 73.28 ± 2.79 | 94.79 ± 1.63 | 95.71 ± 2.06 | 92.46 ± 1.61 | 96.57 ± 1.31 | 98.63 ± 2.67 |
| 0~2 | 65.26 ± 3.01 | 82.20 ± 1.25 | 87.92 ± 2.23 | 82.61 ± 1.62 | 88.41 ± 1.29 | 94.83 ± 1.54 |
| 0~3 | 71.55 ± 3.11 | 91.95 ± 1.34 | 95.46 ± 2.30 | 89.63 ± 1.96 | 95.10 ± 1.29 | 97.49 ± 2.71 |
| 1~2 | 63.22 ± 3.94 | 83.05 ± 1.29 | 87.92 ± 1.71 | 81.50 ± 1.30 | 87.84 ± 2.58 | 93.47 ± 1.15 |
| 1~3 | 72.37 ± 1.91 | 92.66 ± 1.25 | 94.46 ± 1.58 | 92.10 ± 1.71 | 95.59 ± 1.95 | 97.40 ± 1.31 |
| 2~3 | 62.43 ± 2.86 | 82.08 ± 2.31 | 87.77 ± 1.36 | 80.95 ± 1.40 | 87.21 ± 2.11 | 94.26 ± 2.41 |
| 1~0 | 73.05 ± 3.12 | 94.55 ± 1.22 | 97.01 ± 1.43 | 91.94 ± 2.31 | 97.72 ± 1.28 | 97.13 ± 1.98 |
| 2~0 | 62.49 ± 3.44 | 79.98 ± 1.27 | 85.23 ± 2.09 | 81.60 ± 1.66 | 86.38 ± 2.01 | 93.50 ± 2.49 |
| 3~0 | 70.72 ± 2.95 | 84.10 ± 1.53 | 94.53 ± 2.16 | 86.72 ± 1.42 | 93.95 ± 1.27 | 97.84 ± 2.68 |
| 3~1 | 70.40 ± 3.51 | 89.11 ± 1.24 | 91.06 ± 2.52 | 91.14 ± 1.81 | 95.70 ± 1.76 | 97.34 ± 2.30 |
| 3~2 | 60.92 ± 2.99 | 73.03 ± 1.97 | 85.69 ± 3.21 | 70.59 ± 1.89 | 88.28 ± 1.90 | 94.03 ± 1.75 |
| 2~1 | 64.26 ± 2.79 | 74.24 ± 1.61 | 89.27 ± 2.49 | 72.05 ± 1.84 | 88.13 ± 2.53 | 93.80 ± 2.67 |
| Average | 67.50 | 85.15 | 91.00 | 84.44 | 91.74 | 95.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, X.; Zhang, C.; Li, W.; Wang, J.; Li, G.; Bai, C. Dynamic Condition Adversarial Adaptation for Fault Diagnosis of Wind Turbine Gearbox. Sensors 2023, 23, 9368. https://doi.org/10.3390/s23239368
Zhang H, Wang X, Zhang C, Li W, Wang J, Li G, Bai C. Dynamic Condition Adversarial Adaptation for Fault Diagnosis of Wind Turbine Gearbox. Sensors. 2023; 23(23):9368. https://doi.org/10.3390/s23239368
Chicago/Turabian StyleZhang, Hongpeng, Xinran Wang, Cunyou Zhang, Wei Li, Jizhe Wang, Guobin Li, and Chenzhao Bai. 2023. "Dynamic Condition Adversarial Adaptation for Fault Diagnosis of Wind Turbine Gearbox" Sensors 23, no. 23: 9368. https://doi.org/10.3390/s23239368
APA StyleZhang, H., Wang, X., Zhang, C., Li, W., Wang, J., Li, G., & Bai, C. (2023). Dynamic Condition Adversarial Adaptation for Fault Diagnosis of Wind Turbine Gearbox. Sensors, 23(23), 9368. https://doi.org/10.3390/s23239368









