Research on the Mechanical Properties and Temperature Compensation of an Intelligent Pot Bearing for a Pipe-Type Welding Strain Gauge
Abstract
:1. Introduction
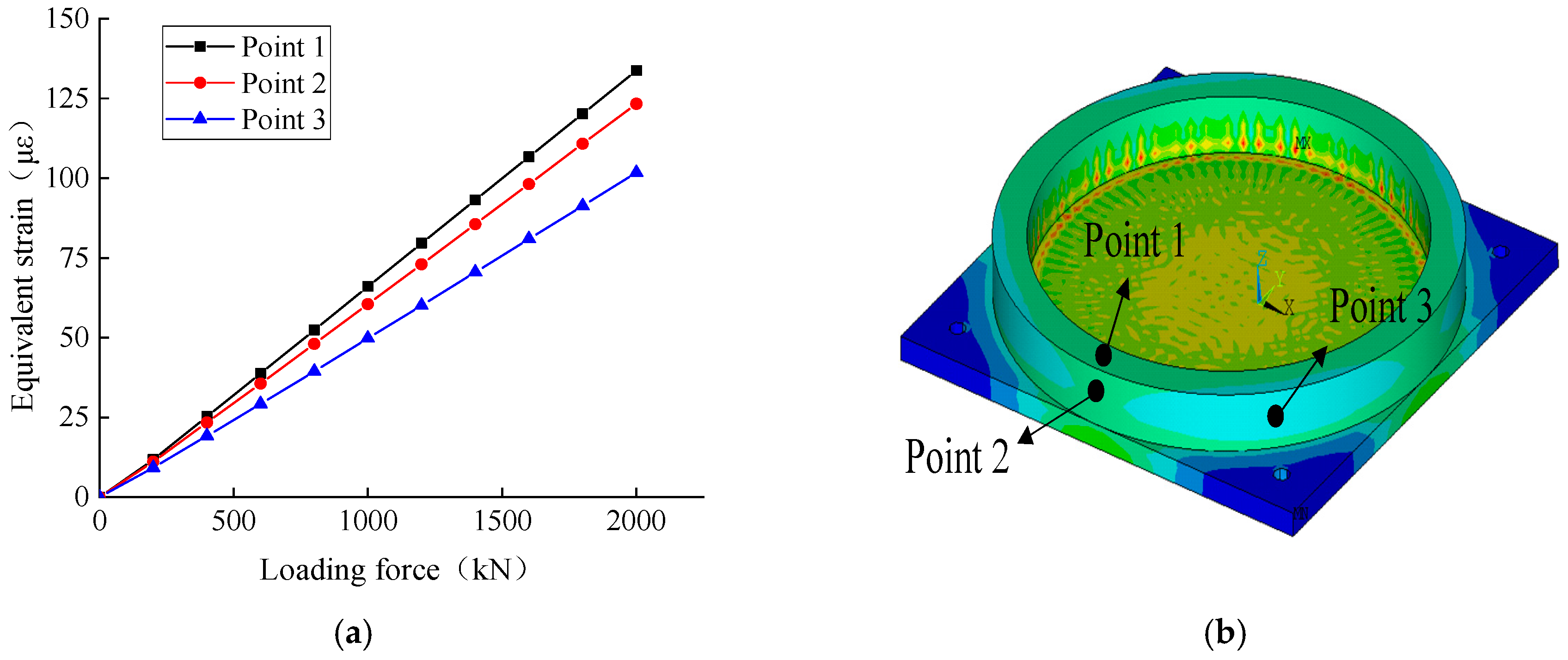
2. Finite Element Analysis of Supports
3. Pipe-Type Welding Strain Gauge Layout
4. Calibration Test of the Vertical Bearing Capacity of the Intelligent Support for Welding Strain Gauges
4.1. Calibration and Temperature Compensation Fitting Method
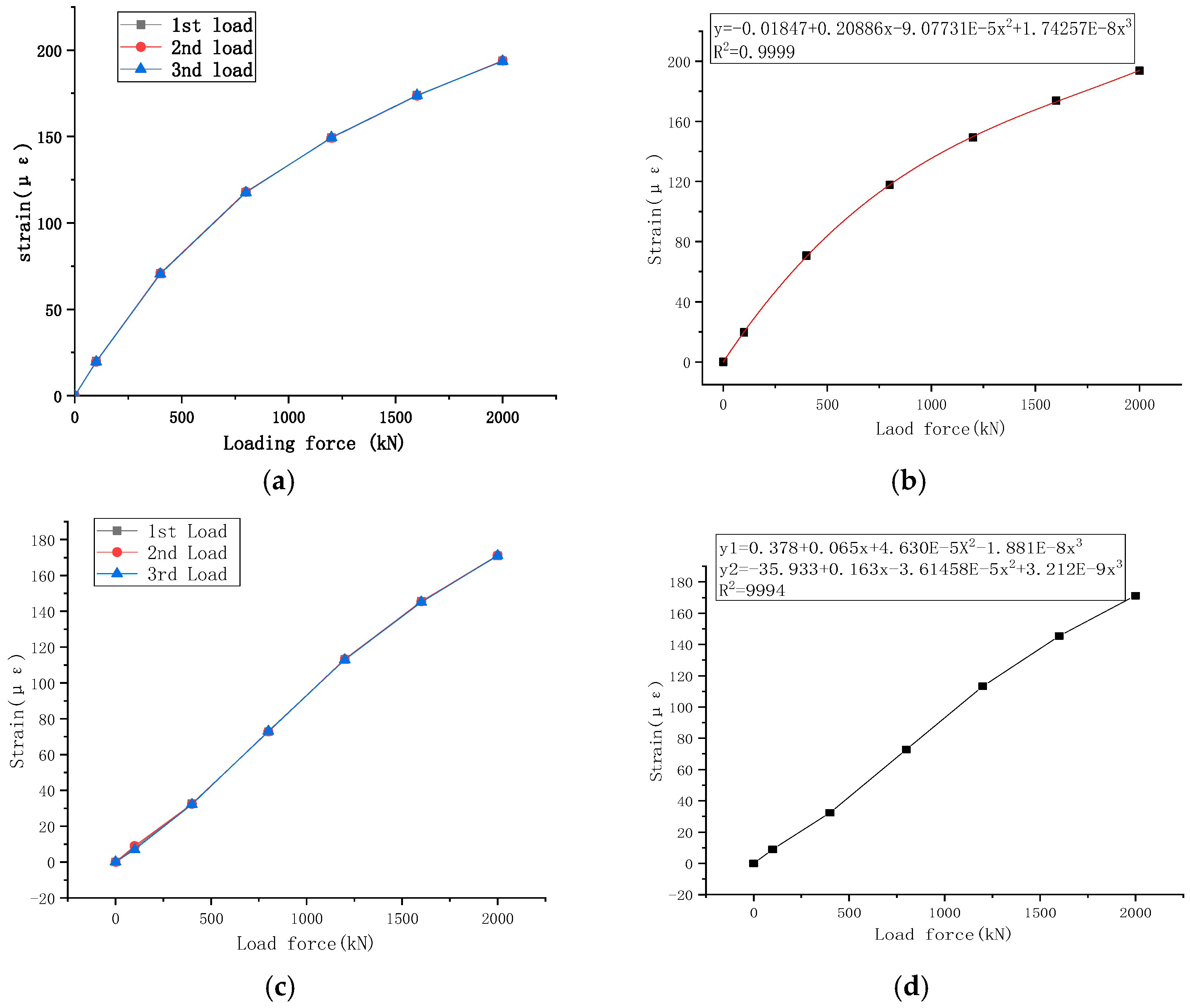
4.2. Calibration Test of the Vertical Bearing Capacity at Normal Temperature
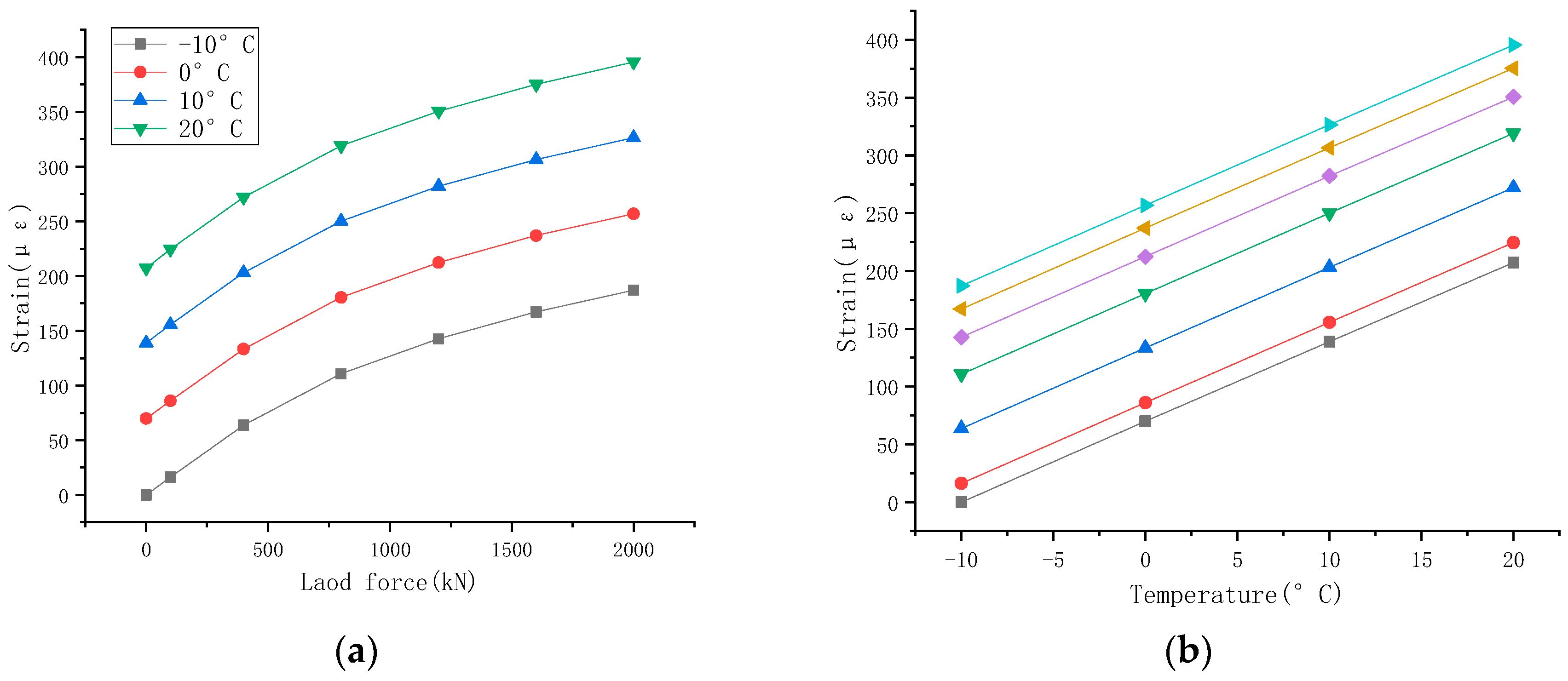
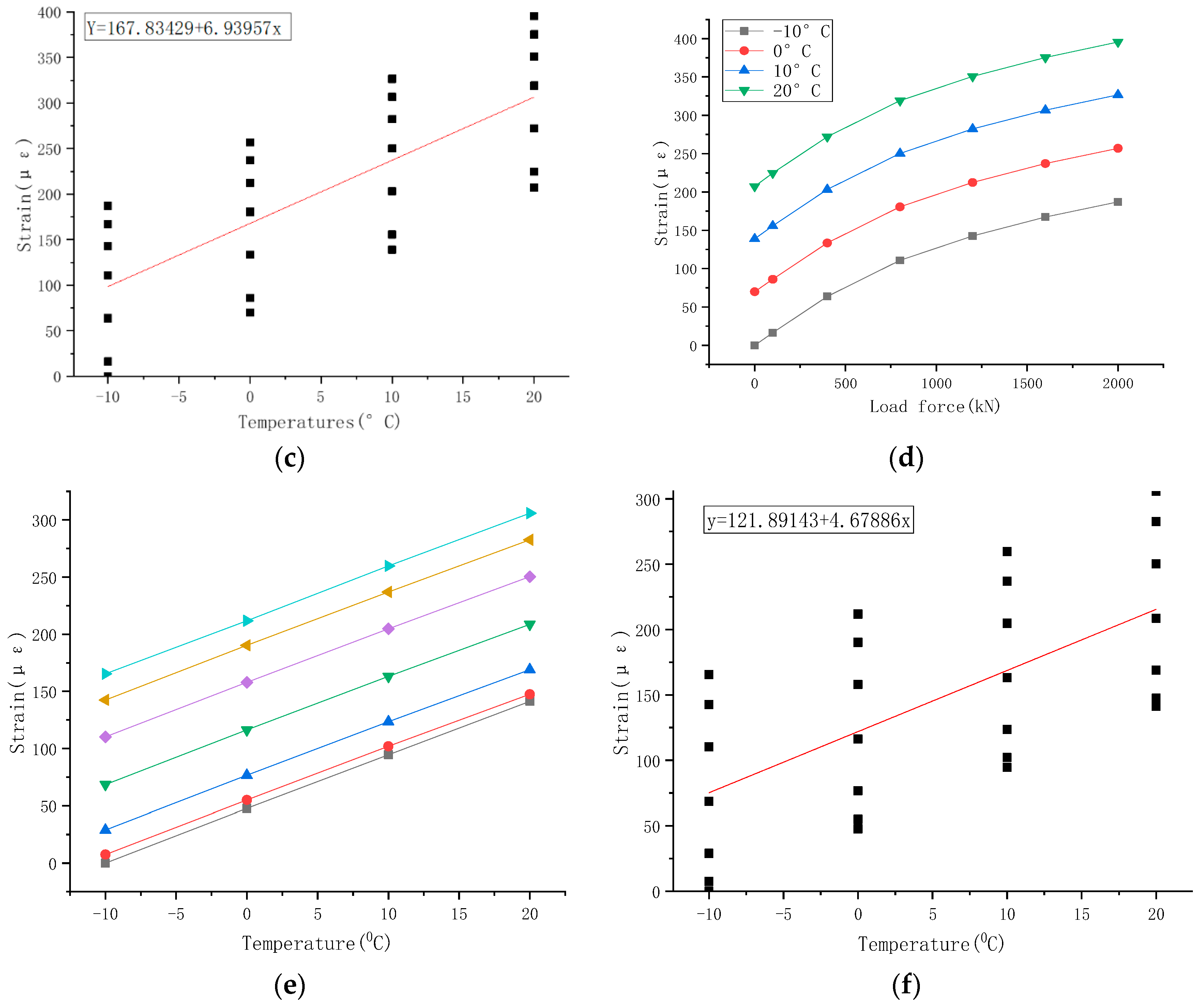
4.3. Temperature Compensation Test
4.4. Error Analysis
5. Support Corner Test
6. Conclusions
- (1)
- A pipe-type spot welding strain gauge comprises a stainless steel tube with a diameter of 1.6 mm welded with a 0.05 mm substrate, and then the resistance strain gauge is threaded into the middle and glued. Using a portable small spot welding machine, it was welded to the pot bearing, which was tested immediately to ensure firmness. This process involves spot welding to the bearing; the voltage is only 3 V to 5 V and will not damage the internal structure of the bearing.
- (2)
- Finite element analysis was conducted on the pot bearing, and the optimal layout of the welded strain gauge on the bearing was obtained. When comparing P1~P4 on the surface of the pot bearing with P5~P8 on the side, P1~P4 on the surface had the best layout.
- (3)
- The calibration test was conducted on the vertical bearing capacity of the bearing compression and shear testing machine at room temperature of the pot-type bearing. Subtractive polynomial cubic polynomial fitting was used, and the curve fitting for each segment was high, with a goodness of fit R2 > 0.999.
- (4)
- Temperature compensation tests were carried out in a temperature chamber using the testing machine to correct measurement errors in the welding strain gauge caused by thermal zero drift and thermal sensitivity drift. A method of minimizing the sum of the squares of the lateral distances of coordinates is proposed, which provides a straight line that minimizes the sum of the squares of the lateral distances of each point from the line. The slope of the line is a coefficient, and the calibration formula equation uses the coefficient for temperature compensation. After considering temperature compensation, the measurement error of the intelligent support of the welding strain gauge was reduced to approximately ±1.8%, which is satisfactory.
- (5)
- The research results can be used in the intelligent monitoring of bridges. The pipe-type structure protected the resistance strain gauge. These sensors can be easily replaced with new sensors when repairs are needed. In the future, a set of monitoring system software for an intelligent pot bearing is developed, which can measure the load value of the pot bearing in real time and bridge damage. The software can be applied to the bridge intelligent support monitoring system to carry out remote intelligent monitoring of the support, grasp the dynamic state of the support in real time and a long time, and then monitor the dynamic health of the bridge.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, X.L.; Chen, L.; Yan, Y.Y.; Xu, X.Y.; Chen, X.Y. Design and Engineering Application of Monitoring System of Force-measuring Bearing for Bridges. High-Speed Railw. Technol. 2021, 12, 50–53. [Google Scholar] [CrossRef]
- Yang, G.J.; Zeng, Y.P.; Gu, H.L. Design and Experimental Study on Automatic Height-adjusting Bearing Based on Elevation Monitoringk. Railw. Stand. Des. 2019, 63, 82–86. [Google Scholar] [CrossRef]
- Yu, F.; Jiang, R.J.; Chen, Y.Y.; Gai, W.M.; Peng, J.; Dong, J.C. An Intelligent High-Damping Rubber Bearing, Bearing Monitoring. Systems, and Intelligent Support. CN205907594U. Available online: https://wenku.baidu.com/view/19835d16961ea76e58fafab069dc5022abea4638.html?fr=hp_Database&_wkts_=1697106600281 (accessed on 25 January 2017).
- Nie, X.M.; Jiang, R.J.; Chen, Y.Y.; Gai, W.M. A New Type of Intelligent Bearing with Force Measuring Rod and Bearing Monitoring System. CN210375597U. Available online: https://wenku.baidu.com/view/8a3202a5ca50ad02de80d4d8d15abe23492f03d3?fr=xueshu&_wkts_=1697099527263 (accessed on 21 April 2020).
- Schulz, W.L.; Udd, E.; Seim, J.M.; McGill, G.E. Advanced Fiber-Grating Strain Sensor Systems for Bridges, Structures, and Highways. SPIE Proc. 1998, 3325, 212–220. [Google Scholar] [CrossRef]
- Subramaniam, K.V.; Pan, Y. Development of Smart Bridge Bearings System: A Feasibility Study; City University of New York: New York, NY, USA, 2005. Available online: https://rosap.ntl.bts.gov/view/dot/16158 (accessed on 12 April 2023).
- Chang, S.J.; Kim, N.S. Development of smart seismic bridge bearing using fiber optic Bragg-grating Sensors. Sens. Smart Struct. Technol. Civ. (SPIE) 2013, 8692, 869228. [Google Scholar] [CrossRef]
- Ha, D.H.; Choo, J.F.; Lee, C.H.; Jang, W.S.; Goo, N.S. Dynamic Characteristics of a Multi-Functional Bridge Bearing with Built-In Piezocomposite Element. Appl. Mech. Mater. 2013, 432, 275–280. [Google Scholar] [CrossRef]
- Xiong, G.B.; Qiu, J.H.; Wei, Y. Research on the Performance of the Spherical Bearing Based on Fiber Bragg Grating Sensing Technology. Prestress. Technol. 2017, 33–34, 38. (In Chinese) [Google Scholar]
- Zhao, X.; Liu, L.; Ji, J.; Li, S.; Zhang, E.; Jin, A. Reliability research on Smart Bridge Cable with Built-in Fiber Bragg Grating Sensors. Piezoelectr. Acoustoopt. 2013, 35, 33–37. [Google Scholar] [CrossRef]
- Guo, J.; Geng, T.; Yan, H.; Du, L.; Zhang, Z.; Sun, C.C. Implementation of a Load Sensitizing Bridge Spherical Bearing Based on Low-Coherent Fiber-Optic Sensors Combined with Neural Network Algorithms. Sensors 2021, 21, 37. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Teng, W.; Liu, F.; Wu, D.; Wu, Y. Measurement of Cable Force through a Fiber Bragg Grating-Type Thin Rod Vibration Sensor and Its Application. Sensors 2022, 22, 8081. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.J.; Kim, N.S.; Baek, J.H. Development of Smart Seismic Device Using FBG Sensor for Measuring Vertical Load. Trans. Korean Soc. Noise Vib. Eng. 2012, 22, 1089–1098. Available online: https://www.researchgate.net/publication/264151753 (accessed on 25 June 2023). [CrossRef]
- Xiong, G.B.; Yang, R.M.; Zou, Q.M. Research on the Performance of Intelligent Isolation Rubber Bearing Based on Hydraulic Sensing Technology. Prestress. Technol. 2016, 20, 16–17. (In Chinese) [Google Scholar] [CrossRef]
- Gu, C.; Cao, X. For a Long-Span Bridge Bearing Risk Detection Intelligent System Design and Implementation. Comput. Meas. Control 2013, 21, 1147–1153. [Google Scholar] [CrossRef]
- Wang, Q. Magneto-Rheological Elastomer Intelligent Isolation Bearing and Its Performance Test. Master’s Thesis, Dalian University of Technology, Dalian, China, 2014. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10141-1015572193.htm (accessed on 7 June 2023).
- Liu, Q.; Li, G.M.; Jiang, R.J.; Yu, F.; Gai, W.M. An intelligent monitoring method and its experiment for bridge bearing. In Proceedings of the International Conference on Civil, Transportation and Environment (ICCTE 2016), Guangzhou, China, 30–31 January 2016; pp. 633–638. [Google Scholar] [CrossRef]
- Hang, X.J. Design, and Research of Bridge Support Multi-Channel Data Acquisition System Based on FPGA. Master’s Thesis, Shandong University, Jinan, China, 2018. [Google Scholar]
- Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P.; Strukova, V.I. Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations. Lubricants 2022, 10, 207. [Google Scholar] [CrossRef]
- Liu, Z.D.; Xiong, G.B.; Tang, M. Study on Performance of A New Type of Ball Bearing for Force Measurement. Build. Technol. Dev. 2019, 46, 96–97. [Google Scholar]
- Yan, B.; Zhang, X.; Zhu, Z. The Influence of Bearing Ring Inclination on Precision Ball Bearing Contact and Heat Generation Performance. Lubricants 2022, 10, 206. [Google Scholar] [CrossRef]
- Ning, F. Coupling Dynamic Response Analysis of Highway Bridge Vehicle-Bridge-Support and Research and Development of Intelligent Support. Master’s Thesis, Guangxi University, Nanning, China, 2022. [Google Scholar] [CrossRef]
- Zhang, R.Y. Electrical Strain Measurement and Sensor; Tsinghua University Press: Beijing, China, 1999; Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=ba64f9ad1ef7cd9151f51371b0955dcf&site=xueshu_se&hitarticle=1 (accessed on 25 April 2023).
- Shen, W.L.; Chen, J.Y.; Song, Y.C.; Liang, S.R.; Peng, J.N. Stress Test for Boiler’s Drum under High-Temperature. Guangxi Electr. Power Technol. 2020, 23, 9–12. [Google Scholar]
- Lv, J.P.; Huang, Y. Discussion on Image Color Classification Method. Comput. Appl. 2002, 22, 1–2. [Google Scholar]
- Zhang, D. The Principle and Application of the Sensor; The University of Electronic Science and Technology of China Press: Chengdu, China, 2013; Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=eb15123dc2b67473b66bad7bfea61173&site=xueshu_se (accessed on 2 May 2023).
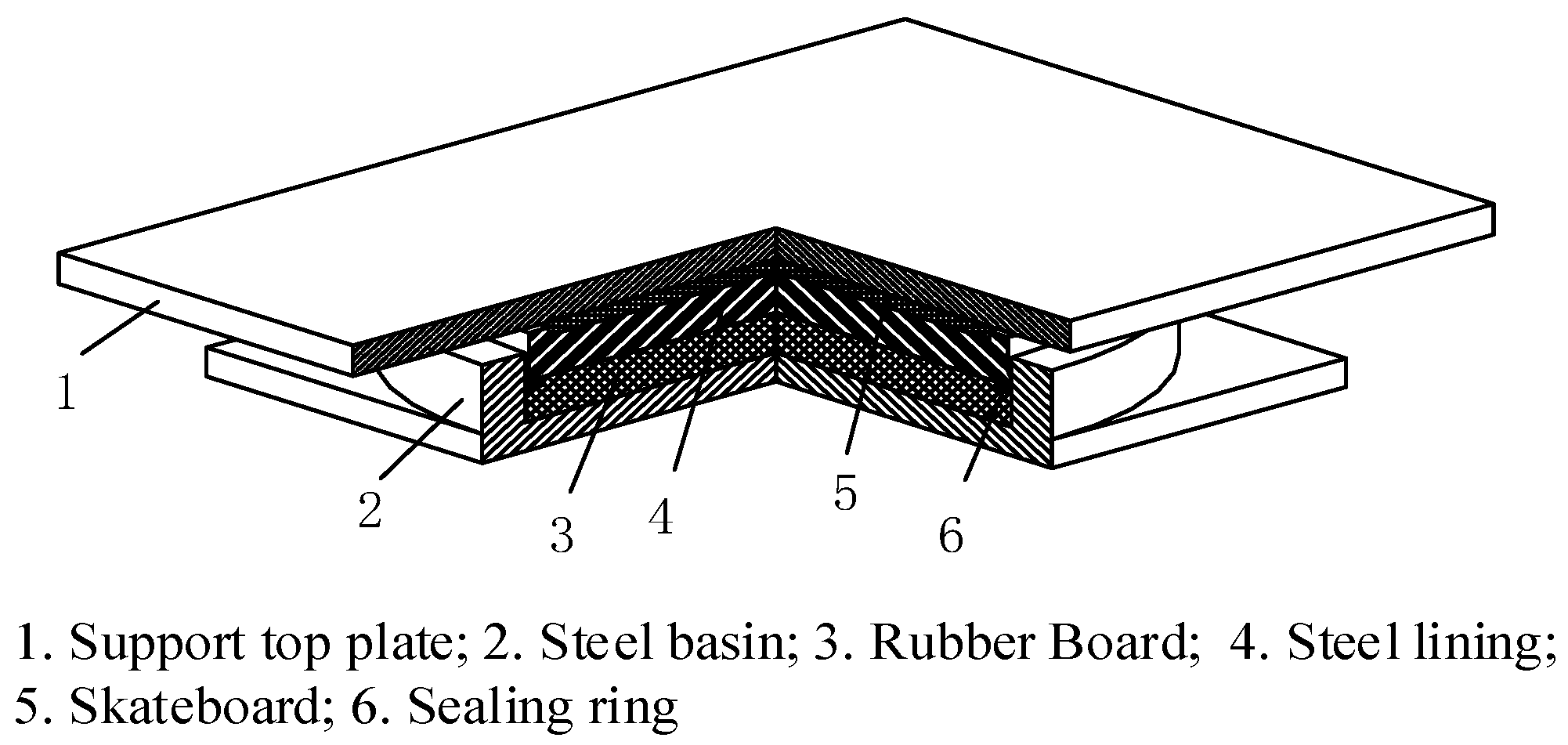
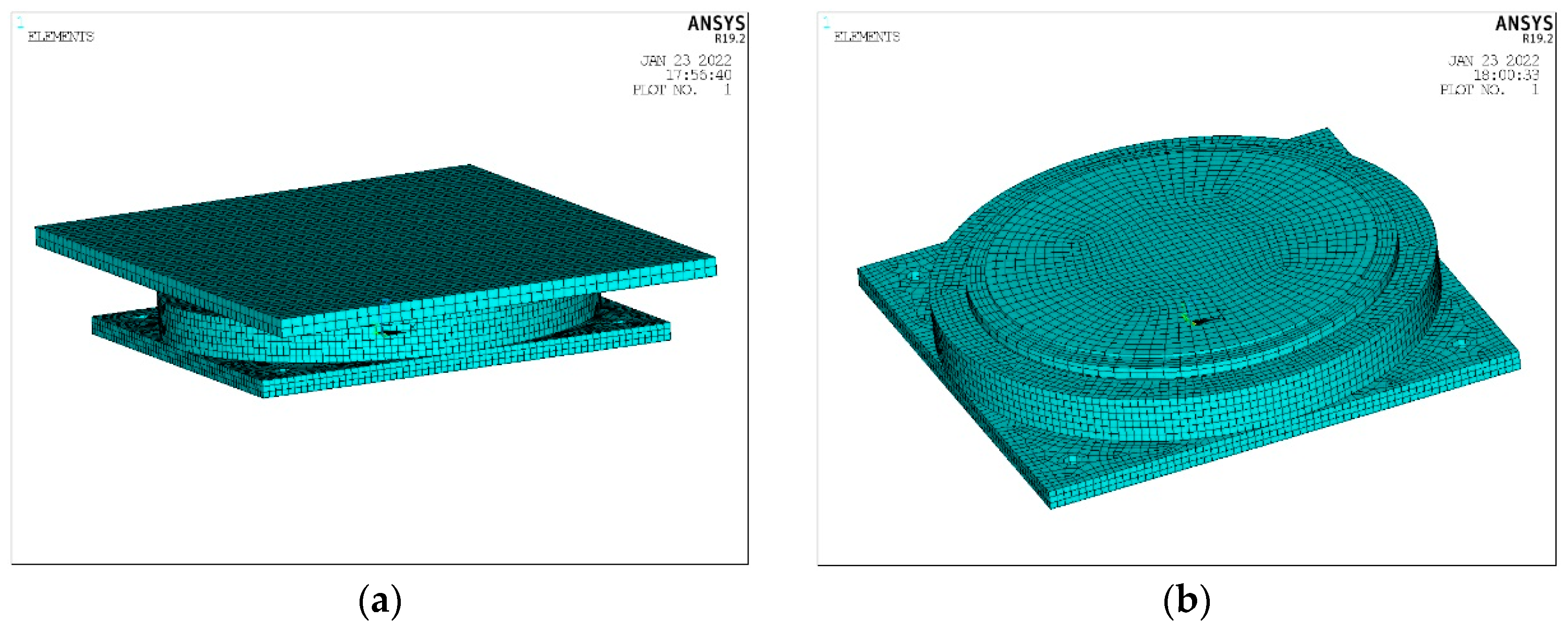

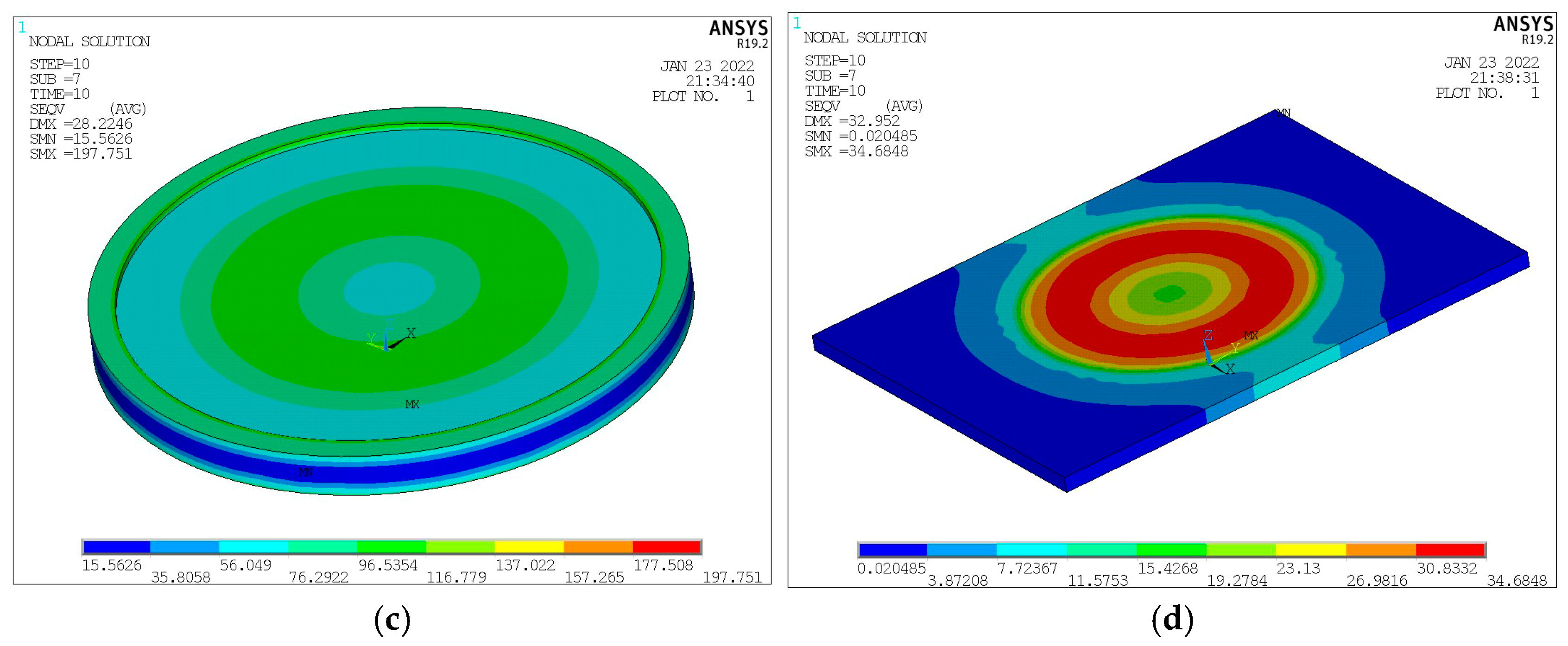
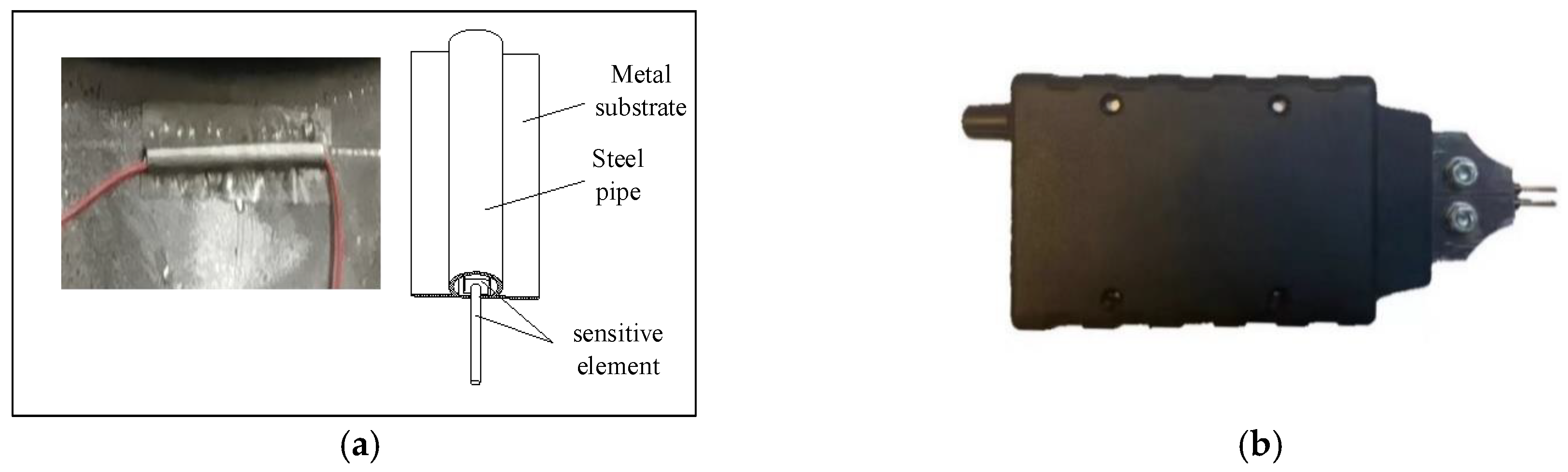



| 6.3 | 1.3 | 0.012 | 5.0 | −0.1 | −2.0 | 2 × 10−4 |
| Component | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|
| Support top plate, steel basin, steel lining plate, stainless steel sliding plate | 2.05 × 105 | 0.3 |
| Pressure-bearing rubber sheet | 4.4 × 103 | 0.5 |
| Teflon skateboard | 1.5 × 103 | 0.4 |
| Test Force Value (kN) | P1~P4 Strain Mean (με) | P5~P8 Strain Mean (με) | ||||
|---|---|---|---|---|---|---|
| 1st Cycle | 2nd Cycle | 3rd Cycle | 1st Cycle | 2nd Cycle | 3rd Cycle | |
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 100 | 19.8 | 19.7 | 19.6 | 8.0 | 9.0 | 7.1 |
| 400 | 70.7 | 70.8 | 70.5 | 32.6 | 32.4 | 32.2 |
| 800 | 117.8 | 117.9 | 117.6 | 72.8 | 72.9 | 73.1 |
| 1200 | 149.3 | 149.3 | 149.5 | 113.1 | 113.3 | 112.9 |
| 1600 | 173.9 | 173.7 | 173.9 | 145.6 | 145.5 | 145.1 |
| 2000 | 193.8 | 193.9 | 193.7 | 170.9 | 171.2 | 171.1 |
| Temperature (°C) | Test Force Value (kN) | P1~P4 Strain Mean (με) | P5~P8 Strain Mean (με) | ||||
|---|---|---|---|---|---|---|---|
| 1st Cycle | 2nd Cycle | 3rd Cycle | 1st Cycle | 2nd Cycle | 3rd Cycle | ||
| −10 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 100 | 16.3 | 16.2 | 16.2 | 7.4 | 8.0 | 7.2 | |
| 400 | 63.7 | 63.8 | 63.7 | 29.1 | 28.8 | 29.0 | |
| 800 | 110.9 | 110.8 | 110.6 | 68.6 | 68.4 | 68.5 | |
| 1200 | 142.6 | 142.7 | 142.8 | 110.1 | 110.4 | 110.2 | |
| 1600 | 167.2 | 167.2 | 167.3 | 142.3 | 142.6 | 142.7 | |
| 2000 | 187.2 | 187.1 | 187.2 | 166.0 | 166.4 | 163.9 | |
| 0 | 0 | 69.7 | 69.9 | 70.1 | 47.9 | 47.8 | 47.6 |
| 100 | 86.2 | 85.9 | 85.9 | 54.7 | 55.7 | 54.7 | |
| 400 | 133.4 | 133.5 | 133.4 | 76.8 | 76.5 | 76.7 | |
| 800 | 180.6 | 180.5 | 180.3 | 116.3 | 116.1 | 116.2 | |
| 1200 | 212.3 | 212.4 | 212.5 | 157.8 | 158.1 | 157.9 | |
| 1600 | 236.9 | 236.9 | 237.2 | 190.1 | 190.3 | 190.4 | |
| 2000 | 256.9 | 256.8 | 256.9 | 213.7 | 214.1 | 207.6 | |
| 10 | 0 | 139.1 | 138.9 | 138.8 | 94.6 | 94.5 | 94.4 |
| 100 | 155.7 | 155.6 | 155.6 | 101.7 | 102.1 | 102.3 | |
| 400 | 203.1 | 203.2 | 203.1 | 123.5 | 123.3 | 123.8 | |
| 800 | 250.3 | 250.2 | 250 | 163.2 | 163.2 | 163.1 | |
| 1200 | 282.1 | 282.1 | 282.2 | 204.7 | 205.3 | 204.6 | |
| 1600 | 306.6 | 306.6 | 306.7 | 237.4 | 237.0 | 236.8 | |
| 2000 | 326.6 | 326.5 | 326.6 | 258.6 | 260.2 | 260.3 | |
| 20 | 0 | 206.3 | 208.1 | 207.3 | 141.1 | 141.3 | 141.3 |
| 100 | 224.6 | 224.6 | 224.7 | 148.1 | 147.1 | 147.1 | |
| 400 | 272.1 | 272.2 | 272.1 | 168.9 | 169.2 | 169.1 | |
| 800 | 319.0 | 319.2 | 319.3 | 208.5 | 208.7 | 208.6 | |
| 1200 | 350.2 | 351.1 | 351.0 | 250.5 | 250.2 | 250.3 | |
| 1600 | 374.7 | 375.6 | 375.7 | 282.7 | 282.4 | 282.8 | |
| 2000 | 395.6 | 395.5 | 395.6 | 306.5 | 306.1 | 305.3 | |
| Standard Pressure Ring Measurements (kN) | Welding Strain Gauge P1~P4 Calculation Force Value (kN) | Average Error (%) | |||
|---|---|---|---|---|---|
| −10 °C | 0 °C | 10 °C | 20 °C | ||
| 100 | 100.0 | 102.3 | 103.8 | 101.4 | 1.8 |
| 400 | 399.1 | 401.3 | 403.4 | 400.7 | 0.28 |
| 800 | 801.9 | 805.1 | 808.4 | 804.3 | 0.61 |
| 1200 | 1198.8 | 1203.3 | 1208.3 | 1197.3 | 0.16 |
| 1600 | 1599.8 | 1606.7 | 1611.2 | 1598.5 | 0.25 |
| 2000 | 2000.5 | 2007.3 | 2014.2 | 2005.6 | 0.34 |
| Standard Pressure Ring Measurements (kN) | Welding Strain Gauge P5~P8 Calculation Force Value (kN) | Average Error (%) | |||
|---|---|---|---|---|---|
| −10 °C | 0 °C | 10 °C | 20 °C | ||
| 100 | 110.2 | 120.7 | 123.8 | 103.2 | 14.4 |
| 400 | 394.7 | 405.4 | 406.4 | 391.5 | -0.12 |
| 800 | 800.1 | 808.7 | 810.3 | 797.5 | 0.51 |
| 1200 | 1199.3 | 1209.0 | 1210.5 | 1196.5 | 0.31 |
| 1600 | 1602.3 | 1616.5 | 1616.6 | 1598.3 | 0.52 |
| 2000 | 1998.2 | 1989.8 | 2012.0 | 2001.5 | 0.02 |
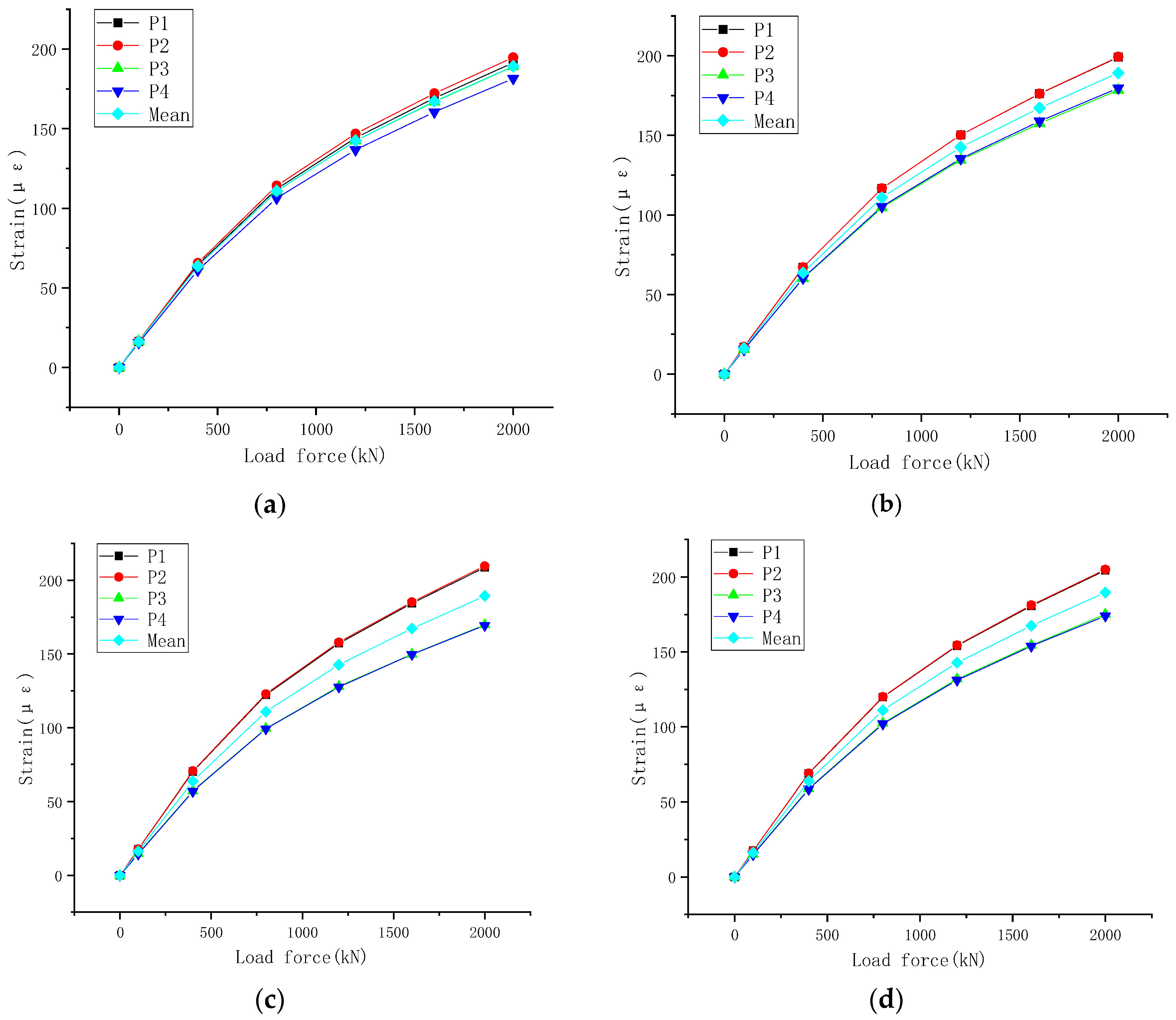
| Angle | Test Force Value | Strain Value (με) | ||||
|---|---|---|---|---|---|---|
| (°) | (kN) | P1 | P2 | P3 | P4 | Mean |
| 0 | 0 | 0 | 0 | 0 | 0 | 0.0 |
| 100 | 16.4 | 16.7 | 16.5 | 15.6 | 16.3 | |
| 400 | 64.4 | 65.6 | 63.7 | 61.1 | 63.7 | |
| 800 | 112.2 | 114.2 | 110.8 | 106.4 | 110.9 | |
| 1200 | 144.3 | 146.8 | 142.5 | 136.8 | 142.6 | |
| 1600 | 169.2 | 172.2 | 166.9 | 160.5 | 167.2 | |
| 2000 | 191.4 | 194.8 | 189.0 | 181.6 | 189.2 | |
| 90 | 0 | 0 | 0 | 0 | 0 | 0 |
| 100 | 17.0 | 17.1 | 15.6 | 15.4 | 16.2 | |
| 400 | 67.0 | 67.1 | 60.1 | 60.4 | 63.7 | |
| 800 | 116.7 | 116.8 | 104.6 | 105.3 | 110.9 | |
| 1200 | 150.2 | 150.2 | 134.5 | 135.4 | 142.6 | |
| 1600 | 176.1 | 176.2 | 157.6 | 158.9 | 167.2 | |
| 2000 | 199.2 | 199.4 | 178.5 | 179.8 | 189.2 | |
| 180 | 0 | 0 | 0 | 0 | 0 | 0 |
| 100 | 17.8 | 17.9 | 14.8 | 14.5 | 16.3 | |
| 400 | 70.2 | 70.61 | 57.2 | 56.9 | 63.7 | |
| 800 | 122.3 | 122.9 | 99.5 | 99.2 | 110.9 | |
| 1200 | 157.3 | 158.0 | 128.0 | 127.6 | 142.7 | |
| 1600 | 184.4 | 185.3 | 149.9 | 149.7 | 167.3 | |
| 2000 | 208.7 | 209.7 | 169.8 | 169.4 | 189.4 | |
| 270 | 0 | 0 | 0 | 0 | 0 | 0 |
| 100 | 17.5 | 17.5 | 15.2 | 14.9 | 16.2 | |
| 400 | 68.8 | 69.0 | 58.9 | 58.5 | 63.8 | |
| 800 | 119.8 | 120.1 | 102.5 | 102.0 | 111.1 | |
| 1200 | 154.1 | 154.5 | 131.9 | 131.1 | 142.9 | |
| 1600 | 180.7 | 181.2 | 154.5 | 153.8 | 167.5 | |
| 2000 | 204.5 | 205.0 | 175.1 | 174.1 | 189.7 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, N.; Zhang, H.; Ning, F.; Tang, Z. Research on the Mechanical Properties and Temperature Compensation of an Intelligent Pot Bearing for a Pipe-Type Welding Strain Gauge. Sensors 2023, 23, 9648. https://doi.org/10.3390/s23249648
Deng N, Zhang H, Ning F, Tang Z. Research on the Mechanical Properties and Temperature Compensation of an Intelligent Pot Bearing for a Pipe-Type Welding Strain Gauge. Sensors. 2023; 23(24):9648. https://doi.org/10.3390/s23249648
Chicago/Turabian StyleDeng, Nianchun, Haitang Zhang, Feng Ning, and Zhiyu Tang. 2023. "Research on the Mechanical Properties and Temperature Compensation of an Intelligent Pot Bearing for a Pipe-Type Welding Strain Gauge" Sensors 23, no. 24: 9648. https://doi.org/10.3390/s23249648
APA StyleDeng, N., Zhang, H., Ning, F., & Tang, Z. (2023). Research on the Mechanical Properties and Temperature Compensation of an Intelligent Pot Bearing for a Pipe-Type Welding Strain Gauge. Sensors, 23(24), 9648. https://doi.org/10.3390/s23249648






