PosturePose: Optimized Posture Analysis for Semi-Supervised Monocular 3D Human Pose Estimation
Abstract
:1. Introduction
- We propose a new posture metric that assesses the similarity between poses by comparing the relative orientation of bones irrespective of the poses’ global positioning and orientation. Unlike existing normalized pose evaluation protocols, our posture metric is better at isolating errors to the defaulting joints and bones.
- The proposed posture metric is fully differentiable and therefore can be directly optimized. We demonstrate its efficacy as a multi-view posture consistency loss function that can be jointly optimized with multi-view pose consistency loss on unlabeled poses in a weakly supervised training pipeline. The addition of these loss terms significantly improves upon monocular pose estimators.
- We present a posture-centric semi-supervised scheme for pose estimation that does not require intrinsic or extrinsic camera parameters and no 2D or 3D pose annotations for the majority of the training data. We significantly improve SOTA semi-supervised pose estimation performance without camera parameter annotations (i.e., no ground truth or estimated camera parameters are used).
2. Related Work
- Fully Supervised 3D-HPE with 3D Pose Ground Truth
- Weakly Supervised 3D-HPE without 3D Pose Ground Truth
- Semi-Supervised 3D-HPE with some 3D Pose Ground Truth
- In the Context of Our Work
3. Method
3.1. Biomechanical Pose Prior Regularization
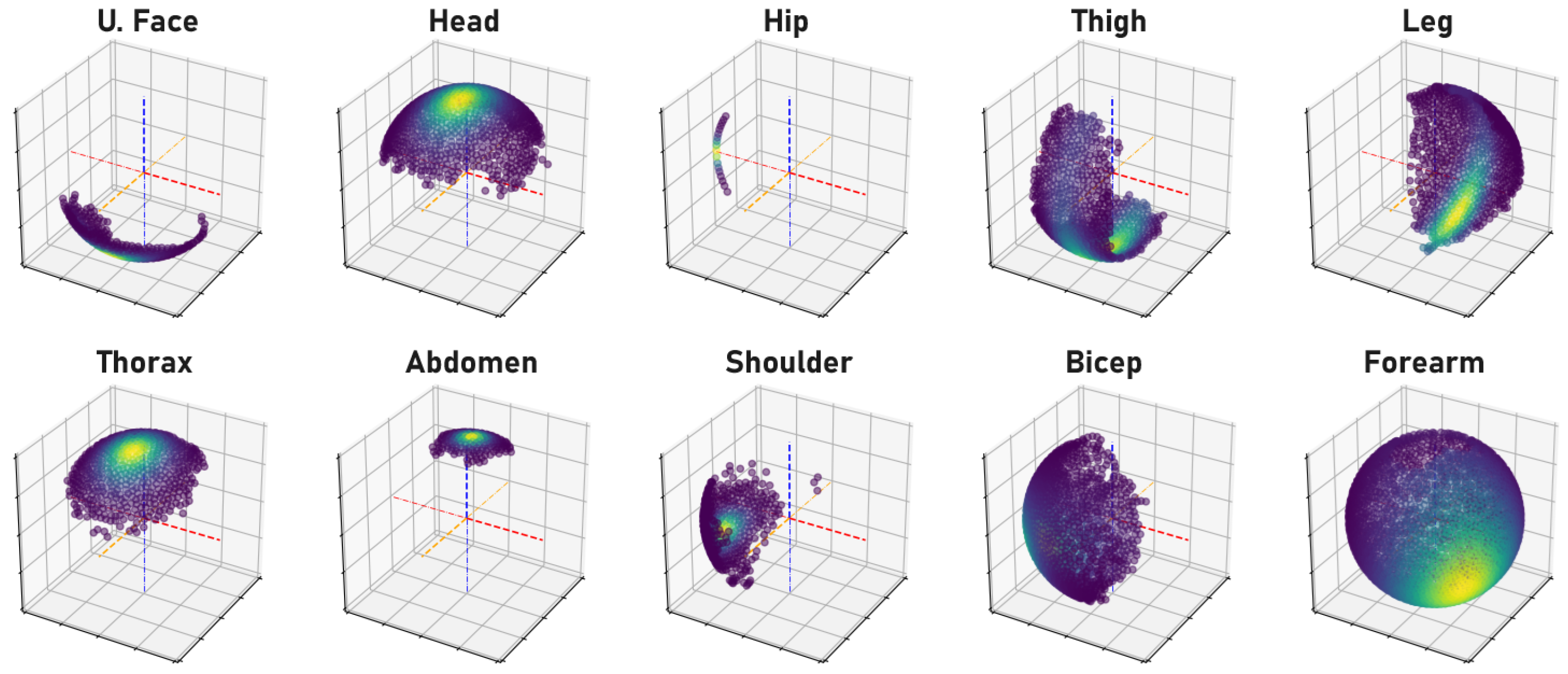
3.2. Differentiable Bone Orientation Alignment
3.3. Bone Orientation Error for Posture Loss
3.3.1. Semi-Supervision with Multi-View Posture Loss
3.3.2. Semi-Supervision without Camera Parameters
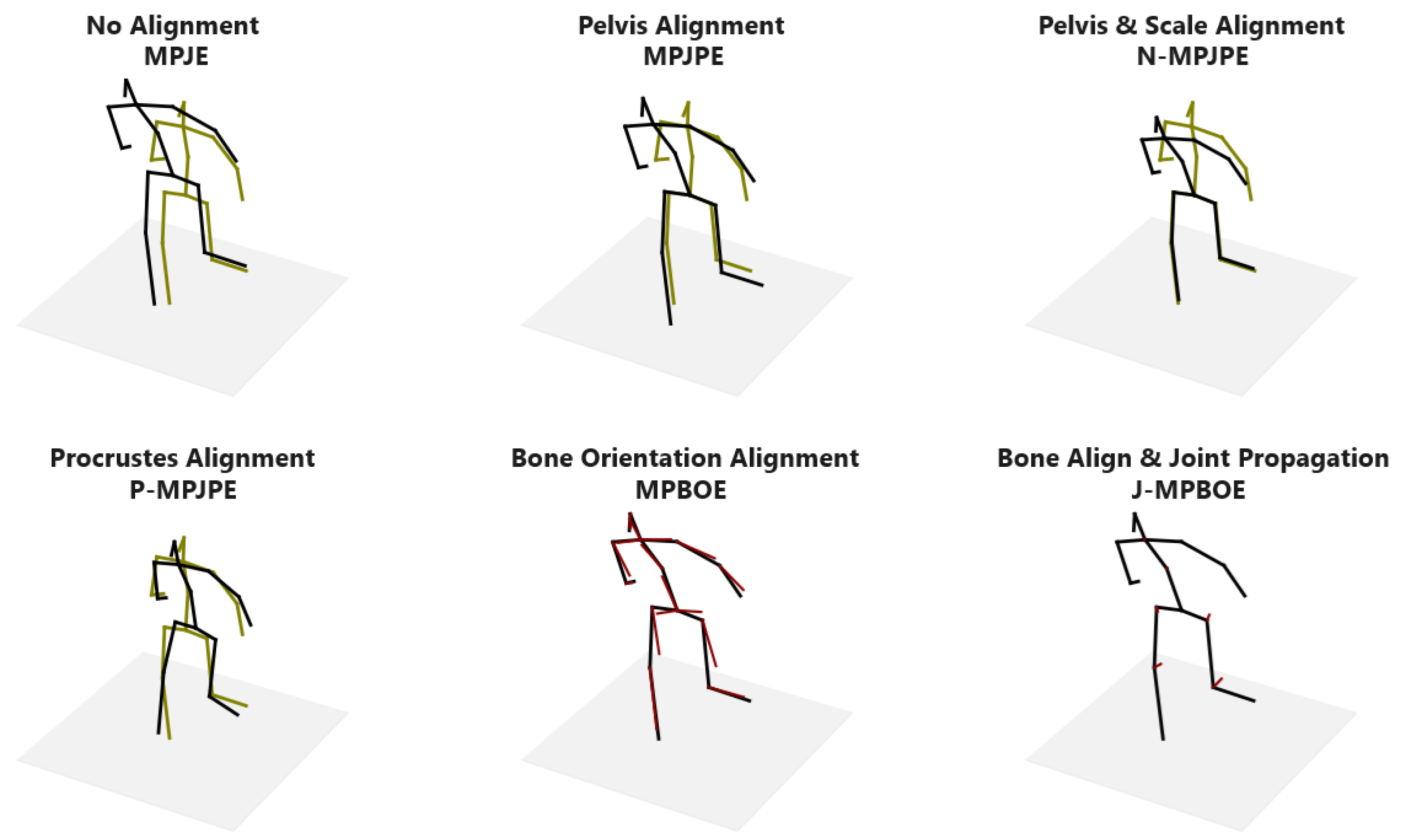
3.4. Bone Orientation Error as a Posture Metric
3.5. Bone Orientation Error Propagated to Joints
4. Experiments and Results
4.1. Experiment Setup
4.1.1. Training and Inference
4.1.2. Datasets and Pose Models
4.2. Results and Comparisons
4.2.1. Semi-Supervision on H36M with Full Supervision on S1
4.2.2. Ablation of Camera Parameters with Increasing Full Supervision
4.2.3. Ablation of Supervision with Little to No 3D Pose Annotations
4.2.4. Cross-Dataset Evaluation on 3DHP
4.2.5. 3D Posture Protocol Assessment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HPE | Human pose estimation |
| 3D-HPE | Three-dimensional human pose estimation |
| GAN | Generative adversarial network |
| Probability density function | |
| MPJPE | Mean per-joint position error |
| N-MPJPE | Scale-normalized mean per-joint position error |
| P-MPJPE | Procrustes-aligned mean per-joint position error |
| MPBOE | Mean per-bone orientation error |
| J-MPBOE | Joint-propagated mean per-bone orientation error |
| H36M | Human3.6M 3D Pose Dataset |
| 3DHP | MPII 3D Human Pose Estimation Dataset |
| VPose3D | VideoPose3D Pose Estimation Network |
| HR-Net | High-Resolution 2D Pose Estimation Network |
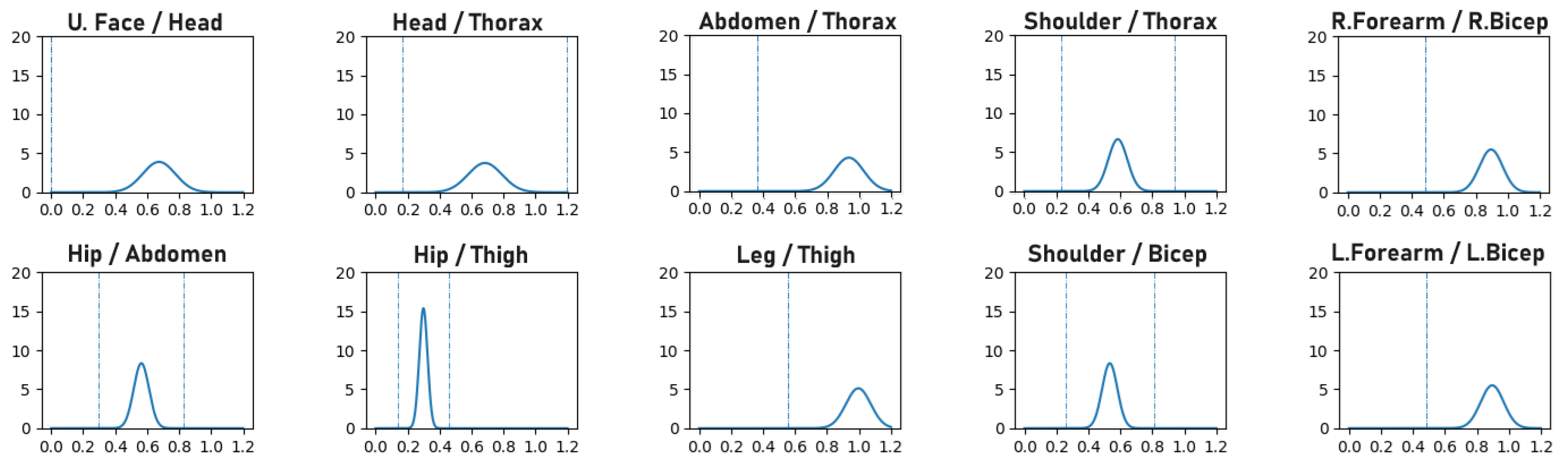
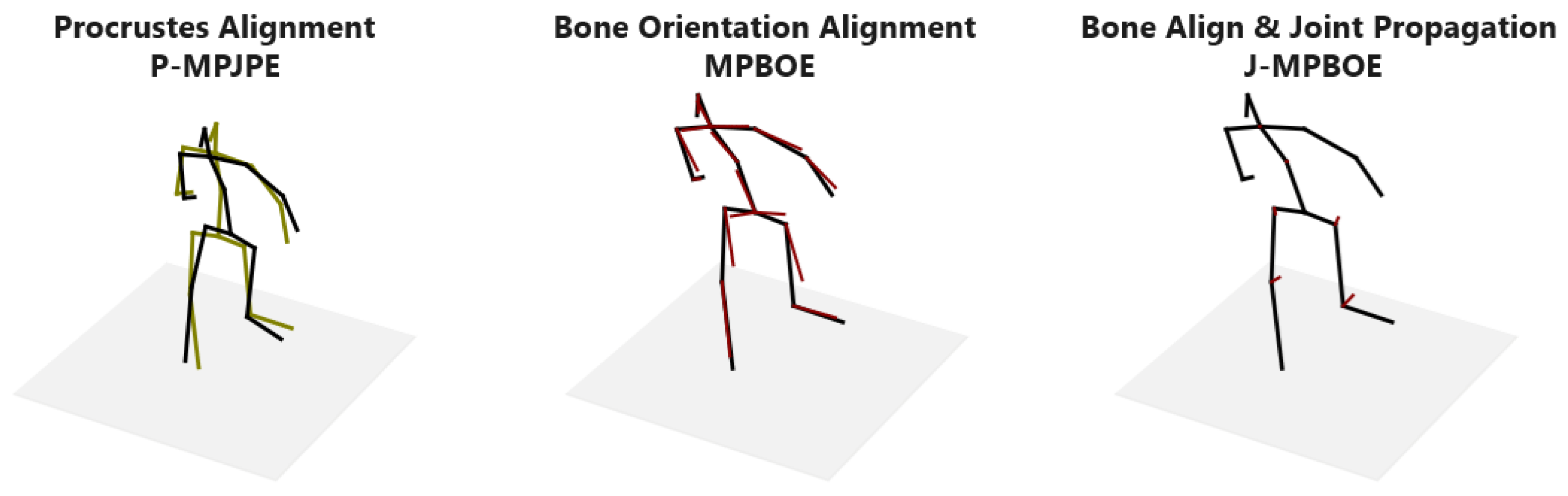
Appendix A. Error Concentration Property of MPBOE and J-MPBOE Illustrated
| Protocol | R.Wrist | L.Wrist | R.Elbow | L.Elbow | R.Shoulder | L.Shoulder | Nose | Skull | Neck | Spine | Pelvis | R.Hip | L.Hip | R.Knee | L.Knee | R.Ankle | L.Ankle |
| MPJPE | 0.19 | 0.23 | 0.20 | 0.24 | 0.28 | 0.27 | 0.31 | 0.34 | 0.27 | 0.20 | 0.15 | 0.17 | 0.13 | 0.16 | 0.13 | 0.20 | 0.23 |
| N-MPJPE | 0.13 | 0.20 | 0.10 | 0.20 | 0.18 | 0.20 | 0.23 | 0.25 | 0.20 | 0.14 | 0.11 | 0.10 | 0.12 | 0.13 | 0.14 | 0.15 | 0.15 |
| P-MPJPE | 0.03 | 0.08 | 0.05 | 0.05 | 0.04 | 0.03 | 0.06 | 0.06 | 0.03 | 0.02 | 0.07 | 0.08 | 0.06 | 0.04 | 0.02 | 0.08 | 0.08 |
| J-MPBOE | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.02 | 0.03 | 0.08 | 0.11 | 0.00 | 0.00 |
| Protocol | R.Radius | L.Radius | R.Humerus | L.Humerus | R.Clavicle | L.Clavicle | Face | Head | Thoracic | Lumbar | R.Waist | L.Waist | R.Femur | L.Femur | R.Tibia | L.Tibia | |
| MPBOE | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.09 | 0.11 | 0.00 | 0.00 |
Appendix B. Configuration of Bone Orientation Alignment Procedure
| Bone or | Quadruplet Keypoints | Superscripts | Axis-Bone | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Body Part | Free | Pivot | Axis | Anchor | Aligned to | |||||
| Face | Nose | Skull | Neck | R. Shoulder | −1 | −1 | Y-Axis | |||
| Head | Skull | Neck | Spine | L. Shoulder | −1 | 1 | Y-Axis | |||
| Thoracic Vertebrae | Neck | Spine | Pelvis | L. Hip | −1 | 1 | Y-Axis | |||
| Lumbar Vertebrae | Spine | Pelvis | Neck | R. Hip | 1 | −1 | Y-Axis | |||
| R. Waist | R. Hip | Pelvis | Spine | L. Hip | 1 | 1 | Y-Axis | |||
| L. Waist | L. Hip | Pelvis | Spine | R. Hip | 1 | −1 | Y-Axis | |||
| R. Femur (Thigh) | R. Knee | R. Hip | Pelvis | Spine | 1 | 1 | X-Axis | |||
| L. Femur (Thigh) | L. Knee | L. Hip | Pelvis | Spine | −1 | 1 | X-Axis | |||
| R. Tibia (Foreleg) | R. Ankle | R. Knee | R. Hip | Pelvis | 1 | 1 | Y-Axis | |||
| L. Tibia (Foreleg) | L. Ankle | L. Knee | L. Hip | Pelvis | 1 | 1 | Y-Axis | |||
| R. Clavicle | R. Shoulder | Neck | Spine | L. Shoulder | −1 | 1 | Y-Axis | |||
| L. Clavicle | L. Shoulder | Neck | Spine | R. Shoulder | −1 | −1 | Y-Axis | |||
| R. Humerus (Bicep) | R. Elbow | R. Shoulder | Neck | Spine | 1 | 1 | X-Axis | |||
| L. Humerus (Bicep) | L. Elbow | L. Shoulder | Neck | Spine | −1 | 1 | X-Axis | |||
| R. Radius (Forearm) | R. Wrist | R. Elbow | R. Shoulder | Neck | 1 | 1 | Y-Axis | |||
| L. Radius (Forearm) | L. Wrist | L. Elbow | L. Shoulder | Neck | 1 | −1 | Y-Axis | |||
- Illustrating the Outcome of Bone Orientation Alignment

References
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3.6M: Large Scale Datasets and Predictive Methods for 3D Human Sensing in Natural Environments. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1325–1339. [Google Scholar] [CrossRef] [PubMed]
- Joo, H.; Simon, T.; Li, X.; Liu, H.; Tan, L.; Gui, L.; Banerjee, S.; Godisart, T.S.; Nabbe, B.; Matthews, I.; et al. Panoptic Studio: A Massively Multiview System for Social Interaction Capture. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3334–3342. [Google Scholar]
- Sigal, L.; Balan, A.O.; Black, M.J. HumanEva: Synchronized Video and Motion Capture Dataset and Baseline Algorithm for Evaluation of Articulated Human Motion. Int. J. Comput. Vis. 2009, 87, 4. [Google Scholar] [CrossRef]
- Mehta, D.; Rhodin, H.; Casas, D.; Fua, P.; Sotnychenko, O.; Xu, W.; Theobalt, C. Monocular 3D Human Pose Estimation in the Wild Using Improved CNN Supervision. In Proceedings of the 3D Vision (3DV), 2017 Fifth International Conference, Qingdao, China, 10–12 October 2017. [Google Scholar] [CrossRef]
- Von Marcard, T.; Henschel, R.; Black, M.J.; Rosenhahn, B.; Pons-Moll, G. Recovering Accurate 3D Human Pose in the Wild Using IMUs and a Moving Camera. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Amadi, L.; Agam, G. Boosting the Performance of Weakly-Supervised 3D Human Pose Estimators with Pose Prior Regularizers. In Proceedings of the 2022 IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022. [Google Scholar]
- Iskakov, K.; Burkov, E.; Lempitsky, V.S.; Malkov, Y. Learnable Triangulation of Human Pose. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 7717–7726. [Google Scholar]
- Reddy, N.; Guigues, L.; Pischulini, L.; Eledath, J.; Narasimhan, S.G. TesseTrack: End-to-End Learnable Multi-Person Articulated 3D Pose Tracking. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 15185–15195. [Google Scholar]
- He, Y.; Yan, R.; Fragkiadaki, K.; Yu, S.I. Epipolar Transformers. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7776–7785. [Google Scholar]
- Zhang, Z.; Wang, C.; Qiu, W.; Qin, W.; Zeng, W. AdaFuse: Adaptive Multiview Fusion for Accurate Human Pose Estimation in the Wild. Int. J. Comput. Vis. 2021, 129, 703–718. [Google Scholar] [CrossRef]
- Remelli, E.; Han, S.; Honari, S.; Fua, P.; Wang, R.Y. Lightweight Multi-View 3D Pose Estimation Through Camera-Disentangled Representation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 6039–6048. [Google Scholar]
- Chun, S.; Park, S.; Chang, J.Y. Learnable Human Mesh Triangulation for 3D Human Pose and Shape Estimation. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; pp. 2849–2858. [Google Scholar]
- Zhang, J.; Tu, Z.; Yang, J.; Chen, Y.; Yuan, J. MixSTE: Seq2seq Mixed Spatio-Temporal Encoder for 3D Human Pose Estimation in Video. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 13222–13232. [Google Scholar] [CrossRef]
- Xu, J.; Yu, Z.; Ni, B.; Yang, J.; Yang, X.; Zhang, W. Deep Kinematics Analysis for Monocular 3D Human Pose Estimation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 19–20 June 2020; pp. 896–905. [Google Scholar]
- Shan, W.; Lu, H.; Wang, S.; Zhang, X.; Gao, W. Improving Robustness and Accuracy via Relative Information Encoding in 3D Human Pose Estimation. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual, 20–24 October 2021. [Google Scholar]
- Hu, W.; Zhang, C.; Zhan, F.; Zhang, L.; Wong, T.T. Conditional Directed Graph Convolution for 3D Human Pose Estimation. In Proceedings of the 29th ACM International Conference on Multimedia (MM ’21), New York, NY, USA, 20–24 October 2021; pp. 602–611. [Google Scholar] [CrossRef]
- Liu, R.; Shen, J.; Wang, H.; Chen, C.; Cheung, S.C.S.; Asari, V.K. Attention Mechanism Exploits Temporal Contexts: Real-Time 3D Human Pose Reconstruction. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5063–5072. [Google Scholar]
- Qiu, H.; Wang, C.; Wang, J.; Wang, N.; Zeng, W. Cross View Fusion for 3D Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4341–4350. [Google Scholar] [CrossRef]
- Rogez, G.; Schmid, C. MoCap-guided Data Augmentation for 3D Pose Estimation in the Wild. In Proceedings of the Annual Conference on Neural Information Processing Systems (NeurIPS), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Zhang, J.; Yu, D.; Liew, J.H.; Nie, X.; Feng, J. Body Meshes as Points. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 546–556. [Google Scholar]
- Mehta, D.; Sridhar, S.; Sotnychenko, O.; Rhodin, H.; Shafiei, M.; Seidel, H.P.; Xu, W.; Casas, D.; Theobalt, C. VNect: Real-Time 3D Human Pose Estimation with a Single RGB Camera. ACM Trans. Graph. 2017, 36, 1–14. [Google Scholar] [CrossRef]
- Li, S.; Ke, L.; Pratama, K.; Tai, Y.W.; Tang, C.K.; Cheng, K.T. Cascaded Deep Monocular 3D Human Pose Estimation With Evolutionary Training Data. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 6172–6182. [Google Scholar]
- Varol, G.; Romero, J.; Martin, X.; Mahmood, N.; Black, M.J.; Laptev, I.; Schmid, C. Learning from Synthetic Humans. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4627–4635. [Google Scholar]
- Chen, W.; Wang, H.; Li, Y.; Su, H.; Wang, Z.; Tu, C.; Lischinski, D.; Cohen-Or, D.; Chen, B. Synthesizing Training Images for Boosting Human 3D Pose Estimation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 479–488. [Google Scholar]
- Gong, K.; Zhang, J.; Feng, J. PoseAug: A Differentiable Pose Augmentation Framework for 3D Human Pose Estimation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8571–8580. [Google Scholar]
- Gholami, M.; Wandt, B.; Rhodin, H.; Ward, R.; Wang, Z.J. AdaptPose: Cross-Dataset Adaptation for 3D Human Pose Estimation by Learnable Motion Generation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 13065–13075. [Google Scholar]
- Yang, C.Y.; Luo, J.; Xia, L.; Sun, Y.; Qiao, N.; Zhang, K.; Jiang, Z.; Hwang, J.N. CameraPose: Weakly-Supervised Monocular 3D Human Pose Estimation by Leveraging In-the-wild 2D Annotations. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–7 January 2023; pp. 2923–2932. [Google Scholar]
- Tung, H.Y.F.; Harley, A.W.; Seto, W.; Fragkiadaki, K. Adversarial Inverse Graphics Networks: Learning 2D-to-3D Lifting and Image-to-Image Translation from Unpaired Supervision. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4364–4372. [Google Scholar]
- Sun, X.; Xiao, B.; Liang, S.; Wei, Y. Integral Human Pose Regression. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Deng, Y.; Sun, C.; Zhu, J.; Sun, Y.C. SVMAC: Unsupervised 3D Human Pose Estimation from a Single Image with Single-view-multi-angle Consistency. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 474–483. [Google Scholar]
- Christidis, A.; Papaioannidis, C.; Pitas, I. Monocular Weakly-Supervised Camera-Relative 3D Human Pose Estimation. In Proceedings of the 2022 IEEE 14th Image, Video, and Multidimensional Signal Processing Workshop (IVMSP), Nafplio, Greece, 26–29 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Wandt, B.; Rosenhahn, B. RepNet: Weakly Supervised Training of an Adversarial Reprojection Network for 3D Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7774–7783. [Google Scholar]
- Zhou, X.; Huang, Q.; Sun, X.; Xue, X.; Wei, Y. Towards 3D Human Pose Estimation in the Wild: A Weakly-Supervised Approach. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 398–407. [Google Scholar]
- Bouazizi, A.; Wiederer, J.; Kressel, U.; Belagiannis, V. Self-Supervised 3D Human Pose Estimation with Multiple-View Geometry. In Proceedings of the 2021 16th IEEE International Conference on Automatic Face and Gesture Recognition (FG 2021), Jodhpur, India, 15–18 December 2021; pp. 1–8. [Google Scholar]
- Hua, G.; Liu, H.; Li, W.; Zhang, Q.; Ding, R.; Xu, X. Weakly-Supervised 3D Human Pose Estimation With Cross-View U-Shaped Graph Convolutional Network. IEEE Trans. Multimed. 2022, 25, 1832–1843. [Google Scholar] [CrossRef]
- Iqbal, U.; Molchanov, P.; Kautz, J. Weakly-Supervised 3D Human Pose Learning via Multi-View Images in the Wild. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5242–5251. [Google Scholar]
- Wandt, B.; Rudolph, M.; Zell, P.; Rhodin, H.; Rosenhahn, B. CanonPose: Self-Supervised Monocular 3D Human Pose Estimation in the Wild. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13289–13299. [Google Scholar]
- Gholami, M.; Rezaei, A.; Rhodin, H.; Ward, R.; Wang, Z.J. TriPose: A Weakly-Supervised 3D Human Pose Estimation via Triangulation from Video. arXiv 2021, arXiv:2105.06599. [Google Scholar] [CrossRef]
- Kocabas, M.; Karagoz, S.; Akbas, E. Self-Supervised Learning of 3D Human Pose Using Multi-View Geometry. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1077–1086. [Google Scholar]
- Martinez, J.; Hossain, R.; Romero, J.; Little, J. A Simple Yet Effective Baseline for 3d Human Pose Estimation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2659–2668. [Google Scholar]
- Pavllo, D.; Christoph Feichtenhofer, D.G.; Auli, M. 3D human pose estimation in video with temporal convolutions and semi-supervised training. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Chu, W.T.; Pan, Z.W. Semi-Supervised 3D Human Pose Estimation by Jointly Considering Temporal and Multiview Information. IEEE Access 2020, 8, 226974–226981. [Google Scholar] [CrossRef]
- Rhodin, H.; Salzmann, M.; Fua, P. Unsupervised Geometry-Aware Representation for 3D Human Pose Estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Wang, C.; Kong, C.; Lucey, S. Distill Knowledge From NRSfM for Weakly Supervised 3D Pose Learning. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 743–752. [Google Scholar]
- Yang, W.; Ouyang, W.; Wang, X.; Ren, J.S.J.; Li, H.; Wang, X. 3D Human Pose Estimation in the Wild by Adversarial Learning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5255–5264. [Google Scholar]
- Akhter, I.; Black, M.J. Pose-conditioned joint angle limits for 3D human pose reconstruction. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1446–1455. [Google Scholar]
- Dabral, R.; Mundhada, A.; Kusupati, U.; Afaque, S.; Sharma, A.; Jain, A. Learning 3D Human Pose from Structure and Motion. In Proceedings of the 2018 Europian Conference on Computer Vision (ECCV), Munich, Germany, 14–18 September 2018; pp. 679–696. [Google Scholar] [CrossRef]
- Spurr, A.; Iqbal, U.; Molchanov, P.; Hilliges, O.; Kautz, J. Weakly Supervised 3D Hand Pose Estimation via Biomechanical Constraints. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Cheng, Y.F.; Yang, B.; Wang, B.; Wending, Y.; Tan, R.T. Occlusion-Aware Networks for 3D Human Pose Estimation in Video. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 723–732. [Google Scholar]
- Rhodin, H.; Spörri, J.; Katircioglu, I.; Constantin, V.; Meyer, F.; Müller, E.; Salzmann, M.; Fua, P. Learning Monocular 3D Human Pose Estimation from Multi-view Images. Proceedings/CVPR, IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit. 2018, 2018, 8437–8446. [Google Scholar] [CrossRef]
- Mitra, R.; Gundavarapu, N.B.; Sharma, A.; Jain, A. Multiview-Consistent Semi-Supervised Learning for 3D Human Pose Estimation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 6906–6915. [Google Scholar]
- Zhao, L.; Peng, X.; Tian, Y.; Kapadia, M.; Metaxas, D.N. Semantic Graph Convolutional Networks for 3D Human Pose Regression. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3420–3430. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–19 June 2019; pp. 5686–5696. [Google Scholar]
- Fang, H.S.; Xie, S.; Tai, Y.W.; Lu, C. RMPE: Regional Multi-person Pose Estimation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Wandt, B.; Little, J.J.; Rhodin, H. ElePose: Unsupervised 3D Human Pose Estimation by Predicting Camera Elevation and Learning Normalizing Flows on 2D Poses. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 6635–6645. [Google Scholar]


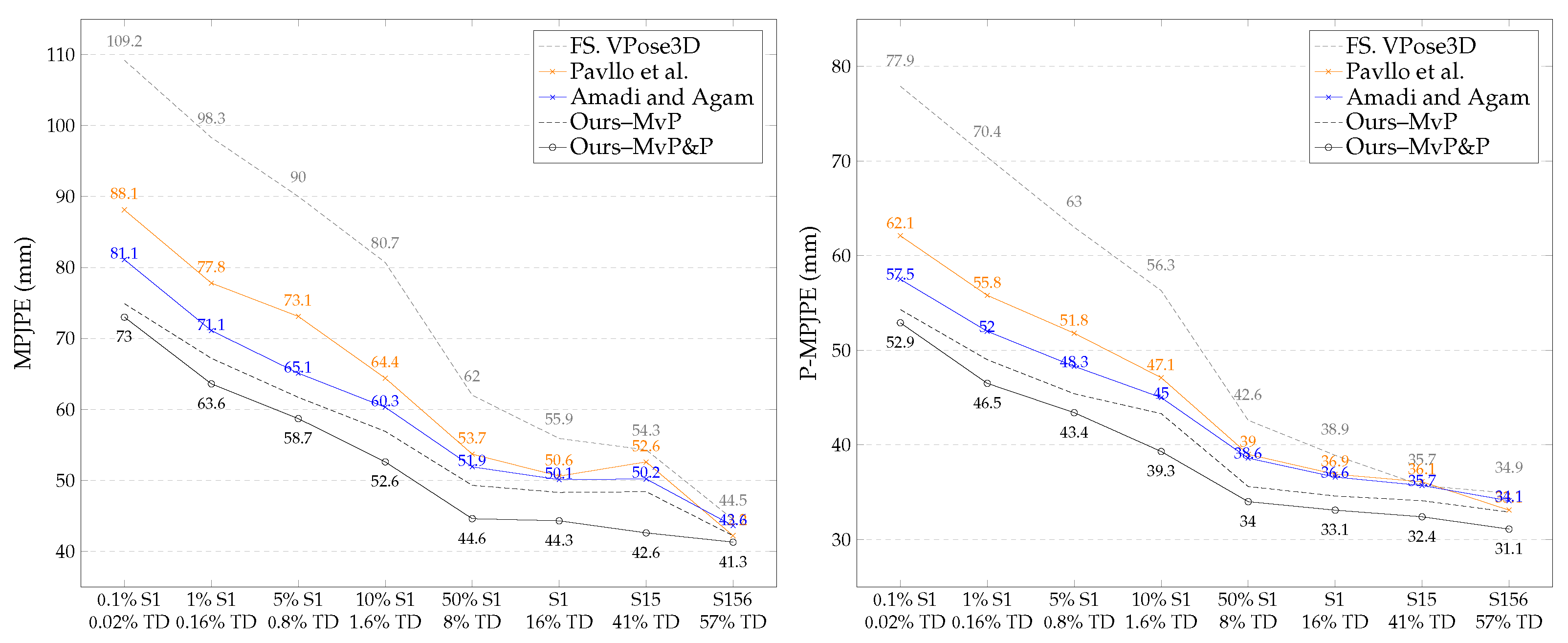

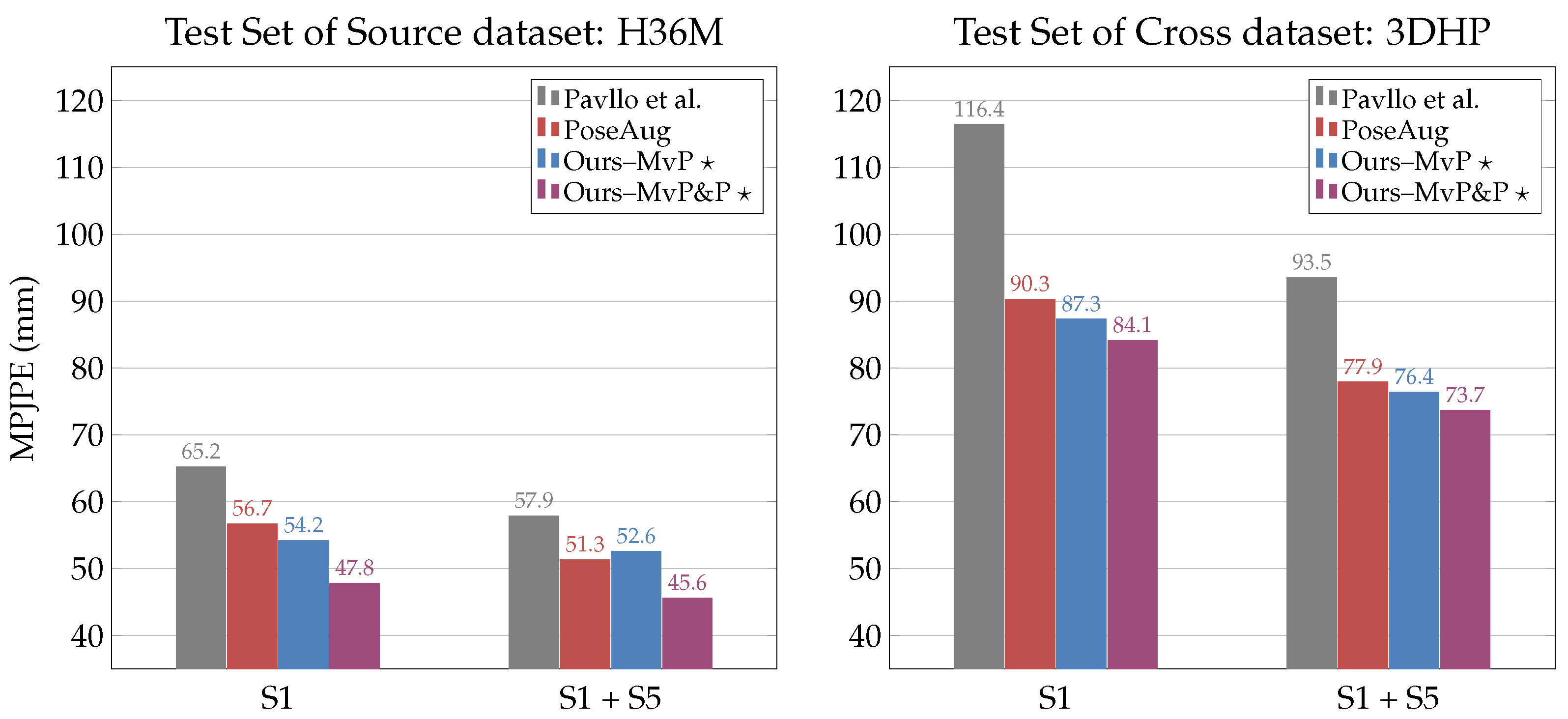
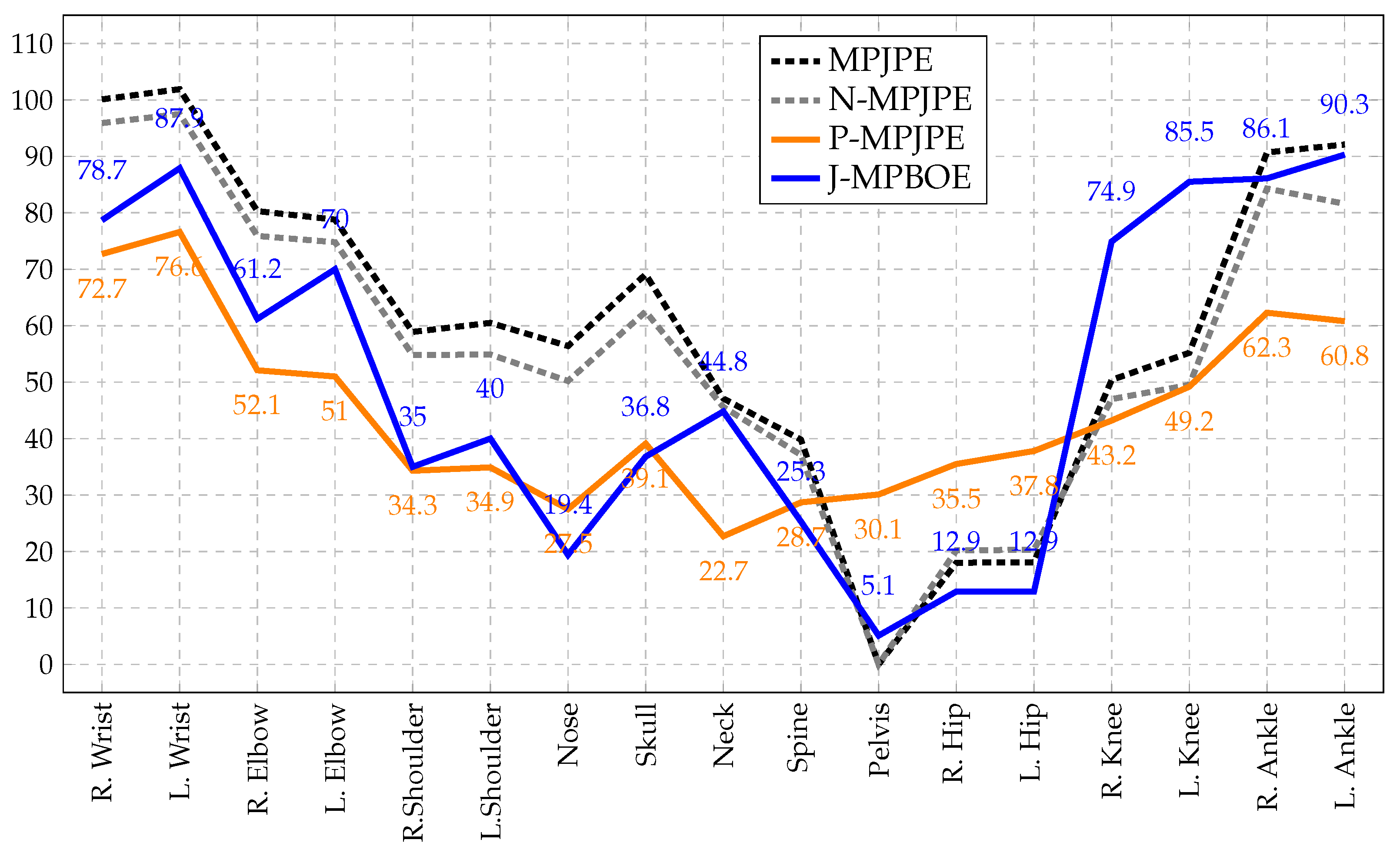
| Semi-Supervision with FS on S1 (16% of TD) and WS on S5–8 | |||||||
|---|---|---|---|---|---|---|---|
| Methods | AG | IM | 2D | MV | MPJPE↓ | P-MPJPE↓ | J-MPBOE↓ |
| EpipolarPose [39] CVPR’19 | 🗸 | FT | 🗸 | 65.3 | 57.2 | - | |
| Iqbal et al. [36] CVPR’20 | 🗸 | † | 🗸 | 62.8 | 51.4 | - | |
| PoseAug [25] CVPR’21 | 🗸 | GT | 56.7 | 42.3 | - | ||
| Amadi and Agam [6] ICIP’22 | GT | 52.6 | 37.3 | 40.6 | |||
| Ours–MvP 🟉 | GT | 🗸 | 48.4 | 34.3 | 37.8 | ||
| Ours–MvP&P 🟉 | GT | 🗸 | 43.5 | 32.7 | 37.2 | ||
| Ours–MvP | HR | 🗸 | 56.1 | 42.2 | 49.2 | ||
| Ours–MvP&P | HR | 🗸 | 54.0 | 41.5 | 49.1 | ||
| Semi-Supervision with FS on S1 (16% of TD) and WS on S5–8 | |||||||
|---|---|---|---|---|---|---|---|
| Methods | AG | IM | 2D | MV | MPJPE↓ | P-MPJPE↓ | J-MPBOE↓ |
| Pavllo et al. [41] CVPR’19 | GT | 49.7 | 36.7 | - | |||
| AdaptPose [26] CVPR’21 | 🗸 | 🗸 | GT | 42.5 | 34.0 | - | |
| Amadi and Agam [6] ICIP’22 | GT | 50.1 | 36.8 | 40.3 | |||
| Ours–MvP 🟉 | GT | 🗸 | 47.0 | 33.3 | 37.2 | ||
| Ours–MvP&P 🟉 | GT | 🗸 | 42.2 | 31.8 | 36.7 | ||
| Ours–MvP | HR | 🗸 | 55.0 | 41.1 | 48.2 | ||
| Ours–MvP&P | HR | 🗸 | 52.4 | 39.7 | 47.5 | ||
| Unpaired 2D–3D Supervision or Weakly/Self-/Unsupervised Methods on S15–8 | |||||||
|---|---|---|---|---|---|---|---|
| Method | NF | IM | 2D | MV | MPJPE↓ | P-MPJPE↓ | J-MPBOE↓ |
| Tung et al. [28] ICCV’17 | 2 | GT | 79.0 | - | - | ||
| Zhou et al. [33] ICCV’17 | 1 | 🗸 | † | 64.9 | - | - | |
| Dabral et al. [47] ECCV’18 ‡ | 20 | 🗸 | † | 52.1 | 36.3 | - | |
| Wang et al. [44] ICCV’19 ‡ | 1 | 🗸 | † | 83.0 | 57.5 | - | |
| RepNet [32] CVPR’19 | 1 | GT | 50.9 | 38.2 | - | ||
| EpipolarPose [39] CVPR’19 | 1 | 🗸 | † | 🗸 | 55.1 | 47.9 | - |
| EpipolarPose [39] CVPR’19 | 1 | 🗸 | FT | 🗸 | 76.6 | 67.5 | - |
| Iqbal et al. [36] CVPR’20 | 1 | 🗸 | † | 🗸 | 69.1 | 55.9 | - |
| TriPose [38] CoRR’21 | 1 | GT | 🗸 | 56.7 | 43.8 | - | |
| TriPose [38] CoRR’21 | 27 | AP | 🗸 | 62.9 | 47.0 | - | |
| CanonPose [37] CVPR’21 | 1 | AP | 🗸 | 74.3 | 53.0 | - | |
| ElePose [55] CVPR’21 | 1 | GT | 64.0 | 36.7 | - | ||
| Ours–MvP&P | 1 | HR | 🗸 | 59.7 | 46.2 | 53.4 | |
| Ours–MvP&P 🟉 | 1 | GT | 🗸 | 52.2 | 39.6 | 46.0 | |
| Ours–MvP&P | 27 | HR | 🗸 | 56.8 | 43.8 | 51.7 | |
| Ours–MvP&P 🟉 | 27 | GT | 🗸 | 48.6 | 37.2 | 44.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amadi, L.; Agam, G. PosturePose: Optimized Posture Analysis for Semi-Supervised Monocular 3D Human Pose Estimation. Sensors 2023, 23, 9749. https://doi.org/10.3390/s23249749
Amadi L, Agam G. PosturePose: Optimized Posture Analysis for Semi-Supervised Monocular 3D Human Pose Estimation. Sensors. 2023; 23(24):9749. https://doi.org/10.3390/s23249749
Chicago/Turabian StyleAmadi, Lawrence, and Gady Agam. 2023. "PosturePose: Optimized Posture Analysis for Semi-Supervised Monocular 3D Human Pose Estimation" Sensors 23, no. 24: 9749. https://doi.org/10.3390/s23249749
APA StyleAmadi, L., & Agam, G. (2023). PosturePose: Optimized Posture Analysis for Semi-Supervised Monocular 3D Human Pose Estimation. Sensors, 23(24), 9749. https://doi.org/10.3390/s23249749








