Crack Monitoring in Rotating Shaft Using Rotational Speed Sensor-Based Torsional Stiffness Estimation with Adaptive Extended Kalman Filters
Abstract
:1. Introduction
2. Design of Adaptive Extended Kalman Filters
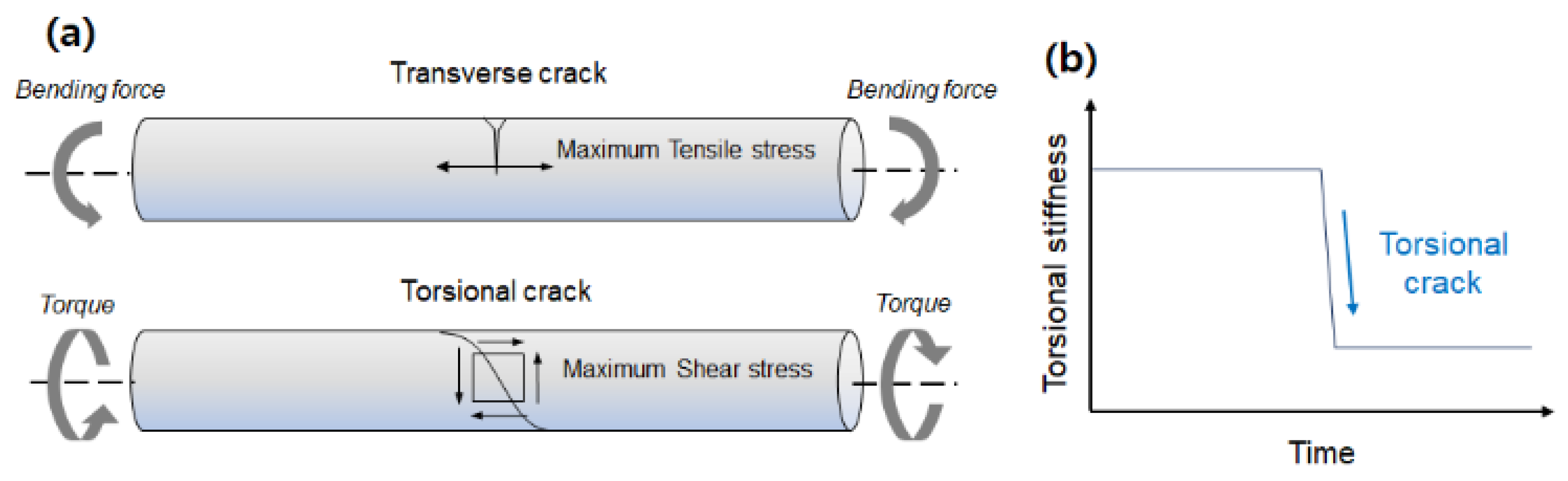
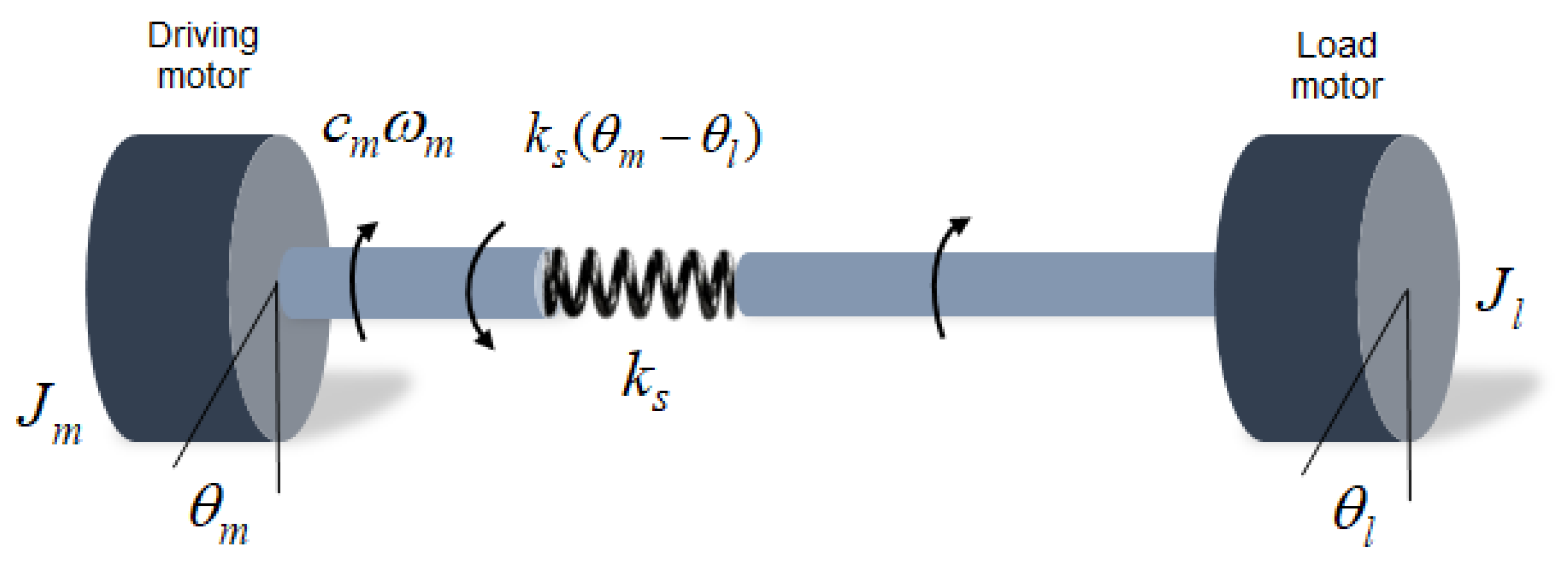
2.1. Dynamic Modeling of Rotating Shaft
2.2. Adaptive Extended Kalman Filters
- ▪
- Initial estimation stage at
- ▪
- Prediction stage
- ▪
- Correction stage
3. Estimation of Shaft Torsional Stiffness
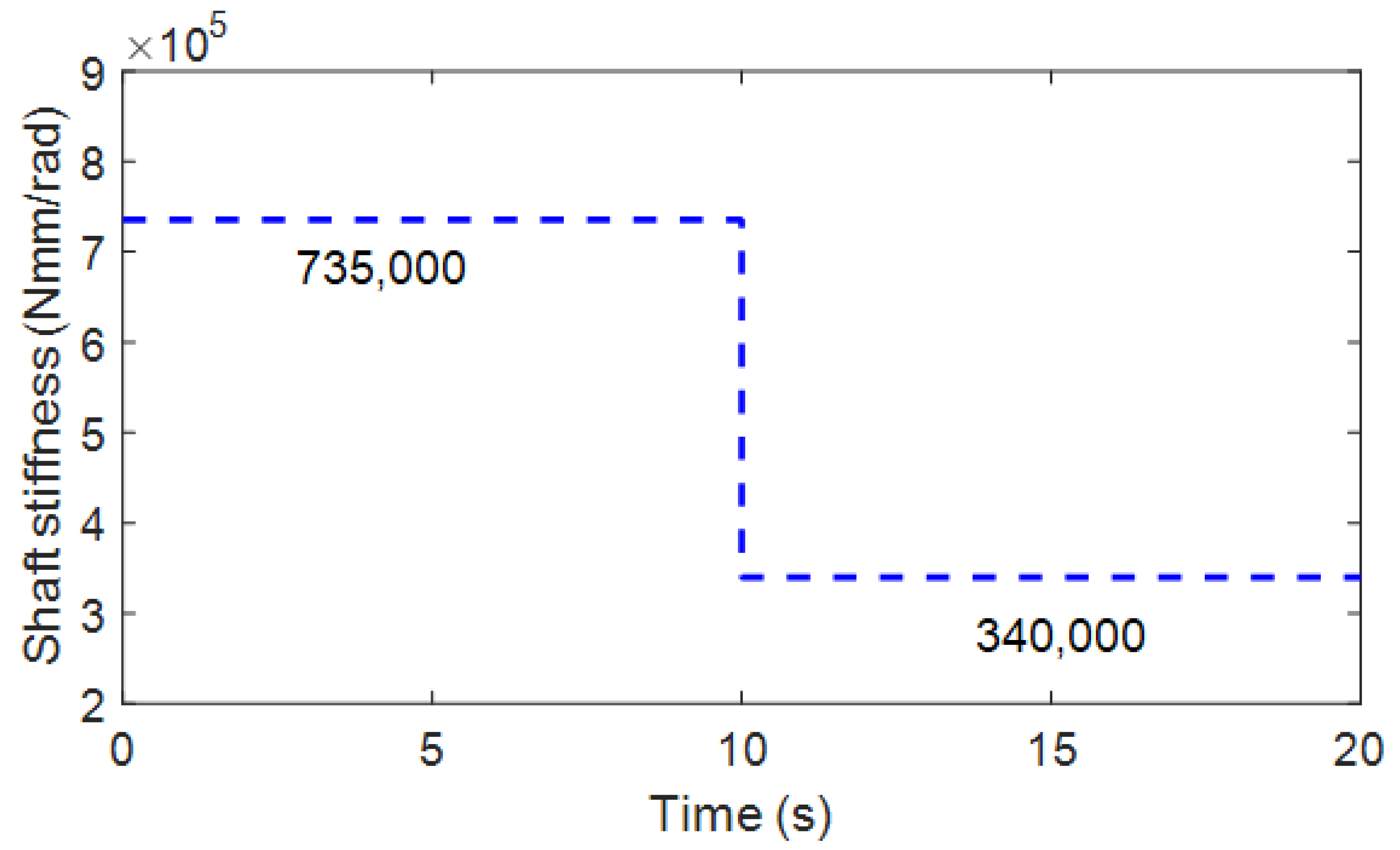
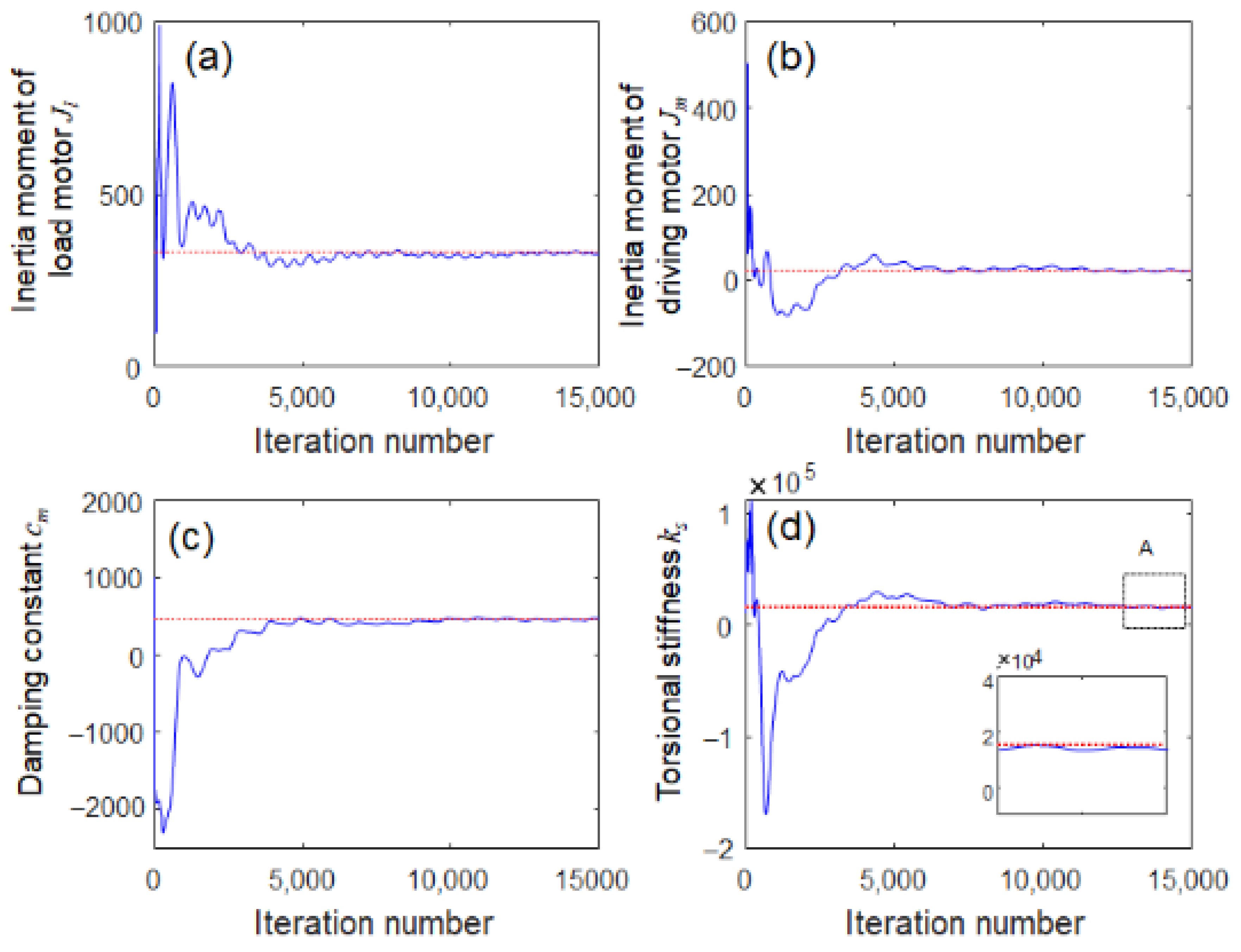
3.1. Simulation Scheme
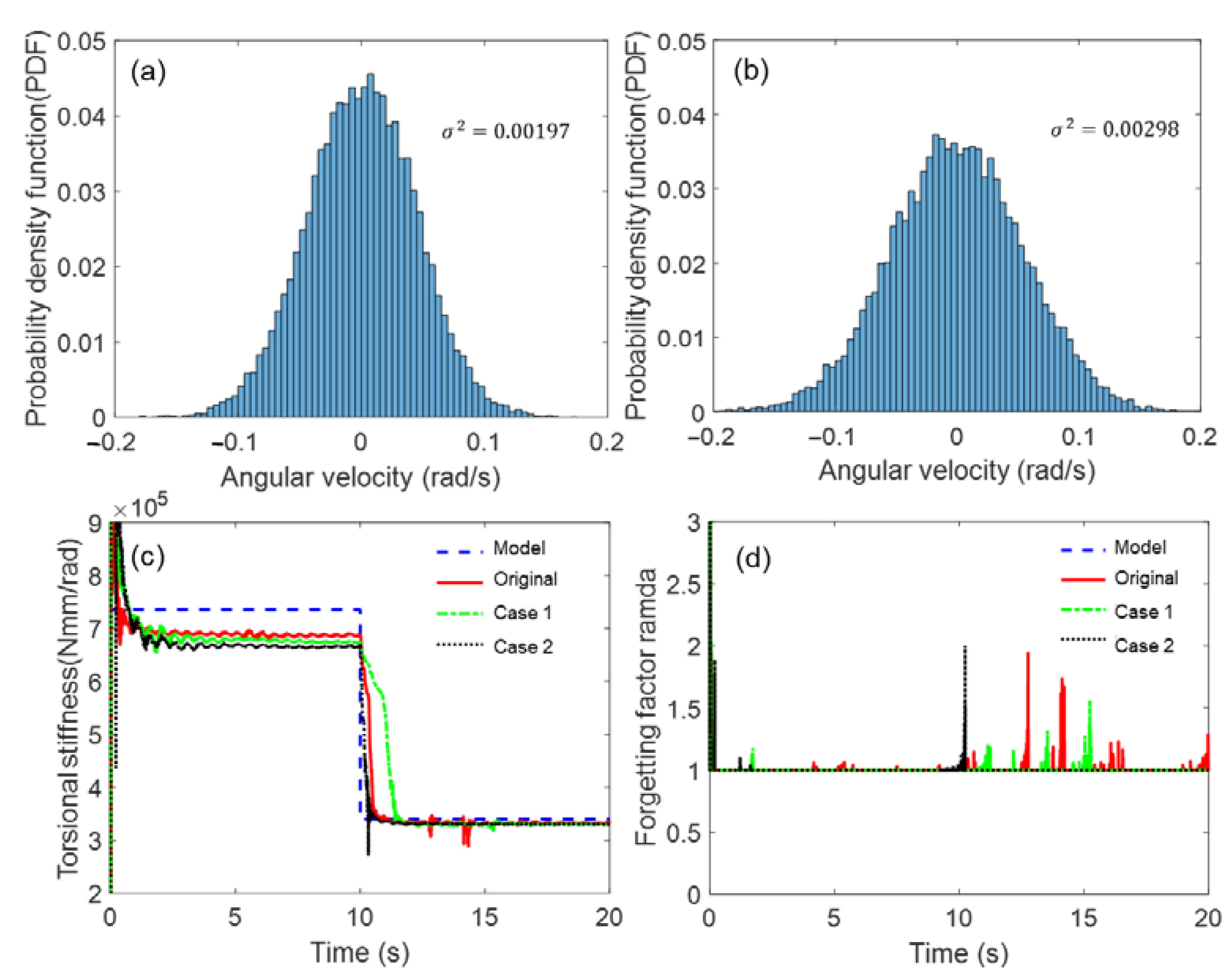
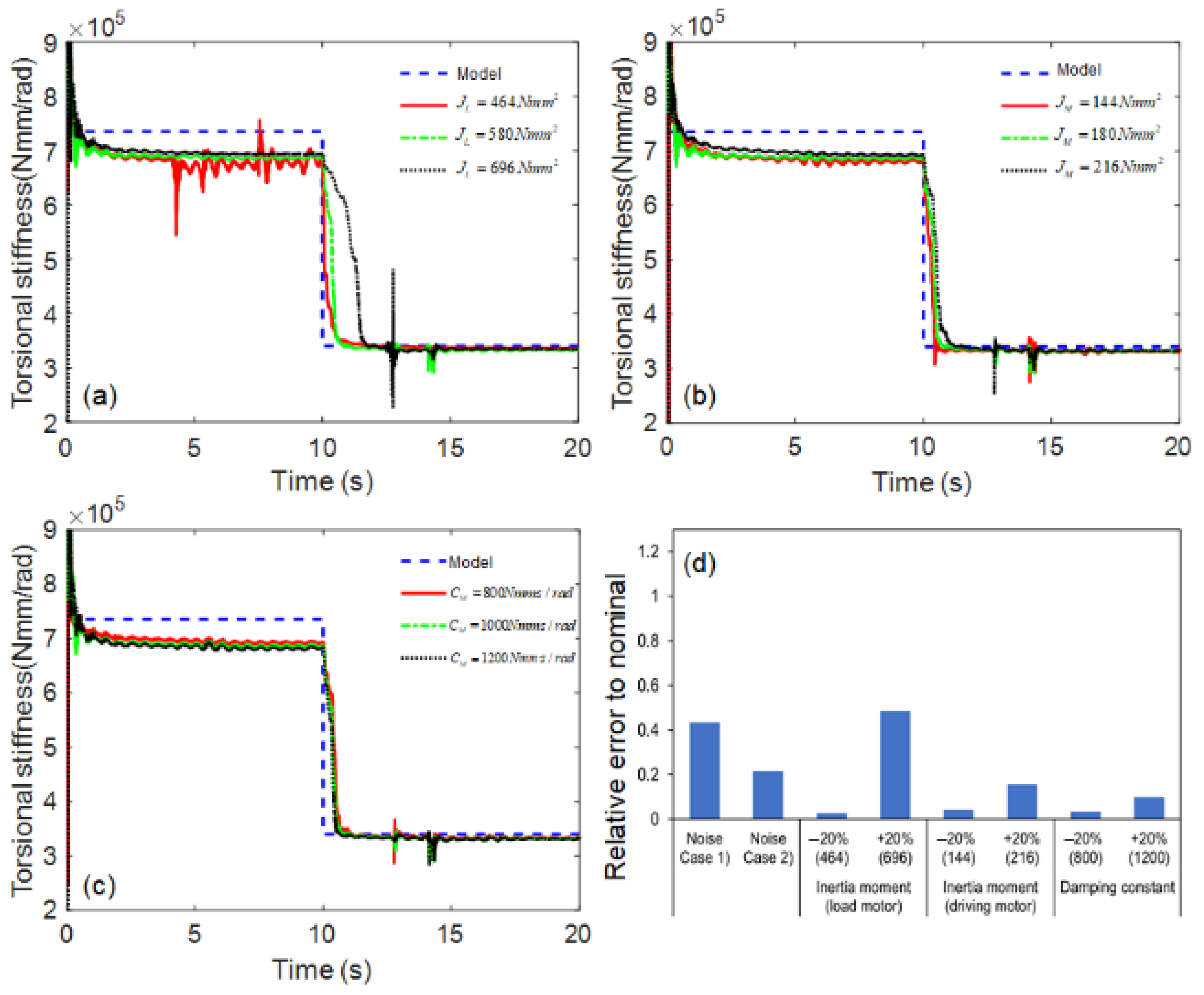
3.2. Robustness Analysis
4. Experimental Validation
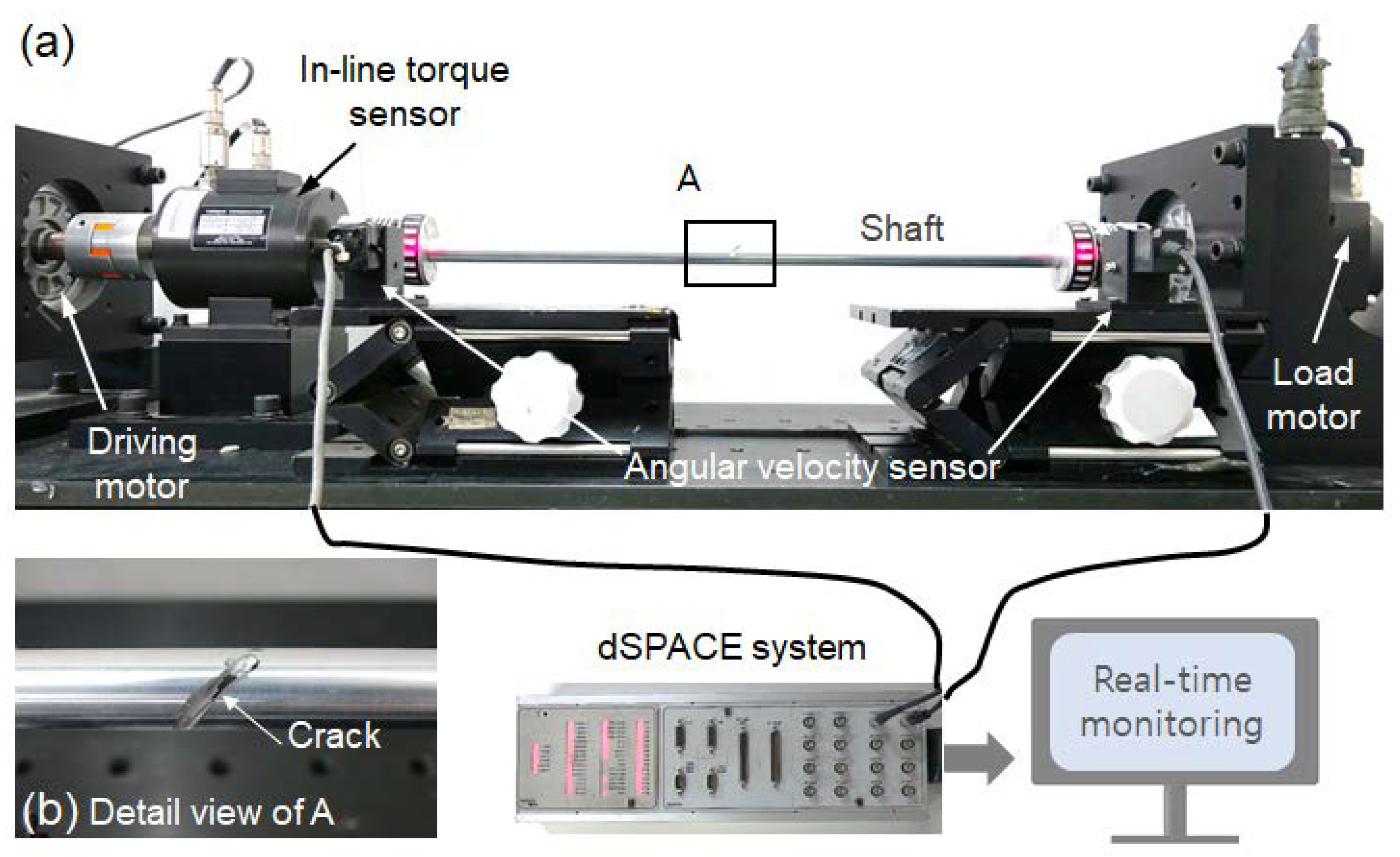
4.1. Experimental Set-Up
- ▪
- Initial estimates
- ▪
- Kalman gain calculation
- ▪
- Parameter update
- ▪
- Covariance update
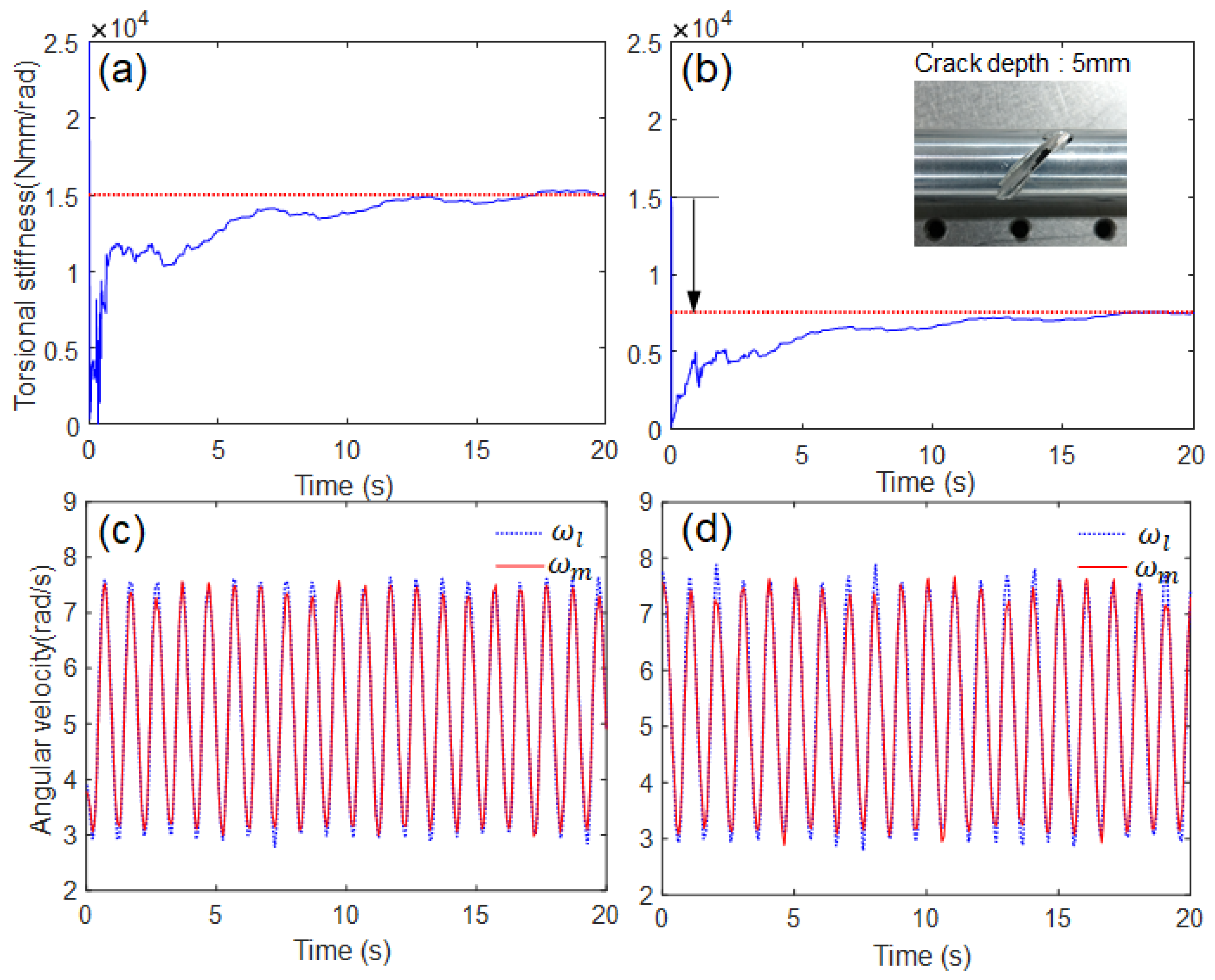
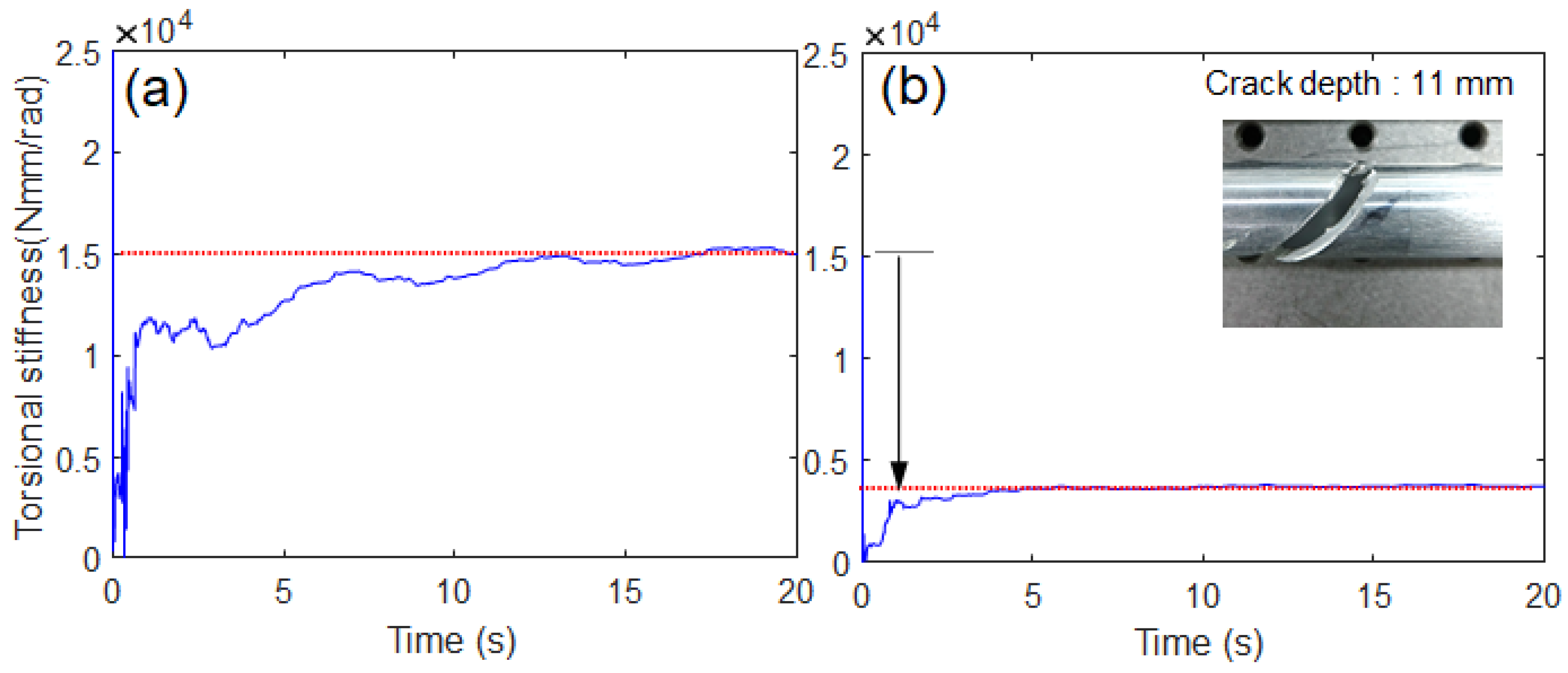
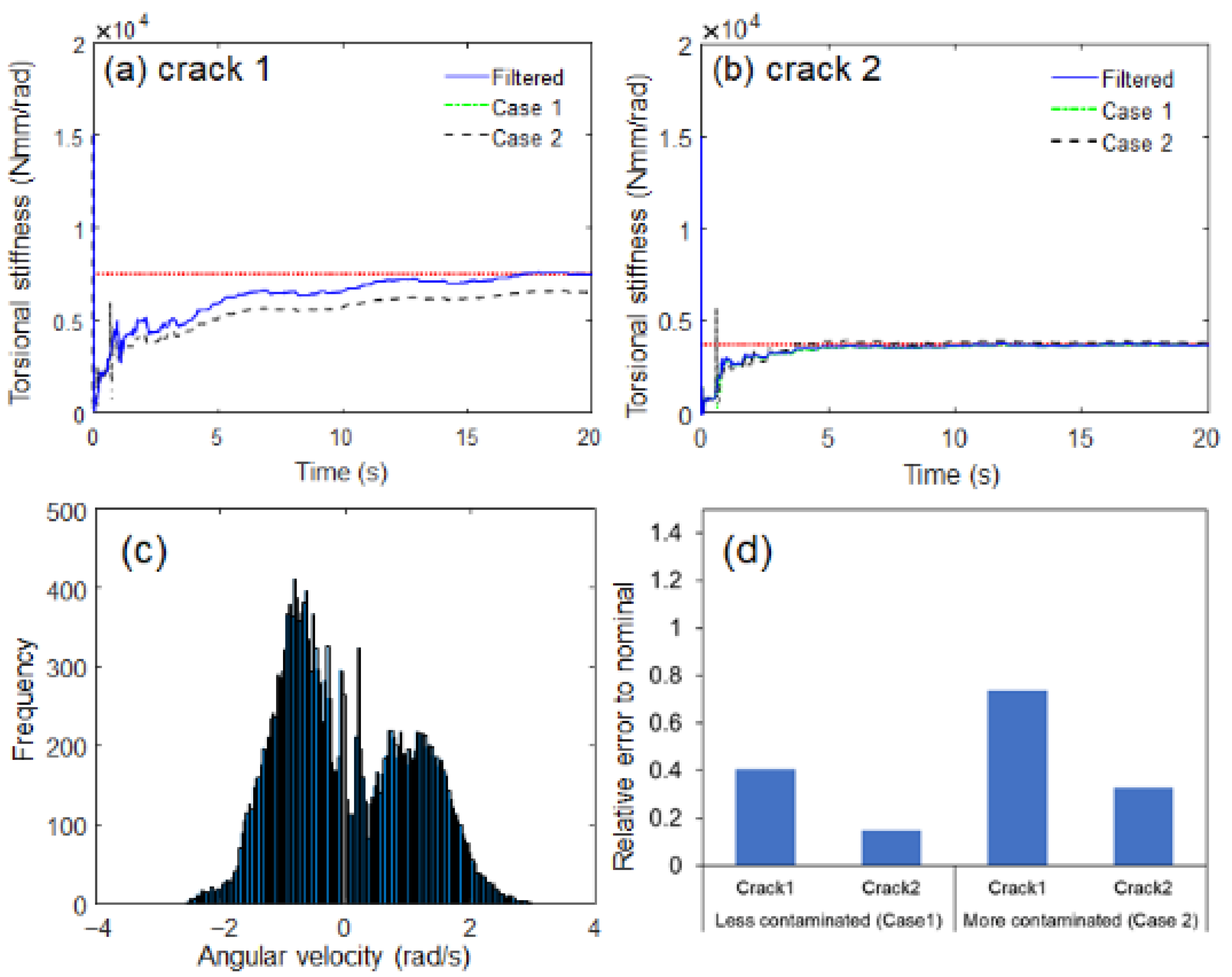
4.2. Results and Discussion
5. Conclusions
- ▪
- We concluded that the proposed approach is a promising alternative means for detecting torsional cracks in rotating shafts despite the difficulty in tuning the Q and R matrices of the AEKF.
- ▪
- The proposed estimation model could not only estimate the decrease in stiffness caused by a crack but also quantitatively evaluate the fatigue crack growth by directly estimating the shaft torsional stiffness.
- ▪
- Another advantage of the proposed approach is that it uses only two cost-effective rotational speed sensors; therefore, it does not require noncontact-type torque sensors, which are typically expensive and suffer from durability limitations.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sabnavis, G.; Kirk, R.G.; Kasarda, M.; Quinn, D. Cracked shaft detection and diagnostics: A literature review. Shock Vib. Dig. 2004, 36, 287. [Google Scholar] [CrossRef]
- Liu, J.; Tang, C.; Pan, G. Dynamic modeling and simulation of a flexible-rotor ball bearing system. J. Vib. Control 2022, 28, 3495–3509. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.; Ni, Q.; Beer, M. A review of vibration-based gear wear monitoring and prediction techniques. Mech. Syst. Signal Process. 2023, 182, 109605. [Google Scholar] [CrossRef]
- Pricop, M.; Pazara, T.; Pricop, C.; Novac, G. Crack detection in rotating shafts using combined wavelet analysis. J. Physics: Conf. Ser. 2019, 1297, 012031. [Google Scholar] [CrossRef]
- Gradzki, R.; Kulesza, Z.; Bartoszewicz, B. Method of shaft crack detection based on squared gain of vibration amplitude. Nonlinear Dyn. 2019, 98, 671–690. [Google Scholar] [CrossRef] [Green Version]
- Kim, G.-W.; Johnson, D.R.; Semperlotti, F.; Wang, K.-W. Localization of breathing cracks using combination tone nonlinear response. Smart Mater. Struct. 2011, 20, 055014. [Google Scholar] [CrossRef]
- Bansode, V.M.; Billore, M. Crack detection in a rotary shaft analytical and experimental analyses: A review. Mater. Today Proc. 2021, 47, 6301–6305. [Google Scholar] [CrossRef]
- Rathna Prasad, S.; Sekhar, A. Detection and localization of fatigue-induced transverse crack in a rotor shaft using principal component analysis. Struct. Health Monit. 2021, 20, 513–531. [Google Scholar] [CrossRef]
- Liang, H.; Zhao, C.; Chen, Y.; Liu, Y.; Zhao, Y. The Improved WNOFRFs Feature Extraction Method and Its Application to Quantitative Diagnosis for Cracked Rotor Systems. Sensors 2022, 22, 1936. [Google Scholar] [CrossRef]
- Sathujoda, P. Detection of a slant crack in a rotor bearing system during shut-down. Mech. Based Des. Struct. Mach. 2020, 48, 266–276. [Google Scholar] [CrossRef]
- Hidle, E.L.; Hestmo, R.H.; Adsen, O.S.; Lange, H.; Vinogradov, A. Early Detection of Subsurface Fatigue Cracks in Rolling Element Bearings by the Knowledge-Based Analysis of Acoustic Emission. Sensors 2022, 22, 5187. [Google Scholar] [CrossRef]
- Reitz, T.; Fritzen, C.-P. A novel baseline-free approach for acousto-ultrasonic crack monitoring of rotating axles. Struct. Health Monit. 2021, 20, 990–1003. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, Z.; Guo, D.; Liu, T.; Xie, Y.; Zhang, D. An Experimental Setup to Detect the Crack Fault of Asymmetric Rotors Based on a Deep Learning Method. Appl. Sci. 2023, 13, 1327. [Google Scholar] [CrossRef]
- Nath, A.G.; Udmale, S.S.; Singh, S.K. Role of artificial intelligence in rotor fault diagnosis: A comprehensive review. Artif. Intell. Rev. 2021, 54, 2609–2668. [Google Scholar] [CrossRef]
- Kim, Y.; Yi, S.; Ahn, H.; Hong, C.-H. Accurate Crack Detection Based on Distributed Deep Learning for IoT Environment. Sensors 2023, 23, 858. [Google Scholar] [CrossRef]
- Yang, J.; Pan, S.; Huang, H. An adaptive extended Kalman filter for structural damage identifications II: Unknown inputs. Struct. Control Health Monit. 2007, 14, 497–521. [Google Scholar] [CrossRef]
- Yang, J.N.; Lin, S.; Huang, H.; Zhou, L. An adaptive extended Kalman filter for structural damage identification. Struct. Control Health Monit. 2006, 13, 849–867. [Google Scholar] [CrossRef]
- Zhou, L.; Wu, S.; Yang, J.N. Experimental study of an adaptive extended Kalman filter for structural damage identification. J. Infrastruct. Syst. 2008, 14, 42–51. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; He, M.; Sun, L.; Wu, D.; Wang, Y.; Qing, X. Weighted adaptive Kalman filtering-based diverse information fusion for hole edge crack monitoring. Mech. Syst. Signal Process. 2022, 167, 108534. [Google Scholar] [CrossRef]
- Wang, Y.; He, M.; Sun, L.; Wu, D.; Wang, Y.; Zou, L. Improved Kalman filtering-based information fusion for crack monitoring using piezoelectric-fiber hybrid sensor network. Front. Mater. 2020, 7, 300. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S.; Adnan, S.B.R.S. Combined state of charge and state of energy estimation of lithium-ion battery using dual forgetting factor-based adaptive extended Kalman filter for electric vehicle applications. IEEE Trans. Veh. Technol. 2021, 70, 1200–1215. [Google Scholar] [CrossRef]
- Al-hababi, T.; Alkayem, N.F.; Zhu, H.; Cui, L.; Zhang, S.; Cao, M. Effective identification and localization of single and multiple breathing cracks in beams under gaussian excitation using time-domain analysis. Mathematics 2022, 10, 1853. [Google Scholar] [CrossRef]
- Lin, Y.; Chu, F. The dynamic behavior of a rotor system with a slant crack on the shaft. Mech. Syst. Signal Process. 2010, 24, 522–545. [Google Scholar] [CrossRef]
- Bishop, G.; Welch, G. An introduction to the Kalman filter. Proc. SIGGRAPH Course 2001, 8, 41. [Google Scholar]
- Chen, B.-C.; Wu, Y.-Y.; Hsieh, F.-C. Estimation of engine rotational dynamics using Kalman filter based on a kinematic model. IEEE Trans. Veh. Technol. 2010, 59, 3728–3735. [Google Scholar] [CrossRef]
- Xia, Q.; Rao, M.; Ying, Y.; Shen, X. Adaptive fading Kalman filter with an application. Automatica 1994, 30, 1333–1338. [Google Scholar] [CrossRef]
- Akhlaghi, S.; Zhou, N.; Huang, Z. In Adaptive adjustment of noise covariance in Kalman filter for dynamic state estimation. In Proceedings of the IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Lee, D.-H.; Yoon, D.-S.; Kim, G.-W. New indirect tire pressure monitoring system enabled by adaptive extended Kalman filtering of vehicle suspension systems. Electronics 2021, 10, 1359. [Google Scholar] [CrossRef]
- Bhalerao, G.N.; Patil, A.A.; Waghulde, K.B.; Desai, S. Dynamic analysis of rotor system with slant cracked shaft. Mater. Today Proc. 2021, 44, 4268–4281. [Google Scholar] [CrossRef]
- Muñoz-Abella, B.; Montero, L.; Rubio, P.; Rubio, L. Determination of the Critical Speed of a Cracked Shaft from Experimental Data. Sensors 2022, 22, 9777. [Google Scholar] [CrossRef]



| Parameters (Unit) | Value |
|---|---|
| Inertia moment of load motor | 580 |
| Inertia moment of driving motor | 180 |
| Damping constant cm (Nmm·s/rad) | 1000 |
| Shaft torsional stiffness ks (Nmm/rad) | 735,000 |
| Parameters (Unit) | Value |
|---|---|
| Inertia moment of load motor | 595 |
| Inertia moment of driving motor | 20 |
| Damping constant cm (Nmm·s/rad) | 280 |
| Shaft torsional stiffness ks (Nmm/rad) | 15,000 |
| P0 | diag[0.1 1 650,000 1] |
| Q | diag[1 2.1 2 2.1] × 10−5 |
| R | diag[9 9] × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, Y.-H.; Lee, H.-B.; Kim, G.-W. Crack Monitoring in Rotating Shaft Using Rotational Speed Sensor-Based Torsional Stiffness Estimation with Adaptive Extended Kalman Filters. Sensors 2023, 23, 2437. https://doi.org/10.3390/s23052437
Park Y-H, Lee H-B, Kim G-W. Crack Monitoring in Rotating Shaft Using Rotational Speed Sensor-Based Torsional Stiffness Estimation with Adaptive Extended Kalman Filters. Sensors. 2023; 23(5):2437. https://doi.org/10.3390/s23052437
Chicago/Turabian StylePark, Young-Hun, Hee-Beom Lee, and Gi-Woo Kim. 2023. "Crack Monitoring in Rotating Shaft Using Rotational Speed Sensor-Based Torsional Stiffness Estimation with Adaptive Extended Kalman Filters" Sensors 23, no. 5: 2437. https://doi.org/10.3390/s23052437
APA StylePark, Y. -H., Lee, H. -B., & Kim, G. -W. (2023). Crack Monitoring in Rotating Shaft Using Rotational Speed Sensor-Based Torsional Stiffness Estimation with Adaptive Extended Kalman Filters. Sensors, 23(5), 2437. https://doi.org/10.3390/s23052437







