Microphones as Airspeed Sensors for Unmanned Aerial Vehicles
Abstract
1. Introduction
2. Design of the Airspeed Instrument
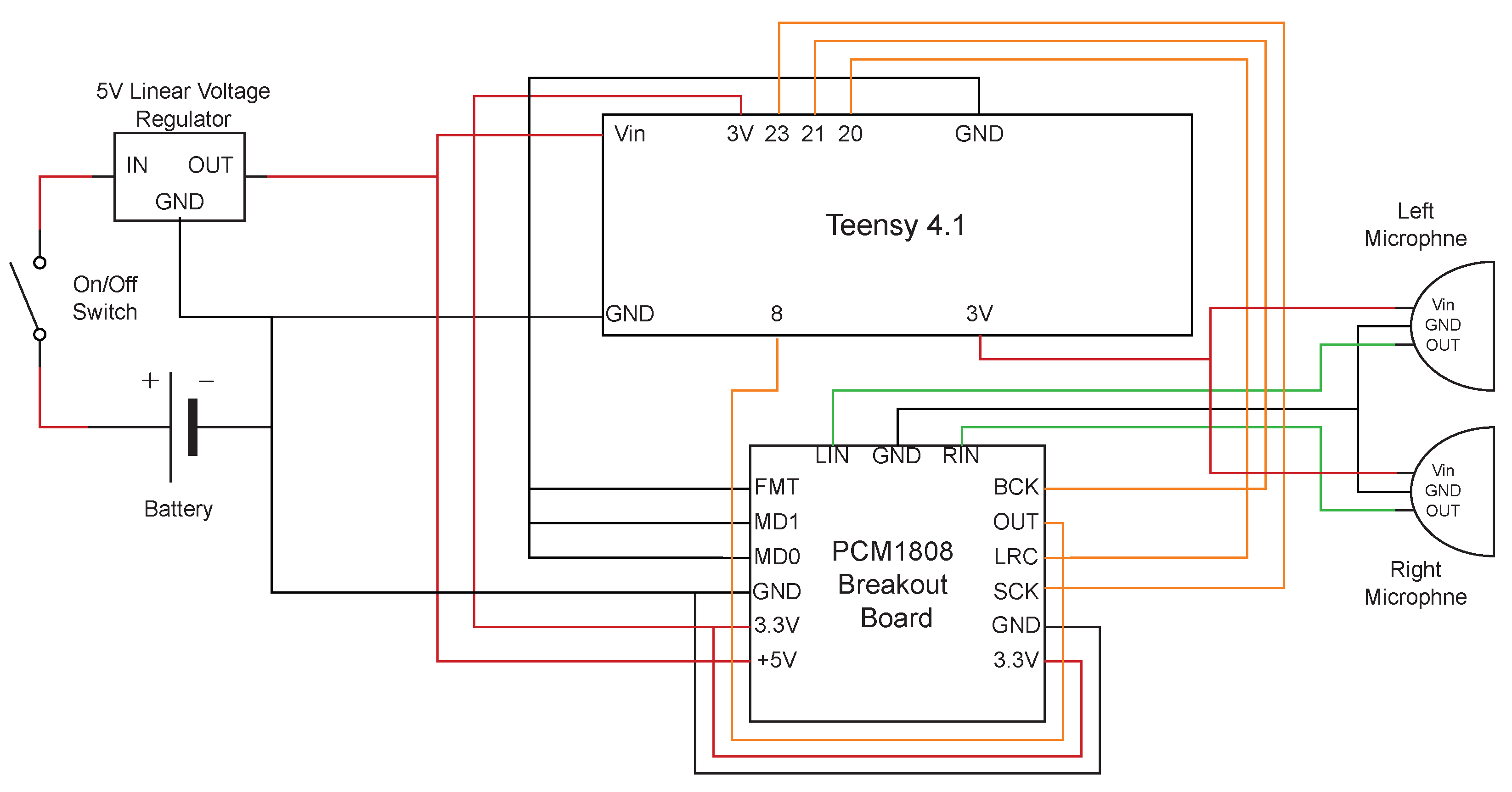
2.1. Microphone Selection and Configuration
2.2. Supporting Components and Configuration of the Instrument Board
3. Experiments
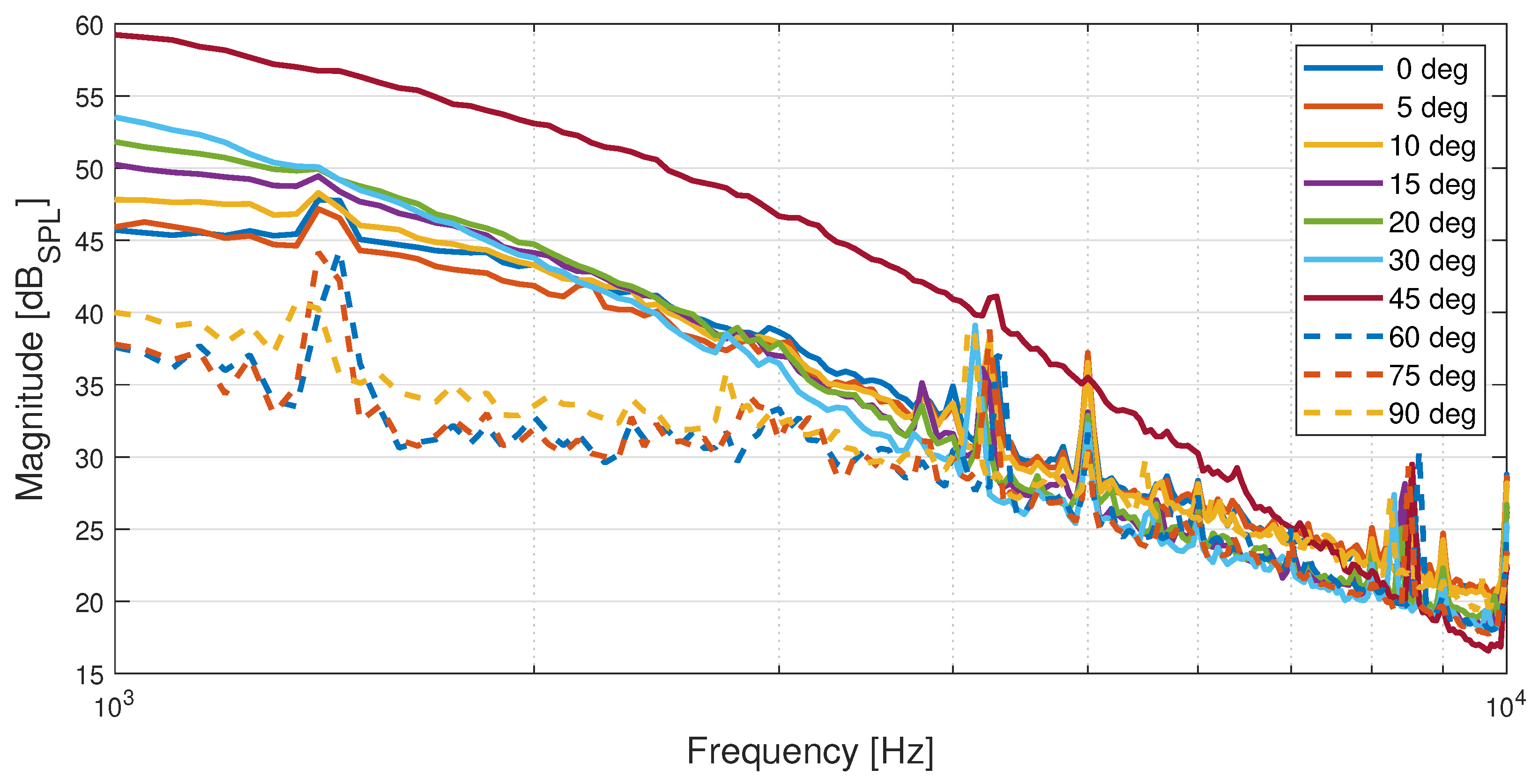
3.1. Wind Tunnel Experiments
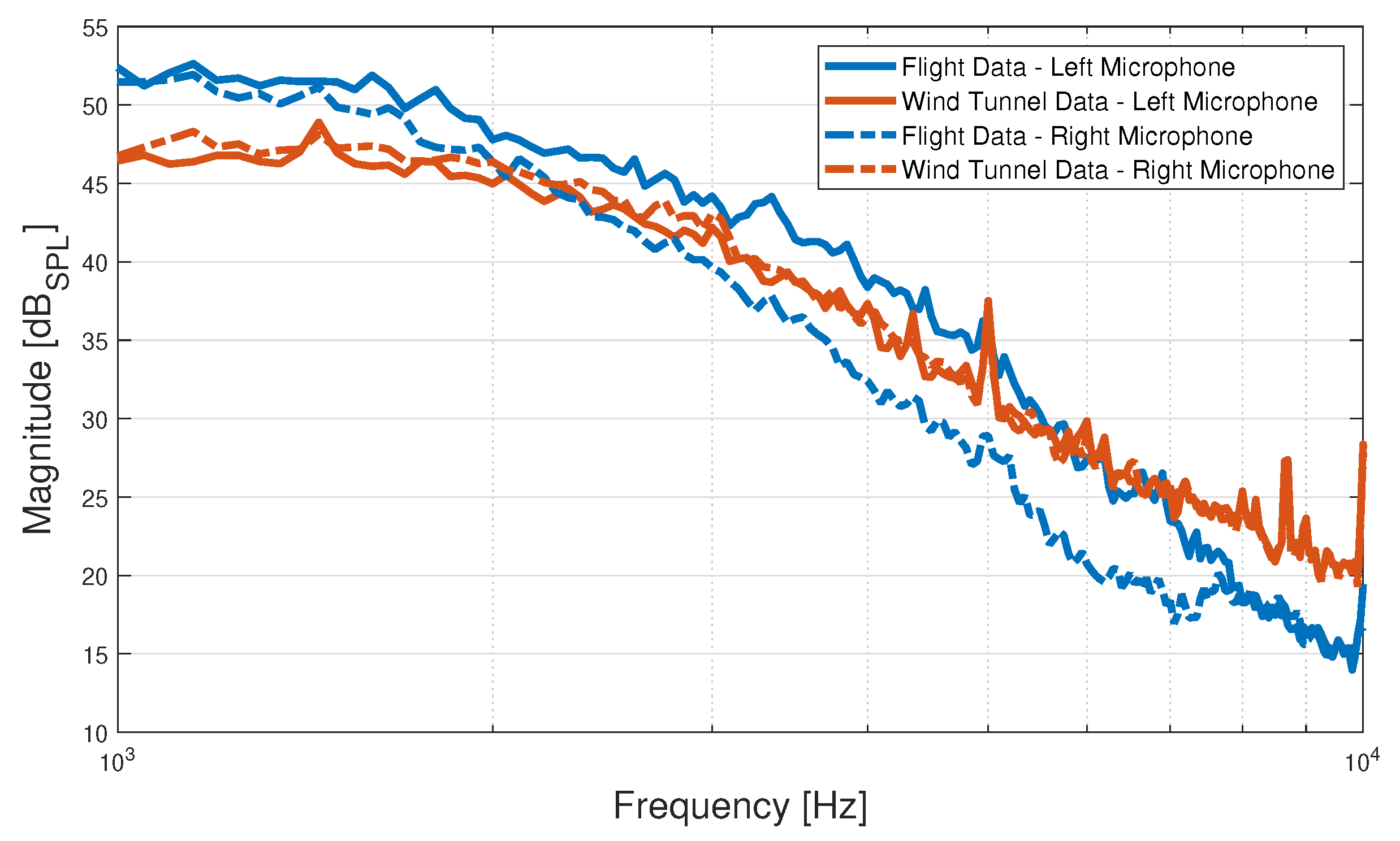
3.2. Flight Experiments
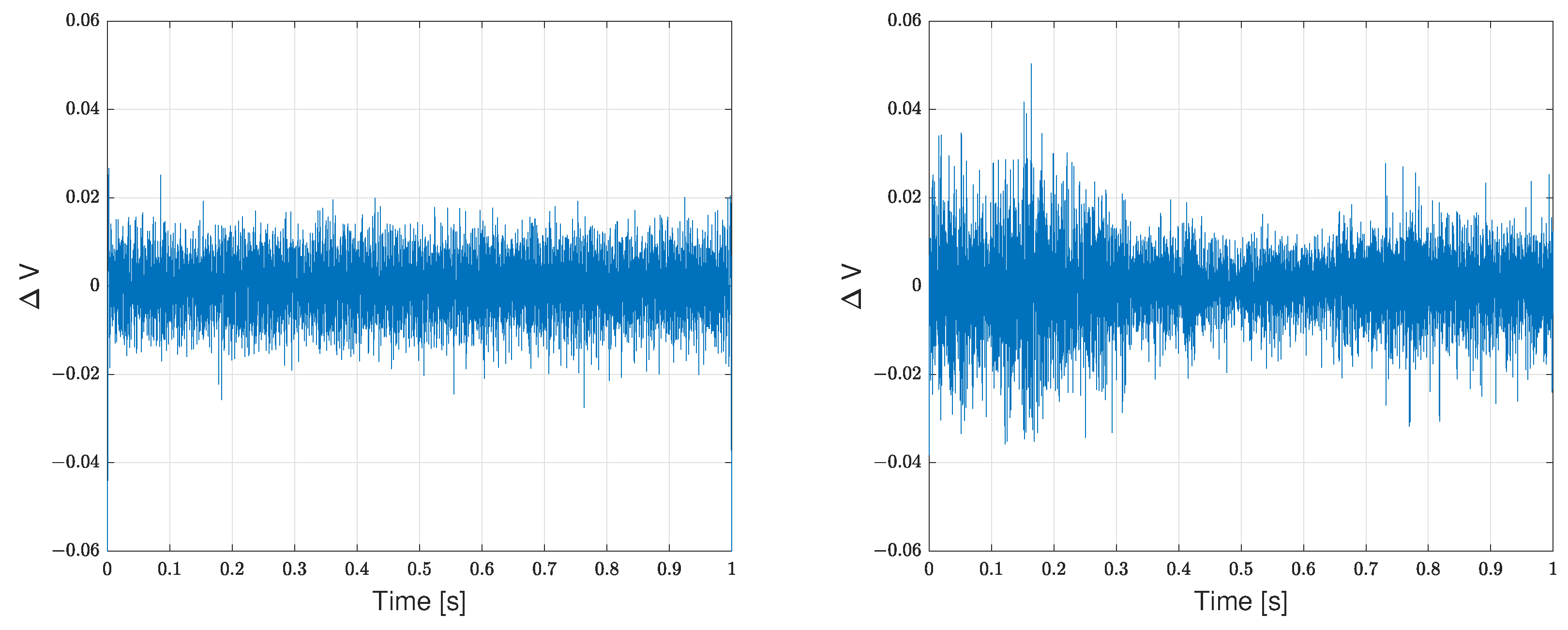
4. Data Processing
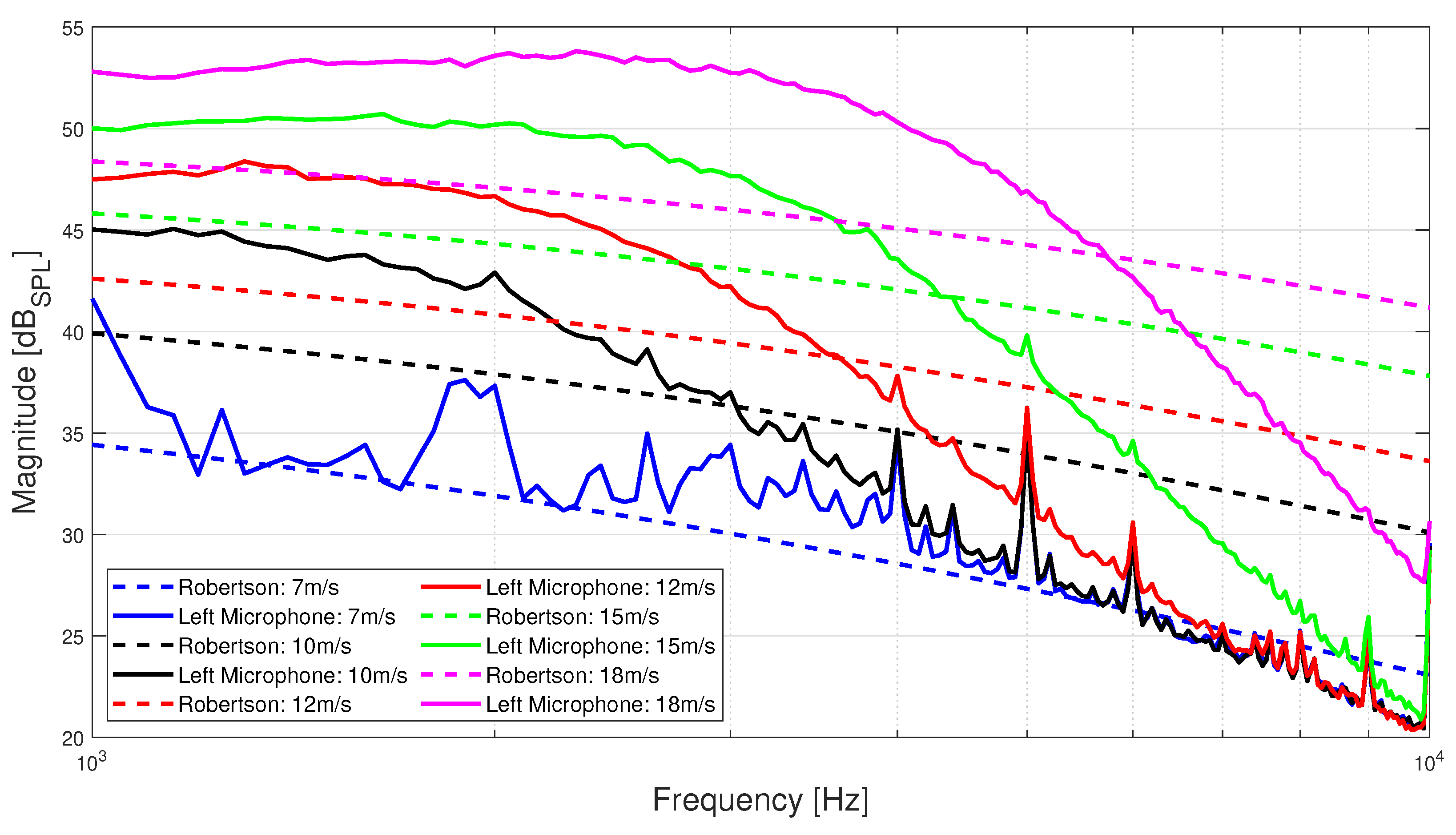
Experimental Data Validation with Semi-Empirical Single-Point Frequency Spectrum Models
5. Modeling
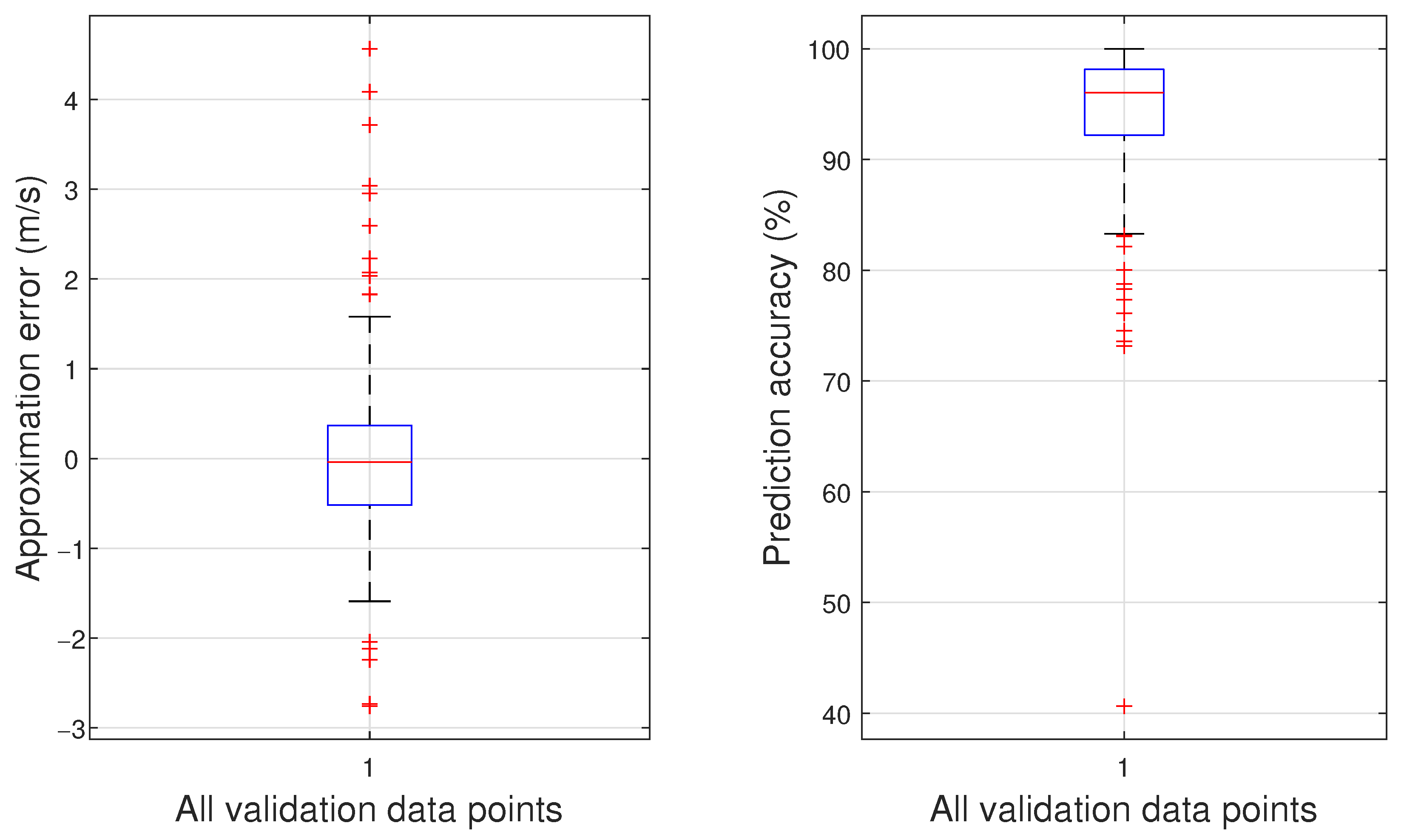
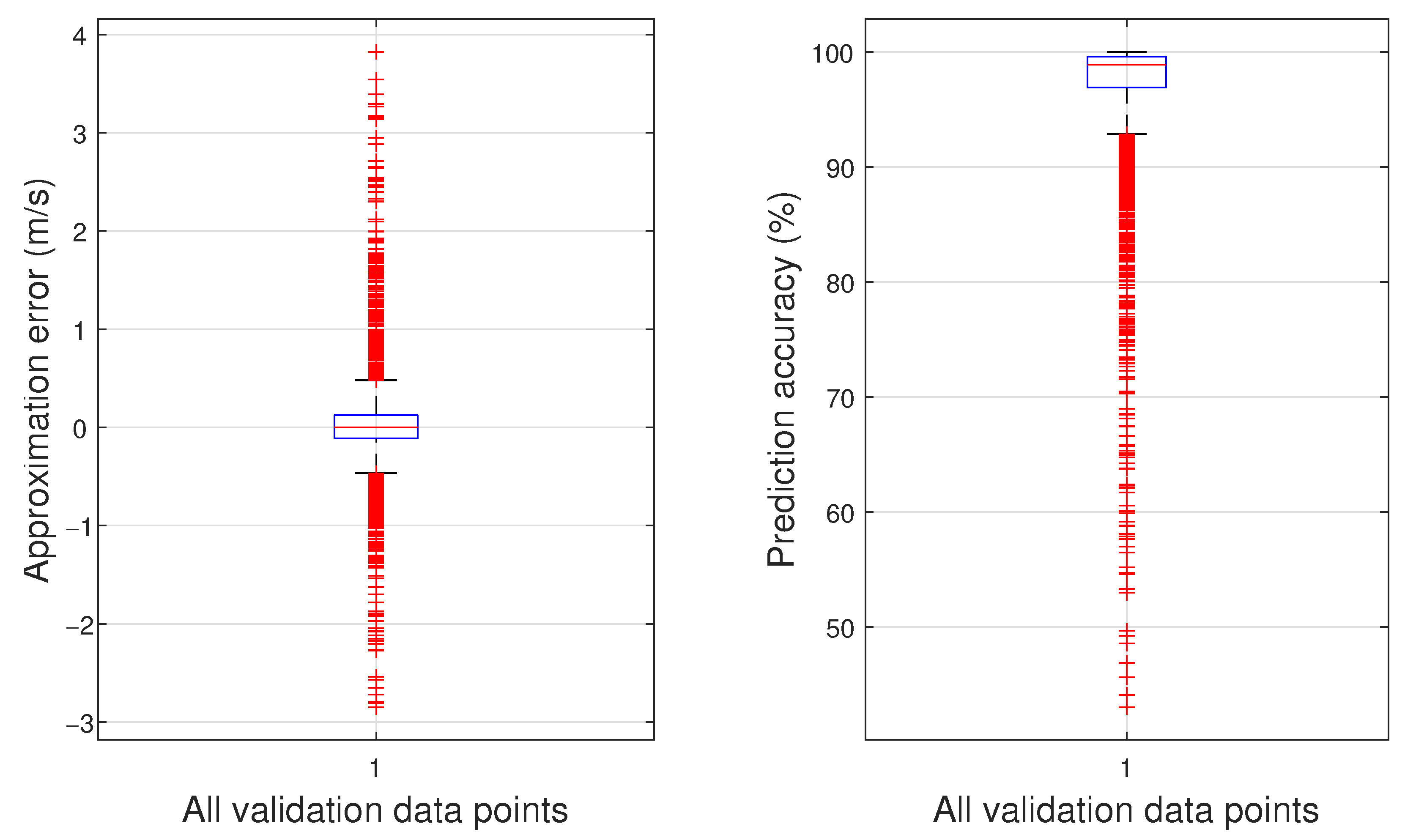
6. Results
Effects of Changing Angle of Attack
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hollister-Short, G.; James, F. History of Technology, 18th ed.; Bloomsbury Publishing: London, UK, 1998; p. 99. [Google Scholar]
- Anderson, J. Fundamentals of Aerodynamics; McGraw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- De Oliveira Buscarini, I.; Barsaglini, A.C.; Jabardo, P.J.S.; Taira, N.M.; Nader, G. Impact of Pitot tube calibration on the uncertainty of water flow rate measurement. J. Phys. Conf. Ser. 2015, 648, 12005–12015. [Google Scholar] [CrossRef]
- Verling, S.L.; Stastny, T.; Siegwart, R. Full Envelope System Identification of a VTOL Tailsitter UAV. In Proceedings of the American Institute of Aeronautics and Astronautics: Scitech Forum 2021, Online, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Hayward, A.T.J. Flowmeters: A Basic Guide and Source-Book for Users, 1st ed.; Palgrave Macmillan: London, UK, 1979. [Google Scholar]
- Wang, S.; Olejnik, D.; Wagter, C.D.; Oudheusden, B.V.; Croon, G.D.; Hamaza, S. Battle the Wind: Improving Flight Stability of a Flapping Wing Micro Air Vehicle Under Wind Disturbance with Onboard Thermistor-Based Airflow Sensing. IEEE Robot. Autom. Lett. 2022, 7, 9605–9612. [Google Scholar] [CrossRef]
- Sikkel, L.; de Croon, G.; De Wagter, C.; Chu, Q. A novel online model-based wind estimation approach for quadrotor micro air vehicles using low cost MEMS IMUs. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 2141–2146. [Google Scholar] [CrossRef]
- Sun, K.; Gebre-Egziabher, D. Air data fault detection and isolation for small UAS using integrity monitoring framework. NAVIGATION J. Inst. Navig. 2021, 68, 577–600. [Google Scholar] [CrossRef]
- Willmarth, W.W. Pressure Fluctuations Beneath Turbulent Boundary Layers. Annu. Rev. Fluid Mech. 1975, 7, 13–36. [Google Scholar] [CrossRef]
- Brungart, T.A.; Lauchle, G.C.; Deutsch, S.; Riggs, E.T. Outer-flow effects on turbulent boundary layer wall pressure fluctuations. J. Acoust. Soc. Am. 1999, 105, 2097–2106. [Google Scholar] [CrossRef]
- Roger, M. Microphone Measurements in Aeroacoustic Installations; Technical Report; University of Lyon: Ecully, France, 2017. [Google Scholar] [CrossRef]
- Smolyakov, A. Calculation of the spectra of pseudosound wall-pressure fluctuations in turbulent boundary layers. Acoust. Phys. 2000, 46, 342–347. [Google Scholar] [CrossRef]
- Rackl, R.G.; Weston, A.R. Modeling of Turbulent Boundary Layer Surface Pressure Fluctuation Auto and Cross Spectra—Verification and Adjustments Based on TU-144LL Data; Technical Report NASA/CR-2005-213938; NASA Center for AeroSpace Information: Hanover, MD, USA, 2005.
- Laganelli, A.L.; Wolfe, H.F. Prediction of fluctuating pressure in attached and separated turbulent boundary-layer flow. J. Aircr. 1993, 30, 962–970. [Google Scholar] [CrossRef]
- Lowson, M.V. Prediction of Boundary Layer Pressure Fluctuations; Technical Report AFFDL-TR-67-167; Air Force Flight Dynamics Laboratory (FDDA): Dayton, OH, USA, 1968.
- Edelman, L.; Pensado, A.; Robinson, S.; Dam, C. Low-Cost Detection of Boundary Layer Separation with Dynamic Pressure Measurements. In Proceedings of the 8TH AIAA Flow Control Conference, Washington, DC, USA, 13–17 June 2016; pp. 1–15. [Google Scholar] [CrossRef]
- Moshkov, P. Experimental determination of wall pressure fluctuations on a Superjet 100 fuselage at level flight conditions. Aerosp. Syst. 2022. [Google Scholar] [CrossRef]
- Panton, R.L.; Goldman, A.; Lowery, R.; Reischman, M. Low-frequency pressure fluctuations in axisymmetric turbulent boundary layers. J. Fluid Mech. 1980, 97, 299–319. [Google Scholar] [CrossRef]
- Bronz, M.; Smeur, E.J.J.; de Marina, H.G.; Hattenberger, G. Development of A Fixed-Wing mini UAV with Transitioning Flight Capability. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Lee, C.; Jiang, X. Flow structures in transitional and turbulent boundary layers. Phys. Fluids 2019, 31, 111301. [Google Scholar] [CrossRef]
- Eargle, J. The Microphone Book: From Mono to Stereo to Surround—A Guide to Microphone Design and Application; Taylor & Francis: Boca Raton, FL, USA, 2012. [Google Scholar]
- Lane, C. Measurement of Turbulent Boundary Layer Induced Surface Pressure Fluctuations. Master’s Thesis, University of Toronto, North York, ON, Canada, 2018. [Google Scholar]
- Van Dercreek, C.; Merino-Martínez, R.; Sijtsma, P.; Snellen, M. Evaluation of the effect of microphone cavity geometries on acoustic imaging in wind tunnels. Appl. Acoust. 2021, 181, 108154. [Google Scholar] [CrossRef]
- Wambsganss, M.W.; Zaleski, P. Measurement, Interpretation, and Characterization of Near-Field Flow Noise; Technical Report; Argonne National Laboratory: Lemont, IL, USA, 1970.
- Simpson, R.L.; Ghodbane, M.; Mcgrath, B.E. Surface pressure fluctuations in a separating turbulent boundary layer. J. Fluid Mech. 1987, 177, 167–186. [Google Scholar] [CrossRef]
- Blitterswyk, J.V.; Rocha, J. Prediction and measurement of flow-induced wall-pressure fluctuations at lowmach numbers. Can. Acoust. 2014, 42, 3–14. [Google Scholar]
- Thomson, N.; Rocha, J. Comparison of Semi-Empirical Single Point Wall Pressure Spectrum Models with Experimental Data. Fluids 2021, 6, 270. [Google Scholar] [CrossRef]
- Merino-Martínez, R.; Rubio Carpio, A.; Lima Pereira, L.T.; van Herk, S.; Avallone, F.; Ragni, D.; Kotsonis, M. Aeroacoustic design and characterization of the 3D-printed, open-jet, anechoic wind tunnel of Delft University of Technology. Appl. Acoust. 2020, 170, 107504. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R. Spectral Analysis of Signals; Pearson Prentice Hall: Hoboken, NJ, USA, 2005. [Google Scholar]
- Harris, F. On the Use of Windows for Harmonic Analysis With the Discrete Fourier Transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Efimtsov, B. The Prediction of the Pressure Fluctuation Field Characteristics of the TBL; Technical Report; TsAGI: Zhukovsky, Russia, 1995. [Google Scholar]
- Goody, M.; Simpson, R.; Chesnakas, C. Surface pressure fluctuations and pressure-velocity correlations produced by a separated flow around a prolate spheroid at incidence. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997. [Google Scholar] [CrossRef]
- Robertson, J.E. Prediction of in Flight Fluctuating Pressure Environments Including Protuberance Induced Flow; Technical Report; Wyle Labs Inc.: El Segundo, CA, USA, 1971. [Google Scholar]
- Parekh, R. Fundamentals of Image, Audio, and Video Processing Using MATLAB®; CRC Press: Boca Raton, FL, USA, 2021; pp. 4–31. [Google Scholar] [CrossRef]
- Ye, C.; Yang, Y.; Fermüller, C.; Aloimonos, Y. On the Importance of Consistency in Training Deep Neural Networks. arXiv 2017, arXiv:1708.00631. [Google Scholar]
- Singh, Y.S.; Devi, B.P.; Singh, K.M. Image compression using Multilayer Feed Forward Artificial Neural Network with Conjugate Gradient. In Proceedings of the 2012 World Congress on Information and Communication Technologies, Trivandrum, India, 30 October–2 November 2012; pp. 976–980. [Google Scholar] [CrossRef]
- Adam, S.; Karras, D.; Magoulas, G.; Vrahatis, M. Solving the linear interval tolerance problem for weight initialization of neural network. Neural Netw. 2014, 54, 17–37. [Google Scholar] [CrossRef] [PubMed]
- Linan, M.N.; Gerardo, B.; Medina, R. Modified weight initialization in the self-organizing map using Nguyen-Widrow initialization algorithm. J. Phys. Conf. Ser. 2019, 1235, 012055. [Google Scholar] [CrossRef]
- Fletcher, L.; Katkovnik, V.; Steffens, F.; Engelbrecht, A. Optimizing the number of hidden nodes of a feedforward artificial neural network. In Proceedings of the 1998 IEEE International Joint Conference on Neural Networks Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98CH36227), Anchorage, AK, USA, 4–9 May 1998; Volume 2, pp. 1608–1612. [Google Scholar] [CrossRef]
- Heaton, J. Introduction to Neural Networks with Java; Heaton Research: Chesterfield, MO, USA, 2008; p. 129. [Google Scholar]
- Mishra, A.; Singh, A. Analysis of flow variation over elliptical nose cone at different angle of attack. Int. J. Adv. Eng. Res. 2020, 20, 1–6. [Google Scholar]






| Airspeed: | 7 m/s | 10 m/s | 12 m/s | 15 m/s | 18 m/s |
| RMSE: | 2.158 dBSPL | 6.294 dBSPL | 8.388 dBSPL | 9.091 dBSPL | 6.857 dBSPL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makaveev, M.; Snellen, M.; Smeur, E.J.J. Microphones as Airspeed Sensors for Unmanned Aerial Vehicles. Sensors 2023, 23, 2463. https://doi.org/10.3390/s23052463
Makaveev M, Snellen M, Smeur EJJ. Microphones as Airspeed Sensors for Unmanned Aerial Vehicles. Sensors. 2023; 23(5):2463. https://doi.org/10.3390/s23052463
Chicago/Turabian StyleMakaveev, Momchil, Mirjam Snellen, and Ewoud J. J. Smeur. 2023. "Microphones as Airspeed Sensors for Unmanned Aerial Vehicles" Sensors 23, no. 5: 2463. https://doi.org/10.3390/s23052463
APA StyleMakaveev, M., Snellen, M., & Smeur, E. J. J. (2023). Microphones as Airspeed Sensors for Unmanned Aerial Vehicles. Sensors, 23(5), 2463. https://doi.org/10.3390/s23052463







