Optical Fiber Magnetic Field Sensors Based on 3 × 3 Coupler and Iron-Based Amorphous Nanocrystalline Ribbons
Abstract
1. Introduction
2. Methods
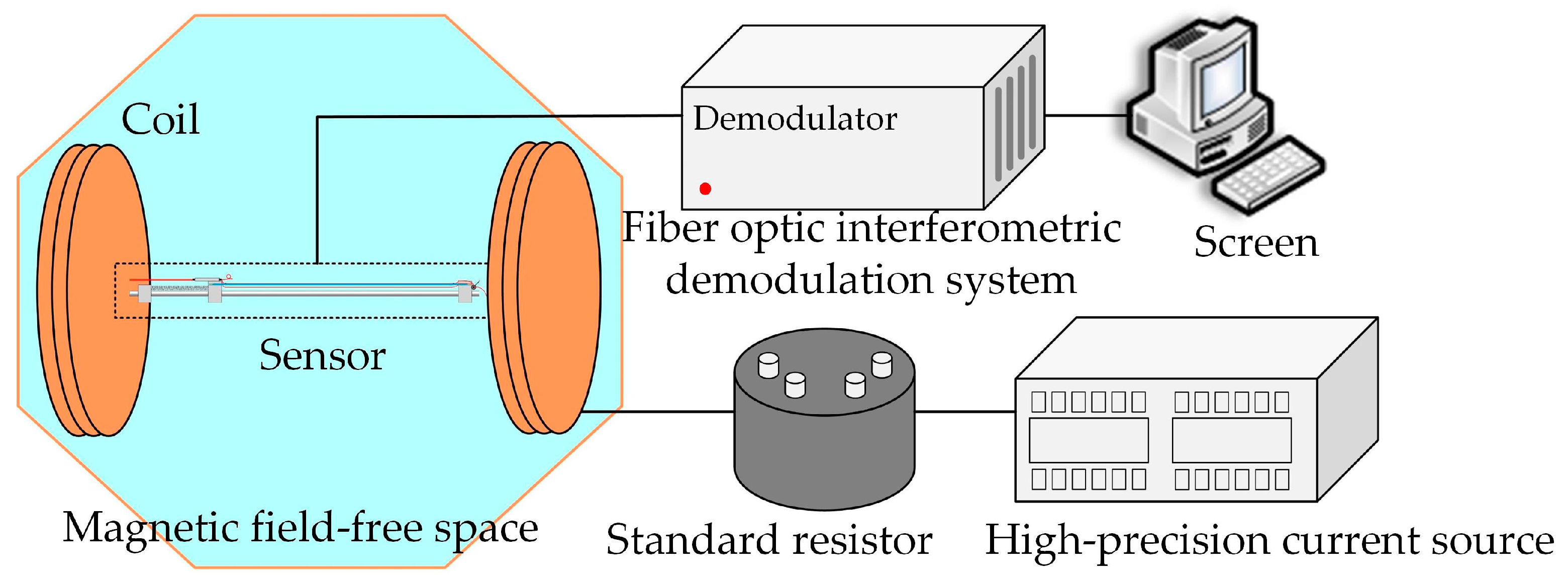
2.1. System Configuration
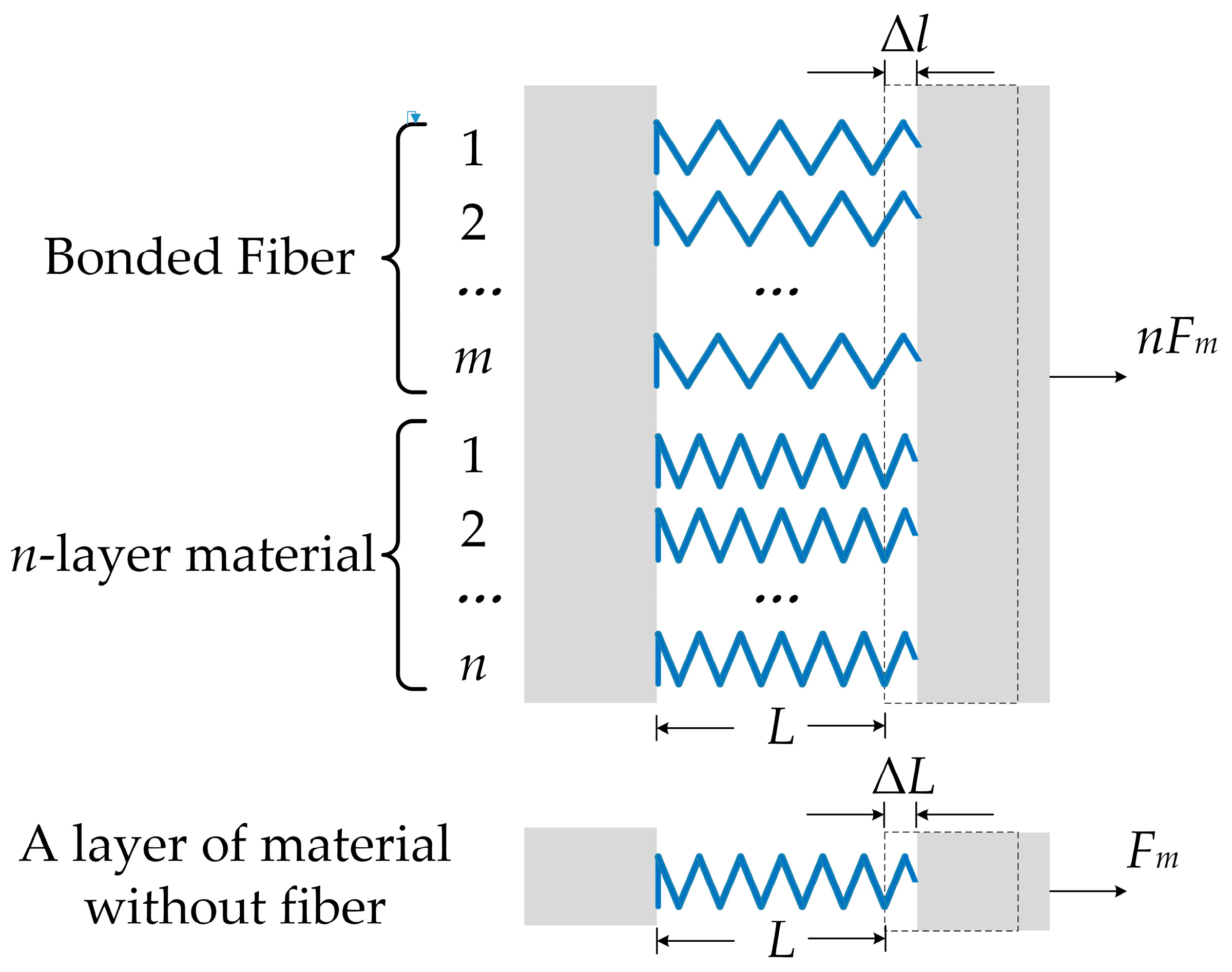
2.2. Theoretical Derivation
- The coefficient q increases with the increase in the magnetic field, but the strain increase is small;
- The coefficient q is a fixed value that does not change with the magnetic field, and the strain and the magnetic field are linear;
- The coefficient q decreases with the increase in the magnetic field, and the magnetostrictive material finally reaches saturation.
2.3. The Principle of Arc Tangent Method
2.4. Experiment Setup
3. Results and Discussion
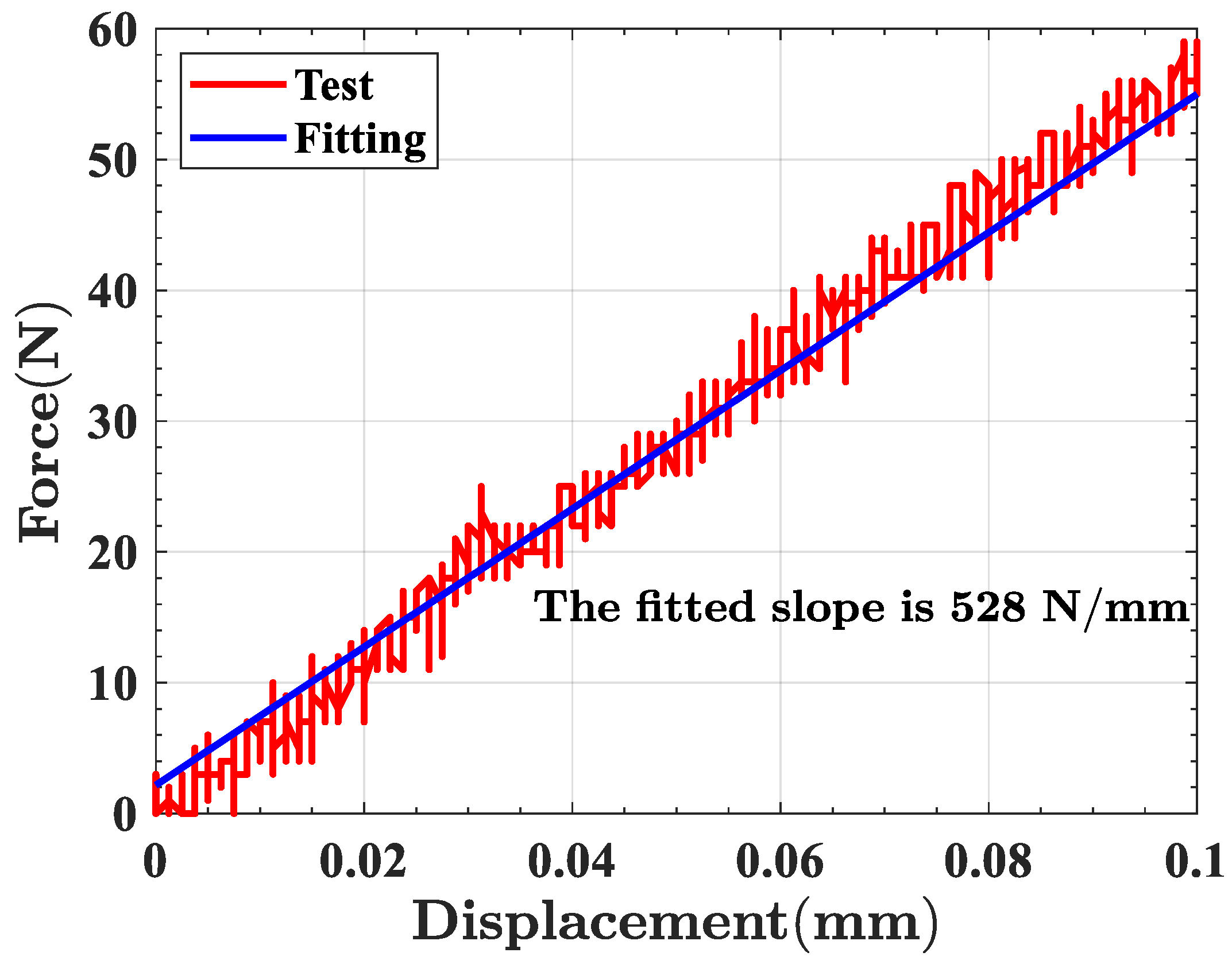
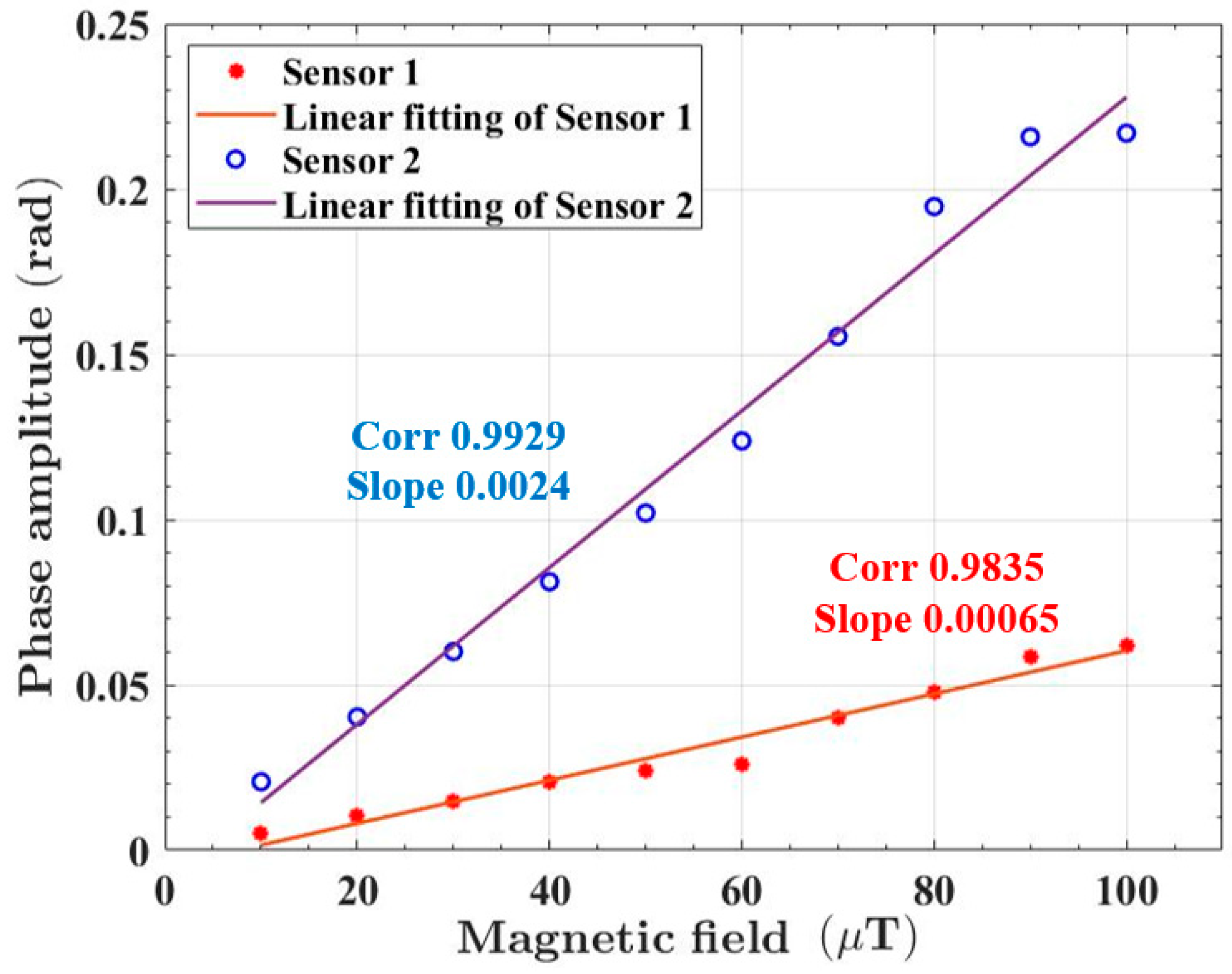
3.1. Linearity
3.2. Frequency Response
3.3. Direction
3.4. Phase Resolution Test of Demodulation System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


Appendix B

References
- Feng, D.Q.; Gao, Y.; Zhu, T.; Deng, M.; Zhang, X.H.; Kai, L. High-Precision Temperature-Compensated Magnetic Field Sensor Based on Optoelectronic Oscillator. J. Light. Technol. 2021, 39, 2559–2564. [Google Scholar] [CrossRef]
- Rui, M.; Wen-tao, Z.; Zhao-gang, W.; Wen-zhu, H.; Fang, L. Magnetic Sensor Based on Terfenol-D Materials and Fiber Bragg Grating Fabry-Perot Cavity. Acta Photonica Sin. 2018, 47, 200–206. [Google Scholar]
- Sun, R.; Zhang, L.; Wei, H.; Gu, Y.; Pang, F.; Liu, H.; Wang, T. Quasi-Distributed Magnetic Field Fiber Sensors Integrated with Magnetostrictive Rod in OFDR System. Electronics 2022, 11, 1013. [Google Scholar] [CrossRef]
- Gerislioglu, B.; Dong, L.; Ahmadivand, A.; Hu, H.; Nordlander, P.; Halas, N.J. Monolithic Metal Dimer-on-Film Structure: New Plasmonic Properties Introduced by the Underlying Metal. Nano Lett. 2020, 20, 2087–2093. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.H.; Wang, M.G.; Wu, B.L.; Han, M.Y.; Yin, B.; Cao, J.H.; Wang, C.C. Temperature-Insensitive Magnetic Field Sensor Based on an Optoelectronic Oscillator Merging a Mach-Zehnder Interferometer. IEEE Sens. J. 2020, 20, 7053–7059. [Google Scholar] [CrossRef]
- Kumar, A.; Kaur, D. Magnetoelectric heterostructures for next-generation MEMS magnetic field sensing applications. J. Alloys Compd. 2022, 897, 163091. [Google Scholar] [CrossRef]
- Fedotov, I.V.; Blakley, S.M.; Serebryannikov, E.E.; Hemmer, P.; Scully, M.O.; Zheltikov, A.M. High-resolution magnetic field imaging with a nitrogen-vacancy diamond sensor integrated with a photonic-crystal fiber. Opt Lett. 2016, 41, 472–475. [Google Scholar] [CrossRef]
- Filograno, M.L.; Pisco, M.; Catalano, A.; Forte, E.; Aiello, M.; Cavaliere, C.; Soricelli, A.; Davino, D.; Visone, C.; Cutolo, A.; et al. Triaxial Fiber Optic Magnetic Field Sensor for Magnetic Resonance Imaging. J. Light. Technol. 2017, 35, 3924–3933. [Google Scholar] [CrossRef]
- Prasai, C.; Krause, B.; McMullin, L.; Tayag, T.J.; Sanders, G.A.; Lieberman, R.A.; Scheel, I.U. Design considerations of a fiber interferometric magnetic sensor. In Proceedings of the Fiber Optic Sensors and Applications XVI, Baltimore, ML, USA, 16-–17 April 2019. [Google Scholar]
- Cui, L. Fiber-Optic All-Polarization Sagnac Magnetic Field Sensor; Zhejiang University: Zhejiang, China, 2021. [Google Scholar]
- Dandridge, A.; Tveten, A.B.; Sigel, G.H.; West, E.J.; Giallorenzi, T.G. Optical fiber magnetic-field sensors. Electron. Lett. 1980, 16, 408–409. [Google Scholar] [CrossRef]
- Hileman, Z.; Homa, D.; Ma, L.M.; Dong, B.; Martin, E.; Pickrell, G.; Wang, A.B. Development of a Multimaterial Optical Fiber for Fully Distributed Magnetic Sensing Applications. IEEE Sens. Lett. 2022, 6, 4. [Google Scholar] [CrossRef]
- Lopez, J.D.; Dante, A.; Carvalho, C.C.; Allil, R.; Werneck, M.M. Simulation and experimental study of FBG-based magnetic field sensors with Terfenol-D composites in different geometric shapes. Measurement 2021, 172, 7. [Google Scholar] [CrossRef]
- Ikeda, A.; Matsuda, Y.H.; Tsuda, H. Note: Optical filter method for high-resolution magnetostriction measurement using fiber Bragg grating under millisecond-pulsed high magnetic fields at cryogenic temperatures. Rev. Sci. Instrum. 2018, 89, 3. [Google Scholar] [CrossRef] [PubMed]
- Cheng, W.R.; Luo, T.M.; Cheng, L.H.; Liang, H.; Guan, B.O. Miniature Fiber-Optic Magnetic Field Sensor Based on Ampere Force and Fiber Laser. Photonic Sens. 2020, 10, 291–297. [Google Scholar] [CrossRef]
- Pang, F.F.; Zheng, H.Q.; Liu, H.H.; Yang, J.F.; Chen, N.; Shang, Y.N.; Ramachandran, S.; Wang, T.Y. The Orbital Angular Momentum Fiber Modes for Magnetic Field Sensing. IEEE Photonics Technol. Lett. 2019, 31, 893–896. [Google Scholar] [CrossRef]
- Yue, C.X.; Ding, H.; Liu, X.F. Magnetic-Field Measurement Based on Multicore Fiber Taper and Magnetic Fluid. IEEE Trans. Instrum. Meas. 2019, 68, 688–692. [Google Scholar] [CrossRef]
- Kaplan, N.; Jasenek, J.; Cervenova, J.; Usakova, M. Magnetic Optical FBG Sensors Using Optical Frequency-Domain Reflectometry. IEEE Trans. Magn. 2019, 55, 4. [Google Scholar] [CrossRef]
- Yariv, A.; Winsor, H.V. Proposal for detection of magnetic-fields through magnetostrictive perturbation of optical fibers. Opt. Lett. 1980, 5, 87–89. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, X.; Hu, Y.; Ni, M.; Yu, Y. All Polarization-Maintaining Fiber Earth Magnetic Field Sensor. Chin. J. Lasers 2005, 32, 1515–1518. [Google Scholar]
- Bibby, Y.W.; Larson, D.C.; Tyagi, S.; Bobb, L.C. Fiber Optic Magnetic Field Sensors Using Metallic-Glass-Coated Optical Fibers. In Proceedings of the Optical Fiber Sensors, Monterey, CA, USA, 29–31 January 1992; p. 22. [Google Scholar]
- Chen, F.; Jiang, Y.; Jiang, L. 3 x 3 coupler based interferometric magnetic field sensor using a TbDyFe rod. Appl. Opt. 2015, 54, 2085–2090. [Google Scholar] [CrossRef]
- Dagenais, D.M.; Bucholtz, F.; Koo, K.P.; Dandridge, A. Demonstration of 3pt-square-root-(hz) at 10hz in a fibre-optic magnetometer. Electron. Lett. 1988, 24, 1422–1423. [Google Scholar] [CrossRef]
- Bucholtz, F.; Villarruel, C.A.; Kirkendall, C.K.; Dagenais, M.; McVicker, J.A.; Davis, A.R.; Patrick, S.S.; Koo, K.P.; Wathen, K.G.; Dandridge, A. Fiber optic magnetometer system for undersea applications. Electron. Lett. 1993, 29, 1032–1033. [Google Scholar] [CrossRef]
- Wang, X.; Chen, S.; Du, Z.; Wang, X.; Shi, C.; Chen, J. Experimental Study of Some Key Issues on Fiber-Optic Interferometric Sensors Detecting Weak Magnetic Field. IEEE Sens. J. 2008, 8, 1173–1179. [Google Scholar] [CrossRef]
- Hongwen, L. Mechanics of Materials I; Higher Education Press: Beijing, China, 2017. [Google Scholar]
- Yanbiao, L.; Min, L.; Li, X. Fiber Optics; Tsinghua University Press: Beijing, China, 2021. [Google Scholar]
- Chikazumi, S. Physics of Ferromagnetism; Lanzhou University Press: Lanzhou, China, 2002. [Google Scholar]
- Feng, X.; Jiang, Y.; Zhang, H. A mechanical amplifier based high-finesse fiber-optic Fabry–Perot interferometric sensor for the measurement of static magnetic field. Meas. Sci. Technol. 2021, 32, 125106. [Google Scholar] [CrossRef]
- Fangyu, J. Research of Fiber Bragg Grating Magnetic Sensor Based on Magnetostrictive Materials. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2018. [Google Scholar]
- Li, H.; Zhang, W.; Zhang, J.; Huang, W. Fiber optic jerk sensor. Opt. Express 2022, 30, 5585–5595. [Google Scholar] [CrossRef] [PubMed]
- Todd, M.D.; Seaver, M.; Bucholtz, F. Improved, operationally-passive interferometric demodulation method using 3 × 3 coupler. Electron. Lett. 2002, 38, 784–786. [Google Scholar] [CrossRef]
- Youlong, Y.; Shengchun, L.; Shikui, L.; Jintao, Z. Method for the measurement of the long difference between two arms of unbalance all-fiber interferometer. J. Nat. Sci. Heilongjiang Univ. 2005, 22, 216–218, 223. [Google Scholar] [CrossRef]






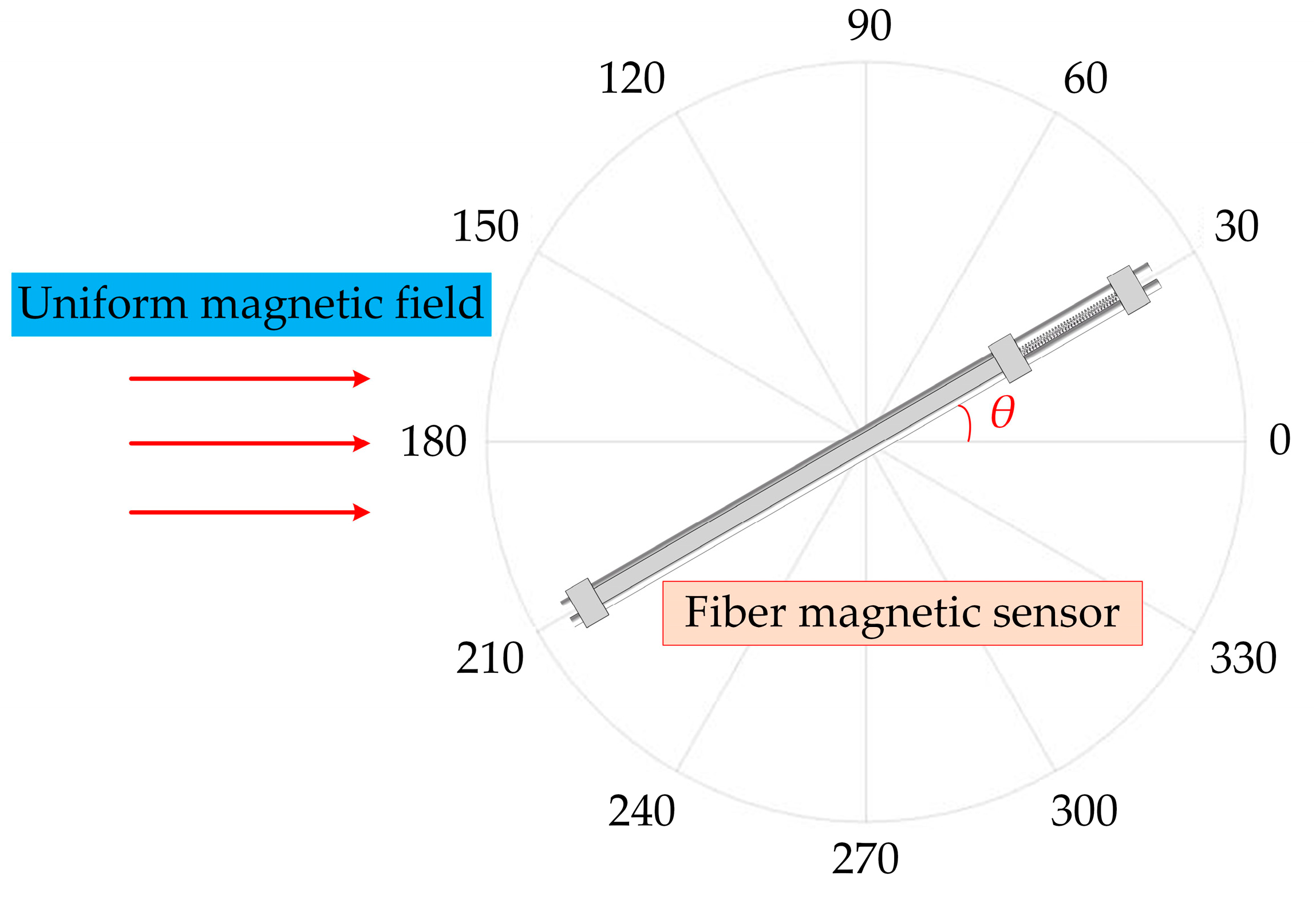
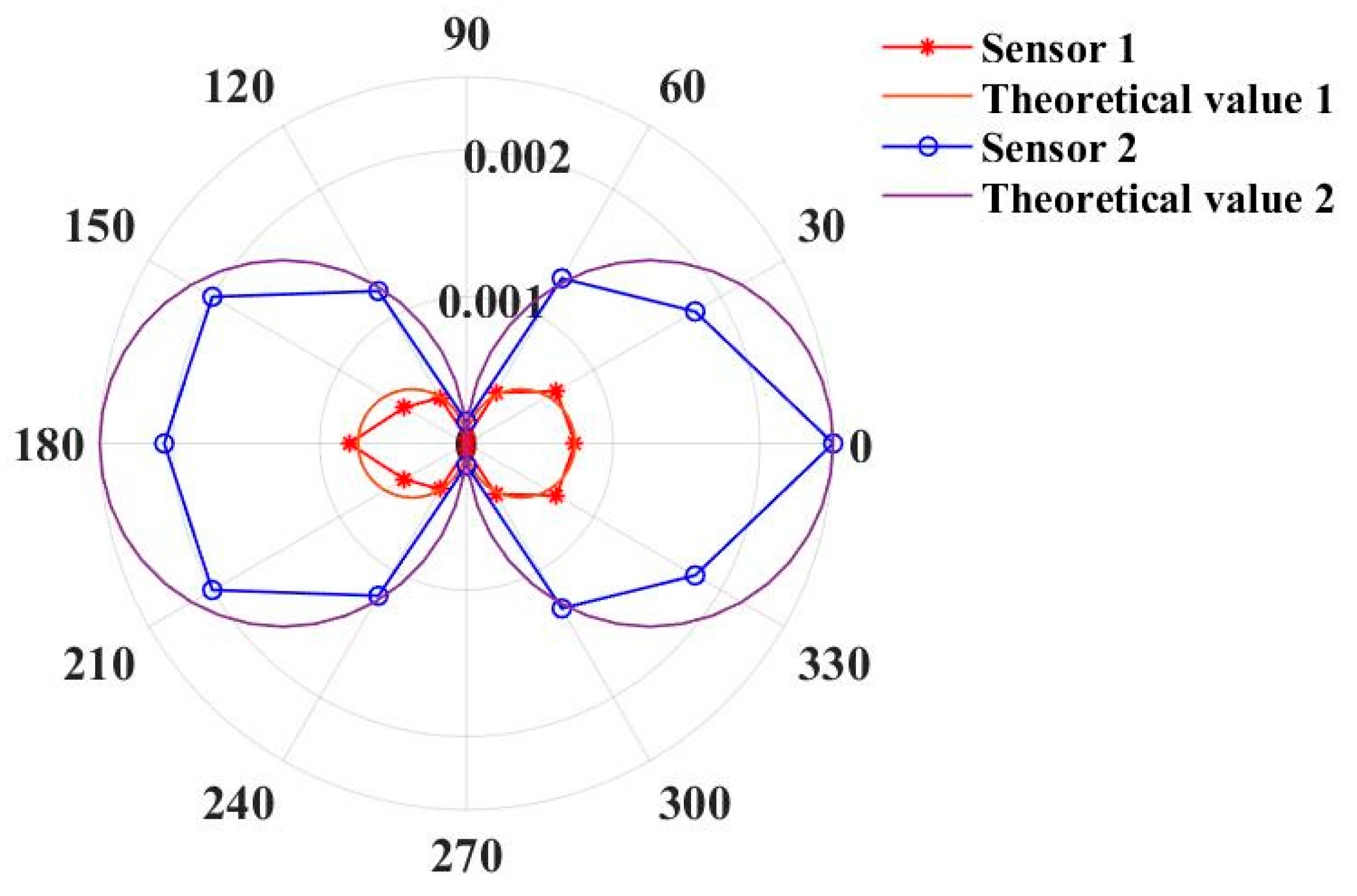

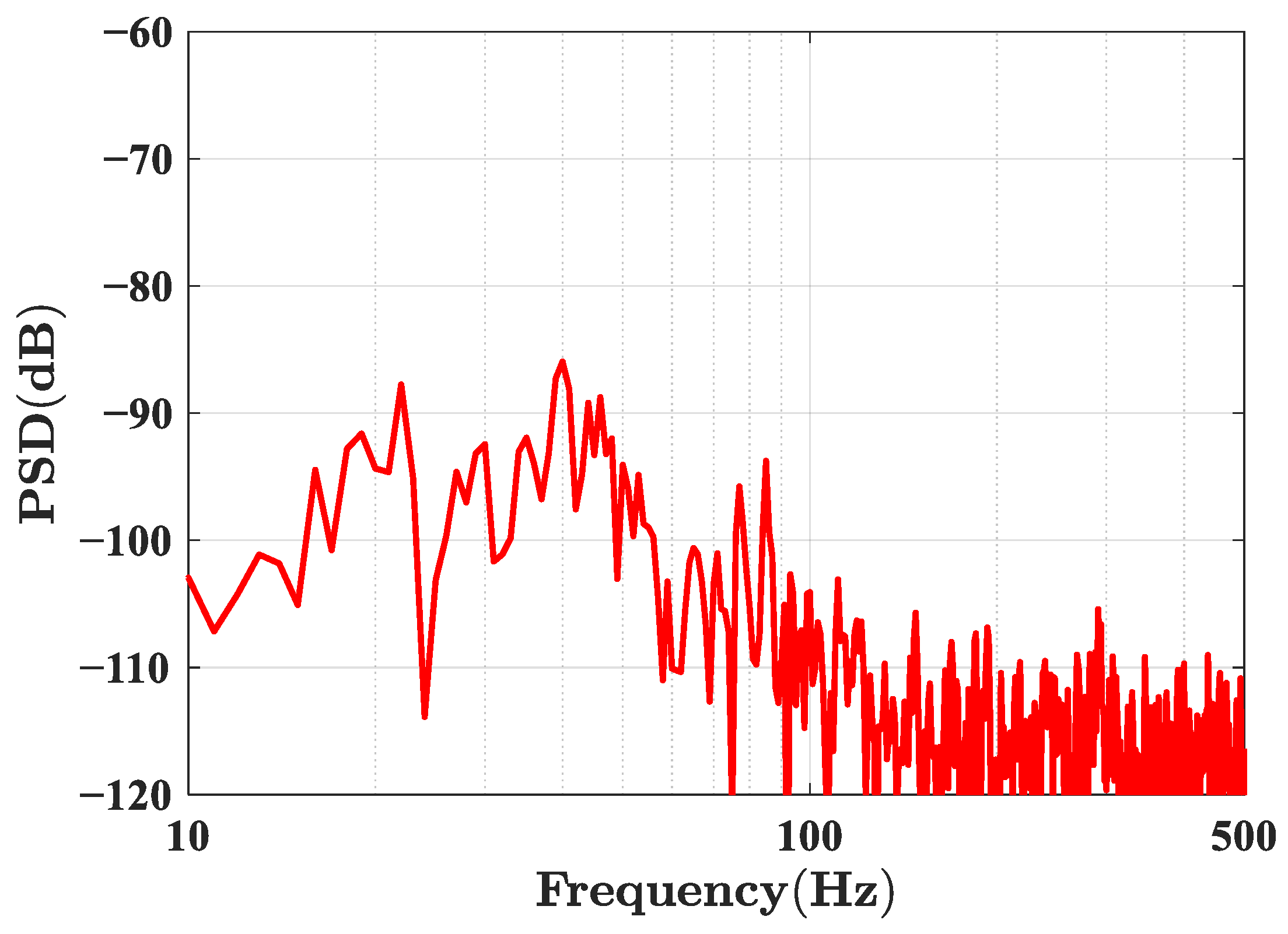
| Parameter | Sensor 1 | Sensor 2 |
|---|---|---|
| neff [31] | 1.4682 | 1.4682 |
| λ0 | 1550 nm | 1550 nm |
| m × L | 1 × 0.25 m | 4 × 0.25 m |
| Q | 0.0004 με/μT | 0.0004 με/μT |
| N | 1 | 2 |
| E | 85.75 GPa | 85.75 GPa |
| Ef | 83.8 GPa | 83.8 GPa |
| A | 0.3325 mm2 | 0.3325 mm2 |
| Af [27] | 0.0123 mm2 | 0.0123 mm2 |
| K (θ = 0) | 0.000574 rad/μT | 0.00222 rad/μT |
| References | Methods | Sensitivity | System Resolution | Magnetic Field Resolution |
|---|---|---|---|---|
| [21] | Mach–Zehnder interferometer Coated Fiber Lock-in-amplifier | 0.0091 rad/μT | 5.6 × 10−4 rad/√Hz @ 245 Hz | 62 nT/√Hz @ 245 Hz |
| [24] | Michelson interferometer Lock-in-amplifier | 0.004 rad/μT | 6 × 10−7 rad/√Hz @ 0.1 Hz | 150 pT/√Hz @ 0.1 Hz |
| [25] | Michelson interferometer Lock-in-amplifier | 105.9 μV/nT | 1.03 × 10−5 V/√Hz @ 1 Hz | 0.1 nT/√Hz @ 1 Hz |
| [22] | Mach–Zehnder interferometer Passive demodulation | 0.06983 rad/μT | 9.17 × 10−5 rad/√Hz @ 200 Hz | 2.14 nT/√Hz @ 200 Hz |
| This paper | Mach–Zehnder interferometer Passive demodulation | 0.00065 rad/μT 0.0024 rad/μT | 1 × 10−5 rad/√Hz @ 10 Hz | 15.4 nT/√Hz @ 10 Hz 4.2 nT/√Hz @ 10 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, M.; Zhang, W.; Huang, W.; Xi, X. Optical Fiber Magnetic Field Sensors Based on 3 × 3 Coupler and Iron-Based Amorphous Nanocrystalline Ribbons. Sensors 2023, 23, 2530. https://doi.org/10.3390/s23052530
Lou M, Zhang W, Huang W, Xi X. Optical Fiber Magnetic Field Sensors Based on 3 × 3 Coupler and Iron-Based Amorphous Nanocrystalline Ribbons. Sensors. 2023; 23(5):2530. https://doi.org/10.3390/s23052530
Chicago/Turabian StyleLou, Minggan, Wentao Zhang, Wenzhu Huang, and Xuekui Xi. 2023. "Optical Fiber Magnetic Field Sensors Based on 3 × 3 Coupler and Iron-Based Amorphous Nanocrystalline Ribbons" Sensors 23, no. 5: 2530. https://doi.org/10.3390/s23052530
APA StyleLou, M., Zhang, W., Huang, W., & Xi, X. (2023). Optical Fiber Magnetic Field Sensors Based on 3 × 3 Coupler and Iron-Based Amorphous Nanocrystalline Ribbons. Sensors, 23(5), 2530. https://doi.org/10.3390/s23052530







