Prediction of State of Health of Lithium-Ion Battery Using Health Index Informed Attention Model
Abstract
1. Introduction
- A convex optimization model is introduced to obtain a health index of a battery, such an index can accurately capture the degradation trajectory of a battery as well as improves the SOH prediction performance.
- An attention-based deep learning predictive algorithm is presented, where an attention matrix referring to the significance level of a time series is adopted in SOH predictions so that the predictive algorithm can utilize the most significant portion of a time series for SOH predictions.
2. Data-Driven Algorithms for SOH Predictions
3. Health Index Informed Attention Model
3.1. Temporal Features Extraction
3.2. Health Index Generation of a Battery
- Attribute 1: The health indices of aging batteries should be piece-wise monotonically decreasing with the increasing number of charge and discharge cycles.
- Attribute 2: The health indices of aging batteries should increase after a complete charge-discharge cycle and a long period of storage.
- Attribute 3: The variance of the failure threshold for the health indices of aging batteries should be minimal.
- Attribute 4: The health indices should be consistent with the true capacity degradation trajectory of batteries.
3.3. Attention-Based Deep Learning Model
4. Case Study
4.1. Dataset Description
4.2. Health Index
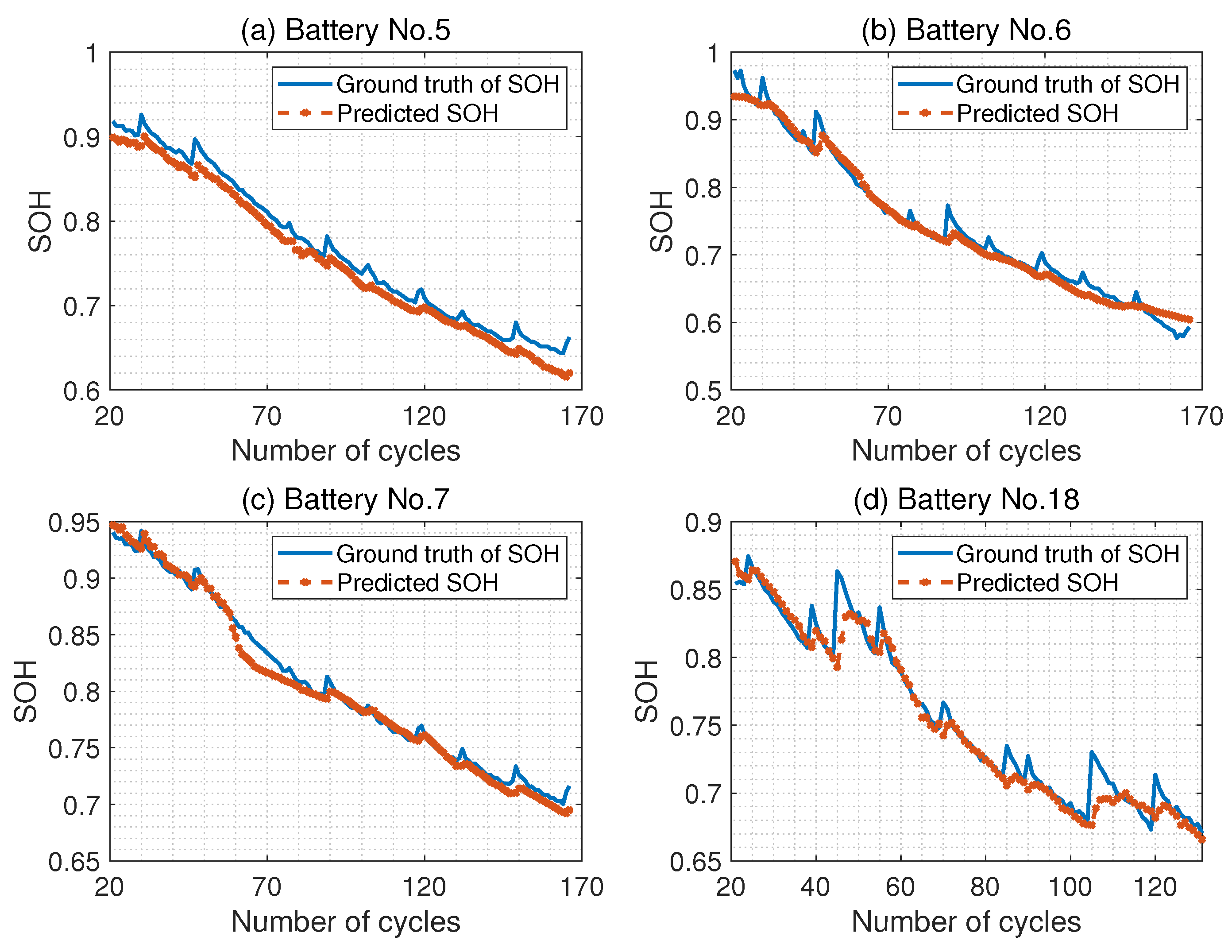
4.3. SOH Estimation
5. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HI | Health Index |
| SOH | State of Health |
| CC | Constant Current |
| CV | Constant Voltage |
| PCoE | Prognostics Center of Excellence |
| RSME | Root Mean Squared Error |
| LSTM | Long Short-term Memory |
| FC | Fully Connected |
References
- Liu, X.; Wu, J.; Zhang, C.; Chen, Z. A method for state of energy estimation of lithium-ion batteries at dynamic currents and temperatures. J. Power Sources 2014, 270, 151–157. [Google Scholar] [CrossRef]
- Xi, Z.; Wang, R.; Fu, Y.; Mi, C. Accurate and reliable state of charge estimation of lithium ion batteries using time-delayed recurrent neural networks through the identification of overexcited neurons. Appl. Energy 2022, 305, 117962. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, G. Developments in nanostructured cathode materials for high-performance lithium-ion batteries. Adv. Mater. 2008, 20, 2251–2269. [Google Scholar] [CrossRef]
- Guo, P.; Song, H.; Chen, X. Electrochemical performance of graphene nanosheets as anode material for lithium-ion batteries. Electrochem. Commun. 2009, 11, 1320–1324. [Google Scholar] [CrossRef]
- Fang, L.; Chen, M.; Nam, K.W.; Kang, Y.M. Redox Evolution of Li-Rich Layered Cathode Materials. Batteries 2022, 8, 132. [Google Scholar] [CrossRef]
- Fang, L.; Zhou, L.; Park, M.; Han, D.; Lee, G.H.; Kang, S.; Lee, S.; Chen, M.; Hu, Z.; Zhang, K.; et al. Hysteresis Induced by Incomplete Cationic Redox in Li-Rich 3d-Transition-Metal Layered Oxides Cathodes. Adv. Sci. 2022, 9, 2201896. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.; Tsui, K.L.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- Fu, P.; Chu, L.; Li, J.; Guo, Z.; Hu, J.; Hou, Z. State of Health Prediction of Lithium-Ion Battery Based on Deep Dilated Convolution. Sensors 2022, 22, 9435. [Google Scholar] [CrossRef]
- Yao, L.; Wen, J.; Xu, S.; Zheng, J.; Hou, J.; Fang, Z.; Xiao, Y. State of Health Estimation Based on the Long Short-Term Memory Network Using Incremental Capacity and Transfer Learning. Sensors 2022, 22, 7835. [Google Scholar] [CrossRef]
- Wei, Y.; Liu, H. Convolutional Long-Short Term Memory Network with Multi-Head Attention Mechanism for Traffic Flow Prediction. Sensors 2022, 22, 7994. [Google Scholar] [CrossRef]
- Meng, J.; Yue, M.; Diallo, D. A degradation empirical-model-free battery end-of-life prediction framework based on gaussian process regression and Kalman filter. IEEE Trans. Transp. Electrif. 2022, 1. [Google Scholar] [CrossRef]
- Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL prediction of lithium-ion batteries based on Gaussian process regression with indirect health indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef]
- Xu, N.; Xie, Y.; Liu, Q.; Yue, F.; Zhao, D. A Data-Driven Approach to State of Health Estimation and Prediction for a Lithium-Ion Battery Pack of Electric Buses Based on Real-World Data. Sensors 2022, 22, 5762. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D.; Terpenny, J. Learning the health index of complex systems using dynamic conditional variational autoencoders. Reliab. Eng. Syst. Saf. 2021, 216, 108004. [Google Scholar] [CrossRef]
- Kumar, A.; Parkash, C.; Vashishtha, G.; Tang, H.; Kundu, P.; Xiang, J. State-space modeling and novel entropy-based health indicator for dynamic degradation monitoring of rolling element bearing. Reliab. Eng. Syst. Saf. 2022, 221, 108356. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D.; Terpenny, J. Constructing Robust and Reliable Health Indices and Improving the Accuracy of Remaining Useful Life Prediction. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2022, 5, 021009. [Google Scholar] [CrossRef]
- Andre, D.; Appel, C.; Soczka-Guth, T.; Sauer, D.U. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries. J. Power Sources 2013, 224, 20–27. [Google Scholar] [CrossRef]
- Xu, W.; Wang, S.; Jiang, C.; Fernandez, C.; Yu, C.; Fan, Y.; Cao, W. A novel adaptive dual extended Kalman filtering algorithm for the Li-ion battery state of charge and state of health co-estimation. Int. J. Energy Res. 2021, 45, 14592–14602. [Google Scholar] [CrossRef]
- Liu, D.; Yin, X.; Song, Y.; Liu, W.; Peng, Y. An on-line state of health estimation of lithium-ion battery using unscented particle filter. IEEE Access 2018, 6, 40990–41001. [Google Scholar] [CrossRef]
- Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation for lithium–iron phosphate batteries. J. Power Sources 2013, 239, 705–710. [Google Scholar] [CrossRef]
- Chen, N.; Hu, X.; Gui, W.; Zou, J. Estimation of li-ion battery state of charging and state of healthy based on unsented Kalman filtering. In Proceedings of the The 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 4725–4729. [Google Scholar]
- Dong, G.; Chen, Z.; Wei, J.; Ling, Q. Battery health prognosis using Brownian motion modeling and particle filtering. IEEE Trans. Ind. Electron. 2018, 65, 8646–8655. [Google Scholar] [CrossRef]
- Thelen, A.; Li, M.; Hu, C.; Bekyarova, E.; Kalinin, S.; Sanghadasa, M. Augmented model-based framework for battery remaining useful life prediction. Appl. Energy 2022, 324, 119624. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.W.; Van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Yayan, U.; Arslan, A.T.; Yucel, H. A novel method for SoH prediction of batteries based on stacked LSTM with quick charge data. Appl. Artif. Intell. 2021, 35, 421–439. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, B. Battery health prognosis using improved temporal convolutional network modeling. J. Energy Storage 2022, 51, 104480. [Google Scholar] [CrossRef]
- Yao, X.Y.; Chen, G.; Pecht, M.; Chen, B. A novel graph-based framework for state of health prediction of lithium-ion battery. J. Energy Storage 2023, 58, 106437. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D.; Terpenny, J. Bearing remaining useful life prediction using self-adaptive graph convolutional networks with self-attention mechanism. Mech. Syst. Signal Process. 2023, 188, 110010. [Google Scholar] [CrossRef]
- Mawonou, K.S.; Eddahech, A.; Dumur, D.; Beauvois, D.; Godoy, E. State-of-health estimators coupled to a random forest approach for lithium-ion battery aging factor ranking. J. Power Sources 2021, 484, 229154. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, Y.; Zhang, B.; Liu, M.; Wang, J.; Liu, C.; Zhang, Y. Method of Predicting SOH and RUL of Lithium-Ion Battery Based on the Combination of LSTM and GPR. Sustainability 2022, 14, 11865. [Google Scholar] [CrossRef]
- Zhou, D.; Li, Z.; Zhu, J.; Zhang, H.; Hou, L. State of health monitoring and remaining useful life prediction of lithium-ion batteries based on temporal convolutional network. IEEE Access 2020, 8, 53307–53320. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D. Prediction of state of health and remaining useful life of lithium-ion battery using graph convolutional network with dual attention mechanisms. Reliab. Eng. Syst. Saf. 2023, 230, 108947. [Google Scholar] [CrossRef]
- Liu, K.; Chehade, A.; Song, C. Optimize the signal quality of the composite health index via data fusion for degradation modeling and prognostic analysis. IEEE Trans. Autom. Sci. Eng. 2015, 14, 1504–1514. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D.; Terpenny, J. Decision-Level Data Fusion in Quality Control and Predictive Maintenance. IEEE Trans. Autom. Sci. Eng. 2020, 18, 184–194. [Google Scholar] [CrossRef]
- Liu, K.; Gebraeel, N.Z.; Shi, J. A data-level fusion model for developing composite health indices for degradation modeling and prognostic analysis. IEEE Trans. Autom. Sci. Eng. 2013, 10, 652–664. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D.; Terpenny, J. Robust incipient fault detection of complex systems using data fusion. IEEE Trans. Instrum. Meas. 2020, 69, 9526–9534. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhudinov, R.; Zemel, R.; Bengio, Y. Show, attend and tell: Neural image caption generation with visual attention. In Proceedings of the International Conference on Machine Learning, PMLR, Miami, FL, USA, 9–11 December 2015; pp. 2048–2057. [Google Scholar]
- Luong, M.T.; Pham, H.; Manning, C.D. Effective approaches to attention-based neural machine translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Saha, B.; Goebel, K. Battery data set. NASA AMES Progn. Data Repos. 2007. [Google Scholar]
- Audin, P.; Jorge, I.; Mesbahi, T.; Samet, A.; De Beuvron, F.D.B.; Boné, R. Auto-encoder LSTM for Li-ion SOH prediction: A comparative study on various benchmark datasets. In Proceedings of the 2021 20th IEEE International Conference on Machine Learning and Applications (ICMLA), online, 13–15 December 2021; pp. 1529–1536. [Google Scholar]
- Yu, J. State of health prediction of lithium-ion batteries: Multiscale logic regression and Gaussian process regression ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
- Qin, P.; Zhao, L.; Liu, Z. State of health prediction for lithium-ion battery using a gradient boosting-based data-driven method. J. Energy Storage 2022, 47, 103644. [Google Scholar] [CrossRef]





| Sequence of Layers | Description | Output Dimensionality |
|---|---|---|
| 1 | Input layer | |
| 2 | LSTM layer | |
| 3 | Attention layer | |
| 4 | Flatten layer | |
| 5 | Output layer |
| Method Symbol | Method Description |
|---|---|
| HI-ALSTM | Health index informed attention-based LSTM model (Proposed methodology) |
| HI-LSTM | Health index-informed LSTM model without using the attention mechanism |
| ALSTM | Attention-based LSTM predictive model without using the health index |
| LSTM | traditional LSTM predictive model |
| Battery No. 5 | Battery No. 6 | Battery No. 7 | Battery No. 18 | Average | |
|---|---|---|---|---|---|
| HI-ALSTM | 0.0149 | 0.0110 | 0.0068 | 0.0083 | 0.0103 |
| HI-LSTM | 0.0380 | 0.0551 | 0.0466 | 0.0222 | 0.0405 |
| ALSTM | 0.0066 | 0.0170 | 0.0133 | 0.0114 | 0.0121 |
| LSTM | 0.0362 | 0.0213 | 0.0372 | 0.0264 | 0.0303 |
| Battery No. 5 | Battery No. 6 | Battery No. 7 | Battery No. 18 | Average | |
|---|---|---|---|---|---|
| HI-ALSTM | 196.30% | 151.03% | 84.17% | 108.29% | 134.95% |
| HI-LSTM | 512.55% | 793.49% | 611.81% | 292.07% | 552.48% |
| ALSTM | 85.89% | 247.20% | 165.64% | 150.38% | 162.28% |
| LSTM | 487.97% | 290.07% | 485.74% | 352.43% | 404.05% |
| Battery No. 5 | Battery No. 6 | Battery No. 7 | Battery No. 18 | Average | |
|---|---|---|---|---|---|
| HI-ALSTM | 0.0165 | 0.0153 | 0.0089 | 0.0139 | 0.0136 |
| HI-LSTM | 0.0399 | 0.0612 | 0.0542 | 0.0274 | 0.0457 |
| ALSTM | 0.0085 | 0.0220 | 0.0145 | 0.0151 | 0.0150 |
| LSTM | 0.0375 | 0.0249 | 0.0427 | 0.0288 | 0.0335 |
| LR-GPR [44] | 0.0168 | 0.0292 | - | 0.0169 | 0.0210 |
| GBDT [45] | 0.0192 | 0.0281 | 0.0157 | - | 0.0210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y. Prediction of State of Health of Lithium-Ion Battery Using Health Index Informed Attention Model. Sensors 2023, 23, 2587. https://doi.org/10.3390/s23052587
Wei Y. Prediction of State of Health of Lithium-Ion Battery Using Health Index Informed Attention Model. Sensors. 2023; 23(5):2587. https://doi.org/10.3390/s23052587
Chicago/Turabian StyleWei, Yupeng. 2023. "Prediction of State of Health of Lithium-Ion Battery Using Health Index Informed Attention Model" Sensors 23, no. 5: 2587. https://doi.org/10.3390/s23052587
APA StyleWei, Y. (2023). Prediction of State of Health of Lithium-Ion Battery Using Health Index Informed Attention Model. Sensors, 23(5), 2587. https://doi.org/10.3390/s23052587





