Convolutional Neural Network-Based Machine Vision for Non-Destructive Detection of Flooding in Packed Columns
Abstract
1. Introduction
- We introduced a deep learning-based machine vision approach using CNNs for non-destructive detection of flooding in packed columns. Different from the results presented in the previous literature [8], which mainly focused on classification, the proposed method offers a real-time pre-alarm approach for early detection of flooding;
- Real-time images of the packed column were captured using a digital camera and analyzed through a pre-trained CNN model. This approach, based on a dataset of recorded images, enabled the prediction of flooding and provides process engineers with a timely indication of potential flooding occurrences;
- Additionally, we also evaluated an integrated approach combining principal component analysis (PCA) [24] and support vector machine (SVM) [25], as well as a deep belief network (DBN) method [26], for flooding detection. These experiments were conducted on a real packed column and demonstrate the feasibility and superiority of our proposed approach.
2. Methodology
2.1. CNN Method
2.2. Integration of PCA and SVM
2.3. Hyperparameter Selection
3. Experimental System
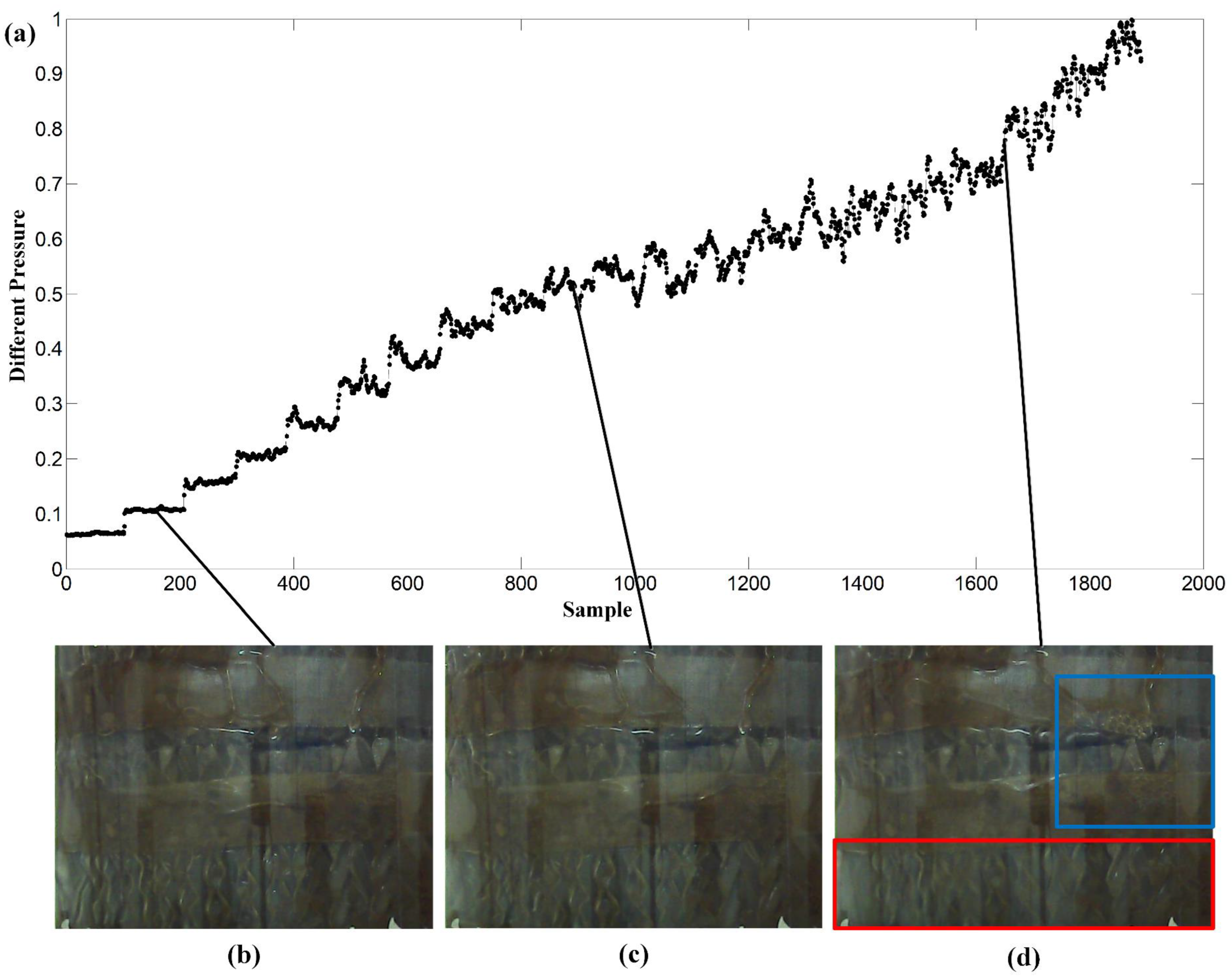
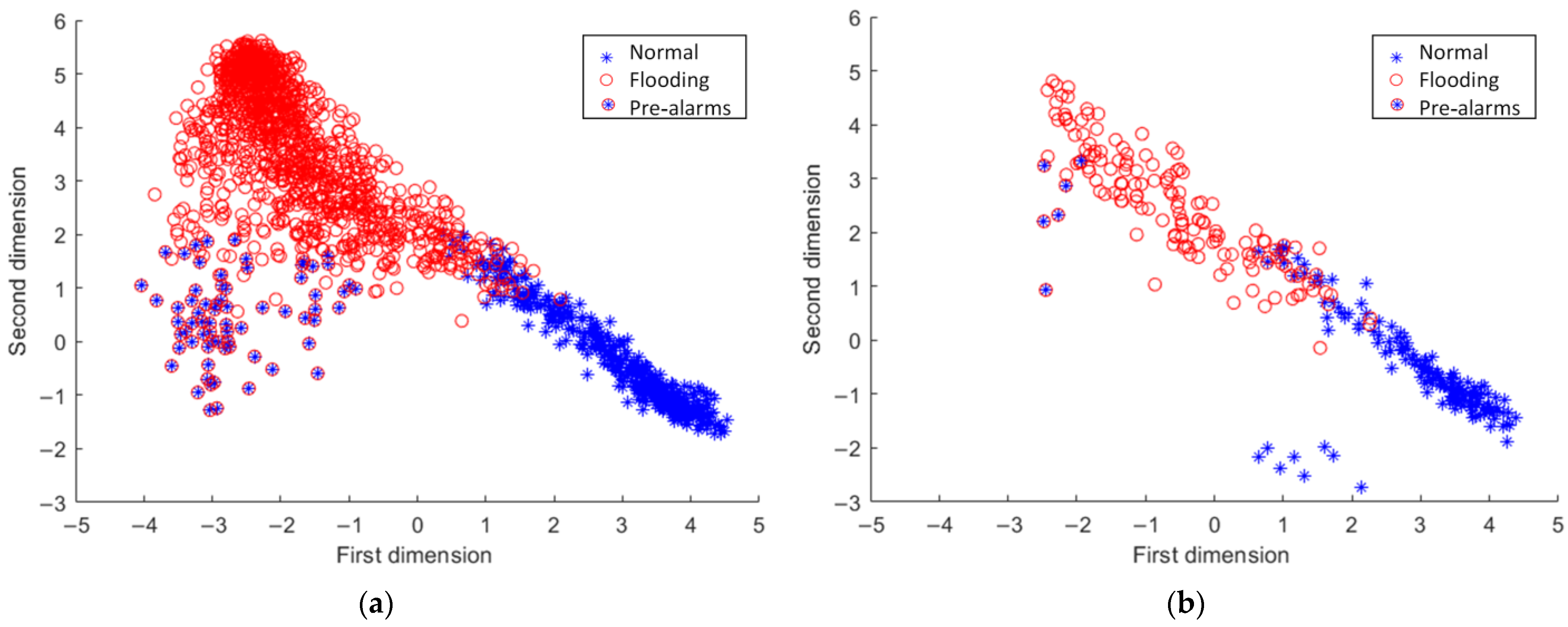
4. Application Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mackowiak, J. Fluid Dynamics of Packed Columns; Springer: New York, NY, USA, 2010. [Google Scholar]
- Brockkötter, J.; Ahndorf, J.; Jupke, A. Prediction of flooding in packed liquid-liquid and high-pressure extraction columns using a gaussian process. Chem. Ing. Tech. 2021, 93, 1907–1916. [Google Scholar] [CrossRef]
- Shoukri, M.; Abdul-Razzak, A.; Yan, C. Hysteresis effects in countercurrent gas-liquid flow limitations in a vertical tube. Can. J. Chem. Eng. 1994, 72, 576–581. [Google Scholar] [CrossRef]
- Strigle, R.F. Packed Tower Design and Applications: Random and Structured Packings; Gulf Publishing Company: Houston, TX, USA, 1994. [Google Scholar]
- Liu, Y.; Hseuh, B.-F.; Gao, Z.; Yao, Y. Flooding prognosis in packed columns by assessing the degree of steadiness (DOS) of process variable trajectory. Ind. Eng. Chem. Res. 2016, 55, 10744–10750. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, Y.; Gao, Z.; Yao, Y. Online flooding supervision in packed towers: An integrated data-driven statistical monitoring method. Chem. Eng. Technol. 2018, 41, 436–446. [Google Scholar] [CrossRef]
- Parthasarathy, S.; Gowan, H.; Indhar, P. Prediction of Flooding in An Absorption Column Using Neural Networks. In Proceedings of the 1999 IEEE International Conference on Control Applications, Kohala Coast, HI, USA, 22–27 August 1999. [Google Scholar]
- Oeing, J.; Neuendorf, L.M.; Bittorf, L.; Krieger, W.; Kockmann, N. Flooding prevention in distillation and extraction columns with aid of machine learning approaches. Chem. Ing. Tech. 2021, 93, 1917–1929. [Google Scholar] [CrossRef]
- Cui, Y.; Pan, T.; Chen, S.; Zou, X. A gender classification method for Chinese mitten crab using deep convolutional neural network. Multimed. Tools Appl. 2020, 79, 7669–7684. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Rizzo, A.; Xibilia, M. Soft Sensors for Monitoring and Control of Industrial Processes; Advances in Industrial Control; Springer: London, UK, 2007. [Google Scholar]
- Han, H.; Qiao, J. Prediction of activated sludge bulking based on a self-organizing RBF neural network. J. Process Control. 2012, 22, 1103–1112. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, Z.; Deng, H.; Zheng, S. Two-stage hybrid model for efficiency prediction of centrifugal pump. Sensors 2022, 22, 4300. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, P.; Gao, X.; Qi, Y.; Gao, H. Amplitude-frequency images-based ConvNet: Applications of fault detection and diagnosis in chemical processes. J. Chemometr. 2019, 33, e3168. [Google Scholar] [CrossRef]
- Zhou, L.; Li, G.; Song, Z.; Qin, J.S. Autoregressive dynamic latent variable models for process monitoring. IEEE Trans. Control Syst. Technol. 2017, 25, 366–373. [Google Scholar]
- Ge, Z.; Song, Z.; Ding, S.X.; Huang, B. Data mining and analytics in the process industry: The role of machine learning. IEEE Access 2017, 5, 20590–20616. [Google Scholar] [CrossRef]
- Jin, H.; Pan, B.; Chen, X.; Qian, B. Ensemble just-in-time learning framework through evolutionary multi-objective optimization for soft sensor development of nonlinear industrial processes. Chemom. Intell. Lab. Syst. 2019, 184, 153–166. [Google Scholar] [CrossRef]
- Brockkötter, J.; Cielanga, M.; Weber, B.; Jupke, A. Prediction and characterization of flooding in pulsed sieve plate extraction columns using data-driven models. Ind. Eng. Chem. Res. 2020, 59, 19726–19735. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Gao, S.; Dai, Y.; Li, Y.; Jiang, Y.; Liu, Y. Augmented flame image soft sensor for combustion oxygen content prediction. Meas. Sci. Technol. 2023, 34, 015401. [Google Scholar] [CrossRef]
- Gao, X.; Shang, C.; Huang, D.; Jiang, Y.; Chen, T. Refinery scheduling with varying crude: A deep belief network classification and multi-model approach. AIChE J. 2014, 60, 2525–2532. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Gao, Z.; Yao, Y. Ensemble deep kernel learning with application to quality prediction in industrial polymerization processes. Chemom. Intell. Lab. Syst. 2018, 174, 15–21. [Google Scholar] [CrossRef]
- Wu, H.; Zheng, K.; Sfarra, S.; Liu, Y.; Yao, Y. Multiview learning for subsurface defect detection in composite products: A challenge on thermographic data analysis. IEEE Trans. Ind. Inform. 2020, 16, 5996–6003. [Google Scholar] [CrossRef]
- Liu, K.; Zheng, M.; Liu, Y.; Yang, J.; Yao, Y. Deep autoencoder thermography for defect detection of carbon fiber composites. IEEE Trans. Ind. Inf. 2022, 1. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Schlköpf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; The MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Xuan, Q.; Chen, Z.; Liu, Y.; Huang, H.; Bao, G.; Zhang, D. Multiview generative adversarial network and its application in pearl classification. IEEE Trans. Ind. Electron. 2019, 66, 8244–8252. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, X.; Xu, X.; Chen, C.P. GCB-Net: Graph convolutional broad network and its application in emotion recognition. IEEE Trans. Affect. Comput. 2022, 13, 379–388. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Cordella, C. Principal component analysis: The basic building block of chemometrics. Actual Chim. 2010, 345, 13–18. [Google Scholar]
- Xu, G.; Wu, H.Z.; Shi, Y.Q. Structural design of convolutional neural networks for steganalysis. IEEE Signal Process. Lett. 2016, 23, 708–712. [Google Scholar] [CrossRef]
- Yuan, X.; Gu, Y.; Wang, Y. Supervised deep belief network for quality prediction in industrial processes. IEEE Trans. Instrum. Meas. 2020, 70, 2503711. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, Y.; Chen, J. Flame images for oxygen content prediction of combustion systems using DBN. Energy Fuels 2017, 31, 8776–8783. [Google Scholar] [CrossRef]
- Liu, K.; Yu, Q.; Liu, Y.; Yang, J.; Yao, Y. Convolutional graph thermography for subsurface defect detection in polymer composites. IEEE Trans. Instrum. Meas. 2022, 71, 4506411. [Google Scholar] [CrossRef]

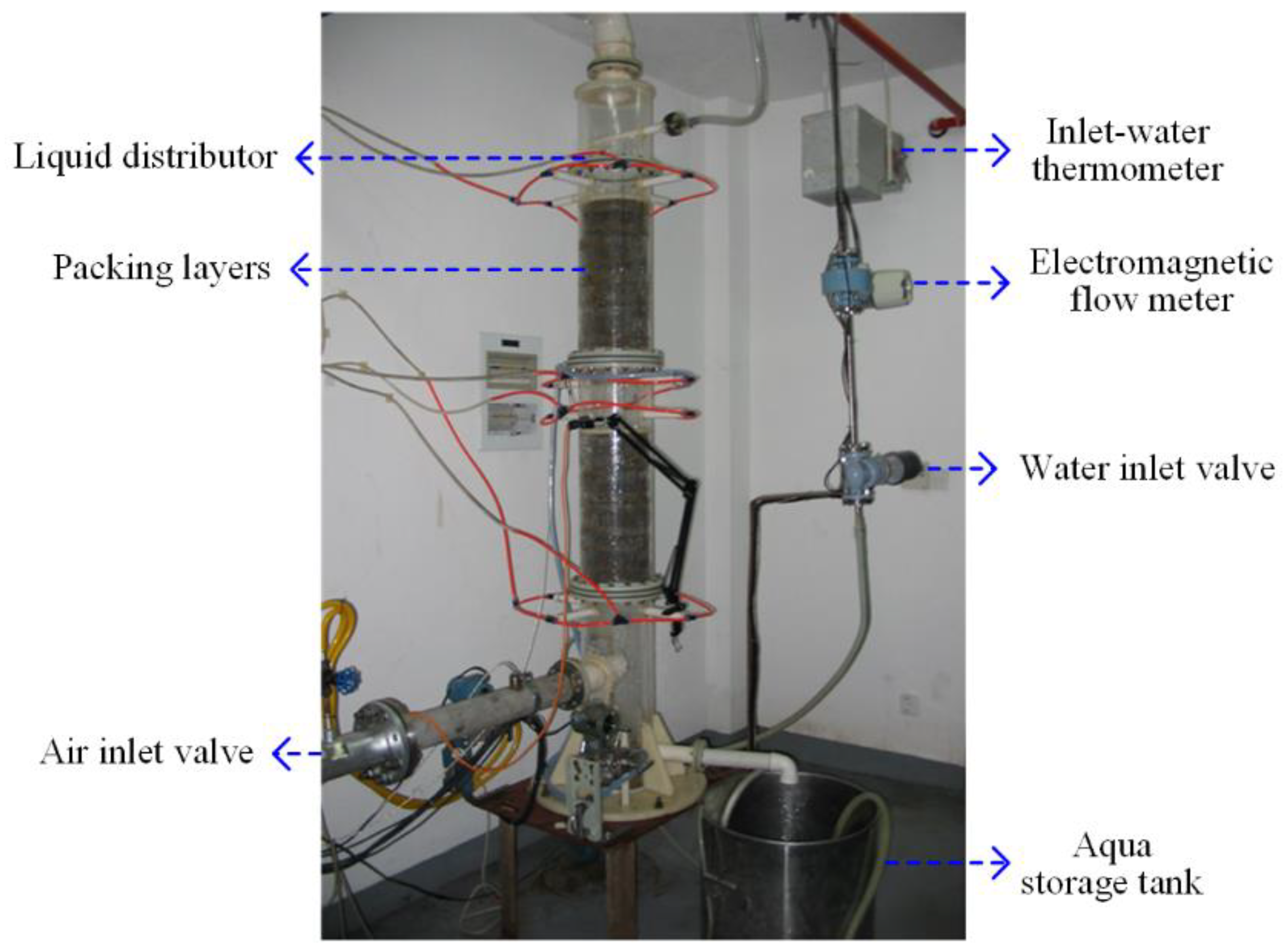




| Components of Packed Column | Size (m) |
|---|---|
| Cylinder diameter | 0.22 |
| Thickness of upper packing layer | 0.46 |
| Thickness of lower packing layer | 0.46 |
| Diameter of air inlet | 0.09 |
| Diameter of water inlet | 0.02 |
| Diameter of air outlet | 0.11 |
| Diameter of water outlet | 0.05 |
| Column height | 2.20 |
| Type | Material | Specific Surface Area (m2/m3) | Corrugation Angle (°) | Wave-Length (mm) | Unit Height (mm) | Porosity (%) | Range of Loading Rate (m3/(m2·h)) |
|---|---|---|---|---|---|---|---|
| CY1700 | Stainless steel | 1700 | 45 | 3.2 | 100 | 85 | 7~24 |
| PCA-SVM | Penalty factor C | 1 | ||
| Kernel function | Radial basis function (RBF) | |||
| Gamma | 1/2 | |||
| Other parameters | Default | |||
| DBN | Number of three hidden layer neurons. | [200 100 100] | ||
| Momentum | 0.5 | |||
| Max epoch | 225 | |||
| Batch size | 1000 | |||
| Penalty | 2 × 103 | |||
| Learning rate | 0.02 | |||
| Activation function | Softmax | |||
| CNN | Input images | 120 × 160 × 3 | ||
| Layer name | Type | Filter size, stride | Output size | |
| C1 | Convolutional layer | 5 × 5, 1 | 116 × 156 × 10 | |
| S1 | Pooling layer | 4 × 4, 4 | 29 × 39 × 10 | |
| C2 | Convolutional layer | 5 × 5, 1 | 25 × 35 × 16 | |
| S2 | Pooling layer | 5 × 5, 5 | 5 × 7 × 16 | |
| H1 | Fully connected layer | 100 × 1 | ||
| H2 | Fully connected layer | 2 × 1 | ||
| Actual Class | |||
|---|---|---|---|
| Normal (Positive) | Flooding (Negative) | ||
| Predicted class | Normal (True) | TP | FN |
| Flooding (False) | FP | TN | |
| PCA-SVM | DBN | CNN | |
|---|---|---|---|
| TP | 118 | 124 | 136 |
| TN | 136 | 141 | 150 |
| FP | 20 | 20 | 6 |
| FN | 26 | 15 | 8 |
| 84.67 | 88.33 | 95.33 | |
| 83.69 | 87.63 | 95.10 | |
| Running time(s) | 17.249 s (training) + 0.001 s (test) | 366.290 s (training) + 0.040 s (test) | 42.415 s (training) + 5.795 s (test) |
| Advantages | Disadvantages | |
|---|---|---|
| PCA-SVM | 1. Improving generalization performance 2. Avoiding structural selection and local minima problems in neural networks | 1. Sensitive to missing samples 2. Cumbersome to adjust parameters |
| DBN | 1. Capable of reflecting the degree of similarity between similar data 2. No need to rely on empirical extraction of data features | 1. Long training time 2. Easy to cause local optimal solutions |
| CNN | 1. High parallel processing capability 2. High nonlinear feature extraction ability 3. Noise-insensitive and highly robust | 1. Timely model updates for application 2. Requires a large number of parameters |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, Y.; Gao, Z.; Liu, K.; Yao, Y. Convolutional Neural Network-Based Machine Vision for Non-Destructive Detection of Flooding in Packed Columns. Sensors 2023, 23, 2658. https://doi.org/10.3390/s23052658
Liu Y, Jiang Y, Gao Z, Liu K, Yao Y. Convolutional Neural Network-Based Machine Vision for Non-Destructive Detection of Flooding in Packed Columns. Sensors. 2023; 23(5):2658. https://doi.org/10.3390/s23052658
Chicago/Turabian StyleLiu, Yi, Yuxin Jiang, Zengliang Gao, Kaixin Liu, and Yuan Yao. 2023. "Convolutional Neural Network-Based Machine Vision for Non-Destructive Detection of Flooding in Packed Columns" Sensors 23, no. 5: 2658. https://doi.org/10.3390/s23052658
APA StyleLiu, Y., Jiang, Y., Gao, Z., Liu, K., & Yao, Y. (2023). Convolutional Neural Network-Based Machine Vision for Non-Destructive Detection of Flooding in Packed Columns. Sensors, 23(5), 2658. https://doi.org/10.3390/s23052658






