Characterization of a Piezoelectric Acoustic Sensor Fabricated for Low-Frequency Applications: A Comparative Study of Three Methods
Abstract
:1. Introduction
2. Design of a Piezoelectric Acoustic Sensor
- Active element (ceramic): This is a piezoelectric material with a given geometry depending on the required use, and very thin electrodes in the whole area perpendicular to the surface that receives the acoustic wave to be recorded.
- Matching layer (ML): They can be one or more layers bonded to the front face of the active element in order to optimize the transmission of acoustic energy between the load and the ceramic, i.e., to adapt the acoustic impedances between the two through the different intermediate layers.
- Housing: This is the component that closes the whole sensor assembly. To avoid electrical ground differential effects as well as the influence of possible electromagnetic waves, it is usually designed with an electrically conductive material.
2.1. Importance of the Ceramic
2.2. Analytical Method: Design for Circular Piezoelectric Ceramics
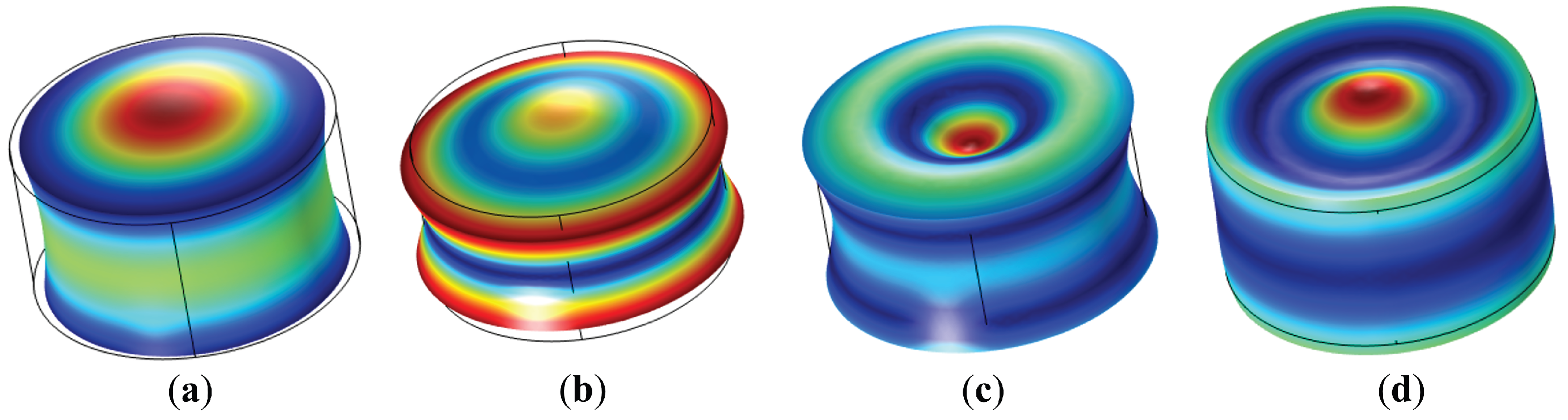
2.3. Numerical Method: Design for Circular Piezoelectric Ceramics
- Preprocessing: The simulations are performed in the structural mechanics module in combination with the piezoelectric devices interface.
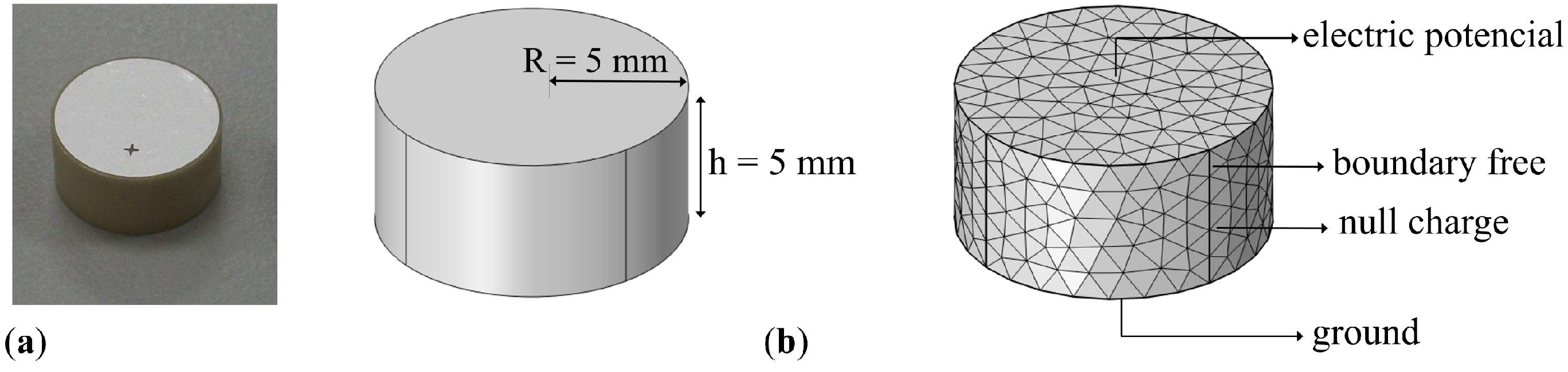
- Geometry: Geometries with a ratio can be approximated by a disk. The piezoelectric ceramic cylinder type PIC255 is simulated and dimensioned in 3D. It has a radius , and a thickness of polarized in the longitudinal axis.
- Frequencies of interest and meshing: In the sizing of the tetrahedral mesh elements, it was taken into account that the minor wavelength (maximum frequency, 250 ) was discretized in 16 parts. Thus, the number of mesh elements with tetrahedral structure was 4318. Figure 2 shows the mesh used to discretize the solutions.
- Boundary conditions:
- –
- Free: This is the mechanical boundary condition, which applies to all ceramic domain boundaries when the ceramic is free-form.
- –
- Null charge: Default electrostatic boundary condition, which has no electrical charge on the boundary and therefore applies to the non-electrode side surface of the ceramics.
- –
- Initial values: These introduce an initial shift of the acoustic field, electric potential, or their derivatives. All initial values are set to 0 and apply to the entire geometry.
- –
- Axial symmetry: This is a default boundary condition used to obtain such symmetry. It is set on the longitudinal axis of the ceramic.
- –
- Electric potential: Sets the electric potential to a value of 1 at one of the electrodes.
- –
- Ground: Sets the electric potential to zero at the boundary applied to the other electrode surface.
- Processing: The input parameters are the coefficients of the elasticity matrix, the coupling matrix, the permittivity matrix, the density, and the mechanical and dielectric losses, respectively. For the development of this numerical model the Frequency Domain study is used, where the displacement field and the electric potential can be obtained from and .
- Post-processing: Two quantities are used to characterize the sensor: electrical impedance and RVR.
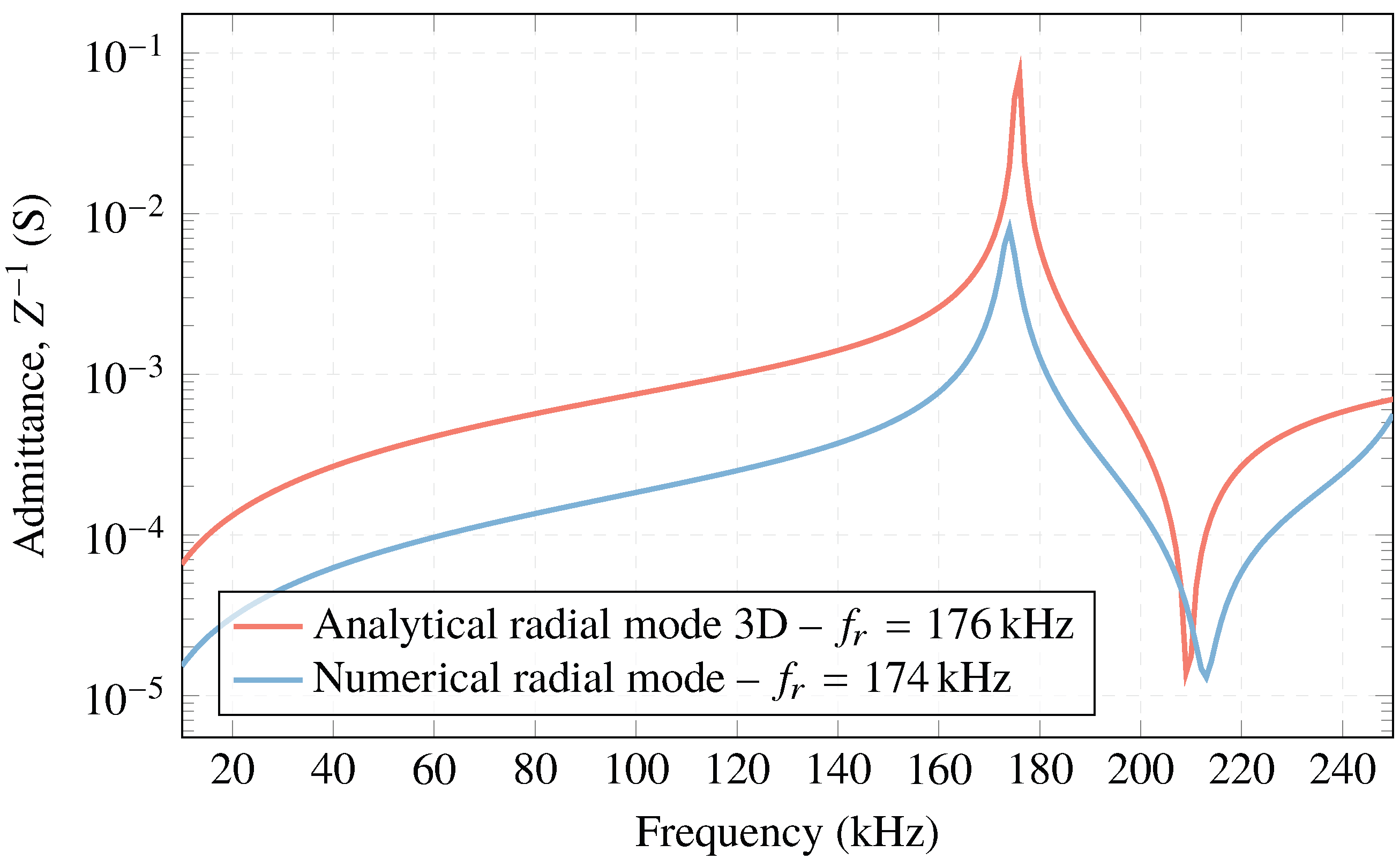
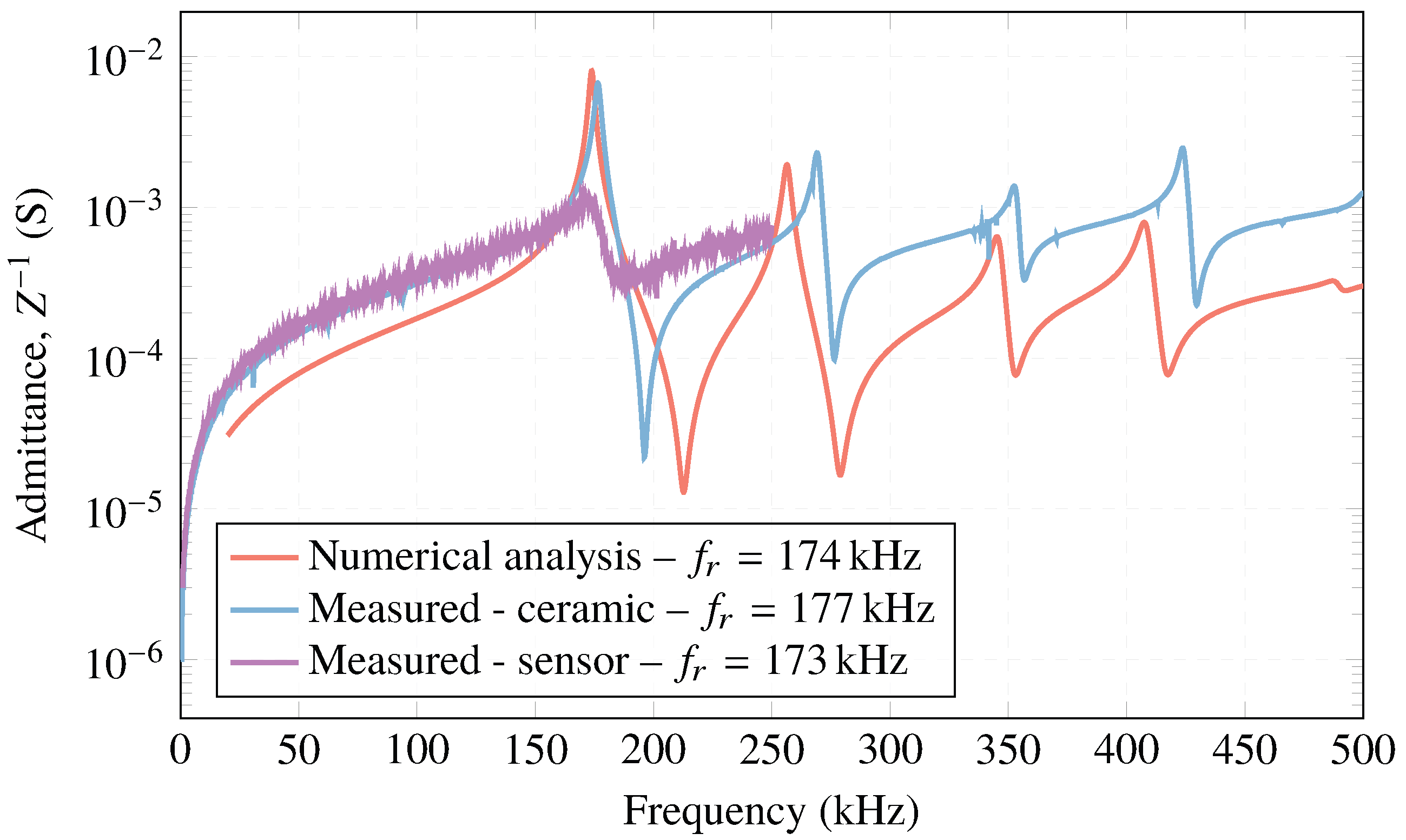
- Electrical impedance: The impedance, Z, is obtained from the inward surface charge density at one of the electrodes, , and the potential difference. The electrical impedance can be obtained as follows [39]:where I is the current intensity across the electrode, being the integral of the inward surface density along the entire surface, S, of the electrode.Deriving the admittance from the impedance is straightforward (Expression (7)). Its calculation allows us to compare the behavior of the ceramic at the resonance frequency with that of the experimental results.
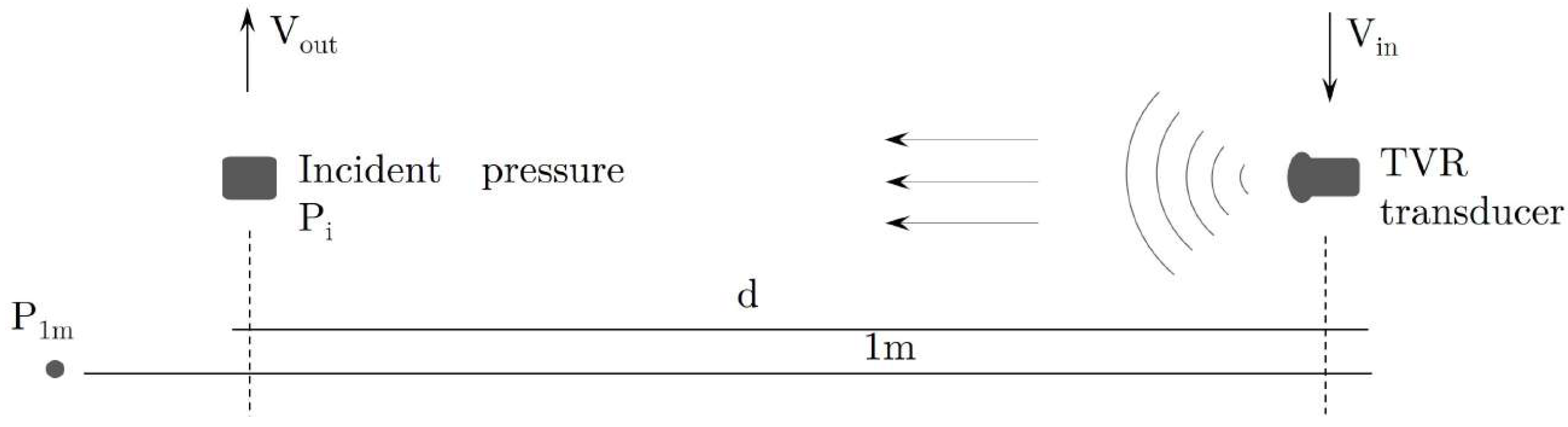
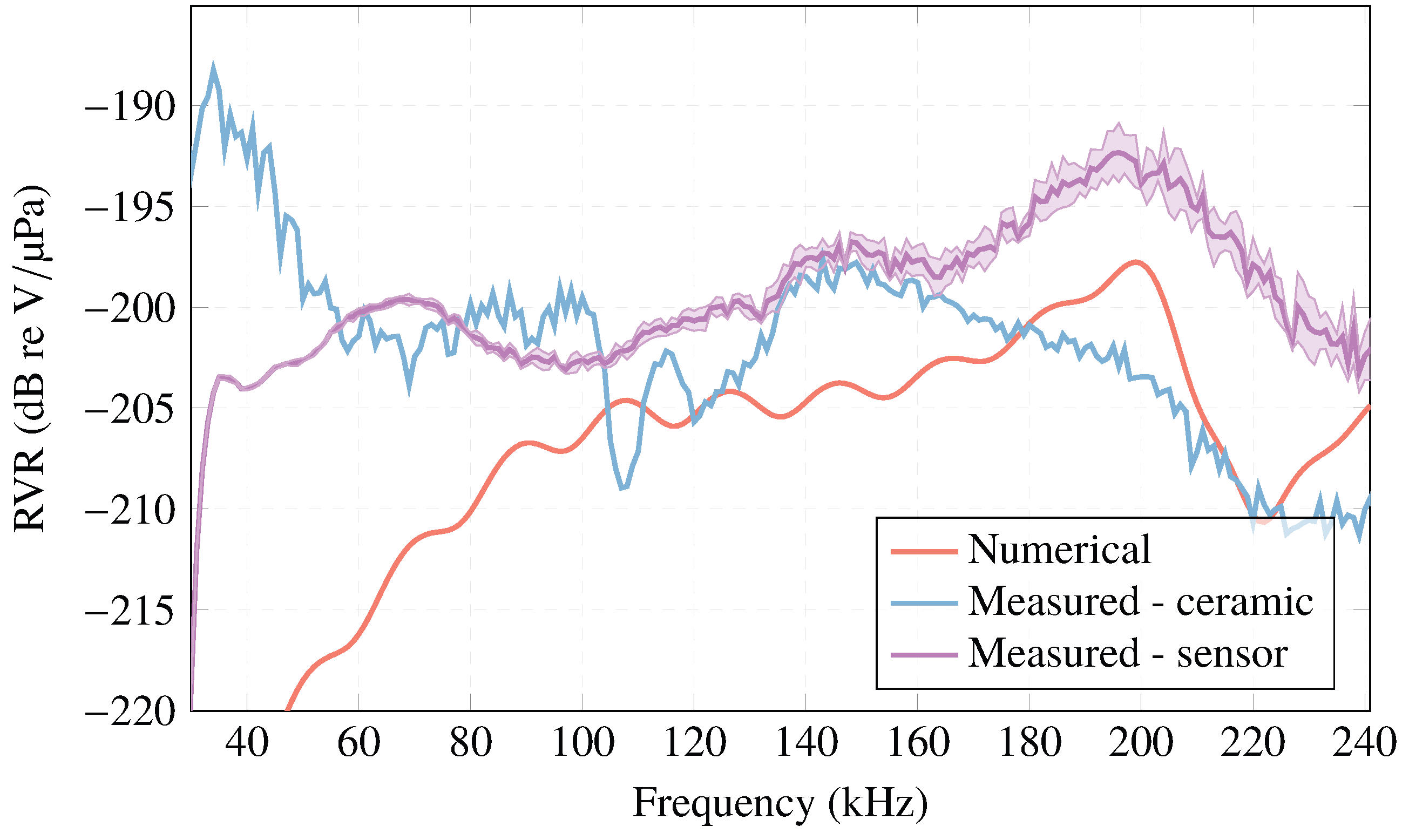
- Receiving Voltage Response: In a linear regime, a ceramic radiates an acoustic wave with an amplitude proportional to its emission sensitivity. Moreover, during the acquisition of acoustic waves, it generates an electrical signal proportional to its reception sensitivity.During transmission, the ceramic voltage sensitivity, , is used to express the pressure P, in Pascals, generated in the medium at a distance of in free field conditions as a function of the input voltage. Thus, given an input voltage, , . This parameter is usually expressed in dB, taking as a reference sensitivity 1 /.The relationship between the voltage and intensity sensitivities is defined as , where is the electrical input impedance of the ceramic.During the reception of acoustic signals, the relationship between the voltage generated in the ceramic when its terminals are in open circuit, , and the reception of an incident acoustic pressure P in Pascals, in a free field, is defined as . This parameter is usually expressed in dB, taking as a reference sensitivity 1 /.The reciprocity principle, (denoted in this paper as instead of J to avoid confusion), is defined as the relation between the ceramic reception and transmission intensity sensitivities [46]. Moreover, the following must hold:where is the wavelength, x is a reference distance of , the water density, 1000 /, and c is the sound’s propagation velocity in water 1480 /.From previous expressions, when the type of waves radiated by the transducer and the sensitivity in one of the two directions are known, the sensitivity in the other direction can be derived from the reciprocity principle. For spherical waves, the relationship between the two sensitivities is given by [46] as:From expression (9), it is straightforward to obtain the RVR using the transmission sensitivity of each of the simulated frequency steps. Thus, the numerical model consists of exciting a point sufficiently far away from the ceramic from the calculation of the sensitivity in emission by applying the reciprocity principle.
Analysis and Numerical Results
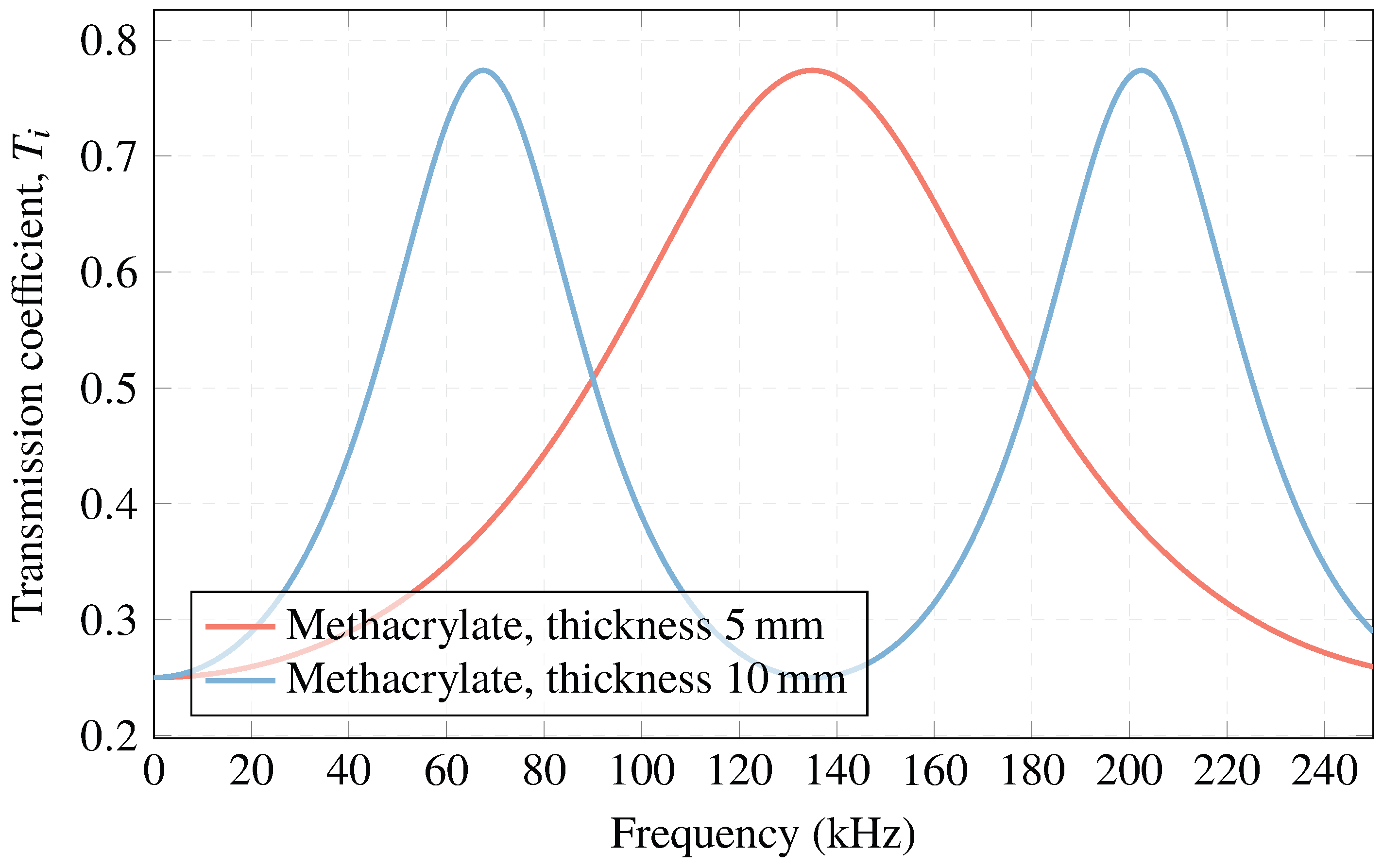
2.4. Importance of the Matching Layer
Analysis
- Zero-layer model: Considering a simple model in which the transmission of an acoustic wave that is generated in a medium and is received by the ceramic is studied (where the electrical signal is recorded), the expected signal loss can be estimated if only the free ceramics are in the water.The sound intensity transmission coefficient, , is derived from the following known expression [47]:
- One-layer model: Understanding the importance of using a matching layer to maximize the acoustic transmission between the water and the ceramic, it is necessary to use an intermediate layer that makes the impedance matching progressive.For the case , the best impedance optimizing the transmission is [18]. Thus, .
2.5. Importance of the Housing
2.6. Sensor Manufacturing
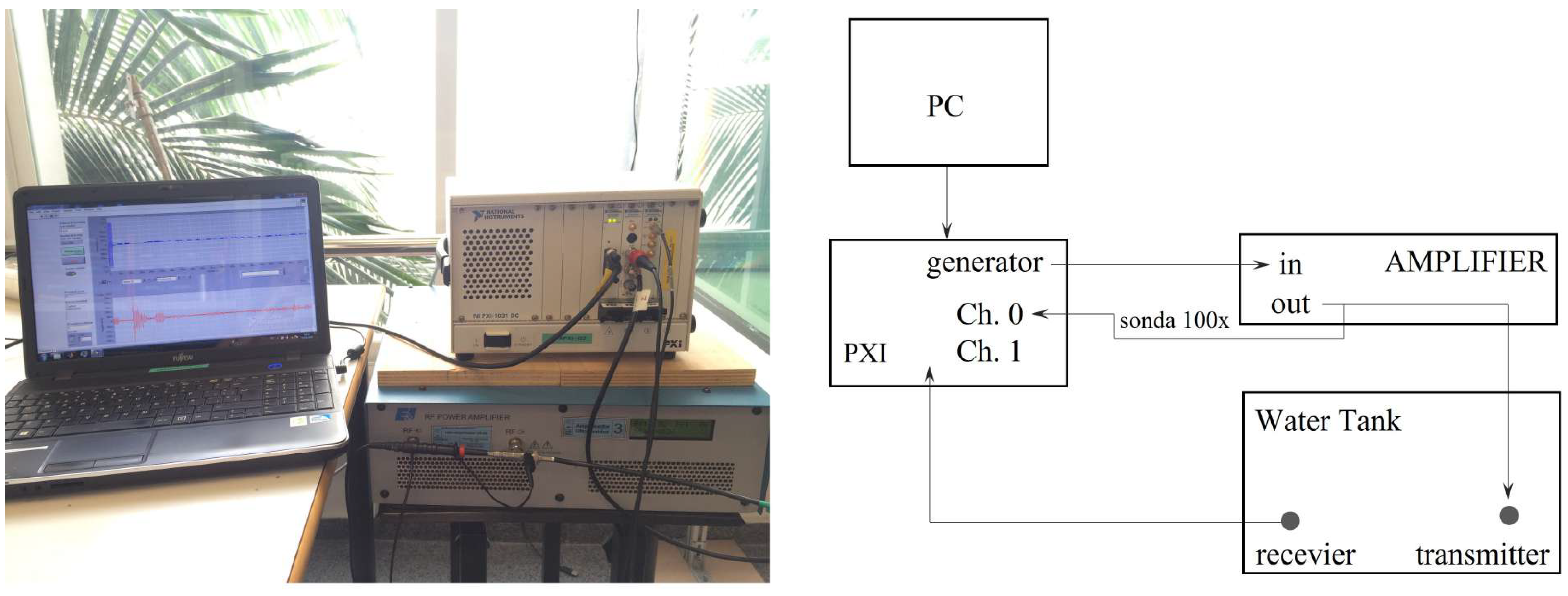
3. Experimental Methods Characterization: Ceramic and Sensor
3.1. Electrical Admittance
3.2. Receiving Voltage Response
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Name/Brand | Serial | Description |
|---|---|---|
| Power amplifier | 2100L | Frequency range: 10 to 12 , Gain: , Nominal output power: 100 |
| Generation and acquisition, National Instruments | NI PXI-1031 | The PXI platform utilized in this study was a 7-slot chassis that accommodated both DC and AC inputs. Its main purpose is to transmit a sequence of signals through channel 0, as determined by the LabVIEW software, and to receive other signals via channel 1. |
| NI PXI card | ExpressCard-8360 | The ExpressCard-8360 is connected to a laptop computer and serves to control the PXI platform. |
| Motor EVA ROBOTICS | EvoDrive ST-23 FW-A201 | 48 DC , which allows millimeter-precision steps. It is used to control the sweep in measurements requiring emitter displacements. Position resolution: . Control resolution: on a motor. |
| Impedance analyzer Wayne Kerr Electronics | WK6500P | Frequency range: 20 –5 , Dissipation factor: , Quality factor: , Capacitance/Inductance/Impedance: |
| Transducer | SX60-FR | TVR: 134 dB re / @ 1 , Capacitance: @ 20 |
| Sensor Design | - | RVR: dB re / |
References
- Duquennoy, M.; Smagin, N.; Kadi, T.; Ouaftouh, M.; Jenot, F. Development of a Broadband (100–240 MHz) Surface Acoustic Wave Emitter Devoted to the Non-Destructive Characterization of Sub-Micrometric Thin Films. Sensors 2022, 22, 7464. [Google Scholar] [CrossRef] [PubMed]
- Le, T.C.; Phan, T.T.V.; Nguyen, T.H.; Ho, D.D.; Huynh, T.C. A low-cost prestress monitoring method for post-tensioned RC beam using piezoelectric-based smart strand. Buildings 2021, 11, 431. [Google Scholar] [CrossRef]
- Andreades, C.; Mahmoodi, P.; Ciampa, F. Characterisation of smart CFRP composites with embedded PZT transducers for nonlinear ultrasonic applications. Compos. Struct. 2018, 206, 456–466. [Google Scholar] [CrossRef]
- Reddy, K.A. Non-destructive testing, evaluation of stainless steel materials. Mater. Today Proc. 2017, 4, 7302–7312. [Google Scholar] [CrossRef]
- Raine, A.B.; Aslam, N.; Underwood, C.P.; Danaher, S. Development of an ultrasonic airflow measurement device for ducted air. Sensors 2015, 15, 10705–10722. [Google Scholar] [CrossRef]
- Yamamoto, S.; Hoshi, T.; Miura, T.; Semboshi, J.; Ochiai, M.; Fujita, Y.; Ogawa, T.; Asai, S. Defect detection in thick weld structure using welding in-process laser ultrasonic testing system. Mater. Trans. 2014, 55, 998–1002. [Google Scholar] [CrossRef] [Green Version]
- Kotze, R.; Wiklund, J.; Haldenwang, R. Optimisation of Pulsed Ultrasonic Velocimetry system and transducer technology for industrial applications. Ultrasonics 2013, 53, 459–469. [Google Scholar] [CrossRef]
- Iglesias, E.; de Frutos, J.; de Espinosa, F.M. Modelado de transductores ultrasónicos piezoeléctricos para fisioterapia. BoletÍN Soc. Espa NOla CerÁMica Vidr. 2015, 54, 231–235. [Google Scholar] [CrossRef] [Green Version]
- Qiu, Y.; Gigliotti, J.; Wallace, M.; Griggio, F.; Demore, C.; Cochran, S.; Trolier-McKinstry, S. Piezoelectric micromachined ultrasound transducer (PMUT) arrays for integrated sensing, actuation and imaging. Sensors 2015, 15, 8020–8041. [Google Scholar] [CrossRef] [Green Version]
- Ter Haar, G.R. High intensity focused ultrasound for the treatment of tumors. Echocardiography 2001, 18, 317–322. [Google Scholar] [CrossRef]
- Khazaee, M.; Rosendahl, L.A.; Rezania, A. Online Condition Monitoring of Rotating Machines by Self-Powered Piezoelectric Transducer from Real-Time Experimental Investigations. Sensors 2022, 22, 3395. [Google Scholar] [CrossRef]
- Villó-Pérez, I.; Alcover-Garau, P.M.; Campo-Valera, M.; Toledo-Moreo, R. A novel 1D-FDTD scheme to solve the nonlinear second-order thermoviscous hydrodynamic model. Commun. Nonlinear Sci. Numer. Simul. 2022, 118, 107015. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Qin, L.; Zhong, C. Wideband and wide beam piezoelectric composite spherical cap transducer for underwater acoustics. Ferroelectrics 2021, 583, 295–305. [Google Scholar] [CrossRef]
- Shi, S.; Geng, W.; Bi, K.; He, J.; Hou, X.; Mu, J.; Li, F.; Chou, X. Design and fabrication of a novel MEMS piezoelectric hydrophone. Sens. Actuators Phys. 2020, 313, 112203. [Google Scholar] [CrossRef]
- Suñol, F.; Ochoa, D.A.; Suñé, L.R.; García, J.E. Design and characterization of immersion ultrasonic transducers for pulsed regime applications. Instrum. Sci. Technol. 2018, 47, 213–232. [Google Scholar] [CrossRef] [Green Version]
- Martins, M.; Correia, V.; Cabral, J.; Lanceros-Mendez, S.; Rocha, J.G. Optimization of piezoelectric ultrasound emitter transducers for underwater communications. Sens. Actuators Phys. 2012, 184, 141–148. [Google Scholar] [CrossRef]
- Sharapov, V. Piezoceramic Sensors; Springer Science & Business Media: Heidelberg, Germany; Dordrecht, The Netherlands; London, UK; New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Arnau Vives, A. Piezoelectric Transducers and Applications; Springer: Berlin/Heidelberg, Germany, 2004; Volume 2008. [Google Scholar] [CrossRef]
- Lin, P.; Zhang, L.; Fei, C.; Li, D.; Wu, R.; Chen, Q.; Hou, C.; Yang, Y. Novel multi-layer-composites design for ultrasonic transducer applications. Compos. Struct. 2020, 245, 112364. [Google Scholar] [CrossRef]
- Pershevska, L.; Drozdenko, O.; Drozdenko, K.; Leiko, O. Study of the influence of the housing on the cooling efficiency of the piezoceramic electroacoustic Langevin-type transducer. Technol. Audit. Prod. Reserv. 2021, 3, 50–55. [Google Scholar] [CrossRef]
- do Nascimento, V.M.; da S. Nantes Button, V.L.; Maia, J.M.; Tabares Costa, E.; Valadares Oliveira, E.J. Influence of backing and matching layers in ultrasound transducer performance. In Proceedings of the SPIE Proceedings; Walker, W.F., Insana, M.F., Eds.; Medical Imaging 2003; SPIE: San Diego, CA, USA, 2003. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Lethiecq, M.; Karlsson, B.; Patat, F. Highly attenuative rubber modified epoxy for ultrasonic transducer backing applications. Ultrasonics 1996, 34, 669–675. [Google Scholar] [CrossRef]
- Sun, D.; Wang, S.; Hata, S.; Shimokohbe, A. Axial vibration characteristics of a cylindrical, radially polarized piezoelectric transducer with different electrode patterns. Ultrasonics 2010, 50, 403–410. [Google Scholar] [CrossRef]
- Dong, S.; Uchino, K.; Li, L.; Viehland, D. Analytical solutions for the transverse deflection of a piezoelectric circular axisymmetric unimorph actuator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007, 54, 1240–1249. [Google Scholar] [CrossRef] [PubMed]
- Ivina, N. Analysis of the natural vibrations of circular piezoceramic plates with partial electrodes. Acoust. Phys. 2001, 47, 714–720. [Google Scholar] [CrossRef]
- Predoi, M.V.; Petre, C.C.; Vasile, O.; Boiangiu, M. High frequency longitudinal damped vibrations of a cylindrical ultrasonic transducer. Shock Vib. 2014, 2014. [Google Scholar] [CrossRef] [Green Version]
- Wauer, J. Vibrations of Piezoceramic Rods. PAMM 2004, 4, 121–122. [Google Scholar] [CrossRef]
- Rogacheva, N.N. The Theory of Piezoelectric Shells and Plates; CRC Press: Boca Ratón, FL, USA, 1994. [Google Scholar] [CrossRef]
- Suhir, E.; Birman, V. Effect of temperature on vibrations of physically nonlinear piezoelectric rods. In Proceedings of the 11th International Workshop on Thermal Investigation of ICs and Systems, THERMINIC 2005, Belgirate, Italy, 27–30 September 2005. [Google Scholar]
- Adelman, N.T.; Stavsky, Y.; Segal, E. Radial vibrations of axially polarized piezoelectric ceramic cylinders. J. Acoust. Soc. Am. 1975, 57, 356–360. [Google Scholar] [CrossRef]
- Jordan, T.L.; Ounaies, Z. Piezoelectric ceramics characterization. In Techreport ICASE No. 2001-28; Institute For Computer Applications in Science and Engineering: Hampton, VA, USA, 2001. [Google Scholar]
- Sherrit, S.; Mukherjee, B.K. Characterization of piezoelectric materials for transducers. arXiv 2007, arXiv:0711.2657. [Google Scholar]
- Kunkel, H.; Locke, S.; Pikeroen, B. Finite-Element Analysis of Vibrational Modes in Piezoelectric Ceramic Disks. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1990, 37, 316–328. [Google Scholar] [CrossRef]
- Zalazar, M.A.; Guarnieri, F.A. Análisis y evaluación del comportamiento de sensores piezoeléctricos. MecÁnica Comput. 2010, 29, 6665–6684. [Google Scholar]
- Melchor, J.; Muñoz, R.; Rus, G. Torsional ultrasound sensor optimization for soft tissue characterization. Sensors 2017, 17, 1402. [Google Scholar] [CrossRef] [Green Version]
- Piao, C.; Kim, J.O. Vibration characteristics of an ultrasonic transducer of two piezoelectric discs. Ultrasonics 2017, 74, 72–80. [Google Scholar] [CrossRef]
- Huang, C.H.; Lin, Y.C.; Ma, C.C. Theoretical analysis and experimental measurement for resonant vibration of piezoceramic circular plates. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 12–24. [Google Scholar] [CrossRef]
- Li, X.; Lyu, D.; Song, Y.; Zhang, S.; Hu, P.; Jeong, H. Simultaneously determining sensitivity and effective geometrical parameters of ultrasonic piezoelectric transducers using a self-reciprocity method. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1649–1657. [Google Scholar] [CrossRef]
- San Emeterio, J.L.; Ramos, A.; Sanz Sánchez, P.T. La impedancia eléctrica normalizada de transductores cerámicos piezoeléctricos como herramiento de evaluación y caracterización. Bol. Soc. Esp. Cerám. Vidr. 1999, 38, 518–521. [Google Scholar] [CrossRef]
- Shahab, S.; Zhao, S.; Erturk, A. Soft and hard piezoelectric ceramics and single crystals for random vibration energy harvesting. Energy Technol. 2018, 6, 935–942. [Google Scholar] [CrossRef]
- Chen, J.; Panda, R. Commercialization of piezoelectric single crystals for medical imaging applications. In Proceedings of the IEEE Ultrasonics Symposium; IEEE: Rotterdam, The Netherlands, 2005; Volume 1, pp. 235–240. [Google Scholar] [CrossRef]
- Berlincourt, D. Piezoelectric ceramics: Characteristics and applications. J. Acoust. Soc. Am. 1981, 70, 1586–1595. [Google Scholar] [CrossRef]
- PI-Ceramic. Piezoelectric Ceramic Products; PI Ceramic: Lederhose, Germany, 2003. [Google Scholar]
- INSPEC 3237638; IEEE Standard on Piezoelectricity. Technical Report; IEEE: Piscataway, NJ, USA, 1987. [CrossRef]
- Comsol. Guide COMSOL Multiphysics User’s; Inc.-2006.-708; Comsol: Burlington, MA, USA, 2012. [Google Scholar]
- Urick, R.J. Principles of Underwater Sound, 3rd ed.; McGraw-Hill Book: New York, NY, USA, 1975. [Google Scholar]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Faraday, M. XLIX. Experimental researches in electricity—Nineteenth series. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1846, 28, 294–317. [Google Scholar] [CrossRef] [Green Version]






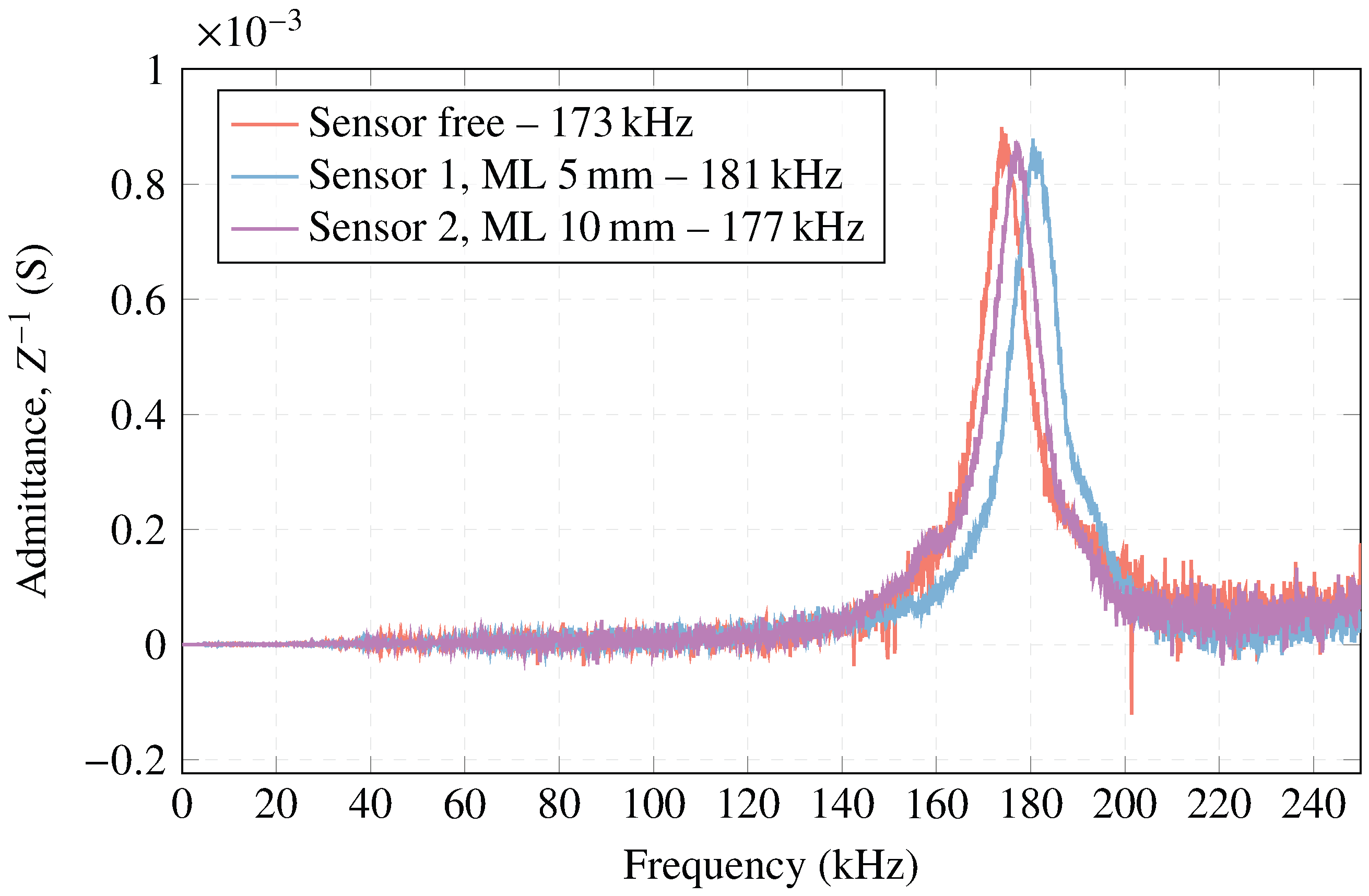
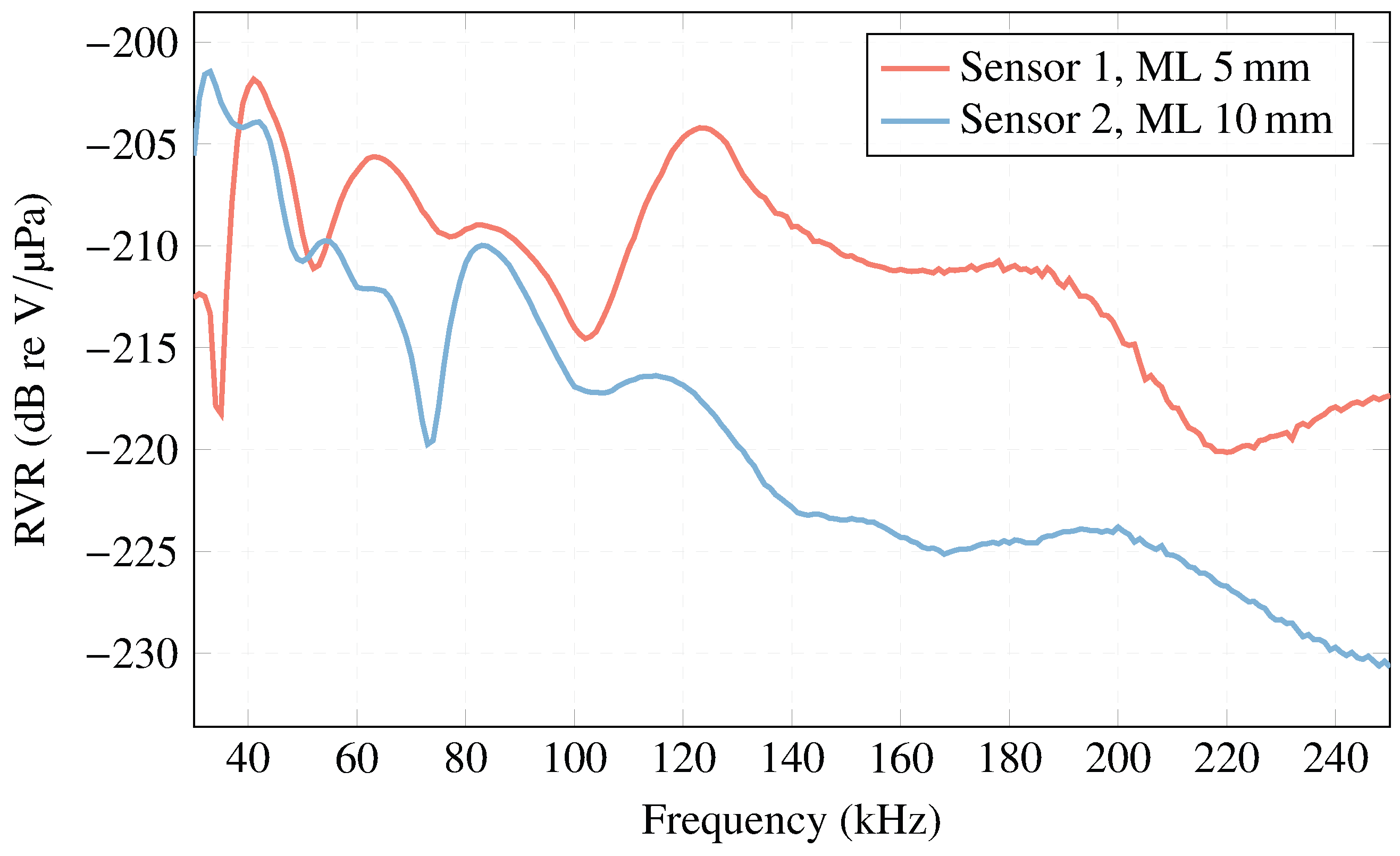
| Element | Velocity m/s | Density kg/m | Acoustic Impedance (MRayl) |
|---|---|---|---|
| Water | 1480 | 1000 | 1.48 |
| Methacrylate | 2700 | 119 | 3.21 |
| Ceramic | 4000 | 7800 | 31.2 |
| Analytical | Numerical | Experimental | |
|---|---|---|---|
| ceramic | |||
| sensor | - | - | |
| sensor (ML—5 ) | - | ||
| sensor (ML—10 ) | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campo-Valera, M.; Asorey-Cacheda, R.; Rodríguez-Rodríguez, I.; Villó-Pérez, I. Characterization of a Piezoelectric Acoustic Sensor Fabricated for Low-Frequency Applications: A Comparative Study of Three Methods. Sensors 2023, 23, 2742. https://doi.org/10.3390/s23052742
Campo-Valera M, Asorey-Cacheda R, Rodríguez-Rodríguez I, Villó-Pérez I. Characterization of a Piezoelectric Acoustic Sensor Fabricated for Low-Frequency Applications: A Comparative Study of Three Methods. Sensors. 2023; 23(5):2742. https://doi.org/10.3390/s23052742
Chicago/Turabian StyleCampo-Valera, María, Rafael Asorey-Cacheda, Ignacio Rodríguez-Rodríguez, and Isidro Villó-Pérez. 2023. "Characterization of a Piezoelectric Acoustic Sensor Fabricated for Low-Frequency Applications: A Comparative Study of Three Methods" Sensors 23, no. 5: 2742. https://doi.org/10.3390/s23052742
APA StyleCampo-Valera, M., Asorey-Cacheda, R., Rodríguez-Rodríguez, I., & Villó-Pérez, I. (2023). Characterization of a Piezoelectric Acoustic Sensor Fabricated for Low-Frequency Applications: A Comparative Study of Three Methods. Sensors, 23(5), 2742. https://doi.org/10.3390/s23052742










