Dynamic Deformation Behaviors of the Levitation Electromagnets of High-Speed Maglev Vehicle Negotiating a Sharp Horizontal Curve
Abstract
1. Introduction
2. Dynamic Model of High-Speed EMS Maglev Vehicle
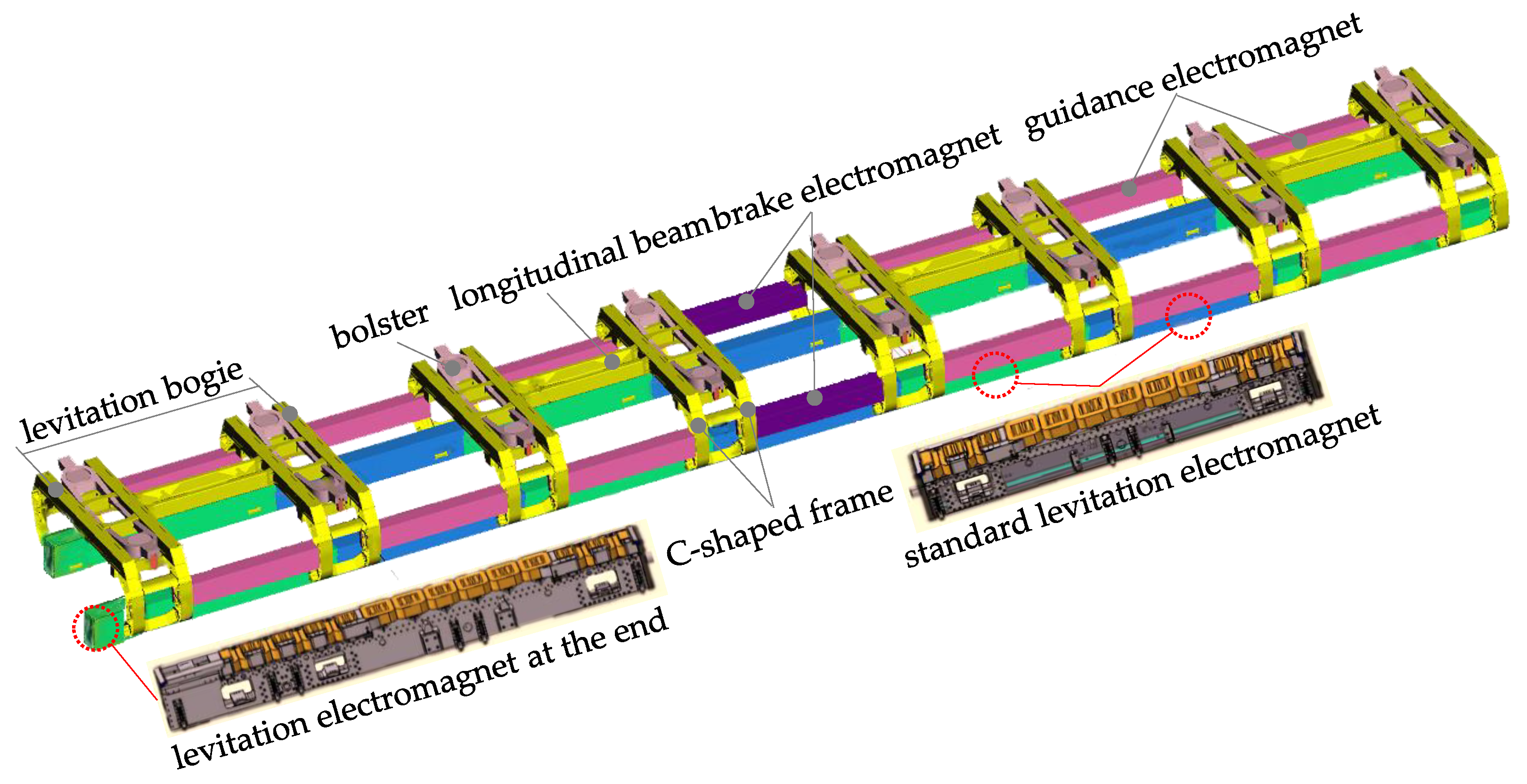
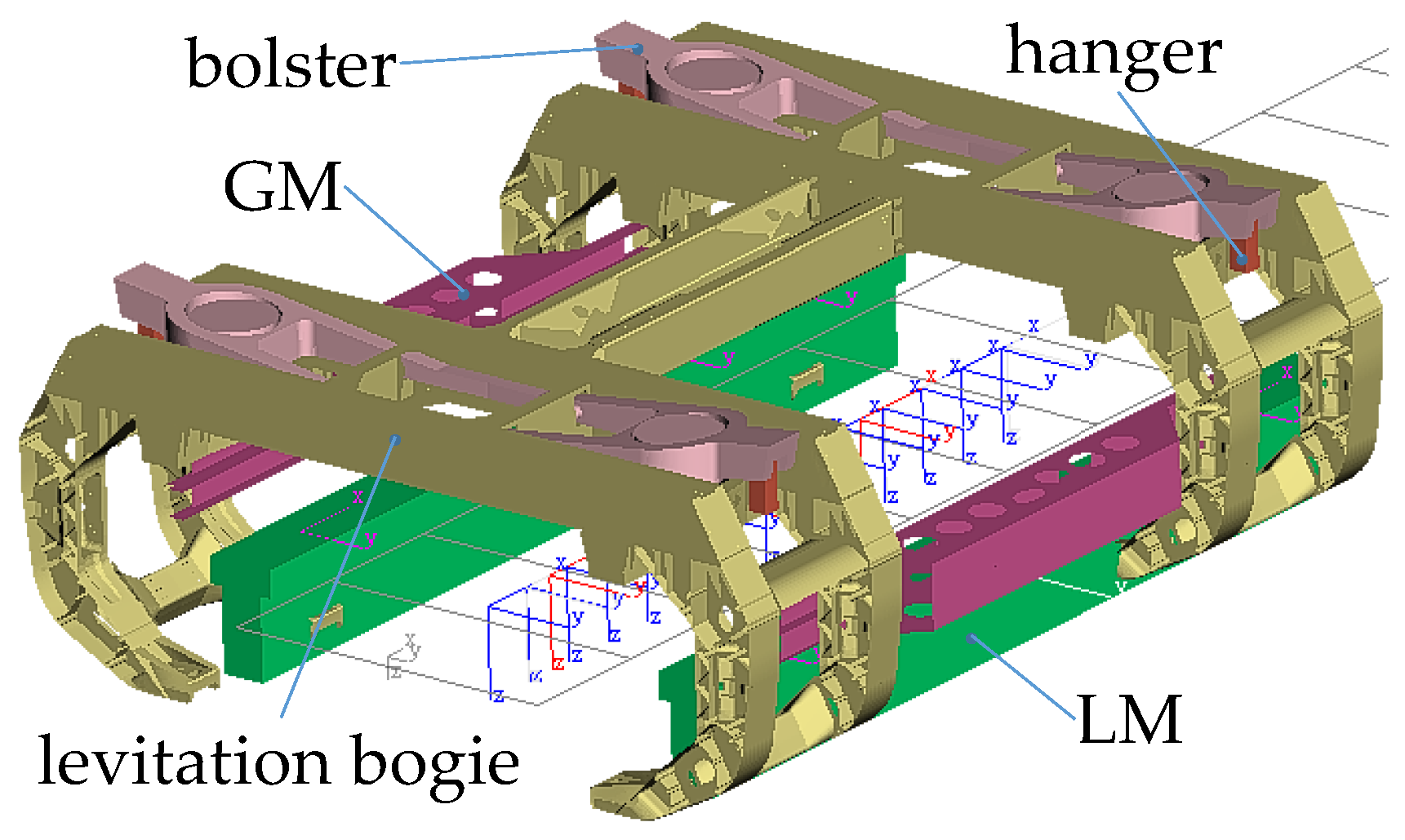
2.1. Flexible Body Dynamic Model of Levitation Bogie and Levitation Electromagnet
2.2. Rigid-Flexible Coupled Dynamic Model of Maglev Vehicle
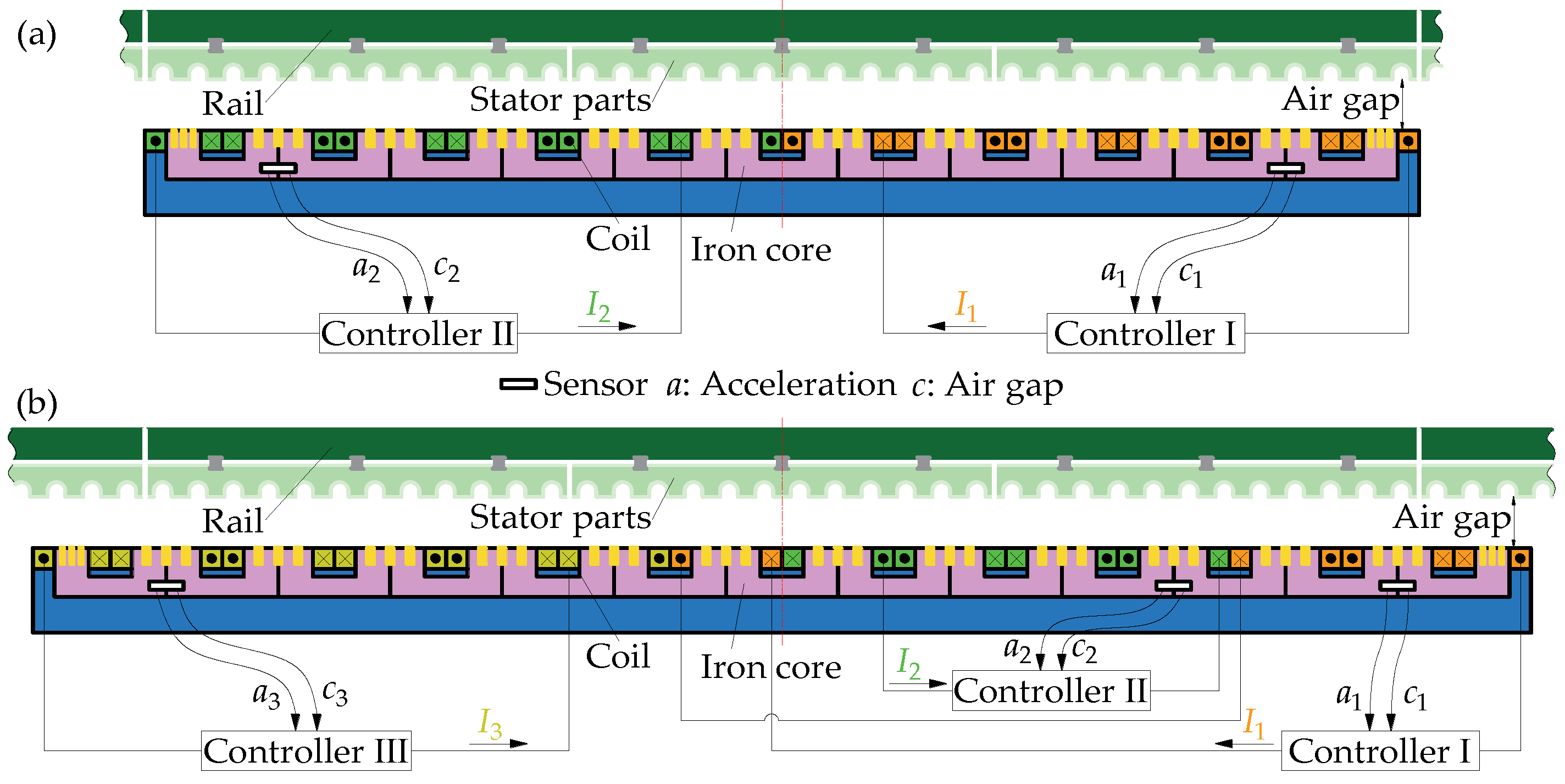
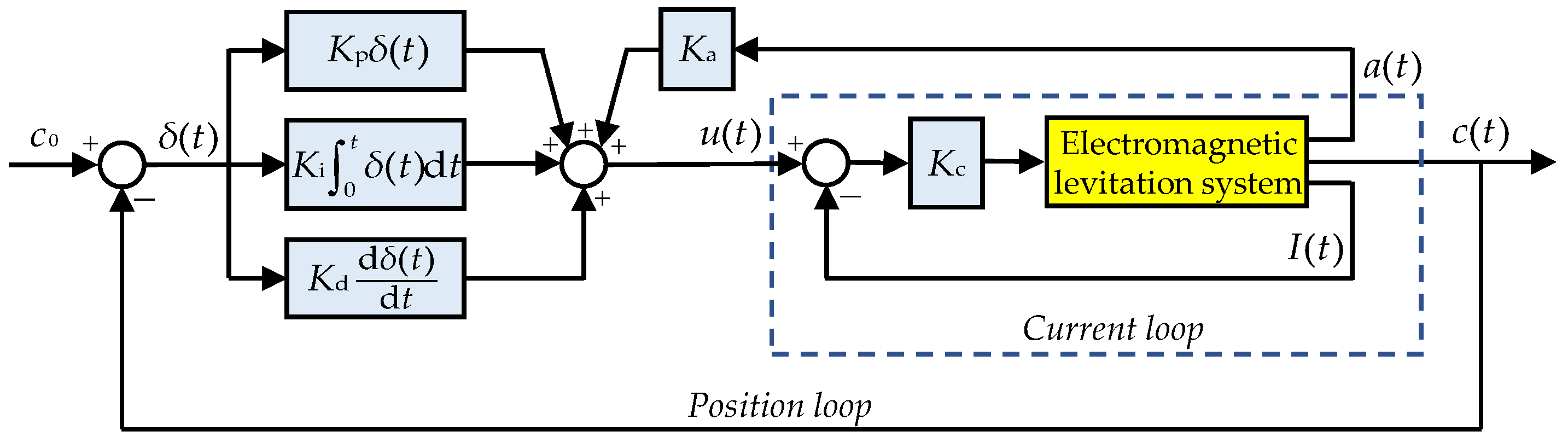
2.3. Dynamic Model of Levitation Control Unit
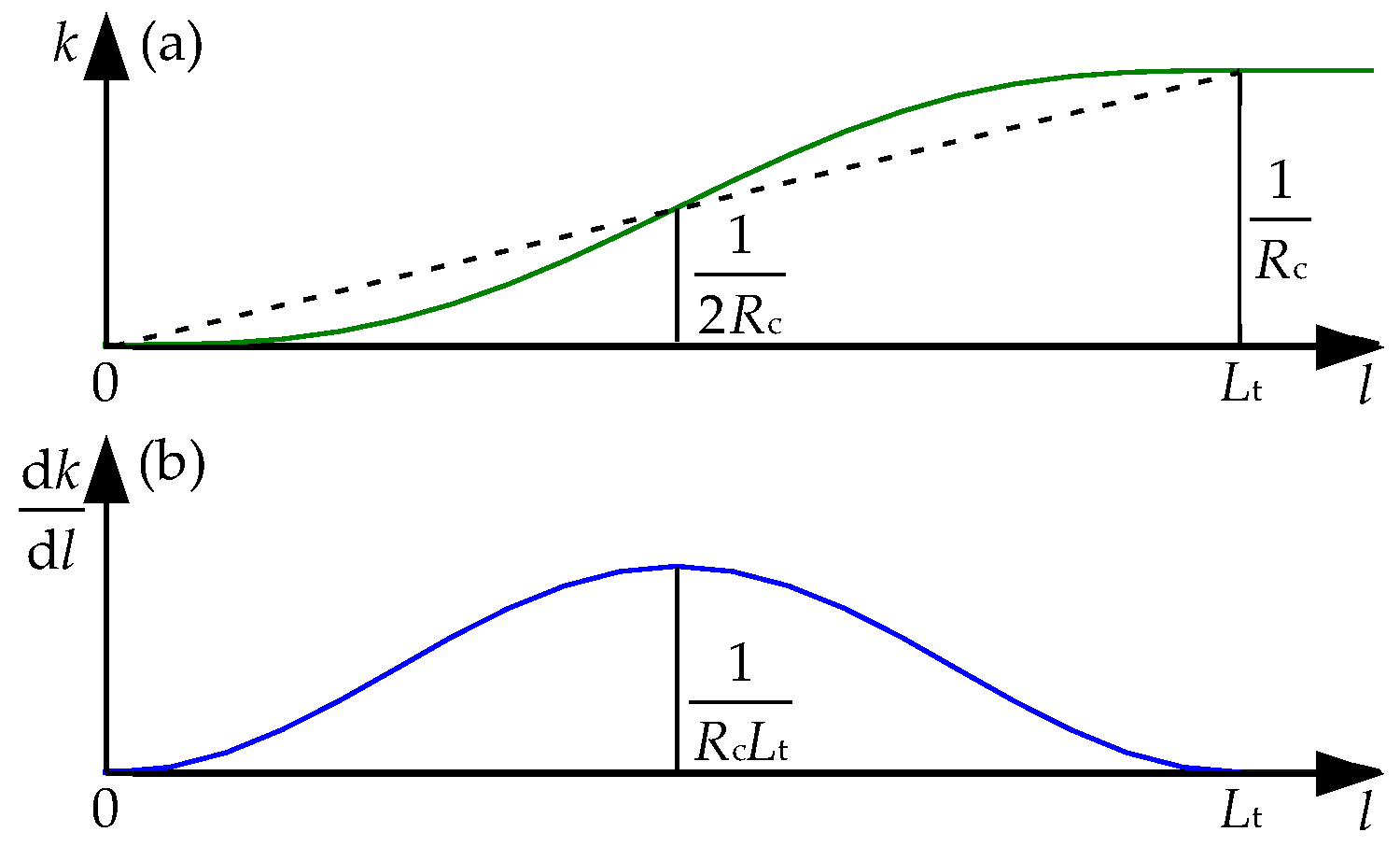
3. Horizontal Curve Model and Its Parameters
4. Deformation Behaviors of the Electromagnets Passing through a Sharp Curve
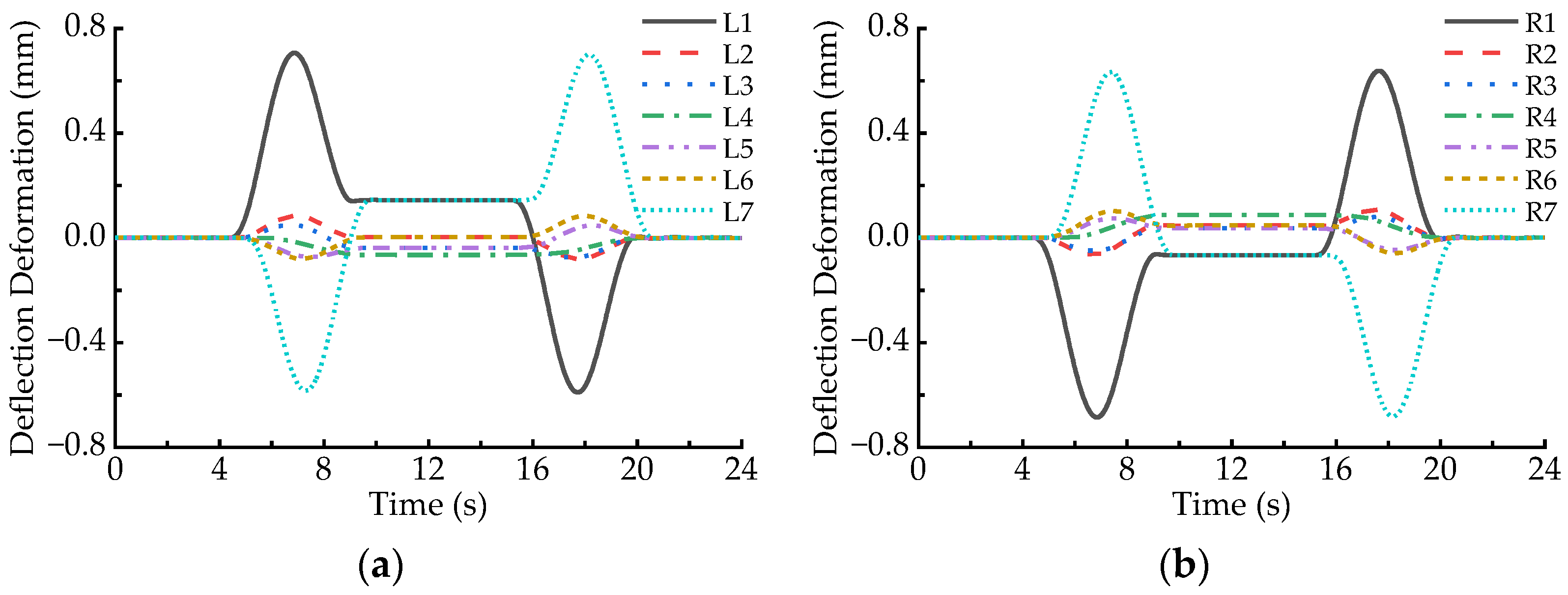
4.1. Deformation Behaviors in the Case of the Balancing Speed
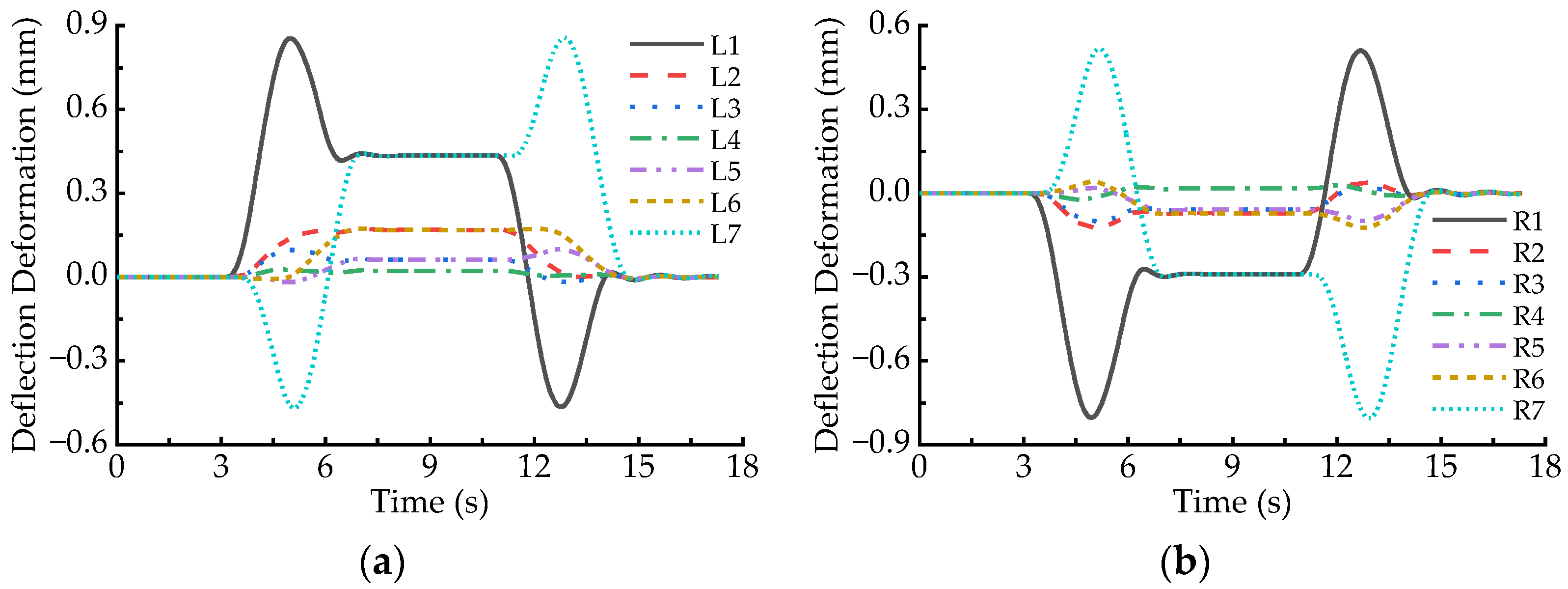
4.2. Deformation Behaviors in the Case of the Maximum Allowable Speed
4.3. Deformation Behaviors in the Case of the Minimum Allowable Speed
4.4. Distribution Feature of Deflection Deformation of All the Electromagnets on the Circular Curve
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, X.M. Maglev Train; Shanghai Science and Technology Press: Shanghai, China, 2003. [Google Scholar]
- Ding, S.S. 600 km/h High-Speed Maglev Transportation System; Science and Technology Press: Shanghai, China, 2022. [Google Scholar]
- Zhao, C.F.; Zhai, W.M. Dynamics of maglev vehicle/guidance system (II)—Modeling and simulation. Chin. J. Mech. Eng. 2005, 41, 163–175. [Google Scholar] [CrossRef]
- Zhao, C.F.; Zhai, W.M.; Ye, X.Y. Dynamic modeling and simulation of high-speed maglev vehicle and its elastic levitation chassis. J. Syst. Simul. 2008, 20, 5718–5721. [Google Scholar]
- Zhao, C.F.; Gu, X.T.; Zhai, W.M. Dynamic model of the levitation chassis of high-speed maglev vehicle. J. Railw. Sci. Eng. 2008, 5, 7–11. [Google Scholar]
- Wang, Z.L.; Xu, Y.L.; Li, G.Q.; Yang, Y.B.; Chen, S.W.; Zhang, X.L. Modelling and validation of coupled high-speed maglev train-and-viaduct systems considering support flexibility. Veh. Syst. Dyn. 2019, 57, 161–191. [Google Scholar] [CrossRef]
- Wang, Z.L.; Xu, Y.L.; Li, G.Q.; Chen, S.W.; Zhang, X.L. Dynamic analysis of a coupled system of high-speed maglev train and curved viaduct. Int. J. Struct. Stab. Dyn. 2018, 18, 1850142. [Google Scholar] [CrossRef]
- Xu, Y.L.; Wang, Z.L.; Li, G.Q.; Chen, S.W.; Yang, Y.B. High-speed running maglev trains interacting with elastic transitional viaducts. Eng. Struct. 2019, 183, 562–578. [Google Scholar] [CrossRef]
- Gong, J.H. Structural form and dynamic characteristics of high-speed maglev separated track beam. J. Vib. Eng. Technol. 2022, 10, 2283–2291. [Google Scholar] [CrossRef]
- Chen, Z.X.; Xu, H.; Li, Z.J.; Li, Y. Research on secondary suspension parameters and track irregularity amplitude of high-speed maglev train. Railw. Stand. Des. 2021, 65, 65–69+76. [Google Scholar]
- Chen, Z.X.; Li, Z.J.; Yang, J.Z.; Wu, X.W.; Zhou, Y.L. Comparison and optimization of secondary suspension structure of high speed ems vehicle. J. OF Mech. Eng. 2022, 58, 160–168+179. [Google Scholar]
- Liang, X.; Zhao, C.F.; Luo, Y.K.; Yu, D.L. Dynamic analysis on high-speed maglev vehicle negotiating a small-radius vertical curve Track. Railw. Locomot. Car 2020, 40, 1–5. [Google Scholar]
- Luo, Y.K.; Zhao, C.F.; Liang, X.; Feng, Y. Dynamic responses of air-spring suspension of a maglev vehicle negotiating a small-radius vertical curved track. J. Vib. Shock 2020, 39, 99–105. [Google Scholar]
- Zhang, B.A.; Yu, D.L.; Li, H.T.; Liang, X.; Huang, C. Influence of flexibility characteristics of levitation chassis on curve negotiation performance of high-speed maglev vehicle. J. Southwest Jiaotong Univ. 2022, 57, 475–482. [Google Scholar]
- He, F.; Feng, Y.; Tong, L.S.; Shu, Y.; Zhao, C.F. Elastic deformation analysis of the levitation bogie and the electromagnet of high-speed maglev vehicle running over the plane curve. Electr. Drive Locomot. 2022, 287, 1–8. Available online: http://edl.csrzic.com/thesisDetails#10.13890/j.issn.1000-128X.2022.04.103 (accessed on 10 October 2022). [CrossRef]
- Li, X.B.; Tang, Z.M.; Wang, S.Y.; Hua, S.; Li, K.C. Deflection deformation displacement compensation technology of maglev electromagnet for high speed maglev train. Electr. Locomot. Mass Transit Veh. 2022, 45, 8–11+46. [Google Scholar]
- Craig, R.R., Jr.; Bampton, M.C.C. Coupling of substructures for dynamic analyses. AIAA J. 1967, 6, 1313–1319. [Google Scholar] [CrossRef]
- Li, Y.G.; Chang, W.S. Cascade control of an EMS maglev vehicle’s levitation control system. Acta Autom. Sin. 1999, 25, 247–251. [Google Scholar]
- Liu, H.K.; Chang, W.S. Double-loop control of maglev train. Control Eng. China 2007, 14, 198–200. [Google Scholar]
- Feng, Y.; Zhao, C.F.; Liang, X.; Jiang, Z.C. Influence of bolster-hanger length on the dynamic performance of high-speed EMS maglev vehicles. Veh. Syst. Dyn. 2022, 60, 3743–3764. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Design of High-Speed Maglev Transit; China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2021; pp. 22–29. [Google Scholar]

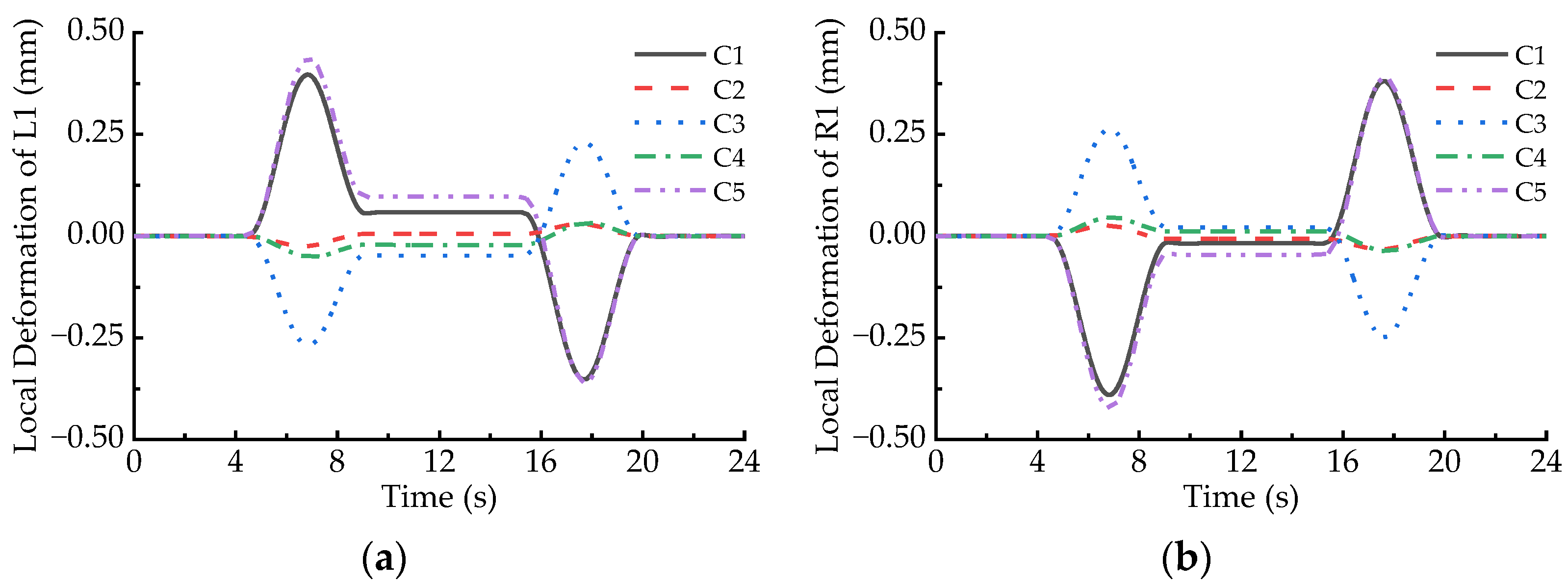
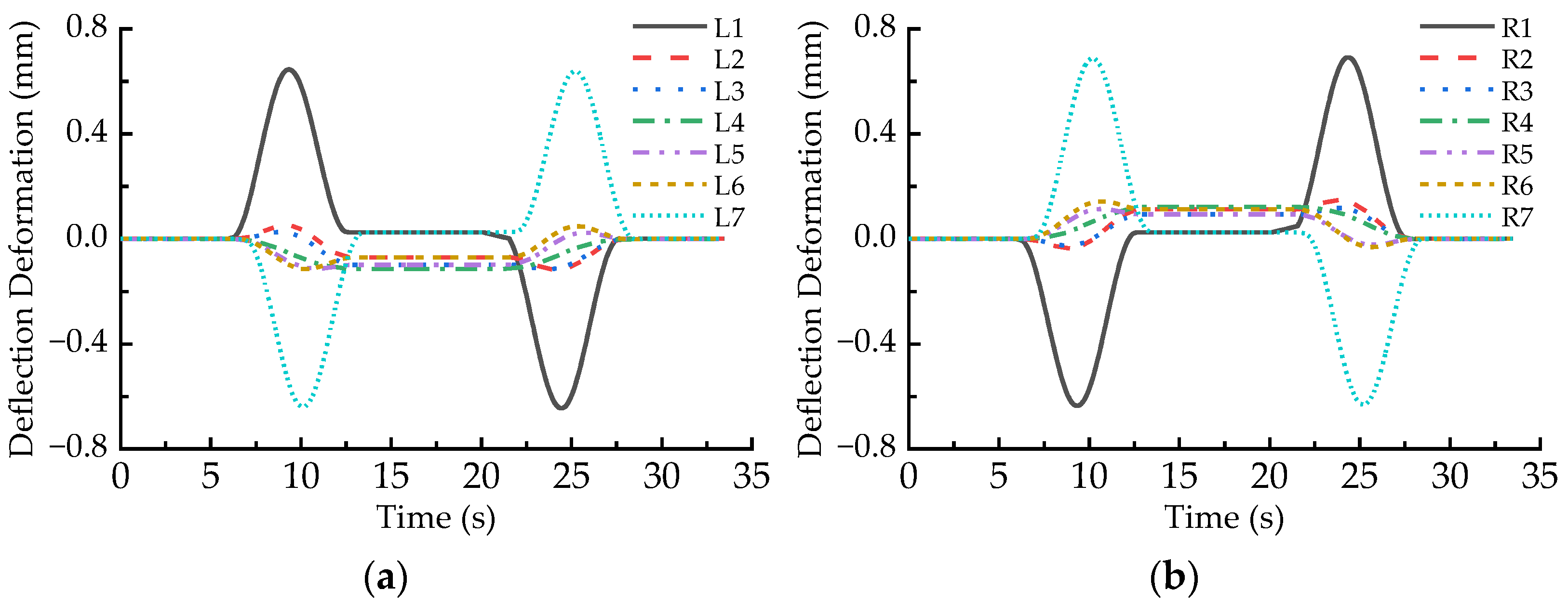
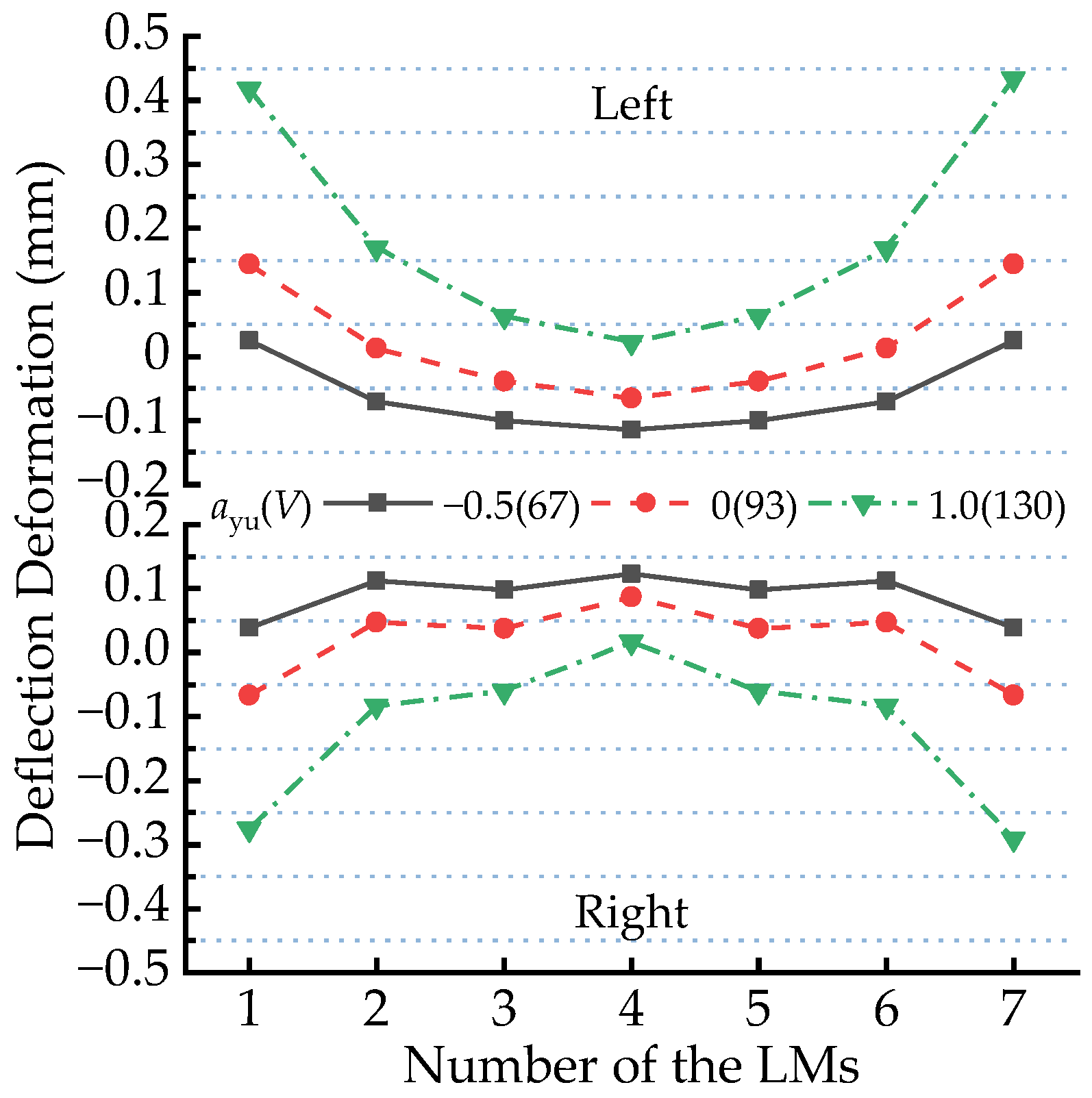
| Position of the LM Measuring Point | L1 | R1 | ||||
|---|---|---|---|---|---|---|
| C1 | C3 | C5 | C1 | C3 | C5 | |
| downward deformation | 0.397 | 0.230 | 0.438 | 0.381 | 0.262 | 0.390 |
| upward deformation | −0.352 | −0.268 | −0.361 | −0.390 | −0.248 | −0.423 |
| Position of the LM | L1 | L7 | R1 | R7 |
|---|---|---|---|---|
| On the transition curve (upward/downward) | 0.706/−0.590 | 0.701/−0.584 | 0.638/−0.685 | 0.634/−0.682 |
| On the circular curve | 0.145 | 0.145 | −0.067 | −0.067 |
| Position of the LM | L1 | L7 | R1 | R7 |
|---|---|---|---|---|
| On the transition curve (upward/downward) | 0.854/−0.464 | 0.857/−0.470 | 0.511/−0.804 | 0.518/−0.805 |
| On the circular curve | 0.435 | 0.435 | −0.290 | −0.290 |
| Position of the LM | L1 | L7 | R1 | R7 |
|---|---|---|---|---|
| On the transition curve (upward/downward) | 0.645/−0.645 | 0.639/−6.40 | 0.692/−0.636 | 0.688/−0.621 |
| On the circular curve | 0.025 | 0.025 | 0.025 | 0.025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Li, X.; Shao, Q.; Han, T.; Zhao, C.; He, F. Dynamic Deformation Behaviors of the Levitation Electromagnets of High-Speed Maglev Vehicle Negotiating a Sharp Horizontal Curve. Sensors 2023, 23, 2785. https://doi.org/10.3390/s23052785
Yu Q, Li X, Shao Q, Han T, Zhao C, He F. Dynamic Deformation Behaviors of the Levitation Electromagnets of High-Speed Maglev Vehicle Negotiating a Sharp Horizontal Curve. Sensors. 2023; 23(5):2785. https://doi.org/10.3390/s23052785
Chicago/Turabian StyleYu, Qingsong, Xiaoqing Li, Qing Shao, Tian Han, Chunfa Zhao, and Feng He. 2023. "Dynamic Deformation Behaviors of the Levitation Electromagnets of High-Speed Maglev Vehicle Negotiating a Sharp Horizontal Curve" Sensors 23, no. 5: 2785. https://doi.org/10.3390/s23052785
APA StyleYu, Q., Li, X., Shao, Q., Han, T., Zhao, C., & He, F. (2023). Dynamic Deformation Behaviors of the Levitation Electromagnets of High-Speed Maglev Vehicle Negotiating a Sharp Horizontal Curve. Sensors, 23(5), 2785. https://doi.org/10.3390/s23052785






