Optical Penetration of Shape-Controlled Metallic Nanosensors across Membrane Barriers
Abstract
:1. Introduction
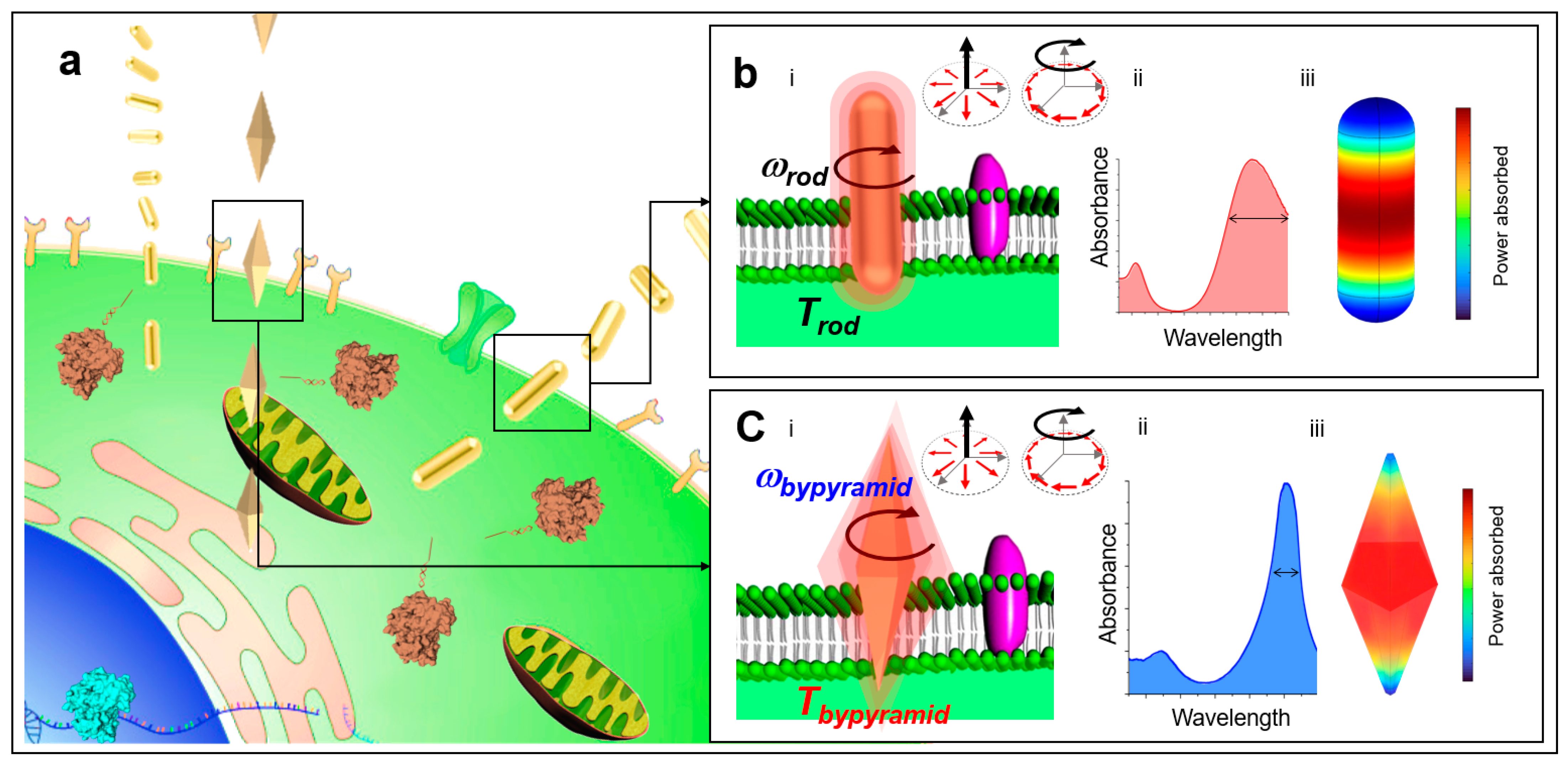
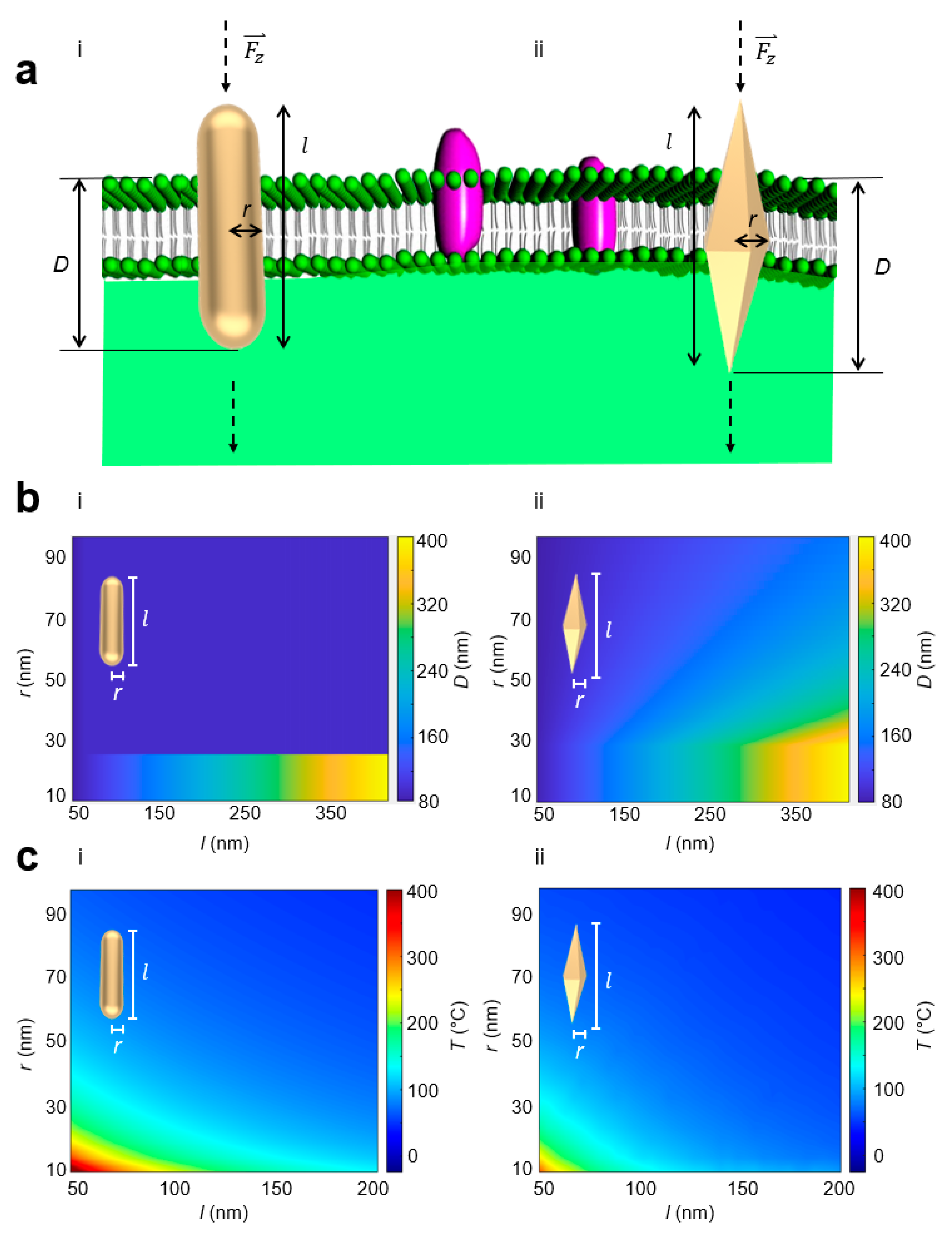
2. Results and Discussion
3. Conclusions
4. Methods
4.1. Normal Stress
4.2. Photothermal Heat
4.3. Lateral Stress
4.4. Shape Factor
4.5. Friction Factor
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knott, G.J.; Doudna, J.A. CRISPR-Cas guides the future of genetic engineering. Science 2018, 361, 866–869. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Jeong, H.; Zu, D.; Zhao, X.; Senaratne, P.; Filbin, J.; Silber, B.; Kang, S.; Gladstone, A.; Lau, M.; et al. Dynamic observations of CRISPR-Cas target recognition and cleavage heterogeneities. Nanophotonics 2022, 11, 4419–4425. [Google Scholar] [CrossRef]
- Fortuna, L.; Buscarino, A. Smart Materials. Materials 2022, 15, 6307. [Google Scholar] [CrossRef]
- Bogyo, M. A ‘Swiss army knife’ probe for metastatic cancers. Nat. Mater. 2021, 20, 1312–1314. [Google Scholar] [CrossRef] [PubMed]
- Dowdy, S.F. Overcoming cellular barriers for RNA therapeutics. Nat. Biotechnol. 2017, 35, 222–229. [Google Scholar] [CrossRef] [PubMed]
- Asuri, P.; Bartel, A.M.; Vazin, T.; Jang, J.-H.; Wong, T.B.; Schaffer, D.V. Directed Evolution of Adeno-associated Virus for Enhanced Gene Delivery and Gene Targeting in Human Pluripotent Stem Cells. Mol. Ther. 2012, 20, 329–338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, W.; Freed, C.R. Adenoviral Gene Delivery Can Reprogram Human Fibroblasts to Induced Pluripotent Stem Cells. STEM CELLS 2009, 27, 2667–2674. [Google Scholar] [CrossRef]
- Ahmed, M.; Narain, R. The effect of molecular weight, compositions and lectin type on the properties of hyperbranched glycopolymers as non-viral gene delivery systems. Biomaterials 2012, 33, 3990–4001. [Google Scholar] [CrossRef]
- Kircheis, R.; Kichler, A.; Wallner, G.; Kursa, M.; Ogris, M.; Felzmann, T.; Buchberger, M.; Wagner, E. Coupling of cell-binding ligands to polyethylenimine for targeted gene delivery. Gene Ther. 1997, 4, 409–418. [Google Scholar] [CrossRef] [Green Version]
- Cemazar, M.; Sersa, G.; Wilson, J.; Tozer, G.M.; Hart, S.L.; Grosel, A.; Dachs, G.U. Effective gene transfer to solid tumors using different nonviral gene delivery techniques: Electroporation, liposomes, and integrin-targeted vector. Cancer Gene Ther. 2002, 9, 399–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Zhang, Z.; Park, Y.; Lee, S.E. Ultraprecision Imaging and Manipulation of Plasmonic Nanostructures by Integrated Nanoscopic Correction. Small 2021, 17, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Marago, O.M.; Jones, P.; Gucciardi, P.G.; Volpe, G.; Ferrari, A.C. Optical trapping and manipulation of nanostructures. Nat. Nanotechnol. 2013, 8, 807–819. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shao, L.; Yang, Z.-J.; Andrén, D.; Johansson, P.; Käll, M. Gold Nanorod Rotary Motors Driven by Resonant Light Scattering. ACS Nano 2015, 9, 12542–12551. [Google Scholar] [CrossRef]
- Berthelot, J.; Aćimović, S.S.; Juan, M.L.; Kreuzer, M.P.; Renger, J.; Quidant, R. Three-dimensional manipulation with scanning near-field optical nanotweezers. Nat. Nanotechnol. 2014, 9, 295–299. [Google Scholar] [CrossRef]
- Spesyvtseva, S.E.S.; Dholakia, K. Trapping in a Material World. ACS Photon. 2016, 3, 719–736. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, Y.Y.; Albella, P.; Rahmani, M.; Giannini, V.; Maier, S.A.; Shimura, T. Plasmonic linear nanomotor using lateral optical forces. Sci. Adv. 2020, 6, eabc3726. [Google Scholar] [CrossRef]
- Toussaint, K.; Liu, M.; Pelton, M.; Pesic, J.; Guffey, M.J.; Guyot-Sionnest, P.; Scherer, N.F. Plasmon resonance-based optical trapping of single and multiple Au nanoparticles. Opt. Express 2007, 15, 12017–12029. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Miljković, V.D.; Käll, M. Alignment, Rotation, and Spinning of Single Plasmonic Nanoparticles and Nanowires Using Polarization Dependent Optical Forces. Nano Lett. 2010, 10, 268–273. [Google Scholar] [CrossRef]
- Shao, L.; Andrén, D.; Jones, S.; Johansson, P.; Käll, M. Optically controlled stochastic jumps of individual gold nanorod rotary motors. Phys. Rev. B 2018, 98, 085404. [Google Scholar] [CrossRef] [Green Version]
- Karpinski, P.; Jones, S.; Šípová-Jungová, H.; Verre, R.; Käll, M. Optical Rotation and Thermometry of Laser Tweezed Silicon Nanorods. Nano Lett. 2020, 20, 6494–6501. [Google Scholar] [CrossRef] [PubMed]
- Shao, L.; Käll, M. Light-Driven Rotation of Plasmonic Nanomotors. Adv. Funct. Mater. 2018, 28, 1706272. [Google Scholar] [CrossRef]
- Kyrsting, A.; Bendix, P.M.; Stamou, D.G.; Oddershede, L.B. Heat Profiling of Three-Dimensionally Optically Trapped Gold Nanoparticles using Vesicle Cargo Release. Nano Lett. 2011, 11, 888–892. [Google Scholar] [CrossRef]
- Li, M.; Lohmüller, T.; Feldmann, J. Optical Injection of Gold Nanoparticles into Living Cells. Nano Lett. 2015, 15, 770–775. [Google Scholar] [CrossRef]
- Cortie, M.B.; Xu, X.; Chowdhury, H.; Zareie, H.; Smith, G. Plasmonic heating of gold nanoparticles and its exploitation. Plasmonic heating of gold nanoparticles and its exploitation. Smart Struct. Devices Syst. II 2005, 565, 5649. [Google Scholar]
- Khlebtsov, B.; Zharov, V.; Melnikov, A.; Tuchin, V.; Khlebtsov, N. Optical amplification of photothermal therapy with gold nanoparticles and nanoclusters. Nanotechnology 2006, 17, 5167–5179. [Google Scholar] [CrossRef]
- Link, S.; El-Sayed, M.A. Shape and size dependence of radiative, non-radiative and photothermal properties of gold nanocrystals. Int. Rev. Phys. Chem. 2000, 19, 409–453. [Google Scholar] [CrossRef]
- Liu, Y.; Bridgette, C.M.; Vo-Dinh, T. Gold nanoparticles-mediated photothermal therapy and immunotherapy. Immunotherapy 2018, 10, 1175–1188. [Google Scholar] [CrossRef]
- Li, X.; Lan, T.-H.; Tien, C.-H.; Gu, M. Three-dimensional orientation-unlimited polarization encryption by a single optically configured vectorial beam. Nat. Commun. 2012, 3, 998. [Google Scholar] [CrossRef] [Green Version]
- Chow, T.H.; Li, N.; Bai, X.; Zhuo, X.; Shao, L.; Wang, J. Gold Nanobipyramids: An Emerging and Versatile Type of Plasmonic Nanoparticles. Accounts Chem. Res. 2019, 52, 2136–2146. [Google Scholar] [CrossRef] [PubMed]
- Koya, A.N. Plasmonic Nanoarchitectures for Single-Molecule Explorations: An Overview. Adv. Photon. Res. 2022, 3, 2100325. [Google Scholar] [CrossRef]
- Murphy, C.J.; Chang, H.-H.; Falagan-Lotsch, P.; Gole, M.T.; Hofmann, D.M.; Hoang, K.N.L.; McClain, S.M.; Meyer, S.M.; Turner, J.G.; Unnikrishnan, M.; et al. Virus-Sized Gold Nanorods: Plasmonic Particles for Biology. Accounts Chem. Res. 2019, 52, 2124–2135. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.E.; Liu, G.L.; Kim, F.; Lee, L.P. Remote Optical Switch for Localized and Selective Control of Gene Interference. Nano Lett. 2009, 9, 562–570. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.E.; Sasaki, D.Y.; Perroud, T.D.; Yoo, D.; Patel, K.D.; Lee, L.P. Biologically Functional Cationic Phospholipid−Gold Nanoplasmonic Carriers of RNA. J. Am. Chem. Soc. 2009, 131, 14066–14074. [Google Scholar] [CrossRef]
- Lee, S.E.; Lee, L.P. Biomolecular plasmonics for quantitative biology and nanomedicine. Curr. Opin. Biotechnol. 2010, 21, 489–497. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.E.; Lee, L.P. Nanoplasmonic gene regulation. Curr. Opin. Chem. Biol. 2010, 14, 623–633. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.E.; Sasaki, D.Y.; Park, Y.; Xu, R.; Brennan, J.S.; Bissell, M.J.; Lee, L.P. Photonic gene circuits by optically addressable siRNA-Au nanoantennas. ACS Nano 2012, 6, 7770–7780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.E.; Alivisatos, A.P.; Bissell, M.J. Toward plasmonics-enabled spatiotemporal activity patterns in three-dimensional culture models. Syst. Biomed. 2013, 1, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.E.; Chen, Q.; Bhat, R.; Petkiewicz, S.; Smith, J.M.; Ferry, V.E.; Correia, A.L.; Alivisatos, A.P.; Bissell, M.J. Reversible Aptamer-Au Plasmon Rulers for Secreted Single Molecules. Nano Lett. 2015, 15, 4564–4570. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Park, Y.; Lee, S.E. Thermo-responsive mechano-optical plasmonic nano-antenna. Appl. Phys. Lett. 2016, 109, 13109. [Google Scholar] [CrossRef]
- Lin, W.; Cui, G.; Burns, Z.; Zhao, X.; Liu, Y.; Zhang, Z.; Wang, Y.; Ye, X.; Park, Y.; Lee, S.E. Optically and Structurally Stabilized Plasmo-Bio Interlinking Networks. Adv. Mater. Interfaces 2021, 8, 2001370. [Google Scholar] [CrossRef]
- Murphy, E.; Liu, Y.; Krueger, D.; Prasad, M.; Lee, S.E.; Park, Y. Visible-Light Induced Sustainable Water Treatment Using Plasmo-Semiconductor Nanogap Bridge Array, PNA. Small 2021, 17, e2006044. [Google Scholar] [CrossRef]
- Saha, T.; Mondal, J.; Khiste, S.; Lusic, H.; Hu, Z.-W.; Jayabalan, R.; Hodgetts, K.J.; Jang, H.; Sengupta, S.; Lee, S.E.; et al. Nanotherapeutic approaches to overcome distinct drug resistance barriers in models of breast cancer. Nanophotonics 2021, 10, 3063–3073. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Yoon, H.J.; Lee, S.E.; Lee, L.P. Multifunctional Cellular Targeting, Molecular Delivery, and Imaging by Integrated Mesoporous-Silica with Optical Nanocrescent Antenna: MONA. ACS Nano 2022, 16, 2013–2023. [Google Scholar] [CrossRef] [PubMed]
- Do, H.; Yoon, C.; Liu, Y.; Zhao, X.; Gregg, J.; Da, A.; Park, Y.; Lee, S.E. Intelligent fusion imaging photonics for real-time object detection. Sensors 2023, 23, 323. [Google Scholar] [CrossRef]
- Liu, Y.; Zu, D.; Zhang, Z.; Zhao, X.; Cui, G.; Hentschel, M.; Park, Y.; Lee, S.E. Rapid Depolarization-Free Nanoscopic Background Elimination of Cellular Metallic Nanoprobes. Adv. Intell. Syst. 2022, 4, 2200180. [Google Scholar] [CrossRef]
- Phelan, C.F.; Donegan, J.F.; Lunney, J.G. Generation of a radially polarized light beam using internal conical diffraction. Opt. Express 2011, 19, 21793–21802. [Google Scholar] [CrossRef]
- Li, H.; Ma, C.; Wang, J.; Tang, M.; Li, X. Spin-orbit Hall effect in the tight focusing of a radially polarized vortex beam. Opt. Express 2021, 29, 39419. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Du, L.; Yuan, X. Structured spin angular momentum in highly focused cylindrical vector vortex beams for optical manipulation. Opt. Express 2018, 26, 23449–23459. [Google Scholar] [CrossRef]
- Zhang, Q.; Tamashunas, A.C.; Agrawal, A.; Torbati, M.; Katiyar, A.; Dickinson, R.B.; Lammerding, J.; Lele, T.P. Local, transient tensile stress on the nuclear membrane causes membrane rupture. Mol. Biol. Cell 2019, 30, 899–906. [Google Scholar] [CrossRef] [PubMed]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Gramse, G.; Dols-Perez, A.; Edwards, M.; Fumagalli, L.; Gomila, G. Nanoscale Measurement of the Dielectric Constant of Supported Lipid Bilayers in Aqueous Solutions with Electrostatic Force Microscopy. Biophys. J. 2013, 104, 1257–1262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bagheri, G.; Bonadonna, C. On the drag of freely falling non-spherical particles. Powder Technol. 2016, 301, 526–544. [Google Scholar] [CrossRef] [Green Version]
- Zwanzig, R. Hydrodynamic fluctuations and Stokes’ law friction. J. Res. Natl. Bur. Stand. Sect. B Math. Math. Phys. 1964, 68, 143. [Google Scholar] [CrossRef]
- Leith, D. Drag on Nonspherical Objects. Aerosol Sci. Technol. 1987, 6, 153–161. [Google Scholar] [CrossRef] [Green Version]
- Ilić, V.; Vincent, J. Sedimentation of complex-shaped particles in a square tank at low Reynolds numbers. Int. J. Multiph. Flow 1994, 20, 445–452. [Google Scholar] [CrossRef]
- Nojima, Y.; Iwata, K. Viscosity Heterogeneity inside Lipid Bilayers of Single-Component Phosphatidylcholine Liposomes Observed with Picosecond Time-Resolved Fluorescence Spectroscopy. J. Phys. Chem. B 2014, 118, 8631–8641. [Google Scholar] [CrossRef]
- Nikoobakht, B.; El-Sayed, M.A. Preparation and Growth Mechanism of Gold Nanorods (NRs) Using Seed-Mediated Growth Method. Chem. Mater. 2003, 15, 1957–1962. [Google Scholar] [CrossRef]
- Gou, L.; Murphy, C.J. Fine-Tuning the Shape of Gold Nanorods. Chem. Mater. 2005, 17, 3668–3672. [Google Scholar] [CrossRef]
- Lehmuskero, A.; Ogier, R.; Gschneidtner, T.; Johansson, P.; Käll, M. Ultrafast Spinning of Gold Nanoparticles in Water Using Circularly Polarized Light. Nano Lett. 2013, 13, 3129–3134. [Google Scholar] [CrossRef]
- Rodríguez, H.R.; Sevilla, P.R.; Rodríguez, E.M.; Ortgies, D.; Pedroni, M.; Speghini, A.; Bettinelli, M.; Jaque, D.; Haro-González, P. Enhancing Optical Forces on Fluorescent Up-Converting Nanoparticles by Surface Charge Tailoring. Small 2015, 11, 1555–1561. [Google Scholar] [CrossRef] [PubMed]
- Nagao, M.; Kelley, E.G.; Faraone, A.; Saito, M.; Yoda, Y.; Kurokuzu, M.; Takata, S.; Seto, M.; Butler, P.D. Relationship between Viscosity and Acyl Tail Dynamics in Lipid Bilayers. Phys. Rev. Lett. 2021, 127, 078102. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Da, A.; Chu, Y.; Krach, J.; Liu, Y.; Park, Y.; Lee, S.E. Optical Penetration of Shape-Controlled Metallic Nanosensors across Membrane Barriers. Sensors 2023, 23, 2824. https://doi.org/10.3390/s23052824
Da A, Chu Y, Krach J, Liu Y, Park Y, Lee SE. Optical Penetration of Shape-Controlled Metallic Nanosensors across Membrane Barriers. Sensors. 2023; 23(5):2824. https://doi.org/10.3390/s23052824
Chicago/Turabian StyleDa, Ancheng, Yanan Chu, Jacob Krach, Yunbo Liu, Younggeun Park, and Somin Eunice Lee. 2023. "Optical Penetration of Shape-Controlled Metallic Nanosensors across Membrane Barriers" Sensors 23, no. 5: 2824. https://doi.org/10.3390/s23052824




