Reduced Order Modeling of Nonlinear Vibrating Multiphysics Microstructures with Deep Learning-Based Approaches
Abstract
:1. Introduction
2. Problem Formulation
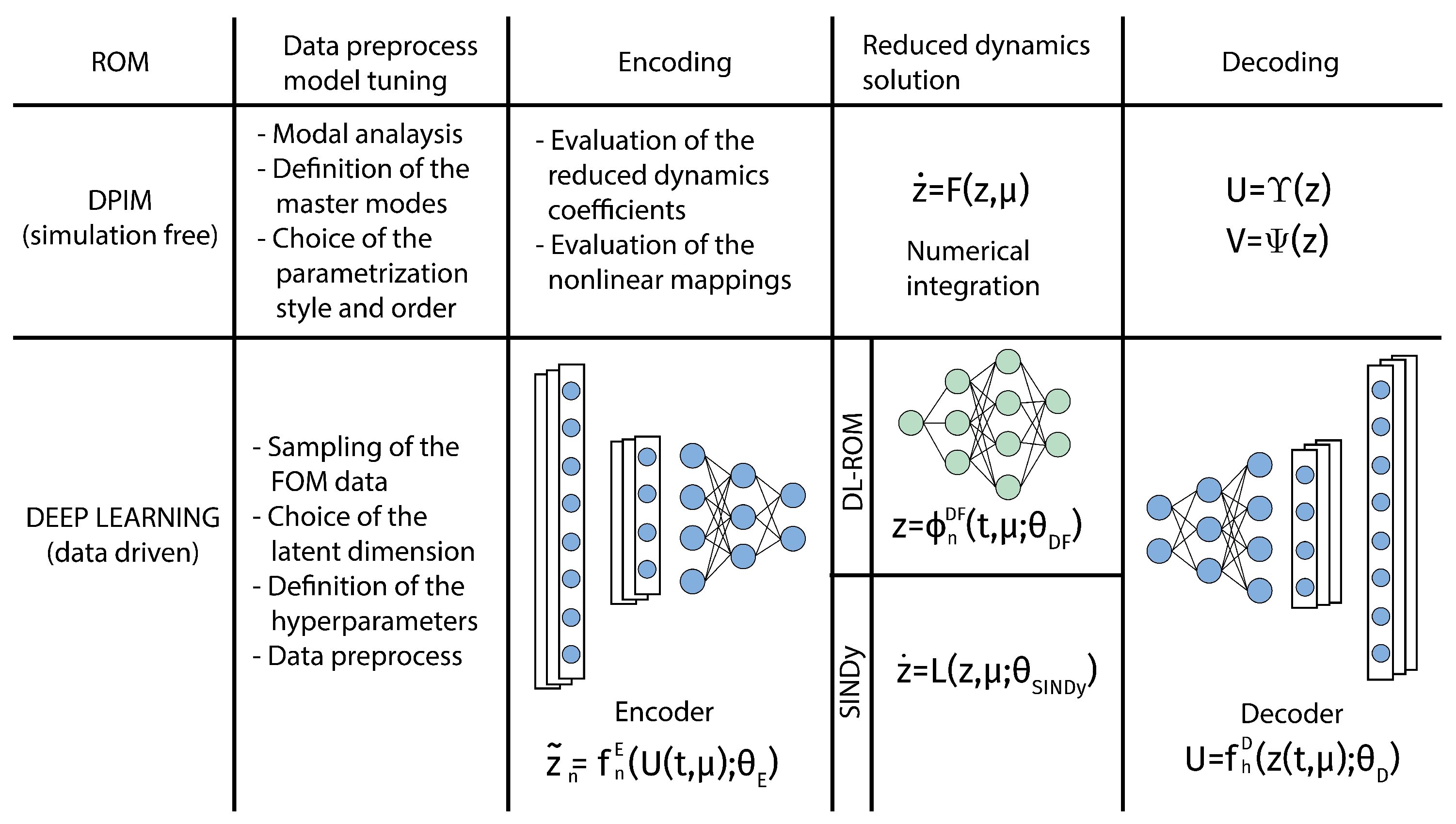
3. Data-Driven Reduced Order Modeling through DL-ROMs
- To map the FOM solutions in a low-dimensional coordinates vector representation (encoding stage), we use the encoder function of a convolutive autoencoder (CAE)where is obtained as the composition of several layers (some of which are convolutional), depending upon a vector of parameters;
- To describe the system dynamics (reduced dynamics learning), the intrinsic coordinates of the ROM approximation are defined aswhere is a DFNN, consisting of the subsequent composition of a nonlinear activation function, applied to a linear transformation of the input, multiple times [36]. Here, denotes the vector of parameters of the DFNN, collecting all of the weights and biases of each layer of the DFNN;
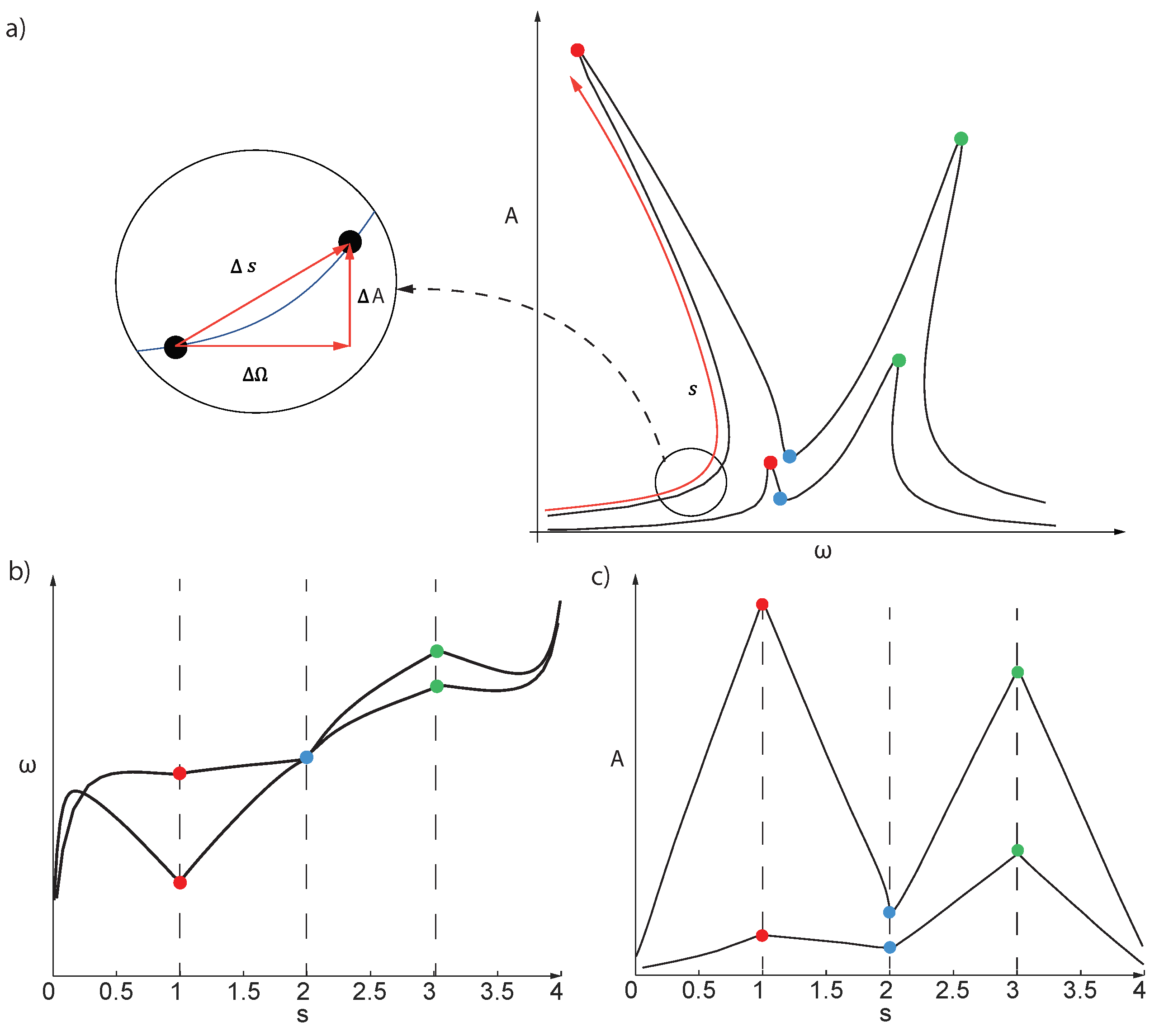
Arc-Length on the FRF as Control Parameter
4. Direct Parametrization of Invariant Manifolds
- (1)
- All of the coefficients and vectors in Equations (15) and (16) are computed offline starting from the FOM, in a preliminary phase, that can be seen as the equivalent of the encoding phase in the DL-ROM. The costly offline training can be performed on dedicated platforms and software. Both approaches hence are based on a FOM, which is typically built exploiting a finite element discretization.
- (2)
- (3)
- Equations (13) and (14) represent the parallel of the decoding phase, which reconstructs the global nodal fields starting from the online integration of the ROM. Thus, both ROMs can reproduce the same richness in details of the original FOM since the decoding phase allows one to generate a full field information.
Computation of the Steady State Response
5. Applications
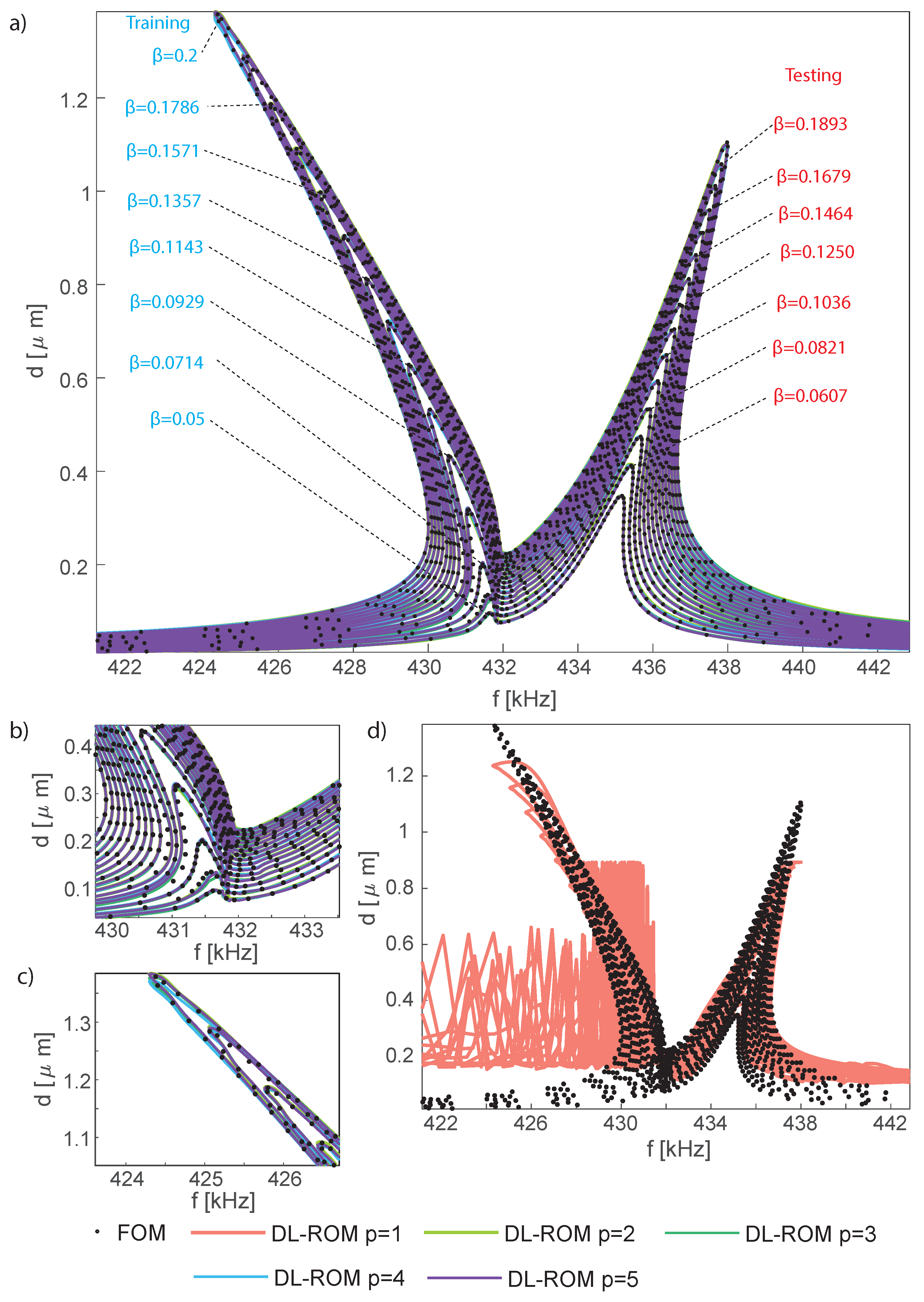
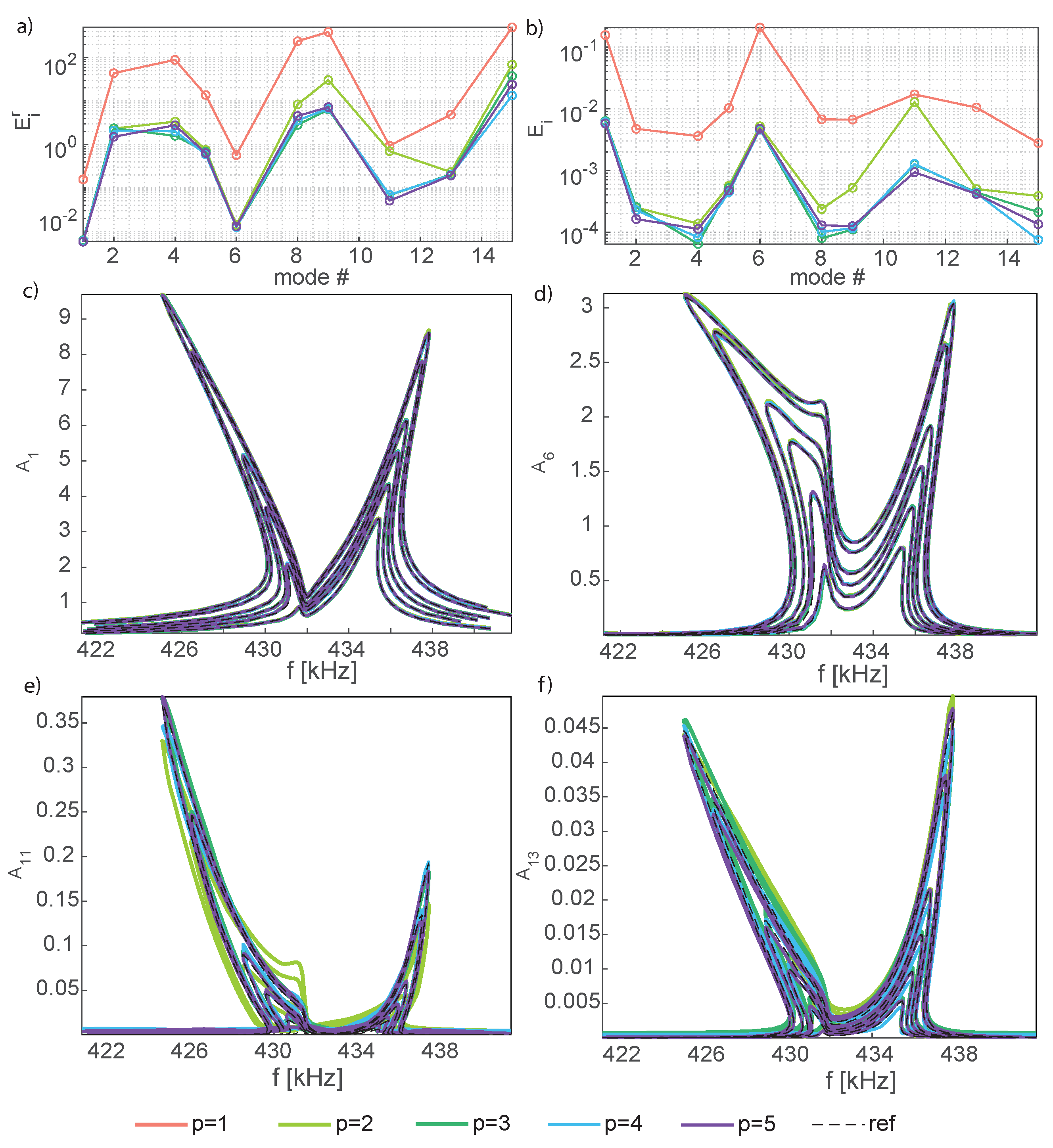
5.1. Reconstruction of the Whole Response
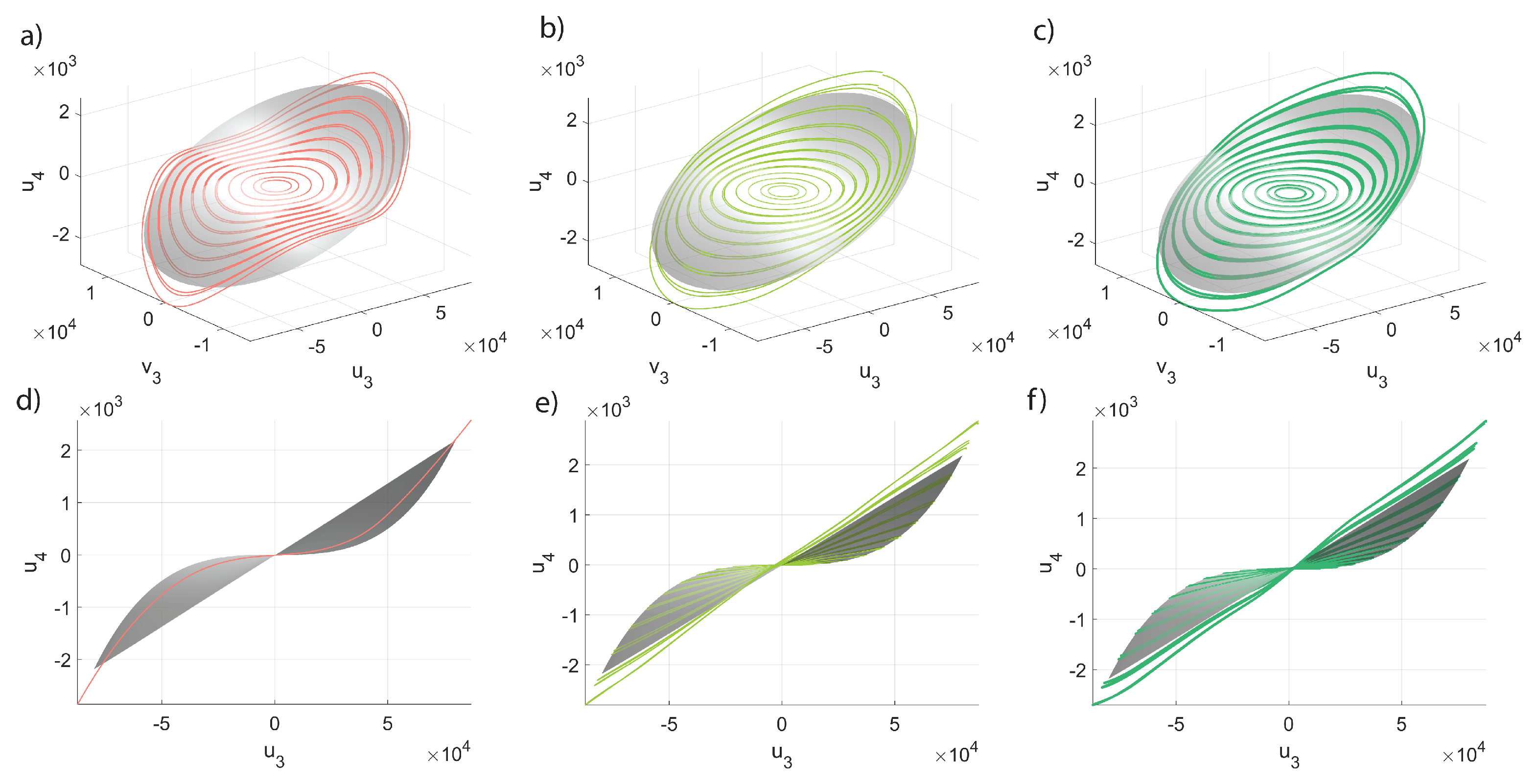
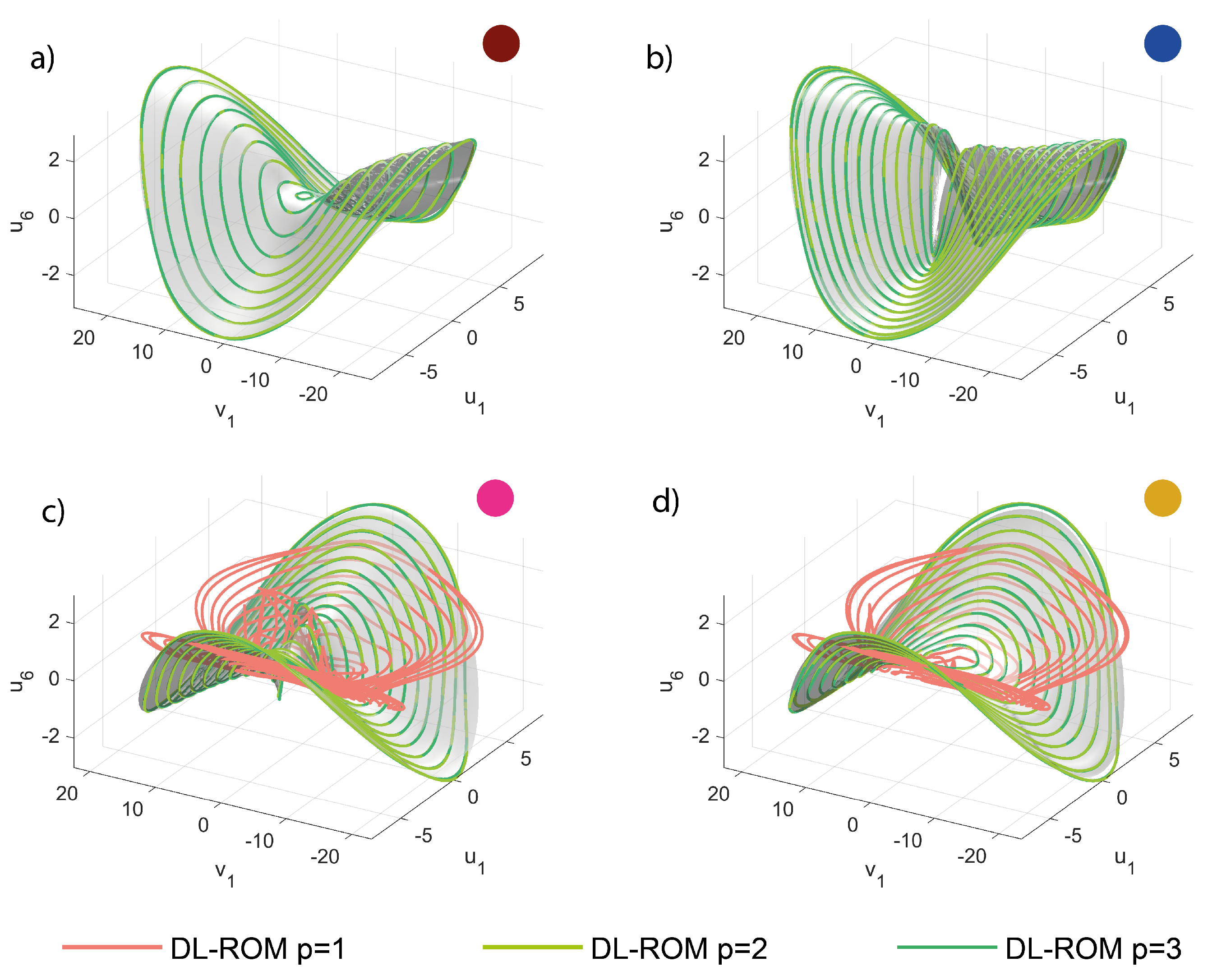
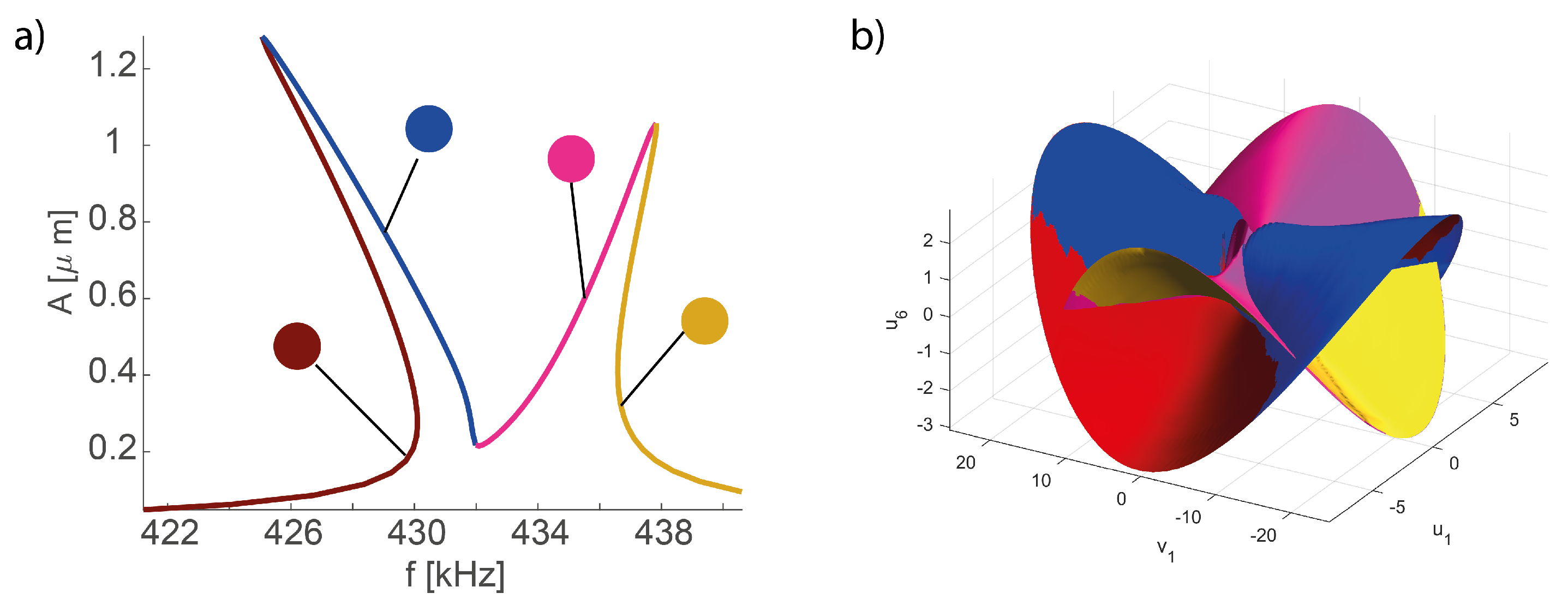
5.2. Computation of Manifolds
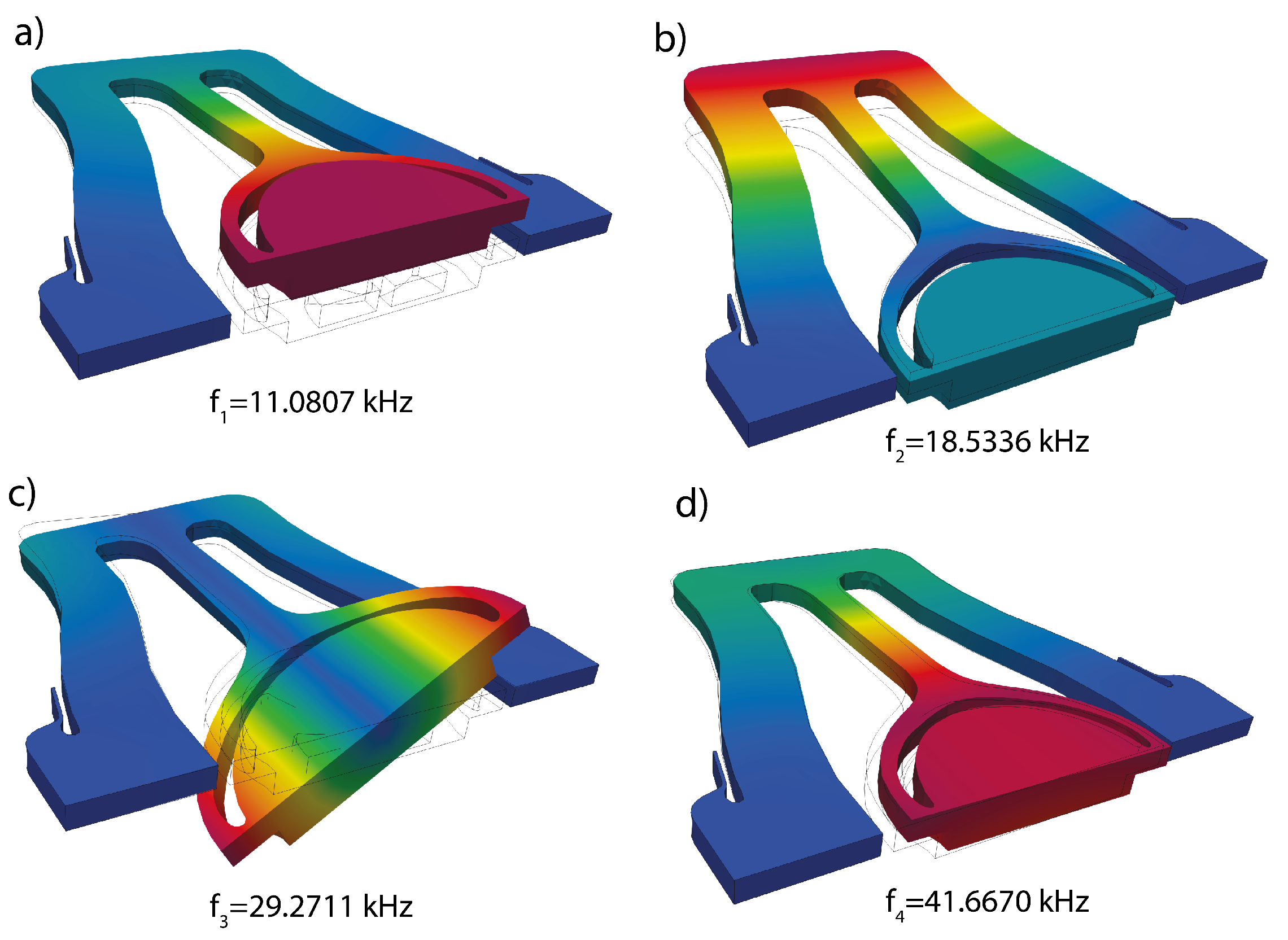
5.3. Micromirror
5.4. Internal Resonance in a Shallow Arch
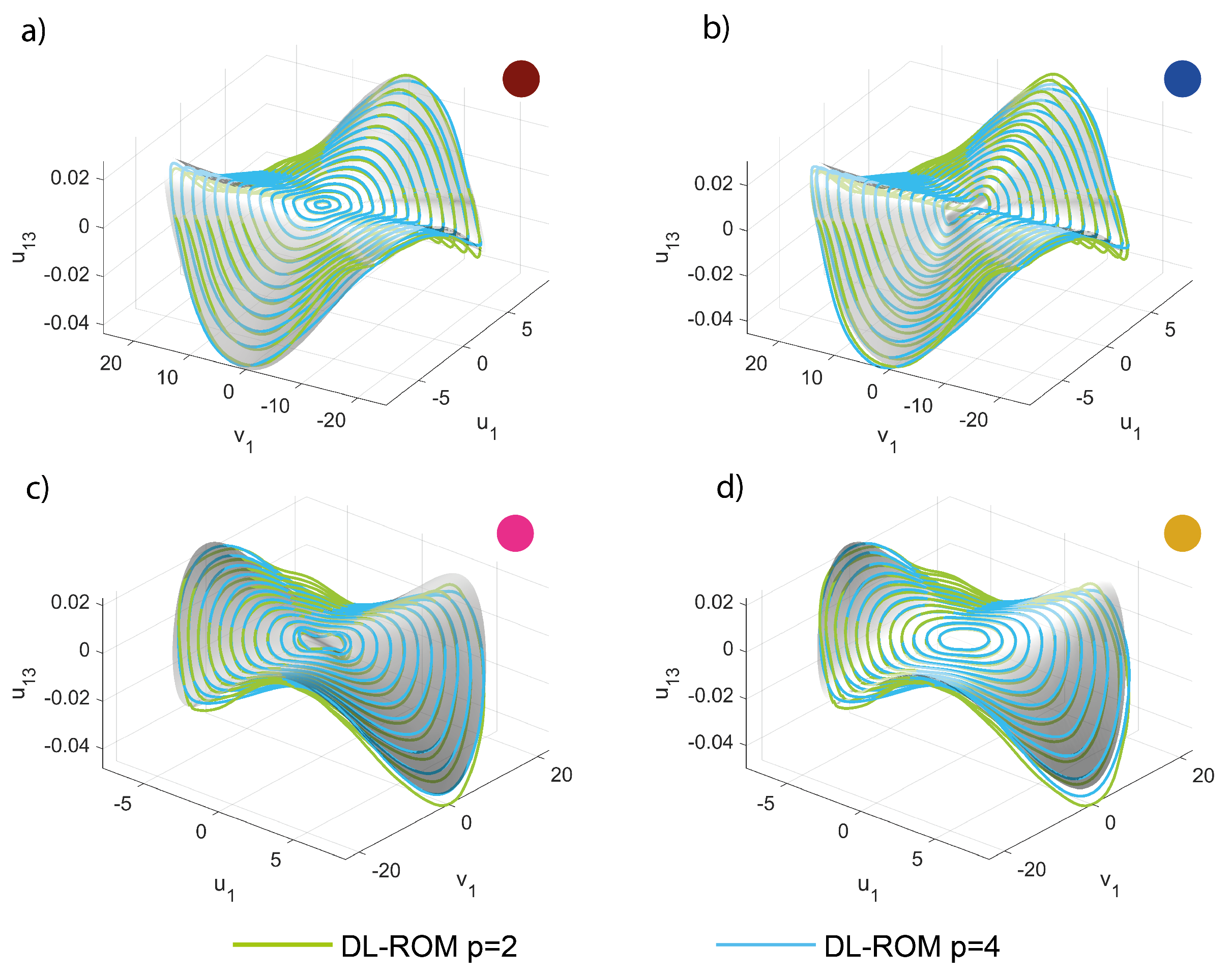
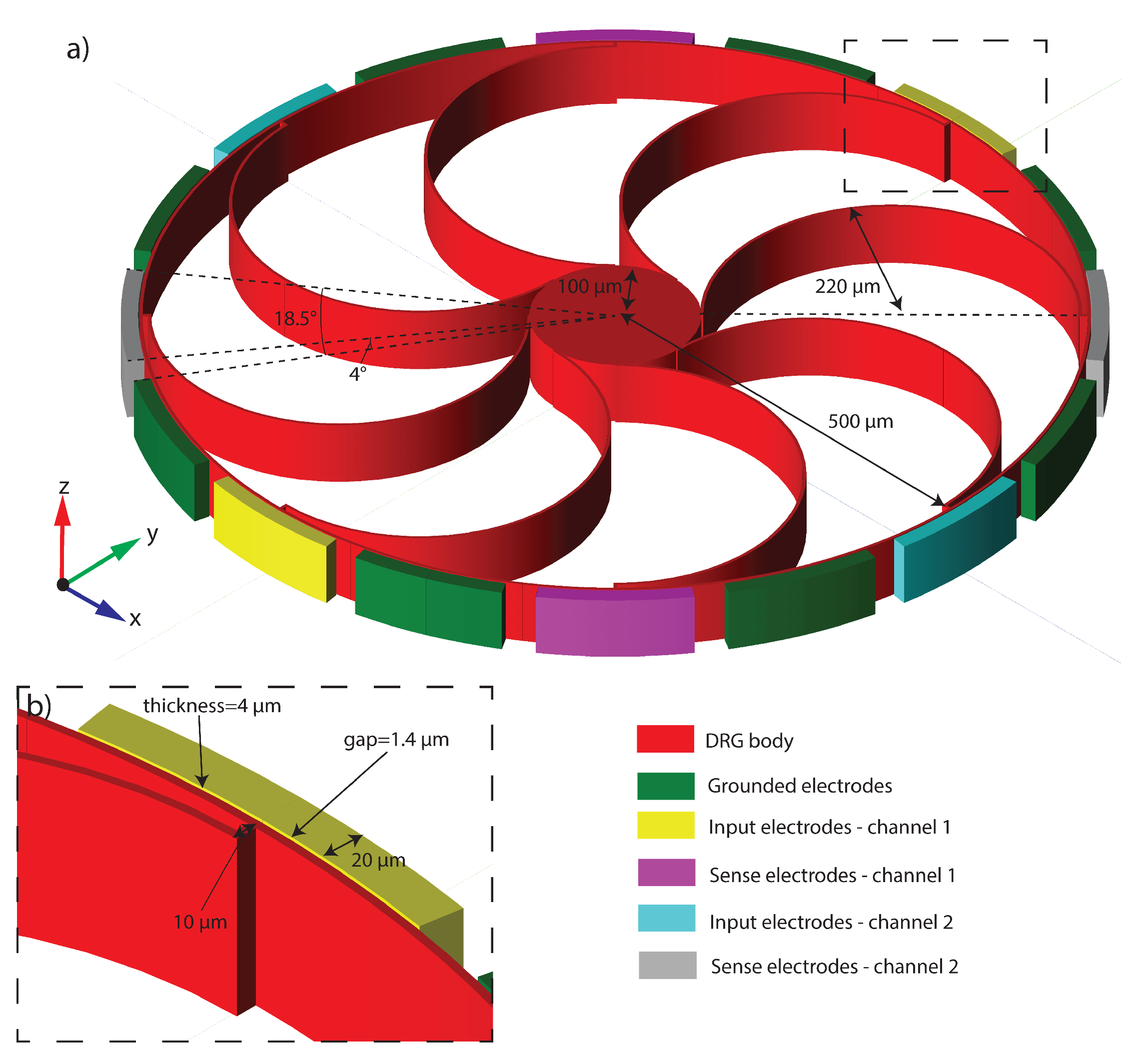
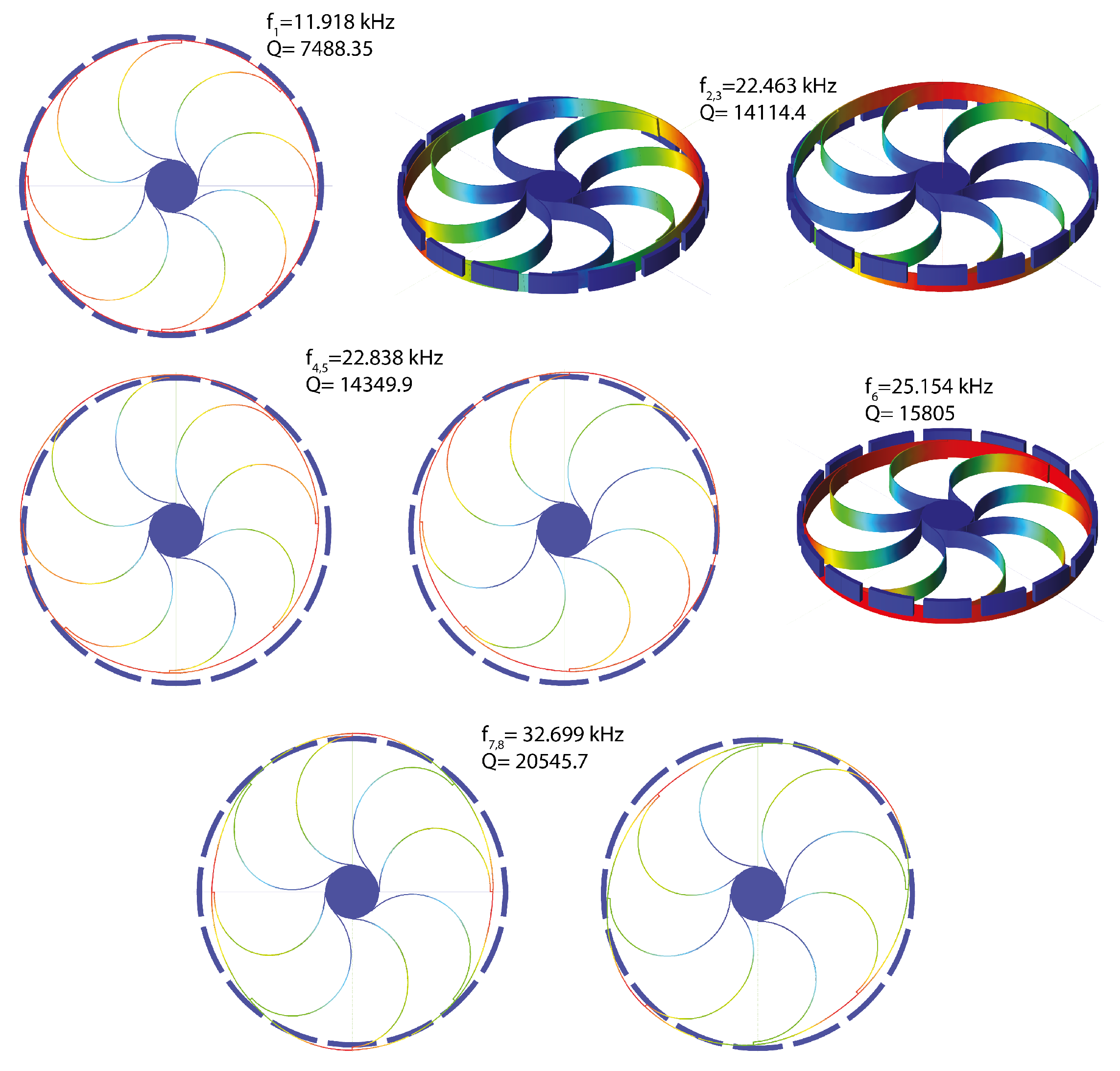
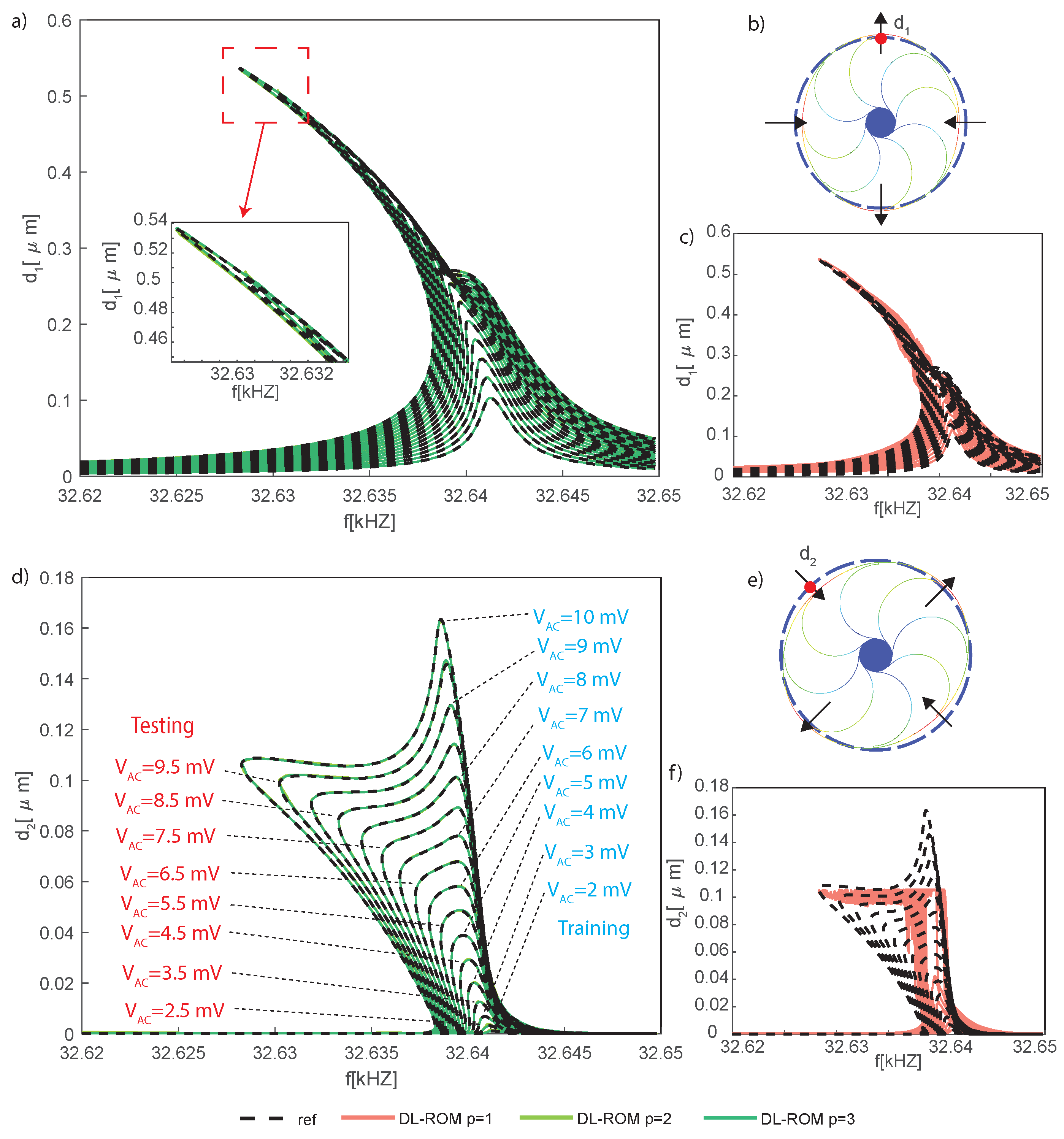
5.5. Electromechanical Disk Resonating Gyroscope
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vizzaccaro, A.; Givois, A.; Longobardi, P.; Shen, Y.; Deü, J.F.; Salles, L.; Touzé, C.; Thomas, O. Non-intrusive reduced order modeling for the dynamics of geometrically nonlinear flat structures using three-dimensional finite elements. Comput. Mech. 2020, 66, 1293–1319. [Google Scholar] [CrossRef]
- Touzé, C.; Vizzaccaro, A.; Thomas, O. Model order reduction methods for geometrically nonlinear structures: A review of nonlinear techniques. Nonlinear Dyn. 2021, 105, 1141–1190. [Google Scholar] [CrossRef]
- Kerschen, G.; Golinval, J.C.; Vakakis, A.F.; Bergman, L.A. The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: An overview. Nonlinear Dyn. 2005, 41, 147–169. [Google Scholar] [CrossRef]
- Amabili, M.; Touzé, C. Reduced-order models for nonlinear vibrations of fluid-filled circular cylindrical shells: Comparison of POD and asymptotic nonlinear normal modes methods. J. Fluids Struct. 2007, 23, 885–903. [Google Scholar] [CrossRef] [Green Version]
- Amabili, M.; Sarkar, A.; Paıdoussis, M. Reduced-order models for nonlinear vibrations of cylindrical shells via the proper orthogonal decomposition method. J. Fluids Struct. 2003, 18, 227–250. [Google Scholar] [CrossRef]
- Gobat, G.; Opreni, A.; Fresca, S.; Manzoni, A.; Frangi, A. Reduced order modeling of nonlinear microstructures through Proper Orthogonal Decomposition. Mech. Syst. Signal Process. 2022, 171, 108864. [Google Scholar] [CrossRef]
- Frangi, A.; Gobat, G. Reduced order modeling of the non-linear stiffness in MEMS resonators. Int. J. Non-Linear Mech. 2019, 116, 211–218. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Salles, L.; Touzé, C. Comparison of nonlinear mappings for reduced-order modeling of vibrating structures: Normal form theory and quadratic manifold method with modal derivatives. Nonlinear Dyn. 2021, 103, 3335–3370. [Google Scholar] [CrossRef]
- Shaw, S.; Pierre, C. Non-linear normal modes and invariant manifolds. J. Sound Vib. 1991, 150, 170–173. [Google Scholar] [CrossRef] [Green Version]
- Shaw, S.W.; Pierre, C. Normal modes for non-linear vibratory systems. J. Sound Vib. 1993, 164, 85–124. [Google Scholar] [CrossRef] [Green Version]
- Ponsioen, S.; Pedergnana, T.; Haller, G. Automated computation of autonomous spectral submanifolds for nonlinear modal analysis. J. Sound Vib. 2018, 420, 269–295. [Google Scholar] [CrossRef] [Green Version]
- Vizzaccaro, A.; Shen, Y.; Salles, L.; Blahoš, J.; Touzé, C. Direct computation of nonlinear mapping via normal form for reduced-order models of finite element nonlinear structures. Comput. Methods Appl. Mech. Eng. 2021, 384, 113957. [Google Scholar] [CrossRef]
- Opreni, A.; Vizzaccaro, A.; Frangi, A.; Touzé, C. Model Order Reduction based on Direct Normal Form: Application to Large Finite Element MEMS Structures Featuring Internal Resonance. Nonlinear Dyn. 2021, 105, 1237–1272. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Opreni, A.; Salles, L.; Frangi, A.; Touzé, C. High order direct parametrisation of invariant manifolds for model order reduction of finite element structures: Application to large amplitude vibrations and uncovering of a folding point. Nonlinear Dyn. 2022, 110, 525–571. [Google Scholar] [CrossRef]
- Jain, S.; Haller, G. How to compute invariant manifolds and their reduced dynamics in high-dimensional finite element models. Nonlinear Dyn. 2022, 107, 1417–1450. [Google Scholar] [CrossRef]
- Opreni, A.; Vizzaccaro, A.; Touzé, C.; Frangi, A. High order direct parametrisation of invariant manifolds for model order reduction of finite element structures: Application to generic forcing terms and parametrically excited systems. Nonlinear Dyn. 2022; accepted for publication. [Google Scholar]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Kim, Y.; Choi, Y.; Widemann, D.; Zohdi, T. A fast and accurate physics-informed neural network reduced order model with shallow masked autoencoder. J. Comput. Phys. 2022, 451, 110841. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Guo, M.; Hesthaven, J.S. Reduced order modeling for nonlinear structural analysis using Gaussian process regression. Comput. Methods Appl. Mech. Eng. 2018, 341, 807–826. [Google Scholar] [CrossRef]
- Guo, M.; Hesthaven, J.S. Data-driven reduced order modeling for time-dependent problems. Comput. Methods Appl. Mech. Eng. 2019, 345, 75–99. [Google Scholar] [CrossRef]
- Lee, K.; Carlberg, K.T. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. J. Comput. Phys. 2020, 404, 108973. [Google Scholar] [CrossRef] [Green Version]
- Fries, W.D.; He, X.; Choi, Y. Lasdi: Parametric latent space dynamics identification. Comput. Methods Appl. Mech. Eng. 2022, 399, 115436. [Google Scholar] [CrossRef]
- Fresca, S.; Dede, L.; Manzoni, A. A comprehensive deep learning-based approach to reduced order modeling of nonlinear time-dependent parametrized PDEs. J. Sci. Comput. 2021, 87, 61. [Google Scholar] [CrossRef]
- Fresca, S.; Manzoni, A. POD-DL-ROM: Enhancing deep learning-based reduced order models for nonlinear parametrized PDEs by proper orthogonal decomposition. Comput. Methods Appl. Mech. Eng. 2022, 388, 114181. [Google Scholar] [CrossRef]
- Fresca, S.; Gobat, G.; Fedeli, P.; Frangi, A.; Manzoni, A. Deep learning-based reduced order models for the real-time simulation of the nonlinear dynamics of microstructures. Int. J. Numer. Methods Eng. 2022, 123, 4749–4777. [Google Scholar] [CrossRef]
- Kaiser, E.; Kutz, J.N.; Brunton, S.L. Sparse identification of nonlinear dynamics for model predictive control in the low-data limit. Proc. R. Soc. A 2018, 474, 20180335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [Green Version]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Sparse identification of nonlinear dynamics with control (SINDYc). IFAC-PapersOnLine 2016, 49, 710–715. [Google Scholar] [CrossRef]
- Champion, K.; Lusch, B.; Kutz, J.N.; Brunton, S.L. Data-driven discovery of coordinates and governing equations. Proc. Natl. Acad. Sci. USA 2019, 116, 22445–22451. [Google Scholar] [CrossRef] [Green Version]
- Simpson, T.; Dervilis, N.; Chatzi, E. Machine Learning Approach to Model Order Reduction of Nonlinear Systems via Autoencoder and LSTM Networks. J. Eng. Mech. 2021, 147, 04021061. [Google Scholar] [CrossRef]
- Li, S.; Yang, Y. Data-driven identification of nonlinear normal modes via physics-integrated deep learning. Nonlinear Dyn. 2021, 106, 3231–3246. [Google Scholar] [CrossRef]
- Fresca, S.; Manzoni, A.; Dedè, L.; Quarteroni, A. Deep learning-based reduced order models in cardiac electrophysiology. PLoS ONE 2020, 15, e0239416. [Google Scholar] [CrossRef]
- Opreni, A.; Boni, N.; Carminati, R.; Frangi, A. Analysis of the nonlinear response of piezo-micromirrors with the harmonic balance method. Actuators 2021, 10, 21. [Google Scholar] [CrossRef]
- Detroux, T.; Renson, L.; Masset, L.; Kerschen, G. The harmonic balance method for bifurcation analysis of large-scale nonlinear mechanical systems. Comput. Methods Appl. Mech. Eng. 2015, 296, 18–38. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Zemel, R. Autoencoders, minimum description length and Helmholtz free energy. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1993; Volume 6. [Google Scholar]
- Halko, N.; Martinsson, P.; Tropp, J.A. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 2011, 53, 217–288. [Google Scholar] [CrossRef]
- Cabré, X.; Fontich, E.; de la Llave, R. The parameterization method for invariant manifolds I: Manifolds associated to non-resonant subspaces. Indiana Univ. Math. J. 2003, 52, 283–328. [Google Scholar] [CrossRef] [Green Version]
- Cabré, X.; Fontich, E.; de la Llave, R. The parameterization method for invariant manifolds II: Regularity with respect to parameters. Indiana Univ. Math. J. 2003, 52, 329–360. [Google Scholar] [CrossRef] [Green Version]
- Cabré, X.; Fontich, E.; De La Llave, R. The parameterization method for invariant manifolds III: Overview and applications. J. Differ. Equ. 2005, 218, 444–515. [Google Scholar] [CrossRef] [Green Version]
- Haro, A.; Canadell, M.; Figueras, J.L.; Luque, A.; Mondelo, J.M. The parameterization method for invariant manifolds. Appl. Math. Sci. 2016, 195. [Google Scholar]
- Opreni, A.; Vizzaccaro, A.; Touzé, C.; Frangi, A. MORFEInvariantManifold. 2022. Available online: https://github.com/aopreni/MORFEInvariantManifold.jl (accessed on 3 March 2023).
- Doedel, E.J.; Champneys, A.R.; Dercole, F.; Fairgrieve, T.F.; Kuznetsov, Y.A.; Oldeman, B.; Paffenroth, R.; Sandstede, B.; Wang, X.; Zhang, C. AUTO-07P: Continuation and Bifurcation Software for Ordinary Differential Equations; Concordia University: Montreal, QC, Canada, 2007. [Google Scholar]
- Guillot, L.; Cochelin, B.; Vergez, C. A Taylor series-based continuation method for solutions of dynamical systems. Nonlinear Dyn. 2019, 98, 2827–2845. [Google Scholar] [CrossRef] [Green Version]
- Guillot, L.; Lazarus, A.; Thomas, O.; Vergez, C.; Cochelin, B. A purely frequency based Floquet-Hill formulation for the efficient stability computation of periodic solutions of ordinary differential systems. J. Comput. Phys. 2020, 416, 109477. [Google Scholar] [CrossRef]
- Krack, M.; Gross, J. Harmonic Balance for Nonlinear Vibration Problems; Springer Nature: Cham, Switzerland, 2019; Volume 1. [Google Scholar]
- Dhooge, A.; Govaerts, W.; Kuznetsov, Y.A.; Mestrom, W.; Riet, A.; Sautois, B. MATCONT and CL MATCONT: Continuation Toolboxes in Matlab; Universiteit Gent: Gent, Belgium; University of Twente: Enschede, The Netherlands; Utrecht University: Utrecht, The Netherlands, 2006. [Google Scholar]
- Dankowicz, H.; Schilder, F. Recipes for Continuation; SIAM (Society for Industrial and Applied Mathematics): Philadelphia, PA, USA, 2013. [Google Scholar]
- Veltz, R. BifurcationKit. jl. HAL. 2020. Available online: https://hal.inria.fr/hal-02902346 (accessed on 3 March 2023).
- Brent, S.; James, A.H.; Nicholas, M.I.; Michael, D.K. Lidar Sensor. US20200033449A1. Available online: https://patents.google.com/patent/US20200033449A1/en?q=Lidar+sensor&oq=Lidar+sensor+ (accessed on 3 March 2023).
- Laser Beam Scanning. Available online: https://www.st.com/content/dam/AME/2019/developers-conference-2019/presentations/STDevCon19_2.4-6-Laser-Beam-Scanners-ST.pdf (accessed on 3 March 2023).
- Microsoft. Microsoft Hololens. Available online: https://www.microsoft.com/it-it/hololens (accessed on 3 March 2023).
- Corigliano, A.; De Masi, B.; Frangi, A.; Comi, C.; Villa, A.; Marchi, M. Mechanical characterization of polysilicon through on-chip tensile tests. J. Microelectromech. Syst. 2004, 13, 200–219. [Google Scholar] [CrossRef]
- Gobat, G.; Guillot, L.; Frangi, A.; Cochelin, B.; Touzé, C. Backbone curves, Neimark–Sacker boundaries and appearance of quasi-periodicity in nonlinear oscillators: Application to 1: 2 internal resonance and frequency combs in MEMS. Meccanica 2021, 56, 1937–1969. [Google Scholar] [CrossRef]
- Opreni, A.; Vizzaccaro, A.; Boni, N.; Carminati, R.; Mendicino, G.; Touzé, C.; Frangi, A. Fast and Accurate Predictions of MEMS Micromirrors Nonlinear Dynamic Response Using Direct Computation of Invariant Manifolds. In Proceedings of the 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), Tokyo, Japan, 9–13 January 2022; pp. 491–494. [Google Scholar]
- Frangi, A.; De Masi, B.; Confalonieri, F.; Zerbini, S. Threshold shock sensor based on a bistable mechanism: Design, modeling, and measurements. J. Microelectromech. Syst. 2015, 24, 2019–2026. [Google Scholar] [CrossRef]
- Zega, V.; Gobat, G.; Fedeli, P.; Carulli, P.; Frangi, A.A. Reduced Order Modeling in a Mems Arch Resonator Exhibiting 1: 2 Internal Resonance. In Proceedings of the 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), Tokyo, Japan, 9–13 January 2022; pp. 499–502. [Google Scholar]
- Sharpe, W.N.; Yuan, B.; Vaidyanathan, R.; Edwards, R.L. Measurements of Young’s modulus, Poisson’s ratio, and tensile strength of polysilicon. In Proceedings of the IEEE the Tenth Annual International Workshop on Micro Electro Mechanical Systems. An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Nagoya, Japan, 26–30 January 1997; pp. 424–429. [Google Scholar]
- Fresca, S.; Manzoni, A. Real-time simulation of parameter-dependent fluid flows through deep learning-based reduced order models. Fluids 2021, 6, 259. [Google Scholar] [CrossRef]
- Coventor Inc., A Lam Research Company. Coventor MEMS+TM. Available online: https://www.coventor.com/ (accessed on 3 March 2023).
- Parent, A.; Krust, A.; Lorenz, G.; Favorskiy, I.; Piirainen, T. Efficient nonlinear simulink models of MEMS gyroscopes generated with a novel model order reduction method. In Proceedings of the 2015 Transducers-2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; pp. 2184–2187. [Google Scholar]
- Parent, A.; Krust, A.; Lorenz, G.; Piirainen, T. A novel model order reduction approach for generating efficient nonlinear verilog-a models of mems gyroscopes. In Proceedings of the 2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS) Proceedings, Hapuna Beach, HI, USA, 23–26 March 2015; pp. 1–4. [Google Scholar]
- Ayazi, F.; Najafi, K. A HARPSS polysilicon vibrating ring gyroscope. J. Microelectromech. Syst. 2001, 10, 169–179. [Google Scholar] [CrossRef] [Green Version]
- Nitzan, S.H.; Zega, V.; Li, M.; Ahn, C.H.; Corigliano, A.; Kenny, T.W.; Horsley, D.A. Self-induced parametric amplification arising from nonlinear elastic coupling in a micromechanical resonating disk gyroscope. Sci. Rep. 2015, 5, 9036. [Google Scholar] [CrossRef] [Green Version]
- Polunin, P.M.; Shaw, S.W. Self-induced parametric amplification in ring resonating gyroscopes. Int. J. Non-Linear Mech. 2017, 94, 300–308. [Google Scholar] [CrossRef]
- Li, D.; Shaw, S.W.; Polunin, P.M. Computational modeling of nonlinear dynamics and its utility in MEMS gyroscopes. J. Struct. Dyn 2022, 1, 217–235. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T.; Holmes, P. Nonlinear Oscillations; WILEY-VCH Verlag GmbH & Co. kgaa: Weinheim, Germany, 1980. [Google Scholar]
- Thomsen, J.J.; Thomsen, J.J.; Thomsen, J. Vibrations and Stability; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Van der Avoort, C.; Van der Hout, R.; Bontemps, J.; Steeneken, P.; Le Phan, K.; Fey, R.; Hulshof, J.; Van Beek, J. Amplitude saturation of MEMS resonators explained by autoparametric resonance. J. Micromech. Microeng. 2010, 20, 105012. [Google Scholar] [CrossRef]
- Gallacher, B.; Burdess, J.; Harish, K. A control scheme for a MEMS electrostatic resonant gyroscope excited using combined parametric excitation and harmonic forcing. J. Micromech. Microeng. 2006, 16, 320. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gobat, G.; Fresca, S.; Manzoni, A.; Frangi, A. Reduced Order Modeling of Nonlinear Vibrating Multiphysics Microstructures with Deep Learning-Based Approaches. Sensors 2023, 23, 3001. https://doi.org/10.3390/s23063001
Gobat G, Fresca S, Manzoni A, Frangi A. Reduced Order Modeling of Nonlinear Vibrating Multiphysics Microstructures with Deep Learning-Based Approaches. Sensors. 2023; 23(6):3001. https://doi.org/10.3390/s23063001
Chicago/Turabian StyleGobat, Giorgio, Stefania Fresca, Andrea Manzoni, and Attilio Frangi. 2023. "Reduced Order Modeling of Nonlinear Vibrating Multiphysics Microstructures with Deep Learning-Based Approaches" Sensors 23, no. 6: 3001. https://doi.org/10.3390/s23063001
APA StyleGobat, G., Fresca, S., Manzoni, A., & Frangi, A. (2023). Reduced Order Modeling of Nonlinear Vibrating Multiphysics Microstructures with Deep Learning-Based Approaches. Sensors, 23(6), 3001. https://doi.org/10.3390/s23063001






