Calibration Model Optimization for Strain Metrology of Equal Strength Beams Using Deflection Measurements
Abstract
1. Introduction
2. Novel Calibration Model and Method
2.1. Theoretical Analysis
2.2. Optimization of the Deflection Method Strain Calibration Model
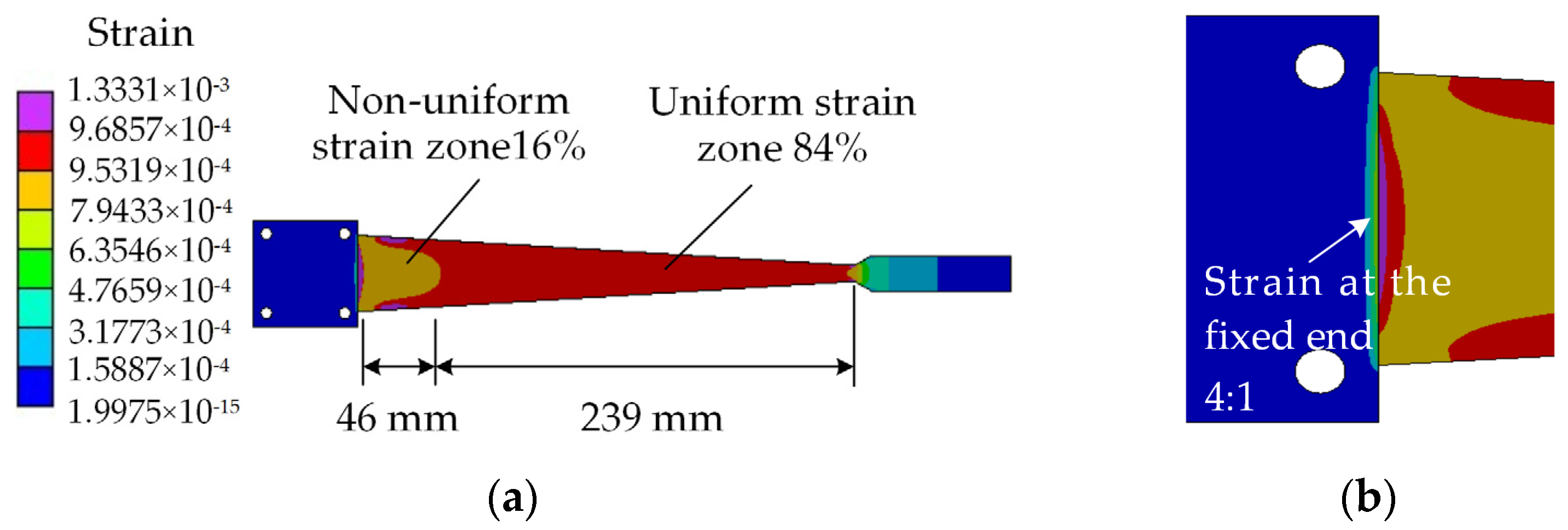
2.2.1. Strain Simulation of Equal Strength Beam
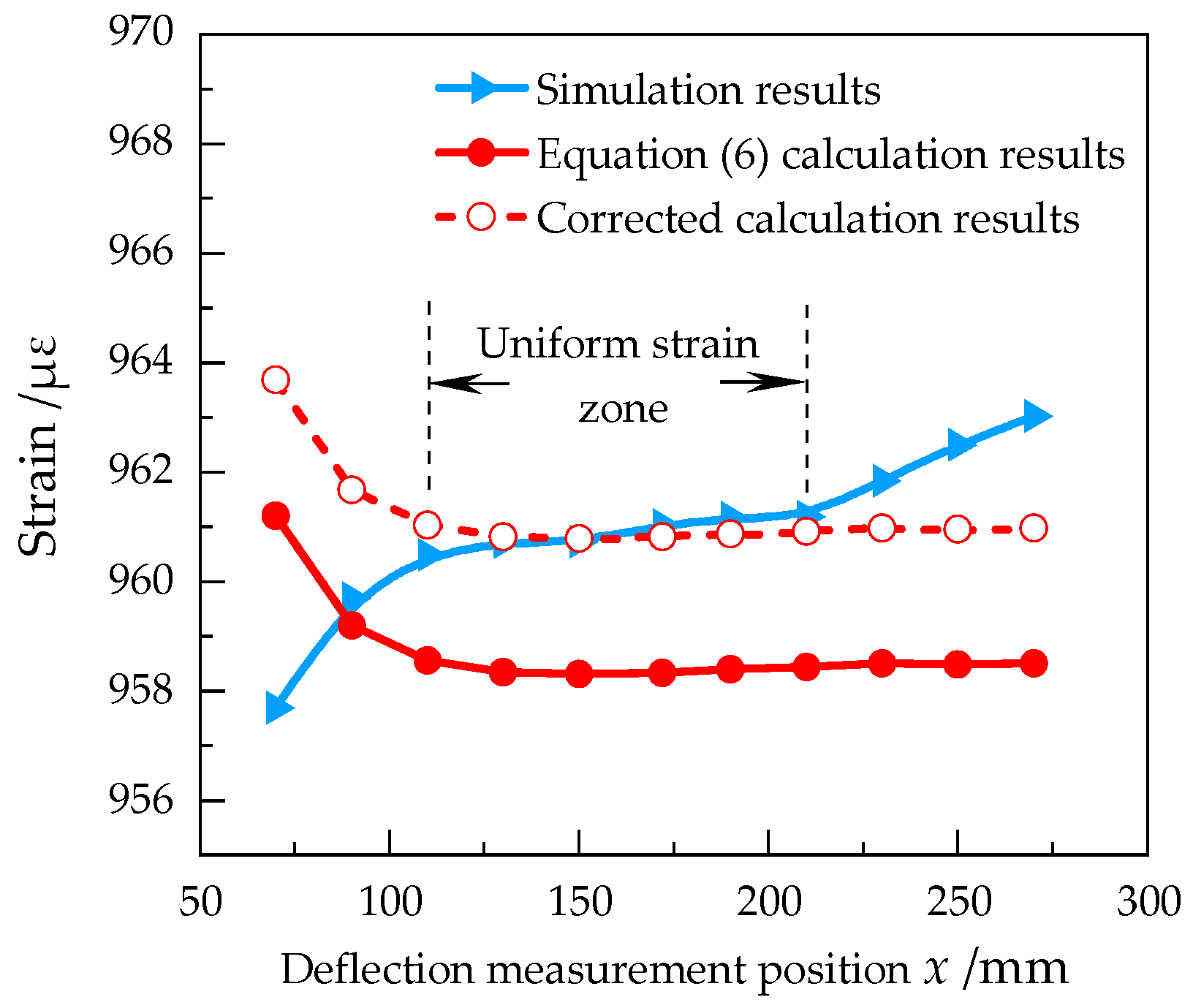
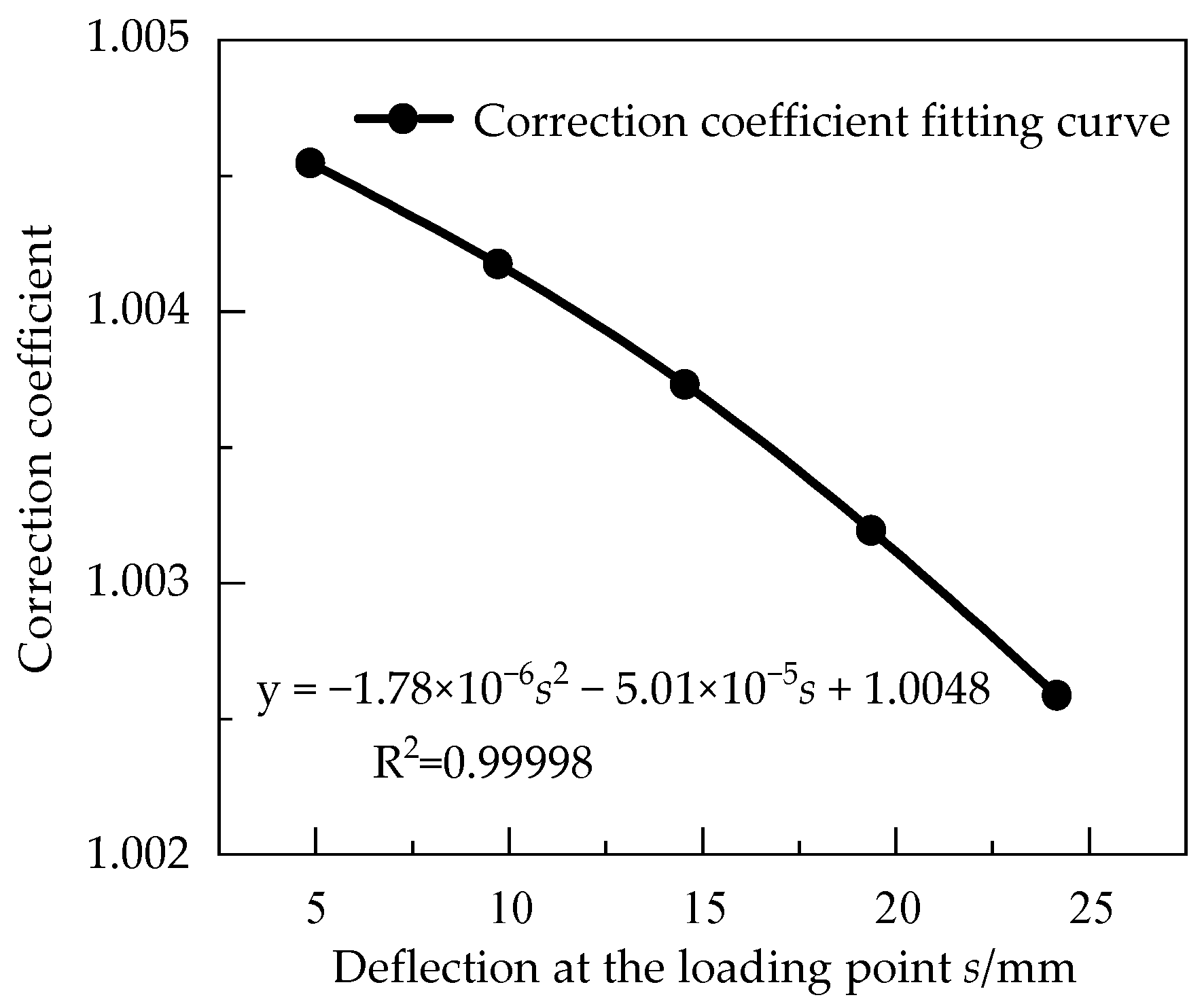
2.2.2. Optimization of the Strain Calculation Model
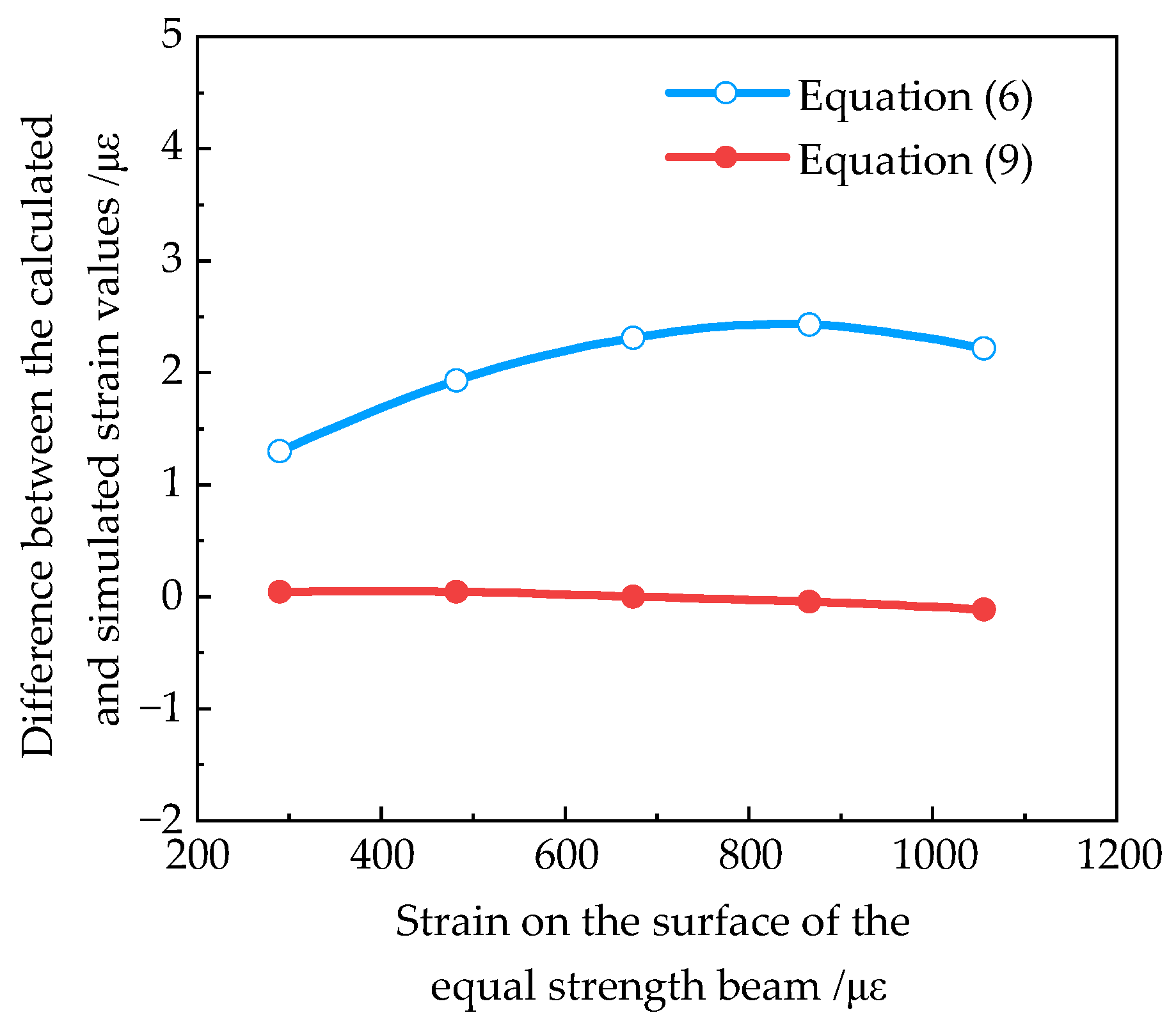
2.2.3. Simulation Result
3. Determination of Deflection Measurement Position
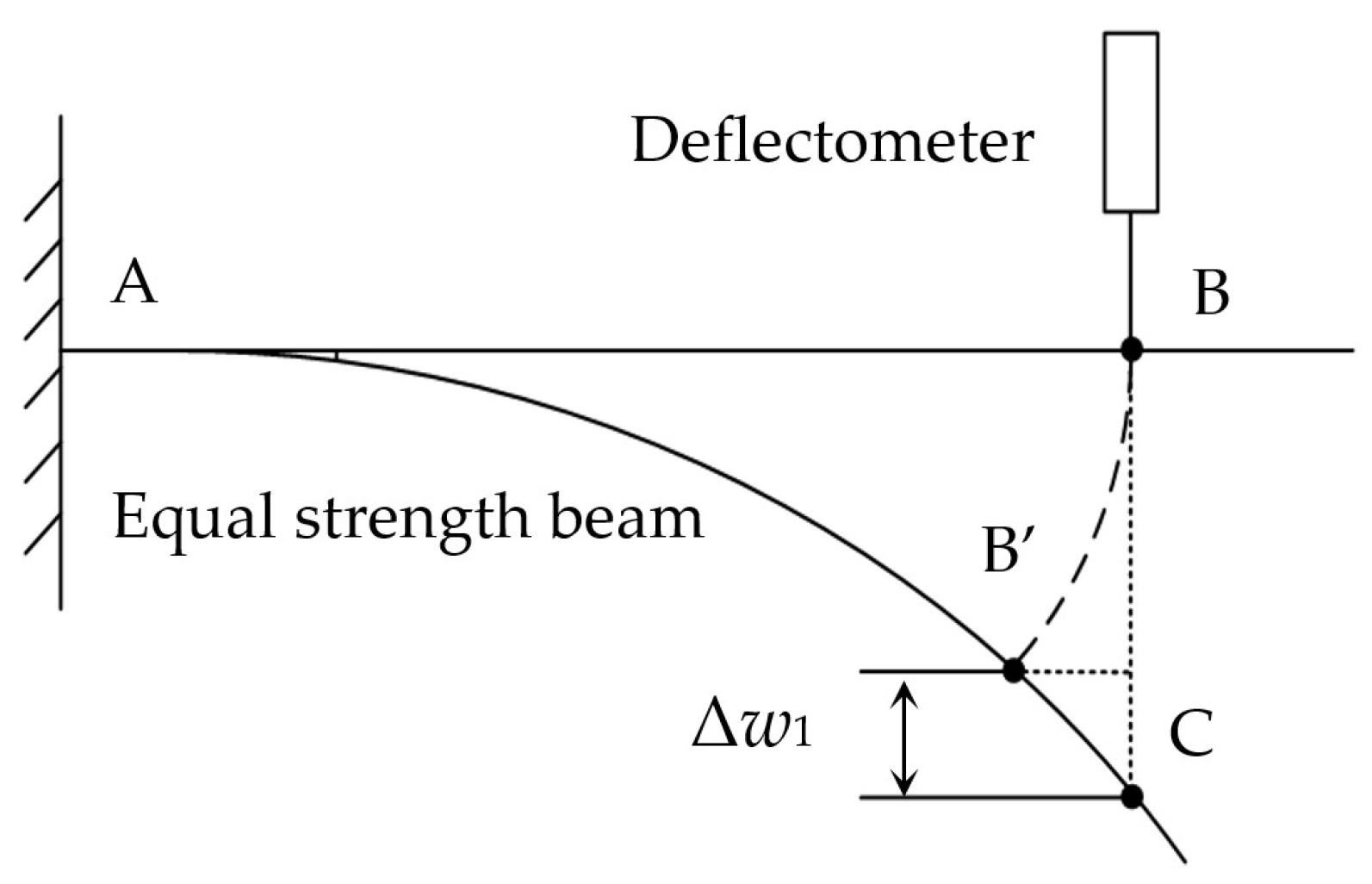
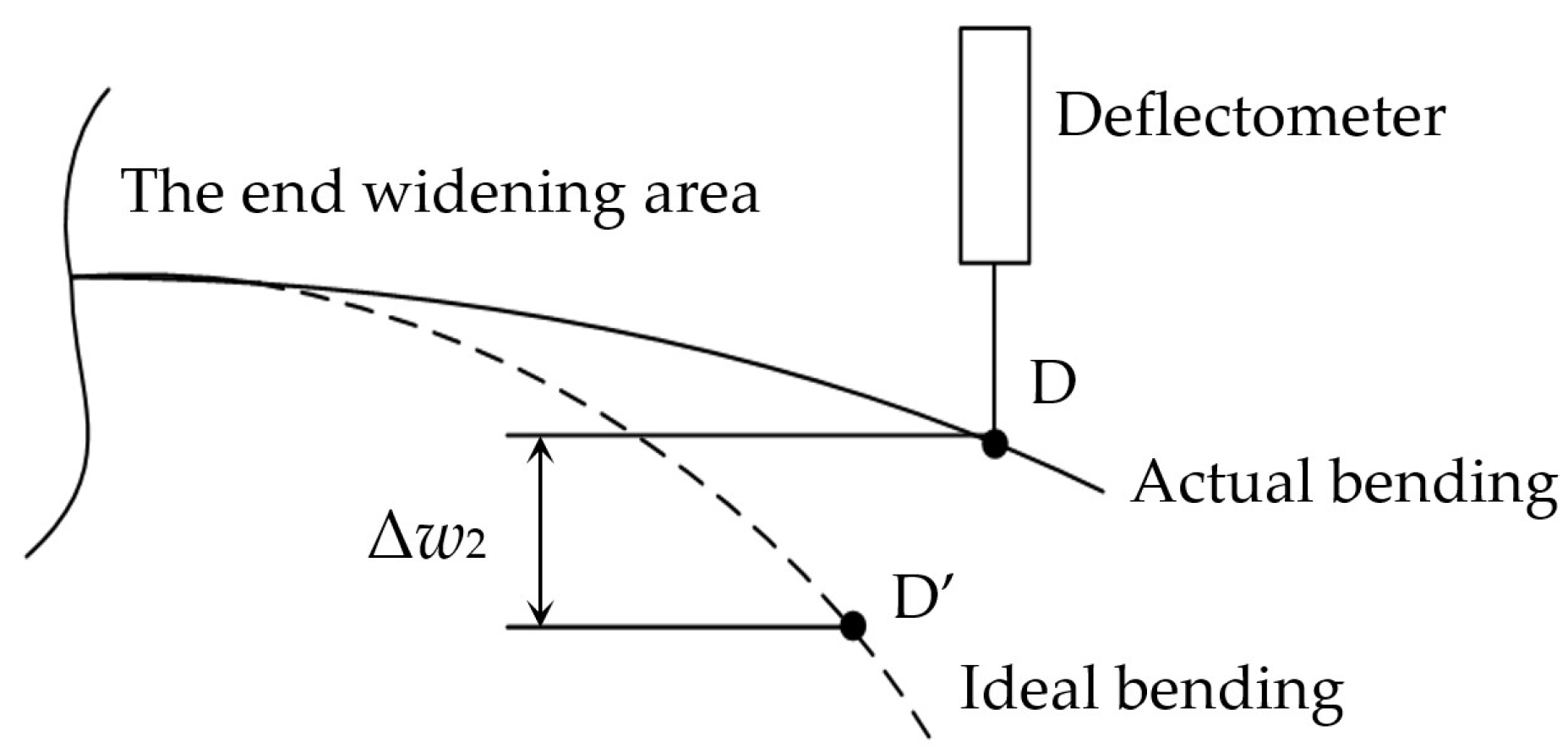
3.1. Error Analysis of Deflection Measurement
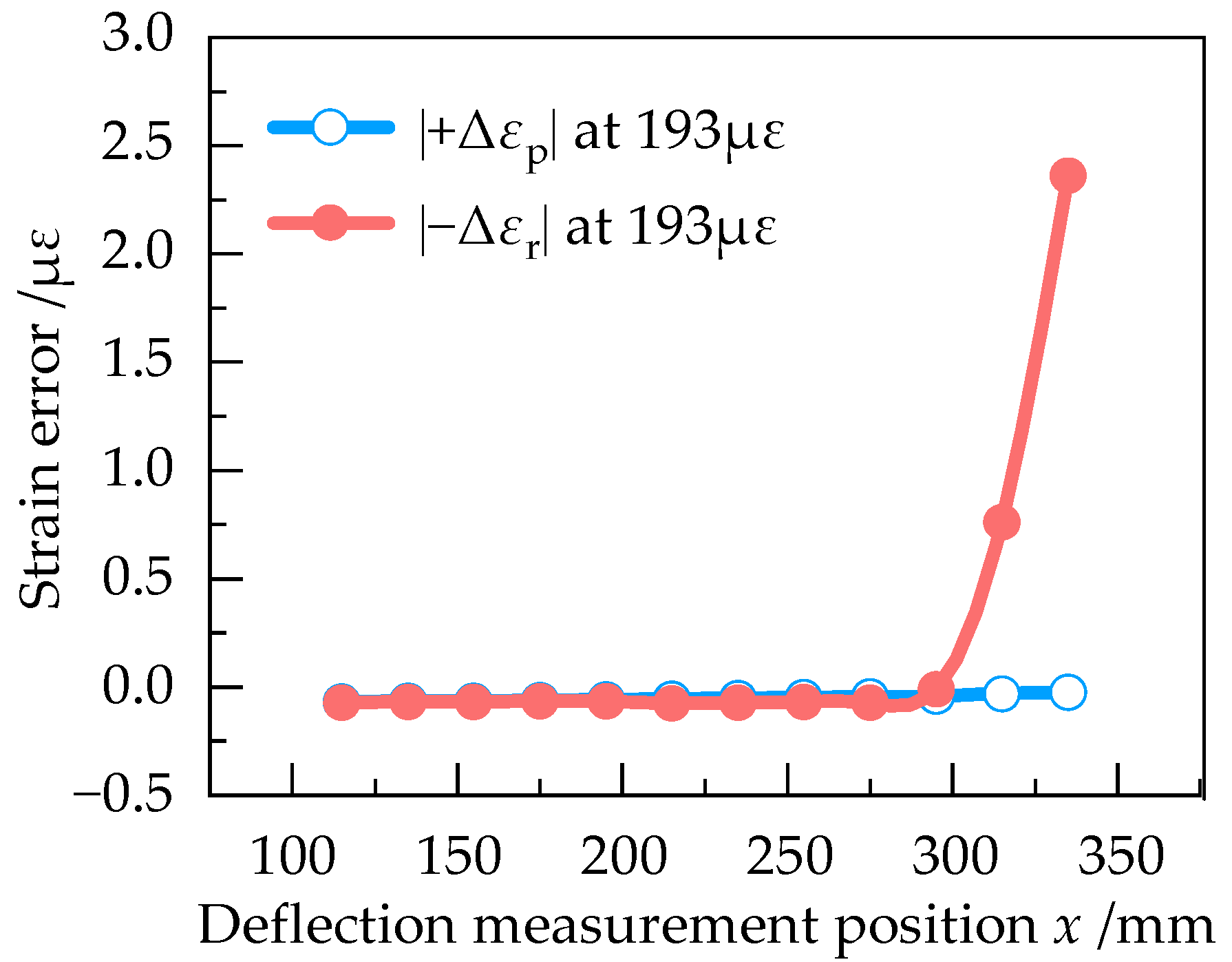
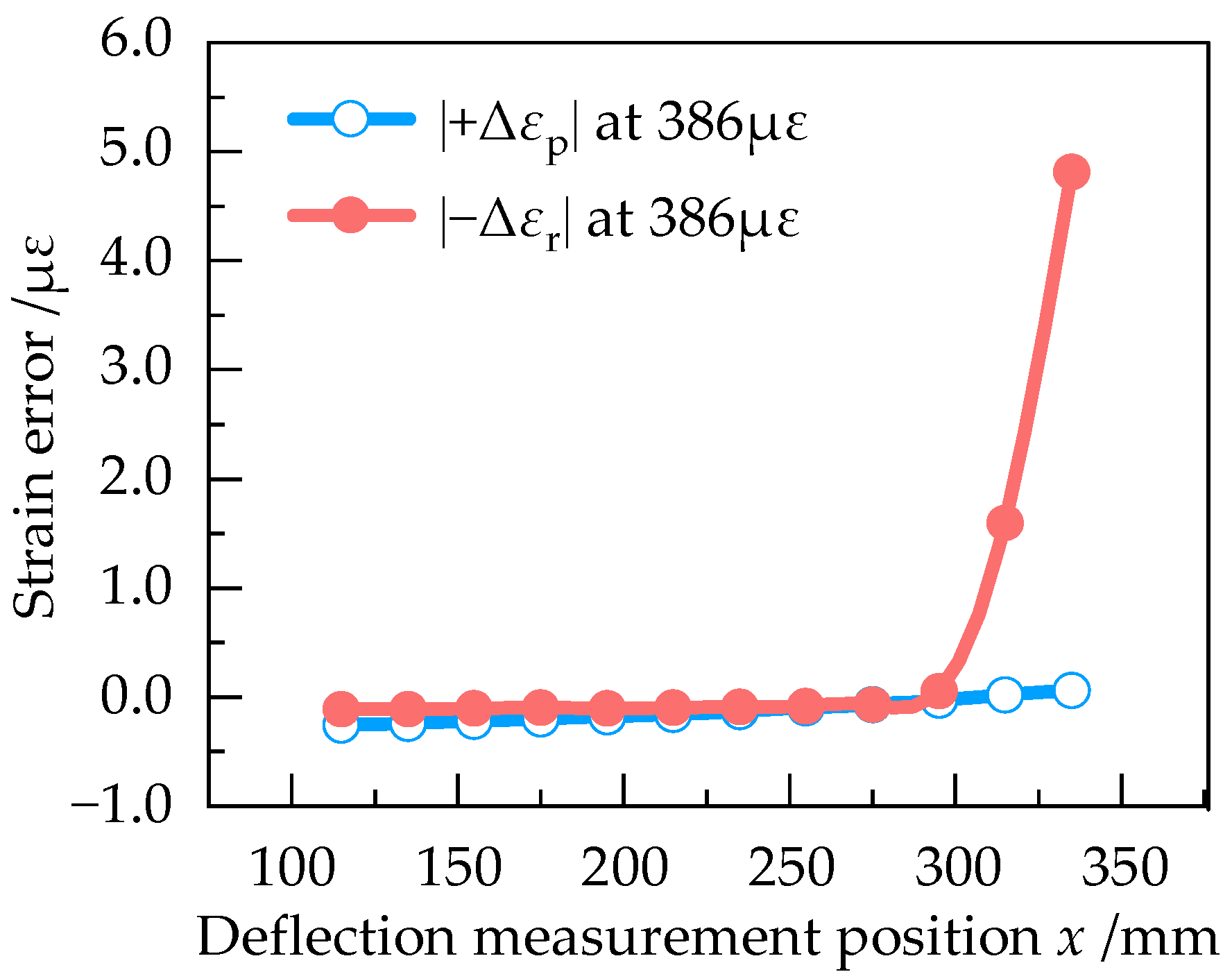
3.2. Numerical Simulation Analysis
4. Experiments
4.1. Experimental Setup
4.2. Strain Measurement Experiment
4.2.1. Validation of the Optimized Strain Calculation Formula
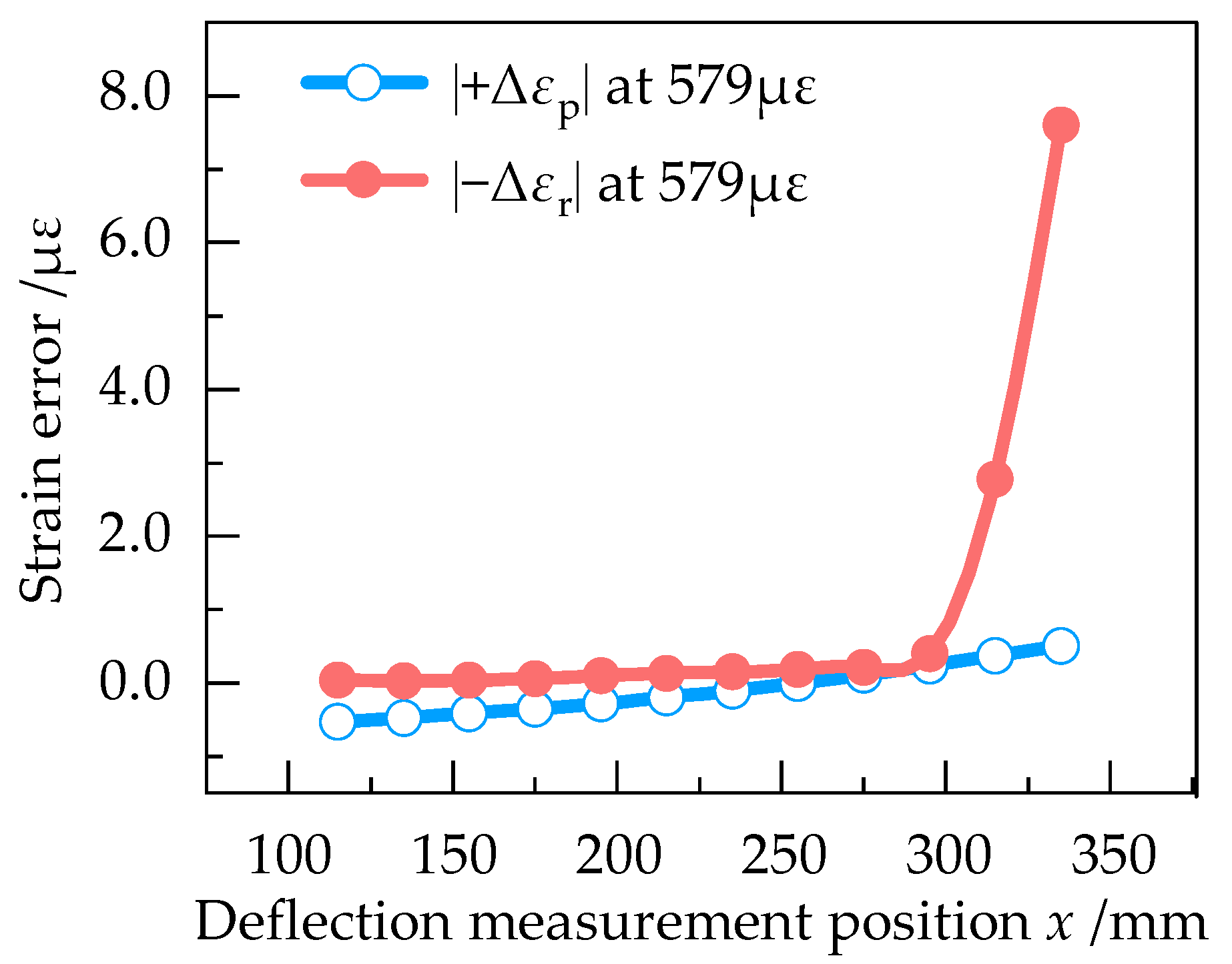
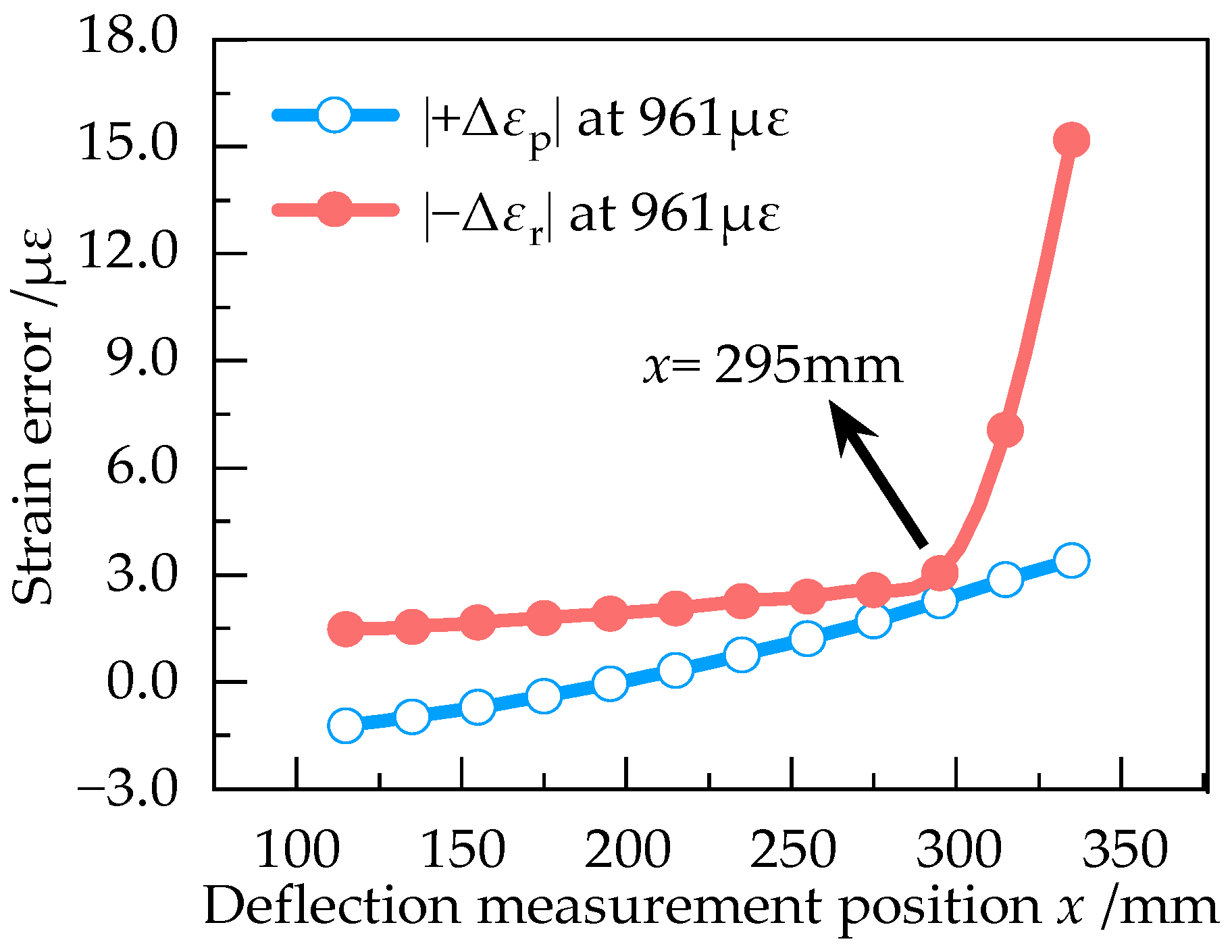
4.2.2. Influence of Deflection Measurement Position on Strain Calculation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goossens, S.; De Pauw, B.; Geernaert, T.; Salmanpour, M.S.; Sharif, K.Z.; Karachalios, E.; Saenz-Castillo, D.; Thienpont, H.; Berghmans, F. Aerospace-grade surface mounted optical fibre strain sensor for structural health monitoring on compositestructures evaluated against in-flight conditions. Smart Mater. Struct. 2019, 28, 065008. [Google Scholar] [CrossRef]
- Buggy, S.J.; James, S.W.; Staines, S.; Carroll, R.; Kitson, P.; Farrington, D.; Drewett, L.; Jaiswal, J.; Tatam, R.P. Railway track component condition monitoring using optical fibre Bragg grating sensors. Meas. Sci. Technol. 2016, 27, 055201. [Google Scholar] [CrossRef]
- Ansari, F. Fiber optic sensors for structural health monitoring of civil infrastructure systems. Struct. Health Monit. Civ. Infrastruct. Syst. 2009, 4, 103–110. [Google Scholar] [CrossRef]
- Jiang, S.; Li, T.; Lin, J.; Ye, Z. Development and application of the FBG strain sensor for ship. Chin. J. Sci. Instrum. 2020, 41, 35–42. [Google Scholar] [CrossRef]
- Richter-Trummer, V.; Silva, S.O.; Peixoto, D.F.C.; Frazão, O.; Moreira, P.M.G.P.; Santos, J.L.; de Castro, P.M.S.T. Fibre Bragg grating sensors for monitoring the metal inert gas and friction stir welding processes. Meas. Sci. Technol. 2010, 21, 085105. [Google Scholar] [CrossRef]
- Qiao, T.; Wang, Z.; Gong, W.; Wang, Z. High Temperature Strain Measurement for Modified C/C Material Beam under Four-Points Bending Load by Fiber Optical Sensor. Struct. Environ. Eng. 2019, 46, 1–6. [Google Scholar] [CrossRef]
- Motwani, P.; Perogamvros, N.; Taylor, S.; Sonebi, M.; Laskar, A.; Murphy, A. Experimental investigation of strain sensitivity for surface bonded fibre optic sensors. Sens. Actuators A Phys. 2020, 303, 111833. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, D.; Zhou, Z.; Zhu, F.; Xiong, L.; Li, T. Cantilever based FBG vibration transducer with sensitization structure. Optoelectron. Lett. 2013, 9, 410–413. [Google Scholar] [CrossRef]
- Ni, N.; Xue, X.; Li, D. Extra-Soft Tactile Sensor for Sensitive Force/Displacement Measurement with High Linearity Based on a Uniform Strength Beam. Materials 2021, 14, 1743. [Google Scholar] [CrossRef]
- Bonopera, M. Fiber-Bragg-Grating-Based Displacement Sensors: Review of Recent Advances. Materials 2022, 15, 5561. [Google Scholar] [CrossRef]
- Cui, Y.; Li, X.; Zhang, T.; Ding, W.; Yin, J. Development of High-Temperature Wire-Grid Thin Film Strain Gauges. Sensors 2022, 22, 7595. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Liang, D.; Li, H. Analysis and Modication of Demarcate Error of FBG Sensor by Equal Strength Beam. J. Optoelectron. Laser 2007, 18, 776–779. [Google Scholar] [CrossRef]
- Xia, P.; Tan, Y.; Yang, C.; Zhou, Z.; Yun, K. A Composite Fabry-Perot Interferometric Sensor with the Dual-Cavity Structure for Simultaneous Measurement of High Temperature and Strain. Sensors 2021, 21, 4989. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Xu, F.; Gao, Q.; Liu, S.; Jin, W.; Xu, Y. A Monitoring Method Based on FBG for Concrete Corrosion Cracking. Sensors 2016, 16, 1093. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.-P.; Dai, J.-G.; Wang, X.-Z. Improved temperature compensation of fiber Bragg grating-based sensors applied to structures under different loading conditions. Opt. Fiber Technol. 2021, 63, 102506. [Google Scholar] [CrossRef]
- Wang, T.; Sun, Q.; Gao, Y.; Liu, L. Strain Characteristics of Fiber Optic Gratings and Application to the Measurement of Slotted Beams. Railw. Eng. 2014, 11, 37–40. [Google Scholar] [CrossRef]
- Xv, Y.; Yang, X.; Wei, T.; Yao, J. Influence of structural parameters of resistancestrain gauge on straintransfer. J. Mech. Electr. Eng. 2018, 35, 352–357. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, N. Design and Study of Fiber Sensor Based on Cantilever Beam of Uniform Strength. Microcomput. Inf. 2010, 26, 107–108. [Google Scholar] [CrossRef]
- Zhu, S.; Zhang, Z.; Qiu, T.; Han, H.; Yin, A.; Lu, W. Optical Fiber Measurement of Surface Strain Distribution on Equal Strength Beam. Piezoelectrics Acoustooptics 2019, 41, 809–813. [Google Scholar]
- Huang, G.; He, Z.; Chen, M.; Wang, X. Sensor Performance Analysis by Equal Strength Beam Test for Crane SHM. Appl. Mech. Mater. 2014, 633, 795–799. [Google Scholar] [CrossRef]
- Luo, B.; Yang, W.; Hu, X.; Lu, H.; Shi, S.; Zhao, M.; Lu, Y.; Xie, L.; Sun, Z.; Zhang, L. Study on vibration sensing performance of an equal strength cantilever beam based on an excessively tilted fiber grating. Appl. Opt. 2018, 57, 2128. [Google Scholar] [CrossRef] [PubMed]
- Xue, Z.; Lv, G. Study on the surface bonding technology of fiber Bragg grating strain sensor. Nat. Sci. J. Harbin Norm. Univ. 2011, 27, 29–32. [Google Scholar] [CrossRef]
- Hu, D.; Guo, Y.; Chen, X.; Zhang, C. Cable Force Health Monitoring of Tongwamen Bridge Based on Fiber Bragg Grating. Appl. Sci. 2017, 7, 384. [Google Scholar] [CrossRef]
- Tu, Y.; Gong, H.; Chen, J.; Jin, Y. Simulation and Experimental Investigations on the Strain Measurement of the Uniform Strength Beam Using a FBG sensor. J. Phys. Conf. Ser. 2011, 276, 012145. [Google Scholar] [CrossRef]
- Hou, J.; Liu, B.; Cui, J.; Wei, J.; Chen, K.; Zhang, P.; Li, X. Calibration and Process Simulation of FBG Strain Deflection Method. Acta Metrol. Sin. 2021, 42, 1472–1481. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Shen, J.; Chen, M.; Yv, X. Large deformation analysis of cantilever beam based on MATLAB. Mech. Eng. 2015, 37, 750–753. [Google Scholar] [CrossRef]
- Polilov, A.N.; Tatus, N.A.; Tian, X. Analyzing the Correctness of Equal Strength Composite Profiled Beam Bending Problems. J. Appl. Mech. Tech. Phy. 2019, 60, 144–155. [Google Scholar] [CrossRef]
- Brojan, M.; Cebron, M.; Kosel, F. Large deflections of non-prismatic nonlinearly elastic cantilever beams subjected to non-uniform continuous load and a concentrated load at the free end. Acta Mech. Sin. 2012, 28, 863–869. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Zhou, Y. A Wavelet Method for Studying Large Deflection Bending Problems of Flexible Beams. Chin. J. Solid Mech. 2013, 33, 159–165. [Google Scholar] [CrossRef]
- Oore, S.; Oore, M. Uniform strength for large deflections of cantilever beams under end point load. Struct. Multidisc. Optim. 2009, 38, 499–510. [Google Scholar] [CrossRef]
- Rahman, M.A.; Kowser, M.A. Inelastic Deformations of Stainless Steel Leaf Springs-Experiment and Nonlinear Analysis. Meccanica 2010, 45, 503–518. [Google Scholar] [CrossRef]
- Wu, G. Large Deflection Analysis of Flexible Beams by Linearization Methods. J. Zhejiang Ocean. Univ. (Nat. Sci.) 2008, 27, 1–4. [Google Scholar] [CrossRef]
- Zheng, W.; Dan, D.; Cheng, W. Calibration of 0.1 με Level Resolution FBG Sensor by the Equal Strength Beam. J. Optoelectron. Laser 2017, 28, 365–370. [Google Scholar] [CrossRef]
- Zang, Y. Comparison and Analysis of Two Kinds of Parameters Testing Apparatus for Electronic Strain Gauges. China Meas. Test 2009, 35, 29–31. [Google Scholar]





| Dimensions | Symbols | Numerical Values/mm |
|---|---|---|
| Thickness | h | 5.0 |
| Width at the fixed end | B | 43.2 |
| Width of the widening area | B | 20.0 |
| Effective length | L0 | 285.0 |
| Working length | L1 | 360.0 |
| Total length | L2 | 375.0 |
| Material | Density | Elastic Modulus | Poisson’s Ratio |
|---|---|---|---|
| 65 Mn | 7850 kg/m3 | 2.08 × 105 Mpa | 0.26 |
| No. | Applied Load/N | Theoretical Value/με | Simulation Value/με | Relative Error |
|---|---|---|---|---|
| 1 | 40 | 384.62 | 385.82 | 0.052% |
| 2 | 60 | 576.92 | 578.25 | 0.230% |
| 3 | 80 | 769.23 | 770.06 | 0.108% |
| 4 | 100 | 961.54 | 961.02 | −0.054% |
| No. | Measurement Position x/mm | Difference before Correction/με | Difference after Correction/με |
|---|---|---|---|
| 1 | 110 | −1.93 | 0.55 |
| 2 | 130 | −2.38 | 0.10 |
| 3 | 150 | −2.42 | 0.06 |
| 4 | 172 | −2.68 | −0.20 |
| 5 | 190 | −2.77 | −0.29 |
| 6 | 210 | −2.74 | −0.27 |
| Average | −2.49 | −0.01 |
| Deflection of Loading Point M/mm | Deviation of Equation (6)/με | Deviation of Equation (9)/με |
|---|---|---|
| 0.0 | 0.00 | 0.00 |
| 1.5 | 0.37 | 0.14 |
| 3.0 | 0.50 | 0.01 |
| 4.5 | 0.85 | 0.10 |
| 6.0 | 0.74 | −0.26 |
| 7.5 | 1.22 | −0.02 |
| 9.0 | 1.76 | 0.31 |
| 10.5 | 2.11 | 0.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Wu, Z.; Cui, J.; Chen, K.; Tang, Y.; Yang, N. Calibration Model Optimization for Strain Metrology of Equal Strength Beams Using Deflection Measurements. Sensors 2023, 23, 3059. https://doi.org/10.3390/s23063059
Yan Y, Wu Z, Cui J, Chen K, Tang Y, Yang N. Calibration Model Optimization for Strain Metrology of Equal Strength Beams Using Deflection Measurements. Sensors. 2023; 23(6):3059. https://doi.org/10.3390/s23063059
Chicago/Turabian StyleYan, Yonggang, Zhengxing Wu, Jianjun Cui, Kai Chen, Yanhong Tang, and Ning Yang. 2023. "Calibration Model Optimization for Strain Metrology of Equal Strength Beams Using Deflection Measurements" Sensors 23, no. 6: 3059. https://doi.org/10.3390/s23063059
APA StyleYan, Y., Wu, Z., Cui, J., Chen, K., Tang, Y., & Yang, N. (2023). Calibration Model Optimization for Strain Metrology of Equal Strength Beams Using Deflection Measurements. Sensors, 23(6), 3059. https://doi.org/10.3390/s23063059





