Rethinking LEO Mega-Constellation Routing to Provide Fast Internet Access Services
Abstract
:1. Introduction
2. Background
2.1. Related Work
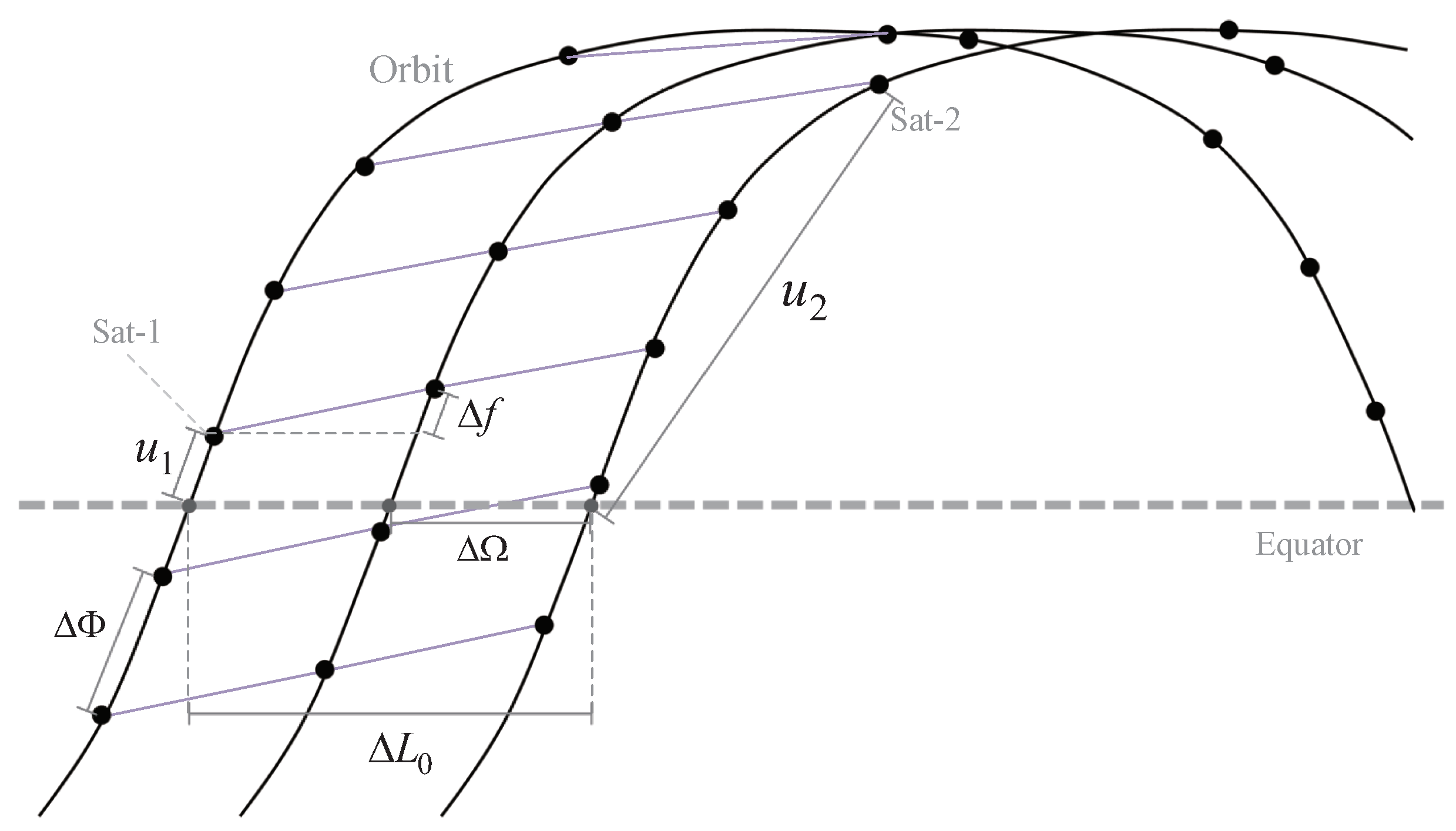
2.2. Satellite Network Model
3. Our Proposed Algorithm
3.1. Minimum Hop Count
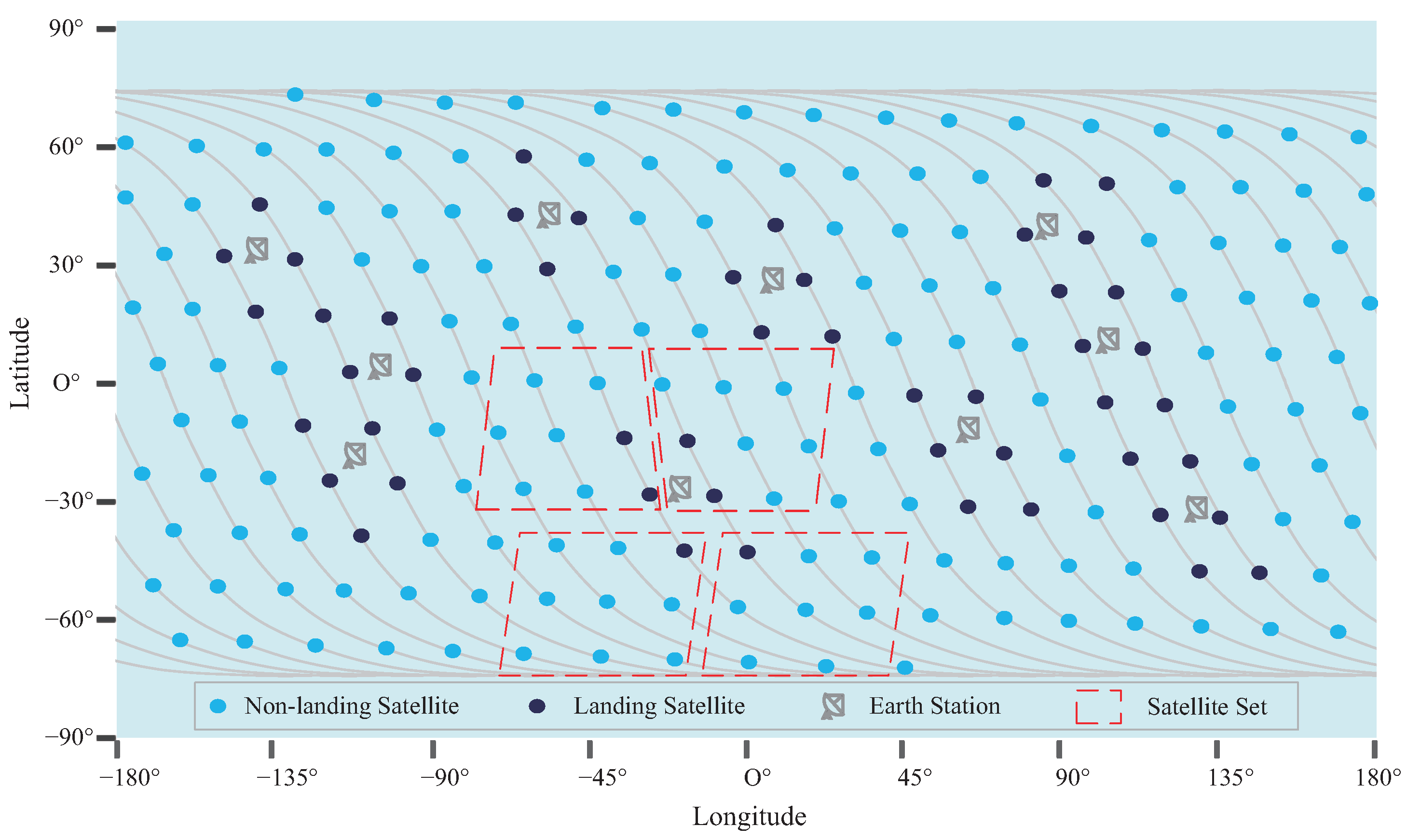
3.2. Satellite Set Matching Strategy
3.3. Forwarding Strategy
4. Evaluation
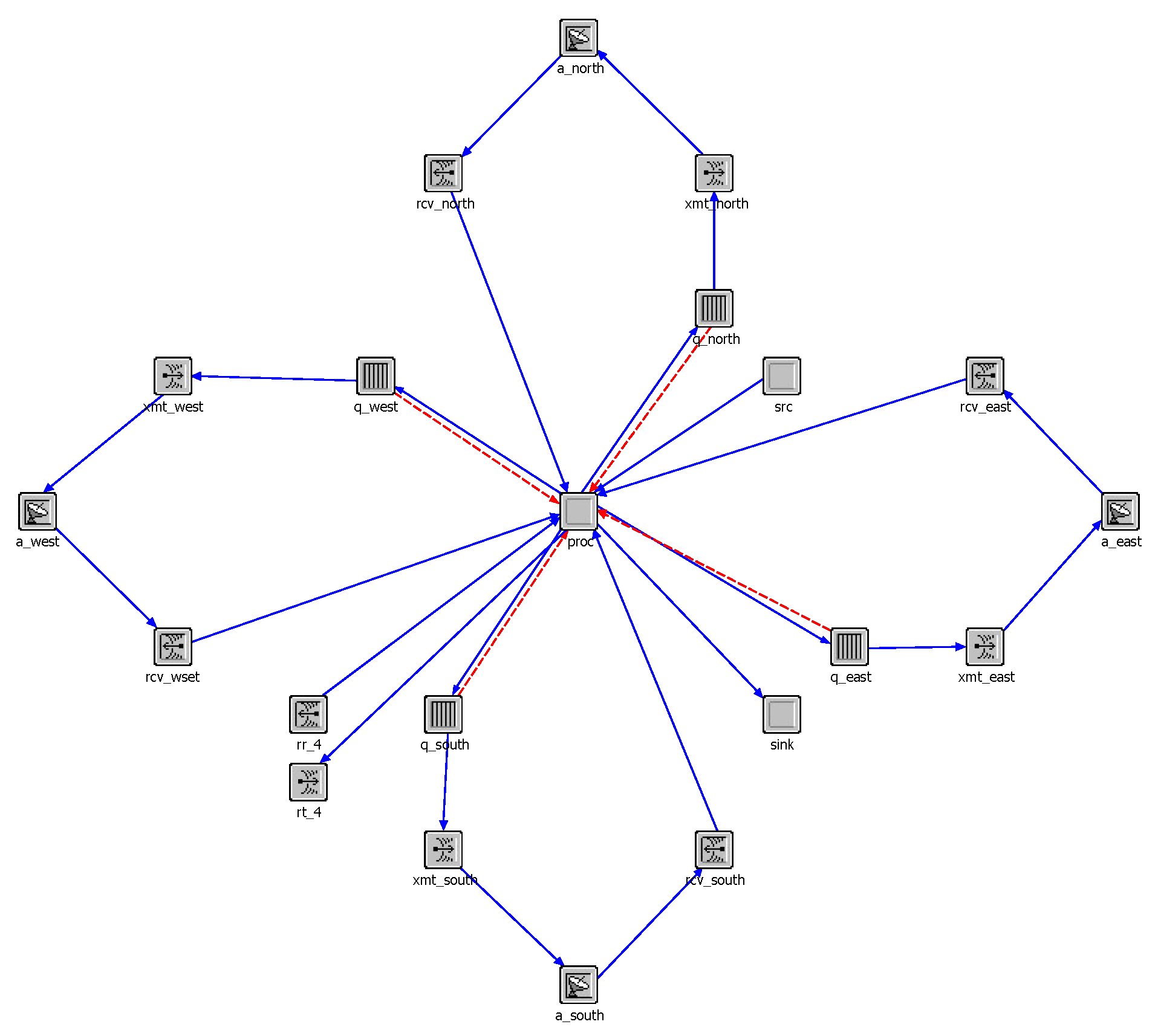
4.1. Experiment Setting
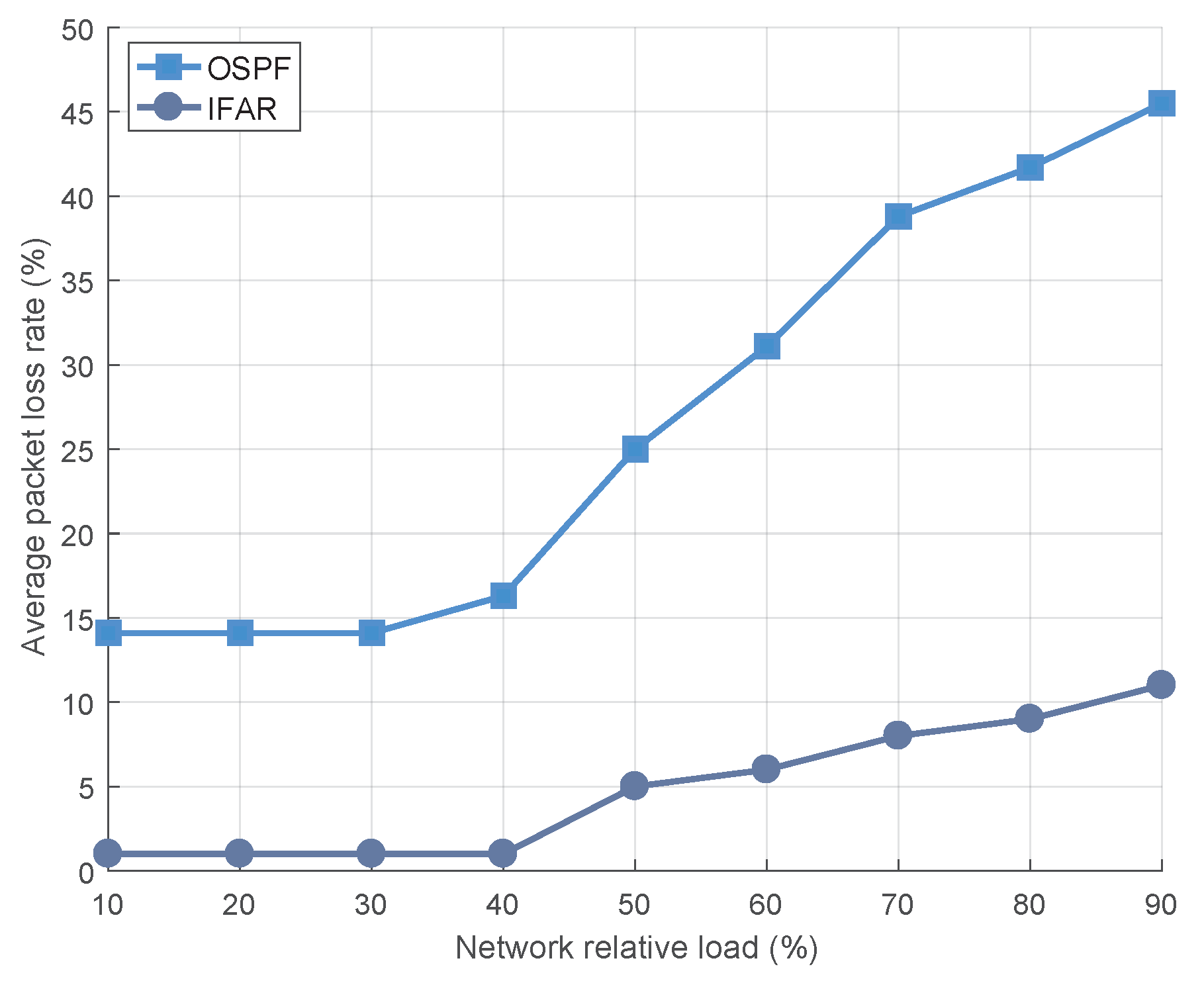
4.2. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yaacoub, E.; Alouini, M. A Key 6G Challenge and Opportunity—Connecting the Base of the Pyramid: A Survey on Rural Connectivity. Proc. IEEE 2020, 108, 533–582. [Google Scholar] [CrossRef] [Green Version]
- Kota, S.; Giambene, G. 6G Integrated Non-Terrestrial Networks: Emerging Technologies and Challenges. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021. [Google Scholar]
- Zhou, D.; Sheng, M.; Li, J.; Han, Z. Aerospace Integrated Networks Innovation for Empowering 6G: A Survey and Future Challenges. IEEE Commun. Surv. Tutor. 2023. early access. [Google Scholar] [CrossRef]
- Dietrich, F.J.; Metzen, P.; Monte, P. The Globalstar cellular satellite system. IEEE Trans. Antennas Propag. 1998, 46, 935–942. [Google Scholar] [CrossRef]
- Pratt, S.R.; Raines, R.A.; Fossa, C.E.; Temple, M.A. An operational and performance overview of the IRIDIUM low earth orbit satellite system. IEEE Commun. Surv. 1999, 2, 2–10. [Google Scholar] [CrossRef]
- Ruiz de Azua, J.A.; Calveras, A.; Camps, A. Internet of Satellites (IoSat): Analysis of Network Models and Routing Protocol Requirements. IEEE Access. 2018, 6, 20390–20411. [Google Scholar] [CrossRef]
- Schneider, K.; Zhang, B.; Benmohamed, L. Hop-by-Hop Multipath Routing: Choosing the Right Nexthop Set. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020. [Google Scholar]
- Wang, C.; Ren, Z.; Cheng, W.; Zhang, H. CDMR. Effective Computing-Dependent Multi-Path Routing Strategies in Satellite and Terrestrial Integrated Networks. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3715–3730. [Google Scholar] [CrossRef]
- Lakew, D.S.; Sa’ad, U.; Dao, N.N.; Na, W.; Cho, S. Routing in Flying Ad Hoc Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2020, 22, 1071–1120. [Google Scholar] [CrossRef]
- Azari, M.M.; Solanki, S.; Chatzinotas, S.; Kodheli, O.; Sallouha, H.; Colpaert, A.; Montoya, J.F.M.; Pollin, S.; Haqiqatnejad, A.; Mostaani, A.; et al. Evolution of Non-Terrestrial Networks from 5G to 6G: A Survey. IEEE Commun. Surv. Tutor. 2022, 24, 2633–2672. [Google Scholar] [CrossRef]
- Ekici, E.; Akyildiz, I.F.; Bender, M.D. A distributed routing algorithm for datagram traffic in LEO satellite networks. IEEE/ACM Trans. Netw. 2001, 9, 137–147. [Google Scholar] [CrossRef]
- Lai, Z.; Liu, W.; Wu, Q.; Li, H.; Xu, J.; Wu, J. SpaceRTC: Unleashing the Low-latency Potential of Mega-constellations for Real-Time Communications. In Proceedings of the IEEE INFOCOM 2022—IEEE Conference on Computer Communications, London, UK, 2–5 May 2022. [Google Scholar]
- Liu, J.; Zhao, B.; Xin, Q.; Su, J.; Ou, W. DRL-ER: An Intelligent Energy-Aware Routing Protocol with Guaranteed Delay Bounds in Satellite Mega-Constellations. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2872–2884. [Google Scholar] [CrossRef]
- Zeng, G.; Zhan, Y.; Pan, X. Failure-Tolerant and Low-Latency Telecommand in Mega-Constellations: The Redundant Multi-Path Routing. IEEE Access. 2021, 9, 34975–34985. [Google Scholar] [CrossRef]
- Grislain, P.; Pelissier, N.; Lamothe, F.; Hotescu, O.; Lacan, J.; Lochin, E.; Radzik, J. Rethinking LEO Constellations Routing with the Unsplittable Multi-Commodity Flows Problem. In Proceedings of the 2022 11th Advanced Satellite Multimedia Systems Conference and the 17th Signal Processing for Space Communications Workshop (ASMS/SPSC), Graz, Austria, 6–8 September 2022. [Google Scholar]
- Chen, Q.; Giambene, G.; Yang, L.; Fan, C.; Chen, X. Analysis of Inter-Satellite Link Paths for LEO Mega-Constellation Networks. IEEE Trans. Veh. Technol. 2021, 70, 2743–2755. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Tian, F.; Jin, J.; Liu, H. Rethinking LEO Mega-Constellation Routing to Provide Fast Internet Access Services. Sensors 2023, 23, 3207. https://doi.org/10.3390/s23063207
Yang Z, Tian F, Jin J, Liu H. Rethinking LEO Mega-Constellation Routing to Provide Fast Internet Access Services. Sensors. 2023; 23(6):3207. https://doi.org/10.3390/s23063207
Chicago/Turabian StyleYang, Zijian, Feng Tian, Jifeng Jin, and Huijie Liu. 2023. "Rethinking LEO Mega-Constellation Routing to Provide Fast Internet Access Services" Sensors 23, no. 6: 3207. https://doi.org/10.3390/s23063207
APA StyleYang, Z., Tian, F., Jin, J., & Liu, H. (2023). Rethinking LEO Mega-Constellation Routing to Provide Fast Internet Access Services. Sensors, 23(6), 3207. https://doi.org/10.3390/s23063207





