An Edge-Filtered Optical Fiber Interrogator for Thermoplastic Polymer Analysis
Abstract
1. Introduction
2. Methods and Experimental Setup
2.1. Optical Fiber Fresnel Reflectometer—Refractive Index Measurement
2.2. Lorentz–Lorenz Model—Correlation of Refractive Index and Thermal Expansion
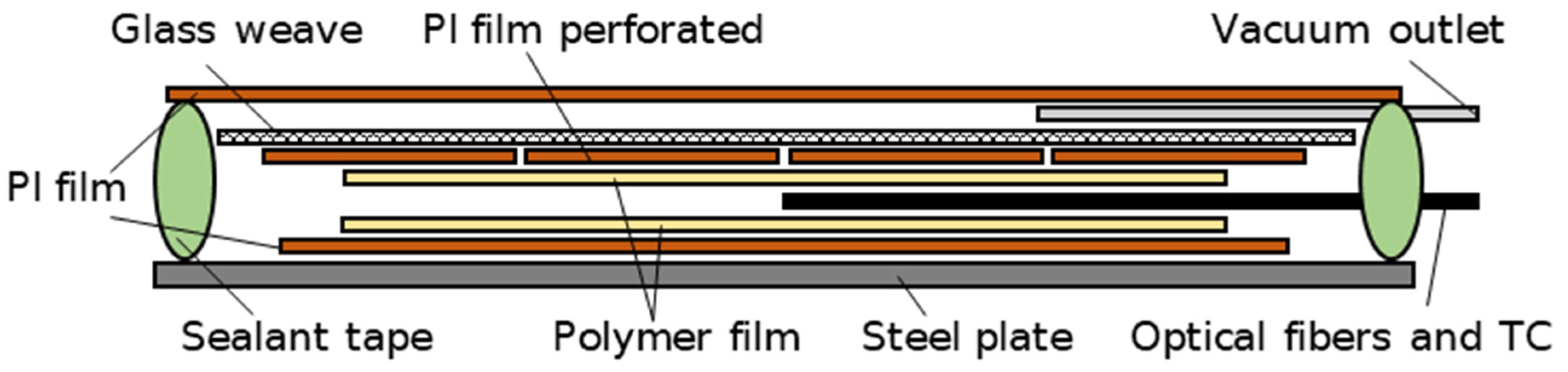
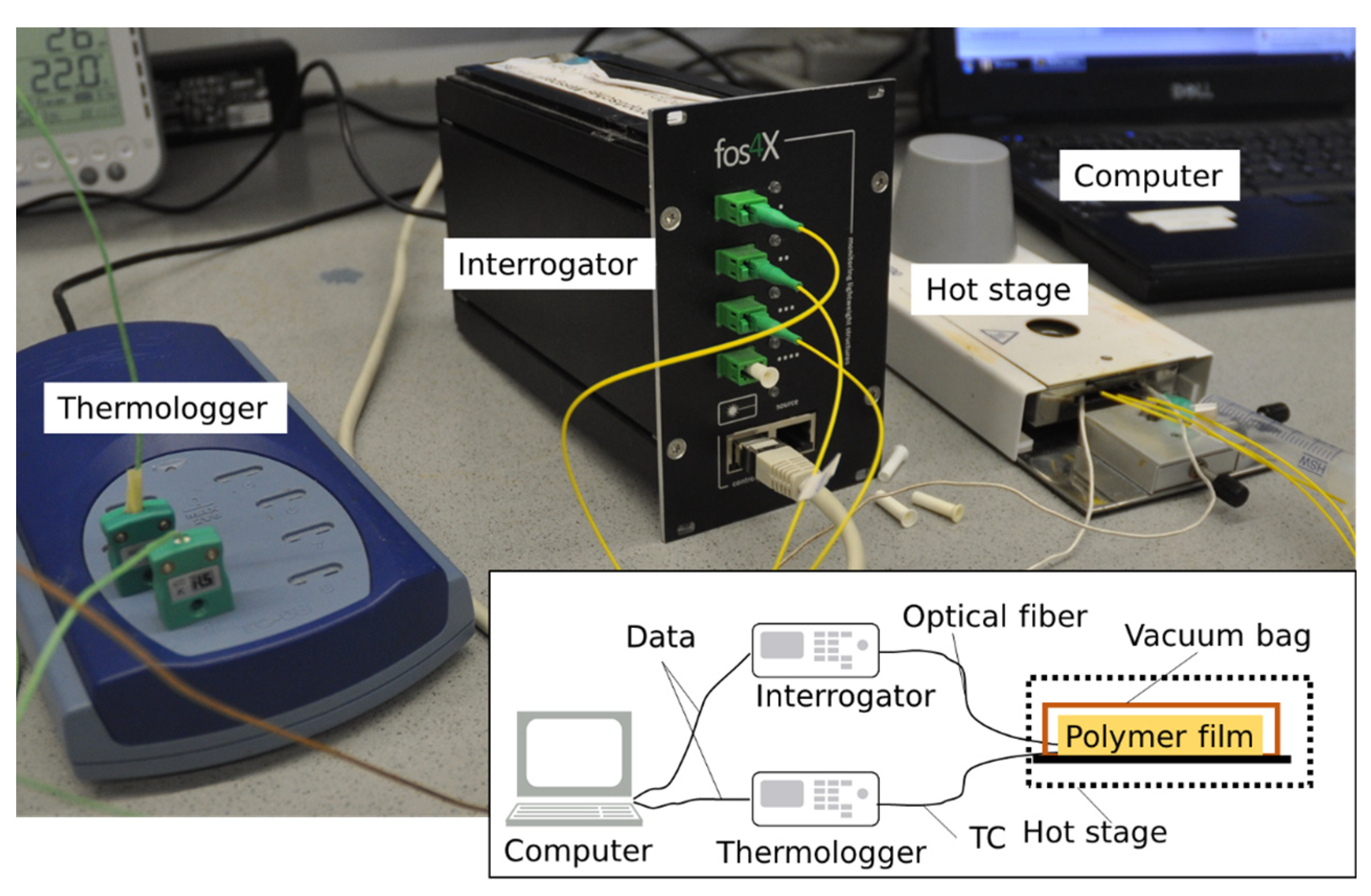
2.3. Experimental Setup
3. Amorphous Thermoplastic Polymers: Polyetherimide (PEI), Polyethersulfone (PES)
3.1. Experimental Details and Materials
3.2. Validation: TMA and DSC
3.3. Results and Discusion
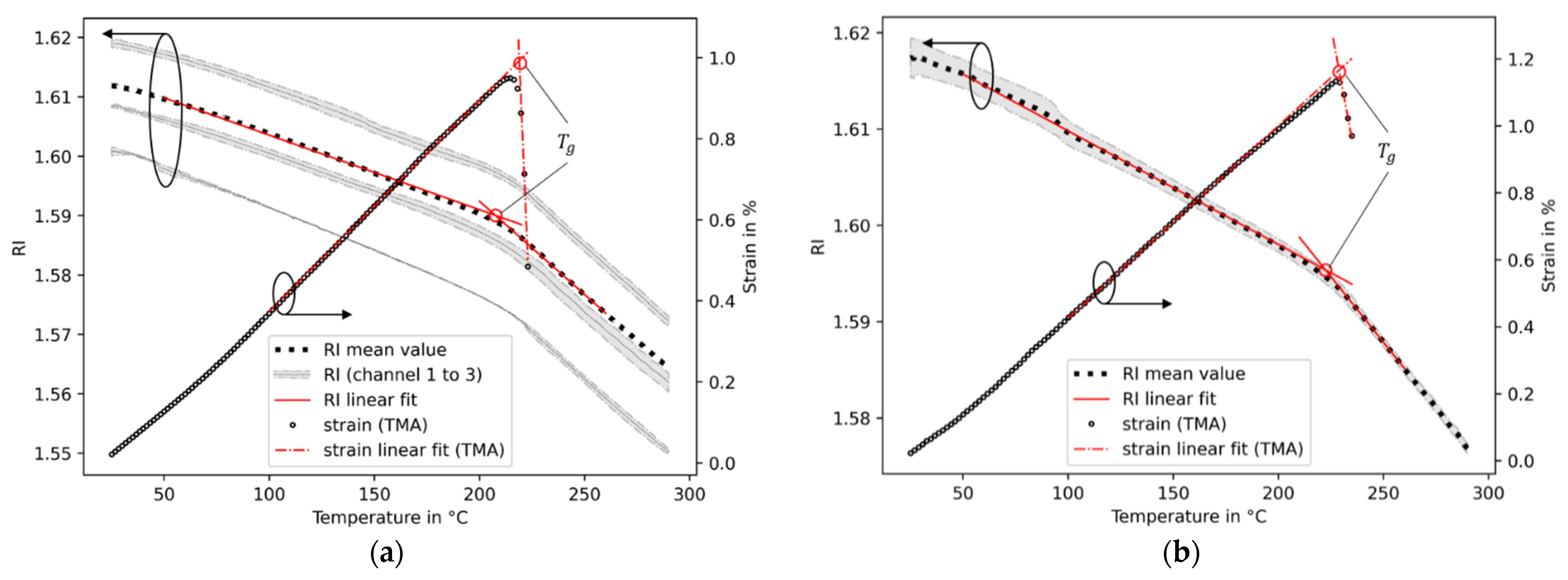
3.3.1. Refractive Indices
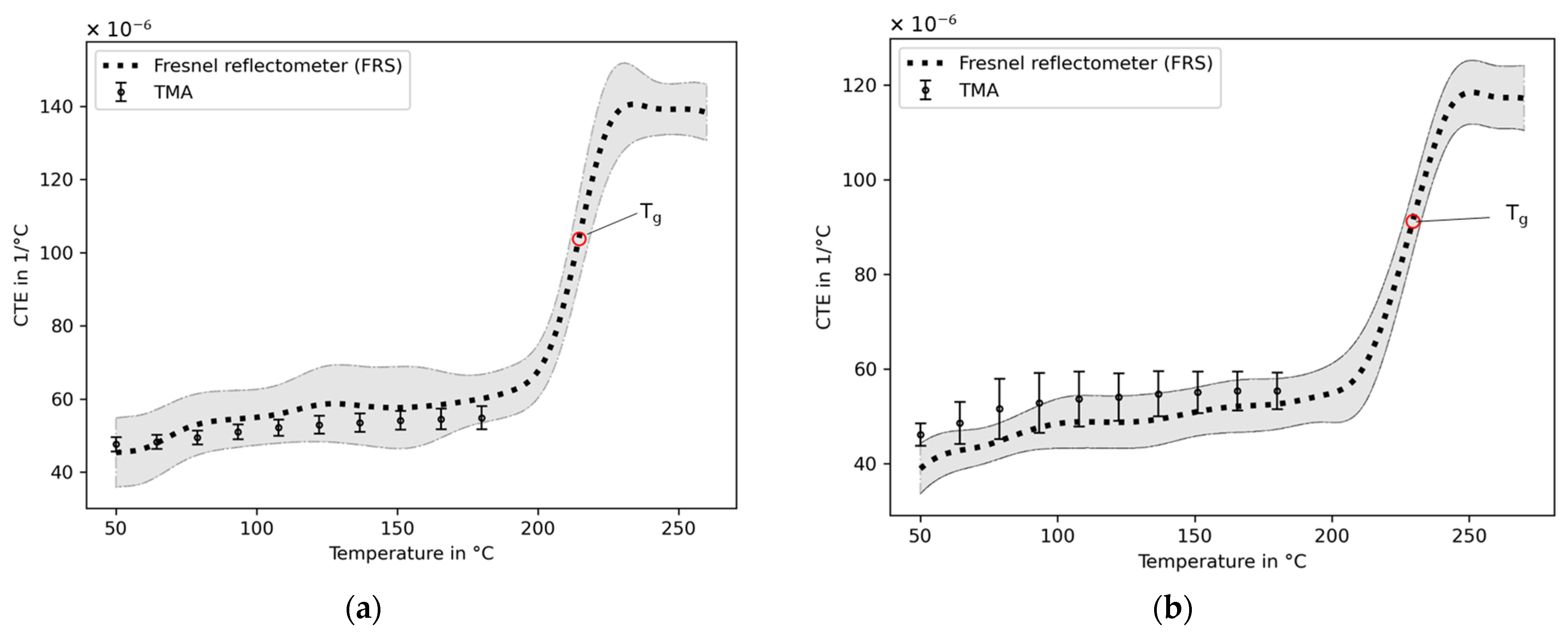
3.3.2. Coefficients of Thermal Expansion
3.3.3. Glass Transition Temperatures
4. Semi-Crystalline Polymer: Polyether Ether Ketone (PEEK)
4.1. Experimental Details and Materials
4.2. Validation: DSC and DMA
4.3. Results and Discussion
4.3.1. Refractive Index
4.3.2. Thermal Expansion
4.3.3. Transition Temperatures
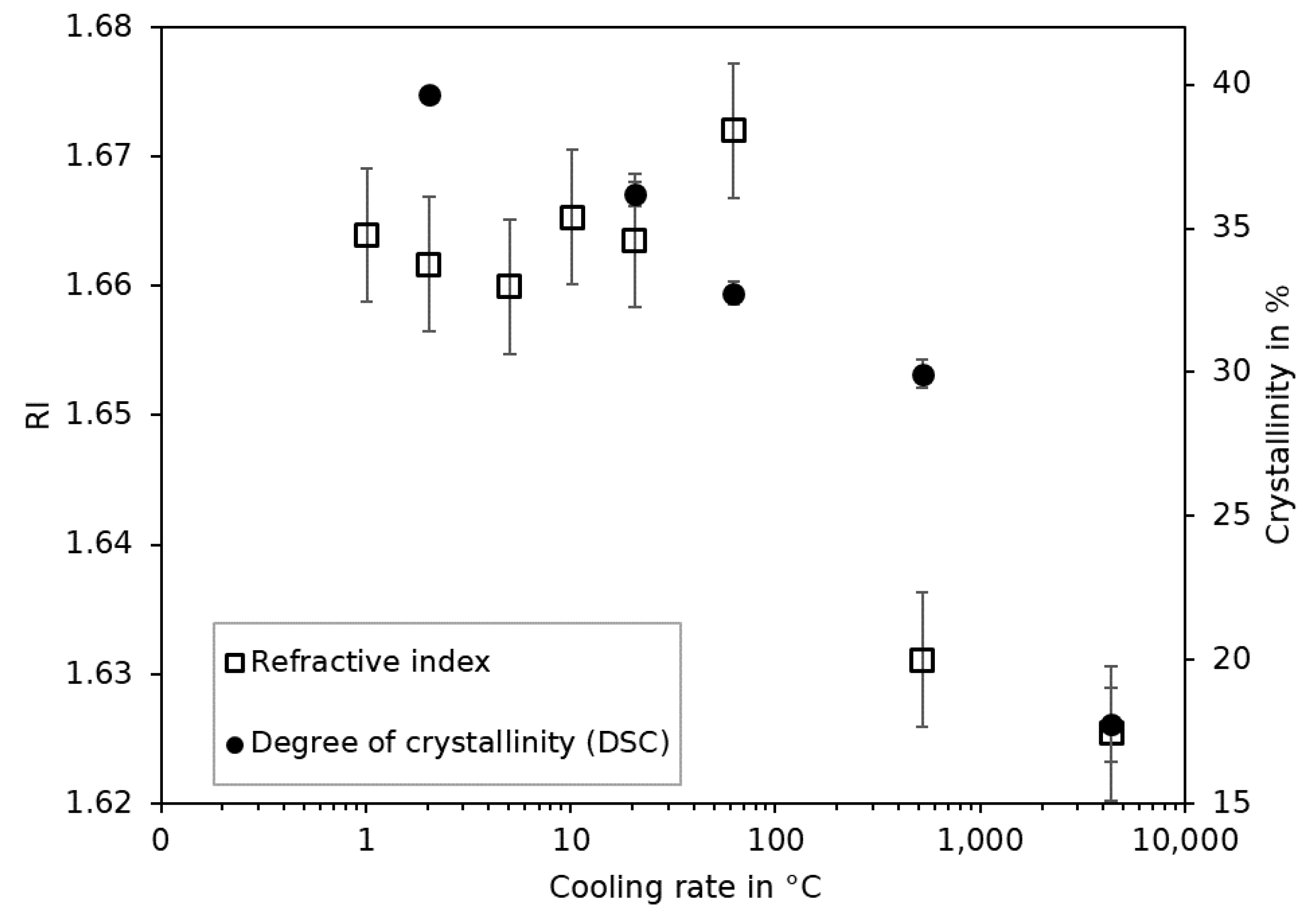
4.3.4. Degree of Crystallinity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Measurement of Thermal Expansion Coefficient Using Strain Gages—Tech Note TN-513-1. Available online: https://www.micro-measurements.com/knowledge-base/technical-notes (accessed on 11 January 2023).
- Chiesura, G.; Lamberti, A.; Yang, Y.; Luyckx, G.; Van Paepegem, W.; Vanlanduit, S.; Vanfleteren, J.; Degrieck, J. RTM Production Monitoring of the A380 Hinge Arm Droop Nose Mechanism: A Multi-Sensor Approach. Sensors 2016, 16, 866. [Google Scholar] [CrossRef] [PubMed]
- Othonos, A.; Kalli, K.; Kohnke, G.E. Fiber Bragg Gratings: Fundamentals and Applications in Telecommunications and Sensing. Phys. Today 2000, 53, 61–62. [Google Scholar] [CrossRef]
- Shivakumar, K.; Emmanwori, L. Mechanics of Failure of Composite Laminates with an Embedded Fiber Optic Sensor. J. Compos. Mater. 2004, 38, 669–680. [Google Scholar] [CrossRef]
- Lu, X.; Chruscicki, S.; Schukar, M.; Münzenberger, S.; Krebber, K. Application of Intensity-Based Coherent Optical Time Domain Reflectometry to Bridge Monitoring. Sensors 2022, 22, 3434. [Google Scholar] [CrossRef] [PubMed]
- Hartog, A.H. An Introduction to Distributed Optical Fibre Sensors, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-351-64530-0. [Google Scholar]
- Luyckx, G.; Voet, E.; Lammens, N.; Degrieck, J. Strain Measurements of Composite Laminates with Embedded Fibre Bragg Gratings: Criticism and Opportunities for Research. Sensors 2011, 11, 384–408. [Google Scholar] [CrossRef]
- Su, H.; Huang, X.G. Fresnel-Reflection-Based Fiber Sensor for on-Line Measurement of Solute Concentration in Solutions. Sens. Actuators B Chem. 2007, 126, 579–582. [Google Scholar] [CrossRef]
- Afromowitz, M.A. Fiber Optic Polymer Cure Sensor. J. Light. Technol. 1988, 6, 1591–1594. [Google Scholar] [CrossRef]
- Afromowitz, M.A.; Lam, K.-Y. The Optical Properties of Curing Epoxies and Applications to the Fiber-Optic Epoxy Cure Sensor. Sens. Actuators A Phys. 1990, 23, 1107–1110. [Google Scholar] [CrossRef]
- Lam, K.-Y.; Afromowitz, M.A. Fiber-Optic Epoxy Composite Cure Sensor. II. Performance Characteristics. Appl. Opt. AO 1995, 34, 5639–5644. [Google Scholar] [CrossRef]
- Cusano, A.; Cutolo, A.; Giordano, M.; Nicolais, L. Optoelectronic Refractive Index Measurements: Application to Smart Processing. IEEE Sens. J. 2003, 3, 781–787. [Google Scholar] [CrossRef]
- Oelhafen, J.; Mayr, T.; Dorner, F.; Moutzouris, K.; Roths, J.; Drechsler, K. Fiber Optic Measurement System for Fresnel Reflection Sensing: Calibration, Uncertainty, and Exemplary Application in Temperature-Modulated Isothermal Polymer Curing. J. Light. Technol. 2018, 36, 939–945. [Google Scholar] [CrossRef]
- Vacher, S.; Molimard, J.; Gagnaire, H.; Vautrin, A. A Fresnel’s Reflection Optical Fiber Sensor for Thermoset Polymer Cure Monitoring. Polym. Polym. Compos. 2004, 12, 269–276. [Google Scholar] [CrossRef]
- Antonucci, V.; Cusano, A.; Giordano, M.; Nasser, J.; Nicolais, L. Cure-Induced Residual Strain Build-up in a Thermoset Resin. Compos. Part A Appl. Sci. Manuf. 2006, 37, 592–601. [Google Scholar] [CrossRef]
- Robert, L.; Dusserre, G. Anisothermal Thermosetting Resin Cure Monitored by Optical Fiber Refractometer. Polym. Eng. Sci. 2014, 54, 626–635. [Google Scholar] [CrossRef][Green Version]
- Cusano, A.; Breglio, G.; Giordano, M.; Nicolais, L.; Cutolo, A. Multifunction Fiber Optic Sensing System for Smart Applications. IEEE/ASME Trans. Mechatron. 2004, 9, 40–49. [Google Scholar] [CrossRef]
- Giordano, M.; Laudati, A.; Russo, M.; Nasser, J.; Persiano, G.V.; Cusano, A. Advanced Cure Monitoring by Optoelectronic Multifunction Sensing System. Thin Solid Films 2004, 450, 191–194. [Google Scholar] [CrossRef]
- Sampath, U.; Kim, H.; Kim, D.; Kim, Y.-C.; Song, M. In-Situ Cure Monitoring of Wind Turbine Blades by Using Fiber Bragg Grating Sensors and Fresnel Reflection Measurement. Sensors 2015, 15, 18229–18238. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction; Wiley: Hoboken, NJ, USA, 2018; ISBN 9781119321590. [Google Scholar]
- Michel, P.; Dugas, J.; Cariou, J.M.; Martin, L. Thermal Variations of Refractive Index of PMMA, Polystyrene, and Poly (4-Methyl-1-Pentene). J. Macromol. Sci. Part B 1986, 25, 379–394. [Google Scholar] [CrossRef]
- Cariou, J.M.; Dugas, J.; Martin, L.; Michel, P. Refractive-Index Variations with Temperature of PMMA and Polycarbonate. Appl. Opt. AO 1986, 25, 334–336. [Google Scholar] [CrossRef]
- Zoller, P.; Kehl, T.A.; Starkweather, H.W.; Jones, G.A. The Equation of State and Heat of Fusion of Poly(Ether Ether Ketone). J. Polym. Sci. B Polym. Phys. 1989, 27, 993–1007. [Google Scholar] [CrossRef]
- Gao, S.-L.; Kim, J.-K. Cooling Rate Influences in Carbon Fibre/PEEK Composites. Part 1. Crystallinity and Interface Adhesion. Compos. Part A Appl. Sci. Manuf. 2000, 31, 517–530. [Google Scholar] [CrossRef]
- Rao, Y.-J. In-Fibre Bragg Grating Sensors. Meas. Sci. Technol. 1997, 8, 355–375. [Google Scholar] [CrossRef]
- Oelhafen, J. Cure and Viscosity Measurement of Thermosetting Epoxy Resin with Fresnel Reflectometer Sensors; Technical University of Munich: Munich, Germany, 2019. [Google Scholar]
- Müller, U.; Philipp, M.; Thomassey, M.; Sanctuary, R.; Krüger, J.K. Temperature Modulated Optical Refractometry: A Quasi-Isothermal Method to Determine the Dynamic Volume Expansion Coefficient. Thermochim. Acta 2013, 555, 17–22. [Google Scholar] [CrossRef]
- Ciddor, P.E. Refractive Index of Air: New Equations for the Visible and near Infrared. Appl. Opt. 1996, 35, 1566. [Google Scholar] [CrossRef] [PubMed]
- Juelich, F.; Roths, J. Determination of the Effective Refractive Index of Various Single Mode Fibres for Fibre Bragg Grating Sensor Applications. Proc. OPTO 2009 2009, 119–124. [Google Scholar] [CrossRef]
- Waxler, R.M.; Cleek, G.W. The Effect of Temperature and Pressure on the Refractive Index of Some Oxide Glasses. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1973, 77, 755. [Google Scholar] [CrossRef]
- Brückner, R. Properties and Structure of Vitreous Silica. I. J. Non-Cryst. Solids 1970, 5, 123–175. [Google Scholar] [CrossRef]
- Jewell, J.M. Thermooptic Coefficients of Some Standard Reference Material Glasses. J. Am. Ceram. Soc. 1991, 74, 1689–1691. [Google Scholar] [CrossRef]
- Tan, C.Z.; Arndt, J. Temperature Dependence of Refractive Index of Glassy SiO2 in the Infrared Wavelength Range. J. Phys. Chem. Solids 2000, 61, 1315–1320. [Google Scholar] [CrossRef]
- Lorenz, L. Ueber Die Refractionskonstante. Ann. Phys. 1880, 247, 70–103. [Google Scholar] [CrossRef]
- LITE I|litefilms.com. Available online: https://www.litefilms.com/de/product/lite-i/ (accessed on 15 July 2022).
- LITE S|litefilms.com. Available online: https://www.litefilms.com/de/product/lite-s/ (accessed on 15 July 2022).
- Cogswell, F.N. Thermoplastic Aromatic Polymer Composites: A Study of the Structure, Processing, and Properties of Carbon Fibre Reinforced Polyetheretherketone and Related Materials; Butterworth-Heinemann: Oxford, UK; Boston, MA, USA, 1992; ISBN 978-0-7506-1086-5. [Google Scholar]
- Voice, A.M.; Bower, D.I.; Ward, I.M. Molecular Orientation in Uniaxially Drawn Poly(Aryl Ether Ether Ketone): 1. Refractive Index and X-Ray Measurements. Polymer 1993, 34, 1154–1163. [Google Scholar] [CrossRef]
- Lu, S.X.; Cebe, P.; Capel, M. Thermal Stability and Thermal Expansion Studies of PEEK and Related Polyimides. Polymer 1996, 37, 2999–3009. [Google Scholar] [CrossRef]
- Blundell, D.J.; Osborn, B.N. Crystalline Morphology of the Matrix of PEEK-Carbon Fiber Aromatic Polymer Composites. II. Crystallization Behavior. SAMPE Q. 1985, 17, 50–57. [Google Scholar]






| Method | ||
|---|---|---|
| Fresnel reflectometer (below Tg) | 54.6 ± 4.3 | 50.9 ± 3.8 |
| TMA (below Tg) | 51.9 ± 2.6 | 56.9 ± 3.9 |
| Fresnel reflectometer (above Tg) | 146.3 ± 3.3 | 124.1 ± 4.4 |
| Method | ||
|---|---|---|
| Fresnel reflectometer (FRS), intersection | 207.6 ± 3.3 | 222.0 ± 3.3 |
| Fresnel reflectometer (FRS), inflection | 214.3 ± 1.2 | 229.4 ± 2.4 |
| TMA, intersection | 219.1 ± 1.8 | 230.1 ± 5.1 |
| DSC, inflection | 217.8 ± 0.2 | 228.5 ± 0.2 |
| Method | ||
|---|---|---|
| Fresnel reflectometer, inflection | 141.9 | 344.6 ± 1.7 |
| Fresnel reflectometer, intersection | - | 346.3 ± 2.5 |
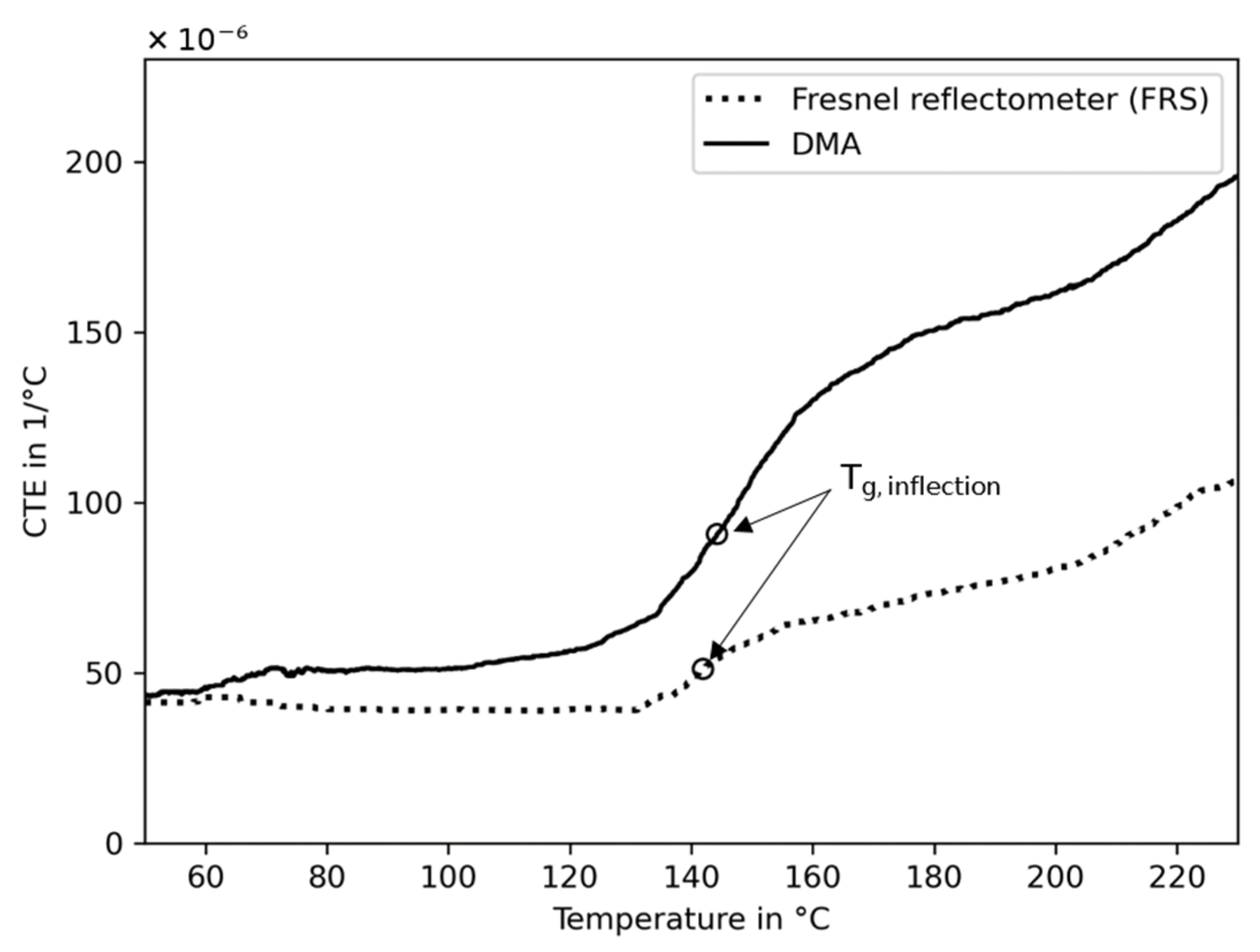
| DMA, inflection | 144.2 | - |
| DSC, inflection | 144.4 ± 1.5 | - |
| DSC, peak heat flow | - | 339.7 ± 1.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Backmann, V.; Dorner, F.; Drechsler, K. An Edge-Filtered Optical Fiber Interrogator for Thermoplastic Polymer Analysis. Sensors 2023, 23, 3300. https://doi.org/10.3390/s23063300
Backmann V, Dorner F, Drechsler K. An Edge-Filtered Optical Fiber Interrogator for Thermoplastic Polymer Analysis. Sensors. 2023; 23(6):3300. https://doi.org/10.3390/s23063300
Chicago/Turabian StyleBackmann, Vincent, Felix Dorner, and Klaus Drechsler. 2023. "An Edge-Filtered Optical Fiber Interrogator for Thermoplastic Polymer Analysis" Sensors 23, no. 6: 3300. https://doi.org/10.3390/s23063300
APA StyleBackmann, V., Dorner, F., & Drechsler, K. (2023). An Edge-Filtered Optical Fiber Interrogator for Thermoplastic Polymer Analysis. Sensors, 23(6), 3300. https://doi.org/10.3390/s23063300






